비내진상세를 가진 기둥용접형 거셋플레이트의 단순화된 유한요소해석모델
Copyright © 2023 by Korean Society of Steel Construction
초록
힘지배요소로 구분되는 거셋플레이트의 압축거동은 철골가새골조의 내진성능에 미치는 영향이 크다. 옥외배관을 지지하는 철골가새골조에는 기둥용접형 거셋플레이트가 흔히 사용된다. 기존 거셋플레이트 압축강도 예측식은 거셋플레이트의 면내방향 강성이 면외방향에 비하여 매우 크다는 가정에서 유도되어 이를 기둥용접형 거셋플레이트에 적용하는 것은 적절하지 않다. 기둥용접형 거셋플레이트의 압축강도를 파악하려면 인접 구조부재가 포함된 거셋플레이트의 유한요소해석모델을 수립해야 하나, 해석시간 등을 고려한 보다 효율적인 방법이 요구된다. 본 연구는 거셋플레이트에 대한 기존 스프링요소모델을 기둥과 가새부재가 포함된 기둥용접형 거셋플레이트의 유한요소해석과 비교·검토하고, 경계조건을 단순화한 유한요소모델을 제안하였다. 기존 강도식과 스프링요소모델은 기둥용접형 거셋플레이트의 압축강도와 면외방향 회전강성 등을 적절하게 예측할 수 없음을 확인하였다. 또한, 본 연구에서 제안한 유한요소해석모델은 기존 스프링요소모델에 비해 기둥용접형 거셋플레이트의 압축거동특성을 잘 반영하는 것으로 나타났다.
Abstract
The seismic performance of a steel braced frame can be affected by the compression behavior of gusset plates which are usually classified into force-governing structural members. Although commonly used in pipeline-supporting steel braced frames, gusset plates welded to a column web only are inappropriate to be subjected to existing formula that were developed under the assumption that gusset plates possess extremely high in-plane rotational stiffness. To evaluate the compression strength of gusset plates welded to a column web only, efficient and simplified finite element models need to be developed considering effects of adjacent structural members. This study investigates existing spring element modeling methodologies for gusset plates for direct comparison with the finite element model including column and bracing members, and proposes a model for gusset plates welded to a column web only using the simplification of boundary conditions. The proposed model adequately predicts the compression strength and out-of-plane rotational stiffness of the gusset plates, compared with the existing formula and spring element models.
Keywords:
Gusset plates welded to a column web only, Non-seismic details, Buckling modes, Boundary conditions, Finite element analysis models키워드:
기둥용접형 거셋플레이트, 비내진상세, 좌굴모드, 경계조건, 유한요소해석모델1. 서 론
석유화학산업단지 내 화학물질을 운반하는 옥외배관은 일반적으로 철골구조물에 의해 지지된다. 철골가새골조와 철골모멘트골조가 주요 횡력저항시스템으로 사용되며, 배관과의 간섭을 피하기 위해 배관의 진행방향(이하 ‘배관방향’)으로는 철골가새골조가 사용되고, 이에 수직한 방향(이하 ‘배관 직각방향’)으로는 철골모멘트골조가 사용된다. 옥외배관지지 구조물의 구조적 손상이 야기할 수 있는 천문학적인 사회·경제적 피해를 최소화하기 위해, 건축물 내진설계기준인 KDS 41 17 00[1]은 이를 “건물외 구조물”로 분류하고 내진설계 대상으로 명시하고 있다. 그러나 국내 상당수 옥외배관지지 구조물은 내진설계기준이 제정되기 전 설계·시공되어, 현행 내진설계기준이 요구하는 내진성능과 부합한다고 볼 수 없다. 이러한 이유로 내진성능이 확보되지 않거나 의심되는 옥외배관지지 철골구조물에 대한 내진성능평가와 내진보강설계 및 공사가 진행되고 있다.
신축구조물의 내진설계뿐만 아닌 기존 구조물의 내진성능평가와 내진보강설계는 역량설계법(capacity design methodology)을 근간으로 하며, 지진력저항시스템 내 구조요소를 변위지배요소와 힘지배요소로 분류한다. 힘지배요소는 충분한 강성 및 강도를 보유하여 설계 수준의 지진강도에 대해서는 탄성거동해야 하며, 변위지배요소는 비선형거동을 통해 지진에너지를 소산할 수 있어야 한다. 철골가새골조의 가새부재는 변위지배요소로 취급되는 반면, 이를 골조에 연결하기 위해 설치되는 거셋플레이트(gusset plate)는 가새부재의 원활한 비선형거동 유도를 위해 충분한 강성 및 강도를 보유해야 하는 힘지배요소이다. 지진력을 받는 철골가새골조 내 거셋플레이트가 항복하거나 파괴되면 골조의 지진응답이 달라질 수 있으므로 내진성능에 미치는 영향이 적지 않다. 그럼에도 불구, 거셋플레이트의 형상 및 상세가 매우 다양하고 거동특성의 모델링이 매우 복잡하여 대부분의 엔지니어들은 거셋플레이트의 강성 및 강도에 대한 별도의 고려 없이 가새부재의 양단을 단순 회전절점으로 가정하여 철골가새골조를 설계한다. 이러한 과도한 가정은 거셋플레이트의 강도 예측과 이에 따른 철골가새골조의 내진성능평가결과의 신뢰성을 저하시킬 수 있다. 이를 개선하면서도 일정 수준 이상 해석의 편이성을 담보할 수 있는 스프링요소(spring elements)를 사용한 해석모델이 다수 연구자에 의해 개발되었다[2],[3]. 그러나 옥외배관 지지를 위해 사용되는 철골가새골조에는 독특한 비내진 상세의 거셋플레이트가 다수 조사되었고, 선행연구를 통해 제시된 스프링요소모델을 이에 적용할 수 있는지 의문시된다.
Fig. 1과 같이 기둥의 웨브에만 용접된 거셋플레이트(기둥용접형 거셋플레이트)는 옥외배관지지 철골가새골조에 주로 쓰이는 비내진 상세이다. 이러한 비내진 상세 기둥용접형 거셋플레이트의 압축거동에 관한 연구는 희소하며, 거셋플레이트의 단순스프링요소모델에 대한 기존 연구도 보와 기둥 부재에 모두 용접된 거셋플레이트(코너용접형 거셋플레이트)의 압축거동에 집중되어 있다. 코너용접형 거셋플레이트는 인접한 보와 기둥에 모두 용접되므로 면내방향으로 큰 강성을 가지며, Fang et al.[4]은 경계조건의 단순화를 위해 거셋플레이트 용접면의 모든 자유도를 구속한 유한요소해석을 수행하였다. 거셋플레이트의 면외방향 회전스프링을 이용한 연구에서도 거셋플레이트의 면내방향 회전은 고정단으로 가정하였다[2],[3]. 그러나 거셋플레이트 면내방향으로 회전강성이 작은 웨브에만 고정된 기둥용접형 거셋플레이트의 웨브와의 용접면을 고정단으로 가정하는 선행연구의 스프링해석모델은 거셋플레이트의 좌굴모드에 따른 압축내력을 과대평가할 수 있다. 코너용접형 거셋플레이트와 구분되는 기둥용접형 거셋플레이트의 이러한 특성은 철골가새골조의 내진성능에도 영향을 줄 수 있으며, Astaneh-Asl et al.은 거셋플레이트의 면내방향 회전강성이 가새부재의 압축내력과 연성에 미치는 영향을 실험적으로 확인하였다[5].

Non-seismically detailed gusset plates welded to a column web only in pipeline supporting braced frames
본 연구에서는 기둥용접형 거셋플레이트의 유한요소해석을 수행하여 기존 연구에서 제시한 회전강성 및 압축내력의 기둥용접형 거셋플레이트에 대한 적용 가능 여부를 파악하고자 한다. 또한, 기둥용접형 거셋플레이트의 유한요소해석결과로부터 응력분포 및 좌굴형상을 분석하고, 이를 바탕으로 기둥용접형 거셋플레이트의 경계조건을 단순화한 유한요소해석모델을 제시하고자 한다. 최종적으로, 경계조건의 단순화를 위해 인접 구조부재와의 용접면을 고정단으로 고려하는 기존의 일반적인 유한요소모델과 본 논문의 단순화된 기둥용접형 거셋플레이트의 유한요소해석모델을 압축내력과 면내·외 방향 회전강성 측면에서 비교하고자 한다.
2. 코너용접형 거셋플레이트의 압축거동 특성
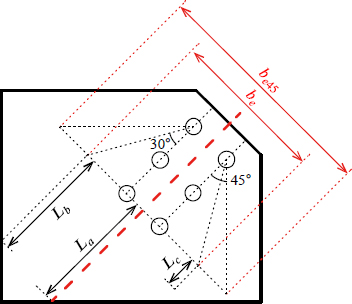
거셋플레이트의 압축내력 계산에는 거셋플레이트를 유효 기둥스트립(effective column strip)으로 고려하는 Thornton 방법이 가장 널리 사용되고 있다[6]. Thornton 방법에서 유효 기둥스트립은 Fig. 2와 같이 위트모어(Whitmore)단면을 유효단면으로 가지며, 위트모어단면의 유효폭 be는 가새쪽 볼트열에서 30° 각도로 방사한 선과, 가력 중심선과 웨브면의 교점(이하 ‘작업점’)과 최단거리에 위치한 볼트열의 연장선이 만나는 두 점 사이의 거리로 결정된다. 유효 기둥스트립은 유효폭 be와 거셋플레이트의 두께 tg를 가지는 사각형 단면(위트모어 단면)과 유효좌굴길이 LE를 가정하여 압축내력 을 다음과 같이 계산할 수 있다.
| (1) |
| (2) |
여기서, λc는 위트모어단면과 유효좌굴길이 LE를 가진 기둥스트립의 세장비, r은 위트모어단면의 단면2차반경이다. LE는 유효좌굴길이계수(effective length factor, K)와 기준길이(reference length, LR)를 곱한 값이며, AISC에서는 Dowswell et al.이 거셋플레이트의 형상과 인접 구조부재와의 경계조건에 따라 구분한 거셋플레이트 유형별로 K와 LR 값을 달리 적용하도록 하고 있다[7],[8].
Fig. 3는 거셋플레이트를 형상에 따라 분류한 것이며, Fig. 3(a)와 Fig. 3(b)는 코너용접형 거셋플레이트로 각각 조밀과 비조밀 거셋플레이트로 분류할 수 있다. Fig. 3(c)는 보 또는 기둥에만 용접되는 거셋플레이트로 기둥용접형 거셋플레이트는 여기에 속한다. Table 1은 거셋플레이트 유형별로 K와 LR을 정리한 것으로, La는 유효폭의 중심과 경계면의 최단거리, Lavg는 La, Lb, Lc의 평균값이다. Yoo[2]는 Thornton 방법이 거셋플레이트의 압축내력을 50 % 이상 과소평가함을 언급하였으며, 식 (1)에 be 대신 45° 분포각으로 정의되는 위트모어단면의 유효폭 be45를 적용하여 이를 보완하였다.
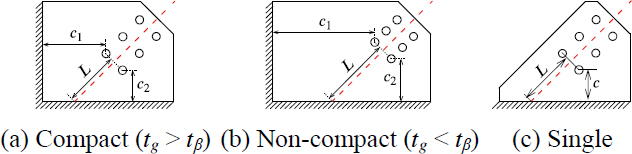
Classification of gusset plates (after Dowswell[7]; tβ=1.5Fyc3/EL, Fy: yield strength, c = min(c1, c2), E: elastic modulus)
면내방향에 비해 거셋플레이트는 골조의 면외방향 회전에 낮은 강성과 저항력을 가지며, 면외방향 회전으로 인한 저항능력 감소는 인접 가새부재의 저항능력 감소를 유발한다. Hsiao et al.은 be45로 정의되는 위트모어단면의 단면2차모멘트를 사용하여 거셋플레이트의 면외방향 회전강성 을 다음과 같이 계산하였다[3].
| (3) |
위 식의 회전강성은 유효 기둥스트립의 위트모어단면에 균일한 응력이 분포한다는 가정에서 도출되었음을 알 수 있다. Hsiao et al.은 거셋플레이트의 면내방향 회전에 대해서는 별도의 스프링요소 없이 고정단으로 고려하였으며, Yoo 역시 동일한 방식을 사용하였다[2],[3].
3. 기둥용접형 거셋플레이트의 유한요소해석
3.1 해석 대상 거셋플레이트
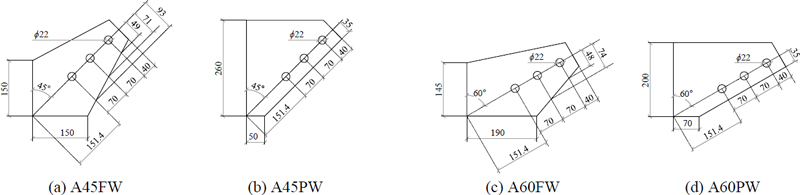
기둥용접형 거셋플레이트의 압축거동을 면밀하게 파악하기 위해 유한요소해석을 수행하였으며, 해석결과를 기존 연구의 방법을 통해 계산한 거셋플레이트의 압축내력 및 회전강성과 비교하였다. 해석 대상인 거셋플레이트의 각 형상은 Fig. 4에 나타냈다. 거셋플레이트는 가력 중심선과 수직선 사이 각도가 각각 45°와 60°인 해석모델 A45와 A60로 구분된다. A45와 A60는 다시 거셋플레이트가 분포각 30°로 정의되는 위트모어단면의 유효폭을 포괄하는 FW(fully-covered within the Whitmore width)모델과, 위트모어단면의 일부만 포괄하는 PW(partially-covered within the Whitmore width)모델로 구분하였으며, 총 4개 형상의 거셋플레이트를 해석대상으로 선정하였다. 국내 대표 석유화학단지 내 옥외배관을 지지하는 철골가새골조의 기둥과 가새가 이루는 각도가 대부분 45°–60°의 분포를 보여 이를 해석대상 선정에 반영하였다.
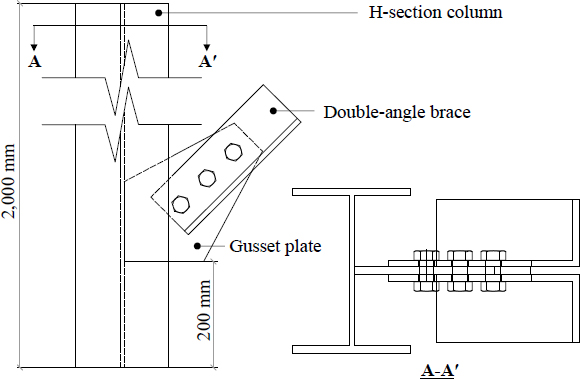
모든 거셋플레이트의 두께는 12 mm로, 조밀 거셋플레이트의 임계두께 tβ인 약 9 mm 이상이 되도록 설정했으며, 식 (1)에서 거셋플레이트 압축내력의 결정 요소 중 하나인 LR은 모두 121 mm로 같게 설정하였다. A45FW와 A45PW의 be는 162 mm와 116 mm, be45는 185 mm와 187 mm로 거의 같다. A60FW와 A60PW의 be는 162 mm와 116 mm로 A45FW, A45PW와 동일하며, be45는 172 mm와 175 mm로 차이가 크지 않다. 모든 모델은 가력 중심선을 따라 일렬로 M20 볼트 3개를 통해 ㄱ-100×100×100t 단면의 가새부재와 접합되는 상세를 가지며, 해석의 단순화를 위해 가새부재는 거셋플레이트와의 접합부를 포괄하는 300 mm 길이로 가정했다. 볼트 구멍 사이 간격, 연단길이 등의 자세한 치수는 Fig. 4와 같다. Fig. 5에 나타난 바와 같이, 각 거셋플레이트는 H-244×175×7×11 단면을 갖는 2 m 길이 기둥의 웨브면에 용접되는 것으로 가정하여, 작업점은 기둥의 하단으로부터 200 mm 떨어진 곳에 위치시켰다. 용접면에서의 손상은 발생하지 않는 것으로 가정했으며, 해석의 편이성을 위해 거셋플레이트 용접면의 자유도를 기둥 웨브면에 맞닿은 부분에 종속시켰다.
상용프로그램 ABAQUS 6.14[9]로 거셋플레이트 해석모델을 수립하였으며, 재료 및 기하 비선형을 모두 반영 가능한 C3D8R 요소를 사용하였고, 해석모델의 형상은 Fig. 6와 같다. 거셋플레이트와 가새를 접합하는 볼트 및 너트는 별도의 나사산 없이 강체거동하도록 모델링하였다. 메쉬 크기는 거셋플레이트와 가새부재의 볼트구멍 주변을 제외한 부분은 약 12 mm, 볼트구멍의 주변부는 볼트와의 접촉조건을 고려해 약 5 mm로, 전체 해석모델 크기에 비해 충분히 작게 나누어 급격한 응력변화가 발생하지 않도록 하였다. 거셋플레이트의 항복강도 Fy는 308 MPa, 탄성계수 E는 220 GPa로 적용하고 등방성 경화모델과 폰 미세스(von Mises) 항복 판정식을 사용하였다.
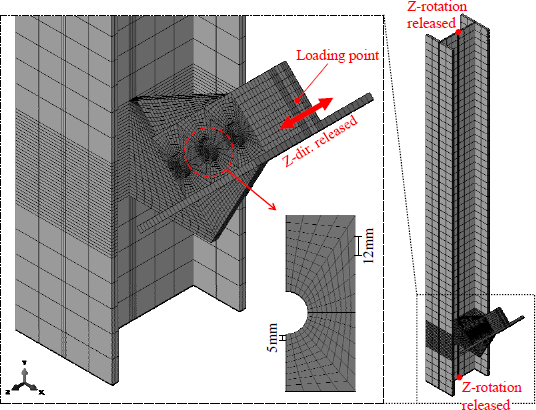
Close-up view of a gusset plate connection and its meshing scheme of a FEA model with a column and brace
거셋플레이트의 응력도-변형도 관계는 Fig. 7과 같이 항복강도 이후 강성을 갖지 않는 이선형(bi-linear) 모델로 정의하였다. 거셋플레이트와 결합되는 기둥의 웨브는 탄성거동하는 것으로 가정, 웨브의 비선형성이 거셋플레이트의 압축거동에 미치는 영향을 배제하였다. 기둥의 웨브에 비해 골조의 면내방향으로 매우 큰 강성을 갖는 기둥의 플랜지는 강체로 가정하였으며, 해석에서 탄성으로 정의된 웨브가 항복강도 이상의 응력을 플랜지에 전달하여 골조의 변형이 해석결과에 과도하게 반영되지 않고 해석결과가 거셋플레이트의 거동에만 의존하도록 하였다. 거셋플레이트-볼트와 거셋플레이트-가새부재 접촉면의 법선방향 접촉조건은 경접촉(hard contact)으로 가정하여 요소 간 침투를 불허하였고, 강재 간 마찰에 대한 접촉조건은 별도의 표면처리가 없는 것으로 가정하여 마찰계수 0.2를 적용하였다.
거셋플레이트 및 기둥부재의 접합상세와 철골가새골조의 일반적인 거동특성을 반영하여 해석모델의 구속조건을 설정하였다. 기둥부재 양단의 단면 내에서 중앙의 절점을 지배절점(reference node)으로 설정하고 나머지 절점은 지배절점에 커플링(coupling)시켰으며, 기둥부재의 약축방향 회전 자유도를 제외한 지배절점의 모든 자유도를 구속하였다. 거셋플레이트-기둥웨브 용접부는 거셋플레이트의 용접면과 웨브면이 일체가 되도록 각 접촉면을 구속하였다. 가새부재에서 볼트가 접합되는 쌍ㄱ형강의 각 다리는, 가력 중심선과 가새부재 끝단 단면의 교점으로 정의되는 가력점이 지배절점인 강체운동을 하도록 모델링하였다. 골조의 면외방향으로 구속되지 않는 거셋플레이트의 실제 상세를 반영하여 가새부재의 가력점은 가력방향과 골조의 면외방향으로 자유도가 구속되지 않도록 하였으며, 이를 제외한 나머지 회전 자유도와 병진방향 자유도는 구속하였다.
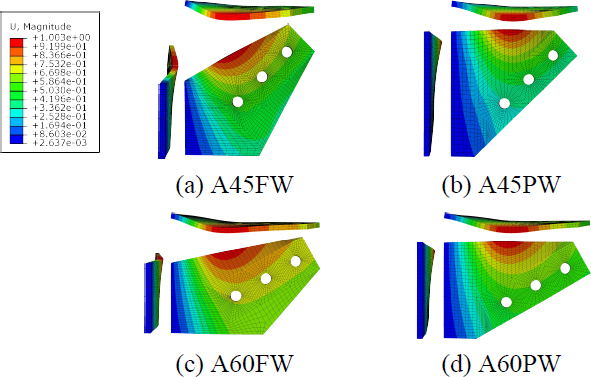
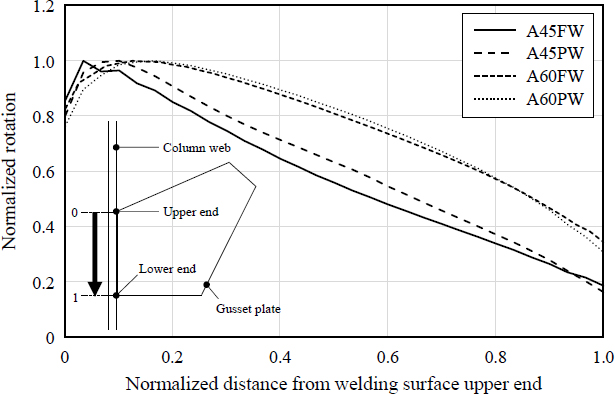
거셋플레이트의 좌굴모드를 해석에 고려하기 위해 고유치해석을 수행하였다. 모든 거셋플레이트 해석모델의 1차 좌굴모드는 거셋플레이트의 면외방향 변위 발생과 동시에 용접면과 가새부재에 의해 횡지지되는 부분이 고정단처럼 변형하는 측방향변형(side-sway) 형상을 보였다. Fig. 8은 각 거셋플레이트 모델의 좌굴모드 형상을 나타낸 것으로, 거셋플레이트 윗면의 면외변형이 두드러졌다. 이는 기둥의 길이방향 축(y축)에 대해 거셋플레이트 용접면에 접한 웨브면의 회전강성이 y축 상의 위치에 따라 상대적인 차이를 가지기 때문이다. 기둥의 상·하단에 위치한 지점과의 거리가 멀수록 웨브면은 작은 회전강성을 발휘하며, 이로 인해 상대적으로 회전강성이 작은 용접면의 상단에 접한 거셋플레이트 윗면에서 좌굴 발생이 두드러진다.
Fig. 9은 Fig. 8의 각 거셋플레이트 모델의 1차 좌굴모드 형상으로부터, 용접면의 상단으로부터 y축 방향으로 떨어진 거리와 용접면에서의 회전량을 각각 정규화하여 나타낸 것이다. 기둥 하단 지점과 멀어질수록 회전강성이 감소하여 회전량이 증가함을 확인할 수 있다. 각 해석모델의 1차 좌굴모드 형상에 대해 1 mm 진폭의 초기 형상결함(imperfection)을 가지는 것으로 가정하였으며, 가력점에 수직방향으로 30 mm 이상의 강제변위를 입력하였다. 초기 가력 단계에서 볼트의 강체운동에 의한 수렴성 문제를 개선하기 위하여 안정화(stabilization) 조건을 적용하였고, 해석결과의 신뢰도를 확보하기 위해 충분히 작은 0.02 %의 감쇠비를 적용하였다. 선행연구[4],[10]에서는 이와 동일한 방법으로 수립된 모델에 대한 유한요소해석결과를 실험결과와 비교하였으며, 해석모델이 실험체의 거동을 전반적으로 적절히 모사함을 확인하였다.
3.2 기둥용접형 거셋플레이트의 압축거동
이 절에서는 4개 모델의 유한요소해석결과를 축력-면외변형, 면외방향 모멘트-회전각, 면내방향 모멘트-회전각 관계를 통해 설명한다. 축력-면외변형에서 면외변위 drf는 작업점과 가력점 사이의 상대변위로 계산하였다. 면외방향 모멘트 Mo는 가력 중심선을 따라 가해지는 축력 P와 drf의 곱으로 다음과 같이 산정하였다.
| (4) |
거셋플레이트의 면외방향 회전각 θo는 작업점에 대한 마지막 볼트열 중심에서의 면외변위 do를 작업점 사이의 거리 Lo로 나누어 다음과 같이 계산하였다.
| (5) |
거셋플레이트 용접면의 도심을 기준으로 작용하는 면내방향 모멘트 Mi는 용접면의 도심으로부터 가력 중심선까지의 수직 길이 Li와 P의 곱으로 다음과 같이 산정하였다.
| (6) |
용접면의 도심을 기준으로 면내방향으로 회전하는 거셋플레이트의 회전각 θi는 가력점에 발생하는 축방향변위 di를 Li로 나누어 다음과 같이 계산할 수 있다.
| (7) |
Fig. 10은 식 (4)–식 (7)로 구한 거셋플레이트의 각 변위 및 회전각에 대해 보여준다.
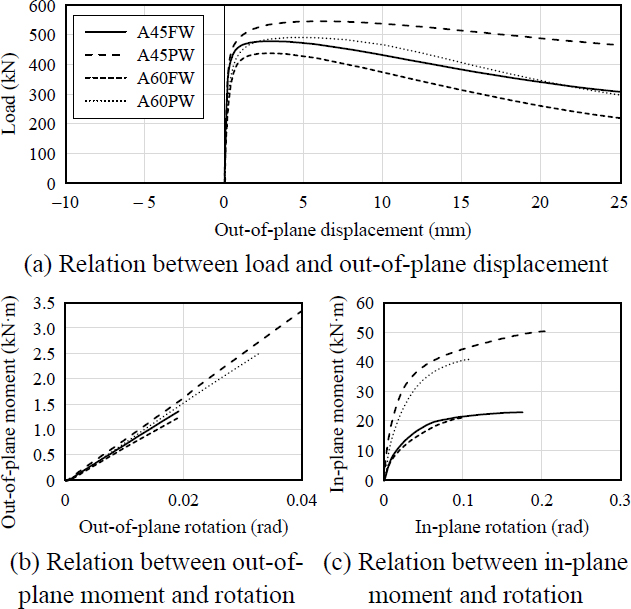
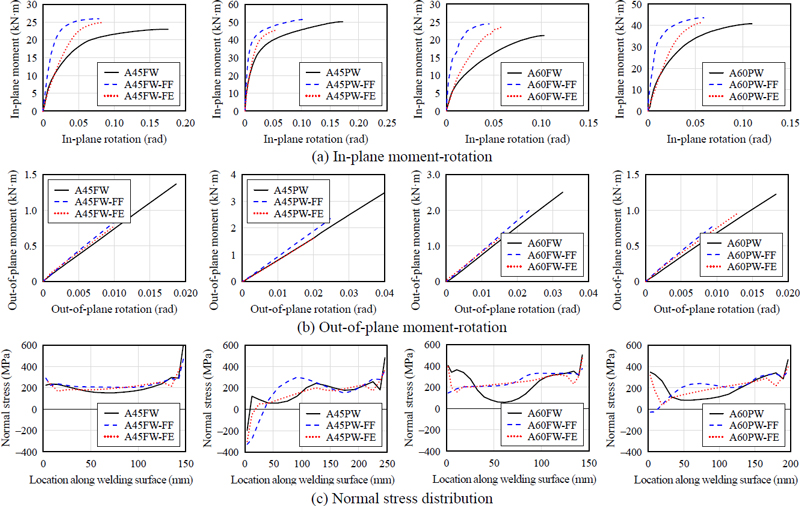
Fig. 11은 4개 거셋플레이트 해석모델의 유한요소해석결과를 나타낸 것으로, 축력-면외변형 관계와 거셋플레이트 최대강도 도달 시점까지의 면외방향 모멘트-회전각, 면내방향 모멘트-회전각 관계를 보여준다. 모든 해석모델은 거셋플레이트의 윗면에서 면외변형이 급증함과 동시에 강성이 감소하였으며, 최대강도 도달 이후 거셋플레이트가 좌굴함과 동시에 급격한 면외변위가 발생하였다. 해석모델에 따라 거셋플레이트의 유효폭이 서로 비슷하여 면외방향 회전강성은 큰 차이가 없음을 볼 수 있다. 반면, 면내방향 회전강성은 A45PW, A60PW가 A45FW, A60FW에 비해 매우 크게 나타났으며, 이는 식 (3)을 통해 알 수 있듯이, 거셋플레이트 유효폭과 두께의 영향을 크게 받는 면외방향 회전강성과 달리 면내방향 회전강성은 용접면의 길이가 길어질수록 기하급수적으로 증가하는 면내방향 회전에 대한 단면2차모멘트와 함께 증가하기 때문이다.
Table 2는 해석모델의 최대강도 Pmax를 식 (1)에 유효폭 be45를 대입하여 계산한 최대강도 과 비교하고, 면외방향 초기회전강성, Kout은 식 (3)을 통해 계산한 와 비교하였다. 또한 해석모델의 면내방향 초기회전강성 Kin을 정리, 제시하였다. 위트모어 단면을 이용한 기존에 제시된 압축강도 산정법은 전반적으로 기둥용접형 거셋플레이트의 압축강도를 과대평가하는 경향을 보임을 확인할 수 있다. Dowswell et al.이 제시한 유효 좌굴길이계수(= 0.7)[7]을 적용한 는 해석결과를 최소 24 %, 최대 35 % 과대평가하였다. AISC에서 제시하는 유효 좌굴길이계수(= 1.2)를 적용한 Pcal은 유효 좌굴길이계수로 0.7을 적용하여 계산된 압축내력에 비하여 향상된 정확도를 보였으나, 최대 22 % 정도 압축강도를 과대평가하였다. 뿐만 아니라, 면외방향 회전강성의 경우, 선행연구에서 제시한 계산식은 해석결과를 평균적으로 약 50 % 수준으로 과소평가하였다.

Comparison of compression behavior obtained from analyses with those calculated equations proposed by previous studies
거셋플레이트의 압축내력과 면외방향 회전강성에 대한 기존 식들이 기둥용접형 거셋플레이트의 압축거동을 적절히 모사하지 못하는 것은 위트모어단면에 대한 가정이 기둥용접형 거셋플레이트에는 부합하지 않기 때문이다. Fig. 12(a)는 A60FW의 폰 미세스(von Mises) 응력분포와 변형형상을 보여준다. 압축력을 받는 거셋플레이트에 대한 대부분의 기존 연구들은 위트모어 유효폭에 걸쳐 균일하게 형성되는 응력분포를 가정하고 있으나, Fig. 12(a)에 나타난 응력분포는 그와 매우 상이하다. 이는 기둥용접형 거셋플레이트가 용접된 웨브의 강성이 매우 낮을 뿐만 아니라, 거셋플레이트의 아랫면이 보에 의해 지지되지 않아 거셋플레이트가 시계방향으로 회전하기 때문이다. 이는 그림에서 각 볼트 구멍 주변부의 변형과 응력이 전파되는 방향이 작용점을 향하지 않고 서로 다른 것을 통해 확인할 수 있다.
Fig. 12(b)는 거셋플레이트로부터 전달되는 압축력에 의해 면외방향으로 변형하는 웨브의 단면을 보여준다. 기둥용접형 거셋플레이트가 웨브에 용접되는 경우 기둥부재의 전체 단면이 거셋플레이트에서 전달되는 압축력에 저항하지 않으며, 면외방향 강성이 작은 웨브에 국부적 변형이 발생한다. 이때 용접면에 접한 웨브는 y축 방향 양단에 지지되면서 휘어지는 것과 유사한 변형형상을 보이며, 용접면 길이에 따라 변하는 수직응력분포를 나타낸 Fig. 12(c)에서도 양단에서 응력의 집중 발생이 확인된다. 용접면에 접한 웨브의 중앙 부근의 수직응력은 약 100 MPa 전후인데 반해, 양단에서는 최대 약 500 MPa까지 큰 폭으로 증가하였다. 이와 같이 응력이 양단에 집중되는 현상은 A60FW를 제외한 다른 거셋플레이트 해석모델에서도 유사하게 나타난다.
4. 기둥용접형 거셋플레이트를 단순화한 유한요소해석모델
기둥용접형 거셋플레이트의 유한요소해석 시 매번 기둥을 해석모델에 포함시키면 과도한 노력과 해석시간이 소요된다. 또한 단부를 고정지점으로 가정해 거셋플레이트만을 고려한 유한요소모델은 단부의 고정도가 증가해 압축강도를 과대평가할 수 있다. 이 장은 3장에 소개된 기둥용접형 거셋플레이트의 유한요소해석모델에서 기둥부재를 배제하고 경계조건을 단순화하는 방법을 제시한다. 유한요소해석모델은 인접 구조부재의 영향이 반영된 다양한 형상의 거셋플레이트에 대한 스프링요소모델의 모델링 변수 결정에 활용될 수 있다.
4.1 기둥용접형 거셋플레이트의 경계조건과 좌굴모드
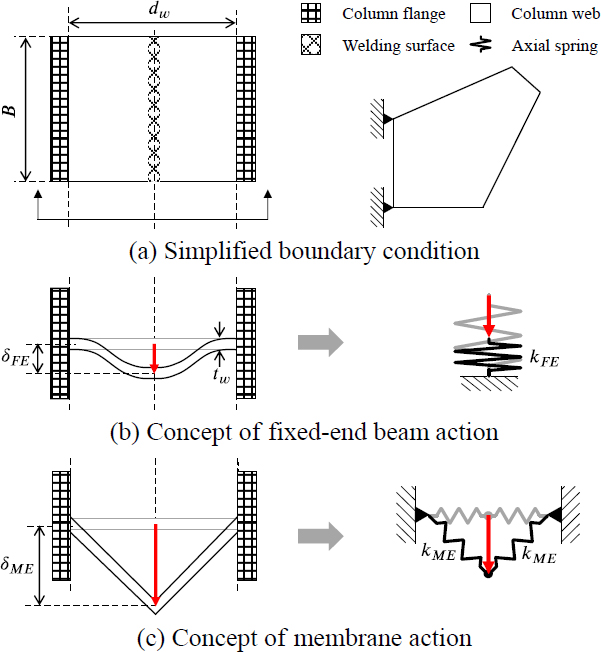
압축력에 대해 용접면의 y축 방향 양단에서 지지되는 것과 같이 거동하는 기둥용접형 거셋플레이트의 경계조건은 Fig. 13(a)와 같이 용접면의 양단부를 회전단으로 가정하여 단순화할 수 있다. 그러나 이는 기둥 웨브의 하중저항 메커니즘을 과도하게 단순화한 것으로, 실제 웨브는 회전단처럼 작용하는 용접면 양단 사이에 연속적으로 변하는 면외방향 강성을 통해 압축력에 저항하게 된다. 이로 인해 양단부를 회전단으로 가정한 거셋플레이트는 용접면 전체에 걸쳐 수직응력이 발생하는 현상을 적절하게 모사하는 데 한계가 있다.
웨브가 용접면 양단 회전단 사이에서 발휘하는 면외방향 강성의 분포는 스프링요소를 추가함으로써 반영가능하며, 하중 크기에 따른 웨브 변형형상의 변화를 고려하면 스프링요소는 Fig. 13(b) 및 Fig. 13(c)와 같이 양단고정단보(fixed-end beam, FE)와 막(membrane, ME)의 거동 특성을 반영할 수 있어야 한다. Fig. 13(b)와 같이 골조에 면내방향으로 가력되는 압축력에 대해 기둥 플랜지는 웨브에 비해 높은 강성을 가지므로, 웨브는 양단이 고정된 보처럼 거동한다고 가정할 수 있다. FE 스프링요소는 가력 초반 단계에서, 즉 가력 변위가 비교적 작을 때의 주요 저항요소로, 요소의 수직강성 KFE는 널리 알려진 양단지지보의 처짐공식으로부터 다음과 같이 계산할 수 있다.
| (8) |
여기서, δmax는 웨브길이 dw를 길이로 갖는 양단이 고정단인 보의 최대처짐이며, B는 용접면에 접한 웨브의 폭, tw는 웨브의 두께이다.
웨브의 면외방향으로 과도한 변형이 발생하게 되면, Fig. 13(c)와 같이 웨브의 전단면에 걸쳐 인장응력만이 발생하는 막과 같이 거동하게 된다. ME 스프링요소는 요소의 길이방향 인장에 대해서만 강성을 발휘하는 두 개의 스프링요소로 구성되며, 각 스프링요소는 기둥 플랜지에 고정되는 것으로 가정할 수 있다. ME 스프링요소는 변형이 적게 발생하는 가력 초반 단계에서는 각 스프링의 길이방향 축과 거셋플레이트로부터 전달되는 압축력의 방향이 거의 수직에 가까움에 따라 강성을 거의 발휘하지 못하지만, 면외방향 변형이 커지면 강성을 발휘하게 된다. 이때 거셋플레이트를 잡아당기는 막의 강성 KME는 웨브의 탄성계수와 단면적의 곱을 길이로 나누어 다음과 같이 계산할 수 있다.
| (9) |
여기서, Aw는 웨브의 단면적이며, KME를 갖는 스프링요소는 Fig. 13과 같이 거셋플레이트를 기준으로 양쪽에 배치된다.
Fig. 14은 서로 다른 4개 조건으로 단순화된 기둥용접형 거셋플레이트의 경계조건을 보여준다. FF(fully-fixed) 경계조건은 거셋플레이트 용접면의 모든 자유도를 구속한 것으로, 거셋플레이트에 관한 기존 연구에서 경계조건의 단순화를 위해 주로 사용된 경계조건이다. NS(no spring) 경계조건은 거셋플레이트 용접면의 양단에만 회전지점을 배치한 단순화 모델링 방식이며, FE와 ME 경계조건은 각각 NS 경계조건에 FE와 ME 스프링요소를 추가한 것이다. 해석의 정확도 향상을 위해 용접면을 그림과 같이 15개 구간으로 나누고, 각 경계조건에 해당하는 스프링요소를 구간의 중심마다 배치하였다. 용접면이 15개 구간으로 나뉨에 따라 총 15개의 스프링요소가 배치되었다. 이때 스프링요소의 강성은 구간마다 동일하며, 15개 스프링요소에서 강성의 총합은 식 (8)과 식 (9)로부터 계산되는 강성과 같다. 스프링요소 또는 회전지점이 용접면의 길이를 따라 절점에 불연속적으로 배치됨으로써 발생할 수 있는 응력 및 변형의 과도한 집중 현상이 나타나지 않도록 각 구간의 면의 자유도를 이들의 중심에 위치한 절점(스프링요소가 배치된 절점)에 구속시켰다. 용접면의 양단에 위치한 구간의 면은 회전지점을 기준으로 z축에 대해 회전할 수 있도록 역학적 커플링(kinematic coupling) 조건을 부여하여 병진방향 자유도를 종속시켰으며, 이를 제외한 모든 구간의 면은 힘과 모멘트를 인접한 구간의 면에 전달할 수 있도록 구조적 커플링(structural coupling) 조건을 부여하여 병진방향과 회전 자유도를 종속시켰다. 또한, 웨브의 면외방향을 제외한 방향과 모든 축에 대한 회전 자유도는 전부 구속하였다.
Fig. 15은 FF, NS, FE, ME 경계조건을 갖는 유한요소해석모델의 좌굴모드를 보여준다. 각 거셋플레이트 모델의 1차 좌굴모드는 용접면으로부터 멀어질수록 거셋플레이트의 측방향변형이 증가하는 변형형상을 보인다. 기둥이 포함된 거셋플레이트 유한요소해석모델과 달리, 어느 한 곳에 면외변형이 집중되는 현상이 완화되었다. 이는 단순화된 경계조건을 적용한 유한요소해석모델에서 웨브의 면외방향을 제외한 모든 자유도를 구속함으로써 웨브 면내의 수직위치에 따른 회전강성의 상대적 차이가 반영되지 않았기 때문이다. 따라서 1차 좌굴모드 형상은 압축력을 받는 거셋플레이트의 임계단면(critical section)이 거셋플레이트 윗면에서 발생하는 실제 거동을 적절하게 반영한다고 볼 수 없다. 실제 경계조건이 반영된 임계단면은 거셋플레이트 윗면에 집중적인 면외변형이 발생하는 좌굴모드를 초기 좌굴모드로 선택해야 한다. Fig. 15에 나타난 바와 같이 유한요소해석모델의 고차 좌굴모드에서 면외변형이 거셋플레이트의 윗면에 형성되는 것을 확인할 수 있으며, 이를 각 유한요소해석모델에 적용하여 좌굴해석을 수행하였다.
4.2 단순화된 경계조건을 가진 거셋플레이트 해석모델의 압축거동 특성 비교
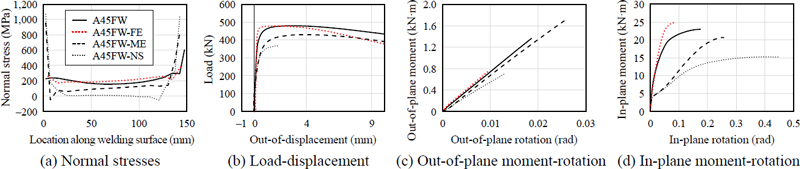
Fig. 16은 A45FW의 형상을 지닌 거셋플레이트의 경계조건을 NS, FE, ME로 단순화한 유한요소해석모델(A45FW-NS, A45FW-FE, A45FW-ME)의 해석결과를 기둥부재를 포함한 해석모델인 A45FW와 비교한 것이다. A45FW-FE가 거셋플레이트의 최대강도 도달 시점에서 용접면에 발생하는 수직응력을 가장 잘 모사하고 있는 것으로 나타났다. A45FW-NS와 A45FW-ME는 용접면 양단부 회전지점 사이는 거셋플레이트의 면내방향 강성이 비교적 적어 양단부에 응력이 집중되는 현상이 나타났다. A45FW-FE/ME/NS의 최대강도는 각각 478 kN, 429 kN, 368 kN이며, A45FW-FE의 최대강도가 기둥부재가 포함된 유한요소해석모델의 최대강도인 479 kN와 가장 유사하다.
거셋플레이트가 최대강도에 도달할 때까지 면외방향 회전각-모멘트 관계는 그래프에서 확인할 수 있듯이 A45FW-FE가 A45FW의 면외방향 회전강성을 가장 잘 모사하고 있다. 최대강도 시점에서 가력점의 면외변위와 축력의 곱으로 구해지는 모멘트는 거셋플레이트의 면외방향 항복모멘트와는 무관한 값으로, A45FW-FE의 최대강도가 A45FW와 유사함에도 불구하고 최대강도 도달 시점에서의 면외방향 모멘트에 차이가 나타나는 것은 가력점의 면외방향 변위 차이 때문이다. 거셋플레이트의 면내방향 회전강성의 측면에서도 A45FW-FE가 A45FW를 가장 잘 모사하였으며, 가력 초기 이후 A45FW-FE의 강성이 더 큰 것은 웨브의 면외방향 변형이 적은 가력 초반 단계에서는 웨브면이 FE와 같이 저항하지만, 변형이 점차 커짐에 따라 ME와 가깝게 변해가기 때문이다. 이에 따라 A45FW의 최대강도 도달하는 시점에서의 면내방향 회전각이 그래프 상에서 A45FW-FE와 A45FW-ME의 회전각의 값 사이에 위치한다고 할 수 있다. 스프링요소모델은 거셋플레이트의 회전거동에 대해 항복모멘트와 초기 회전강성만을 요구하며, 일반적으로 기둥용접형 거셋플레이트의 강도가 면외방향 좌굴에 의해 결정되고 좌굴과 동시에 면내방향 회전에 대한 저항능력을 거의 상실한다는 측면에서 A45FW-FE는 초기 회전강성을 충분히 잘 모사하고 있으므로, FE 스프링요소의 강성으로부터 ME 스프링요소의 강성으로 변화하는 웨브의 거동특성을 단순화된 경계조건에 반영하는 것은 불필요할 것으로 판단된다.
Fig. 17은 경계조건을 단순화한 FE 해석모델(A45FW-FE, A45PW-FE, A60FW-FE, A60PW-FE)과 FF 해석모델(A45FW-FF, A45PW-FF, A60FW-FF, A60PW-FF)의 해석결과를, 인접 구조부재를 직접적으로 모델링한 거셋플레이트(A45FW, A45PW, A60FW, A60PW)의 해석결과와 비교하여 보여준다. Fig. 17(a)는 면내방향 모멘트-회전각 관계를 나타내며, FF 경계조건으로 단순화된 모델들의 면내방향 회전강성은 기둥부재를 직접적으로 모델링한 거셋플레이트에 비해 초기 회전강성이 전반적으로 크게 나타났다. FF 경계조건의 모델에 비해 FE 경계조건으로 단순화된 모델이 초기 회전강성을 보다 잘 예측하는 것으로 나타났다. 거셋플레이트의 면외방향 회전강성에 대해서도 FE 경계조건의 단순화 모델은 FF 경계조건의 단순화 모델에 비교하여 근소하지만 정확도가 향상된 것을 Fig. 17(b)에서 볼 수 있으며, Fig. 17(c)에 나타낸 거셋플레이트 용접면 상의 응력분포에서도 FE 경계조건의 해석모델이 FF 경계조건에 비교하여 높은 정확도를 보였다. A45FW-FF와 A45FW-FE는 모두 A45FW의 응력분포와 유사한 결과를 나타냈으며, A45PW에 대해서는 A45PW-FE가 더 유사한 응력분포를 보였다. A60FW-FF와 A60PW-FF는 거셋플레이트 용접면 상단에 집중되는 응력을 모사하지 못하였다. 이는 기둥용접형 거셋플레이트의 좌굴에 대한 임계단면이 용접면 상단에 근접한 거셋플레이트 윗면에 형성된다는 측면에서 FF 모델이 거셋플레이트의 좌굴 형상 및 강도를 모사하는 데 적합하지 않음을 보여준다. 반면 A60FW-FE와 A60PW-FE는 용접면 상단에 집중되는 응력을 잘 모사하고 있다.
Table 4는 FF와 FE 경계조건으로 단순화한 해석모델의 최대강도(와 ), 면외방향 초기 회전강성(와 ), 그리고 면내방향 초기 회전강성(와 )을 기둥부재가 포함된 유한요소해석결과와 비교하여 보여준다. 와 는 4개 형상의 거셋플레이트에 대해 기둥부재가 포함된 유한요소해석결과에 비교하여 10 % 이내의 오차를 나타냈다. 강도와 회전강성 측면에서 전반적으로 FE 경계조건 해석모델은 FF 경계조건 해석모델과 비교하여 높은 정확도를 가졌으며, 이는 면내방향 회전강성에서 크게 두드러진다. FF 경계조건으로 단순화한 해석모델로 구한 면내방향 회전강성이 기둥부재가 포함된 해석모델과 비교하면 186 %–377 % 수준으로 나타났으며, FE 경계조건을 적용하였을 때는 110 %–112 % 수준으로 감소한다.
5. 결 론
본 연구는 기존에 제시된 거셋플레이트의 압축내력 및 회전강성 예측 방법에 대해 고찰하고, 비내진 설계된 파이프랙 철골가새골조에 설치되는 기둥용접형 거셋플레이트에 대한 적용 가능 여부를 검토하였다. 이를 위해 기둥용접형 거셋플레이트의 경계조건을 반영한 유한요소해석을 수행하고, 해석결과로부터 응력분포 및 좌굴형상을 분석하였다. 이를 바탕으로 기둥용접형 거셋플레이트의 경계조건을 단순화하여 해당 거셋플레이트가 포함된 철골가새골조의 내진성능평가에 사용될 수 있는 유한요소해석모델을 제안하였으며, 이를 기존의 일반적인 방법으로 경계조건이 단순화된 해석모델과 비교하여 다음과 같은 결론을 도출하였다.
- (1) 기존 예측식은 거셋플레이트의 압축내력과 면내·외 방향 회전강성에 대해 응력이 균일하게 분포하는 위트모어단면을 가정하나, 기둥용접형 거셋플레이트는 골조의 면내방향으로 회전함에 따라 위트모어단면 내 균등 응력분포에 대한 가정이 타당하지 않음을 해석적으로 확인하였다.
- (2) 기둥용접형 거셋플레이트의 용접면에 접한 웨브의 변형형상과 수직응력 분포를 바탕으로 경계조건을 단순화하여 등가의 유한요소해석모델을 수립할 수 있으며, 경계조건이 단순화된 유한요소해석모델에 실제 발생하는 좌굴모드를 고려하려면 거셋플레이트 윗면의 면외변형에 의한 좌굴형상을 기둥용접형 거셋플레이트의 1차 좌굴모드로 반영해야 한다.
- (3) 본 연구에서 제시된 FE 경계조건으로 단순화한 해석모델은 FF 경계조건을 가진 해석모델에 비해 기둥용접형 거셋플레이트의 압축내력, 면내·외 방향 초기 회전강성을 비교적 잘 예측하는 것으로 나타났다. 다만, FE 경계조건으로 단순화한 해석모델은 거셋플레이트의 최대강도 도달 시점에서 용접면의 중심을 기준으로 회전하는 거셋플레이트의 회전각을 과소평가하는 경향이 있는데, 내진성능평가 시 거셋플레이트는 주로 힘지배요소로 취급되므로, 이와 같은 변형능력보다 최대강도를 적절하게 예측 가능한 단순화된 해석모델이 필요하다는 점에서 FE 경계조건으로 단순화한 해석모델의 적용은 무리가 없을 것으로 판단된다.
- (4) 본 연구에서 수행된 해석은 옥외배관을 지지하는 철골가새골조의 현장조사를 통해 기둥과 가력 중심선 사이의 각도가 45°와 60°이며 조밀 거셋플레이트의 임계두께 이상의 두께를 갖는 기둥용접형 거셋플레이트를 대상으로 하므로, 다른 각도와 두께를 가지는 거셋플레이트에 본 연구의 결과를 적용할 경우 추가적인 해석이 필요하다.
Acknowledgments
이 연구는 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20017750).
References
- Ministry of Land, Infrastructure and Transport (2021) Seismic Design Standard for Buildings (KDS 41 17 00: 2021), Korea (in Korean).
- Yoo, J.H. (2006) Analytical Investigation on the Seismic Performance of Special Concentrically Braced Frames, Ph.D. Dissertation, University of Washington, USA.
-
Hsiao, P.-C., Lehman, D.E., and Roeder, C.W. (2012) Improved Analytical Model for Special Concentrically Braced Frames, Journal of Constructional Steel Research, Elsevier, Vol.73, pp.80–94.
[https://doi.org/10.1016/j.jcsr.2012.01.010]

-
Fang, C., Yam, M.C.H., Zhou, X., and Zang, Y. (2015) Post-Buckling Resistance of Gusset Plate Connections: Behaviour, Strength, and Design Considerations, Engineering Structures, Elsevier, Vol.99, pp.9–27.
[https://doi.org/10.1016/j.engstruct.2015.04.043]

-
Astaneh-Asl, A., and Goel, S.C. (1984) Cyclic In-Plane Buckling of Double Angle Bracing, Journal of Structural Engineering, American Society of Civil Engineers, Vol.110, No.9, pp.2036–2055.
[https://doi.org/10.1061/(ASCE)0733-9445(1984)110:9(2036)]

- Thornton, W.A. (1984) Bracing Connections for Heavy Constructions, Engineering Journal, American Institute of Steel Construction, Vol.21, No.3, pp.139–148.
- Dowswell, B. (2006) Effective Length Factors for Gusset Plate Buckling, Engineering Journal, American Institute of Steel Construction, Vol.43, No.2, pp.91–102.
- American Institute of Steel Construction (2001) Manual of Steel Construction: Load and Resistance Factor Design (3rd Ed.), AISC, USA.
- Dassault Systèmes Simulia Corp. (2014) Abaqus Analysis User’s Manual, Ver. 6.14, DSS, USA.
- Shin, Y.-S., Go, H., and Kim, H.-J. (2023) Compression Buckling Behavior and Stress Distribution of Non-Seismically Detailed Gusset Plates Welded to a Column, Journal of the Architectural Institute of Korea, AIK, Vol.39, No.6, pp.235–243 (in Korean).