T-형 보강재로 보강된 판의 압축강도 산정에 형상비를 고려한 좌굴계수 식의 적용성 평가
Copyright © 2023 by Korean Society of Steel Construction
초록
종방향 보강재로 보강된 판에서 보강재의 제원을 합리적으로 결정하기 위해 Wang et al.은 형상비(β)를 고려한 좌굴계수 식(kfc)을 최근 제안하였다. 본 연구에서는 kfc 식의 적용 시 AASHTO LRFD 교량설계기준의 압축강도가 합리적으로 산정되는지에 대한 해석적 연구를 수행하였다. 보강재 개수는 3개까지 고려하였으며, 주요 변수로서 형상비와 조밀, 비조밀 및 세장 판을 포함하도록 판의 폭-두께비와 보강재의 휨강성 조합을 고려하였다. 비선형해석으로부터 압축강도를 평가한 결과 β < 1.4βcr(βcr: kfc가 최소값이 되는 한계세장비)일 때에는 one half sine-wave의 종국변형을 보이며 AASHTO 기준의 압축강도가 얻어졌다. 반면, β ≥ 1.4βcr일 때에는 two half wave 형태의 종국변형을 보였으며 설계기준의 압축강도에 도달하지 못하였다. 따라서 횡방향 보강재의 최대 간격에 대한 규정이 필요할 것으로 판단되었다.
Abstract
Wang et al. recently proposed a buckling coefficient equation(kfc) to determine a reasonable size of stiffener considering the aspect ratio(β) in longitudinally stiffened plates. In this study, a series of numerical analysis was conducted on whether the compressive strength stipulated in the AASHTO LRFD bridge design specifications is reasonably estimated when the kfc equation is applied. The number of stiffener was considered up to 3. As major variables, the aspect ratio and plate width-to-thickness ratio in combination with flexural stiffness of stiffeners were considered to include compact, noncompact and slender plates. As a result of evaluating compressive strength from nonlinear analysis, when β < 1.4βcr (βcr: critical aspect ratio corresponding to minimum value of kfc), the final deformation showed one half sine-wave form and the compressive strength of the AASHTO standards was obtained. On the other hand, when β ≥ 1.4βcr, it showed a deformation in the form of two half waves and did not reach the compressive strength of the design standards. Accordingly, it is considered that a regulation on the maximum spacing of transverse stiffeners would be necessary.
Keywords:
Stiffened plate, Aspect ratio, Tee stiffener, Buckling coefficient, Compressive strength키워드:
보강판, 형상비, T-형 보강재, 좌굴계수, 압축강도1. 서 론
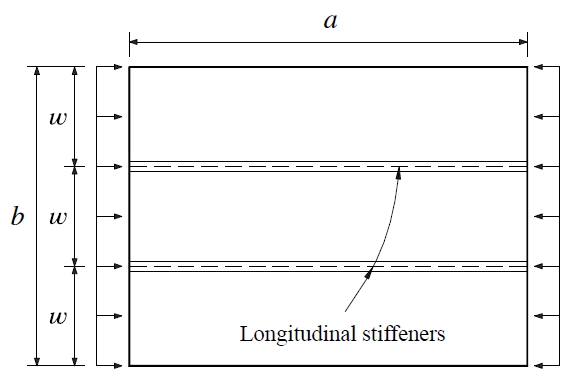
박스거더교의 압축플랜지는 좌굴강도의 향상을 위해 Fig. 1과 같이 종방향 보강재를 통상 설치한다. AASHTO LRFD 교량설계기준[1](이하 AASHTO LRFD 기준)에서는 횡비틀림좌굴에 유리한 T-형 보강재를 사용토록 하고 있으며, 보강재의 단면2차모멘트(Is)에 따른 보강판의 좌굴계수 식을 본문 6.11.11.2에 제시하고 있다. 이 식은 종래의 설계기준인 AASHTO Standard Specifications[2]에서 보강재 개수(n)가 5개 이하일 때 적용하는 좌굴계수 식을 그대로 가져온 것이다.
그러나, n ≥ 3인 경우 보강재의 제원이 매우 커지는 문제점이 있는데, 그 이유는 횡방향 보강재(transverse stiffener)에 의한 구속 효과를 무시하고 종방향 보강재가 매우 길다고 가정하였기 때문이다. 즉, 보강판의 형상비(aspect ratio) β(= a/b, Fig. 1 참조)가 무한한 값으로 고려됨에 따라 보강재 제원이 과도하게 되어 AASHTO LRFD 본문 기준에서는 n ≤ 2로 제한하고 있다. 한편, AASHTO LRFD 해설부 C6.11.11.2에서는 n ≤ 5일 때 적용할 수 있는 별도의 좌굴계수 식을 제시하고 있다. 하지만 이 식은 본 논문의 2.1.2에서 제시한 바와 같이 보강재의 크기를 유연하게 결정할 수 없는 등의 문제점이 있다.
보강판의 좌굴계수 식에 대한 AASHTO 기준의 문제점을 보완하고자 Wang et al.[3]은 T-형 보강재로 보강한 판에 대해 형상비를 고려한 좌굴계수 식을 제시하였다. 이들은 에너지법으로 유도된 식의 타당성을 평가하기 위해 n ≤ 3인 경우에 대해 좌굴고유치해석을 수행하고, 그 결과를 토대로 보정계수를 적용함으로써 최종 좌굴계수 식을 제안하였다.
한편, AASHTO LRFD 기준과 국내 강구조부재설계기준인 KDS 14 31 10[4]은 보강판의 압축강도를 조밀(λp) 및 비조밀 한계세장비(λr)에 따라 산정하는 식을 제시하고 있는데, 이들 한계세장비는 좌굴계수 k의 함수이다. 따라서 보강판의 압축강도를 합당하게 예측하기 위해서는 k 값을 합리적으로 평가하여야 한다.
본 연구의 목적은 Wang et al.이 제안한 판의 형상비를 고려하는 좌굴계수 식의 적정성을 평가하는 것이다. 절차는 이들이 제안한 식으로 k 값을 산정하고 이로부터 AASHTO LRFD 기준의 λp와 λr을 계산한 후 이를 토대로 계산된 보강판의 압축강도를 전산해석에 의한 압축강도와 비교하는 과정으로 수행하였다. 보강판의 압축강도는 재료 및 기하비선형해석으로 평가하였으며, 보강재 3개까지에 대해 판의 형상비, 폭-두께비(또는 판의 세장비), 그리고 보강재의 휨강성을 변수로 하였다.
2. 좌굴계수 및 압축강도에 관한 기준
2.1 AASHTO LRFD 기준의 좌굴계수 식
AASHTO LRFD 기준[1] 본문 6.11.11.2의 보강재 단면2차모멘트(Is)와 좌굴계수 관계는 AASHTO Standard Specifications의 다음 식 (1a)와 식 (1b)를 토대로 하였다.
| (1a) |
| (1b) |
여기서, n: 보강재 개수, w: 서브패널 폭, tf: 압축플랜지 두께, Is: 압축플랜지 면에 대한 보강재의 단면2차모멘트이다.
전술한 바와 같이 식 (1a)와 식 (1b)는 보강재가 매우 길다는 가정(즉 형상비 = ∞)으로부터 도출된 것이다. 이로 인해 특히 n ≥ 3일 때 보강재 제원이 지나치게 커지는 문제가 있어 본문 기준은 n ≤ 2로 제한하고 있다.
상기의 문제점을 보완하고자 AASHTO LRFD 기준[1]의 해설부 C6.11.11.2에 다음 식을 제시하고 있다.
| (2) |
여기서, β: 보강판의 형상비(= a/b), a: 횡방향 보강재 간격, b: 압축플랜지 폭이다.
식 (2)는 n ≤ 5이고 β ≤ 3인 조건에서 적용 가능하며 보강재의 단면2차모멘트는 식 (3)을 만족하여야 한다.
| (3) |
식 (3)의 Is 요건은 서브패널의 형상비 α(= a/w)가 4일 때 k 값이 약 4.0이 되도록 결정한 것이다. 따라서 식 (2)는 α < 4일 때 임의의 좌굴계수 크기, 즉 k < 4.0에 상응하는 보강재 제원을 고려할 수 없고, 이로 인해 형상비가 작을수록 불필요하게 큰 보강재를 적용하게 된다. 더욱이 β > 3인 경우에는 식 (2)의 적용이 제한된다.
2.2 Wang et al.의 좌굴계수 제안식
Wang et al.[3]은 에너지법으로부터 유도된 이론적 좌굴계수 식[5],[6]의 검증을 위해 서브패널의 폭-두께비(λf = w/tf), 형상비, 그리고 보강재의 휨강성을 변수로 하여 보강재 3개까지에 대해 좌굴고유치해석을 수행하였다. 수치해석 결과를 바탕으로 에너지법으로부터 유도된 좌굴계수 식에 수정계수(cf)를 도입하여 최종 좌굴계수 식(여기서, AASHTO LRFD 기준의 k와 구분하기 위하여 kfc로 표기하기로 함)을 식 (4a) 및 식 (4b)로 제안하였다.
• β/βcr ≤ 1.0일 때:
| (4a) |
• β/βcr > 1.0일 때:
| (4b) |
여기서, βcr은 좌굴계수 kfc가 최소값을 보이는 한계 형상비로서 다음과 같다.
| (5) |
| (6) |
| (7) |
| (8) |
그리고, D = Et3f/12(1 – v2): 판의 휨강성, v(= 0.3): 포아송 비, Al: 보강재 1개의 단면적이며, γ와 δ는 각각 보강재 1개의 ‘휨강성비’와 ‘단면적비’이다.
2.3 AASHTO LRFD 기준의 압축강도
본 기준[1]의 6.11.8.2에서 비틀림 영향을 포함한 플랜지의 공칭압축강도 Fnc를 식 (9)로 제시하고 있다.
| (9) |
여기서, Fcb: 압축력만에 의한 플랜지 좌굴강도, fv: St. Venant 비틀림에 의한 플랜지의 전단응력, Fcv: 전단에 대한 플랜지 좌굴강도, ϕv: 전단에 대한 저항계수이다.
본 기준에서 서브패널의 폭-두께비(λf)에 따라 Fcb를 다음과 같이 규정하고 있다.
• λf ≤ λp일 때:
| (10a) |
• λp < λf ≤ λr일 때:
| (10b) |
• λf > λr일 때:
| (10c) |
여기서,
| (11a) |
| (11b) |
| (12) |
이고 Rb: 압축플랜지 응력감소계수, Rh: 하이브리드 계수, E: 강재의 탄성계수(= 210,000 MPa), Fyc: 압축플랜지의 항복강도, Fyr: 잔류응력 효과를 고려한 항복강도이다.
본 논문에서는 Rb = 1.0, Rh = 1.0이고 비틀림 영향이 없이 압축력만 작용하는 경우로 국한하기로 한다. 이 때 fv = 0이므로 식 (12)의 ∆ = 1.0이 되고 식 (9)와 식 (10a)–식 (10c)에서 Fnc = Fcb가 된다.
3. 전산해석 방안
3.1 전산 모델
보강판의 압축강도는 ABAQUS 프로그램[7]을 사용하여 재료 및 기하비선형해석으로부터 평가하였다. Fig. 2는 경계조건과 하중을 포함한 전산모델의 개요도이다. 여기서, U는 이동변위, R은 회전변위이다. Line A에는 x-방향 이동변위(Ux)를 동일하게 적용하기 위해 ‘Coupling: kinematic’ 옵션을 적용하였다. 본 해석 모델은 4변 단순지지 조건에 해당하므로 종방향으로 인접패널에 의한 ‘연속효과(continuity effect)’를 고려하지 않아 안전측의 압축강도로 고려된다. 하중은 플랜지와 T-형 보강재에 각각 판두께에 해당하는 선하중을 재하하였는데, 이는 단위 압축응력(1 MPa)에 해당하는 셈이다.
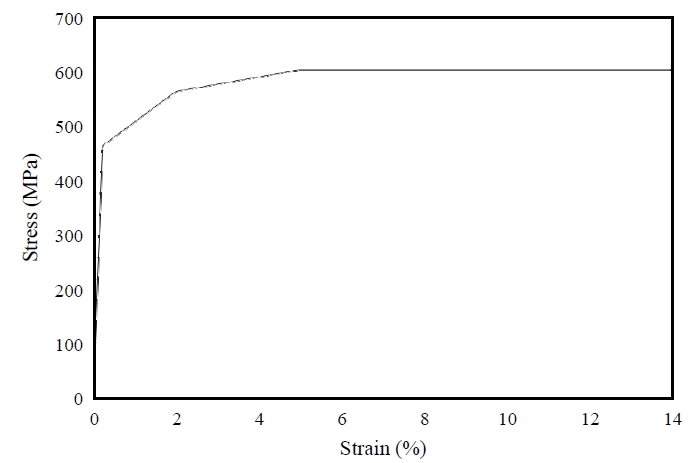
강재는 플랜지 및 보강재 모두 HSB460을 고려하였으며, 응력-변형률 선도는 Fig. 3와 같이 이상화하였다. 재료 및 기하비선형해석 시 하중 증가는 Rik’s method를 적용하였다. 항복기준은 Von Mises 기준을 적용하였고 변형률경화 구간에는 isotropic strain hardening 모델을 사용하였다. 플랜지 및 T-형 보강재 모두 S4R 쉘요소로 모델링하였다. 본 연구에서 고려한 보강판의 서브패널 폭(w)은 n = 1일 때 800 mm이고 n = 2,3일 때 600 mm이다. 전산 쉘요소 모델에서 플랜지 부의 개별 요소의 크기는 20 mm × 20 mm로 충분히 세분화하였으며, T-형 보강재도 비슷한 요소 크기로 분할하였다.
3.2 잔류응력 및 초기처짐
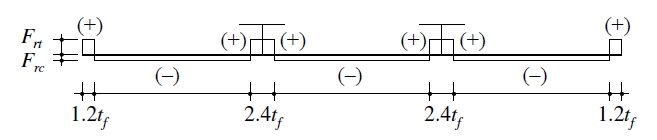
Chacón et al.[8]은 용접 제작한 I-거더에 대해 다양한 잔류응력 모델로 휨강도 비교 평가를 수행하였는데, 이에 따르면 잔류응력 모델에 따른 종국강도의 차이는 크지 않다. 본 연구에서는 플랜지와 T-형 보강재 스템의 용접접합에 의한 잔류응력을 Fig. 4와 같이 고려하였다. 본 모델은 Chacón et al.이 비교 해석에 고려한 모델 중 Granath의 모델을 기반으로 한 것이다. 용접 잔류응력의 크기는 인장 잔류응력 (+)Frt는 0.9Fy(= 414 MPa)으로 하였고 폭은 편측당 1.2tf로 하였다. 이 때 압축 잔류응력 (–)Frc의 크기는 자체 평형(self-equilibrium)으로부터 결정된다.
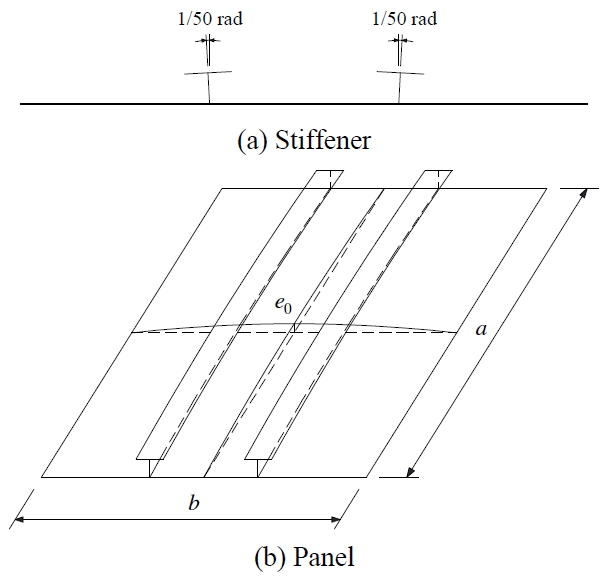
초기처짐은 보강재의 초기처짐과 보강판의 전체적인 초기처짐을 고려하였다. 보강재의 초기처짐은 Fig. 5(a)와 같이 중앙점을 기준으로 1/50 rad 회전된 것으로 고려하였다. 보강판의 전체적인 초기처짐은 Fig. 5(b)와 같이 e0 만큼 면외 초기처짐으로 고려하였으며, Eurocode 3[9]에 기반하여 e0 = min(a/400, b/400)으로 하였다. 보강재의 초기처짐은 전산모델 작성 시 직접 정의하였으며, 판의 전체적인 초기처짐은 좌굴고유치해석을 수행한 후 첫번째 좌굴모드를 e0만큼 스케일하여 모사하였다.
4. 압축강도 해석 및 결과 분석
4.1 해석 경우
본 연구에서는 종방향 보강재 개수(n)를 3개까지 고려하였다. 주요 변수로 보강판의 형상비(β), 서브패널의 폭-두께비(λf), 보강재의 휨강성비(γ)를 고려하였다. 판의 폭-두께비와 보강재의 휨강성을 조합함으로써 조밀, 비조밀 및 세장판(slender plate)의 범위를 포함하였다. 이로부터 결정한 해석 경우는 보강재 개수별로 Table 1에서 Table 3과 같다. T-형 보강재의 제원 표기는 T-형강의 표기 방식에 따른 것이며, 보강재의 플랜지 폭(B)은 스템 높이(H)의 1.5배 내외로 하였다. βcr은 식 (5)로 정의된 한계 형상비이다.
Table 1–Table 3에서 kFEA는 ABAQUS 프로그램의 고유치해석에 의한 좌굴계수이다. kfc는 Wang et al.이 제안한 식 (4a) 및 식 (4b)로부터 산정한 것이며, λp와 λr은 식 (11a)와 식 (11b)에 kfc를 적용하여 산정한 것이다. Fnc는 식 (9)에서 fv = 0(또한 ∆ = 1.0)일 때 AASHTO LRFD 기준의 압축강도이며, Fu,FEA는 비선형해석에 의한 압축강도이다.
첫번째 좌굴모드가 one half sine-wave이고 이를 초기처짐으로 적용하였을 때 비선형해석으로부터 종국변형 형상 역시 one half wave 형태를 보였는데, 그 예를 Fig. 6(a)에 제시하였다. 한편, Table 1–Table 3에서 * 마크로 표시한 경우는 첫번째 좌굴모드가 two half wave를 보이는 최소 횡방향 보강재 간격(a)에 해당하는 것이다. 최소 a 값은 반복 해석으로부터 근사적으로 결정하였으며, 보강재 개수와 무관하게 β/βcr ≒ 1.4이었다. 비선형해석에서 이를 초기처짐으로 적용하였을 때 종국변형 형상 또한 two half wave 형태를 보였으며, Fig. 6(b)에 n = 1일 때의 예를 제시하였다. 참고로, β/βcr ≒ 1.4일 때 초기처짐의 크기는 a/400이 아닌 b/400이 적용된다.
4.2 결과 분석
보강재 개수별 Fu,FEA/Fyc 결과를 Fig. 7(a)에서 Fig. 7(c)에 도시하였다. Fig. 7에서 가로축 는 정규화한 세장비로서 다음 식으로 정의하였다.
| (13) |
식 (11b)에서 Fyr을 0.7Fyc로 설정하면
| (14) |
이 된다. Rb = 1.0, Rh = 1.0인 조건에서 AASHTO LRFD 기준에 의한 압축강도와 항복강도의 비(Fnc/Fyc)를 에 대해 정리하면 식 (10a)–식 (10c)로부터 다음과 같다.
• 조밀판: ≤ 1.0
| (15a) |
• 비조밀판: 1.0 < ≤ 1.992
| (15b) |
• 세장판: > 1.992
| (15c) |
먼저, β/βcr < 1.4일 때 1 ≤ n ≤ 3 경우 모두 종국 변형형상은 one half wave를 보였으며, Table 1–Table 3으로부터 Fu,FEA/Fnc 비의 최소값은 n = 2 및 n = 3의 일부 조밀판 또는 조밀에 가까운 비조밀판에서 0.99를 보인다. n이 증가할수록 Fu,FEA/Fnc 비가 조금 감소하는 경향을 보이는데, 추후 n ≥ 4에 대해 보완 검토가 필요하다고 판단된다. 단 이 값(0.99)은 인접 패널에 의한 ‘연속효과’를 고려하지 않은 것이므로 안전측의 압축강도임을 감안할 필요가 있다. 그 외의 경우는 모두 1.0 이상의 값을 보이며, 비조밀 및 세장판 영역에서는 판의 세장비가 증가할수록 안전측의 결과를 보인다. 따라서 β/βcr < 1.4일 때 Wang et al.이 제안한 식 (4a)와 식 (4b)는 합리적인 크기의 보강재를 결정하는데 적용 가능하다고 판단된다.
한편, 1 ≤ n ≤ 3 경우 모두 β/βcr ≒ 1.4에서 two half wave의 종국 변형형상을 보였다. Fu,FEA/Fnc 비는 비조밀판 영역에서 n = 1일 때 0.94–0.85, n = 2일 때 0.94–0.92, n = 3일 때 0.96–0.93의 범위를 보였으며, 세장판 영역에서는 n = 2일 때 0.95, n = 3일 때 1.19를 보였다. 따라서 β/βcr ≥ 1.4일 때 설계기준의 압축강도에 미치지 못하는 결과를 보일 수 있고, 이러한 경향은 n이 작을수록 두드러진다. Table 1과 Table 2에서 β ≒ 1.4βcr에 해당하는 횡방향 보강재 간격(a)은 판의 세장비에 따라 n = 1일 때 4,400 mm–4,500 mm, n = 2일 때 6,500 mm–7,300 mm이다. 이러한 간격은 실제 박스거더교에서 생길 수 있으므로 횡방향 보강재의 최대 간격에 대한 규정이 필요하다고 판단된다.
참고로 Table 1과 Table 2에 β/βcr ≒ 1.4(* 마크 표시)인 경우들에 대해 식 (1a)와 식 (1b)의 AASHTO 기준에 의한 k 값을 괄호 내에 제시하였다. 이로부터 식 (4a) 및 식 (4b)의 kfc가 AASHTO 기준의 k 값보다 같거나 작게 산출되었다. 따라서 AASHTO 기준의 k를 적용하는 것에 비해 kfc의 적용으로 인해 압축강도를 크게 평가하지는 않았다. 이로부터, 보강판에서 횡방향 보강재의 최대 간격은 AASHTO LRFD 기준의 식 (1a) 및 식 (1b) 또는 Wang et al.의 식 (4a) 및 식 (4b)의 적용 시 β/βcr < 1.4로 제한할 필요가 있다. 현재 AASHTO LRFD 기준에서는 식 (1a) 및 식 (1b)의 적용 시 횡방향 보강재의 최대 간격에 대한 언급은 없다.
5. 결 론
본 연구에서는 압축력을 받는 보강판에서 T-형 보강재의 제원을 합리적으로 결정하기 위해 Wang et al.[3]이 형상비를 고려하여 제안한 좌굴계수 식의 적용 시 AASHTO LRFD 기준의 압축강도가 타당하게 산정되는지 여부를 평가하기 위한 연구를 수행하였다. 종방향 보강재는 1~3개까지 고려하였으며 주요 변수로 형상비(β), 판의 폭-두께비 및 보강재의 휨강성을 고려하였다. 압축강도의 평가는 재료 및 기하비선형해석에 의하였으며, 본 연구의 주요 결론은 다음과 같다.
- (1) β < 1.4βcr일 때 FE 해석에 의한 좌굴모드 및 비선형해석에 의한 종국 변형은 one half wave를 보였다. 해석에 의한 압축강도(Fu,FEA)는 Wang et al.이 제안한 식 (4a)와 식 (4b)로부터 kfc를 산정하고 이로부터 AASHTO LRFD 기준의 한계세장비 λp와 λr을 계산한 후 식 (10a)–식 (10c)로 산정한 압축강도(Fnc)를 만족 또는 상회하는 것으로 나타났다.
- (2) 보강재 개수(n) 1~3개 경우 모두 β ≥ 1.4βcr일 때 좌굴모드 및 비선형해석의 종국 변형은 two half wave를 보였다. 이 때 비조밀판 및 세장판 영역에서 AASHTO LRFD 기준의 압축강도에 미치지 못하는 결과를 보였으며, 이러한 경향은 n이 작을수록 두드러졌다.
- (3) 한편 β = 1.4βcr에 해당하는 횡방향 보강재 간격은 보강재 개수가 2개 이하일 때 실제 박스거더교에서 생길 수 있어 횡보강재의 최대 간격에 대한 고려가 필요한 것으로 판단되었다. 이에 잠정적으로 횡방향 보강재의 최대 간격은 AASHTO LRFD 기준의 식 (1a) 및 식 (1b) 또는 Wang et al.의 식 (4a) 및 식 (4b) 적용 시 β < 1.4βcr로 제한할 필요가 있다.
본 연구에서는 강재를 HSB460 강재로 한정하고 비선형해석에 의한 해석적 연구를 수행하였는데, 향후 고강도강과 더불어 실험적 연구에 의한 검증이 필요하다.
Acknowledgments
이 논문은 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
References
- American Association of State Highway and Transportation Officials (2020) AASHTO LRFD Bridge Design Specifications (9th Ed.), USA.
- American Association of State Highway and Transportation Officials (2002) Standard Specifications for Highway Bridges (17th Ed.), USA.
-
Wang, L., Park, Y.M., Liu, Y., and Choi, B.H. (2021) Proposal of Buckling Coefficient Equation Considering Aspect Ratio of Compression Plates Stiffened with Tees, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.5, pp.275–283 (in Korean).
[https://doi.org/10.7781/kjoss.2021.33.5.275]

- Ministry of Land, Infrastructure and Transport (2017) Design Standard of Steel Structural Members (Load and Resistance Factored Design) (KDS 14 31 10: 2018), Korea (in Korean).
- Timoshenko, S.P., and Gere, J.M. (1961) Theory of Elastic Stability, McGraw-Hill, USA.
- Choi, B.-H. (2002) Design Requirements for Longitudinal Stiffeners for Horizontally Curved Box Girders, Ph.D. Dissertation, Auburn University, USA.
- Dassault Systèmes Simulia Corp. (2022) Abaqus Analysis User’s Manual, DSS, USA.
-
Chacón, R., Serrat, M., and Real E. (2012) The Influence of Structural Imperfections on the Resistance of Plate Girders to Patch Loading, Thin-Walled Structures, Elsevier, Vol.53, pp.15–25.
[https://doi.org/10.1016/j.tws.2011.12.003]

- European Committee for Standardization (2006) Eurocode 3: Design of Steel Structures, Part 1-5: Plated Structural Elements (EN 1993-1-5: 2006), Belgium.