정현파형 주름웨브 보를 적용한 합성보의 휨거동 및 설계

2.1 현행설계기준 분석

국내 건축물 강구조 설계기준 KDS 41 30 10^[11]에서는 강재앵커를 갖는 노출형 합성보의 휨강도와 전단강도 산정법을 다음과 같이 제시하고 있다.

판폭두께비(h_w/t_w)가 3.76$$ \sqrt{E/F_y}$$보다 작은 조밀웨브 단면의 휨강도는 소성응력분포 가정에 따라 소성모멘트로 산정하고, 3.76$$ \sqrt{E/F_y}$$보다 큰 단면의 휨강도는 항복한계상태에 대한 탄성응력을 중첩하여 항복모멘트로 산정한다. 압연 H형강을 적용한 노출형 합성보는 통상적으로 소성응력분포법을 적용하며, 정모멘트에 대한 휨강도는 식 (1)을 따른다. 식 (1)의 콘크리트 슬래브 압축력 C는 식 (2)와 같다. 만일 강종 또는 항복강도가 다른 판재로 구성된 조립 강재보를 사용하는 경우에는 식 (2)의 인장항복강도 F_yA_s는 강재보 각 부분에 대한 항복강도의 합으로 산정한다. 압축응력블럭 깊이 a는 식 (3)으로 산정할 수 있다.

Fig. 1.

Geometry and dimensional symbols for sinusoidal corrugated web beam

여기서, P_y는 강재보의 인장항복강도, d₁은 콘크리트 슬래브 내 압축력의 중심으로부터 강재 단면 윗면까지의 거리, d₂는 강재 단면 내 압축력 중심으로부터 강재 단면 윗면까지의 거리(강재 단면 내 압축력 부재 시 d₂ = 0), d₃는 P_y가 작용하는 강재 단면의 중심으로부터 강재 단면 윗면까지의 거리를 나타낸다.

여기서, f_ck는 콘크리트 압축강도, A_c는 유효폭 내 콘크리트 슬래브의 단면적, F_y는 강재보의 항복강도, A_s는 강재보의 단면적, ΣQ_n은 정모멘트가 최대가 되는 위치와 모멘트가 0이 되는 위치 사이 전단연결재의 공칭강도의 합, b_e는 콘크리트 슬래브의 유효폭을 나타낸다.

노출형 합성보의 전단강도는 안전측으로 KDS 41 30 10에 따라 강재보 웨브만의 전단강도로 산정한다^[11]. 그러나 KDS 41 30 10에는 파형웨브 보에 관련된 설계조항이 전무하므로, 파형웨브 보의 한계상태에 따른 휨 및 전단강도가 제시된 Eurocode 3(이하 EC3) Part 1-5의 Annex D에 따라 전단강도를 산정한다(식 (4) - 식 (6))^[12].

여기서, F_yw, h_w, t_w는 각각 파형웨브의 항복강도, 춤 및 두께이다.

식 (4)의 χ_c는 웨브의 좌굴을 고려한 강도저감계수로, 국부좌굴에 의한 저감계수 χ_c,l과 전체좌굴에 의한 저감계수 χ_c,g 중 작은 값을 사용한다. χ_c,l과 χ_c,g는 각각 식 (5)와 식 (6)을 따른다.

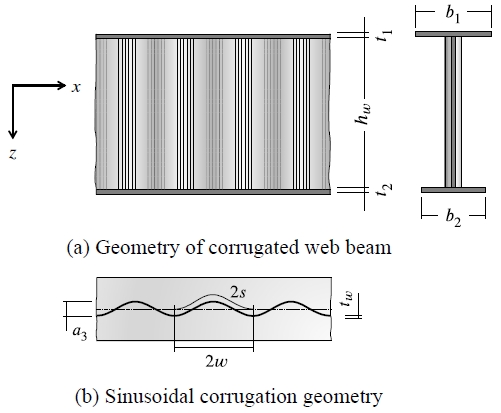
여기서, a₃, s, w는 파형웨브의 기하학적 형상에 대한 변수로 각각 웨브 진폭, 반파장의 전개길이, 반파장의 길이를 나타내며(Fig. 1(b) 참고), E, υ는 강재의 탄성계수 및 포아송비, I_z는 보의 약축에 대한 파형웨브 반파장의 단면2차모멘트를 의미한다.

2.2 파형웨브 합성보 설계법 제안

파형웨브 합성보의 전단강도는 순철골 파형웨브 보의 전단강도(EC3 Part 1-5의 Annex D)에 따라 산정하면 될 것이나, 휨강도와 관련해서 고려할 사항이 두 가지 있다.

첫째는 소성응력분포법 적용 가능 여부이다. 노출형 합성보의 휨강도를 비교적 계산하기 편한 소성응력분포법에 따라 산정하기 위해서는 앞서 언급한 웨브의 조밀단면 조건($$ h_w/t_w\le 3.76\sqrt{E/F_y}$$)을 만족하여야 한다. 파형웨브 보의 경우에는 국내 자동생산 규격 중 가장 낙관적인 조건(웨브 최소 춤 333 mm, 최대 두께 3 mm)을 적용하더라도 이 폭두께비를 만족하지 못한다. 그러나 이 웨브 조밀단면 조건은 일반 H형강에서 웨브의 좌굴이 선행될 경우 강재보의 전소성모멘트 강도 발현이 어려워지기 때문에 마련된 것에 지나지 않는다. 웨브의 면외좌굴 저항성능이 H형강보다 높은 파형웨브 보가 웨브의 국부좌굴 및 전체좌굴에 대한 전단강도를 보장할 수 있다면, 웨브 조밀단면 규정을 만족하지 않더라도 파형웨브 합성보는 소성모멘트를 충분히 발휘할 수 있으리라 판단된다.

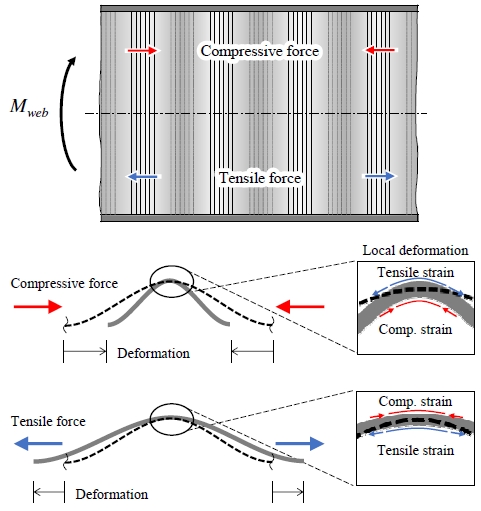
두 번째는 파형웨브의 아코디언 효과에 의한 축강도 저하이다. Fig. 2에 도시한 바와 같이 주름의 직각방향으로 인장 또는 압축을 받을 때 신축의 발생이 쉬우므로 휨 저항이 낮다. 따라서 파형웨브의 휨설계에서는 파형웨브의 휨강도 기여를 제외하는 것이 일반적이다.

Fig. 2.

Accordion effect in corrugated web subjected to horizontal axial forces

이 연구에서는 위 두 가지 사항을 고려하여, 파형웨브 합성보의 강도를 소성응력분포법을 통해 산정할 경우, 식 (1)과 식 (2)에서 적용되는 강재 단면의 인장강도에서 파형웨브를 제외하고 산정하는 방법을 제안한다(식 (7) 참고).

여기서 F_yft와 A_ft는 상부플랜지의 항복강도와 단면적, F_yfb와 A_fb는 하부플랜지의 항복강도와 단면적이다.

파형웨브 합성보의 사용성 평가를 위해서는 휨강성에 대한 정의가 필요하다. 강구조물의 휨재는 강도뿐만 아니라 처짐에 의해 지배되는 경우도 많으므로 올바른 유효탄성강성 (EI)_eff을 산정하여 사용하중 하에서 발생하는 처짐을 예측하는 것이 중요하다. 이 연구에서는 파형웨브 합성보의 유효탄성강성을 일반적인 노출형 합성보에서의 비균열단면강성으로 적용하되, 휨강도 산정과 동일하게 파형웨브의 기여를 제외하였다. 식 (8)과 같이 환산단면을 통한 탄성중립축을 산정하고, 식 (9)를 통해 파형웨브 합성보의 처짐 산정을 위한 휨강성을 계산한다.

여기서, y_ENA는 탄성중립축의 위치, y와 $$ \stackrel{-}{y}$$는 각각 면적이 dA인 요소의 도심으로부터 콘크리트 슬래브 윗면 또는 탄성중립축까지의 거리, A_c와 A_sf는 유효폭 내의 콘크리트 슬래브 단면적과 파형웨브 보의 플랜지 면적, E_c와 E_sf는 각각 콘크리트와 파형웨브 보 플랜지의 탄성계수, n = E_sf/E_c를 나타낸다.

이 연구에서는 파형웨브 합성보의 합성률을 변수로 한 실물대 휨실험으로 그 성능을 확인하고, 앞서 제시한 소성응력분포 가정에 따른 휨강도 산정과 유효탄성강성의 적합성을 검증하였다.

3.1 실험체 설계 및 제작

실험체의 휨강도는 2.2절에서 기술한 바와 같이 파형웨브를 제외한 소성응력분포법에 따라 검토하였으며, 전단강도는 EC3 Part 1-5의 Annex D에 따라 검토하여 소성휨강도에 도달하기 전에 웨브 좌굴이 발생하지 않음을 확인하였다.

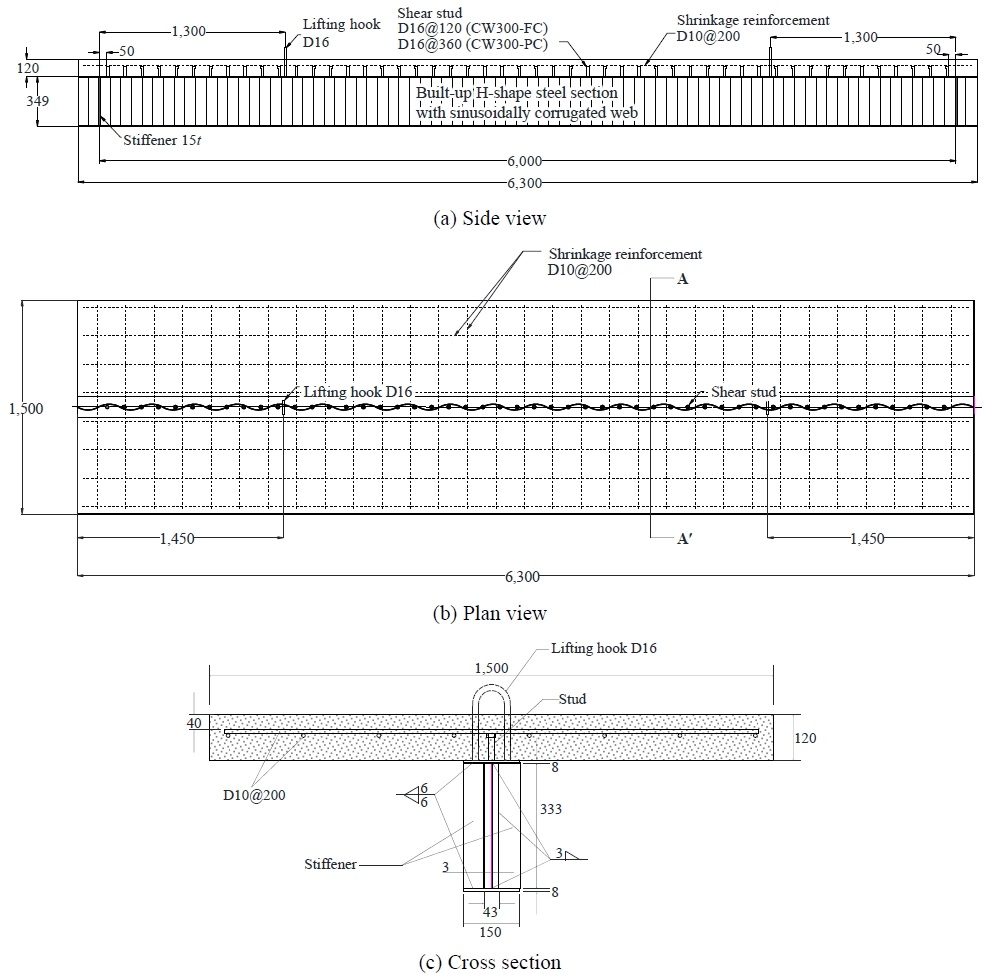
Table 1과 Fig. 3는 실험체 상세를 보여준다. 실험체의 파형웨브에는 SS275, 플랜지에는 SM355 강을 적용하여 조립단면을 구성하였다. 두께 3 mm인 파형웨브의 춤은 333 mm를 선정하였는데, 이는 H형강 평웨브를 기준으로 하는 폭두께비가 111인 비조밀단면에 해당한다. 모든 실험체에서 파형웨브 진폭 a₃는 43 mm, 한 파장의 길이 2w는 155 mm, 파장의 전개길이 2s는 178 mm이다(Fig. 1 참조). 파형웨브와 플랜지 간 용접은 한 패스의 일면 모살용접으로 이루어졌으며, 용접사이즈는 3 mm이다. 실험체의 지점 간 거리는 6 m이다.

Table 1.

Test specimens

Fig. 3.

Details of test specimens

콘크리트 슬래브의 폭은 유효폭 기준에 따라 보 경간 6 m의 1/4인 1.5 m로 하였다. 슬래브의 두께는 120 mm로 하였고, SD400 ϕ10 철근을 슬래브 길이 및 직각방향으로 간격 200 mm 단배근하였다. 높이 70 mm, 직경 ϕ16인 전단스터드를 1열 배열함으로써 콘크리트 슬래브와 파형웨브 보 사이에서 수평전단력을 전달하도록 하였다. 완전합성보 실험체인 CW333-FC의 스터드 설치 간격은 120 mm이고, 부분합성보 실험체인 CW333-PC의 스터드 간격은 360 mm이다. 합성률(C.R.)은 식 (10)과 같이 산정하였으며, 스터드 공칭강도 및 콘크리트와 강재의 재료계측강도로 계산하였을 때 CW333-PC 실험체의 합성률은 약 56 % 수준이다.

여기서, ΣQ_n은 정모멘트가 최대가 되는 위치와 모멘트가 0이 되는 위치 사이 전단스터드의 공칭강도의 합이다.

전단스터드의 개당 공칭강도 Q_n은 식 (11)과 같다^[11].

여기서 A_sa는 전단스터드의 단면적, R_g와 R_p는 각각 데크플레이트의 골방향과 스터드 배치에 의한 강도저감계수이다. 이 연구에서는 골데크플레이트를 사용하지 않았으므로 R_g와 R_p에 따라 각각 1.0과 0.75를 적용하였으며^[11], 스터드의 공칭인장강도 F_u는 400 MPa를 적용하였다.

Table 2는 실험체에 사용된 강판의 인장시험 평균 결과를 정리한 것이다. 웨브에 사용된 3 mm 두께의 SS275 판재와 플랜지에 사용된 8 mm 두께의 SM355 판재에서 인장시편을 각각 3개씩 절취하여 시험 후 평균을 냈다. 세 개의 콘크리트 공시체에 압축실험을 수행한 결과, 평균 압축강도는 41.6 MPa로 나타났다. 이 결괏값은 실험결과의 분석과 해석연구에 재료물성으로 적용하였다.

Table 2.

Tensile coupon test results

3.2 실험 세팅 및 가력방법

Fig. 4는 실험 셋업 전경을 보여준다. 모든 실험은 4점가력으로 진행되었다. Fig. 4(a)에는 실험체의 기하학적 변수(Table 1 참고), 횡지지 위치, 수직처짐 및 단부회전각 측정을 위한 수직변위계(LVDT1 - LVDT2) 위치를 표시하였다. 변형률 게이지는 실험체 중앙단면의 상하부 플랜지의 하부와 파형웨브 골에 부착하였다. 실험체 지점부에는 집중하중에 대한 보강을 위해 전높이 스티프너를 적용하였다. 반면, 가력부는 파형웨브 보에 직접적으로 집중하중이 작용하지 않고 콘크리트 슬래브를 통해 하중이 전달되기 때문에 별도의 스티프너를 적용하지 않았다. 연속된 슬래브의 다이어프램 효과를 모사하기 위해 Fig. 4(c)와 같이 지점부를 구속시켰다.

Fig. 4.

Overall view of test setup and 4-point loading condition

4.1 휨성능 및 거동 평가

Fig. 5와 Fig. 6는 각각 CW333-FC와 CW333-PC 실험체의 변형 및 파괴모드를 보여준다. 두 실험체 모두 파형웨브 보에서는 전단에 의한 파형웨브 좌굴을 포함하여 어떠한 파괴도 관측되지 않았다. 완전합성보 실험체인 CW333-FC는 가력구간에서 콘크리트 압괴가 진행되며 실험이 종료되었다(Fig. 5(b)). CW333-PC는 부분합성보의 전형적인 거동인 강재보와 콘크리트 슬래브의 분리가 육안으로 확인되었으며(Fig. 6(c)), 이로 인해 콘크리트 압괴에 도달하지 않고 슬래브 하부에 인장으로 의한 균열만 발생한 것을 Fig. 6(b)를 통해 볼 수 있다.

Fig. 5.

Failure mode of CW333-FC

Fig. 6.

Failure mode of CW333-PC

Table 3는 앞서 언급한 재료실험에서 계측된 소재강도의 평균값에 기반하여 산정한 소성모멘트(M_p,m) 및 실험체 최대모멘트(M_u), 최대모멘트 도달 시점에서의 실험체 중앙부 처짐(δ_u) 및 단부회전각(θ_u)을 보여준다. 소성모멘트에 최대모멘트를 비교하면 CW333-FC는 130 %, CW333-PC는 142 %로, 두 실험체 모두 소성응력분포법으로 산정한 강도를 훨씬 상회하는 휨강도를 발현하였다. Table 3의 D_e와 D_p는 계측된 재료물성에 기반하여 산정한 탄성중립축 및 소성중립축의 위치이다.

Table 3.

Summary of test results

Fig. 7은 각 실험체의 모멘트-단부회전각(M-θ) 관계를 나타낸 것이다. Fig. 7에서 보듯이 두 실험체 모두 항복 이후 최대강도에 도달하기까지 충분한 연성능력을 가지며, 최대강도는 제안방법에 따른 휨강도를 상회하는 것을 알 수 있다.

Fig. 7.

Moment-rotation relationship of test specimens

또한, 두 실험체의 단면이 동일하므로 부분합성 실험체(CW333-PC)가 부담할 수 있는 수평전단력 수준의 하중까지는 완전합성 실험체(CW333-FC)와 동일한 강성이 나타났으며, 비균열단면강성으로 산정한 이론적인 휨강성(식 (9) 참조)과 거의 일치함을 알 수 있다. 부분합성 실험체의 전단스터드가 분담할 수 있는 수평전단력을 초과하는 하중인 약 220 kN·m - 230 kN·m에 도달했을 때, 부분합성 실험체의 파형웨브 보와 콘크리트 슬래브 간에 슬립이 발생하여 강성이 저하되는 것으로 파악된다.

실험에서 관측된 파괴모드와 모멘트-단부회전각 관계를 비추어볼 때, 파형웨브가 조밀단면 기준을 만족하지 않더라도 2.2절에서 제시한 소성응력분포법을 통해 파형웨브 합성보의 휨강도와 휨강성을 산정해도 무방하다고 판단된다.

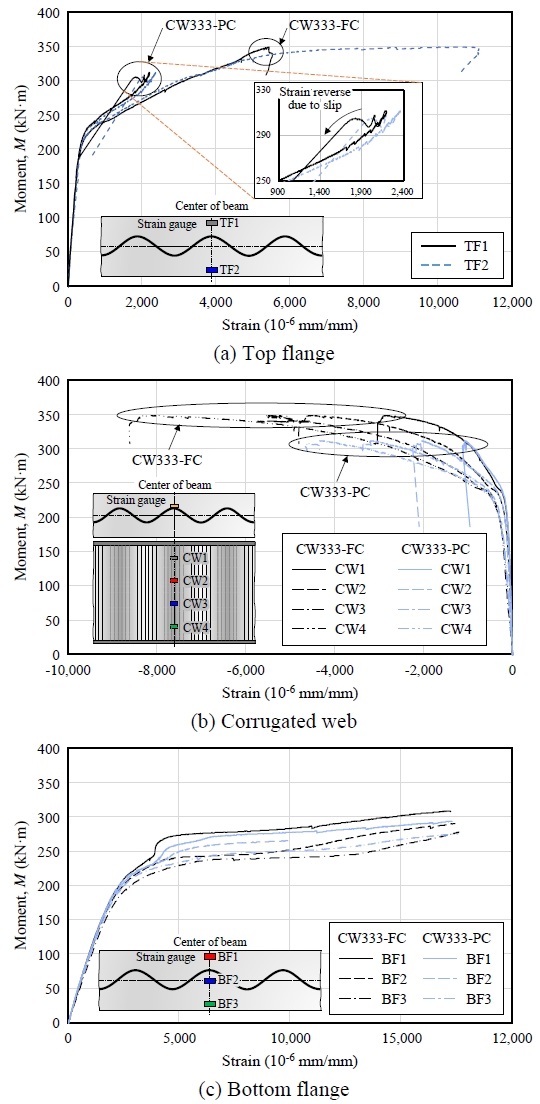
Fig. 8은 실험체 중앙의 플랜지와 파형웨브 골 외측에서 계측한 변형률이다. 두 실험체 모두 가력하는 동안 상·하부플랜지에서 인장변형만이 발생하여 슬래브 내에 중립축이 존재함을 알 수 있다. 부분합성인 CW333-PC의 상부플랜지에서는 하중 증가에 따른 변형률의 증가를 보이다가 최대하중 도달 이후에 변형률이 역전하는 것을 볼 수 있다(Fig. 8(a)). 이는 전단스터드와 콘크리트 슬래브 간 부착파괴가 발생하여 상부플랜지로 더 이상의 수평전단력 전달이 불가능해졌기 때문이다. Fig. 8(b)에서 파형웨브의 골 외측에서는 압축변형이 발생한 것으로 나타났다. 이는 Fig. 2에서 보듯 인장력을 받은 파형웨브 골이 펴지며 골의 곡률이 감소하여 골의 외측에 압축변형이 발생한 것으로, 아코디언 효과를 아주 분명하게 보여주는 사례이다. Fig. 8(c)에 나타낸 하부플랜지의 변형률 데이터의 계측은 과도한 인장변형 발생으로 인해 실험종료 전에 중단되었다. 같은 하중 하에서 하부플랜지의 변형률은 골 내부(BF2, BF3)보다 외부(BF1)에서 더 작게 나타났다. 이는 파형웨브의 국부적인 변형(외측: 압축변형, 내측: 인장변형)이 플랜지 변형에도 영향을 미친 것으로 판단된다.

Fig. 8.

Strain response measured at mid-span of test specimens

4.2 변형률적합법과의 비교

이 절에서는 변형률적합법을 통해 파형웨브 합성보의 휨성능을 수치해석적으로 파악하고자 하였다. 단, 부분합성보의 강-콘크리트 단면 분리거동을 해석에 반영하기 어려워 완전합성(CW333-FC) 실험체와 결과만 비교하였다.

4.2.1 해석 알고리즘 및 재료모델

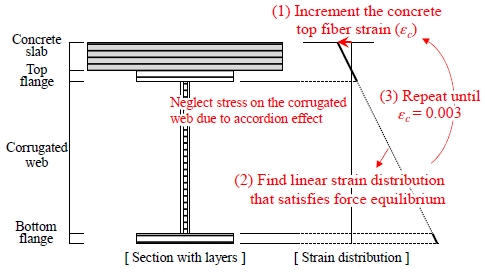
MATLAB 프로그램을 이용하여 합성보 단면에 대한 변형률적합 해석을 수행하였다. Fig. 9에 도시한 바와 같이 합성보의 춤 방향으로 두께 1 mm의 레이어를 적용하였고, 단면의 변형률은 선형분포를 가정하였다.

Fig. 9.

Analysis method for strain compatibility method

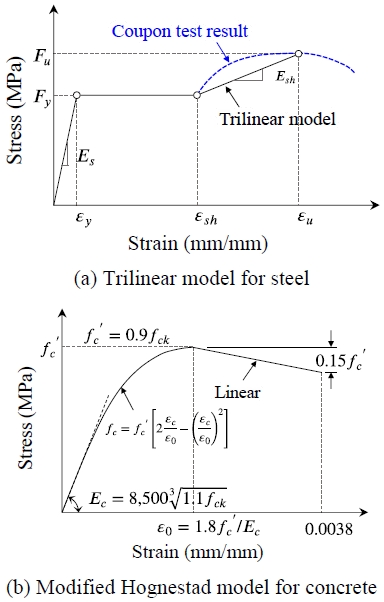
파형웨브 단면 내 응력은 아코디언 효과를 감안하여 무시하였다. 플랜지의 각 레이어별 응력을 계산하기 위해 Fig. 10(a)와 같이 삼선형곡선 모델을 적용하였다. 플랜지의 항복강도 F_y, 인장강도 F_u, 탄성계수 E_s는 Table 2에 나타낸 SM355 시편 물성을 적용하였다. 항복변형률 ε_y와 변형경화계수 E_sh는 이 물성들에서 역으로 산출하였다. 변형경화시점의 변형률 ε_sh와 극한변형률 ε_u는 각각 1 %, 10 %를 적용하였다.

Fig. 10.

Material models for strain compatibility method

콘크리트 슬래브 단면의 인장응력은 0으로 하였고, 압축응력-변형률 관계에는 수정된 Hognestad 모델^[13]을 적용하였다(Fig. 10(b) 참고). 압축강도 f_ck는 3.1절에서 언급한 공시체 압축강도 평균값을 적용하였고, 탄성계수 E_c는 KDS 14 20 10^[14]에 따라 산정하였다.

해석은 콘크리트 슬래브 최상단 레이어의 압축변형률을 증가시키며 수행하였다. 특정 최상단 압축변형률에 대해 인장력과 압축력의 평형을 만족하는 선형 변형률 분포를 결정하였고, 이를 통해 각 레이어의 변형률과 응력으로부터 중립축의 위치와 휨모멘트를 산정하였다. 이 과정은 슬래브 최상단부의 압축변형률이 0.003에 도달할 때까지 반복되었다.

4.2.2 CW333-FC 실험결과와의 비교

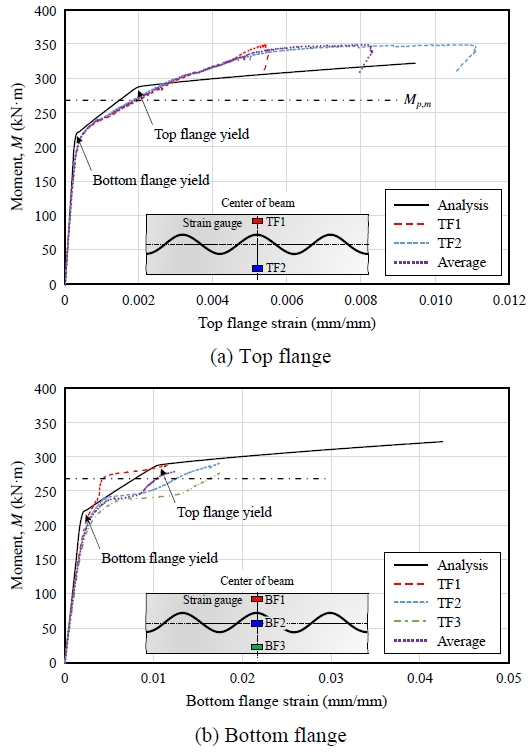
Fig. 11은 변형률적합법 및 완전합성보(CW333-FC)의 실험결과에서 얻은 모멘트와 플랜지의 인장변형률 관계를 비교한 것이다. Fig. 11(a)에서 보듯이 상부플랜지의 실험 및 해석에 따른 모멘트-변형률 관계가 해석에 도출한 상부플랜지 항복시점(약 280 kN·m)까지는 상당히 잘 부합하는 것을 확인할 수 있다. 280 kN·m 이후부터는 해석결과가 강도를 낮게 예측하였다. 이는 플랜지의 삼선형 재료모델에서 변형경화 영역의 응력분포를 실제 응력분포보다 낮은 직선 형태로 가정했기 때문으로 판단된다. 하부플랜지의 변형률 데이터의 계측은 과도한 인장변형 발생으로 인해 실험종료 전에 중단되었다. 그럼에도 불구하고 Fig. 11(b)는 계측이 중단된 시점까지 실험결과와 해석결과가 잘 부합함을 보여준다. 또한, 플랜지 양 측면에서 계측된 데이터의 평균값(Fig. 11의 average)은 해석결과에 더욱 유사하게 나타났다.

Fig. 11.

Comparison of moment-strain relationship between analysis and test of CW333-FC

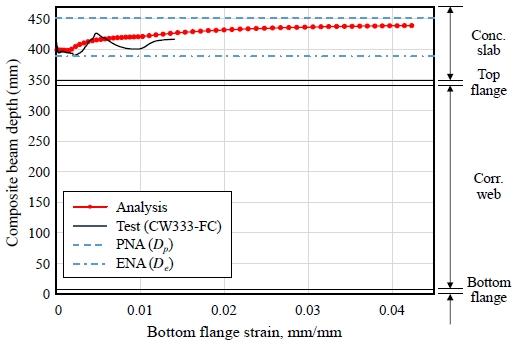
Fig. 12는 변형률적합 해석과 CW333-FC 실험을 통해 얻은 중립축의 위치변화 및 식 (8)에 따라 산정한 탄성중립축(ENA)의 위치와 소성중립축(PNA)을 함께 나타낸 것이다. 실험에서 얻은 중립축 위치는 계측 변형률로부터 상·하부플랜지 각각의 평균변형률을 산정하고, 변형률 선형분포 가정에 따라 변형률이 0이 되는 지점을 계산한 것이다. 다만, 실험종료 이전 하부플랜지의 변형률 계측이 조기에 중단되어 중립축 위치변화 경향 또한 끝까지 얻을 수 없었다.

Fig. 12.

Comparison of neutral axis between analysis and test of CW333-FC

해석결과를 살펴보면, 초기에는 이론적인 탄성중립축(일점 쇄선) 근방에 중립축이 위치하다가 하중이 증가함에 따라 (또는 하부플랜지의 인장변형률이 증가함에 따라) 이론적인 소성중립축(쇄선)에 가까워지는 것을 확인할 수 있다. 다소 변동성이 있으나 실험에서 계측된 중립축 또한 해석결과와 같은 경향을 나타내고 있다.

실험을 통해 얻은 모멘트-변형률 관계와 중립축의 위치변화 경향성이 파형웨브를 제외한 단면해석결과와 잘 부합함을 비추어 볼 때, 2.2절에서 제시한 파형웨브 합성보의 휨강도 및 휨강성 산정법은 타당하다고 판단된다.