프리스트레스트 CFT 보강 강박스거더의 크리프로 인한 프리스트레스 손실 평가
Copyright © 2022 by Korean Society of Steel Construction
초록
이 연구에서는 프리스트레스트 CFT로 보강된 강박스거더의 프리스트레스 손실 평가방법을 제안하기 위해 AEMM을 기반으로 CFT의 장기거동해석을 수행하였다. 이전 연구자들의 실험결과를 기반으로 CFT의 건조 크리프 특성을 분석하여 CFT의 크리프 계수 수정모델을 제안하였으며, 나아가 기존의 설계기준모델들과 비교를 통해 수정모델의 타당성을 검증하였다. 이후 수정모델을 적용한 프리스트레스 손실 평가방법의 예측 성능을 평가하기 위해 프리스트레스트 CFT로 보강된 강박스거더 목업 시험체를 제작하여 약 90일간 장기변형을 측정하였으며, 결과적으로 예측값은 목업 시험체의 장기 계측 데이터와 잘 일치하는 것으로 확인되었다.
Abstract
In this study, a long-term behavior analysis of the CFT was conducted based on AEMM to establish the prestress loss evaluation method of steel box girder reinforced with prestressed CFT. The drying creep characteristic of CFT was analyzed by referring to the experimental result of previous researchers, and a modified creep coefficient model of CFT was proposed. Furthermore, the modified model was verified by comparing it with the existing design model. After that, in order to confirm the predictive performance of the prestress loss evaluation method using modified model, an steel box girder reinforced with prestressed CFT mock-up specimen was manufactured and long-term deformation was measured for about 90 days. As a result, it was confirmed that the predicted values shows good agreement with the long-term measurement data of mock-up specimens.
Keywords:
Prestressed CFT, Steel box girder, Prestress losses, Drying creep, Age-adjusted effective modulus method키워드:
프리스트레스트 CFT, 강박스거더, 프리스트레스 손실, 건조 크리프, 재령 보정 유효탄성계수법1. 서 론
합성교량의 연속교는 지점부의 부모멘트로 인해 교량 상부 바닥판에 인장응력으로 인한 균열이 발생될 수 있으며, 이로 인해 교량 단면의 강성이 감소하는 문제가 발생할 수 있다. 따라서 교량을 설계할 때 지점부의 단면을 보강하기 위해 변단면을 적용하는 등의 방법을 사용하나, 이럴 경우 합성 교량의 경제성 및 구조 효율성이 감소하는 단점을 갖는다. 이전 연구자들은 연속교의 지점부를 보강하면서도 구조적 효율성을 도모하기 위한 다양한 연구를 수행해왔으며[1]-[5] 대표적인 방법으로는 부모멘트부 교량 하부에 PS강재를 이용하여 프리스트레스를 도입하거나[6] 콘크리트를 타설하는 등의 공법이 있다. 최근에는 경제성뿐만 아니라 구조적으로도 뛰어난 성능을 갖는 CFT(concrete filled steel tube) 부재를 활용한 합성 교량의 시공이 증가하고 있다. CFT는 각형 또는 원형 강관에 콘크리트가 충전된 합성 부재로 내부 콘크리트는 강관의 구속으로 인해 강도가 증진되는 효과를 얻으며 강관은 내부 콘크리트에 의해 국부좌굴이 방지되는 효과를 얻을 수 있다[7]. 또한 콘크리트 외부를 둘러싼 강관으로 인해 외기와 접촉이 차단되어 건조 수축 및 건조 크리프로 인한 변형이 매우 미소하기[8] 때문에 장기적인 변형 측면에 있어 일반 콘크리트 부재보다 뛰어난 구조성능을 발휘한다.
이러한 이유로 CFT 부재를 활용하여 강박스거더 하부에 프리스트레스를 도입함으로써 부모멘트부의 단면을 보강하는 공법이 제안되었다. 그러나 CFT 부재는 건조에 의한 변형에 대해서는 뛰어난 성능을 가지지만 기본 크리프에 의한 변형은 일반 콘크리트 부재와 동일하게 발생하기 때문에 결과적으로 시간이 지남에 따라 강박스거더에 도입된 프리스트레스의 손실을 유발할 수 있다[9],[10]. 따라서 CFT 부재의 장기거동 특성으로 인한 프리스트레스 손실을 정확히 예측하여 설계와 시공에 반영하는 것이 중요하다.
콘크리트의 크리프 및 수축에 관한 연구[11]-[14]와 크리프 및 수축 등으로 인해 프리스트레스트 콘크리트 교량에 발생하는 손실에 관한 연구[15]-[17]는 다양하게 수행되어왔으며, fib model code 2010[18], ACI 209[19],[20] 등의 설계기준은 프리스트레스 교량에서 발생하는 콘크리트의 장기변형을 예측하기 위한 모델식을 제안해 왔으나 아직까지도 CFT 부재를 사용한 프리스트레스 구조물의 장기거동에 대한 연구는 매우 미흡한 실정이다.
따라서 이 연구에서는 선행연구의 CFT 크리프 실험결과와 fib model code 2010[18]의 콘크리트 크리프 계수 모델을 기반으로 CFT 크리프 계수 수정모델을 제안하였으며, 수정모델의 예측 성능을 평가하기 위하여 기존 설계기준식들과의 비교를 수행하였다. 이후 재령 보정 유효탄성계수법(AEMM, age-adjusted effective modulus method)[21]을 기반으로 강박스 교량의 장기거동해석을 수행하였으며, 실제 강박스 목업 시험체의 장기변형 데이터와 해석 데이터를 비교하여 수정모델을 적용한 프리스트레스 손실 평가방법의 타당성을 검증하고자 하였다.
2. 프리스트레스트 CFT 보강 강박스거더 공법 및 제작 단계별 프리스트레스 손실 특성
2.1 공법개요
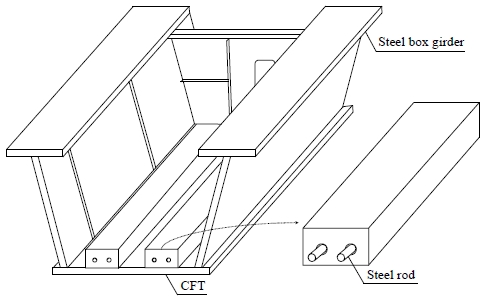
프리스트레스트 CFT 보강 강박스거더 공법은 Fig. 1과 같이 강박스거더 하부에 CFT 부재를 이용하여 프리스트레스를 도입함으로써 지점부의 단면을 보강시키는 공법이다. 해당 공법은 CFT 부재의 제작부터 프리스트레스 도입까지 전 과정이 공장에서 진행되기 때문에 현장 타설 작업을 배제할 수 있으며, 강박스거더 내 균일한 프리스트레스를 도입할 수 있을 뿐만 아니라 강박스 대비 강재량 절감 효과까지 발휘할 수 있어 우수한 시공성 및 경제성을 얻을 수 있다.
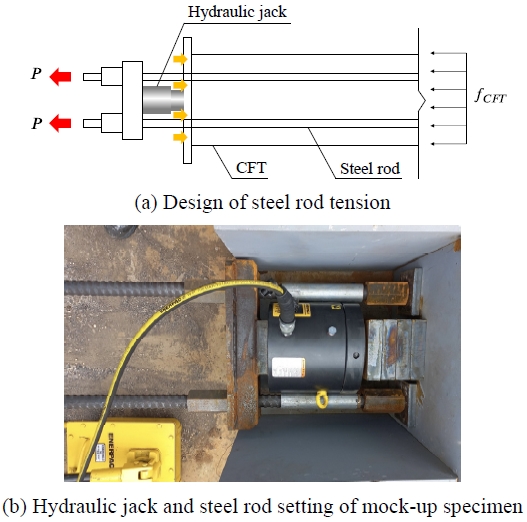
프리스트레스 도입을 위한 CFT 부재는 강박스 하부플랜지와 원활한 부착을 위해 직사각형으로 설계되었으며, CFT의 중간 높이에는 인장력을 도입하기 위해 임시로 강봉을 삽입하기 위한 두 개의 구멍이 뚫려있는 형태로 강박스거더 내부에는 부벽을 사이에 두고 총 4개의 CFT 부재가 부착된다. Fig. 2는 CFT에 압축력을 도입하기 위해 유압잭을 이용하여 강봉을 인장하는 과정으로 도입 순서는 다음과 같다.
- (1) 유압잭을 이용하여 4개의 CFT의 강봉을 차례로 긴장시킨 후 너트를 조여 반력판과 밀착시킨다.
- (2) 반력판과 부벽, CFT 하면과 마감판을 강박스에 용접한 후 강봉과 유압잭, 너트를 모두 제거한다.
(2)에서 강봉 및 유압잭 등이 제거된 이후부터 강박스거더 하부에는 CFT 부재의 복원력으로 인한 프리스트레스가 도입된다[22].
2.2 제작 단계별 프리스트레스 손실특성
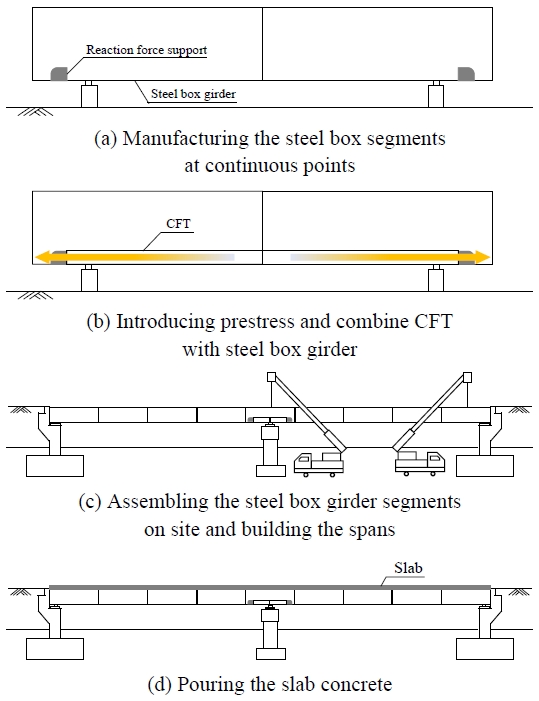
Fig. 3는 프리스트레스트 CFT 보강 강박스거더 공법의 시공단계를 나타낸다. 시공단계는 총 4단계로 구성되며, 시공 위치에 따라 공장 제작 단계와 현장 제작 단계로 나뉜다. 공장 제작 단계는 강박스 제작 단계 및 프리스트레스 도입 단계로 구성되며, 현장 제작 단계는 강박스거더의 현장 조립 및 경간 가설 단계와 콘크리트 슬래브 타설 단계로 구성된다.
시공단계별로 강박스거더에 추가적으로 도입되는 하중에 의해 발생하는 프리스트레스의 손실은 4단계로 분류할 수 있다.
- (1) 강박스 하부에 프리스트레스 도입 시 발생하는 손실(1차 프리스트레스 손실)
- (2) 교각 위 강박스거더 가설 시 강박스거더의 자중으로 인해 발생하는 손실(2차 프리스트레스 손실)
- (3) 슬래브의 하중에 의해 발생하는 손실(3차 프리스트레스 손실)
- (4) 차량 활하중에 의해 발생하는 손실(4차 프리스트레스 손실)
일반적으로 강박스거더에는 프리스트레스 도입 시 축력만 작용하나 CFT와 강박스의 하부플랜지가 합성된 이후에는 강박스거더가 콘크리트의 크리프 변형을 구속함으로써 축력뿐만 아니라 휨모멘트가 함께 발생하기 때문에 장기거동해석 시 축력과 휨모멘트를 동시에 고려해야 한다. 또한, 프리스트레스 손실이 1차에서 4차까지 발생하는 동안 손실량은 중첩적으로 증가하여 교량의 장기적인 구조성능에 영향을 미칠 수 있기 때문에 각 시공단계에 따라 정확한 프리스트레스 손실량을 예측하여 설계에 반영하는 것이 중요하다. 따라서 이 연구에서는 CFT의 구조적 특성을 고려할 수 있도록 CFT 장기거동 예측모델을 제안하여 최종적으로 프리스트레스트 CFT로 보강한 강박스거더에서 발생하는 프리스트레스 손실을 평가하기 위한 방법을 제안하고자 한다.
3. CFT 장기거통 특성에 따른 크리프 예측모델 적용 방안
3.1 CFT의 크리프
크리프란 콘크리트 구조물에 하중이 일정하게 가해질 경우 시간이 지남에 따라 변형이 증가하는 현상으로, 크리프 변형의 정도를 판단하기 위한 지표로 식 (1)과 같이 탄성 변형률과 크리프 변형률의 비인 크리프 계수를 사용한다.
| (1) |
일반적으로 크리프는 콘크리트와 외기의 접촉 유무에 따라 기본 크리프와 건조 크리프로 분류할 수 있는데, 건조한 환경에 놓인 콘크리트일수록 기본 크리프 이외에 건조 크리프가 함께 발생하여 더 큰 변형이 발생한다[23]. 그러나 CFT의 경우 강관에 의해 내부 콘크리트가 외기와의 접촉이 차단되어 건조 크리프로 인한 변형은 일반 콘크리트 부재에 비해 매우 미소하게 발생하기 때문에[8] 일반 콘크리트에 비해 장기적인 크리프 변형에 있어서 유리한 구조적 성능을 갖는다.
3.2 기존의 크리프 계수 예측모델
fib model code 2010[18] 모델은 시간 t일 때의 콘크리트 크리프 계수 ϕ(t,t′)를 계산하기 위해 식 (2)와 같이 개념 크리프 계수 ϕ0와 시간 함수 β(t,t′)의 곱으로 표현되며, 여기서 개념 크리프 계수는 콘크리트 재령 28일을 기준으로 재령에 따른 강도 변화를 시간의 함수로 나타낸 값이다.
| (2) |
- 여기서, t′: 하중 가압 시 재령(일).
ACI 209[19],[20] 모델은 식 (3)과 같이 극한 크리프 계수 ϕ′와 시간함수의 곱으로 표현되며, 극한 크리프 계수는 양생조건, 습도, 부재 치수, 슬럼프 등을 고려하도록 하는 보정계수가 도입되어 계산된다.
| (3) |
기존의 설계기준들은 콘크리트의 장기거동실험 데이터를 기반으로 유도된 경험식으로 기존의 설계기준을 보정 없이 CFT 부재의 장기거동해석에 적용할 경우 실제 구조물에 발생하는 프리스트레스 손실량과 예측값의 차이가 상당하게 발생할 수 있으며, 이로 인해 CFT 부재를 이용한 구조물에 예기치 못한 문제를 초래할 수 있다[24].
3.3 CFT의 장기거동 특성 분석
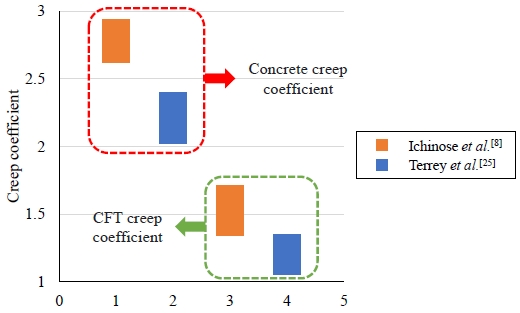
Fig. 4는 이전 연구자들에 의해 수행된 CFT 부재의 건조 크리프 특성에 관한 실험적인 연구결과 데이터로[8],[25] 같은 조건 하에서 일반 콘크리트 시험체와 CFT 시험체의 크리프 변형을 비교하였다. 일반 콘크리트 시험체의 평균 크리프 계수는 각각 2.23, 2.78로 나타났으며, CFT 시험체의 평균 크리프 계수는 각각 1.20, 1.53으로 나타났다. 일반 콘크리트 시험체의 크리프 계수 대비 CFT 시험체의 크리프 계수 감소율은 약 53.9 %, 54.9 % 정도로 두 실험 모두 일반 콘크리트에 비해 CFT의 크리프 계수가 절반가량 작게 나타났다. 이를 통해 CFT 시험체의 경우 내부 콘크리트를 둘러싼 강관으로 인해 외기와의 접촉이 차단되는 구조적 특성에 의해 건조 크리프로 인한 변형은 매우 미소하게 발생하며, CFT 시험체의 평균 크리프 계수 감소율이 약 54 % 정도임을 고려했을 때 건조 크리프는 총 크리프의 절반 수준으로 발생함을 알 수 있다. 여기서 총 크리프는 기본 크리프와 건조 크리프의 합을 의미한다.
3.4 CFT의 크리프 계수 예측 수정모델 제안 및 기존 설계식과의 비교
이 연구에서는 프리스트레스트 CFT 보강 강박스거더의 정확한 장기거동해석을 위해 식 (4)와 같이 크리프 계수 수정모델을 적용하였다. CFT 크리프 계수 수정모델은 fib model code 2010[18] 모델의 콘크리트 크리프 계수식을 기반으로 건조 크리프 보정계수 α를 도입하여 수정되었으며, 여기서 α는 선행연구의 실험결과에[8],[25] 기반하여 0.46을 적용하였다.
| (4) |
- 여기서, ϕCFT: CFT의 크리프 계수,
- α: 건조 크리프 보정계수(α = 0.46),
- ϕt: 콘크리트의 총 크리프 계수.
제안한 CFT 크리프 계수 수정모델의 타당성을 확인하기 위해 Terrey et al.[25]의 CFT 크리프 시험 데이터를 기반으로 기존 설계모델들과 장기거동 예측 성능을 비교하였다. 실험은 약 145일간 수행되었으며, 실험조건은 Table 1과 같다. Fig. 5는 비교 결과 그래프로 실험 데이터에 따르면 145일 기준 CFT 크리프 계수는 약 0.8 정도로 나타난다. 수정모델의 크리프 계수 예측 데이터는 약 0.9 정도로 실험결과와 근접하게 나타났으나, fib model code 2010[18] 모델과 ACI 209[19],[20]의 크리프 계수 예측 데이터는 각각 1.8과 2.4로 실제 CFT 크리프 계수에 비해 약 2.3~3배가량 과대평가함을 확인할 수 있다. 결과적으로 기존의 설계모델들에 비해 수정모델은 실험 데이터와 비교적 잘 일치하는 것으로 판단된다.
4. CFT 구조물의 장기거동해석법
이 연구에서는 프리스트레스트 CFT로 보강된 강박스거더의 장기거동을 해석하기 위해 재령 보정 유효탄성계수법(AEMM)을 사용하였으며, 단면의 응력 해석방법으로는 Bresler and Selna[26]가 제안한 RA(relaxation approach)를 적용하였다. 장기거동해석은 콘크리트와 강재가 일체 거동한다는 가정하에 수행하였으며, CFT의 경우 구조 특성상 건조수축이 거의 발생하지 않는다는 점을 고려하여 건조수축에 의한 변형은 무시하였다.
Bazant[12]에 의해 제안된 재령 보정 유효탄성계수법(AEMM)은 시간에 따른 콘크리트의 재령효과를 고려하기 위해 유효탄성계수법(EMM)에 재령계수 χ(t,t′)를 도입하는 방법으로 시간 t에서 발생하는 총 변형률 ϵ(t)은 식 (5)와 같이 초기 응력과 시간이 지남에 따라 발생하는 응력 변화량의 합으로 표현된다. 여기서 재령 보정 유효탄성계수(Ee)는 식 (6)과 같이 표현된다.
| (5) |
| (6) |
- 여기서, σ0: 초기응력(MPa),
- ∆σ(t): 응력 변화량(MPa),
- Ee: 재령 보정 유효탄성계수(MPa),
- Ec(t′): 콘크리트 재령 t′일 때 탄성계수(MPa).
강박스 교량에 축력 Ni와 휨모멘트 Mi가 작용할 때 중립축으로부터 y만큼 떨어진 거리에서 발생하는 초기응력 σi는 식 (7)과 같이 계산된다.
| (7) |
- 여기서, ϵoi: 초기변형률,
- ki: 초기곡률(mm-1).
RA(relaxation approach) 방법은 릴랙세이션에 기초한 개념으로 콘크리트의 장기거동에 따라 발생하는 실제 응력 변화량 ∆σ은 식 (8)과 같이 릴랙세이션에 의해 발생하는 응력 변화량 ∆σrelax와 부재 내 힘의 평형 조건을 만족시키기 위해 도입하는 응력 변화량 ∆σrestore의 합으로 표현할 수 있다. 이때, 응력 변화량 ∆σrelax와 ∆σrestore는 각각 식 (9), 식 (10)와 같이 계산된다.
| (8) |
| (9) |
| (10) |
여기서, 변형률 변화량 ∆ϵo 및 곡률 변화량 ∆k은 식 (11), 식 (12)에 의해 계산할 수 있으며, 이때 축력 변화량과 휨모멘트 변화량은 크리프 및 릴랙세이션에 의해 부재 내 발생한 응력 변화량을 전단면에 대해 적분함으로써 계산할 수 있다.
| (11) |
| (12) |
- 여기서, ∆M: 휨 모멘트 변화량(kN·m),
- ∆N: 축력 변화량(kN),
- Ae, Be, Ie: 재령 보정 유효탄성계수 Ee(t,t′)를 적용하여 산정된 등가 환산 단면적, 단면 1차 모멘트, 단면 2차 모멘트.
5. 프리스트레스트 CFT 보강 강박스 목업 시험체 프리스트레스 손실량 평가
5.1 목업 시험체 제작 및 계측 방법
CFT 부재를 이용한 프리스트레스 도입 강박스거더의 실제 장기거동 데이터와 CFT 크리프 계수 수정모델을 적용한 프리스트레스 손실 평가방법의 예측치를 비교·분석하기 위해 목업 시험을 수행하였다. 모든 시공단계에서 발생하는 프리스트레스 손실 데이터를 축적하기에는 실험적인 제약이 있기 때문에 강박스 하부 프리스트레스 도입 후 발생하는 1차 프리스트레스 손실에 대해서만 비교를 수행하였다.
실제 제작한 강박스 목업 시험체는 Fig. 6와 같으며, 상부플랜지 폭 800 mm, 하부플랜지 폭 2,150 mm, 높이 2,000 mm, 길이 9 m의 오픈형 강박스거더로 제작되었다. 강박스거더 하부에 프리스트레스 도입을 위한 CFT 규격은 가로 500 mm, 세로 400 mm의 직사각형 부재를 사용하였으며, 시험체에 사용된 재료의 물성치는 Table 2와 같다. 강봉을 통한 프리스트레스 도입은 콘크리트 재령 13일에 수행되었으며, 강봉 인장시 2,000 kN급의 액추에이터를 사용하였다. 강봉 1개당 약 750 kN의 하중을 도입하였으며, 1개의 CFT 부재에는 유압잭 최대 용량의 약 75 % 정도인 1,500 kN이 도입되었다.
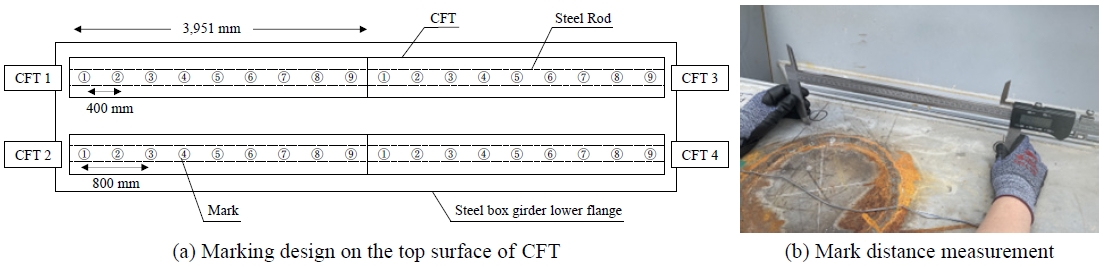
장기변형은 약 90일간 목업 시험체의 CFT 부재 상면에서 측정하였으며, 온도 데이터는 강박스거더 상부플랜지와 복부, 하부플랜지 각각에서 측정하였다. 측정 방법은 강박스거더 하부에 프리스트레스를 도입하기 전에 Fig. 7(a)와 같이 CFT 상면에 400 mm 간격으로 사전에 표점을 표시하여 Fig. 7(b)와 같이 버니어 캘리퍼스를 이용해 400 mm 간격과 800 mm 간격으로 4개의 CFT 부재를 각각 측정하였다. 측정 간격은 하중 도입 초기 변형이 빠르게 발생하는 크리프 변형의 특성을 고려하여 강봉 인장 후 1·2주차는 1주에 1회, 3주차 이후부터는 4주에 1회씩 측정을 실시하였다.
5.2 결과 데이터 분석
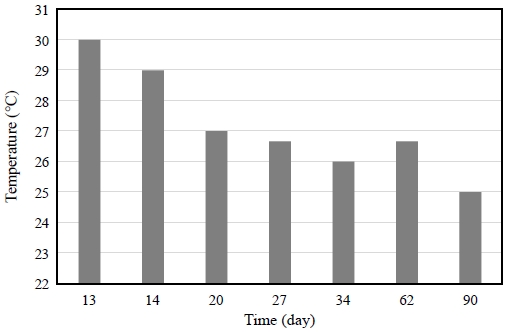
프리스트레스트 CFT 보강 강박스거더 목업 시험체의 장기변형은 약 90일간 측정되었으며, 표점과 표점 사이의 길이와 측정일별 온도 데이터를 측정하였다. Fig. 8은 시험에서 측정된 온도 데이터의 분포로 온도 데이터는 목업 시험체의 계측 데이터의 보정을 위해 측정되었으며, 강박스거더의 상부플랜지, 복부, 하부플랜지에서 각각 측정된 세 개의 값의 평균값을 사용하였다.
실외 장기계측실험의 경우 온도에 따라 열팽창 계수에 의해 계측치에 오차가 발생할 수 있기 때문에 실험 데이터의 비교 전 사전에 식 (13)과 같이 온도 보정식을 사용하여 보정 처리 후 예측 데이터와 비교하였다.
| (13) |
- 여기서, LT: 온도 보정 후 계측 길이(mm),
- L: 온도 보정 전 계측 길이(mm),
- C: 열팽창 계수,
- ∆T: 온도 변화량(℃).
Fig. 9은 목업 시험체의 시간에 따른 변형률 그래프로 프리스트레스는 콘크리트 재령 13일에 도입되었으며, 탄성 변형률은 약 223 μϵ이 발생하였다. 목업 시험체의 총 변형률은 프리스트레스 도입 이후 약 한 달간 급격히 증가하였으며, 40일 이후부터는 완만하게 증가하였다. 측정 90일을 기준으로 발생한 총 변형률은 약 494 μϵ으로 초기 탄성 변형률에 비해 약 45 % 가량 증가하였다. 프리스트레스 도입 이후 약 30일 전후로 계측 데이터의 그래프 형상은 굴곡이 존재하고 변형률이 비교적 작게 측정된 경향이 있으며, 이는 계측 시 버니어 캘리퍼스를 이용하여 측정하는 과정 중 발생했던 오차에 의한 영향일 것으로 판단된다.
5.3 목업 시험 데이터와 예측값 비교·분석
Fig. 10(a)는 목업 시험 계측 데이터와 장기거동해석을 통한 예측 데이터의 변형률을 비교한 그래프이다. 예측 데이터의 초기 탄성 변형률은 약 285 μϵ 정도로 계측 데이터의 초기 탄성 변형률에 비해 약 1.27배가량 크게 산정되었으나, 시간이 장기적으로 흐를수록 두 그래프는 일치하는 경향을 보였으며, 측정 90일을 기준으로 비교한 예측 데이터의 변형률은 약 460 μϵ 정도로 실제 계측 데이터와 약 10.7 % 정도의 차이를 보였다.

Comparison of experimental data and predicted value of CFT-steel box girder according to prestress introduction
Fig. 10(b)는 시간에 따른 강박스거더 하부의 응력 비교 데이터로 강박스의 하부 응력은 변형률 데이터에 강재의 탄성계수 205 GPa을 곱하여 계산하였다. 연속교의 부모멘트부에서 강박스거더 하부플랜지는 CFT 프리스트레스 부재에 의해 인장력이 도입되며, 도입 이후에는 CFT 내부 콘크리트의 크리프로 인해 콘크리트에 발생하는 응력 손실량만큼의 하중을 강재가 추가적으로 받아주기 때문에 시간이 지남에 따라 강박스 하부의 응력이 증가하는 현상이 나타난다.
실제 목업 시험체에서 하중 도입 이후 강박스 하부에서 발생한 초기응력은 약 45 MPa 정도이며, 측정 90일 기준 실험 계측 데이터와 예측값의 장기응력 변화량은 각각 101 MPa, 113 MPa 정도로 하중 도입 초기응력에 비해 각각 2.24배, 2.51배가량 증가하였음을 알 수 있다. 또한 목업 시험체의 데이터와 예측 데이터의 장기응력 차이는 약 8.9 % 정도로 하중 도입 이후부터 시간이 지남에 따라 예측값과 실제 계측 데이터의 응력이 거의 유사하게 증가함을 알 수 있다. 즉 두 그래프의 모두 예측 데이터는 실제 목업 시험의 장기 데이터와 대체로 유사한 결과를 보였으며, 이를 통해 CFT 부재의 장기거동해석 시 건조 크리프 보정계수를 적용한 CFT 수정 크리프 계수 모델의 적용이 타당하였음을 알 수 있다.
단, 목업 시험체의 계측 과정 중 발생할 수 있는 오차나 온습도에 민감한 장기거동실험의 특성에 따라 실험 중 발생했을 수 있는 추가적인 변형 등을 고려했을 때, 목업 시험체의 장기변형 및 응력변화에 대한 수정모델의 대략적인 예측 성능을 알 수 있으나 정확한 성능 평가에는 한계가 있다고 판단된다. 따라서 CFT 부재를 이용한 프리스트레스 구조물의 장기거동해석 시 CFT 수정 크리프 계수 모델 적용의 정확한 성능 평가를 위해서는 통제된 실험조건에서 수행되는 실험 데이터에 기반하여 비교·분석하기 위한 추가 연구가 필요할 것으로 판단된다.
6. 결 론
이 연구는 CFT를 이용한 강박스거더 프리스트레싱 공법 적용 시 발생하는 프리스트레스 손실을 평가하기 위하여 CFT 부재의 장기거동 실험결과 및 설계기준식을 기반으로 CFT 부재의 손실 평가방법을 제안하였다. 또한 해당 방법의 타당성을 입증하기 위해 기존의 설계기준들과의 예측 성능을 비교하였으며, 실제 강박스거더 목업체를 제작하여 약 90일간의 주기적인 계측을 통해 얻은 실험 데이터를 기반으로 장기거동해석을 통해 얻은 예측 데이터와의 비교를 실시함으로써 다음과 같은 결론을 도출하였다.
- (1) CFT와 일반 콘크리트의 장기거동 특성의 차이를 분석하기 위해 이전 연구자들의 비교 실험결과를 참고하였으며, 이를 통해 CFT 시험체에서 발생하는 크리프 변형은 일반 콘크리트에서 발생하는 총 크리프 변형의 약 절반 수준으로 발생하며, 그 이유는 CFT의 구조 특성상 강관으로 인해 내부 콘크리트와 외기와의 접촉이 차단되어 건조 크리프로 인한 변형이 거의 발생하지 않기 때문이라고 판단하였다.
- (2) CFT의 구조적 특성을 고려하여 CFT 부재를 이용한 프리스트레스 구조물의 프리스트레스 손실 평가방법을 제안하기 위해 fib model code 2010[18] 모델을 기반으로 건조 크리프 보정계수를 도입한 수정모델을 제안하였다. 수정모델의 타당성 확보를 위해 선행연구의 실험 데이터를 기반으로 기존의 설계기준식과 비교하였으며, 그 결과 수정모델의 CFT 크리프 계수가 실험 데이터와 유사함을 확인하였다.
- (3) 목업 시험체의 장기변형 데이터는 온도에 대한 영향을 무시하기 위해 강봉이 인장되는 날을 기준으로 온도 보정 후 사용되었다. 결과적으로 시간에 따른 변형률 데이터의 계측 데이터와 예측값의 차이는 약 10.7 % 정도로 나타났고 강박스 하부 응력 데이터의 계측 데이터와 예측값의 차이는 약 8.9 % 정도로 나타나 예측 데이터와 실제 목업 시험체의 데이터가 대체로 잘 일치하고 있음을 확인하였다. 다만 계측 과정 중 발생할 수 있는 오차나 온습도에 의한 오차 등을 고려했을 때, CFT 수정 크리프 계수 모델의 대량적인 예측 성능을 파악할 수 있으나, 정확한 성능의 평가를 위해서는 추가적인 연구가 필요할 것으로 판단된다.
- (4) 목업 시험체에 프리스트레스를 도입한 이후 하부플랜지에서 발생한 초기응력은 약 45 MPa이며 90일 기준 CFT의 내부 콘크리트에서 발생하는 크리프로 인해 증가한 강재의 응력은 약 101 MPa로 초기응력 대비 약 2.24배 정도 증가하였다. 재령 보정 유효탄성계수법(AEMM)을 기반으로 CFT 크리프 계수 수정모델을 적용하여 수행한 장기거동 해석결과에 따르면 시험 90일 기준 강재의 응력은 약 113 MPa로 초기응력 대비 약 2.51배 정도 증가한 것으로 나타났다. 결과적으로 장기거동해석결과는 하중 도입 초기부터 크리프로 인해 시간이 지남에 따라 목업 시험체에 발생하는 응력 변화와 유사한 거동을 보였으며 이를 통해 프리스트레스 CFT로 보강된 강박스거더의 프리스트레스 손실을 예측함에 있어 제안한 프리스트레스 손실 평가방법의 적용이 타당함을 검증하였다.
Acknowledgments
본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 21CTAP-C163558-01).
References
-
Saul, R. (1996) Bridge with Double Composite Action, Structural Engineering International, Taylor & Francis, Vol.6, No.1, pp.32-36.
[https://doi.org/10.2749/101686696780496067]

-
Su, Q.-T., and Yang, G.-T. (2012) Experimental Investigation on Inelastic Behavior of Composite Box Girder Under Negative Moment, International Journal of Steel Structures, KSSC, Vol.12, No.1, pp.71-84.
[https://doi.org/10.1007/s13296-012-1007-0]

-
Kim, S.H., Choi, S.M., and Yom, K.S. (2021) Evaluation of Flexural Performance of Composite Girder Consisting of Square Steel Pipes and Reinforced Lattice, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.4, pp.247-255 (in Korean).
[https://doi.org/10.7781/kjoss.2021.33.4.247]

-
Men, P., Zhou, X., Zhang, Z., Di, J., and Qin, F. (2021) Behavior of Steel-Concrete Composite Girders Under Combined Negative Moment and Shear, Journal of Constructional Steel Research, Elsevier, Vol.179, 106508.
[https://doi.org/10.1016/j.jcsr.2020.106508]

-
Kim, D.S., Choi, Y.G., Park, K.Y., and Kim, K.D. (2022) Method of Reducing Negative Moments of Two-Span Continuous Beam, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.5, pp.251-258 (in Korean).
[https://doi.org/10.7781/kjoss.2022.34.5.251]

-
Saadatmanesh, H., Albrecht, P., and Ayyub, B.M. (1989) Experimental Study of Prestressed Composite Beams, Journal of Structural Engineering, American Society of Civil Engineers, Vol.115, No.9, pp.2348-2363.
[https://doi.org/10.1061/(ASCE)0733-9445(1989)115:9(2348)]

-
Cheon, J.U., Lee, S.H., and Kim, S.H. (2022) A Study on Lateral Torsional Buckling in I-Section Plate Girder with Concrete Filled Half Pipe Stiffner, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.1, pp.1-11 (in Korean).
[https://doi.org/10.7781/kjoss.2022.34.1.001]

-
Ichinose, L.H., Watanabe, E., and Nakai, H. (2001) An Experimental Study on Creep of Concrete Filled Steel Pipes, Journal of Constructional Steel Research, Elsevier, Vol.57, No.4, pp.453-466.
[https://doi.org/10.1016/S0143-974X(00)00021-3]

-
Sharif, A., Taher, S.E.F., and Basu, P.K. (1993) Time-Dependent Losses in Prestressed, Continuous Composite Beams, Journal of Structural Engineering, American Society of Civil Engineers, Vol.119, No.11, pp.3151-3168.
[https://doi.org/10.1061/(ASCE)0733-9445(1993)119:11(3151)]

- Oh, B.-H., Yang, I.-H., and Kim, J.-S. (2001) A Study on the Estimation of Prestress Losses in Prestressed Concrete Box Girder Bridges, Journal of Korea institute for Structural Maintenance and Inspection, KSMI, Vol.5, No.2, pp.111-120 (in Korean).
-
Mozer, J.D., Gerstle, K.H., and Tulin, L.G. (1970) Time-Dependent Behavior of Concrete Beams, Journal of Structural Division, American Society of Civil Engineers, Vol.96, No.3, pp.597-612.
[https://doi.org/10.1061/JSDEAG.0002532]

-
Bazant, Z.P. (1972) Prediction of Concrete Creep Effects Using Age-Adjusted Effective Modulus Method, Journal of the American Concrete Institute, ACI, Vol.69, No.4, pp.212-217.
[https://doi.org/10.14359/11265]

-
Cluley, N.C., and Shepherd, R. (1996) Analysis of Concrete Cable-Stayed Bridge for Creep, Shrinkage and Relaxation Effects, Computers & Structures, Elsevier, Vol.58, No.2, pp.337-350.
[https://doi.org/10.1016/0045-7949(95)00131-Y]

-
Huo, X.S., Al-Omaishi, N., and Tadros, M.K. (2001) Creep, Shrinkage, and Modulus of Elasticity of High-Performance Concrete, ACI Materials Journal, American Concrete Institute, Vol.98, No.6, pp.440-449.
[https://doi.org/10.14359/10842]

-
Shenoy, C.V., and Frantx, G.C. (1991) Structural Tests of 27-Year-Old Prestressed Concrete Bridge Beams, PCI Journal, Precast/Prestressed Concrete Institute, Vol.36, No.5, pp.80-90.
[https://doi.org/10.15554/pcij.09011991.80.90]

-
Roberts-Wollmann, C.L., Arrellaga, J.A., Breen, J.E., and Kreger, M.E. (1996) Field Measurement of Prestress Losses in External Tendons, ACI Structural Journal, American Concrete Institute, Vol.93, No.5, pp.595-601.
[https://doi.org/10.14359/9718]

-
Barr, P.J., Kukay, B.M., and Halling, M.W. (2008) Comparison of Prestress Losses for a Prestress Concrete Bridge Made with High-Performance Concrete, Journal of Bridge Engineering, American Society of Civil Engineers, Vol.13, No.5, pp.468-475.
[https://doi.org/10.1061/(ASCE)1084-0702(2008)13:5(468)]

- International Federation for Structural Concrete (2013) fib Model Code for Concrete Structures 2010, Ernst & Sohn, Switzerland.
- American Concrete Institute (1997) Prediction of Creep, Shrinkage and Temperature Effects in Concrete Structures (ACI 209R-92, Reapproved 1997), USA.
- American Concrete Institute (2008) Guide for Modeling and Calculating Shrinkage and Creep in Hardened Concrete (ACI 209.2R-08), USA.
- Gilbert, R.I. (1988) Time Effects in Concrete Structures, Elsevier Science Ltd., USA.
- Lee, H.J., Kim, R.-H., Cho, K.-I., and Ahn, J.-H. (2022) Prestressing Inducing Effect of Continuous Open-Top Steel Box Girder Using Modular CFT Members, Journal of Korea Institute for Structural Maintenance and Inspection, KSMI, Vol.26, No.3, pp.111-119 (in Korean).
-
Pickett, G. (1942) The Effect of Change in Moisture-Content on the Creep of Concrete Under a Sustained Load, Journal of the American Concrete Institute, ACI, Vol.38, pp.333-355.
[https://doi.org/10.14359/8607]

-
Youakim, S.A., Ghali, A., Hida, S.E., and Karbhari, V.M. (2007) Prediction of Long-Term Prestress Losses, Journal of Precast/Prestressed Concrete Institute, PCI, Vol.52, No.2, pp.116-130 .
[https://doi.org/10.15554/pcij.03012007.116.130]

-
Terrey, P.J., Bradford, M.A., and Gilbert, R.I. (1994) Tubular Structures VI, Creep and Shrinkage in Concrete-Filled Steel Tubes, Routledge, Netherlands, pp.293-298.
[https://doi.org/10.1201/9780203735015-43]

- Bresler, B., and Selna, L. (1964) Analysis of Time-Dependent Behavior of Reinforced Concrete Structures, Symposium on Creep of Concrete (ACI Special Publication SP-9), American Concrete Institute, pp.115-128.