
고강도 강재보의 비탄성 횡-비틀림좌굴 제어를 위한 횡지지 거리
초록
본 연구에서는 공칭인장강도 800MPa를 지니는 고강도 강재로 조립된 H형강보의 횡지지거리에 따른 횡비틀림 좌굴강도를 현행 강구조설계기준(KBC 2009, AISC-LRFD 2010)을 바탕으로 평가하였다. 현행 기준은 고강도 강재와 응력도-변형도 특성이 확연히 다른 항복강도 350MPa 이하의 일반강을 전제로 정립된 것으로서, 고강도 강재에 대한 현행 기준의 적합성 여부가 우선 검토되어야 한다. 본 연구의 실험체는 모두 컴팩트 단면으로서 춤-폭비(H/B) 1.7을 갖는 실험군 A(상대적 뒤틀림 강성을 통한 모멘트전달이 작은 경우)와 2.7을 갖는 실험군 B(상대적으로 모멘트전달에 뒤틀림 강성 크게 기여하는 경우)로 구성하였다. 항복 이후의 응력도-변형도 특성의 영향을 받는 비탄성 횡좌굴 거동이 유발되도록 횡지지거리를 제어하면서 횡지지 구간 내에 균등모멘트가 작용하도록 가력하였다. 두 실험군 모두 현행 기준에 요구하는 강도를 충분히 상회하였고, 특히 뒤틀림 거동을 통한 모멘트전달이 크지 않은 실험군 A의 일부실험체는 소성설계에서 요구하는 수준의 회전능력까지 발휘하였다. 이들 실험결과는 현행 기준을 고강도 강재에 보수적으로 확대하여 적용할 수 있음을 보여준다. 실험결과를 좀 더 심층적으로 분석하기 위해 일반강 및 고강도강의 응력도-변형도 특성을 고려한 H형강보의 횡지지거리에 따른 비탄성 횡좌굴강도 산정식을 유효접선계수를 반영하여 해석적으로 유도하였다. 이를 통해 소재의 항복강도와 탄성계수만을 고려하여 산정되는 현행 기준의 소성횡지지거리() 제한식은, 항복참(yield plateau)없이 즉시 변형경화하는 고강도 강재에 적용하는 경우 보수적인 결과로 귀결됨을 입증하였다. 비탄성 횡좌굴 제어를 위한 횡지지거리는 소재의 항복강도 뿐만 아니라 항복 이후의 변형경화특성까지 반영하여 정의되는 타당하므로 이에 대한 개선의 필요성이 있다.
Abstract
In this study, lateral-torsional buckling (LTB) strength of high-strength H-beams built up from 800MPa tensile-strength steel was experimentally and analytically evaluated according to current lateral stability provisions (KBC 2009, AISC-LRFD 2010). The motivation was to evaluate whether or not current LTB provisions, which were originally developed for ordinary steel with different stress-strain characteristics, are still applicable to high-strength steel. Two sets of compact-section specimens with relatively low (Set A) or high (Set B) warping stiffness were prepared and tested under uniform moment loading. Laterally unbraced lengths of the test specimens were controlled such that inelastic LTB could be induced. All specimens exhibited LTB strength exceeding the minimum limit required by current provisions by a sufficient margin. Moreover, some specimen in Set A reached a rotation capacity required for plastic design, although its laterally unbraced length belonged to the inelastic LTB range. All the test results indicated that extrapolation of current provisions to high-strength steel is conservative. In order to further analyze the test results, the relationship between inelastic moment and laterally unbraced length was also derived in explicit form for both ordinary- and high-strength steel based on the effective tangent modulus of inelastic section. The analytical relationship derived again showed that extrapolation of current laterally unbraced length limit leads to a conservative design in the case of high-strength steel and that the laterally unbraced length to control the inelastic LTB behavior of high-strength steel beam should be specified by including its unique post-yield strain-hardening characteristics.
키워드:
고강도 강재, 횡-비틀림좌굴, 횡지지길이, 좌굴강도, 항복참Keywords:
high-strength steel, inelastic lateral-torsional buckling, unbraced length, buckling strength, yield plateau1. 서 론
고강도강을 건축구조물에 적절히 적용할 경우 부재 사이즈 축소에 따른 여러 구조적 측면의 장점은 물론 운송, 양중, 시공, 건축계획 등 여러측면에서 이득을 취할 수 있다. 외국의 경우 항복강도 690MPa급 고강도강재의 개발은 Haaijer[1], McDermott 등[2] 1960년대까지 거슬러 올라간다
최근 국내에서도 인장강도 800MPa급 강재(HSA800, HSB800)가 KS에 등록되고 현장 적용이 시작되는 등 기준화를 위한 연구가 활발히 진행되고 있다. 800MPa 급 강재는 일반강재(SM490)강재에 비해 높은 강도, 우수한 인성(응력-변형률 곡선하의 면적) 및 양호한 용접성능을 가진 소재이다(Fig. 1).
|
Fig. 1 Stress-strain characteristic of various grades of steel(SM490,SM570 and HSA800) |
|
|
Fig. 2 Stress-strain curve model with a yield plateau |
가장 널리 사용되는 H형강 휨재가 소정의 강도와 변형능력을 발휘하기 위해서는 국부좌굴, 횡비틀림좌굴, 파단, 소성항복 등의 한계상태가 적절히 제어되어야 한다. 현행 강구조기준(KBC 2009[3], AISC-LRFD 2010[4])의 제반 좌굴제어 조항은 항복강도 350MPa 이하의 일반강을 전제로 정립된 것이다. 즉 Fig. 1(a) 곡선에서 보듯이 일반강은 분명한 항복점, 상당한 항복참(yield plateau)이 존재한 후 변형경화하는 특성을 지니고 있으나 고강도강의 경우(Fig. 1(c)) 이런 특성이 존재하지 않는다.
해석적 연구에서는 일반강의 경우 종종 Fig. 2와 같은 3선형 모형이 사용된다. 이와 같이 상이한 항복후 변형특성은 비탄성 국부좌굴 또는 비탄성 횡좌굴에 영향을 미치게 되므로 우선적으로 현행 기준의 비탄성 좌굴조항을 고강도강에도 그대로 확장하여 적용할 수 있는가에 대한 검증이 필요하다. 이와 관련한 국내외 연구는 대부분 국부좌굴 제어를 위한 폭-두께비 제한조건의 검토에 집중되어 있을 뿐(김종락 등[5], 이철호 등[6], 유정한 등[7], Rasmussen 등[8], Ricles 등[9], Green[10]) 횡좌굴에 미치는 영향을 수행한 연구는 매우 희소하다. 본 연구는 이를 감안하여 수행되었다.
2. 현행 기준의 횡좌굴강도 산정식 고찰
|
(a) Lateral buckling of an H-section under uniform moment |
|
(b) Unbraced length versus beam flexural strength curve |
Fig. 3 Lateral buckling strength in current design code(KBC 2009, AISC-LRFD 2010) |
현행 기준의 경우 횡지지 구간내에 모멘트 구배가 존재하는 경우 상대적으로 횡좌굴 저항에 유리한 조건이 되므로 이를 반영하는 보정계수(
 )를 곱하여 횡좌굴강도를 산정한다(Fig. 3(b)).
)를 곱하여 횡좌굴강도를 산정한다(Fig. 3(b)).
이하에서는 일반강을 전제로 제시된 현행 기준의 탄성한계횡지지거리(
 , 식 (3)) 및 소성한계횡지지거리(
, 식 (3)) 및 소성한계횡지지거리(
 , 식 (4))의 배경을 간략히 고찰하고자 한다. Fig. 3(a) 조건에 대한 탄성횡비틀림좌굴모멘트(
, 식 (4))의 배경을 간략히 고찰하고자 한다. Fig. 3(a) 조건에 대한 탄성횡비틀림좌굴모멘트(
 )의 수학적 정해는 4계 상미분 방정식의 해로 아래 (1)식과 같이 이미 잘 알려져 있다(Timoshenko[11]).
)의 수학적 정해는 4계 상미분 방정식의 해로 아래 (1)식과 같이 이미 잘 알려져 있다(Timoshenko[11]).
 (1)
(1)
여기서,
 =횡지지거리,
=횡지지거리,
 =전단탄성계수,
=전단탄성계수,
 =탄성계수,
=탄성계수,
 =약축휨강성,
=약축휨강성,
 =뒤틀림(warping)강성, GJ=비틀림강성을 나타낸다.
=뒤틀림(warping)강성, GJ=비틀림강성을 나타낸다.
위 식에서 근호의 첫항과 두째항은 각각 St. Venant 비틀림(순수비틀림)과 뒤틀림에 의해 제공되는 횡좌굴 저항성분을 나타내는데 일반적으로 폭에 비해 춤이 큰 H형강일수록 뒤틀림 저항성분에 대한 의존성이 증대된다. 한편 잔류응력을 고려한 탄성한계모멘트(
 )는 아래 (2)식과 같다.
)는 아래 (2)식과 같다.
 (2)
(2)
여기서,
 =탄성단면계수,
=탄성단면계수,
 =잔류응력을 나타낸다.
=잔류응력을 나타낸다.
위 식(1) 및 식(2)를 등치시킨 후
 에 대해서 풀면 이것이 곧 아래의 (3)식으로 주어지는 탄성한계횡지지거리(
에 대해서 풀면 이것이 곧 아래의 (3)식으로 주어지는 탄성한계횡지지거리(
 )가 된다. 참고로 현행 기준에서는 압연 또는 조립형강 모두 잔류응력으로 항복강도의 30%(
)가 된다. 참고로 현행 기준에서는 압연 또는 조립형강 모두 잔류응력으로 항복강도의 30%(
 )로 권고하고 있다. 탄성한계횡지지거리(
)로 권고하고 있다. 탄성한계횡지지거리(
 )은 단면의 탄성물성에만 관계되므로 잔류응력의 크기만 같다면 일반강이건 고강도강이건 차별 없이 적용될 수 있다.
)은 단면의 탄성물성에만 관계되므로 잔류응력의 크기만 같다면 일반강이건 고강도강이건 차별 없이 적용될 수 있다.
 (3)
(3)
 ,
,

한편 현행 소성한계횡지지거리(
 )는 Lay[12]와 Galambos[13]의 연구에 근간을 두고 제시되었다. Lay는 Fig. 2의 3선형 모델에 슬립밴드이론(slip band theory)을 추가하여 회전능력까지 고려된 일반적 한계횡지지거리(
)는 Lay[12]와 Galambos[13]의 연구에 근간을 두고 제시되었다. Lay는 Fig. 2의 3선형 모델에 슬립밴드이론(slip band theory)을 추가하여 회전능력까지 고려된 일반적 한계횡지지거리(
 ) 아래 식(4)와 같이 제안하였다. 슬립밴드이론에 대해서는 본 논문의 후반부에서(6절) 소개한다.
) 아래 식(4)와 같이 제안하였다. 슬립밴드이론에 대해서는 본 논문의 후반부에서(6절) 소개한다.
 (4)
(4)
여기서,
 =약축단면2차반경(mm),
=약축단면2차반경(mm),
 =항복변형도,
=항복변형도,
 =회전능력(최대강도의 95% 저하시의 소성회전각을 기준),
=회전능력(최대강도의 95% 저하시의 소성회전각을 기준),
 = 변형경화계수(=
= 변형경화계수(=
 ),
),
 (=항복참길이계수, Fig. 2참조).
(=항복참길이계수, Fig. 2참조).
현행 기준에서 제시하고 있는 아래 (5)식은 위 (4)식에 345MPa 까지의 구조용 탄소강의 전형적인 값
 =10.5,
=10.5,
 =45, R=3을 대입하여 도출된 것이다.
=45, R=3을 대입하여 도출된 것이다.
 (5)
(5)
만일 강재의 항복후 물성이 이와 같은 조건에서 현저하게 벗어나는 경우라면 아래 (5)식은 그 적용의 타당성을 잃게 되는데 바로 HSA800 같은 고강도 강재가 이 경우에 해당한다.
3. 실험체 설계 및 제작
2장에서 언급한 문제를 지닌 식(5)의 고강도강 적용시의 적합성 여부를 평가하기 의해 수행된 실험연구 내용을 우선 소개하고 이후 관련 해석적 연구를 논의하고자 한다.
3.1 실험체 재료 및 단면 특성
Table 1에 실험체의 주요 단면특성 및 물성정보를 요약하였다. 150mm인 플랜지의 폭을 일정하게 유지하면서 높이의 변화를 통해 두 실험군을 만들었다. 모두 컴팩트 단면으로서 춤-폭비(H/B) 1.7을 갖는 실험군 A(상대적으로 뒤틀림 강성을 통한 모멘트전달이 작은 경우)와 2.7을 갖는 실험군 B(상대적으로 모멘트전달에 뒤틀림 강성 크게 기여하는 경우)로 구성하여 실무에서 취급되는 대표적 단면형상을 포괄하고자 하였다. 실험군 A와 실험군 B의 약축단면모멘트(
 )는 유사하며, 춤이 높은 실험군 B의 소성단면계수(
)는 유사하며, 춤이 높은 실험군 B의 소성단면계수(
 ),웨브 판폭두께비(
),웨브 판폭두께비(
 ) 및 뒤틀림계수(
) 및 뒤틀림계수(
 )는 실험군 A에 비해 상대적으로 큰 값을 갖는다. 조립에 사용된 HSA800 판재의 인장시험(KS-4호 시험편)에서 얻어진 전형적 응력도-변형도 곡선을 Fig.1(c)에 도시하였고 0.2% 오프셋법을 이용한 항복점 산정 등의 기타 주요 변형도값은 Table 1하단에 정리하였다.
)는 실험군 A에 비해 상대적으로 큰 값을 갖는다. 조립에 사용된 HSA800 판재의 인장시험(KS-4호 시험편)에서 얻어진 전형적 응력도-변형도 곡선을 Fig.1(c)에 도시하였고 0.2% 오프셋법을 이용한 항복점 산정 등의 기타 주요 변형도값은 Table 1하단에 정리하였다.
Table 1. Section Information and key properties |
||||
Specimen |
S1~S3 (Group A) |
S4~S6 (Group B) |
||
Section properties |
(1) Dimension |
H-250×150×15×15 |
H-400×150×15×15 |
|
(2) Plastic modulus,
|
710,250 |
1,379,625 |
||
(3) Radius of gyration,
|
33.0 |
29.2 |
||
(4) Moment of inertia,
|
8,499,375 |
8,541,563 |
||
(5) Warping constant,
|
1.16×
|
3.13×
|
||
(6) Torsional constant,
|
601,875 |
770,625 |
||
(7) Flange slenderness,
|
5.0 (6.2)a |
5.0 (6.2)a |
||
(8) Web slenderness,
|
15.0 (61.7)a |
25.0 (61.7)a |
||
Material strength (
|
(9) Steel plate |
Modulus |
|
|
Nominal |
|
|||
Measured |
|
|||
(10)b Weld metal |
Measured |
|
||
Key strainc (%) |
(11) Yield point,
|
0.388 |
||
(12) Strain at maximum stress,
|
4.5~5.0 |
|||
(13) Fracture strain,
|
11.0~12.0 |
|||
a:Width-to-thickness ratio limits for compact section (AISC and KBC code) b:Weld metal(K-120TG) spec. c:KS-1A coupon test result |
||||
3.2 실험체 제작
Fig. 4는 용접제작 실험체 단면 및 스티프너 상세를 보여주고 있다. 웨브의 양측을 5mm씩 45도 개선을 실시한 후 K-120TG 용접재를 사용하여 부분용입용접으로 제작되었다. K-120TG는
|
Fig. 4 Welding details of built-up section and stiffeners |
 )를 보유하고 있어 사용하였다.
)를 보유하고 있어 사용하였다.
반력지점의 스티프너는 스티프너는 S1~S5 실험체의 경우 삼면을 5mm 개선한 후 상하부 플랜지 및 웨브와 일체화되도록 전높이 스티프너로 제작하였다. S6 실험체의 경우는 전춤스티프너 사용 시 예상되는 부정적 영향인 소성힌지부 인장플랜지 열영향과 응력집중을 배제하기 위해 부분높이 스티프너를 적용하였다.
4. 실험체 셋업
4.1 실험체 셋업
Fig. 5~6은 실험체의 가력조건 및 횡지지 상세의 셋업을 보여주고 있다. 횡좌굴 성능 실험을 위해 사용된 실험조건은 현행 설계식 도출에 직·간접적으로 영향을 준 Lay-Galambos[12] 및 Dibley[14]의 실험조건을 참고하여, 모멘트구배를 갖는 사이드스팬(
 )을 두어 동일한 테스트 셋업으로 다양한 횡지지거리를 갖는 균등모멘트 가력조건이 구현될수 있도록 고려하였다. 사이드스팬의 길이가 길 경우 의도치 않는 횡좌굴이 사이드스팬에서 발생할 염려가 있으므로 경간이 짧은 것이 선호되나, 전단거동 등의 영향을 고려하여 가력지점길이(
)을 두어 동일한 테스트 셋업으로 다양한 횡지지거리를 갖는 균등모멘트 가력조건이 구현될수 있도록 고려하였다. 사이드스팬의 길이가 길 경우 의도치 않는 횡좌굴이 사이드스팬에서 발생할 염려가 있으므로 경간이 짧은 것이 선호되나, 전단거동 등의 영향을 고려하여 가력지점길이(
 )의 S/5~S/6정도의 길이를 갖도록 선정하였다. 전춤스티프너를 적용한 S1~S5(1차 실험) 실험 시 사이드스팬의 길이는 610mm로 선정하였으나, 가력지점과 반력지점사이가 근접하여 UTM 부속장비와 반력지점 롤러 혼잡으로 셋업을 위한 공간확보에 불리한 측면이 존재하였다. 따라서, 부분춤스티프너를 적용한 S6(2차 실험)은 사이드스팬의 길이를 실험실 바닥 반력지점의 기본이격거리인 150mm를 늘려 760mm로 선정하였다.
)의 S/5~S/6정도의 길이를 갖도록 선정하였다. 전춤스티프너를 적용한 S1~S5(1차 실험) 실험 시 사이드스팬의 길이는 610mm로 선정하였으나, 가력지점과 반력지점사이가 근접하여 UTM 부속장비와 반력지점 롤러 혼잡으로 셋업을 위한 공간확보에 불리한 측면이 존재하였다. 따라서, 부분춤스티프너를 적용한 S6(2차 실험)은 사이드스팬의 길이를 실험실 바닥 반력지점의 기본이격거리인 150mm를 늘려 760mm로 선정하였다.
횡지지는 상하부 플랜지 모두를 “point bracing”에 가깝게 하였다(Fig. 6, 8, 9, 15 횡지지 참조) 즉, 실험체의 횡변위와 단면의 비틀림은 구속하고 단면의 뒤틀림은 허용하는 조건이 적용되었다. 횡지지는 등분포모멘트를 갖는 구간 내에 위치하며 유효횡좌굴길이계수(
 ) 0.575를 갖는 횡지지조건과 유효횡좌굴길이계수(
) 0.575를 갖는 횡지지조건과 유효횡좌굴길이계수(
 ) 1.0을 갖는 횡지지조건으로 구성이 되어있다.
) 1.0을 갖는 횡지지조건으로 구성이 되어있다.
|
Fig. 5 Test setup and lateral bracing conditions |
|
|
Fig. 6 Top plan view and effective length factor(
|
|
Fig. 7 Comparison of the effective length factor (
|
 는 인접스팬(
는 인접스팬(
 )에 횡구속 효과에 따른 유효횡좌굴길이계수가 0.575이므로 테스트스팬(
)에 횡구속 효과에 따른 유효횡좌굴길이계수가 0.575이므로 테스트스팬(
 )의 유효횡지지거리는
)의 유효횡지지거리는
 을 갖는다. 횡지지조건
을 갖는다. 횡지지조건
 는 인접스팬(
는 인접스팬(
 )에 의한 구속효과가 없으므로 유효횡좌굴길이계수가 1.0으로 테스트스팬(
)에 의한 구속효과가 없으므로 유효횡좌굴길이계수가 1.0으로 테스트스팬(
 )의 횡지지거리가 동일하게 유효횡지지거리(
)의 횡지지거리가 동일하게 유효횡지지거리(
 )가 된다.
)가 된다.
유효횡좌굴길이계수 값
 =0.575는 Fig. 7(a)에서 보듯이 유한요소 좌굴해석에 의해 횡좌굴 발생시 약축휨의 변곡점간 거리로서 산정하였다. 해석은 유한요소해석프로그램 중의 하나인 ABAQUS의 8절점 고체요소(C3D8R)를 사용하여 수행하였다. Fig. 7(b)는 계측과 해석에 의한 약축휨의 변곡점간의 거리를 보여주고 있다. 계측과 해석에 의한 유효횡좌굴길이계수(
=0.575는 Fig. 7(a)에서 보듯이 유한요소 좌굴해석에 의해 횡좌굴 발생시 약축휨의 변곡점간 거리로서 산정하였다. 해석은 유한요소해석프로그램 중의 하나인 ABAQUS의 8절점 고체요소(C3D8R)를 사용하여 수행하였다. Fig. 7(b)는 계측과 해석에 의한 약축휨의 변곡점간의 거리를 보여주고 있다. 계측과 해석에 의한 유효횡좌굴길이계수(
 )는 대체로 일치하나 실험상에서는 횡지지와 실험체 사이의 접촉조건 및 횡좌굴 시 횡지지보의 미소한 변형에 따라 완벽한 비틀림단순지지조건의 구현은 어려워 계측 값에서 조금 더 큰 유효횡좌굴길이계수 값을 보이는 것으로 파악된다.
)는 대체로 일치하나 실험상에서는 횡지지와 실험체 사이의 접촉조건 및 횡좌굴 시 횡지지보의 미소한 변형에 따라 완벽한 비틀림단순지지조건의 구현은 어려워 계측 값에서 조금 더 큰 유효횡좌굴길이계수 값을 보이는 것으로 파악된다.
한편, Fig. 8과 같이 반력부의 하부는 롤러로 지지했을 뿐 별도의 지점 구속이나 지지상세를 추가하지 않았다.
4.2 계측계획
Fig. 9는 실험체의 횡-비틀림 좌굴을 관찰하기 위해서 실험체의 하부플랜지에 설치된 변위계, 상하부플랜지 및 웨브에 설치된 변형률계 설치위치를 보여주고 있다. 하부플랜지에 설치된 변위계는 실험체의 수직처짐 및 비틀림각(
 ) 변화를 관찰하여 횡좌굴 개시점을 포착하는데 사용되었다. 상부플랜지 변형률계는 길이방향 폭의 좌우변형률 분포를 계측하여 횡-비틀림정도에 따른 횡곡률분포 등을 관찰하였다. 웨브 변형률계는 휨 거동시 평면유지 만족여부 등을 계측하여 횡좌굴이 면내변형률 변
) 변화를 관찰하여 횡좌굴 개시점을 포착하는데 사용되었다. 상부플랜지 변형률계는 길이방향 폭의 좌우변형률 분포를 계측하여 횡-비틀림정도에 따른 횡곡률분포 등을 관찰하였다. 웨브 변형률계는 휨 거동시 평면유지 만족여부 등을 계측하여 횡좌굴이 면내변형률 변
|
|
Fig. 9 Location of displacement and strain measurement instrument |
|
Fig. 8 Overall view of test setup |
5. 실험변수 및 결과
5.1 강도, 변형능력 및 파괴모드
Table 2는 횡좌굴 실험체 주요변수 및 실혐결과를 정리한 것이다. Table 2 제5열의 횡좌굴 개시점 강도는 횡비틀림좌굴 발생 시점이 육안으로 관측하기 어려우므로 Fig. 10과 같이 실험체 보 중앙에서 계측된 수직변위(
 )와 비틀림각(
)와 비틀림각(
 )의 관계에서 수직변위의 변화에 비해 중앙부 단면 비틀림 변형이 급격하게 증가하는 시점을 기준으로 산정되었다. 즉, 기하학적 불완전이 전혀없는 “perfect beam”이라면 임계좌굴 하중 도달이전에는 횡비틀림이 전혀 없다가 임계하중 도달순간 횡비틀림 변형이 발생하겠으나 실제보(real beam)의 경우 기하학적 불완전(geometric imperfection)과 가력 시 편심 등에 의해 Fig. 10과 같은 거동을 보인다.
)의 관계에서 수직변위의 변화에 비해 중앙부 단면 비틀림 변형이 급격하게 증가하는 시점을 기준으로 산정되었다. 즉, 기하학적 불완전이 전혀없는 “perfect beam”이라면 임계좌굴 하중 도달이전에는 횡비틀림이 전혀 없다가 임계하중 도달순간 횡비틀림 변형이 발생하겠으나 실제보(real beam)의 경우 기하학적 불완전(geometric imperfection)과 가력 시 편심 등에 의해 Fig. 10과 같은 거동을 보인다.
즉, 가력 초기부터 수직변위의 증가에 따라 미소한 횡비틀림변형이 수반되다가 임계하중점 부근을 분기점으로 횡비틀림변형이 급격히 증가하는 거동을 볼 수 있다.
Table 2의 제6열 최대강도는 횡좌굴 이후 변형경화 등에 의한 추가적인 내력 증가분을 포함한 것이다. Table 2의 제7열 회전능력은(R)은 Fig. 11과 같이 소성모멘트 강도에서의 탄성회전각(
 )과 모멘트 강도가 최대강도에 도달한 후 비탄성 변형증가에 따라 소성모멘트강도(
)과 모멘트 강도가 최대강도에 도달한 후 비탄성 변형증가에 따라 소성모멘트강도(
 )로 저하되는 시점까지의 비로 산정되었다.
)로 저하되는 시점까지의 비로 산정되었다.
Table 2 Key parameters and test results |
|||||||
Specimen (1) |
Unbraced length (
(2) |
Effective length factor (
(3) |
Effective lateral slenderness (
(4) |
Buckling strength (
(5) |
Maximum strength (
(6) |
Rotation capacity (
(7) |
|
Group A
|
S1 |
2,800 |
1.0 |
84.8(5.44)a |
0.90 |
1.00 |
0.67 |
S2 |
2,400 |
1.0 |
72.7(4.66)a |
1.01 |
1.16 |
3.00 |
|
S3 |
1,800 |
0.575 |
31.4(2.01)a |
1.08 |
1.18 |
2.77 (HAZ crack) |
|
Group B
|
S4 |
2,800 |
1.0 |
95.9(6.15)a |
0.66 |
0.86 |
Not applied |
S5 |
1,800 |
0.575 |
35.5(2.27)a |
0.98 |
1.10 |
1.32 |
|
S6 |
1,400 |
0.575 |
27.6(1.76)a |
1.04 |
1.12 |
1.77 |
|
※ Measured material strengths and effective length factor(
a: Effective unbraced length(
|
|||||||
|
(a) Vertical deflection versus torsional angle curves(S1~S3) |
|
(b) Vertical deflection versus torsional angle curves(S4~S6) |
Fig. 10 Determination of the critical buckling point(
|
 ) 대비 5.44(
) 대비 5.44(
 )배의 횡지지를 간격으로 횡지지를 한 것이다.
)배의 횡지지를 간격으로 횡지지를 한 것이다.
|
Fig. 11 Definition of rotation capacity |
|
|
Fig. 12 End rotation versus bending moment curves (S1~S3) |
 )는 소성모멘트(
)는 소성모멘트(
 )의 0.90(
)의 0.90(
 )배, 회전능력(
)배, 회전능력(
 )은 0.67(
)은 0.67(
 )을 발휘하였다. 본실험체는
)을 발휘하였다. 본실험체는
 로서 탄성한계횡지지거리에 가깝게 횡지지된 것으로 Fig. 13에서 보듯이 상당한 횡-비틀림이 발생하여 파괴되었다.
로서 탄성한계횡지지거리에 가깝게 횡지지된 것으로 Fig. 13에서 보듯이 상당한 횡-비틀림이 발생하여 파괴되었다.
실험체 S2의 경우
 거리로 횡지지된 것으로
거리로 횡지지된 것으로
 인 S1에 비해 훨씬 뛰어난 강도 및 변형능력을 발휘하였다. 즉
인 S1에 비해 훨씬 뛰어난 강도 및 변형능력을 발휘하였다. 즉
 와
와
 의 성능을 발휘하였다.
의 성능을 발휘하였다.
|
Fig. 13 Failure modes(S1~S3) |
|
|
Fig. 14 End rotation versus bending moment curve (S4~S6) |
실험체 S3의 경우,
 의 횡지지를 한 것으로
의 횡지지를 한 것으로
 ,
,
 을 발휘하였다.
을 발휘하였다.
 인 시점에서 실험체의 추가적인 연성거동이 예상되었으나 실험체 우측 가력지점 스티프너 하단 용접부 균열이 발생하여 안정상의 이유로 실험을 중단하였다(Fig. 13). 횡비틀림좌굴 발생시점은 단부회전각(
인 시점에서 실험체의 추가적인 연성거동이 예상되었으나 실험체 우측 가력지점 스티프너 하단 용접부 균열이 발생하여 안정상의 이유로 실험을 중단하였다(Fig. 13). 횡비틀림좌굴 발생시점은 단부회전각(
 ) 2.2(
) 2.2(
 ) 부근이나 비틀림의 크기가 작아 실험 종료 후 육안으로는 횡비틀림좌굴을 관찰하기 어려웠다. 위에서 논의한 강도는 변위계로 관측한 횡좌굴 개시점 강도(
) 부근이나 비틀림의 크기가 작아 실험 종료 후 육안으로는 횡비틀림좌굴을 관찰하기 어려웠다. 위에서 논의한 강도는 변위계로 관측한 횡좌굴 개시점 강도(
 )이다. 횡좌굴 이후 변형경화 등에 의한 강도증진분 10~15%를 포함한 최대강도(
)이다. 횡좌굴 이후 변형경화 등에 의한 강도증진분 10~15%를 포함한 최대강도(
 )는 3개 시험체 모두 소성모멘트 강도를 상회하였다(Table 2 제6열 참조).
)는 3개 시험체 모두 소성모멘트 강도를 상회하였다(Table 2 제6열 참조).
|
Fig. 15 Failure modes(S4~S6) |
 로서 탄성횡좌굴의 발생이 예측되는 실험체로서
로서 탄성횡좌굴의 발생이 예측되는 실험체로서
 의 강도를 발휘하였다. 실험체 S5는
의 강도를 발휘하였다. 실험체 S5는
 로서
로서
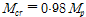 ,
,
 의 강도를 발휘하였다. 실험체 S6은
의 강도를 발휘하였다. 실험체 S6은
 로서
로서
 ,
,
 의 회전능력이 발휘되었다. 실험군 B 역시 좌굴발생이후 변형경화 등에 의해 10~30%정도의 강도증진을 볼 수 있다.
의 회전능력이 발휘되었다. 실험군 B 역시 좌굴발생이후 변형경화 등에 의해 10~30%정도의 강도증진을 볼 수 있다.
5.2 현행기준의 강도식과의 비교 및 변형능력평가
Fig. 16은 Table 2에 정리된 횡세장비에 따른 횡좌굴 개시점의 좌굴강도(
 )를 현행 설계식과 비교한 것이다. Fig. 16에서 보듯이 HSA800강재보는 현행기준이 제시하는 강도곡선을 크게 상회하는 강도를 발휘하며, “perfect beam” (곧 기하학적 불완전과 잔류응력이 존재하지 않는 이상적인 보)의 탄성횡좌굴-소성강도(elastic lateral buckling-plastic strength curve)에 더욱 일치하는 실험결과 값을 보였다.
)를 현행 설계식과 비교한 것이다. Fig. 16에서 보듯이 HSA800강재보는 현행기준이 제시하는 강도곡선을 크게 상회하는 강도를 발휘하며, “perfect beam” (곧 기하학적 불완전과 잔류응력이 존재하지 않는 이상적인 보)의 탄성횡좌굴-소성강도(elastic lateral buckling-plastic strength curve)에 더욱 일치하는 실험결과 값을 보였다.
즉 제한된 실험결과이긴 하지만, 비탄성 횡좌굴 영역의 강도를 소성모멘트(
 )와 탄성한계모멘트(
)와 탄성한계모멘트(
 )로서 직선보간하는 현행설계기준의 방식은 HSA800 강재보의 경우 매우 보수적인 결과를 준다. 현행 기준의 이러한 보수성은 잔류응력(
)로서 직선보간하는 현행설계기준의 방식은 HSA800 강재보의 경우 매우 보수적인 결과를 준다. 현행 기준의 이러한 보수성은 잔류응력(
 )을 강종에 상관없이 항복강도의 30%(
)을 강종에 상관없이 항복강도의 30%(
 )로 취하는 것과도 상관이 있어 보인다. 선행연구(Ramussen-Hancock[7], 이철호 등[15], Lee 등[16])에 의해 잔류응력의 크기는 항복강도에 무관한 것으로 확인된 바가 있는데, HSA800강재 보의 경우 항복강도 10% 정도로 계측된바가 있다. 이를 반영하여 비탄성 횡좌굴 강도를 규정한다면 현행기준의 고강도 강재에 대한 보수성이 일정부분 개선될 수 있다.
)로 취하는 것과도 상관이 있어 보인다. 선행연구(Ramussen-Hancock[7], 이철호 등[15], Lee 등[16])에 의해 잔류응력의 크기는 항복강도에 무관한 것으로 확인된 바가 있는데, HSA800강재 보의 경우 항복강도 10% 정도로 계측된바가 있다. 이를 반영하여 비탄성 횡좌굴 강도를 규정한다면 현행기준의 고강도 강재에 대한 보수성이 일정부분 개선될 수 있다.
|
(a) S1~S3 (relatively low warping constant specimens) |
|
(b) S4~S6 (relatively high warping constant specimens) |
Fig. 16 Comparison beam strength design curve (AISC 2010,KBC2009) with experiment results |
 )의 1.76, 2.27, 4.66배로 설계된 비탄성 횡좌굴 영역(
)의 1.76, 2.27, 4.66배로 설계된 비탄성 횡좌굴 영역(
 ) 실험체 S6, S3, S2 모두 소성강도(
) 실험체 S6, S3, S2 모두 소성강도(
 )를 상회하는 강도를 발현하였다. 이는 HSA800강재가 비탄성영역에서 높은 비탄성좌굴성능(유효단면강성)을 지니는 것을 시사하는 것으로 다음장의 이론적인 고찰을 통해 이점을 분명히 하고자 한다.
)를 상회하는 강도를 발현하였다. 이는 HSA800강재가 비탄성영역에서 높은 비탄성좌굴성능(유효단면강성)을 지니는 것을 시사하는 것으로 다음장의 이론적인 고찰을 통해 이점을 분명히 하고자 한다.
본 실험체는 현행기준에 의할 때 비탄성 LTB 영역 (즉
 )에 속하므로 소성회전능력에 대한 요구조건이 전혀 없었지만 소정의 회전능력이 발휘되었다. 그러나 비탄성회전능력의 존재는 예기치 않는 과하중 작용시 힘의 재분배에 의한 구조내력 증진에 중요한 역할을 하므로 바람직한 구조적 특성이 분명하다. 같은 스케일로 그려진 Fig. 12 및 14의 비교에서 보듯이 실험군 B의 변형능력이 상대적으로 열등한 것을 알 수 있다. 가령 대표적인 예로서
)에 속하므로 소성회전능력에 대한 요구조건이 전혀 없었지만 소정의 회전능력이 발휘되었다. 그러나 비탄성회전능력의 존재는 예기치 않는 과하중 작용시 힘의 재분배에 의한 구조내력 증진에 중요한 역할을 하므로 바람직한 구조적 특성이 분명하다. 같은 스케일로 그려진 Fig. 12 및 14의 비교에서 보듯이 실험군 B의 변형능력이 상대적으로 열등한 것을 알 수 있다. 가령 대표적인 예로서
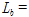
 로서
로서
 에 비해 훨씬 양호한 횡지지 조건을 지니는 S6의 경우
에 비해 훨씬 양호한 횡지지 조건을 지니는 S6의 경우
 으로서 S2의
으로서 S2의
 보다 미달하는 결과를 보여주고 있다. 이미 언급한 바와 같이 실험군 B는 실험군 A에 비해 뒤틀림에 의한 횡좌굴에 저항하는 성분이 큰 단면형상을 지니고 있다. 이 경우 횡좌굴 발생 이후 플랜지의 면외 변형이 증대되고 압축플랜지와 연속적으로 결합된 웨브의 변형까지 야기하여 단면전체의 강성저하를 유발하기 때문으로 추정된다.
보다 미달하는 결과를 보여주고 있다. 이미 언급한 바와 같이 실험군 B는 실험군 A에 비해 뒤틀림에 의한 횡좌굴에 저항하는 성분이 큰 단면형상을 지니고 있다. 이 경우 횡좌굴 발생 이후 플랜지의 면외 변형이 증대되고 압축플랜지와 연속적으로 결합된 웨브의 변형까지 야기하여 단면전체의 강성저하를 유발하기 때문으로 추정된다.
실험군 A 및 B에 속하는 실험체 S2,S3 및 S5,S6 웨브에서 계측된 변형률 자료를 비교한 결과 뒤틀림 강성에 의존도가 작은 S2,S3의 계측치는 횡좌굴 이후에도 초등휨이론에서 가정하는 평면유지상태가 유지되었다. 반면 실험체 S5,S6은 횡좌굴 이후 이런 상태가 유지되지 않았다. 이는 전술한 바와 같이 상부플랜지의 약축 면외변형(곧 뒤틀림 변형)의 결과로서 웨브에 국부변형이 유입된 때문으로 추측된다(참고로 실험군 A와 실험군 B의 웨브 폭-두께비는 각각 15.0와 25.0로서 실험군 B가 상대적으로 세장하다). 이러한 웨브의 국부변형은 황좌굴과 상호작용(interaction)하여 실험군 B에서 관측된 조기강도저하 및 회전능력의 저하를 야기한 것으로 판단된다. 이 실험결과는 횡좌굴과 국부좌굴의 상호작용 내지는 커플링(coupling)을 시사하는 것으로 이와 관련된 본격적 논의는 후속연구로 미루고자 한다.
실험체 S3의 스티프너 파단과 관련된 계측사항으로서 전높이스티프너 하단에 관찰된 플랜지 변형률은 단부회전각 2.2(
 )가 넘어서는 순간부터 변형률이 급격히 증가하기 시작하여 11% 변형률(인장시편 파단 변형률과 일치)에서 파단이 발생하였다. 이는 선행연구(이철호 등[6], Lee 등[15])에서 지적된 바와 같이 전높이스티프너 사용 시, 인장플랜지에 용접열영향이 유입되고 항복이후 큰 비탄성변형이 스티프너 하단에 집중될 수 있으므로 소성힌지 위치에는 가능하면 부분높이스티프너를 이용한 제작이 바람직하다. 본 실험에서도 부분높이스티프너를 사용한 실험체 S6은 실험종국까지 변형집중이 일어나지 않고, 파단현상이 발생하지 않았다.
)가 넘어서는 순간부터 변형률이 급격히 증가하기 시작하여 11% 변형률(인장시편 파단 변형률과 일치)에서 파단이 발생하였다. 이는 선행연구(이철호 등[6], Lee 등[15])에서 지적된 바와 같이 전높이스티프너 사용 시, 인장플랜지에 용접열영향이 유입되고 항복이후 큰 비탄성변형이 스티프너 하단에 집중될 수 있으므로 소성힌지 위치에는 가능하면 부분높이스티프너를 이용한 제작이 바람직하다. 본 실험에서도 부분높이스티프너를 사용한 실험체 S6은 실험종국까지 변형집중이 일어나지 않고, 파단현상이 발생하지 않았다.
6. H형강보 비탄성 횡좌굴 거동의 이론적 고찰
본 장에서는 일반강 및 고강도 강의 응력도-변형도 특성을 반영한 횡지지거리에 따른 비탄성 횡좌굴 강도식을 해석적으로 유도한 후 추가적인 고찰을 진행코자 한다.
|
Fig. 17 Typical moment-curvature relationship of H-section with SM490 and HSA800 steel |
대표적인 일반강으로서 항복참이 존재하는 SM490강재와 항복참이 없는 HSA800강재의 전형적 모멘트-곡률관계를 우선파악할 필요가 있다. Fig. 17은 실험군 A(H-250×150 ×15×15)단면에 각 강재의 대표 물성치를 넣어 해석한 결과를 보여주고 있다.
설계 시 가정한 소성모멘트강도(
 )를 기준으로 단면 내 곡률의 변화를 비교해보면 아래와 같다. SM490강재는 항복(
)를 기준으로 단면 내 곡률의 변화를 비교해보면 아래와 같다. SM490강재는 항복(
 ) 이후 항복참구간(
) 이후 항복참구간(
 )을 가짐으로 인해서 소성모멘트 도달시까지 상당한 비탄성변형을 필요로 한다. 소성모멘트 발현시점은 항복참구간의 길이에 비례하여 커지며 곡률
)을 가짐으로 인해서 소성모멘트 도달시까지 상당한 비탄성변형을 필요로 한다. 소성모멘트 발현시점은 항복참구간의 길이에 비례하여 커지며 곡률
 인 곳에서 발현된다.
인 곳에서 발현된다.
반면 HSA800강재는 SM490강재와 달리 항복참을 거치지 않고 조기에 변형경화가 발생함에 따라 곡률

 인 곳에서 소성강도가 발현되는 것을 알 수 있다. 이를 통해 항복참이 없는 고강도 강재의 경우 소성모멘트 발현을 위해 일반강재에 비해 상당히 작은 비탄성변형이 필요하며 항복참의 존재로 인해 발생하는 비탄성구간(
인 곳에서 소성강도가 발현되는 것을 알 수 있다. 이를 통해 항복참이 없는 고강도 강재의 경우 소성모멘트 발현을 위해 일반강재에 비해 상당히 작은 비탄성변형이 필요하며 항복참의 존재로 인해 발생하는 비탄성구간(

 )이 상당부분 축소될 수 있음을 간접적으로 보여주고 있다.
)이 상당부분 축소될 수 있음을 간접적으로 보여주고 있다.
6.2 횡지지거리 대 횡비틀림좌굴강도 일반관계식의 유도
본 절에서 앞의 모멘트-곡률관계를 통해 얻은 결과를 이용하여 항복참이 있는 강재(SM490)와 항복참이 없는 강재(HSA800)의 소성강도 발현에 필요한 횡지지거리(
 )를 도출하도록 한다. 소성횡지지거리를 제안을 위해서는 비탄성영역에서 단면이 지니는 유효강성을 분석하는 방법이 필요하며 본 연구에서는 비탄성상태의 강재가 보이는 슬립밴드(slip- band)거동까지 반영한 유효단면강성법을 응용하여 접근하였다. 유효단면강성법은 항복모멘트 이상의 휨을 받아 비탄성상태의 응력-변형률 보이는 단면의 등가유효강성을 산정하여 탄성이론해를 활용하는 방법이다.
)를 도출하도록 한다. 소성횡지지거리를 제안을 위해서는 비탄성영역에서 단면이 지니는 유효강성을 분석하는 방법이 필요하며 본 연구에서는 비탄성상태의 강재가 보이는 슬립밴드(slip- band)거동까지 반영한 유효단면강성법을 응용하여 접근하였다. 유효단면강성법은 항복모멘트 이상의 휨을 받아 비탄성상태의 응력-변형률 보이는 단면의 등가유효강성을 산정하여 탄성이론해를 활용하는 방법이다.
본 연구에서 도출하고자 하는 비탄성상태의 소성횡지지거리(식(6))을 수학적으로 축약하여 표현하면 아래와 같다. 식(6)은 앞의 Timosenko가 제시한 횡좌굴 강도곡선(식 (1))을 횡지지거리(
 )의 양함수 형태로 표현하고, 식(7)을 구성하는 유효약축휨강성
)의 양함수 형태로 표현하고, 식(7)을 구성하는 유효약축휨강성
 ,유효뒤틀림강성
,유효뒤틀림강성
 ,유효비틀림강성
,유효비틀림강성
 을 재산정하여 비탄성상태에서 적합한 횡지지거리를 도출하고, 횡지지거리대 횡좌굴모멘트 강도를 단일식 형태로 유도하기 위함이다.
을 재산정하여 비탄성상태에서 적합한 횡지지거리를 도출하고, 횡지지거리대 횡좌굴모멘트 강도를 단일식 형태로 유도하기 위함이다.
 (6)
(6)
 ,
,
 (7)
(7)
여기서,
 은 면내모멘트 강도를 의미하며,
은 면내모멘트 강도를 의미하며,
 는 유효약축휨강성,
는 유효약축휨강성,
 는 유효뒤틀림강성,
는 유효뒤틀림강성,
 는 유효비틀림강성을 의미한다.
는 유효비틀림강성을 의미한다.
6.2.1 SM490, HSA800 강재 비탄성상태의 접선계수변화
항복참이 있는 강재와 항복참이 없는 강재에 유효강성을 도출하기 위해서는 아래와 같이 각 강재의 변형률에 따른 비탄성구간 유효강성계수 값을 명확히 정의할 필요가 존재하였다. 항복 참이 있는 강재의 경우, 비탄성구간의 접선계수를 정의하기 위해 Nadal[17], Donnell[18] 등에 의해 제시된 슬립밴드 이론을 이용하였다.
슬립밴드 이론은 삼선형 모델에서 항복참구간의 실제 접선계수(
 )가 0이 아닌 유한 값을 지닌다는 논리로 재료공학적으로 잘알려져 있듯이 항복참구간의 변형은 Fig. 18에서 보듯이 다양한 슬립평면(Slip plane,
)가 0이 아닌 유한 값을 지닌다는 논리로 재료공학적으로 잘알려져 있듯이 항복참구간의 변형은 Fig. 18에서 보듯이 다양한 슬립평면(Slip plane,
 )이 발생하면서 나타나는 소성흐름(Plastic flow)의 결과이다. 즉, 슬립이 발생한 평면이 강재의 소성변형에 기여를 하고, 슬립이 생기지 않은 면은 강재의 탄성변형에만 기여를 하게 된다. 따라서 강재의 소성변형을 슬립이 발생한 구간의 기여분과 발생하지 않는 구간의 기여분으로 나누어 항복참구간(
)이 발생하면서 나타나는 소성흐름(Plastic flow)의 결과이다. 즉, 슬립이 발생한 평면이 강재의 소성변형에 기여를 하고, 슬립이 생기지 않은 면은 강재의 탄성변형에만 기여를 하게 된다. 따라서 강재의 소성변형을 슬립이 발생한 구간의 기여분과 발생하지 않는 구간의 기여분으로 나누어 항복참구간(

 )의 평균비탄성계수를 산출하면 0이 아닌 탄성계수(
)의 평균비탄성계수를 산출하면 0이 아닌 탄성계수(
 )와 경화접선계수(
)와 경화접선계수(
 )의 중간 값을 가지는 식(8)을 도출할 수 있다.
)의 중간 값을 가지는 식(8)을 도출할 수 있다.
|
Fig. 18 Conceptual diagram of slip deformation of steel for deriving tangent modulus in a yield plateau region |
 (단,
(단,
 ) (8)
) (8)
|
(a) Stress-strain curve(SM490) |
|
(b) Variation of tangent modulus(SM490) |
Fig. 19 Inelastic characteristic and tangent modulus variation of SM490 steel for theoretical analysis |
 는 항복참구간에서 접선계수,
는 항복참구간에서 접선계수,
 는 1축인장시편테이터에서 나타난 항복참구간의 변형률로 항복변형률(
는 1축인장시편테이터에서 나타난 항복참구간의 변형률로 항복변형률(
 )과 변형경화변형률(
)과 변형경화변형률(
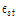 )사이의 값을 지닌다.
)사이의 값을 지닌다.
|
(a) Stress-strain curve(HSA800) |
|
(b) Variation of tangent Modulus(HSA800) |
Fig. 20 Inelastic characteristic and tangent modulus variation of HSA800 steel for theoretical analysis |
슬립밴드이론을 적용한 항복참이 있는 SM490강재의 응력-변형도 곡선 및 비탄성계수 변화는 Fig. 19와 같이 나타난다. Fig19(b)에서 보듯이 슬립밴드 이론을 적용하면 항복참구간에서 평균비탄성계수(식(8)) 값이 0이 아닌 탄성계수와 경화접선계수 중간의 값을 지니며 변형률에 따라 변화하는 형태의 곡선을 보인다.
반면, 항복참이 없는 강재 접선계수는 항복참구간 없이 바로 변형경화하므로 Fig. 20와 같이 응력-변형률을 미분한 값(
 )으로 비탄성영역의 접선계수를 산출할 수 있다.
)으로 비탄성영역의 접선계수를 산출할 수 있다.
6.2.2 항복참이 존재하는 일반강재의 유효약축단면강성
앞에서 구한 접선계수(
 ) 값을 바탕으로 소성모멘트 시 유효약축단면강성(
) 값을 바탕으로 소성모멘트 시 유효약축단면강성(
 )은 식 (9)와 같이 나타날 수 있다.
)은 식 (9)와 같이 나타날 수 있다.
 (9)
(9)
여기서,
 는 곡률변화에 따른 유효약축강성,
는 곡률변화에 따른 유효약축강성,
 는 유효접선계수를 나타낸다.
는 유효접선계수를 나타낸다.
|
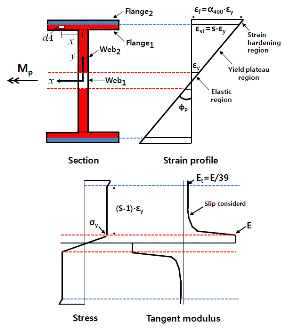
Fig. 21 Distribution of strain and tangent modulus of SM490 H-section at beam plastic moment(
|
 (10)
(10)
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
여기서,
 =탄성상태 웨브의 약축단면강성(식 (11)),
=탄성상태 웨브의 약축단면강성(식 (11)),
 =항복참구간 웨브의 약축단면강성(식(12)),
=항복참구간 웨브의 약축단면강성(식(12)),
 =항복참구간 플랜지의 약축단면강성(식 (13)),
=항복참구간 플랜지의 약축단면강성(식 (13)),
 =변형경화상태 플랜지의 약축단면강성(식 14))을 나타낸다.
=변형경화상태 플랜지의 약축단면강성(식 14))을 나타낸다.
 는 춤 높이,
는 춤 높이,
 플랜지 폭,
플랜지 폭,
 는 플랜지 두께,
는 플랜지 두께,
 웨브의 두께를 나타내며,
웨브의 두께를 나타내며,
 는 소성모멘트 도달 시 상부플랜지 변형률(
는 소성모멘트 도달 시 상부플랜지 변형률(
 )을 정의하기 위한 값이며,
)을 정의하기 위한 값이며,
 는 강재의 항복참길이로 SM490 강재의 경우 13을 나타내며,
는 강재의 항복참길이로 SM490 강재의 경우 13을 나타내며,
 는 변형경화시의 접선계수(=
는 변형경화시의 접선계수(=
 )를 나타내는 것으로 SM490 강재의 경우 39를 나타낸다.
)를 나타내는 것으로 SM490 강재의 경우 39를 나타낸다.
6.2.3 항복참이 없는 고강도 강재의 유효약축단면강성
Fig. 22은 항복참이 없는 HSA800 강재의 소성모멘트 발현 시 단면 내 변형률, 응력 및 접선계수 값들의 분포를 나타낸다. 이때의 유효약축단면강성은 식 (15)~(18)과 같이 표현된다.
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
여기서,
 =탄성상태 웨브의 약축단면강성(식(16)),
=탄성상태 웨브의 약축단면강성(식(16)),
 =변형경화구간 웨브의 약축단면강성(식(17)),
=변형경화구간 웨브의 약축단면강성(식(17)),
 =변형경화구간 플랜지의 약축단면강성(식(18))을 나타낸다.
=변형경화구간 플랜지의 약축단면강성(식(18))을 나타낸다.
 는 항복참이 없는 강재에서 할선에 의한 접선계수(Fig. 22(b))값을 나타내는 것으로 HSA800 강재의 경우
는 항복참이 없는 강재에서 할선에 의한 접선계수(Fig. 22(b))값을 나타내는 것으로 HSA800 강재의 경우
 의 값을 지닌다.
의 값을 지닌다.
6.2.4 유효뒤틀림 강성
유효뒤틀림강성
 은 플랜지가 지니는 유효강성(
은 플랜지가 지니는 유효강성(
 )을 통해 산출가능한 것으로 SM490강재의 경우 식(13),(14)를 통해 식 (19a)와 같이 표현가능하다.
)을 통해 산출가능한 것으로 SM490강재의 경우 식(13),(14)를 통해 식 (19a)와 같이 표현가능하다.
Table 3. Comparison of the effective section stiffness and lateral slenderness at beam plastic moment(
|
|||
Section |
Key results |
SM490 |
HSA800 |
H-250×150×15×15 |
(1) Effective lateral bending stiffness,
|
|
|
(2) Warping stiffness,
|
|
|
|
(3) Torsional stiffness,
|
4.70×
|
||
(4) Lateral slenderness(
|
17.8 |
20.7 |
|
 (19a)
(19a)
HSA800강재의 경우는 식 (18)를 통해 식 (19b)와 같이 표현가능하다.
 (19b)
(19b)
6.2.5 유효비틀림 강성
유효비틀림강성
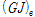 은 식(20)과 같이 탄성비틀림 강성과 동일한 강성이 유지된다고 보았는데 이는 선행연구 Neal[19], Galambos[20]에 의해 등분포모멘트와 같이 단면 내 전단력이 없는 경우 재료의 항복과 무관하게 탄성비틀림 강성이 유지된다고 것을 기초로 적용하였다.
은 식(20)과 같이 탄성비틀림 강성과 동일한 강성이 유지된다고 보았는데 이는 선행연구 Neal[19], Galambos[20]에 의해 등분포모멘트와 같이 단면 내 전단력이 없는 경우 재료의 항복과 무관하게 탄성비틀림 강성이 유지된다고 것을 기초로 적용하였다.
|
Fig. 22 Distribution of strain and tangent modulus of HSA800 H-section at beam plastic moment(
|
 (20)
(20)
Table 3은 식(6)~(20)을 실험군 A 단면에 적용했을 때의 유효강성 및 소성횡세장비 결과 값을 보여주고 있다. Table 3(4)에서 보듯이 HSA800강재의 요구되는 횡세장비는 20.7로 SM490강재에 요구되는 횡세장비 17.8 보다 더 길더라도 소성강도가 발현되는 것을 볼 수 있다. 위 결과는, 소성모멘트 발현 시 HSA800강재가 SM490강재에 비해 유효약축휨강성
 ,유효뒤틀림강성
,유효뒤틀림강성
 이 큰 값을 가지는 것에 기인하는 것으로 항복응력만 고려하는 현행기준의 산정식에서 고려하지 못하고 있는 거동이다.
이 큰 값을 가지는 것에 기인하는 것으로 항복응력만 고려하는 현행기준의 산정식에서 고려하지 못하고 있는 거동이다.
6.3 횡세장비에 따른 횡좌굴 강도곡선 비교
Fig. 23은 앞서 단면의 유효강성 계산 시 사용했던 Fig. 22(b)의 할선계수 값이 아닌 Fig. 22(a) 변형률에 따른 실제 접선계수 값(Fig. 19, 20)을 적용하여 SM490 강재 및 HSA800 강재의 횡세장비 대 모멘트강도를 구현한 결과를 보여주고 있다. 식 (6)에서 모멘트 강도를 소성모멘트(
 )에 국한시키지 않고, 단면의 곡률 변화에 따른 전 영역(탄성,비탄성,소성)에서의 모멘트강도(
)에 국한시키지 않고, 단면의 곡률 변화에 따른 전 영역(탄성,비탄성,소성)에서의 모멘트강도(
 )로 변경, 유효강성을 대입, 반복계산을 실행하면 1개의 식을 통해 전 영역에서의 횡세장비에 따른 모멘트 강도 곡선이 도시 할 수 있다.
)로 변경, 유효강성을 대입, 반복계산을 실행하면 1개의 식을 통해 전 영역에서의 횡세장비에 따른 모멘트 강도 곡선이 도시 할 수 있다.
Fig. 23의 횡세장비에 따른 면내강도곡선를 통해 고강도(HSA800)와 일반강재(SM490)의 차이를 비교해보면 고강도 강재는 항복모멘트가 커짐에 따라 탄성구간(Elastic Region)이 증가하고, 조기에 소성모멘트가 도달함에 따라 비탄성구간(Inelastic Region)이 짧아지고, 전소성모멘트구간(Plasic Region)이 증가하는 것을 관찰가능하다.
위 결과를 현행기준식(AISC-LRFD, KBC-2009)의 소성횡세장비(
 )와 비교하면 아래와 같다. 일반강(SM490)의 경우 현행기준식에 의한
)와 비교하면 아래와 같다. 일반강(SM490)의 경우 현행기준식에 의한
 =21.1이고, 본 연구 이론식에 의한 것은
=21.1이고, 본 연구 이론식에 의한 것은
 =17.8로서 현행 기준식이 더 낙관적인 값을 준다. 반면 고강도 강의 경우, 현행식은
=17.8로서 현행 기준식이 더 낙관적인 값을 준다. 반면 고강도 강의 경우, 현행식은
 =16.2이고 본 연구 이론식은
=16.2이고 본 연구 이론식은
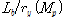 =19.9로서 현행식이 도리어 더 보수적인 결과를 준다.
=19.9로서 현행식이 도리어 더 보수적인 결과를 준다.
위 결과가 시사하는 것은 아래와 같다. 현행식은 기존 삼선형 재료모델에 재료의 항복강도변화에 따른 비탄성 거동 변화 특성을 반영하지 않고 항복강도 제곱근에 반비례적으로 일괄적으로 소성횡지지거리식을 규정하고 있다.
|
Fig. 23 Lateral slenderness ratio versus flexural strength curves (H-250*150*15*15, SM490, HSA800) |
하지만, 고강도 강재는 일반강재와 달리 항복참 없이 항복이후 조기 변형경화를 발현함에 따라 소성모멘트(
 )발현시 비탄성유효강성이 일반강재에 비해 크다. 이를 통해 강도발현 측면에서 현행식의 HSA800로의 확대,연장 적용은 보수적인 결과를 줄 수밖에 없음을 증명하였다. 또한, 비탄성 유효강성을 설계식에 적절히 고려한다면 고강도강재(HSA800)강재의 소성강도 발현을 위해 요구되는 횡지지거리가 일반강재(SM490)강재에 비해 도리어 완화하여 설계가능하며, 현행식을 통해 소성모멘트 이상(
)발현시 비탄성유효강성이 일반강재에 비해 크다. 이를 통해 강도발현 측면에서 현행식의 HSA800로의 확대,연장 적용은 보수적인 결과를 줄 수밖에 없음을 증명하였다. 또한, 비탄성 유효강성을 설계식에 적절히 고려한다면 고강도강재(HSA800)강재의 소성강도 발현을 위해 요구되는 횡지지거리가 일반강재(SM490)강재에 비해 도리어 완화하여 설계가능하며, 현행식을 통해 소성모멘트 이상(
 )의 초과강도를 발현시킬 수 있음을 시사한다.
)의 초과강도를 발현시킬 수 있음을 시사한다.
7. 요약 및 결론
본 연구에서는 국내에서 최근에 개발된 인장강도 800MPa급 고강도강 조립보의 비탄성 횡좌굴 거동에 대한 실험 및 해석적 연구를 수행하였다. 현행 국내외 비탄성 횡좌굴 기준은 분명한 항복참이 존재하는 일반 강재보의 실험을 바탕으로 제시된 것으로서, 항복참이 존재하지 않고 높은 항복비를 지니는 고강도 강재의 경우 현행 기준의 적용성 여부가 우선적으로 검증되어야 했기 때문이다.
(1)실험결과 고강도 강재는 현행식 대비 상당한 초과강도 및 소정의 회전능력을 발휘하였다. 실험에서 보인 좌굴강도는 완전보(perfect beam)의 탄성횡좌굴-소성강도곡선에 더욱 일치하는 현상을 보였다.
(2)회전능력은 뒤틀림강성에 의존가 작은 단면의 경우 횡좌굴 이후에도 초등휨이론에 따른 평면 유지상태가 유지되어 연성거동이 관찰되었다. 하지만, 뒤틀림강성에 의존도가 큰 실험체의 경우 횡좌굴 이후 횡좌굴 이후 상하플랜지에서 서로 반대방향으로 발생하는 약축휨의 결과로서 웨브에 국부변형이 유입되어 회전능력이 저하되는 것으로 판단되었다. 이는 개방형 단면의 횡좌굴시 횡좌굴과 웨브 국부좌굴과의 상호작용을 시사하는 것으로 고강도 적용시 웨브 판폭두께비와 관련한 추가적인 후속연구가 필요하다고 본다.
(3)실험에서 보인 높은 비탄성 좌굴 강도를 유효단면강성법을 이용하여 해석적으로 분석하였다. 고강도 강재보의 경우 비탄성 횡좌굴 영역에서 유효약축휨강성,유효뒤틀림강성이 일반강재에 비해 큰 값을 발휘됨이 확인되었다. 이는 고강도 강재보의 경우 비탄성 모멘트 도달시 항복참을 거치지 않고 즉시 변형경화하는 특성 때문에 비탄성 유효강성이 일반강재에 비해 상대적으로 크기 때문이다. 결과적으로 현행 기준의 횡지지 거리 산정식을 고강도 강재보에 그대로 적용하면 보수적인 결과로 귀결된다. 현행 기준의 횡지지 거리 산정식은 소재의 항복강도만 반영할 뿐 항복 후의 물성(가령 항복참의 존재 유무, 변형경화의 정도)을 반영하지 못하는데 그 이유가 있다.
(4)본 연구에서는 일반강재와 고강도강재로 제작된 완전보 각각에 대해 탄성, 비탄성, 그리고 소성강도에 이르는 전영역에 대해 적용이 가능한 “횡지지지 거리 대 횡좌굴모멘트 강도”를 단일식의 형태로 유도하고 SM490 및 HSA800의 물성을 사례로 활용방안을 예시하였다. 이 관계식은 비탄성 횡좌굴에 미치는 강재물성의 여러 영향인자를 누락없이 분명하게 보여주므로 특정 강재의 탄소성물성을 반영한 횡지지거리 산정식의 정립에 기초로 활용할 수 있다.
Acknowledgments
본 연구는 국토해양부 “고성능재료 및 첨단시공기술 개발” 사업, POSCO “고성능강의 건축현장 적용성 향상을 위한 기초 및 응용기술연구” 사업, 교육과학기술부 “지속가능 건설을 위한 창의적 글로벌 신기술 개발” 사업에 의해 수행되었기에 이에 깊은 감사드립니다.
References
- Haaijer, G. (1961) Economy of high strength steelstructural members, Journal of Structural Division, ASCE, 87 (ST8), pp.1-23.
- McDermott, J.F. (1969) Plastic bending of A514 steel beams, Journal of Structural Division, ASCE, 95 (ST9), pp.1851-1871.
- 대한건축학회(2010) 건축구조기준 및 해설(KBC 2009), 기문당.AIK (2009) Koreabuildingcodeandcommentary-structural, Architectural Institute of Korea(in Korean).
- AISC (2010) Specification for Structural Steel Buildings, American Institue of Steel Construction, Chicago.
- 김종락 등(2011) 800MPa 고강도강 설계기준제정연구, 연구보고서, 한국강구조학회.Kim, J.R. et al.(2011) Research on Standardization of High-strength Steel, Research Report, KSSC, Korea (in Korean).
- 이철호, 한규홍, 박창희, 김진호, 이승은, 하태휴(2011) 국부좌굴을 고려한 고강도 조립 H형강 부재의 휨성능 실험, 한국강구조학회논문집, 한국강구조학회, 제23권, 제4호, pp.417-428.Lee, C.H., Han, K.H., Park, C.H., Kim, J.H., Lee, S.E., and Ha, T.H. (2011) Local Buckling and Inelastic Behavior of 800MPa High-Strength Steel Beams, Journal of Korean Society of Steel Construction, KSSC, Vol. 23, No. 4. pp.417-428 (in Korean).
- 유정한, 김주우, 양재근, 강주원, 이동우(2012) 중심압축력을 받는 건축구조용 고성능강(HSA800) 용접각형강관 압축재의 국부좌굴, 한국강구조학회논문집, 한국강구조학회, 제24권, 제4호, pp.435-442.Yoo, J.H., Kim, J.W., Yang, J.G., Kang, J.W., and Lee, D.W. (2012) Local Buckling of Built-up Square Tubular Comp-ression Members Fabricated with HSA800 High Performance Steels under Concentric Axial Loading,Journal of Korean Society of Steel Construction, KSSC, Vol. 24, No. 4. pp.435-442 (in Korean).
- Rasmussen, K.J.R. and Hancock, G.J. (1992) Slenderness Limits for High Strength Steel Sections,Journal of Constructional Steel Research, Vol. 23, pp.73-96.
- Ricles, J.M., Sause, R. and Green, P.S. (1998) High-Strength Steel:Implications of Material and Geometric Characteristics On Inelastic Flexural Behavior, Journal of Engineering Structures, Vol. 20, No. 4-6, pp.323-335.
- Green, P.G. (2000) The Inelastic Behavior of Flexural Members Fabricated from High PerformanceSteel, Ph.D. Dissertation, Lehigh University, Bethlehem, PA.
- Timoshenko, S.P. (1945) Theory of Bending, Torsion, and Buckling of Thin-Walled Members of Open Cross Section, Journal of the Franklin Institue, Vol. 239, No. 3,4,5, March, April, May 1945.
- Lay, M.G. and Galambos, T.V. (1965) Inelastic Steel Beams Under Uniform Moment, Journal of Structural Engineering, ASCE, Vol. 91, No. 5, pp.320-327.
- Galambos, T.V. (1968) Structural Members and Frames, Prentice-Hall, New York.
- Dibley, J.E. (1969) Lateral Torsional Buckling of I-Sections in Grade 55 Steel, Proceedings of Institution of Civil Engineers, Vol. 43, London, pp.559-327.
- 이철호, 김대경, 한규홍, 김진호, 이승은, 하태휴(2012) 고강도강재 단주의 압축강도 및 잔류응력 평가, 한국강구조학회논문집, 한국강구조학회, 제24권, 제1호, pp.23-34.Lee, C.H., Kim, D.K., Han, K.H., Kim, J.H., Lee, S.E., and Ha, T.H. (2012) Compressive strength and residual stress evaluation of stub columns fabricated of high strength steel, Journal of Korean Society of Steel Construction, KSSC, Vol. 24, No. 1. pp.23-34 (in Korean).
- Lee, C.H., Han, K.H., Uang., C.M., Kim, D.K., Park, C.H., and Kim, J.H. (2012) Flexural Strengthand Rotation Capacity of I-shaped Beams Fabricated from 800MPa Steel, ASCE, web-posted.
- Nadal, A. (1961) Theory of Flow and Fracture in Solids, Vol. 1, McGraw-Hill, New York.
- Donnell, L.H. (1942) Plastic Flow as an Unstable Process, Journal of Applied Mechanics, ASME, Vol. 9, June, 1942.
- Neal, B.G. (1950) The lateral Instability of Yielded Mild Steel Beams of Rectangular Cross- Section, Philosophical Transaction of the Royal Society of London, Series A, Mathematical and Physical Science, Vol. 242, No. 846, pp.197-242.
- Galambos, T.V. (1963) Inelastic Lateral Buckling of Beams, Journal of Structural Engineering, ASCE, pp.217-241.




 (
(
 )
) (
(
 )
) (
(
 )
) (
(
 )
)

 (
(
 )
)

 )
) =200,470
=200,470 =650,
=650,
 =800
=800 =775,
=775,
 =860
=860 =788 (Minimum:745)
=788 (Minimum:745) =842 (Range:830~970)
=842 (Range:830~970)





 )
)

 =0.575) between F.E.M and test
=0.575) between F.E.M and test 


 ,mm)
,mm) )
) )
) )
) )
) )
) =550 kN-m
=550 kN-m =15.6
=15.6 =102.1
=102.1 =1,069 kN-m
=1,069 kN-m =15.6
=15.6 =90.6
=90.6 ) were applied to
) were applied to
 and
and
 .
.  ) to unbraced length for plastic moment(
) to unbraced length for plastic moment(
 ) ratio.
) ratio. 

 )
)











 )
)  )
) [
[
 ]
]

 [
[
 ]
]

 [
[
 ]
]
 )
)
 )
)