지지형 전단연결재를 활용한 지하합성벽의 휨성능 평가
Copyright © 2022 by Korean Society of Steel Construction
초록
지하합성벽을 위한 전단연결재로 지지형 전단연결재(support type shear connector)가 개발되었다. 지지형 전단연결재를 활용한 지하합성벽의 구조성능을 평가하기 위해 휨실험을 실시하였다. 지지형 전단연결재 실험체의 감소계수를 적용하지 않은 공칭강도에 대한 항복하중의 비는 0.82, 최대하중의 비는 1.19로 나타났다. 감소계수를 적용한 공칭강도에 대한 항복하중의 비는 0.99, 최대하중의 비는 1.43으로 나타났다. 따라서 지지형 전단연결재를 활용한 지하합성벽은 합성보와 동일하게 설계 가능하며, 감소계수를 적용하지 않은 공칭강도로 설계할 수 있을 것으로 판단된다.
Abstract
A support type shear connector was developed as a shear connector for the basement composite wall. A bending test was conducted to evaluate the structural performance of the basement composite wall using the support type shear connector. The ratio of the yield load to the nominal strength without applying the reduction factor of the bending specimens using the support type shear connector was 0.82, and the ratio of the maximum load was 1.19. In addition, the ratio of the yield load to the nominal strength to which the reduction factor was applied was 0.99, and the ratio of the maximum load was 1.43. Therefore, the basement composite wall using the support type shear connector can be designed in the same way as composite beams, and it can be designed with the nominal strength without the reduction factor applied.
Keywords:
Basement, Composite wall, Shear connector, Structural performance, Bending performance키워드:
지하층, 합성벽, 전단연결재, 구조성능, 휨성능1. 서 론
건축물 지하공사는 흙막이 공사와 지하구조물 공사로 구분할 수 있다. 흙막이 공사에서 CIP공법, SCW공법 등으로 형성되는 흙막이 주열벽은 충분한 강도 및 강성을 가지고 있음에도 단순 가설흙막이로 활용되어 건설재료의 효율성이 저하되고 있다. 현재 건축구조기준에서는 지하구조물의 내진성능 검토를 의무화하고 있는데[1], 이는 지하외벽 두께 증가 및 지하공간 감소의 요인이 된다.
흙막이 공사의 CIP공법에서 엄지말뚝으로 사용되는 H파일은 띠장 설치가 용이하며 주열벽의 일체성 확보 및 횡력 저항 등의 역할을 한다. 가설흙막이로 사용되고 있는 H파일과 지하외벽을 합성한다면, 지하구조물 내진설계를 위해 지하외벽 두께를 크게 증가시키지 않고, 건설재료를 보다 효율적으로 활용할 수 있다. 따라서 건축물 지하구조물의 구조안전성과 경제성을 확보하기 위해서는 H파일과 지하외벽을 일체화시킨 지하합성벽의 개발이 필요하다.
전단연결재로 스터드 앵커를 활용한 지하합성벽의 휨 및 전단성능에 대한 연구는 다수 수행된 바 있다[2]-[5]. 그리고 H파일에 띠장 설치를 용이하게 하는 지지형 전단연결재(support type shear connector)가 개발되었다[6]. 지지형 전단연결재는 Fig. 1과 같이 띠장 지지용 브라켓 역할과 전단연결재 역할을 겸하며, 형상은 Fig. 2와 같이 2개의 웨브를 갖는다. 또한 강판을 절곡하여 제작하기 때문에 용도에 따라 다양한 크기로 사용 가능하다.
선행연구에서는 push-out 실험을 통해 지지형 전단연결재의 구조성능을 평가하였으며[6], 본 연구에선 지지형 전단연결재를 활용한 지하합성벽의 휨성능을 평가하고자 한다.
2. 실험계획
2.1 실험체 계획
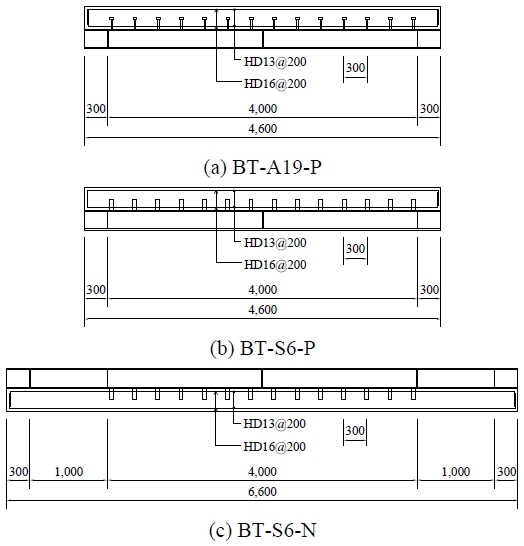
지지형 전단연결재를 활용하여 흙막이와 지하벽체를 합성한 지하합성벽의 구조성능을 평가하기 위해 Table 1과 같이 휨실험체를 제작하고 휨실험을 실시하였다. 휨실험체는 비교를 위해 전단연결재의 종류에 따라 스터드 앵커 실험체, 지지형 전단연결재 실험체로 구분하였다. 스터드 앵커는 D19를 적용하였으며, 지지형 전단연결재는 Fig. 2와 같이 높이 150 mm, 너비 150 mm, 길이 50 mm, 강재두께 6 mm를 적용하였다. 또한 가력방법에 따라 단순보 정모멘트로 가력하는 스터드 앵커 실험체(BT-A19-P)와 지지형 전단연결재 실험체(BT-S6-P), 연속보 부모멘트로 가력하는 지지형 전단연결재 실험체(BT-S6-N)로 각각 계획하였다.
휨실험체의 형상은 Fig. 3와 같으며, H형강(H-250×250×9×14) 상부 플랜지에 전단연결재를 용접한 후, 철근배근 및 콘크리트를 타설하여 실험체를 제작하였다. 단순보 정모멘트 실험체(BT-A19-P, BT-S6-P)는 합성률 60 %로 계획하여 전단연결재를 배치하였다. 연속보 부모멘트 실험체(BT-S6-N)는 단순보 정모멘트 실험체(BT-S6-P)와 동일하게 전단연결재를 배치하였으며, 지하합성벽 기초부의 거동을 확인하기 위해 지점과 반력장치 사이에는 전단연결재를 배치하지 않았다. 슬래브 두께는 지하벽체 두께를 고려하여 300 mm로 계획하였으며, 슬래브 폭은 합성보 유효폭을 고려하여 1,000 mm로 계획하였다.
2.2 가력 및 측정 방법
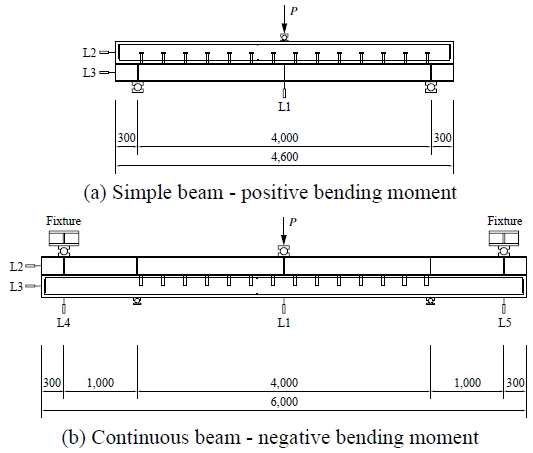
휨실험은 단순보 및 연속보 가력을 위해 실험체를 Fig. 4와 같이 설치하였다. 단순보 정모멘트 실험은 2개의 지점 위에 실험체를 설치하여 수행하였고, 연속보 부모멘트 실험은 2개의 지점 위에 실험체를 설치한 후 양단에 반력장치를 설치하여 수행하였다. 가력은 2,000 kN 용량의 actuator를 이용하여 1.5 mm/min의 속도로 단조가력하였다.
실험체 변위를 측정하기 위해 하단 중앙에 LVDT(L1)를 설치하였으며, H형강·슬래브의 슬립을 측정하기 위해 단부 각 단면의 중심에 LVDT(L2, L3)를 설치하였다. 연속보 부모멘트 실험의 경우 단부 슬래브의 처짐을 측정하기 위해 반력장치 하단 중앙에 LVDT(L4, L5)를 추가로 설치하였다.
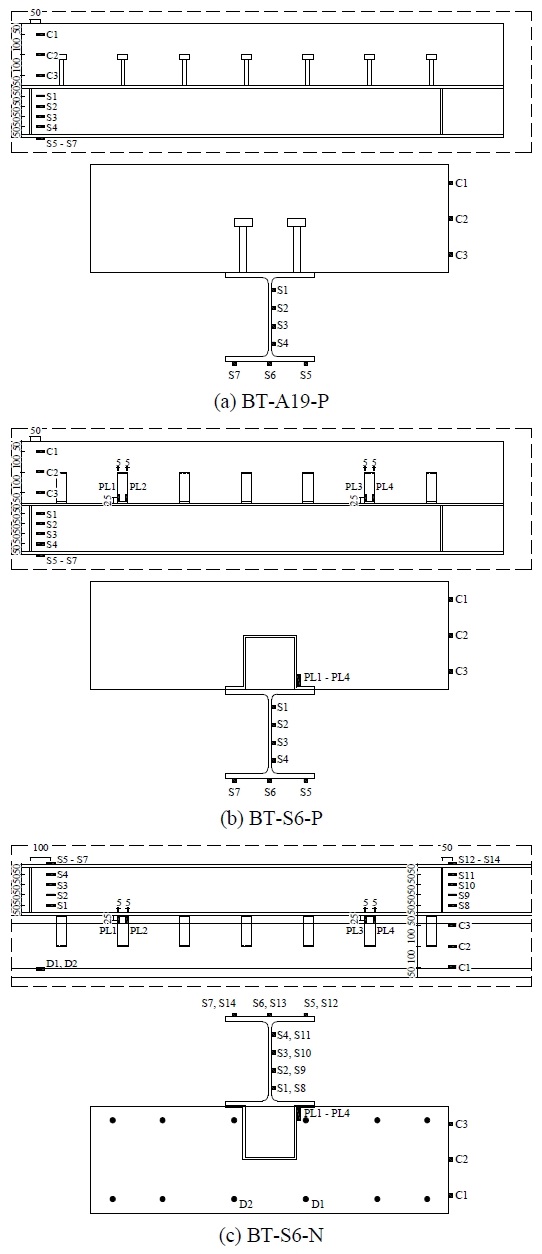
실험체의 변형률을 측정하기 위해 Fig. 5와 같이 스트레인 게이지를 부착하였다. 단순보 정모멘트로 가력하는 스터드 앵커 실험체(BT-A19-P)의 경우 실험체 중앙에서 50 mm 이격된 위치에 슬래브 측면은 100 mm 간격, H형강 웨브는 50 mm 간격, H형강 플랜지는 100 mm 간격으로 스트레인 게이지를 부착하였다.
단순보 정모멘트로 가력하는 지지형 전단연결재 실험체(BT-S6-P)의 경우 실험체 중앙에서 50 mm 이격된 위치에 슬래브 측면은 100 mm 간격, H형강 웨브는 50 mm 간격, H형강 플랜지는 100 mm 간격으로 스트레인 게이지를 부착하였다. 또한 지점 및 가력점에서 2번째에 위치한 지지형 전단연결재에는 H형강 플랜지에서 25 mm, 전단연결재의 단부에서 5 mm 이격된 위치에 스트레인 게이지를 부착하였다.
연속보 부모멘트로 가력하는 지지형 전단연결재 실험체(BT-S6-N)의 경우 실험체 중앙에서 100 mm 이격된 위치에 H형강 웨브는 50 mm 간격, H형강 플랜지는 100 mm 간격, 지점에서 50 mm 이격된 위치에 슬래브 측면은 100 mm 간격, H형강 웨브는 50 mm 간격, H형강 플랜지는 100 mm 간격으로 스트레인 게이지를 부착하였다. 또한 지점 및 가력점에서 2번째에 위치한 지지형 전단연결재에는 H형강 플랜지에서 25 mm, 전단연결재의 단부에서 5 mm 이격된 위치에 스트레인 게이지를 부착하였다.
3. 실험체의 공칭강도
3.1 전단연결재의 공칭강도
스터드 앵커의 공칭강도는 건축물 강구조설계기준(KDS 41 31 00, 이하 ‘기준’) 4.6.8에 따라 식 (1)과 같이 산정하였다[7]. Rg와 Rp는 슬래브 및 데크플레이트 조건에 따른 감소계수로, 골데크플레이트를 사용하지 않는 경우 Rg는 1.0, Rp는 0.75를 사용하고 있다. 본 연구에서는 실험결과와 비교하기 위해 Rg와 Rp에 1.0을 적용하여 공칭강도(Qn1)를 산정하였으며, 감소계수의 영향을 검토하기 위해 Rg는 1.0, Rp는 0.75를 적용하여 공칭강도(Qn2)를 산정하였다.
| (1) |
여기서, fck: 콘크리트의 압축강도,
- Ec: 콘크리트의 탄성계수,
- Asa: 스터드 앵커의 단면적,
- Fu: 스터드 앵커의 인장강도,
- Rg, Rp: 감소계수.
선행연구에서는 기준 4.6.8을 참조하여 지지형 전단연결재의 공칭강도를 식 (2)와 같이 산정하였으며[6],[7], 지지형 전단연결재의 길이가 35 mm - 100 mm일 경우 감소계수를 적용하지 않은 공칭강도로 설계할 수 있음을 확인하였다. 본 연구에서는 실험결과와 비교하기 위해 Rs는 1.0을 적용하여 공칭강도(Qn1)를 산정하였으며, 강재의 전단파괴 영향을 검토하기 위해 Rs는 0.6을 적용하여 공칭강도(Qn2)를 산정하였다[8]-[10].
| (2) |
여기서, Asw: 강재 웨브의 단면적,
- Fu: 강재의 인장강도,
- Rs: 감소계수.
3.2 합성보의 공칭휨강도
정모멘트를 받는 노출형 합성보의 공칭휨강도는 소성중립축 산정 후 소성응력분포(Fig. 6)에 따라 식 (3)과 같이 산정한다[10]. 정모멘트가 최대가 되는 위치와 모멘트가 0이 되는 위치 사이의 총수평전단력은 콘크리트의 압괴, 강재단면의 인장항복, 그리고 강재앵커(전단연결재)의 강도의 3가지 한계상태로부터 구한 값 중에서 최솟값으로 한다[7]. 본 연구에서는 휨실험체의 공칭휨모멘트를 산정 후 가력조건을 반영하여 공칭강도를 산정하였으며, 재료시험결과를 사용하였다.
| (3) |
여기서, C: 0.85fckAc, FyAs, ΣQn 중 최솟값,
- Ac: 유효폭 내의 콘크리트 단면적,
- As: 강재단면적,
- ΣQn: 정모멘트 최대 및 0 사이의 강재앵커 공칭강도 합,
- Py: 강재단면의 인장강도, Py = FyAs,
- d1: 콘크리트의 압축력 C의 중심으로부터 강재단면의 상단까지 거리,
- d2: 강재단면의 압축력 중심으로부터 강재단면의 상단까지 거리,
- d3: Py가 작용하는 강재 단면의 중심으로부터 강재단면의 상단까지 거리.
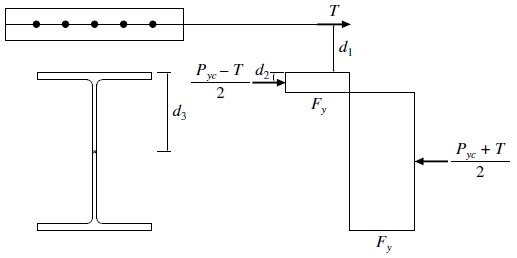
부모멘트를 받는 노출형 합성보의 공칭휨강도는 소성중립축 산정 후 소성응력분포(Fig. 7)에 따라 식 (4)와 같이 산정한다[10]. 부모멘트가 최대가 되는 위치와 모멘트가 0이 되는 위치 사이의 총수평전단력은 슬래브철근의 항복과 강재앵커(전단연결재)의 강도의 2가지 한계상태로부터 구한 값 중에서 최솟값으로 한다[7]. 본 연구에서는 휨실험체의 공칭휨모멘트를 산정 후 가력조건을 반영하여 공칭강도를 산정하였으며, 재료시험결과를 사용하였다.
| (4) |
여기서, T: FyrAr, ΣQn 중 최솟값,
- Ar: 유효폭 내의 길이방향철근 단면적,
- Fyr: 철근의 설계기준항복강도,
- ΣQn: 부모멘트 최대 및 0 사이의 강재앵커 공칭강도 합,
- Pyc: 강재단면의 압축강도, Pyc = FyAs,
- d1: 길이방향 슬래브철근의 중심으로부터 강재단면의 상단까지 거리,
- d2: 강재단면의 인장력 중심으로부터 강재단면의 상단까지 거리,
- d3: Pyc로부터 강재단면의 상단까지 거리.
4. 실험결과
4.1 재료시험결과
휨실험체 제작에 사용된 재료 특성을 파악하기 위해 재료시험을 실시하였다. 스터드 앵커 HS1(D19), 강판 SS275(6 mm, 9 mm, 14 mm), 철근 SD400(D13, D16)에 대한 강재 인장시험과 콘크리트 압축강도시험을 수행하였다.
강재 인장시험결과는 항복강도 및 인장강도, 연신율로 정리하였으며, Table 2와 같다. 콘크리트 압축강도시험결과는 Table 3와 같다.
4.2 휨실험결과
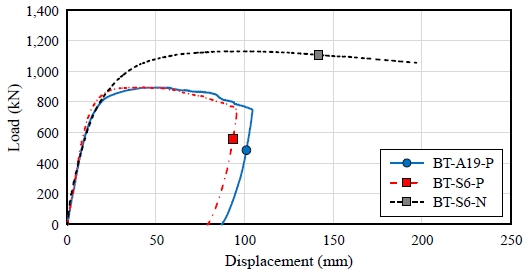
휨실험체의 하중-변위 곡선은 Fig. 8과 같다. BT-S6-N 실험체의 경우 가력과정에서 탈락된 슬래브 콘크리트 조각이 LVDT를 충격하여 충격 이전까지의 하중-변위 곡선을 나타낸 것이다.
휨실험결과를 초기강성, 하중 및 변위로 정리하면 Table 4와 같다. Pmax는 실험시 최대하중이며, δPmax는 최대하중시 변위이다. K는 초기강성으로 최대하중의 20 % - 40 % 하중구간의 기울기로 산정하였다. Pyield는 항복하중, δPyield는 항복하중시 변위로, 초기강성의 1/3 기울기를 갖는 선분을 하중-변위 곡선과 접하도록 평행이동하고, 초기강성 선분과 만나는 점으로 산정하였다[6],[11]-[14]. 변형능력은 항복하중시 변위에 대한 최대하중시 변위의 비(δPmax/δPyield)로 평가하였다.
BT-A19-P 실험체는 전단연결재로 D19 스터드 앵커를 적용한 단순보 정모멘트 가력 실험체이다. 해당 실험체의 초기강성은 61.8 kN/mm, 항복하중은 633.0 kN, 항복하중시 변위는 10.0 mm로 나타났다. 최대하중은 899.2 kN으로 항복하중의 1.42배이며, 최대하중시 변위는 52.3 mm로 항복하중시 변위의 5.23배로 나타났다.
BT-S6-P 실험체는 전단연결재로 두께 6 mm, 길이 50 mm인 지지형 전단연결재를 적용한 단순보 정모멘트 가력 실험체이다. 해당 실험체의 초기강성은 68.0 kN/mm, 항복하중은 674.4 kN, 항복하중시 변위는 9.9 mm로 나타났다. 최대하중은 900.0 kN으로 항복하중의 1.33배이며, 최대하중시 변위는 42.3 mm로 항복하중시 변위의 4.27배로 나타났다. 동일한 성능으로 계획한 실험체(BT-A19-P)와 비교하면 BT-S6-P 실험체가 초기강성과 항복하중은 높고, 최대하중은 유사하며, 변형능력은 작게 나타났다.
BT-S6-N 실험체는 전단연결재로 두께 6 mm, 길이 50 mm인 지지형 전단연결재를 적용한 연속보 부모멘트 가력 실험체이다. 해당 실험체의 초기강성은 48.4 kN/mm, 항복하중은 713.3 kN, 항복하중시 변위는 12.6 mm로 나타났다. 최대하중은 1,136.5 kN으로 항복하중의 1.59배이며, 최대하중시 변위는 90.5 mm로 항복하중시 변위의 7.18배로 나타났다. 전단연결재 배치가 동일한 실험체(BT-S6-P)와 비교하면 BT-S6-N 실험체가 초기강성은 낮지만, 항복하중 및 최대하중은 높고, 변형능력은 크게 나타났다.
4.3 파괴양상
BT-A19-P 실험체의 파괴양상은 Fig. 9과 같이 실험체의 처짐과 함께 휨파괴의 경향을 나타내며, 가력점 부근 콘크리트 슬래브의 균열과 압축파괴가 나타났다. H형강과 슬래브의 슬립을 측정하기 위해 단부 각 단면의 중심에 설치한 LVDT(L2, L3)의 슬립 곡선은 최대하중 이전에는 H형강과 슬래브가 합성 거동을 하며, 최대하중 이후 H형강과 슬래브 사이의 슬립을 발생하였음을 나타낸다. 각 단면의 중심에서 측정한 값의 차이는 최대 4.3 mm이며, 실험종료 후 H형강과 슬래브 사이의 슬립은 12 mm로 나타났다.
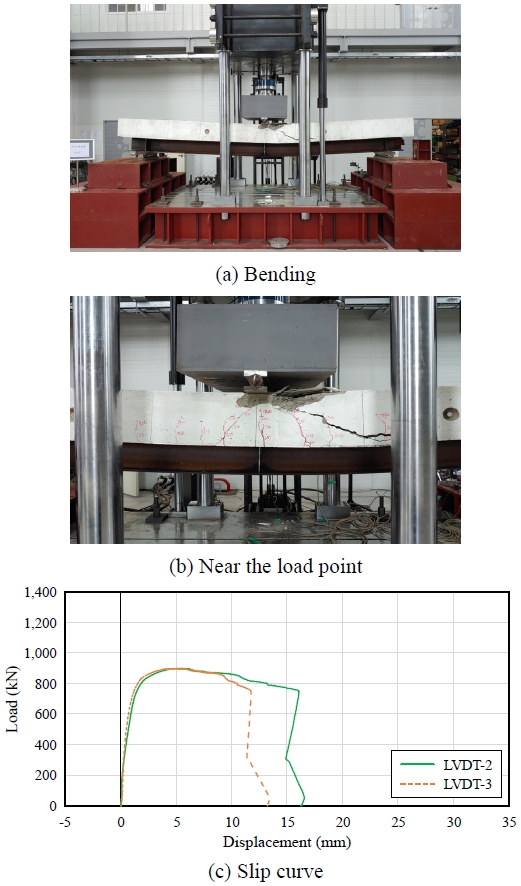
BT-S6-P 실험체의 파괴양상은 Fig. 10과 같이 실험체의 처짐과 함께 휨파괴의 경향을 나타내며, 가력점 부근 콘크리트 슬래브의 균열과 압축파괴가 나타났다. LVDT(L2, L3)의 슬립 곡선은 최대하중 이전에는 H형강과 슬래브가 합성 거동을 하며, 최대하중 이후 H형강과 슬래브 사이의 슬립을 발생하였음을 나타낸다. 각 단면의 중심에서 측정한 값의 차이는 최대 4.3 mm이며, 실험종료 후 H형강과 슬래브 사이의 슬립은 8 mm로 나타났다. BT-S6-P 실험체는 BT-A19-P 실험체와 파괴양상이 동일하게 나타났으며, 초기강성, 하중 및 변형능력으로 미루어보아 지지형 전단연결재(두께 6 mm, 길이 50 mm)와 스터드 앵커(D19)는 동일한 성능을 발휘하는 것으로 판단된다.
BT-S6-N 실험체의 파괴양상은 Fig. 11과 같이 실험체의 처짐과 함께 휨파괴의 경향을 나타내고 있으며, 가력점 부근 콘크리트 슬래브의 균열과 H형강의 국부좌굴이 나타났다. LVDT(L2, L3) 슬립 곡선에서 슬래브 단부의 변형은 거의 없었으나, H형강 단부의 변형은 크게 나타났다. 각 단면의 중심에서 측정한 값의 차이는 최대 32.1 mm이며, 실험종료 후 H형강과 슬래브 사이의 슬립은 27 mm로 나타났다. 또한 단부 슬래브의 처짐을 측정하기 위해 반력장치 하단 중앙에 설치한 LVDT(L4, L5)의 곡선에서 단부 슬래브의 처짐은 5 mm - 7 mm로 나타났다. 지하합성벽 기초부의 거동을 확인하기 위해 지점과 반력장치 사이에는 전단연결재를 배치하지 않았다. LVDT(L2, L3, L4, L5)에서 측정한 BT-S6-N 실험체의 단부 거동은 지점 부근 콘크리트 슬래브의 균열, 지점과 반력장치 사이의 전단연결재 부재로 인한 것으로 판단된다.
4.4 내력비교
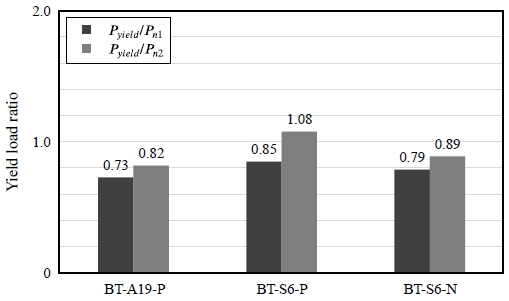
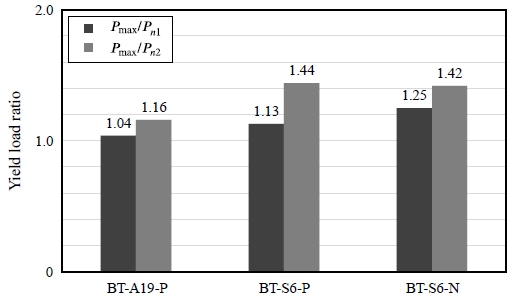
휨실험결과의 항복하중과 최대하중을 공칭강도와 비교하면 Table 5, Figs. 12-13과 같다. Pn1은 감소계수를 적용하지 않은 공칭강도이며, 스터드 앵커는 Rp = 1.0을 적용한 공칭강도, 지지형 전단연결재는 Rs = 1.0을 적용한 공칭강도이다. Pn2는 감소계수를 적용한 공칭강도이며, 스터드 앵커는 Rp = 0.75를 적용한 공칭강도, 지지형 전단연결재는 Rs = 0.6을 적용한 공칭강도이다.
BT-A19-P 실험체는 전단연결재로 D19 스터드 앵커를 적용한 단순보 정모멘트 가력 실험체이다. 감소계수를 적용하지 않은 공칭강도(Pn1)에 대한 항복하중의 비는 0.73, 최대하중의 비는 1.04로 나타났다. 감소계수를 적용한 공칭강도(Pn2)에 대한 항복하중의 비는 0.82, 최대하중의 비는 1.16으로 나타났다.
BT-S6-P 실험체는 전단연결재로 두께 6 mm, 길이 50 mm인 지지형 전단연결재를 적용한 단순보 정모멘트 가력 실험체이다. 감소계수를 적용하지 않은 공칭강도(Pn1)에 대한 항복하중의 비는 0.85, 최대하중의 비는 1.13으로 나타났다. 감소계수를 적용한 공칭강도(Pn2)에 대한 항복하중의 비는 1.08, 최대하중의 비는 1.44로 나타났다.
BT-S6-N 실험체는 전단연결재로 두께 6 mm, 길이 50 mm인 지지형 전단연결재를 적용한 연속보 부모멘트 가력 실험체이다. 감소계수를 적용하지 않은 공칭강도(Pn1)에 대한 항복하중의 비는 0.79, 최대하중의 비는 1.25로 나타났다. 감소계수를 적용한 공칭강도(Pn2)에 대한 항복하중의 비는 0.89, 최대하중의 비는 1.42로 나타났다.
지지형 전단연결재 실험체(BT-S6-P, BT-S6-N)의 감소계수를 적용하지 않은 공칭강도(Pn1)에 대한 항복하중의 비는 0.82, 최대하중의 비는 1.19로 나타났다. 감소계수를 적용한 공칭강도(Pn2)에 대한 항복하중의 비는 0.99, 최대하중의 비는 1.43으로 나타났다. 따라서 지지형 전단연결재를 활용한 지하합성벽은 합성보와 동일하게 설계 가능하며, 감소계수를 적용하지 않은 공칭강도로 설계할 수 있을 것으로 판단된다. 또한 지지형 전단연결재의 안전율을 높게 설계할 경우 강재의 전단파괴를 고려하여 감소계수를 적용한 공칭강도로 설계할 수 있을 것으로 판단된다.
4.5 변형률
BT-A19-P 실험체 가력점 부근(정모멘트 구간)의 변형률 분포를 300 kN, 500 kN, 633 kN(항복하중), 800 kN, 899 kN(최대하중)의 하중별로 나타내면 Fig. 14(a)와 같다. 강재 단면의 S1, S2, S3, S4, S6 변형률은 인장변형률로 나타났으며, 하중의 증가에 따라 인장변형률이 증가하였다. 콘크리트 단면의 C2, C3 변형률은 인장변형률로 나타났으며, 하중의 증가에 따라 인장변형률이 증가하였다. Fig. 14(b)와 같이 콘크리트 슬래브의 균열이 스트레인 게이지를 지나며 인장변형률이 나타난 것으로 판단된다. 콘크리트 단면의 C1 변형률은 896 kN 이전 압축변형률, 896 kN 이후 인장변형률로 나타났다. BT-A19-P 실험체는 불완전 합성보 거동을 하며, 콘크리트 압축응력은 C1 부근, 소성중립축은 플랜지 부근에 형성된 것으로 판단된다.
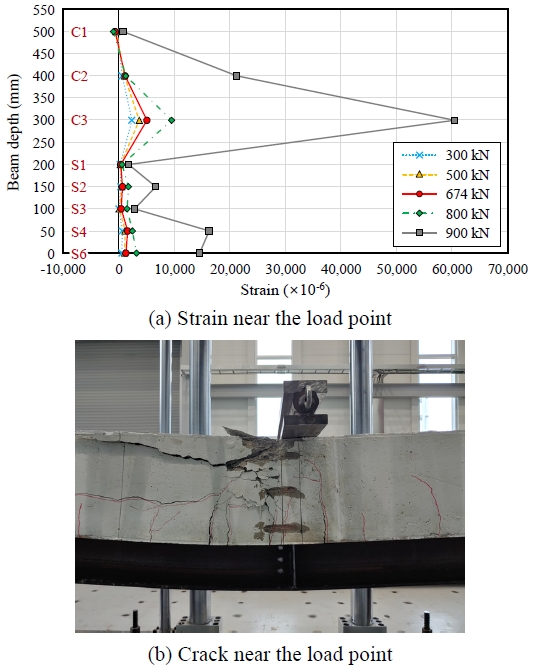
BT-S6-P 실험체 가력점 부근(정모멘트 구간)의 변형률 분포를 300 kN, 500 kN, 674 kN(항복하중), 800 kN, 900 kN(최대하중)의 하중별로 나타내면 Fig. 15(a)와 같다. 강재 단면의 S1, S2, S3, S4, S6 변형률은 인장변형률로 나타났으며, 하중의 증가에 따라 인장변형률이 증가하였다. 콘크리트 단면의 C2, C3 변형률은 압축변형률로 나타났으며, 하중의 증가에도 변형률은 크게 변하지 않았다. Fig. 15(b)와 같이 콘크리트 슬래브의 균열이 스트레인 게이지의 양옆을 지나며 변형률이 크게 변하지 않은 것으로 판단된다. 콘크리트 단면의 C1 변형률은 230 kN 이전 압축변형률, 230 kN 이후 인장변형률로 나타났다. BT-S6-P 실험체는 불완전 합성보 거동을 하며, 콘크리트 압축응력은 C1 부근, 소성중립축은 플랜지 부근에 형성된 것으로 판단된다. Fig. 15(c)는 지지형 전단연결재의 변형률을 나타낸 것이다. H형강과 슬래브 사이의 슬립으로 지지형 전단연결재에 변형률이 나타나며, 800 kN 이후 지지형 전단연결재의 파괴가 발생한 것으로 판단된다.
BT-S6-N 실험체 가력점 부근(부모멘트 구간)의 변형률 분포를 300 kN, 500 kN, 713 kN(항복하중), 900 kN, 1,000 kN, 1,137 kN(최대하중)의 하중별로 나타내면 Fig. 16(a)와 같다. 철근의 D1 변형률은 인장변형률로 나타났다. 강재 단면의 S2, S3, S4, S6 변형률은 압축변형률로 나타났으며, 하중의 증가에 따라 압축변형률이 증가하였다. 강재 단면의 S1 변형률은 375 kN 이전 압축변형률, 375 kN - 860 kN 인장변형률, 860 kN 이후 압축변형률로 나타났다. Fig. 16(b)와 같이 웨브에 국부좌굴이 발생해 860 kN 이후 S1이 압축변형률로 나타난 것으로 판단된다. BT-S6-N 실험체의 부모멘트 구간 소성중립축은 S1 부근에서 형성된 것으로 판단된다.
BT-S6-N 실험체 지점 부근(정모멘트 구간)의 변형률 분포는 Fig. 16(c)와 같다. 강재 단면의 S10, S11, S13 변형률은 인장변형률로 나타났으며, 하중의 증가에 따라 인장변형률이 증가하였다. 강재 단면의 S8, S9 변형률은 압축변형률로 나타났으며, 하중의 증가에 따라 압축변형률이 증가하였다. 콘크리트 단면의 C2, C3 변형률은 인장변형률로 나타났으며, 하중의 증가에 따라 인장변형률이 증가하였다. Fig. 16(d)와 같이 콘크리트 슬래브의 균열이 스트레인 게이지를 지나며 인장변형률이 나타난 것으로 판단된다. 콘크리트 단면의 C1 변형률은 891 kN 이전 압축변형률, 891 kN 이후 인장변형률로 나타났다. 지점 사이에는 전단연결재는 배치하였지만, 지점과 반력장치 사이에는 배치하지 않아 BT-S6-N 실험체 정모멘트 구간의 콘크리트 압축응력은 C1 부근, 소성중립축은 S9 부근에 형성된 것으로 판단된다. Fig. 16(e)는 지지형 전단연결재의 변형률을 나타낸 것이다. H형강과 슬래브 사이의 슬립으로 지지형 전단연결재에 변형률이 나타나며, 1,100 kN 이후 지지형 전단연결재의 파괴가 발생한 것으로 판단된다.
따라서 지지형 전단연결재를 활용한 지하합성벽은 합성보와 동일하게 설계 가능하며, 감소계수를 적용하지 않은 공칭강도로 설계할 수 있을 것으로 판단된다.
5. 결 론
지하합성벽을 위한 전단연결재로 지지형 전단연결재(support type shear connector)가 개발되었다. 지지형 전단연결재를 활용한 지하합성벽의 구조성능을 평가하기 위해 휨실험을 실시하였으며, 다음과 같은 결론을 도출하였다.
- (1) 휨실험 결과, 스터드 앵커 실험체의 감소계수를 적용하지 않은 공칭강도(Pn1)에 대한 항복하중의 비는 0.73, 최대하중의 비는 1.04로 나타났다. 감소계수를 적용한 공칭강도(Pn2)에 대한 항복하중의 비는 0.82, 최대하중의 비는 1.16으로 나타났다.
- (2) 지지형 전단연결재 실험체의 감소계수를 적용하지 않은 공칭강도(Pn1)에 대한 항복하중의 비는 0.82, 최대하중의 비는 1.19로 나타났다. 감소계수를 적용한 공칭강도(Pn2)에 대한 항복하중의 비는 0.99, 최대하중의 비는 1.43으로 나타났다.
- (3) 따라서 지지형 전단연결재를 활용한 지하합성벽은 합성보와 동일하게 설계 가능하며, 감소계수를 적용하지 않은 공칭강도로 설계할 수 있을 것으로 판단된다. 또한 지지형 전단연결재의 안전율을 높게 설계할 경우 강재의 전단파괴를 고려하여 감소계수를 적용한 공칭강도로 설계할 수 있을 것으로 판단된다.
Acknowledgments
본 연구는 과학기술정보통신부 한국건설기술연구원 연구운영비지원(주요사업)사업으로 수행되었습니다(과제번호 20210098-001, 흙막이를 이용한 지하합성벽 개발).
References
- Ministry of Land, Infrastructure and Transport (2019) Seismic Design Standard for Buildings (KDS 41 17 00: 2019), Korea (in Korean).
-
Kim, S.-M., Li, C.-H., Seo, S.-Y., and Lee, L.-H. (2002) Shear Capacity of Composite Basement Walls, Journal of the Korea Concrete Institute, KCI, Vol.14, No.3, pp.321-330 (in Korean).
[https://doi.org/10.4334/JKCI.2002.14.3.321]

- Seo, S.-Y., Park, J.-H., and Lee, L.-H. (2006) Verification on the Flexural Behavior of Inverted T-Shaped Composite Basement Wall Subjected to Lateral Earth Load, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.22, No.2, pp.11-18 (in Korean).
- Yoon, Y.-D., Seo, S.-Y., and Kim, S.-S. (2009) Shear Strength of Composite Basement Wall with Various Shear Span-to-Depth Ratio, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.25, No.11, pp.61-69 (in Korean).
- Seo, S.Y., Kim, S.S., and Yoon, Y.D. (2010) The Effect of Composite Ratio and Wall Thickness on the Shear Behavior of Composite Basement Wall, Journal of the Korea Institute for Structural Maintenance and Inspection, KSMI, Vol.14, No.1, pp.93-101 (in Korean).
-
Choi, Y.H., Heo, B.W., and Chae, J.Y. (2022) Structural Performance Evaluation of Shear Connectors for Basement Composite Walls, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.3, pp.173-184 (in Korean).
[https://doi.org/10.7781/kjoss.2022.34.3.173]

- Ministry of Land, Infrastructure and Transport (2019) Korean Building Code for Steel Structures (KDS 41 30 00: 2019), Korea (in Korean).
- Segui, W.T. (2013) Steel Design (5th Ed.), Cengage Learning, USA.
- Salmon, C.G., Johnson, J.E., and Malhas, F.A. (2009) Steel Structures: Design and Behavior (5th Ed.), Prentice Hall, USA.
- KSSC (2019) Steel Structures Design for New Korean Standard, Goomiseogwan, Korea (in Korean).
- Lee, S.D., Kim, P.J., and Kim, K.S. (2004) The Strength of Square Steel Tubular Column to H-Beam Connections: Focused on the Connections with Outside-Type Diaphragm, Journal of Korean Society of Steel Construction, KSSC, Vol.16, No.1, pp.11-20 (in Korean).
- Heo, B.W., Kwak, M.K., Bae, K.W., and Jeong, S.M. (2007) Flexural Capacity of the Profiled Steel Composite Beams: Deep Deck Plate, Journal of Korean Society of Steel Construction, KSSC, Vol.19, No.3, pp.247-258 (in Korean).
-
Lee, D.Y., Cho, B.H., Hong, P.G., and Ha, T.H. (2019) Seismic Performance Evaluation of Beam-Column Connection of Unitized Floor System, Journal of Korean Society of Steel Construction, KSSC, Vol.31, No.2, pp.85-96 (in Korean).
[https://doi.org/10.7781/kjoss.2019.31.2.085]

-
Oh, S.H., and Park, H.Y. (2020) Experimental Study About Flexural Strength of H-Shaped Compact Stud Column Under Varying Axial Load, Journal of Korean Society of Steel Construction, KSSC, Vol.32, No.5, pp.297-308 (in Korean).
[https://doi.org/10.7781/kjoss.2020.32.5.297]