용접형강의 직접강도법 개발에 관한 연구 고찰

1. 서 론

압연형강이 주로 조밀단면(간혹 비조밀단면) 요소로 구성되는데 반하여 용접형강은 단면의 규격, 경제성 및 시공성 등의 여러 가지 이유로 비조밀단면요소나 세장판단면요소로 제작되는 경우가 흔히 있다. 이러한 경우에는 박판 냉간성형강 부재보다는 덜 치명적이기는 하지만 국부좌굴이나 뒤틀림좌굴이 부재의 전체좌굴(overall buckling)과 함께 발생하기 때문에 부재의 구조적인 거동은 물론 부재의 강도산정을 복잡하게 만드는 요인이 된다(Fig. 1).

비조밀단면 및 세장판단면이 사용된 강구조물의 설계에서는 단면요소의 국부좌굴의 후좌굴강도를 고려한 합리적인 부재강도의 산정이 반드시 필요하며, 이를 통하여 강구조물의 경제성을 확보할 수 있다. 국부좌굴의 거동이 부재의 강도에 미치는 영향을 파악하기 위하여 최근 고성능강(HSA800, HSB800) 단면요소의 압축부재(Lee et al., 2013^[1], Yoo et al., 2013^[2]) 및 플레이트거더(Kim et al., 2014^[3])의 강도에 관한 연구가 수행 된 바 있다. 국부좌굴은 판폭두께비가 큰 판요소로 구성된 모든 형태의 용접단면에서 발생하는데 반하여, 뒤틀림좌굴은 종방향보강재로 보강된 대형 박스단면, 수평 보강재가 부착된 플레이트거더 웨브 및 연속플레이트거더교의 지점부근 외에서는 발생하는 경우가 거의 없다. 그러나 뒤틀림좌굴의 경우에도 국부좌굴과 같이 상당한 크기의 후좌굴강도가 존재하므로 이것을 설계에 고려하는 것이 부재 단면의 합리적인 강도 산정에 중요한 요소가 된다.

본 논문에서는 세장판단면 요소로 구성된 용접형강 압축 및 휨 부재의 설계강도 산정 시에 판요소의 국부좌굴과 뒤틀림좌굴의 후좌굴강도를 고려하기 위하여 최근에 개발된 설계법인 직접강도법의 최근 연구동향을 살펴보고자 한다.

2. 세장판단면(slender sections)의 설계법

현재 부재를 구성하는 판요소의 국부좌굴의 후좌굴강도를 고려하여 부재 강도를 산정하는 방법은 두 가지가 있다. 범세계적으로 70여 년간 사용되어 오고 있는 유효폭법(effective width method)과 최근에 북미주와 호주/뉴질랜드에서 냉간성형강 부재의 설계에 적용되고 있는 직접강도법(direct strength method)이다^[4],[5]. 이 방법은 아직 용접형강이나 압연형강 부재의 설계기준에 채택된 예는 없다.

2.1 유효폭법

유효폭법의 개념은 이미 강구조공학 교과서에 잘 설명되어 있으며, 현행 설계기준^{[6],[7],[8],[9]}에 널리 채택되어 설계에 적용되고 있는 방법이다. 국부좌굴이 발생하게 되면 후좌굴강도를 발현하므로 이를 고려하는 방법으로 단면의 일부분의 강성을 무시하는(유효단면적) 개념으로 1940년대부터 선진국의 강구조설계기준에서 채택되고 있는 방법이다. EC3^[7]나 AISI^[9] 설계기준과 같이 보강요소와 비보강요소로 구분하여 각각 실험에 근거하여 제시된 유효폭식을 적용하여 개별 단면 요소의 유효단면적을 구하여 전체 유효단면적을 구하거나, AISC 설계기준^[8]의 Q-계수 설계와 같이 보강요소에는 유효폭 개념으로 그리고 비보강요소에는 평균응력 개념을 적용하는 방법으로 감소계수를 구하여 세장판단면의 후좌굴강도를 고려할 수 있는 설계방법이다. 그러나 유효폭법에서는 1970년대에 관심을 끌기 시작한 뒤틀림좌굴을 고려하지 못하고, 반복적인 계산에 의하여 개별 요소의 유효폭을 독립적으로 산정해야하는 계산상의 단점이 있다. 또한 인접 요소간의 구속정도를 정확하게 산정하지 못하므로 단면의 형상이 복잡해지면 폭두께비 한계값에 대한 신뢰성에 의문이 있을 수 있다.

2.2 직접강도법

직접강도법은 국부좌굴 및 뒤틀림좌굴과 전체좌굴의 혼합이 발생하는 냉간성형강 부재의 설계강도를 편리하게 산정하고자 많은 연구자(Lau and Hancock, 1990^[10], Kwon and Hancock, 1992^[11], Hancock et al., 1994^[12])들에 의하여 수행된 연구결과에 근거하여 Schafer(1998)^[13]에 의해서 처음 제안되었으며, AISI 설계기준(2004)^[14] 및 AS/NZS (2005)^[15]에서 냉간성형강구조물의 설계에 공식적으로 채택되어 사용하고 있다.

전통적인 유효폭법이 단면 개별요소에 대하여 독립적으로 반복적인 계산에 의하여 유효폭을 산정하고 두께를 곱하여 유효단면적을 계산하고, 이렇게 계산된 유효단면적을 합하여 전체 단면의 유효단면적을 계산해야하는 복잡성과 개별 요소간의 구속정도를 결정하기가 어려운 문제를 해결하기 위하여, 탄성좌굴응력을 근거로 하며, 전단면적(gross area)을 사용하고 다양한 단면의 실험결과에 근거하여 제시된 부재 강도식을 사용하는 직접강도법을 개발하였다. 현재 유한요소법 또는 유한대판법에 의해서 구한 탄성국부좌굴 또는 탄성뒤틀림좌굴응력은 정해로 받아들여지기 때문에 이를 직접 이용하여 강도를 구하는 데는 별다른 이의의 소지가 없다고 사료된다.

3. 직접강도법 개발

최근 개발된 직접강도법은 단면의 탄성국부좌굴응력 및 뒤틀림좌굴응력과 현행 설계기준의 국부좌굴을 고려하지 않은 부재강도(전체좌굴에 근거한 기둥강도 및 휨강도)를 제안된 강도식에 직접 적용하여 국부좌굴의 후좌굴강도를 고려한 부재강도를 구하는 선진 설계방법이다. 각 국의 현행 설계기준에 근거한 플랜지나 웨브의 국부좌굴을 고려하지 않은 압축강도나 휨강도가 약간씩 차이가 있으므로 적용하는 설계기준에 따라서 설계강도는 약간의 차이는 있을 수 있다. 직접강도법의 부재별 강도 산정식과 방법을 간단히 기술하면 아래와 같다.

3.1 압축부재의 강도

국부좌굴이 발생 가능한 원형강관을 제외한 용접형강의 압축강도식을 개발하기 위하여 판폭두께비가 큰 단면 요소로 구성된 용접 H, C형강의 압축실험결과에 근거하여 아래와 같은 압축강도식을 제안하였다(Kwon and Kim, 2007^[4]).

 (1)

여기서 

 (2a)

                (2b)

 (3)

 :공칭압축강도 

 :탄성국부좌굴응력 

 :휨/휨비틂좌굴 응력에 근거한 AISC 기준, EC3 등 현행설계기준에 따른 기둥강도

일반적으로 탄성국부좌굴응력은 유한요소법이나 유한대판법을 사용하여 구할 수 있다. 그러나 정사각형단면이나 면내 휨강성이 국부좌굴의 절선의 역할을 하기에 충분한 크기의 종방향보강재의 간격이 동일한 박스단면의 경우 다음의 이론식을 적용할 수도 있다.

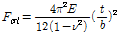 (4)

여기서 는 포와송비 이다.

또한 직사각형의 경우에도 다음 식 (5)와 같은 등가 판폭두께비 개념을 이용하여 식 (4)를 적용할 수 있다.

 (5)

여기서, 는 단변의 폭이다.

위에서 제안된 강도식과 H 및 C형강 기의 압축실험결과(Kwon et al., 2007^[16], Davids et al., 1986^[17], Rasmussen and Hancock, 1989^[18])를 Fig. 2에서 비교하여 보았다. 제안된 강도식은 몇 개의 아주 세장한 C형강을 제외한 실험결과들에 대하여 보수적인 강도를 산출하는 것을 알 수 있다.

제안된 식을 용접 사각형(RHS) 기둥의 압축실험결과(Usami and Fukumoto, 1982^[19]; 1984^[20], Degée et al., 2008^[21], Kwon and Seo, 2013^[22])와 Fig. 3에서 비교하여 보았다. Fig. 3에서 나타난 것처럼 제안된 식 (2a), (2b)는 용접 사각형기둥에 대하여 일부 실험결과에 대하여 비보수적인 압축강도를 산출하고 있다. 이것은 개단면과 폐단면인 사각형단면의 국부좌굴의 후좌굴강도의 크기와 잔류응력의 분포 등의 차이에서 나타나는 결과로 판단된다. 따라서 합리적인 사각형단면의 압축강도를 산정하기 위하여 위에서 제시된 식 (2a), (2b)에 의한 강도를 실험결과와의 비교를 근거로 약간 조정할 필요가 있다고 판단되어 다음 식과 같이 수정하였다.

 (6a)

          (6b)

Fig. 3에서 식 (2a), (2b) 및 실험결과와 비교하여 수정된 식 (6a), (6b)가 사각형단면에 관하여 비교적 합리적인 강도를 산출하는 것을 알 수 있다. 따라서 단면의 형상에 따른 정확한 강도를 산정하기 위하여 별도의 식을 적용하여야 하지만 설계의 편의상 단면형상에 관계없이 동일한 강도식을 적용하고자 한다면 개단면에 대하여는 조금 더 보수적이기는 하지만 수정된 강도식 (6a), (6b)를 적용하여야 한다.

3.2 원형강관 기둥의 압축강도

원형강관단면(circular hollow sections)은 탄성국부좌굴응력의 크기가 직경두께비에 의해서 결정되므로 요소의 판폭두께비에 따라 정해지는 개단면이나 사각형단면과는 동일한 압축강도식을 적용할 수는 없다. Kwon et al.(2011)^[23]은 실험 및 해석결과에 근거하여 원형강관단면의 압축강도식을 다음과 같이 제안하였다.

 (7a)

 

          (7b)

여기서 탄성국부좌굴응력은 구조해석프로그램에 의한 탄성국부좌굴응력 대신에 다음 식 (8)을 적용할 수도 있다. 강성이 충분한 종방향보강재가 등간격으로 부착된 대형 원형강관 단면의 경우에도 보수적으로 식 (8)은 적용이 가능하다

(8)

Fig. 4에서 원형 및 각형강관 실험결과들(Usami and Hancock, 1982^[19], 1984^[20], Kwon et al., 2011^[23]) 및 AISC 설계기준^[8]의 Q계수와 비교하여 보았다. 비교결과를 보면 AISC Q계수 설계법은 원형강관의 실험결과에 비하여 너무 보수적인 강도를 산출하는 것을 알 수 있다.

3.3 뒤틀림좌굴이 발생하는 보강판의 압축강도

용접형강의 경우에는 냉간성형강재와는 달리 종방향보강재로 구성된 박스단면 외에는 뒤틀림좌굴이 발생하는 단면이 흔하지 않다. 뒤틀림좌굴이 발생하는 냉간성형강 압축부재의 강도식은 Kwon and Hancock(1992)^[11]에 의하여 처음 제안되었으며, 수평보강재로 보강된 용접 보강판의 실험결과에 근거하여 용접형강의 설계를 위한 뒤틀림좌굴을 고려한 공칭강도식은 다음과 같다(Kwon and Park, 2011)^[24].

 (9a)

          (9b)

여기서, 

 (10)

는 탄성뒤틀림좌굴응력이다.

Fig. 5에서 용접 제작된 종방향보강재로 보강된 보강판의 압축실험결과(Choi et al., 2009^[25], Kwon and Park, 2011^[24], Ghavami and Khedmati, 2008^[26])와 강도식을 비교하여 보았다. AISI standard (2012)^[8] 강도식을 함께 비교하여 보았다. 제안된 강도식은 실험결과에 대하여 비교적 합리적인 강도를 산출하는 것으로 나타났다.

3.4 콘크리트충전(CFT) 합성기둥의 강도

국부좌굴이 발생하는 비조밀 및 세장판 요소로 구성된 사각형 및 원형 강관에 콘크리트를 충전한 충전합성기둥 단주의 파괴(극한)강도는 다음 식으로 제안하였다(Kwon et al., 2011^[23], Kwon and Jung, 2014^[27]). 외부 강재의 설계강도는 보수적으로 속이 빈 강재단면(HSS)의 강도식을 채택하였고, 강재의 구속 효과를 콘크리트 설계강도에 고려하였다. 기둥의 세장효과는 현행 AISC 기준^[7]이나 EC4^[28]의 규정을 적용하여 고려할 수 있다.

(11)

1) 사각형 단면의 강도

강재강도

) (12a)

 

        ( ) (12b)

 (13)

콘크리트강도

 (14)

) (15a)

 

        ( )         (15b)

2) 원형단면의 강도

강재강도

) (16a)

 

        ( ) (16b)

콘크리트강도

                                (17)

)          (18a)

        ( ) (18b)

제안된 파괴강도와 원형 및 사각형 콘크리트충전합성 단주의 실험결과를 Fig. 6(a), (b)에서 각각 비교하여 보았다. Fig. (6a), (b)에서 알 수 있듯이 식 (11)은 원형 및 사각형 충전합성단면의 파괴강도를 합리적으로 산출하는 것을 알 수 있다. 충전단면의 휨강도도 위의 압축강도의 경우와 유사한 방법으로 구할 수 있다. 다만, 계산상의 편의를 위하여 압축측 콘크리트단면의 응력은 의 크기를 갖는 사각형 분포로 가정하여 직접 휨강도를 산정할 수 있다.

3.5 플레이트거더의 휨강도

플랜지나 웨브에 국부좌굴이 발생하는 플레이트거더의 휨강도는 플레이트거더의 순수휨실험결과에 근거하여 다음과 같이 제안하였다(Kwon and Seo, 2012^[29]).

 (19a)

 

          (19b)

 (20)

여기서,

 :공칭압축강도 

)

 :횡-비틀림좌굴에 근거한 현행 설계기준의 공칭휨강도

 :탄성국부좌굴응력

 :탄성단면계수 

제안된 휨강도식의 형태는 압축부재의 경우와 동일하지만 휨강도를 산정하기 위하여 전단면적 대신에 전단면의 탄성단면계수를 사용하여야 하고, 또한 탄성국부좌굴응력은 압축부재의 그것과 형태는 같지만 순수휨에 대한 단면의 탄성국부좌굴응력으로 압축부재에 사용되는 등분포압축하중에 대한 단면의 탄성국부좌굴응력보다는 상당히 크다.

플레이트거더의 실험결과(Kwon and Seo, 2012^[29],Kuhlman, 1989^[30])와 제안된 강도식을 Fig. 7에서 비교하여 보았다. 실험결과와의 비교결과를 보면 유사한 강도식을 적용하는 압축강도에 비하여 휨강도는 상당히 보수적인 강도를 산출하는 것을 알 수 있다. 따라서 현재는 설계식의 형식의 단순화를 위하여 압축과 휨부재에 동일한 강도식을 적용하고 있지만 향후 더 많은 실험결과에 근거하여 수정할 요소가 충분히 있다고 판단된다.

3.6 플레이트거더 웨브의 전단강도

주로 전단을 받아서 파괴되는 플레이트거더의 실험결과에 근거하여 직접강도법의 휨강도와 유사한 형식으로 플레이트거더 웨브의 전단강도식을 다음과 같이 제안할 수 있다. 이 식은 플레이트거더에서 인장역작용(Basler, 1961^[31])으로 잘 알려진 전단좌굴의 후좌굴강도를 효과적으로 고려할 수 있다.

) (21a)

        ( ) (21b)

여기서,

 (22)

 (23)

 (24)

 (25a)

 (25b)

 : 웨브 높이

 : 중간보강재 간격

 : 웨브 두께

제안한 전단강도식을 AISC 설계기준식 및 실험결과(Lee and Yoo, 1999^[32], Lee et al., 2003^[33], Shanmugam and Baskar, 2003^[34], Ryu and Kim, 2014^[5])와 Fig. 8에서 비교하여 보았다. Fig. 8에서 보면 제안한 전단강도식은 인장역작용을 고려한 변장비가 3인 경우의 강도식과 유사하며, 실험결과에 대하여 보수적인 강도를 산출하는 것을 알 수 있다.

전단좌굴하중의 계산에서 전통적으로 사용하는 사변 단순지지로 가정한 판의 전단좌굴이론에 의한 전단좌굴응력 식 (20), (21a), (21b)를 사용하는 대신에 플랜지의 구속효과가 웨브의 좌굴강도에 미치는 영향을 고려할 수 있는 방법으로 유한요소법에 의하여 구한 탄성순수전단좌굴하중을 사용할 수도 있다. 이렇게 구한 전단좌굴하중은 단순지지된 판의 이론식에 의한 식 (20)에 의한 값보다 크므로 Fig. 8에서 실험결과의 표기 위치를 왼쪽으로 이동시키는 결과를 초래하여 제안된 전단강도식보다 아래에 위치할 수 있다. 이렇게 플랜지의 영향을 고려할 경우에는 제안된 식을 수정하여 사용하여야 할 것이다.

4. 신뢰성 검토 및 향후 연구과제

문헌상의 실험결과들과 직접강도법에 의한 설계강도에 대한 비( )의 평균값, 표준편차 및 분산계수를 Table 1에 정리하여 보았다. Table 1에서 보면 직접강도법은 비교적 신뢰할 수준의 설계강도를 산출할 수 있는 것으로 판단된다. 기둥강도에 대한 비교 결과에 비하여 플레이트거더의 비교 결과는 대단히 크기 때문에 플레이트거더의 직접강도법에 의한 설계휨강도는 너무 보수적인 것을 알 수 있다. 그러나 휨강도에 관한 연구결과(Kwon and Seo, 2012^[29])에 의하면 EC3나, AISC 규정과 비교하여 상당히 합리적인 설계강도인 것으로 평가되었다.

신뢰성지수 β를 2.5라고 가정하고 Ravindra and Galambos​(1978)^[35]에 의해 제안된 아래의 식 (26)에 따라 저항계수를 산정해보면 기둥의 경우 ϕ=0.89 그리고 플레이트거더의 경우ϕ=1.06이 된다. 이 값은 합리적인 값으로 판단되어 제안된 직접강도법의 적용 가능성을 보여준다고 판단된다.

 (26)

Table 1에서 알 수 있듯이 강도식의 개발에 참고한 실험결과가 충분한 자료라고 볼 수는 없다고 판단되므로, 개발된 직접강도법의 적용을 위하여 세계의 냉간성형강 연구자그룹에서 진행되고 있는 것과 같이 추가적으로 다양한 단면 조건에 따른 관련 실험들이 많은 연구자들에 의하여 수행되어야 할 것으로 판단된다. 제안된 강도식 개발의 근거로 사용된 부재는 고강도강재가 포함되어 있기는 하지만 주로 SM400, SM490 강재로 용접 제작된 부재였으므로 최근에 개발된 고성능강재에 대한 적용성을 당연히 검증하여야 한다. 또한 대형 구조물에 흔히 적용되는 수평보강재가 부착된 플레이트거더와 하이브리드거더에 대한 휨 및 전단실험이 수행되어야 할 것이다. 보강재가 부착된 사각형기둥의 실험이 수행되어야 하며, 가능한 모든 실험결과를 근거로 필요에 따라서 강도식은 수정되어야 할 것이며 신뢰성 검토가 당연히 수행되어야 할 것이다.

5. 결 론

본 논문에서는 용접형강의 설계에 직접강도법을 적용하기 위하여 최근에 수행된 실험 및 문헌상의 실험결과들을 근거로 개발된 부재별 강도식을 정리하여 직접강도법의 타당성을 제시하고자 하였다. 전체좌굴과 혼합하여 발생하는 국부좌굴의 후좌굴강도를 효과적으로 고려하기 위하여 제안된 직접강도법의 압축, 휨 및 전단 강도식은 국부좌굴 또는 뒤틀림좌굴이 발생하는 비조밀 및 세장판 요소로 구성된 용접형강 부재의 강도를 합리적으로 산정할 수 있는 설계법으로 판단된다. 그러나 실무적용을 위하여 계속적인 많은 연구자들의 후속 연구가 수행되어야 할 것이다. 직접강도법 관련 연구자들이 참고할 수 있도록 가능한 한 많은 참고문헌을 목록에 정리하였다.

Acknowledgments

본 연구는 한국연구재단의 지원(2012R1A1B3002777)으로 수행되었습니다. 이에 감사드립니다.

References

• 이강민, 이명재, 오영석, 김태수, 김도환(2013) 중심압축력을 받는 건축구조용 고성능(HSA800) 용접H형 단주의 국부좌굴거동, 한국강구조학회논문집, 한국강구조학회, 제25권, 제3호, pp.289-297.
  Lee, K.M., Lee, M.J., Oh, Y.S., Kim, T.S., and Kim, D.H. (2013) Local Buckling Behavior of Stub H-Shaped Columns Fabricated with HSA800 High Performance Steels Under Concentric Axial Loading, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.3, pp.289-​297 (in Korean). [ https://doi.org/10.7781/kjoss.2013.25.3.289 ]
• 유정한, 김주우, 양재근, 강주원, 이동우(2013) 국부좌굴을 고려한 건축구조용 고성능강(HSA800) 조립각형강관 압축재의 적용성 평가, 한국강구조학회논문집, 한국강구조하기회, 제25권, 제3호, pp.223-231.
  Yoo, J.H., Kim, J.W., Yang, J.G., Kang, J.W., Lee, D.W. (2013) Evaluation on Applicability of Built-up Square Tubular Compression Members Fabricated with HSA800 High Performance Steel Considering Local Buckling, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.3, pp.223-231 (in Korean). [ https://doi.org/10.7781/kjoss.2013.25.3.223 ]
• 김정훈, 김경열, 이정화, 김경식, 강영종(2014) 고성능강재(HSB 800)를 적용한 플레이트 거더의 휨강도에 대한 플랜지 국부좌굴, 한국강구조학회논문집, 한국강구조학회, 제26권, 제2호, pp.91-103.
  Kim, J.H., Kim, K.Y., Lee, J.H., Kim, K.S., and Kang, Y.J. (2014) Flange Local Buckling (FLB) for Flexural Strength of Plate Girders with High Performance Steel (HSB800), Journal of Korean Society of Steel Construction, KSSC, Vol.26, No.2, pp.91-103 (in Korean). [ https://doi.org/10.7781/kjoss.2014.26.2.091 ]
• 권영봉, 김낙구(2007) 혼합좌굴이 발생하는 압축부재의 강도에 관한 연구, 대한토목학회논문집 A, 대한토목학회, 제27권, 제4A호, pp.569-578.
  Kwon, Y.-B., and Kim, N.G. (2007) A Study on the Strengths of Compression Members Undergoing Buckling Interaction, Journal of the Korean Society of Civil Engineers A, KSCE, Vol.27, No.4A, pp.569-578 (in Korean).
• 류승완, 권영봉(2014) 직접강도법에 의한 플레이트거더 웨브의 극한전단강도 평가, 한국강구조학회 2014년 학술발표대회 논문집, 한국강구조학회, pp.83-84.
  Ryu, S.W., and Kwon, Y.B. (2014) Prediction of the Ultimate Shear Strengths of Plate Girders by the Direct Strength Method, Proceedings of Annual Conference of Korean Society of Steel Construction Conference, KSSC, pp.83-84 (in Korean).
• 국토해양부(2009) 하중저항계수설계법에 의한 강구조설계기준.
  Ministry of Land, Transportation and Maritime Affairs (2009) Steel Structure Design Code (Load and Resistant Factored Design), Korea (in Korean).
• European Committee for Standardization (2006) Eurocode 3: Design of Steel Structures, Part 1-5: Plated Structural Elements (EN 1993-1-5: 2006), Belgium.
• American Iron and Steel Institute (2012) North American Specification for the Design of Cold-Formed Steel Structural Members (AISI S100-12), USA.
• American Institute of Steel Construction (2010) Specification for Structural Steel Buildings (ANSI/AISC 360-​10), USA.
• Lau, S.C.W., and Hancock, G.J. (1990) Inelastic Buckling of Channel Columns in the Distortional Mode, Thin-​Walled Structures, Elsevier, Vol.10, No.1, pp.59-84. [https://doi.org/10.1016/0263-8231(90)90005-J]
• Kwon, Y.B., and Hancock, G.J. (1992) Tests of Cold-​Formed Channels with Local and Distortional Buckling, Journal of Structural Engineering, American Society of Civil Engineering, Vol.118, No.7, pp.1786-1803. [https://doi.org/10.1061/(ASCE)0733-9445(1992)118:7(1786)]
• Hancock, G.J., Kwon, Y.B., and Bernard, E.S. (1994) Strength Design Curves for Thin-Walled Sections Undergoing Distortional Buckling, Journal of Constructional Steel Research, Elsevier, Vol.31, pp.169-186. [https://doi.org/10.1016/0143-974X(94)90009-4]
• Schafer, B.W., and Peköz, T. (1998) Direct Strength Prediction of Cold-Formed Steel Members Using Numerical Elastic Buckling Solutions, Thin-Walled Structures: Research and Development (Proceedings of the 2nd International Conference on Thin-Walled Structures), National University of Singapore, Singapore, pp.137-144.
• American Iron and Steel Institute (2005) Supplement 2004 to the North American Specifications for the Design of Cold-Formed Steel Structural Members (AISI/COS/​NASPEC-SUP04), USA.
• Standards Australia, and Standards New Zealand (2005) Cold-Formed Steel Structures (AS/NZS 4600: 2005), Australia/New Zealand.
• Kwon, Y.B., Kim, N.G., and Hancock, G.J. (2007) Compression Tests of Welded Section Columns Undergoing Buckling Interaction, Journal of Constructional Steel Research, Elsevier, Vol.63, No.12, pp.1590-1602. [https://doi.org/10.1016/j.jcsr.2007.01.011]
• Davids, A.J., and Hancock, G.J. (1986) Compression Tests of Long Welded I-Section Columns, Journal of Structural Engineering, American Society of Civil Engineers, Vol.112, No.10, pp.2281-2297. [https://doi.org/10.1061/(ASCE)0733-9445(1986)112:10(2281)]
• Rasmussen, K.J.R., and Hancock, G.J. (1989) Compression Tests of Welded Channel Section Columns, Journal of Structural Engineering, American Society of Civil Engineers, Vol.115, No.4, pp.789-808. [https://doi.org/10.1061/(ASCE)0733-9445(1989)115:4(789)]
• Usami, T., and Fukumoto, Y. (1982) Local and Overall Buckling of Welded Box Columns, Journal of the Structural Division, American Society of Civil Engineers, Vol.​108, No.3, pp.525-542.
• Usami, T., and Fukumoto, Y. (1984) Welded Box Column Members, Journal of Structural Engineering, American Society of Civil Engineers, Vol.110, No.10, pp.2457-​2470. [https://doi.org/10.1061/(ASCE)0733-9445(1984)110:10(2457)]
• Degée, H., Detzel, A., and Kuhlmann, U. (2008) Interaction of Global and Local Buckling in Welded RHS Compression Members, Journal of Structural Engineering, Elsevier, Vol.64, pp.755-765. [https://doi.org/10.1016/j.jcsr.2008.01.032]
• Kwon, Y.B., and Seo, E.G. (2013) Prediction of the Compressive Strength of Welded RHS Columns Undergoing Buckling Interaction, Thin-Walled Structures, Elsevier, Vol.68, pp.141-155. [https://doi.org/10.1016/j.tws.2013.03.009]
• Kwon, Y.B., Seo, S.J., and Kang, D.W. (2011) Prediction of the Squash Loads of Concrete-Filled Tubular Section Columns with Local Buckling, Thin-Walled Structures, Elsevier, Vol.49, No.1, pp.85-93. [https://doi.org/10.1016/j.tws.2010.08.009]
• Kwon, Y.B., and Park, H.S. (2011) Compression Tests of Longitudinally Stiffened Plates Undergoing Distortional Buckling, Journal of Constructional Steel Research, Elseiver, Vol.67, No.8, pp.1212-1224. [https://doi.org/10.1016/j.jcsr.2011.02.015]
• Choi, B.H., Hwang, M.-O., Yoon, T.-Y., and Yoo, C.H. (2009) Experimental Study of Inelastic Buckling Strength and Stiffness Requirements for Longitudinally Stiffened Panels, Engineering Structures, Elsevier, Vol.31, pp.1141-​1153. [https://doi.org/10.1016/j.engstruct.2009.01.010]
• Ghavami, K., and Khedmati, M.R. (2006) Numerical and Experimental Investigations on the Compression Behavior of Stiffened Plates, Journal of Constructional Steel Research, Elsevier, Vol.62, No.11, pp.1087-1100. [https://doi.org/10.1016/j.jcsr.2006.06.026]
• Kwon, Y.B., and Jung, I.K. (2014) Resistance of Rectangular Concrete-Filled Tubular (CFT) Sections to the Axial Load and Combined Axial Compression and Bending, Thin-Walled Structures, Elsevier, Vol.79, pp.178-186. [https://doi.org/10.1016/j.tws.2014.02.019]
• European Committee for Standardization (2004) Eurocode 4: Design of Composite Steel and Concrete Structures, Part 1-1: General Rules and Rules for Building (EN 1994-​1-1: 2004), Belgium.
• Kwon, Y.B., and Seo, G.H. (2012) Prediction of the Flexural Strengths of Welded H-Sections with Local Buckling, Thin-Walled Structures, Elsevier, Vol.54, pp.126-139. [https://doi.org/10.1016/j.tws.2012.02.005]
• Kuhlmann, U. (1989) Definition of Flange Slenderness Limits on the Basis of Rotation Capacity Values, Journal of Constructional Steel Research, Elsevier, Vol.14, No.1, pp.21-40. [https://doi.org/10.1016/0143-974X(89)90068-0]
• Basler, K. (1961) Strength of Plate Girders in Shear, Journal of the Structural Division, American Society of Civil Engineers, Vol.87, No.7, pp.151-180.
• Lee, S.C., and Yoo, C.H. (1999) Experimental Study on Ultimate Shear Strength of Web Panels, Journal of Structural Engineering, American Society of Civil Engineers, Vol.125, No.8, pp.838-846. [https://doi.org/10.1061/(ASCE)0733-9445(1999)125:8(838)]
• Lee, S.C., Yoo, C.H., and Yoon, D.Y. (2003) New Design Rule for Intermediate Transverse Stiffeners Attached on Web Panels, Journal of Structural Engineering, American Society of Civil Engineers, Vol.129, No.12, pp.1607-​1614. [https://doi.org/10.1061/(ASCE)0733-9445(2003)129:12(1607)]
• Shanmugam, N.E., and Baskar, K. (2003) Steel-Concrete Composite Plate Girders Subjected to Shear Loading, Journal of Structural Engineering, American Society of Civil Engineers, Vol.129, No.9, pp.1230-1242. [https://doi.org/10.1061/(ASCE)0733-9445(2003)129:9(1230)]
• Ravindra, M.K., and Galambos, T.V. (1978) Load and Resistance Factor Design for Steel, Journal of the Structural Division, American Society of Civil Engineers, American Society of Civil Engineers, Vol.104, No.9, pp.1337-1353.