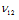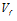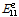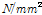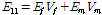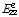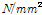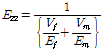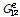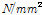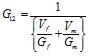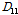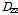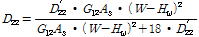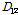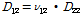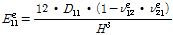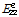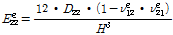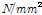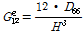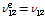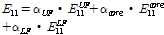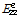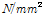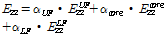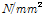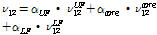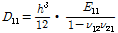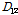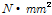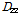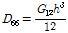GFRP 복합소재 바닥판의 간편해석법
ⓒ KSSC 2013
초록
본 논문은 중공튜브 및 샌드위구조 형식을 주로 갖는 GFRP 복합소재 바닥판의 기본설계에서 전체 유한요소 모델링을 이용하지 않고 탄성등가 모델링을 이용한 간편 해석 방법을 제시하였다. 제시된 간편 해석 방법의 타당성 검증을 위해서 ANSYS 프로그램이 사용되었으며, 전체 유한요소 모델링과 탄성등가모델링을 이용한 해석값을 각각 비교하였다. 또한 본 논문에서 제안된 GFRP 복합소재 바닥판 간편 해석법에 의한 해석 결과를 비교하기 위해 각형 튜브를 갖는 샌드위치 구조형식 GFRP 복합소재 바닥판의 4점 휨시험인 실내실험결과를 수행하였다. 해석 결과와 실험 결과 내용을 비교분석하였다. 제시된 간편해석 방법은 GFRP 복합소재 바닥판의 기본설계시 사용하기에 적용성이 있음을 확인되었다.
Abstract
This paper presents a simplified analysis method using the elastic equivalent modelling not using the global finite element modelling of deck for the basic design GFRP composites deck with cellular tubes or sandwich structural type. In order to verify the validation of the simplified method ANSYS software package is used and compared the results analyzed on the global finite element modelling and the elastic equivalent modelling. And the laboratory testing by 4-point bending is conducted to compare the results based on the simplified analysis method proposed in this paper. The comparison of the results based on the analysis and the testing are discussed. It is found that the presented simplified analysis is applicable to the use in the basic design GFRP composite deck.
키워드:
GFRP 복합소재 바닥판, 간편해석법, ANSYS, 실내실험Keywords:
GFRP composites deck, simplified analysis method, ANSYS, laboratory testing1. 서 론
FRP(Fiber Reinforced Polymer) 재료는 비강도(항복강도를 밀도로 나눈 값), 비강성(탄성계수를 밀도로 나눈 값)이 기존의 일반 콘크리트나 강재에 비해 상대적으로 높고(Table 1), 내부식성, 경량성, 비전기성 등 재료의 장점을 갖고 있다. 또한 방향성을 이용하여 우수한 재료 성질을 얻을 수 있고 다양한 형태로 만들 수 있는 우수한 성형성을 가지고 있다. FRP 재료는 섬유(fiber)를 기지(matrix)인 수지(resin)에 함침시켜 만들어진다. 설계자는 FRP 재료설계를 통해 구조부재의 재료 성질을 사용자의 요구대로 설계할 수 있다. 최근에 FRP 재료로 만든 복합소재 바닥판에 대한 연구가 국내외적으로 활발히 이루어지고 있으며, 신설교량 및 노후교량 철근콘크리트 바닥판 교체 공사에 복합소재 바닥판이 많이 적용되고 있다. 선진국을 중심으로 FRP 재료를 이용하여 만든 다양한 복합소재 바닥판 형식이 교량 바닥판 건설에 적용되어지고 있다[1],[2]. 국내에서도 FRP 재료 복합소재 교량 바닥판이 개발되어 신설 교량 바닥판 공사에 적용되고 있다[3]. 대부분 교량 건설용 복합소재 바닥판 시스템은 인발(pultrusion) 성형된 단위 모듈(unit module) 중공 튜브(tube)를 현장에서 교량 바닥판의 폭에 맞추어 접착제로 연결하여 전체 교량 바닥판을 제작하는 시스템이다. 이러한 인발 성형된 단위 모듈 중공 튜브로 제작된 교량용 FRP 복합소재 바닥판의 연구[4],[5],[6]가 활발하게 연구되고 있으나 국내 교량용 바닥판 건설적용에 여러 가지 이유로 지연되고 있다. 주요 지연 원인으로는 기존 건설재료인 콘크리트, 강재와 비교하였을 때 FRP 재료로 만든 구조부재는 이방성 구조체로서 해석[7]이 복잡하여 대부분의 구조설계자가 복합소재구조 설계에 익숙하지 못할 뿐만 아니라 복합소재 구조 설계기준이 아직 까지 제정되지 못해 활용 정도가 저조했기 때문이다. 지금까지 국내외적으로 개발되어 상용중인 FRP 재료 복합소재 바닥판의 형식은 FRP 재료의 특성에 부합한 샌드위치 구조[8],[9]와 인발 성형하여 만든 플랜지(flange)와 웨브(web)를 갖는 중공 튜브 형태의 단위 모듈 구조이다. FRP 복합소재 바닥판에 대한 주요 설계 변수는 단면의 휨강성이다. 이러한 점에서 FRP 재료 복합소재 바닥판의 단면 형상 결정을 위한 기본 및 상세 설계는 주로 상용 유한요소 프로그램을 이용하여 이루어지고 있으며, 바닥판 대해 전체 유한요소 모델링을 구성하여 해석을 실시한다. 비등방성인 복합소재 바닥판에 대한 전체 유한요소 모델링을 구성한 구조해석은 많은 해석 시간이 소요된다. 복합소재 바닥판 설계가 휨강성이 지배적임을 감안할 때 실제 기본설계의 단계에서 복합소재 바닥판 설계의 주요 인자는 설계하중 하에서 최대 처짐을 계산하여 그 값이 허용 처짐 이내 여부의 확인이다. 이와 같이 복합소재 바닥판 처짐 계산 간편화를 위해서는 복합소재 바닥판 단면의 휨강성과 동일한 휨강성을 갖는 등가직교이방성판 모델로 치환하여 탄성등가모델링을 이용하여 처짐 해석을 수행하는 간편해석법이 필요하다[10],[11].
본 논문에서는 복합소재 바닥판의 폭과 두께를 유지하면서복합소재 바닥판을 동일한 휨강성을 갖는 등가 직교이방성판으로 변환하여 해석할 수 있는 탄성등가모델링을 이용한 간편 해석방법을 제시하였다. 본 간편 해석 방법의 검증을 위해서 복합소재 바닥판 전체 유한요소 모델링을 이용한 해석 값과 탄성등가모델링을 이용한 해석 값과 비교하였으며, 최종적으로 복합소재 바닥판에 대한 실내 시험인 4점 휨시험 결과와 비교 분석하였다. 따라서 본 논문은 FRP 복합소재 바닥판 형식이 주로중공튜브 구조 또는 샌드위치 구조이므로, 본 연구에서 제시된 간편 해석 방법이 복합소재 구조 설계에 익숙하지 못한 설계 기술자에게 유용하게 사용될 수 있도록 하는 데 그 목적이 있다.
2. GFRP 복합소재 바닥판 해석
현재까지 국내외적으로 샌드위치 구조 및 중공 튜브를 갖는 GFRP(glass fiber reinforced polymer) 복합소재 바닥판은 단위 모듈간 접착제로 플랜지와 웨브 연결로 제작되고 있다. 이러한 형식을 갖는 GFRP 복합소재 바닥판의 구조해석은 상용 유한요소해석 프로그램을 사용하고 있으며, 전체 복합소재 바닥판에 대한 요한요소 모델링을 구성하여 해석하고 있다. 상기 1장에서 언급하였듯이 복합소재 바닥판의 주요 설계인자는 설계하중 하에서 발생 처짐이 최대 처짐 한계 이내 여부를 확인하는 것이다. 이러한 점에서 기본 설계단계에서 전체 유한요소 모델링을 구성하여 유한요소 해석을 하는 데 있어서 많은 시간이 소요되고 있고 복합소재에 익숙하지 못한 설계자가 해석을 하는 데 있어서 많은 어려움이 수반된다. 따라서 본 논문에서는 기본설계단계에서 설계자가 복합소재 바닥판 단면설계를 위한 간편 해석방법으로 대표적인 샌드위치 및 중공 형태를 갖는 복합소재 바닥판을 직교이방성 등가직교이방성판으로 변환하시키어 얻은 휨강성 값을 기반으로 탄성등가모델링을 이용하여 수행하는 방법으로서, 그 진행과정을 다음과 같이 기술한다.
2.1 GFRP 복합소재 바닥판 단면가정
인발성형된 중공 튜브 형태를 갖는 복합소재 바닥판은 플랜지와 웨브 접착부에서 박리파괴모드와 같은 주요 파괴양상을 보이고 있다. 본 논문에서는 이러한 파괴모드를 줄이면서 복합소재 바닥판 구조성능을 높일 수 있는 바닥판 단면을 고려하였다. Fig. 1과 같이 인발 성형된 GFRP 튜브를 갖는 심재(core)와 GFRP 면재(facing)로 구성된 단면으로 가정한다.
2.2 적층 설계
FRP 재료는 수지(resin)와 섬유(fiber)로 구성되어 있어 구조물의 부재에 대한 적층 설계가 중요하다. 적층 설계에 있어서 가장 중요한 요구 사항으로서 구조 부재 두께를 계산하기 위해서 사용하는 수지와 섬유의 중량이다. 설계자가 선택하는 수지와 섬유의 중량에 대한 두께의 값으로 부터 섬유가 수지에 함침된 적층(Lamina)의 두께를 계산할 수 있다. 섬유를 이용한 적층 형태는 종방향(0°), 횡방향(90°) 그리고 사선방향(±45°)으로 나타낸다. 설계자는 FRP 재료 구조 부재의 GFRP 복합소재 바닥판, 간편해석법, ANSYS, 실내실험두께에 맞추어 다양한 섬유 방향의 배열로 적층 설계를 설계할 수 있다. FRP 재료의 물성은 섬유의 분포나 배열에 따라 크게 좌우된다. 재료 물성을 추정하는 방법에는 재료역학적인 방법인 혼합법(rules of mixture)과 변분의 원리를 이용한 방법 등이 있으나, 본 논문에서는 섬유와 수지의 함량에 따라 계산되는 혼합법을 이용하였다. 본 논문에서 사용된 FRP 재료는 유리섬유(glass fiber)와 비닐 에스터(vinyl ester)를 사용하였으며 각 재료의 물성을 Table 2에 나타내었다.
Table 2의 섬유와 수지의 재료 물성을 가지고 혼합법을 사용하여 계산된 적층 재료(lamina)의 물성은 Table 3에 나타내었다.
복합소재 바닥판의 적층설계는 상부 플랜지는 [
 /
/
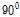 /
/
 /
/
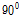 /
/
 /
/
 ], 하부플랜지는 일방향 [
], 하부플랜지는 일방향 [
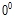 /
/
 /
/
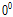 /
/
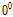 /
/
 /
/
 ]으로 설계하였으며 심재는 일방향으로 설계하였다. 복합소재 바닥판 구성 부재의 두께별로 Table 4 와 같이 나타내었다.
]으로 설계하였으며 심재는 일방향으로 설계하였다. 복합소재 바닥판 구성 부재의 두께별로 Table 4 와 같이 나타내었다.
2.3 탄성 등가 모델링
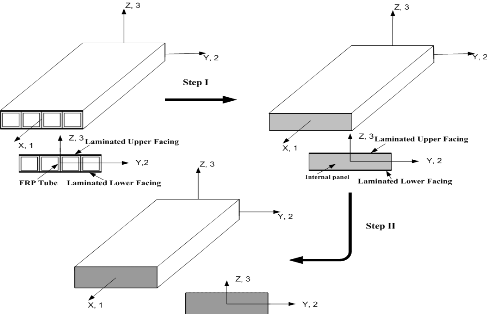
상기 절에서 기술하였듯이 FRP 복합소재 바닥판은 비등방성 재료로 단면형태가 샌드위치 및 중공형태의 구조이다. 기본 설계단계에서 실제 모델에 대한 해석이 요구되지만 간편 설계를 위해서 탄성 등가 모델링을 이용한 간편 해석 방법이 필요하다. 복합소재 바닥판은 해석을 위해서 동일한 폭과 두께를 갖는 탄성 등가의 직교이방성판으로 나타낼 수 있다. 본 논문에서 제시하는 간편 해석 방법은 Fig. 2 와 같이 복합소재 바닥판을 등가 직교이방성판으로 모델링하여 해석하는 방법으로서 단계 I, II를 통하여 동일한 바닥판의 폭과 두께를 가지는 등가 직교이방성판, 즉 1개 층 적층판(laminated plate)으로 모델링한다. 본 간편 해석방법은 교량 설계자가 쉽게 1개 층의 적층판 이론을 사용하여 해석할 수 있는 장점을 가지고 있다. 다음은 해석 시 필요한 등가직교이방성판의 x-방향, y-방향의 재료 성질을 구하는 과정을 기술한다.
2.3.1 등가직교이방성판 재료적 성질
등가직교이방성판 재료적 성질은 상・하층 면재의 재료적 성질과 심재의 재료적 성질을 계산하여 각각 구한 후 등가직교이방성판 재료적 성질을 구할 수 있다. Table 5는 재료 물성을 추정하는 방법인 혼합법[12]을 사용하여 계산한 면재의 등가재료물성을 나타내고 있다. Table 5에서 사용된 공식 아래첨자 f 와 m 은 섬유(fiber)와 수지(matrix)을 나타낸다. 여기서
 ,
,
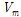 은 각각 섬유와 수지의 부피비를 나타낸다.
은 각각 섬유와 수지의 부피비를 나타낸다.
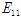 ,
,
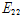 는 각각 Lamina의 섬유방향 및 섬유직각방향의 탄성계수를 나타내며,
는 각각 Lamina의 섬유방향 및 섬유직각방향의 탄성계수를 나타내며,
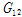 ,
,
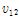 는 lamina의 면내 전단탄성계수 및 프와송 비를 나타낸다. 윗 첨자 e는 등가재료물성을 나타낸다.
는 lamina의 면내 전단탄성계수 및 프와송 비를 나타낸다. 윗 첨자 e는 등가재료물성을 나타낸다.
다음은 심재의 등가재료물성을 계산하는 과정을 나타낸다. 대부분의 복합소재 바닥판의 심재는 다실(multi cell) 형태를 이루고 있다. 물성은 동일한 높이에 대한 등가강성을 사용한 적층판의 재료적 성질을 계산하여 구할 수 있다. 먼저 심재의 튜브 강성을 아래 식을 이용하여 계산할 수 있다. 튜브는 등가직교이방성판으로 동일한 길이와 폭 그리고 두께로 모델화할 수 있다. 1개의 직사각형 튜브 단면은 상기 2.1 절의 Fig. 1에 나타내었다. Fig. 1로부터 등가직교이방성판의 직교이방성 휨강성 계수를 다음 식 (1)-(4)로부터 계산할 수 있다. 종방향 휨강성
 은 다음 식 (1)로 부터 구한다.
은 다음 식 (1)로 부터 구한다.
 (1)
(1)
여기서
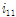 은 튜브의 종방향 단위길이당 단면 2차 모멘트이며,
은 튜브의 종방향 단위길이당 단면 2차 모멘트이며,
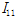 는 튜브 전체단면 2차모멘트이고
는 튜브 전체단면 2차모멘트이고
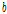 는 튜브단면 폭이다.
는 튜브단면 폭이다.
횡방향 휨강성
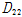 은 튜브 웨브는 두께가 얇기 때문에 횡방향 휨강성 계산시 뒤튈림 단면에 의한 전단변형을 고려해야한다. 따라서 다음 식 (2)을 이용하여 구할 수 있다[13].
은 튜브 웨브는 두께가 얇기 때문에 횡방향 휨강성 계산시 뒤튈림 단면에 의한 전단변형을 고려해야한다. 따라서 다음 식 (2)을 이용하여 구할 수 있다[13].
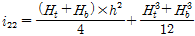 (2a)
(2a)

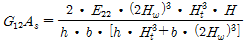 (2b)
(2b)
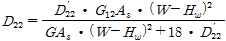 (2c)
(2c)
여기서
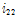 은 튜브의 횡방향 단위길이당 단면 2차 모멘트,
은 튜브의 횡방향 단위길이당 단면 2차 모멘트,
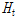 ,
,
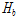 는 튜브 상・하부 플랜지의 두께,
는 튜브 상・하부 플랜지의 두께,
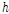 는 튜브 의 높이,
는 튜브 의 높이,
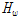 는 튜브 웹의 두께,
는 튜브 웹의 두께,
 는 복합소재 바닥판 폭,
는 복합소재 바닥판 폭,
 는 튜브 단면적,
는 튜브 단면적,
 는 복합소재 바닥판의 총 두께를 나타낸다.
는 복합소재 바닥판의 총 두께를 나타낸다.
그리고
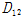 는 다음 식 (3)로부터 쉽게 구할 수 있다.
는 다음 식 (3)로부터 쉽게 구할 수 있다.
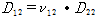 (3)
(3)
마지막으로 뒤튈림 휨강성
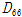 다음 식 (4)로 부터 구할 수 있다.
다음 식 (4)로 부터 구할 수 있다.
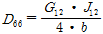 (4)
(4)
여기서,
 는 튜브의 전단탄성계수,
는 튜브의 전단탄성계수,
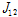 는 튜브의 뒤틀림 강성값이다. 상기 식을 이용하여 튜브에 대한 휨강성값을 계산하여 다음 Table 6과 같이 나타낼 수 있다.
는 튜브의 뒤틀림 강성값이다. 상기 식을 이용하여 튜브에 대한 휨강성값을 계산하여 다음 Table 6과 같이 나타낼 수 있다.
상기 Table 6을 사용하여 심재 튜브단면을 한 개의 층으로 나타낸 등가직교이방성판으로 변환하여 등가직교이방성판 재료 성질을 다음 식 (5)으로 구할 수 있다[14].
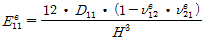 (5a)
(5a)
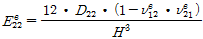 (5b)
(5b)
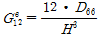 (5c)
(5c)
포아송 비는 다음 식과 같이 구할 수 있다.
 (5d)
(5d)
상기 식을 사용하여 등가 심재에 대한 재료 성질을 Table 7과 같이 나타낼 수 있다.
Table 6과 7을 이용하여 중공형태의 심재를 갖는 샌드위치 구조인 복합소재 바닥판을 한 개 층(single-layer)인 등가 직교이방성판을 변환하여 등가 직교이방성판에 대한 재료 물성과 휨강성을 최종적으로 Table 8, 9 와 같이 얻을 수 있다.
여기서,
 ,
,
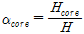 ,
,
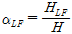 이며, 첨자
이며, 첨자
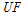 (upper facings)는 샌드위치 구조의 상층면재, 첨자 core는 심재 그리고 첨자
(upper facings)는 샌드위치 구조의 상층면재, 첨자 core는 심재 그리고 첨자
 (lower facings)는 하층면재를 뜻한다. 그리고
(lower facings)는 하층면재를 뜻한다. 그리고
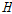 는 복합소재 바닥판의 총 두께,
는 복합소재 바닥판의 총 두께,
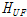 ,
,
 ,
,
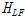 는 각각 상층면재 두께, 심재두께, 하층면재의 두깨를 나타낸다.
는 각각 상층면재 두께, 심재두께, 하층면재의 두깨를 나타낸다.
2.3.2 등가직교이방성판 엄밀해석 기본 이론
일반적으로 교량 바닥판은 일단 단순지지(simple support)와 타단 자유(free support)를 갖는 경계조건(SSFF)으로 해석한다. 이러한 경계조건을 갖는 직교이방성 복합소재 바닥판의 지배방정식의 식 (6)은 Levy 방법을 사용하여 Table 9에서 제시한 휨강성(
 )값을 사용하여 엄밀 해석으로 처짐(
)값을 사용하여 엄밀 해석으로 처짐(
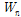 )을 구할 수 있다.
)을 구할 수 있다.
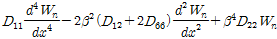

(6)

 (7)
(7)
여기서,
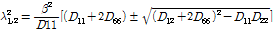 이다.
이다.
식 (7)에서 처짐(
 )은 경계조건에 따라 상수값
)은 경계조건에 따라 상수값
 ,
,
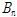
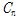 ,
,
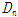 을 구할 수 있다. 그러나 FRP 재료 구조 설계에 익숙하지 못한 건설 기술자에게 기본설계에서 이러한 식을 이용하여 처짐을 구하기 쉽지 않을 수 있다.
을 구할 수 있다. 그러나 FRP 재료 구조 설계에 익숙하지 못한 건설 기술자에게 기본설계에서 이러한 식을 이용하여 처짐을 구하기 쉽지 않을 수 있다.
2.3.3 등가직교이방성판에 대한 유한요소 모델
상기 2.3.1 절에서 제시한 Table 8과 Table 9를 사용하여 유한요소 해석 프로그램을 이용하여 한 개의 적층판인 등가직교이방성판에 대한 유한요소 모델링을 할 수 있다. 본 논문에서는 상용 유한요소 해석 프로그램인 ANSYS 7.0[15]를 사용하였다. 적용한 요소는 하나의 절점에 6개의 자유도를 가지는 4절점 쉘 요소(Shell element 181)이다. 본 요소는 면내 방향(X, Y 방향)으로 2차 변형 형상함수를 가지고 있기 때문에 직교이방성 재료를 적합하게 모델링 할 수 있다. 경계조건은 단순 지지이며 Table 3의 Lamina의 물성을 이용하여 유한요소 해석을 수행하였다. Fig. 3은 상기 2.1절에서 가정한 단면에 대한 복합소재 바닥판에 대한 쉘요소를 사용하여 등가직교이방성판 모델링을 나타낸 것이다.
작용하중은 지간 중앙에 파괴하중 300kN하에서 처짐을 구하였다. Fig. 4는 등가직교이방성판 유한요소 모델링을 이용하여 해석한 결과를 나타낸 것이다.
3. 등가직교이방성판 모델 검증
등가직교이방성판 모델의 검증을 위해서 2.3.1절에서 계산한 Table 5와 9의 재료물성과 휨강성을 이용하여 비등방성 적층보 해석, 복합소재 바닥판 전체 유한요소 해석 모델과 실내실험을 통하여 등가직교이방성판 모델에 대한 검증을 실시하였다. 상기 2.3.3절에서 언급하였듯이 작용하중은 파과하중 300kN 하에서 각각 해석을 실시하였으며, 경계조건은 일단(길이방향) 단순지지, 타단(폭방향) 자유(SSFF)이다.
3.1 비등방성 적층보해석
본 연구에서는 Table 9에서 제시한 등가 직교이방성판에 대한 휨강성 값을 이용하여 간편 구조해석으로 비등방성 적층보 식 (8)을 이용하여 중앙지점에서의 처짐을 쉽게 구할 수 있다.
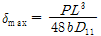 l(8)
l(8)
여기서,
 는 집중하중이고,
는 집중하중이고,
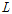 은 보의 지간이다. 그리고
은 보의 지간이다. 그리고
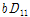 은 휨강성이다.
은 휨강성이다.
3.2 전체 유한요소해석 모델
복합소재 바닥판 전체 유한요소 해석 모델에 의한 결과와 등가직교이방성판 유한요소 해석 모델에 의한 해석과 비교하였다. 경계조건은 일단(길이방향) 단순지지, 타단(폭방향) 자유(SSFF)이다. Fig. 5는 ANSYS 7.0를 사용한 복합소재 바닥판 전체에 대한 유한요소 해석 모델을 나타내고 있다. 2.3.2절에서 언급하였듯이 동일한 요소를 사용하여 유한요소해석을 수행하였다.
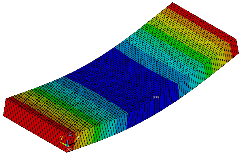
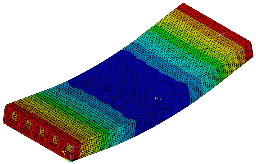
Fig. 6은 복합소재 바닥판 전체에 대한 유한요소 해석한 변위 분포도를 보여 주고 있다.
Table 10은 비등방성 적층보해석, 등가직교이방성판 유한요소 해석 모델에 의한 값과 복합소재 전체 유한요소 해석 모델에 의한 값을 비교하여 나타낸 것이다. 등가직교이방성판 모델링 해석값이 전체 모델링 해석 값 보다 6.08% 높은 것으로 나타났으며, 비등방성 적층보 해석보다는 18.9% 적게 나타났다. 이러한 차이는 실제 FRP 재료 복합소재 바닥판이 얇은 두께의 복부를 갖는 튜브형태의 심재이기 때문에 이 부분의 국부거동의 결과로 기인된 것으로 사료된다.
3.3 실내 휨 성능시험
3.3.1 시험 개요
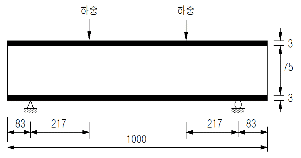
본 실험은 상기 2.1절에서 제안된 단면의 GFRP 복합소재 바닥판에 대해 구조적인 특성을 파악하기 위해 휨성능 시험을 수행하였으며, 시험체 제작은 한국화이바(주)에 의뢰하여 이루어 졌다. 본 바닥판 형식은 샌드위치 구조로서 심재(core)인 박스튜브는 인발공법(pultrusion)으로 제작하였으며, 상층면재(upper facing)과 하층면재(lower facing)를 수적층(hand lay-up)하여 오토클레이브(autoclave) 몰딩(molding)공법으로 제작하였다. 각 구성요소의 접합은 2가지 방법을 사용하였으며, 순수한 접착제 접합에 의한 시험체 제작과 접착제 접합을 포함한 기계적 이음에 의한 시험체 제작을 이용하여 각각 2 종류의 시험체를 제작하였다. 접착제로는 에폭시 접착제이며, 사용된 볼트 직경은 5mm이다. 볼트 체결 위치에 미리 에폭시/glass powder를 주입시켜 볼트 체결시 응력집중의 손상을 방지하였다. 총 3개의 시험제를 제작하였으며, 시험체 2개는 완전 접착제만을 사용하여 제작되었으며, 나머지 1개 시험체는 접착제와 볼트를 사용하여 제작하였다. 구조성능을 확인하기 위해 4점 휨(4-Point Bending) 시험을 하였다. GFRP 복합소재 바닥판 시험체의 제원과 가력 방향은 Fig. 7에 보인 바와 같다. 실험체의 지점간격은 1.0m 이고, 보 지점부의 지지조건은 단순지지로 하였다. Fig. 8과 같이 하중은 국내사의 100kN 용량의 구조 모형틀 시험기를 사용하였다. GFRP 복합소재 바닥판의 처짐과 변형률 등은 데이터 로거(data logger)를 사용하여 측정하였다.
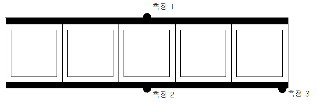
처짐은 Fig. 9와 같이 측정 2의 위치에서 측정하였으며, 변형률은 지간 중앙부 3개의 점에서 측정하였다. 동일한 시험 체 3개에 대하여 0.05mm/sec의 속도로 변위를 제어하여 바닥판이 완전히 파괴되거나 더 이상의 하중증가가 없을 때까지 하중을 재하 하였다.
3.3.2 시험결과 및 분석
Fig. 10은 극한하중에 대한 하중-처짐 곡선을 나타낸 것으로 Test 1은 접착제와 볼트에 의한 제작한 GFRP 복합소재 바닥판 시험체이며, Test 2는 완전 접착제만을 사용하여 제작한 복합소재 바닥판 시험체를 뜻한다. 시험체의 경계조건은 일단(길이방향) 단순지지, 타단(폭방향) 자유(SSFF)이다.
Table 11은 파괴하중 300kN의 작용하중 하에서 식 (8)에 의한 비등방성 적층보 해석, 등가직교이방성판 유한요소 해석 모델에 의한 값과 실내 시험을 통하여 측정한 값과 비교하여 나타낸 것이다. 식 (8)에 적용된 휨강성
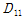 값은 Table 9에서 제시된 등가직교이방성판의 휨강성 값이다. 등가직교이방성판 모델링 해석 값이 접착제 접합만으로 제작한 시험체(test2)에 대한 실내시험의 파괴하중에서 측정한 처짐 값 보다 19.24% 낮게 나타났으며, 접착제와 볼트로 제작한 시험체(test1)에 대한 처짐 값보다 32.19% 높게 나타났다.
값은 Table 9에서 제시된 등가직교이방성판의 휨강성 값이다. 등가직교이방성판 모델링 해석 값이 접착제 접합만으로 제작한 시험체(test2)에 대한 실내시험의 파괴하중에서 측정한 처짐 값 보다 19.24% 낮게 나타났으며, 접착제와 볼트로 제작한 시험체(test1)에 대한 처짐 값보다 32.19% 높게 나타났다.
4. 결 론
지금까지 GFRP 복합소재 바닥판 설계는 휨강성(stiffness)에 의해서 이루어지고 있음을 많은 연구를 통해서 확인되었다. 이러한 점에서 GFRP 복합소재 바닥판 설계에서 주요 설계인자는 설계하중에서 발생 처짐이 처짐 한계 이내에 있도록 단면설계가 되어야 함을 알 수 있다. 그러므로 기본설계에서 가정한 GFRP 복합소재 바닥판의 단면설계에 대한 설계하중 하에서 간편한 복합소재 바닥판의 최대 처짐 계산이 중요하다.
본 연구는 GFRP 복합소재 바닥판의 해석의 기본설계에서 최대 처짐 계산을 위해 많은 시간이 소요되는 전체 유한요소 해석 모델링을 이용하지 않고 탄성 등가 모델링을 이용한 간편 해석 방법을 제시하였다. 본 간편 해석 방법에 의한 탄성등가모델링을 이용한 직교이방성판의 해석결과와 전체 유한요소해석 모델링을 이용한 해석결과와 비교 검토하였다. 또한 복합소재 바닥판의 실내 정적하중 시험을 통하여 측정한 처짐 값과 본 논문에서 제시한 탄성등가모델링을 구성하여 이용한 간편 해석 방법의 결과와 비교하여 타당성을 검증하기 위해 세 가지 방법으로서, 1) 전체 유한요소 모델링 해석, 2) 비등방성 적층보 이론, 3) 휨성능 실험을 이용하였다.
결과 분석결과 본 연구에서 제시한 간편 해석방법인 등가직교이방성판 모델링 해석 값(9.24mm)이 비등방성 적층보이론값(11.40mm)보다 18.9% 낮으며, 전체 유한요소 모델링 해석 값(8.71mm)보다 6.08% 높은 것으로 나타났다. 이러한 분석을 통해서 단면결정을 위한 기본설계 단계에서 GFRP 복합소재 바닥판 단면설계시 탄성등가 모델링 해석을 이용한 해석방법으로도 설계할 수 있음을 확인할 수 있다. 그리고 휨성능 실험 결과에서, 등가직교이방성판 모델링 해석 값(9.24mm)이 접착제 접합과 기계적 접합(볼트)로 제작된 시험체(test1)의 측정된 처짐 값(6.99mm)보다 32.1% 높게 나타났으며, 접착제 접합만으로 제작한 시험체(test2)의 측정된 처짐 값(11.444mm)보다 23.8% 낮게 나타났다. 등가직교이방성판 모델링 해석 값과 휨성능 시험 값과의 오차 발생원인은 시험체의 제작과 주로 관련이 있다고 사료된다. 접착제 접합으로 만 제작한 시험체는 접착제의 충분한 접착강도가 확보되지 않아 복합소재 바닥판의 전체 휨강성이 발휘되지 못한 것으로 분석되며, 한편 접착제 접합과 기계적 접합(볼트)을 사용하여 제작한 시험체는 충분한 휨강성이 확보된 것으로 판단된다.
기존 철근콘크리트 바닥판 설계는 엄밀해석인 평판 해석이 아닌 보 해석을 통하여 단면결정을 하고 있다. 이러한 점에서 본 논문에서 제시한 간편 해석 방법은 비등방성 적층보의 해석보다 크고 전체 유한요소해석 모델링을 사용한 해석 값 보다 큰 오차(6.08%∼18.9%)가 발생하고 있지만 기존 철근콘크리트 바닥판 설계에서 나타난 해석 값의 흐름과 유사한 순서를 보이고 있기 때문에 본 논문에서 제시한 간편해석 방법이 기본 설계 단계에서 단면결정을 위해서는 사용가능하다고 사료된다.
GFRP 복합소재 바닥판 형식이 GFRP 재료의 특성에 맞는 중공튜브 구조 또는 샌드위치 구조이다. 따라서 복합소재구조 설계에 익숙하지 못한 설계자가 단면설계를 위한 기본설계 단계에서 비교적 난해한 복합소재 바닥판 전체 유한요소 해석 모델링을 사용하여 최대 처짐 계산하는 방법 보다 본 연구에서 제시된 탄성 등가 모델링을 이용하여 간편하게 GFRP 복합소재 바닥판의 최대 처짐을 계산할 수 있으며, 최적의 GFRP 복합소재 바닥판의 단면형식을 결정할 수 있을 것으로 사료된다.
References
- Zhou, A. (2002) Stiffness and strength of fiber reinforced polymer composite bridge deck systems, Ph.D. Thesis, Virginia Polytechnic Institute and State University.
-
Cai, C.S., Oghumu, S.O., and Meggers, D.A. (2009) Finite element modeling and development of equivalent properties for FRP bridge panels, Journal of Bridge Engineering, ASCE, Vol. 14, No. 2, pp.112-121.
[https://doi.org/10.1061/(ASCE)1084-0702(2009)14:2(112)]

- Lee, S.W., Lee, S.G., and Kim, J.H. (2001) Development of light weight and high durable composite bridge deck, Proceedings of Korean Society of Civil Engineers, KSCE (in Korean).
- Ji, H.S., Son, B.J., and Chang, S.Y. (2004) A Experimental Study on Behavior of FRP Materials Bridge Deck for Use in Deteriorated Bridge Decks Replacement, Journal of Korean Society of Steel Construction, KSSC, Vol. 13, No. 6, pp.631-640 (in Korean).
-
Ji, H.S., Son, B.J., and Ma Z. John. (2009) Evaluation of Composite Sandwich Bridge Decks with Hybrid FRP-Steel Core, Journal of Bridge Engineering, ASCE, Vol. 14, No. 1, pp.36-44.
[https://doi.org/10.1061/(ASCE)1084-0702(2009)14:1(36)]

- Ji, H.S. and Chun, K.S. (2010) A Experimental Study on Behavior of Modular GFRP Deck for Use in Deteriorated Bridge Decks Replacement, Journal of Korean Society for Advanced Composites Structures, KOSACS, Vol. 1, No. 2, pp.44-50 (in Korean).
- Chun, K.S. and Ji, H.S. (2011) A Simple Modification of the First-Order Shear Deformation Theory for the Analysis of Composite Laminated Structures, Journal of Korean Society of Steel Construction, KSSC, Vol. 23, No. 4, pp.475-481 (in Korean).
- Allen, H.G. (1969) Analysis and Design of Structural Sandwich Panels, Pergamon, Oxford.
-
Ji, H.S. (2012) Long-term performance evaluation of a GFRP slab bridge, Journal of Korean Society of Steel Construction, KSSC, Vol. 24, No. 3, pp. 349-360 (in Korean).
[https://doi.org/10.7781/kjoss.2012.24.3.349]

- Ji, H.S. and Chun, K.S. (2010) A Experimental Study on Behavior of Modular GFRP Deck for Use in Deteriorated Bridge Decks Replacement, Journal of Korean Society for Advanced Composites Structures, KOSACS, Vol. 1, No. 2, pp.44-50 (in Korean).
-
Qiao, P., Davalos, J.F., and Brown, B. (2000) A Systematic Analysis and Design Approach for Single-span FRP Deck/stringer Bridges, Composites Part B, Vol. 31, pp.593-609.
[https://doi.org/10.1016/S1359-8368(99)00044-X]

- Jones, R.M. (1999) Mechanics of Composite Materials 2nd Edition, Taylor & Francis Inc.
- O'Brien, E.J. and Keogh, D.L. (1999) Bridge Deck Analysis, E&FN Spon of the Taylor & Francis Group, New York, NY, USA.
- Reddy, J.N. (1997) Mechanics of Laminated Composite Plates, CRC Press, New York, USA.
- ANSYS Inc. (2005) ANSYS 7.0 documentation, Canonsburg, PA, USA.

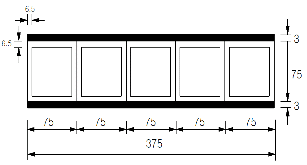
 (GPa)
(GPa)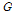 (GPa)
(GPa)
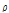 (
(
 )
)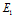
 )
)
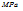 )
)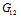
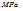 )
)