하이브리드 해상풍력 파일 기초 콘크리트 지지구조(MCF) 개발

1. 서  론

풍력에너지는 석탄, 석유와 같은 기존 화석자원의 고갈과  탄소 배출로 인한 환경 파괴 문제를 해결하기 위한 대체 에너지로 주목 받고 있으며, 부존량이 풍부하여 수천 년 전부터 인류가 이용해 오고 있다. 육상 풍력 발전은 부지 확보와 같은 지역적 제한 조건, 진동 및 소음 등의 민원, 낮은 발전량 등의 문제를 갖고 있어, 최근에는 풍황 및 제한조건이 비교적 양호한 해상풍력발전이 각광받고 있으며, 경제성, 환경성 및 사회적 편익 등이 고려된 효율적인 해상 풍력발전 구조물을 개발하기 위한 노력이 계속 되고 있다.

수심 및 지반 조건 등을 고려한 많은 형식의 해상 풍력발전 지지구조물들이 개발되어 왔으나, 가장 많이 쓰인 형식은 모노파일 형식으로 육상 풍력발전 형식과 유사하고 전이구조를 갖고 있다. 또한, 시공이 간단한 장점이 있으나, 충분한 강성과 적절한 고유 진동수의 확보를 위해서는 직경이 커져야 한다는 단점을 갖고 있어, 대용량의 터빈과 깊은 수심에 적용하여 경제성을 확보하기가 쉽지 않다. 한편, 주로 연안지역에 설치된 중력식 기초 형식도 널리 사용 되었으며, 석유나 가스 시추 구조물에도 중력식 기초 형식이 이용되어 왔다. 전이구조가 없고 견고하며, 전도 모멘트에 대한 저항력으로 기초 구조물 자중을 이용하므로 지반의 굴착이 필요 없는 구조 형식이다. 일반적으로 육상에서 사전 제작 후 직립 상태로 해상의 설치 위치까지 이동되어 해저면에 놓여진다. 최초의 콘크리트 중력식 기초 구조물은 1975년 노르웨이 Stavanger에서 제조된 ‘Condeep B’로, Beryl 지역의 깊은 수심에 설치되었다[1]. 석유나 가스 시추 구조물과 같은 해상 구조물에만 쓰이던 중력식 기초 구조물이 해상 풍력 발전 기초 구조물 형식으로 쓰이기 시작하였다. 1991년 처음으로 덴마크 lolland 해안 연안에 중력식 해상 풍력 기초 구조물로 이루어진 5MW급 해상 풍력 단지가 조성되었는데, 평균 908톤의 해상 풍력 구조물 11기가 설치되었다[2]. 2009년 벨기에 Vlaanderen 지역 해상의 ‘Thornton Bank 1’은 27.5m 수심에 5MW 터빈의 지지구조로 중력식이 사용되었고[3], 2010년 덴마크의 남해상 ‘Red Sand 2’에 적용 수심 7.5~15m의 2.3MW 중력식 지지구조물이 COWI사에 의해 설치되었다[4].

최근에는 해상운반을 고려한 대수심 지역에 적용이 가능한 중력식 지지구조물의 개념 개발이 유럽을 중심으로 활발하다. 대표적으로, Vici Ventus에서는 수심 30~100m에 적용 가능한 대형 콘크리트 지지 구조물을 개발하였다. 중력식을 기반으로 타워기초까지 콘크리트를 이용하여, 시공이 간단하고 지반 조건에 따라 중력식 혹은 스커트 파일식 등으로 변경가능 하도록 설계되었다[5].

일반적으로 사용되던 강재를 이용한 해상풍력발전 지지구조물은 단지의 규모가 커지고 수심이 깊어지면 경제성을 확보하기 어려워 구조적 안정성을 보장하면서도 경제적인 콘크리트를 이용한 지지구조물 개발이 진행되고 있으나, 콘크리트를 이용한 중력식 지지구조는 규모가 크고 중량이 무거워 운반·설치 비용이 오히려 증가할 수도 있다. 따라서, 강재와 콘크리트를 이용한 부재의 최적 배치는 자중을 줄이고 시공성을 확보할 수 있는 좋은 대안이 될 것으로 판단된다. 모노파일 및 중력식과 같은 기존의 지지구조물이 갖는 단점을 보완하여 Fig. 1과 같이 강재 샤프트와 원추형 콘크리트로 이루어진 새로운 형식의 파일지지 하이브리드 지지구조(MCF: Multi-pile Concrete Foundation)를 본 연구에서 제안하였다.

하이브리드 지지구조는 하단에 원추형의 두꺼운 콘크리트 지지구조를 가지고 있기 때문에, 등가의 빔 요소를 이용한 해석 방법은 적절하지 않다. 따라서, 정확한 기하형상을 모델링할 수 있고, 파랑하중에의한 3차원 해석이 가능한 입체요소 혹은 쉘요소의 개발이 요구된다. Ahmad등은 대부분의 쉘 요소 식에 사용되는 ‘degenerate’ 모델을 소개하였고[6], 얇거나 두꺼운 플레이트 혹은 쉘 요소에 모두 적용 할 수 있어 널리 사용되어 왔다. Degenerated 쉘 요소의 대안으로 Hauptmann과 Schweizerhof[7], Sze와 Yao[8]은 솔리드-쉘 요소(Solid-shell)요소를 소개하였는데, 이는 회전 자유도를 사용하지 않는다는 점에서 주목을 받았다. 솔리드-쉘 요소는 degenerated 쉘 요소와 비교하여 수식과 모델링이 간단하고 더 효과적이나, 두께가 얇아지면 잠김 현상으로 인해 성능이 급격히 떨어지는 단점을 갖고 있어 보다 정확하고 안정적인 솔리드-쉘 요소의 개발이 요구되었다.

Simo와 Rifai[9]는 가정된 변형률 방법을 체계적으로 개발하였고, 미소 변형률을 가지는 휨 지배 문제에 대한 성능 향상이 가능한 저차 요소 개발의 틀을 마련하였다. 또한, 수렴성과 안정성에 대한 문제를 해결하기 위해 노력하였고, EAS를 포함하는 비접합 모드의 고전적 방법을 사용하였다. EAS 법을 사용한 요소는 휨뿐 만 아니라 비압축성 한계에 대해서도 좋은 결과를 보이므로 EAS법은 널리 사용되어 오고 있다. Hauptmann과 Schweizerhof[7]는 선형 및 비선형 해석을 위한 ‘Solid- shell’ 요소를 개발하였는데, 이 요소에는 자연 변형률 방법(ANS)과 EAS 방법이 적용되어 잠김 현상을 제거 할 수 있었다. Sze와 Yao[8]는 두께 방향 잠김과 사다리꼴 잠김을 제거하기 위해 가정 자연 변형률법이 적용된 복합 응력 솔리드-쉘 요소를 제안하였고, 직각 가정 응력 모드를 사용하여 기존 복합 요소보다 더 좋은 성능을 보였다.

EAS 방법은 쉘과 솔리드 요소의 잠김이 없는 거동을 위한 복합 응력 방법의 대안이 될 수 있고, 복합 응력 방법과 비교해 볼 때 재료 비선형 정식화에서 큰 장점을 가진다. 하지만 비선형 해석을 위한 추가적인 자유도(D.O.F)의 계산을 위해 EAS와 복합 응력 두 방법 모두 역행렬을 필요로 하고, 이 자유도의 계산을 위해선 더 많은 계산 시간을 필요로 한다.

8절점 솔리드 요소에 대한 잠김 문제를 해결하기 위한 방법 중 감소된 가우스 적분을 사용하는 또이 방법은 모래시계 문제(hourglass problem)를 일으켜, 강성 행렬과 내력 벡터를 안정화시키는 제어 기술이 필요하다.

김기두 등의 쉘 요소는 전체 좌표, 국부좌표와 자연좌표계가 쉘 형상을 모델링하는데 사용되었고[10], 김기두 등은 기하 비선형 해석을 위한 8절점 resultant 솔리드-쉘 요소 식과 검증된 수치 예제를 제시하였다[11]. 미소변형률 및 대변위 개념과 다양한 잠김 현상 해결을 위한 ANS 방법이 사용되었고, 기하학적 비선형 정식화를 위해 수정된 라그랑지안(updated Lagrangian)법이 사용되었다. 평행방정식을 유도하기 위해 Resultant force form이 사용되었고, 강성행렬의 계산을 위해선 두께 방향으로 적분한 2x2 가우스 적분법을 사용하여 계산 시간을 단축시켰다. 두께 방향의 변위와 좌표에 대해 선형 보간하는 방법을 솔리드-쉘 요소에 적용하였다.

본 연구에서는 김기두[12],[13]에 의하여 제시된 신형식 해상풍력 하이브리드 지지구조물의 개념도를 활용하여 기본 설계를 위한 기초 연구를 수행하였다. 하이브리드 지지조물의 효율적인 해석을 위하여 솔리드-쉘 요소에 절점 보간법이 적용된 새로운 솔리드-쉘 요소를 해상 풍력지지 구조물의 3차원 응력해석이 가능하도록 개발하고, 건국대학교에서 개발된 정·동적 구조해석 프로그램인 XFINAS로부터 해양구조물 전용 해석프로그램으로 재개발된 XSEA에 탑재 되었다[14].

2. 신형식 지지구조

최근 유럽의 기업들을 중심으로 콘크리트를 이용한 지지구조물에 대한 연구가 활발하나, 대부분 중력식에 기반하고 있어, 해저 지반조건이 양호한 지역에서만 사용할 수 있다. 우리나라 서남해안과 같이 연약지반 심도가 깊은 지역에서는 안정성을 확보하기 어려워, 파일기초의 사용이 가장 유력한 대안이 될 수 있다. 그러나, 비용증가에 대한 부담으로 인해 지지구조물의 전체적인 비용절감은 불가피한 선택이 된다.

콘크리트 재료의 장점은 비용적인 측면에서 강재의 절반정도이며, 다른 재료보다 강한 내구성을 갖고 있으며, 낮은 유지관리 비용이 소요된다. 또한, 침식에 대한 저항성이 높고, 아주 높은 감쇄특성을 가지고 있어, 증가되는 하중에 대처하기 쉽고 강재 자켓(Jacket)보다 짧은 기간에 신속히 설치할 수 있다. 이러한 장점에도 불구하고, 콘크리트 재료를 이용할 경우 제작 후 플로팅 또는 대형바지선을 이용하여 운반하고 설치하여야 하므로, 무거운 자중이 걸림돌로 작용한다. 따라서, 해저 지반으로부터 최하단의 기초는 콘크리트재료를 이용하고, 타워기초 또는 플랫폼까지는 모노파일과 유사한 강재를 이용한 샤프트(Shaft)를 채용한 하이브리드 형식을 적용하면, 경제성을 확보할 수 있다.

콘크리트와 강재를 이용한 새로운 개념의 해상풍력 지지구조의 형상을 Fig. 2에 나타내었다.

이 모델은 전형적인 중력식 기초로부터 콘크리트와 강재를 이용한 하이브리드 구조형식으로 수정되었다. 해저지반(Mudline)으로부터 원추형 형상이 시작되어 강재 샤프트(Shaft)까지 콘크리트로 이루어져 있고, 강재 파일 슬리브(Sleeve)를 감싸고 있는 콘크리트와 연결되어 있다. 원추형 콘크리트의 내부에는 가로보로 보강되어 있다. 이 가로보는 철골철근콘크리트(SRC)구조재로, 불안정한 횡력에 대해 저항할 수 있는 구조로 구성되어 있다.

파일 지지된 하이브리드 구조물의 기하형상 제원은 Table 1에 나타내었다.

3. 솔리드-쉘 요소 개발

3.1 개발 개요

다양한 종류의 역학적 문제에 적용 가능한 3차원 솔리드요소와 쉘요소가 구조해석을 위해 널리 사용되어 왔으나, 이 요소들은 잠김현상으로 인해 두께가 얇아짐에 따라 정확도가 떨어지는 단점을 보였다. 또한, 감절점 쉘요소는 구조물의 단면 형상에 정확히 적용 할 수 없고, 솔리드 요소를 이용할 경우에는 긴 해석시간이 요구된다는 제약이 있다. 따라서, 모델링이 간편하고 효율적인 8절점 솔리드-쉘 요소(resultant 8-node solid-shell element)가 김기두 등[15]에 의해 개발되었다. 본 연구에서는 국부좌표계를 이용하여 요소 중간면에서의 응력을 구할 수 있는 기존의 솔리드 쉘요소를 Result Forces Form과 새로운 개념의 Stress Nodal Interpolation을 사용하여 8절점에서의 응력 계산이 가능하도록 개발하였다.

솔리드-쉘 요소의 합력 정식화(resultant force formu-lation)는 쉘요소의 접근법에 의해 이루어졌고, 얇은 평판과 쉘에서 발생하는 다양한 잠김현상을 제거하기 위해 평면응력(plane stress)개념의 ANS(Assumed Natural Strain)기법과 EAS(Enhanced Assumed Strain)기법을 이용하였다. 요소 강성행렬의 계산을 위해 2x2 가우스 적분을 이용하였고, 합력은 평형방정식으로부터 유도 되었다. 또한, 변위와 절점좌표의 선형보간을 이용하여 두께 방향으로 pre- integration기법이 솔리드-쉘요소에 적용되었다.

3.2 기하학적 형상

기존 솔리드 요소가 전체 좌표계 와 자연 좌표계 만을 고려하는 반면에, 솔리드-쉘 요소는 Fig. 3과 같이 전체 좌표계 및 자연 좌표계 와 함께 요소의 중간면에 위치한 국부 직각 좌표계 도 고려한다. 따라서 8절점 솔리드-쉘 요소는 쉘의 기하학적 형상 및 운동학의 관점에서 표현될 수 있다.

전체 좌표계에서, 요소 내 한 절점의 위치 벡터 는 와 쌍일차 형상 함수 에 의해 아래 식 (1)과 같이 나타낼 수 있다.

 (1)

 (2)

여기서, 는 요소 중간면에 위치한 위치 벡터, 는 요소 하단에서 상단 방향으로의 절점 벡터의 절반, 그리고 는 각각 요소의 상단과 하단에 대한 절점 벡터이다.

위치 벡터의 보간법과 비슷하게 국부 변위 벡터는 국부 좌표계에서 아래 식 (3)과 같이 보간 된다.

 (3)

 (4)

여기서, 와 는 요소 중간면의 변위 벡터 및 요소 하단에서 상단 방향으로의 절점 벡터의 절반이다.

변환 행렬 로 인해, 아래 식 (5)와 같이 위치 벡터 는 전체 좌표계에서 국부 좌표계로 변환 될 수 있다. 따라서 모든 변위, 변형률 그리고 응력 또한 국부 좌표계에서 계산되어진 후 변환 행렬 와 함께 전체 좌표계에 대한 값으로 변환 될 수 있다.

 (5)

여기서, 와 는 전체 좌표계에 대한 위치 벡터와 변위 벡터, 와 는 국부 좌표계에 대한 위치벡터와 변위 벡터이다.

결국, 식 (1)과 (3)에 따라 솔리드-쉘 요소는 두께 방향으로 선형 보간된 쉘 요소와 비슷한 역학적 특성을 가지게 된다.

3.3 변형률-변위 관계식

다음에 언급 될 식들은 업데이티드 라그랑지안(Updated Lagrangian)법에 기초하였기 때문에, 모든 변형률, 응력, 변위는 증분형태로 표현된다.

식 (3)에서의 변위 벡터는 식 (6)과 같이 구성되어 있다.

 (6)

선형 변형률은 멤브레인 변형률 , 휨 변형률 , 면외 방향 전단 변형률 , 면외 방향 수직 변형률 로 구분되고 이는 다음과 같다.

,    

    (7)

3.4 구성 방정식

응력과 변형률과의 관계를 나타내는 구성 방정식은 4차 탄성 텐서로 표현되고, 응력 텐서 를 변형률 텐서 의 함수로 나타내어 다음과 같이 간단하게 정의될 수 있다.

 (8)

응력 텐서 와 변형률 텐서 는 대칭성을 지니고, 4차 탄성 텐서 는 의 행렬로 표현된다. 국부좌표계에서의 일반화된 plane-stress 텐서는 다음 식에 의해 얻어진다.

 (9)

여기서, , , 는 탄성계수,

는 포아슨 비이다.

멤브레인-휨 응력은 면외 방향 변형률과는 직접적으로 관계가 없으며, 따라서 멤브레인-휨 응력-변형률, 면외 방향 수직 응력-변형률, 면외 방향 전단 응력-변형률에 대한 , , 는 각각 다음과 같이 정의된다.

 (10)

,

따라서, 멤브레인-휨 응력은 식 (11)과 같이 정의되고, 면외 방향 전단 응력 및 면외 방향 수직 응력은 식 (12)와 같이 정의된다.

 (11)

, (12)

요소 구성 행렬은 위의 식 (8)의 행렬을 두께 방향에 대해 적분함으로써 식 (13)과 같이 얻을 수 있고, 이로부터 식 (14)와 같이 합응력을 구할 수 있다.

 (13)

 (14)

여기서, 은 멤브레인 합응력, 은 휨 합응력, 는 면외 방향 수직 합응력, 는 면외 방향 전단 합응력을 나타낸다.

3.5 요소강성 행렬

선형 변형률로부터 계산되는 요소 변형률 에너지는 다음과 같다.

 (15)

여기서 는 변형률 텐서로, 요소 중간면에서의 절점 변위 및 변형률-변위 행렬 로부터 다음과 같이 나타낼 수 있다.

 (16)

식 (15)와 (16)으로부터 요소 변형률 에너지는 식 (17)과 같이 나타낼 수 있고, 여기서 는 국부 요소 강성 행렬을, 는 국부 변위를 의미한다.

 (17)

 (18)

변환 행렬 로 인해 국부 좌표에서의 변위 는 전체 좌표계에 대한 변위 로 식 (19)와 같이 표현되고, 식 (19)를 식 (17)에 대입함으로써 전체 요소 강성 행렬 을 구할 수 있다.

 (19)

 (20)

3.6 절점 보간법

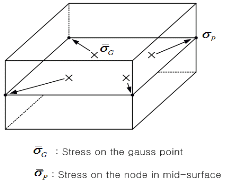
기존 솔리드-쉘 요소는 중간면에 위치한 가우스 적분점에서의 응력을 구할 수 있었으나, 구조물의 실제 거동에 기초한 응력 분포를 구하기 위해서는 절점에서의 응력을 구할 수 있어야 한다. 따라서, 본 논문에서는 응력 및 변형률, 변위와의 선형적 관계를 이용하여 솔리드-쉘 요소의 절점응력을 구하는 방법을 제시하였다.

요소 상․하단 절점에서의 응력을 구하기 위해, 먼저 중간면에 위치한 가우스 적분점에서의 응력을 앞서 설명한 구성 방정식에 의해 구하고, Fig. 4와 같이 중간면의 임의의 절점 응력으로 보간한다. 중간면의 절점은 실제 요소에서 존재하지 않는 절점이나, 요소 절점 응력을 구하기 위해 임의로 응력을 보간하는 절점이다. 가우스 적분점에서의 응력을 절점으로 보간하기 위해서는 식 (21)에 나타낸 2차원 형상함수를 이용하여야 한다.

 (21)

또한, 식 (4)의 관계식을 이용하여 중간면에서의 변위를 구하기 위해, 요소 각 절점에서의 변위( )를 먼저 구하여야 한다. 이것은 앞 절에서 구한 전체 요소 강성 행렬 과 외력 의 평형방정식 관계를 나타낸 식 (22)를 이용하여 얻을 수 있다.

 (22)

요소에서 응력과 변형률, 그리고 변위는 앞서 살펴본 변형률-변위 및 응력-변형률 관계에 의해 선형적 관계를 갖고 있있어, Fig. 5와 같이 1번 절점과 5번 절점 그리고 중간면 절점 에서의 변형률-변위의 관계로 나타낼 수 있다. 이것을 중간면과 각 절점에 대한 응력-변위 비로 표현하면 식 (23)과 같이 나타낼 수 있다.

 (23)

앞서 나타낸 식들에 의해, 식 (23)의 중간면 절점에서의 응력 와 변위 그리고 상․하단 절점에서의 변위 를 구할 수 있고, 요소 상․하단에서의 절점 응력은 식 (24)를 통해 구해진다.

 (24)

4. 환경조건

극한조건을 이용한 기초적인 설계를 위해 파일 지지된 원추형 하이브리드 지지구조에 해양학적 조건들이 적용되었다. 폭풍(storm)의 내습에도 견딜 수 있는 파일 기초 하이브리드 지지구조에 대한 타당성 연구가 목적이다. 하중은 터빈의 비정상운전모드(abnormal turbine wind)가 적용되었다. 1시간 평균풍속, 유의파고(significant wave height), 수심, 폭풍해일높이(storm surge height), 조수고(tide height)와 해류속등이 50년 재현주기로 적용되었다.

4.1 풍하중 모델링

평균 풍속은 가까운 지역 또는 해수면위의 하부구조나 타워에서 평가되어 작성된 데이터베이스에 의해 결정된다. 풍하중 모델은 동일한 거칠기의 수평면위 10m 높이에서의 평균풍속변화는 지수로 나타낸 파워로(power law)로 식 (25)와 같이 나타낼 수 있다.

 (25)

여기서, 는 높이에서의 평균풍속(m/s), 는 계수를 나타낸다.

4.2 파랑하중 모델링

파일지지된 원추형 해상풍력 지지구조는 해류나 파랑과 같은 동적 유체하중(hydrodynamic loading)이 작용한다. 해류(sea current)는 대부분 조류(tide wave)와 해양순환(ocean cir-culation)에 의해 발생되고, 큰 조차가 발생하는 지역 또는 해저지형이 조류에 급격히 영향을 미치는 지역에서 가장 크게 나타난다. 수심에 따른 해류의 속도 변화는 식 (27)의 조류의 영향에 관한 식과 식 (28)의 바람에 의해 발생하는 식으로 나타낼 수 있으며, 식 (26)은 그 합을 나타낸다[16].

 (26)

 (27)

 (28)

여기서, z는 평수위의 수직좌표를 나타내고 , 는 각각 평수위의 조류속과 바람에 의한 유속을 나타낸다. 는 평수위의 수심, 는 바람에 의한 조류속의 기준수심( )를 나타낸다.

하부 구조에 적용된 파랑하중은 모리슨(Morison, 1950)식에 의해 고려되었다. 항력과 관성력에 의해 외력은 작용된다. 이 두가지 항목은 각각 유체의 속도와 가속도의 제곱으로 나타낼수 있다. 속도와 가속도는 적절한 파랑이론에 의해 계산될 수 있다. 파랑하중은 주기, 파고, 수심을 갖는 규칙파(regular wave)가 해석모델로 고려되었고, 적용이론으로는 주어진 도표를 이용하여 선택된 Stream Function 7차 이론이 적용되었다[17]. 그 일반식은 식 (29)와 같다.

 (29)

여기서, 는 파속, 는 수심을 나타내고 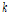는 파수를 나타내며, 은 차수를 나타낸다.

4.3 파랑하중의 입체요소 적용

앞서 언급된 모리슨식은 대부분의 자켓 해양구조물 해석에 적용되어왔으며, Fig. 6과 같이 뼈대(보)요소를 이용하여 길이방향에 따라 파랑하중을 적용하였다.

그러나 콘크리트 해양 구조물의 경우는 표면적에 작용하는 파랑하중에 의하여 응력 집중 및 국부 변형이 발생할 수 있으므로 뼈대 요소의 가정을 사용할 수 없다. 본 논문에서는 모리슨 방정식과 솔리드-쉘 입체요소를 이용하여 실제 지지구조물과 유사하게 모델링 할뿐만 아니라, 기존의 모리슨 방정식을 입체요소 단면에 적용할 수 있도록 식 (30)과 같이 투영 면적을 적용하였다[15]. Fig. 7은 입체요소에 적용된 파랑하중의 개념도를 나타낸다.

 (30)

여기서, 는 물의 밀도, 는 실린더 표면의 압력계수(pre-ssure coefficient), 는 관성압력계수(inertia pressure coefficient), 는 투영면적, 은 대체된 유체의 부피를 나타낸다.

4.4 적용지역의 환경변수

극한 파랑조건은 파랑의 방향에 따라 50년 재현주기로 가정되었다. 유한요소 해석을 위해 적용지역의 특성을 고려한 유체하중 매개변수가 필요하다. 해상풍력발전에 관한 매개변수를 선택하는 것은 바람에 관한 사항뿐만 아니라, 해양의 수심과 관련된 다양한 항목들이 포함된다. 이러한 항목에 대한 분석을 통해 한국전력(KEPCO)은 서남해안에서 가까운 위도 지역을 해상풍력단지 최적지로 선정한 바 있다[18].

본 연구에서도 새롭게 제시한 하이브리드 지지구조의 적용성 검토를 위해 동일한 조건의 환경변수를 적용하였으며, Table 2에 나타내었다.

5. 적용하중 및 조합

5.1 자중 및 터빈 모델링

풍력터빈의 공기역학(Aerodynamic)과 바람의 유입(wind- inflow)조건에 대한 구조물 응답은 비선형 운동방정식(nonli- near equations of motion)에 의해 결정된다. 풍력터빈은 기본적으로 비선형성과 시간에 따른 변동특성이 있다.

공기역학적 회전(torques)과 휨모멘트는 풍속, 회전각(pitch angle), 타워와 블레이드의 처짐과 같은 비선형 특성으로부터 발생한다. 기본설계를 위한 선형해석은 타워상단의 터빈에 적용된 풍하중과 모멘트는 준정적(quasi-statically)으로 적용된 풍속을 기초로 계산된다.

일반적으로, 추력(thrust)을 추정하여 초기설계나 연구목적으로 타워상단에 적용시키거나 타워하단부의 작용력을 적용하는 경우가 많다. 터빈은 제작사 고유의 특성치를 갖고 있기 때문이다. 본 연구에서는 구조해석에 적용되는 터빈 모델로 NREL 5MW 모델을 적용하였다[19]. FAST를 이용하여 타워상단의 값으로 Table 3의 값을 얻었다.

사하중 또는 영구하중은 구조물 자중을 포함하여 지속적으로 작용되는 하중을 말한다. 설계자는 시공재료의 양이나 밀도로부터 사하중의 크기를 결정할 수 있다. 해상풍력발전 하이브리드 지지구조의 자중은 유한요소 프로그램인 XSEA의 자중계산 모듈을 이용하여 자동으로 계산할 수 있다[19]. 타워부분에 적용된 프레임 요소와 하이브리드 지지구조에 사용된 쉘요소에 의해 제시된 모델의 자중을 계산한 결과, 타워를 포함한 하부지지구조의 자중은 1,173톤, 원추형 콘크리트 지지구조의 자중은 907.65톤으로 나타났다. 콘크리트가 사용되는 지지구조물의 경우 그 자중으로 인해, 운반 및 설치에 필요한 장비의 제약과 공사비 증가에 주의할 필요가 있다.

5.2 하중조합

상부구조에 작용하는 풍하중을 비롯하여, 파랑하중, 해류, 터빈하중, 자중 등을 구조물 전체에 적용시켜 구조해석을 수행하게 된다. 풍하중과 파랑하중 및 해류하중은 기본설계 검토 목적의 연구이므로 동일한 방향으로 작용하는 것으로 가정하였다. 각각 다른 방향으로 작용시켰을 경우보다 주요 단면력, 응력, 변위가 커 보수적이라고 판단되지만, 기존 연구를 참고하여 수행하였으며 추가적인 연구가 필요할 것으로 판단된다. Fig. 8은 구조해석을 위한 하중의 작용각도를 나타낸다.

본 연구에서는 XSEA의 자동 하중조합 옵션이 사용되었다. 원추형 하이브리드 지지구조 형식의 형상은 하부가 원형으로 이루어져 평면상의 x, y축에 대하여 대칭구조이다. 그러나, 파일이 사각형으로 배치되는 것을 고려하면, 파일이 없는 부분에 직각으로 작용하는 하중도 고려해야 하므로 45〫 각도의 하중조합을 고려하였다.

IEC나 API 설계기준에 제시된 하중적용 조건에 따라, 극한상태의 조건을 고려하는 경우 DLC1.3, DLC1.4, DLC 6.2a 등과 같이 선택될 수 있고, 터빈 시뮬레이션 프로그램을 이용할 경우에도 DLC1.3(extreme turbulence)과 DLC1.4 (extreme coherent gust)의 적용으로 얻은 6-DOF의 풍하중과 조합 될 수 있다.

6. 모델링 및 해석

6.1 해석 모델

본 연구에서 제안한 신형식 하이브리드 지지구조물의 준정적 해석 및 고유진동수 해석을 위해, 유한요소 프로그램인 XSEA를 이용하여 Fig. 9와 같이 모델링 하였다. 강재 샤프트와 원추형 콘크리트 및 파일 슬리브는 총 510개의 솔리드-쉘 요소로 나누어 3차원 모델링 하였고, 타워 및 하단 가로보는 총 123개의 프레임 요소로 모델링하였다.

지반조건을 고려한 구조물 전체의 거동해석을 위해서는 파일을 동시에 모델링하여 지반과 구조물과의 상호작용을 고려할 필요가 있으나, 본 연구는 새롭게 제시된 하이브리드 지지구조 형식의 적정성에 대해 검토하는 것이 목적이므로 연구범위에서 제외 하였다. 또한, 파일을 모델링 할 경우 더 유연한 구조로 응력집중부의 변화가 예상될 뿐 아니라, 콘크리트부의 단면 적정성 평가를 위해서는 최대 단면력을 얻을 수 있어야 하므로, 파일 슬리브 하단의 중심점과 해저지반 지지조건을 고정단으로 가정하였다. 콘크리트의 두께는 50cm를 적용하였다.

6.2 하중 적용

앞서 다룬 환경하중, 터빈 하중 및 자중을 XSEA 프로그램을 이용하여 유한요소 모델에 Fig. 10과 같이 적용하였다. XSEA 프로그램에 하중 파라미터를 입력하고, 터빈하중은 타워 상단에, 풍하중은 해수면에서 부터 타워상단에 적용하였고, 파랑하중과 해류하중은 콘크리트 지지구조물에 적용하였다. 또한, 자중 계산 모듈을 통해 전체 구조물의 자중을 적용하고, 유한 요소 모델에 가해진 모든 하중들을 조합하여 이에 따른 구조물의 거동 해석이 가능토록 하였다.

7. 해석결과

앞서 언급된 조건에 기초하여 환경하중이 작용하는 하이브리드 지지구조의 해석에는 XSEA 프로그램이 사용되었다. 입체요소인 솔리드-쉘요소로 3차원으로 모델링하고 타워의 모델링에는 프레임 요소를 이용하였다. 설계기준에 제시된 수심에 따른 파랑이론의 적용범위에 의거하여 Stream Func-tion을 모리슨 방정식을 통해 적용하였다.

해석결과, 준정적 하중(quasi-static loading)이 작용하는 동안 MCF의 응답은 구조물 전체적인 응력분포와 변위로 나타난다. 하중의 적용방향에 따라 하중조합이 달라지며, 지지구조의 변형을 볼 수 있다. 타워상단에서의 최대변위는 하중작용각도가 0〫 일 때 0.126m, 45〫 일 때는 0.125m로 나타났다.

해상풍력 구조물은 사용자가 있는 육상에서의 일반시설물과는 달리 전력생산이 목적이므로, 사용성과 관련하여 수평변위에 대한 제한규정은 없는 것으로 추정된다. 일반적인 해양플랜트 상품은 각 기업의 설계 안전률 확보에 대한 노하우로 알려져 있고, 그 적용기준 또한 서로 상이하다. 그러나, DNV 설계기준[15]에 수직처짐에 대한 제한 규정이 나타나 있는데, 캔틸레버의 경우에는 2L/200이하로 제한하였다. 이 규정에 따르면 타워상단에서의 처짐은 2*101/200 = 1.01m로 충분히 안전측이 된다. 또한, 원추형 콘크리트보다 타워부분의 처짐이 큰 것은 강성의 차이보다는 캔틸레버 구조의 기하형상 때문이다.

Fig. 11은 타워를 포함한 하이브리드 지지구조의 전체 변위도를 나타낸다.

Fig. 12는 해석결과 휨응력 분포를 변형된 형상과 함께 낸다. 환경하중이 적용된 하이브리드 지지구조의 응력결과를 보면, 강재의 응력은 허용응력 이내로 충분히 안전측이며, 콘크리트의 경우 압축응력은 충분히 안전측이 되지만, 휨부재의 경우 대부분 콘크리트의 인장응력을 무시하고 설계되므로, 인장이 발생하는 부분은 PS강재를 이용하여 압축지배 되도록 충분히 보강되어야 한다. 또한, 콘크리트와 강재샤프트가 연결되는 부분에서 응력집중현상으로 큰 값이 발생하지만, 연결부의 검토는 별도의 상세 해석을 통해 검토 되어야 할 부분이다. 따라서, 본 제시된 하이브리드 지지구조는 콘크리트부분에서 발생하는 인장력에 저항할 수 있는 프리스트레스트 콘크리트를 적용할 경우, 해석결과는 충분히 안전하게 나타났다.

고유진동은 구조물의 물리적 특성으로 경계조건에 따라 크게 달라진다. 일반적으로 감쇄(damping)를 무시한 구조물의 고유진동수와 모드형상(mode shape)을 먼저 해석하게 되고 그 결과가 구조물의 기본적인 동적특성 나타낼 뿐 아니라, 동적하중에 대한 구조물 응답 예측이 가능하다. 고유진동은 외력이 작용할 때 구조물 고유의 진동에 대한 주파수를 나타내며, 특성주파수(characteristic frequency), 기초주파수(fun-damental frequency), 공진주파수(resonant frequency) 및 일반주파수(normal frequency)로 구분된다.

진동에 대한 특정 고유주파수에서 구조물의 변형형상은 일반 진동모드(normal mode)로 나타내고, 모드형상(mode shape), 특성 형상(characteristic shape), 기본형상(fun-da--mental shape)이 설명을 위해 사용된다.

해상풍력 하이브리드 지지구조의 고유진동수 해석은 XSEA를 이용하여 수행하였다. 해상풍력발전기의 주요 외력은 바람에 의한 로터의 회전과 블레이드가 회전할 때 마다 발생하는 주파수 및 육상풍력과는 다른 파랑에 의한 주기적인 하중이다. 동적효과를 줄이기 위해서는 고유주파수가 작용주파수 근처의 범위에서 나타나는 것을 피해야 한다. 구조물에 큰 변위와 응력을 유발하는 공진과 동적응답이 증가되기 때문이다. 일반적으로 로터의 회전이 증가하면, 그 에너지를 이용하여 나셀(nacelle)이 전력을 생산하는데, 이때 회전주파수(rotational frequency) 효과가 나타난다. Fig. 13은 로터의 회전주파수 영역을 나타낸다.

또한, 바람의 작용으로 블레이드 주변에 집중되는 공기역학적 하중(aerodynamic load)은 블레이드 통과주파수(blade passing frequency)를 증가시킨다. 풍력터빈 제작사들은 주파수범위의 상․하위 10%를 추가적인 여유(safety margin)로 권장하고 있다. 이 두 가지 주파수가 Fig. 13에 나타나 있다. 가로축은 주파수를 나타내고 세로축은 값이 없는 임의의 응답을 나타낸다. 고차의 외력(higher order excitations)이 작용하지만, 여기서는 회전주파수 범위와 블레이드 통과주파수 범위가 주요 외력으로 고려되었다.

공진을 피하기 위해 구조물은 첫 번째 진동수가 로터의 회전주파수나 블레이드 통과주파수의 작용과 동시에 발생하지 않아야 한다. 이것을 피하기 위한 3가지 구역이 있는데, 블레이드 통과주파수 이상에서 첫 번째 주파수를 갖는 매우 강한 구조물을 ‘stiff-stiff structure’라고 부른다. 첫 번째 고유주파수가 회전주파수 영역과 블레이드 통과주파수 영역 사이로 떨어진다면 구조물이 ‘soft-stiff’ 되었다고 말할 수 있다. 또한, 로터의 회전주파수영역 아래에 있는 연성구조물은 ‘soft-soft structure’로 불린다.

고유진동수 해석결과 파일 지지된 원추형 하이브리드 지지구조에 대한 1차 고유진동수는 0.970Hz로 나타났다. 콘크리트 중력식 지지구조는 통상 0.96Hz정도를 나타내는 것으로 알려져 있으나, 모노파일의 경우는 0.4Hz이하, 일반적인 강재 트라이포드가 0.277Hz를 보이는 것을 감안하면 상당히 비교되는 값을 보였다. 강재 자켓이나 트라이포드 설계시에는Soft-Stiff 영역에 위치하도록 최적화 시키는데, Stiff-Stiff 영역에 주파수가 있는 경우 구조체의 강성은 커지지만, 경제적이지 못하게 된다.

본 논문에서 제시한 신형식 하이브리드 지지구조물은 고유진동수가 파랑주파수 영역과 터빈 주파수영역을 벗어나 Stiff-Stiff 영역에 있으므로, 강재 자켓이나 트라이포드의 고유주파수 범위인 Soft-Stiff로부터 Stiff-Stiff 영역으로 충분히 발전시킬 수 있는 가능성이 보여 졌다. 콘크리트 재료가 가지는 우수한 장점 중 진동특성 때문으로 판단된다.

한편, 파도의 고유주파수(natural wave frequency)는 시간에 따라 주기가 변하기 때문에 주파수 영역에서 넓게 분포된다. 즉, 파도의 주파수가 변하는 여러 경우의 수만큼 분포곡선으로 표현할 수 있는데, 일반적으로 로터의 고유주파수 이하에 분포된다. Table 5는 파일 지지된 원추형 하이브리드 지지구조의 모드별 주파수와 주기를 나타낸다.

고유진동수 해석을 통해 MCF의 동적거동에 영향을 미치는 기본 진동수를 파악하였다. XSEA는 물리적 거동에 대한 고유벡터(eigen-vector)를 계산하기 위한 수학적 모델을 제공한다. Fig. 14에 파일 지지된 하이브리드 형식의 실질적인 물리적 거동 5가지 모드형상을 타나내었다.

XSEA 모듈에 의해 자동 계산된 하이브리드 지지구조의 자중은 타워를 포함할 경우 1,173톤이지만, 원추형 콘크리트 지지구조의 자중은 907.65톤으로, 해상운반 및 설치에 사용되는 일반적인 장비를 이용하여 쉽게 가설할 수 있다. 또한, 원추형 콘크리트 지지구조의 하부에 임시 물막이를 설치한 후 플로팅 상태로 운반이 가능하므로, 부력을 고려한 이동 중 작용하중에 대한 별도의 구조검토가 필요할 것으로 판단된다. 본 구조물의 기초파일은 일반적인 말뚝 기초, 석션 기초 혹은 헬리컬 파일등 여러 가지 파일을 사용 할 수 있는 장점도 가지고 있다.

8. 결  론

기존의 해상풍력 지지구조물은 대부분이 강재로 만들어져 왔다. 콘크리트는 저수심 지역에서 지지구조물로 사용된 사례가 다수 있으나, 최근 들어 경제성 때문에 더 주목받고 있다. 강재와 비교해 볼 때 콘크리트는 낮은 재료비, 제작비용 및 유지관리비, 내구수명이 길다. 강재에 비하여 구조물의 피로 및 동적거동에 대한 저항성이 우수하여 발전기 작동시 기계에 부담감을 줄여 주어서 발전기 고장을 방지 할 수 있는 등의 많은 장점을 갖고 있다. 본 논문에서 제안된 하이브리드 지지구조물은 기존의 중력식 지지구조물과 파일기초가 결합된 형식으로 지반조건이 불량한 지역은 물론 수심이 깊은 곳에 적용이 가능하도록 개발되었다. 그리고 경우에 따라서는 전체 구조물을 콘크리트로 제작할 수 있는 장점도 있다.

구조해석을 통해 극한조건에서 타워 상단에 발생한 변위가 허용변위보다 작아 충분히 안전하나 구조물임을 확인하였으며, 고유 진동수 및 모드형상을 평가하여 향후 연구의 동적 해석 기반 특성을 파악하였다. 구조물의 고유 진동수 평가 결과, 주요 외력인 바람과 파도에 의한 고유진동수가 공진을 피할 수 있는 안전한 영역에 있고, 우수한 동적특성을 나타내었다.

본 논문에서 제안한 파일 기초 하이브리드 지지구조물은 연약지반이 있는 우리나라 서남해의 극한 조건하에서 충분한 내력을 가진 것으로 평가되었다.

향후, 하중 작용 하에 지지구조물에 발생하는 반력으로부터 파일의 크기가 결정되어야하고, 제안된 모델의 개발을 위해, 기본설계, 운반 및 설치 방법에 대한 연구와, 동적해석에 의한 최적 설계가 요구된다. 본 연구는 Morrison 방정식이 적용된 범위에 한하여 연구하였으며 향후 Differaction 및 radiation 이론에 의한 대형 구조물의 3차원 요소 하중의 개발이 필요 할 것으로 판단된다. 

Acknowledgments

이 논문은 2013년 해양수산부 재원으로 한국해양과학기술진흥원의 지원을 받아 수행된 연구임(해상풍력 지지구조 설계기준 및 콘크리트 지지구조물 기술개발)

References

• Subrata, Chakrabarti., Handbook of offshore engineering , (2005), U.S.A., Elsevier Science Ltd.
• Nikolasos, N., Deep water offshore wind tech-nologies , (2004), University of Strathclyde.
• Kenneth, Perire., Hendrick, Nonneman., Eric, Bosschem., Gravity Base Foundation for the Thornton Bank Offshore Wind Farm , Terra et Aqua, (2009), 115, p19-29.
• COWI, Gravity Base Foundation for Red Sand2 , (2010), Denmark.
• Vici, Ventus., Offshore Wind Turbines: Con-crete Foundations , (2010), Norway.
• Ahmad, S., Irons, B.M., Zienkiewicz, O.C., Analysis of Thickand Thin Shell Structures by Curved Finite Elements , 10.1002/nme.1620020310Meth. Eng, (1970), 2, p419-451.
• Hauptmann, R., Schweizerhof, K., A systematic development of solid-shell element formulations for linear and non-linear analysis employing only displacement degrees of freedom , 10.1002/(SICI)1097-0207(19980515)42:1<49::AID-NME349>3.0.CO;2-2Meth. Eng, (1998), 42, p49-69.
• Sze, K.Y., Yao, L.Q., A hybrid stress ANS solid-shell element and its generalization for smart structure modeling, Part I:Solid-shell element formulation , 10.1002/(SICI)1097-0207(20000610)48:4<545::AID-NME889>3.0.CO;2-6Meth. Eng, (2000), 48, p545-564.
• Simo, J.C., Rifai, M.S., A class of mixed assumed strain methods and the methods of incompatible modes , 10.1002/nme.1620290802Meth. Eng, (1990), 29, p1595-1638.
• Kim, K.D., Lomboy, G.R., Han, S.C., A co-rotational 8-node assumed strain shell element for postbuckling analysis of laminated composite plates and shells , 10.1007/s00466-003-0415-6Comput. Mech, (2003), 30(4), p330-342.
• Kim, K.D., Liu, G.Z., Han, S.C., A Resultant 8-node Solid-shell Element for Geome-trically Nonlinear Analysis , 10.1007/s00466-004-0606-9Comput. Mech, (2005), 35, p315-331.
• Kim, K.D., Sim, J.S., Choi, S.Y., New concrete and steel support structure of offshore wind turbine using pile foundation in 40m depth , KSCE, (2012), 60(7), p33-38.
• Kim, K.D., Anaphat, Manovachirasan., New Development of Cost-Efficient Multi-pile Concrete Foundation (MCF) for Offshore Wind Turbine , (2013), Hamburg, German, International Conference.
• Konkuk Univ, Nonlinear dynamic analysis , (2012), Konkuk Univ.
• Pramin, Norachan, A Co-Rotational 8-Node Solid-Shell Element for Three-Dimensional Analysis of Prestressed Concrete Structures, Ph.D. Thesis , (2012), Konkuk University.
• DNV-OS-J101, Design of Offshore Wind Turbine Structures , (2011), Det Norske Veritas, Offshore Standard.
• DNV-RP-C205, Environmental Conditions and Environmental Loads, Recommended Practice , (2007), Det Norske Veritas, Offshore Standard.
• Oh, K.Y., Kim, J.Y., Lee, J.S., Preliminary evaluation of monopile foundation dimensions for an offshore wind turbine by analyzing hydrodyna-mic load in the frequency domain , 10.1016/j.renene.2012.08.007Renewable Energy, (2013), 54, p211-218.
• Jonkman, J., Butterfield, S., Musial, W., Scott, G., Definition of a 5-MW Reference Wind Turbine for Offshore System Development , (2009), National Renewable Energy Laboratory.