부분 매입형 셀룰러 합성보의 휨-전단 성능에 대한 실험적 평가
Copyright © 2024 by Korean Society of Steel Construction
초록
본 논문에서는 층고절감 및 장스팬 구조에 효과가 탁월하고, 설비 배관을 자유롭게 관통형으로 설계할 수 있는 부분 매입형 셀룰러 합성보를 제안하였다. 제안된 합성보의 휨-전단 성능을 규명하고자 일련의 실험적 평가를 수행하였다. 제안된 셀룰러 합성보의 경우, 콘크리트 슬래브의 휨 및 전단 저항 기여도 덕분에, 셀룰러 강재보 T단면에 발생되는 비렌딜 휨과 압축에 의한 좌굴을 완화시킬 수 있었으며, 이로 인해 비합성 셀룰러 보 대비 하중 저항 및 연성 능력을 크게 향상시키는 결과를 거둘 수 있었다. AISC Steel Desgn Guide 31에 근거한 설계 이론값들은 제안 합성보의 내력을 평가하기에 충분히 보수적이었다. 그러나 유효 단면2차모멘트를 산정하는 방식은 실험 결과 대비 약 20 % – 30 % 과대 평가되는 부분이 확인되어, 추가적인 연구로 검증하는 것이 필요하였다.
Abstract
In this paper, a partially embedded cellular composite beam was proposed that is excellent in reducing floor height and suitable for long-span structures. Service facilities such as pipes or ducts can be designed integrally with the proposed composite beams by penetrating the web openings. A series of experimental tests were conducted to investigate the flexural-shear performance of the proposed composite beam. For the proposed composite beams, the Vierendeel bending and compression-induced buckling occurring at the T-section of the cellular steel beams can be alleviated due to the contribution of the concrete slab to flexural and shear resistance. This results in significantly improved load resistance and ductility compared to noncomposite cellular beams. Theoretical design values based on AISC Steel Design Guide 31 were sufficiently conservative to evaluate the flexural strength of the proposed composite beam. However, the method for estimating the effective moment of inertia was found to be overestimated by about 20 % – 30 % compared to experimental results, requiring verification through further research.
Keywords:
Cellular beam, Vierendeel bending, Web post buckling, Flexural behavior, Composite beam키워드:
셀룰러 보, 비렌딜 휨, 웨브 포스트 좌굴, 휨 거동, 합성보1. 서 론
2000년대 초반부터 국내에는 다양한 용도 및 성능 개선을 목적으로 다수의 합성보 개발 연구가 진행되어 왔다. 층고 절감 및 설비 통합형 합성보로 개발된 iTECH 합성보[1]와 Smart Beam[2]이 있으며, 냉간성형 박판을 거푸집 대용 및 구조재로 활용한 TSC 합성보[3] 및 TU합성보[4]가 그 대표적 사례라 할 수 있다. 또한, PC부재를 강재보와 함께 공장에서 제작하여 별도의 거푸집 없이 현장 타설을 통해 완성하는 MHS 합성보[5]와 바닥슬래브 춤 내부로 강재보를 완전 매입시킨 Slim Floor 유형의 합성보[6]-[8]까지 그 형상 및 구성 요소도 다양하다. 최근 이러한 연구 개발 추세는 데이터 및 물류 센터 그리고 장스팬 공장용 구조물에 대한 수요 증가와 더불어, 경제적이며 폭넓은 실내 공간을 확보할 수 있는 대공간형 강구조 시스템으로 관심이 옮겨지고 있다. 특히, 내부에 배치되는 다양한 설비 시설물들을 구조체와 일체화 및 선조립화하여 Unit 단위로 생산할 수 있는 방안이 지속적으로 모색되고 있다.
셀룰러 보(Cellular beam)는 1980년대 유럽 등지에서 개발되어 현재까지 수많은 프로젝트에 적용되어 온 강재 보 시스템으로, 구조체를 외부에 노출시켜 의장적인 효과를 거둘 수 있으며, Fig. 1[9]-[10]과 같은 생산방식을 통해 강재 물량을 극단적으로 효율화하여 장스팬 구조에 적합하도록 개발되었다[11]. 특히, 연속된 웨브 개구부를 설비 관통 용도로 사용할 수 있어 층고 절감 효과에도 탁월한 장점이 있다. 그러나 해당 장점에도 불구하고, 비렌딜(Vierendeel) 거동 및 웨브 포스트 좌굴 등과 같은 복잡한 추가 설계 고려 사항들 때문에 국내에서는 아직 널리 활용되고 있지 못한 실정이다.
본 연구에서는 대공간 장스팬 구조물을 대상으로 적용할 수 있는 합성보를 셀룰러 보와 춤이 깊은 데크 슬래브(또는 중공형 PC 슬래브)를 이용하여 새롭게 제안하였으며, 해당 합성보에 대한 구조 성능을 실험적으로 평가하고자 하였다.
2. 부분 매입형 셀룰러 합성보
2.1 개 요
개발된 합성보에 대한 개념도를 Fig. 2에 나타냈다. Fig. 2(a)와 같이 셀룰러 보 웨브 측면에 데크를 얹을 수 있는 지지대를 설치하고 웨브 개구부의 상단 일부가 콘크리트 슬래브에 매입되도록 제작한다. 이때 사용되는 데크는 춤이 250 mm 이상으로 전체 슬래브 두께는 350 mm 이상이 되며, 춤이 깊은 골 데크를 통해 8 m까지 슬래브의 스팬을 구현할 수 있도록 고려하였다. 경우에 따라 해당 Deep Deck은 등가의 중공 PC 슬래브로 대체될 수 있다.
콘크리트 슬래브와 셀룰러 보 사이의 합성 거동을 유도하기 위해, Fig. 2(b좌)처럼, 셀룰러 보 상단에 스터드와 같은 전단연결재를 부착한다. 초장스팬 구조물의 경우에는, Fig. 2(b우)와 같이, 스터드의 부착 위치를 셀룰러 보 웨브 측면으로 옮겨 콘크리트 슬래브의 매입 깊이를 증가시키고 합성보의 전체 춤을 절감할 수 있도록 하였다. 이때, 두 소재 사이의 합성 거동은 증가된 매입 깊이로 웨브 개구부에 충진된 콘크리트 슬래브의 지압력을 스터드와 함께 추가로 고려할 수 있다.
고안된 합성보를 적용할 경우, Fig. 2(c)와 같이, 장스팬 바닥판을 형성하는 데 필요한 작은 보를 제거할 수 있으며, 이를 통해 사용되는 강재 물량을 절감할 수 있다. 또한, 작은 보 제거를 통해 바닥 하부 구조에 웨브 개구부를 가지는 셀룰러 보만이 위치하게 되어, 배관 및 덕트와 같은 설비 시설의 관통 배치 설계에 자유로움을 얻을 수 있다.
2.2 내력 평가 이론식
본 연구에서 제안된 합성보는 AISC Steel Desgn Guide 31 내용을 바탕으로 이론적으로 평가할 수 있다[12]. 셀룰러 보는, Fig. 3에 정리된 바와 같이, 총 8가지 한계상태를 고려하여 구조 설계를 수행해야 된다. 해당 한계상태 중 1, 2, 7, 8 한계상태는 일반 강재보를 설계할 때 고려하는 사항들로 셀룰러 보에서는 그 외에 3~6 한계상태를 추가로 검토해야만 한다. Fig. 4에 웨브 개구부 주변에서 발생할 수 있는 다양한 파괴 모드를 나타냈다.
웨브에 개구부를 가지는 비합성 강재 보의 경우, Fig. 5(a상)에 나타낸 바와 같이, 단면에 발생되는 휨모멘트를 상·하부 T단면의 압축과 인장력으로 저항하게 된다. 또한, 수직 전단력은 개구부의 전단변형과 함께 T단면 단부에 부가적인 저항 모멘트를 발생시키게 된다(Fig. 5(b상)). 이때 전단력에 의해 발생되는 2차 휨모멘트를 비렌딜 모멘트라 명명한다. 개구부의 형상이 원형일 경우, 비렌딜 모멘트가 형성되는 위치를 명확히 규정하기 어렵기 때문에, 관련 설계 기준에서는 개구부 중심으로부터 0.225D0 떨어진 위치로 가정하며, 해당 위치의 단면을 임계 단면(Critical section)이라 정의한다. 여기서 D0는 원형 개구부의 지름을 나타낸다. 따라서, 임계 단면에 위치한 상·하부 T단면은 비렌딜 모멘트와 축력(상부 T는 압축, 하부 T는 인장)을 동시에 저항해야 되는 상태에 놓이게 되고 이에 대한 안전성 검토를 추가로 진행해야 한다.
휨모멘트와 전단력에 의해 임계 T단면에 발생되는 축력 및 비렌딜 모멘트는 다음과 같이 계산할 수 있다.
| (1) |
| (2) |
여기서, Ptop (or bot) = 상·하부 T단면에 발생되는 축력, M = 개구부 중심 단면에서의 휨모멘트, deffec = 상·하부 T단면의 도심 사이의 거리, Mv = 임계단면 상·하부 T에 발생되는 비렌딜 모멘트, V = 개구부 중심 단면에서의 전단력, Acrit = 임계 단면 상·하부 T의 단면적 합, Atee-crit = 임계 단면 내 상부 또는 하부 T의 단면적을 각각 나타낸다. 여기서, 비렌딜 모멘트를 구하기 위한 팔거리(moment arm)는 D0/4로 가정한다[14].
주어진 T단면의 축강도 산정 시, 압축력을 받는 상부 T단면은 휨좌굴과 휨-비틀림 좌굴을 고려하며, 인장을 받는 하부 T단면은 전단면이 항복응력에 도달하는 것을 기준으로 저항력을 평가한다. 관련 설계식은 강구조 압축재 및 인장재 설계에 사용되는 식들과 동일하며[15], 단지 좌굴 내력 산정에 필요한 유효좌굴길이계수로 Kx = 0.65, Ky = 1.0를 적용하고, T단면의 비지지길이 L = D0/2로 가정하여 설계를 진행한다.
T단면의 휨강도는 Fig. 3에서 확인할 수 있는 바와 같이, 총 4개의 한계상태를 고려하여 제일 작은 값을 공칭 휨강도로 결정한다. 다만, 압축을 받는 T단면이 휨에 의해 소성모멘트까지 도달하기 어려운 점을 감안하여 항복(Yielding)에 의한 휨강도는 Mn = Mp = My로 고려, 항복강도에 탄성단면계수 Sx-tee를 곱한 값으로 해당 저항 성능을 산정한다.
현장 콘크리트가 타설되고 합성거동이 인정된 이후의 셀룰러 보 내부에 형성되는 축력과 비렌딜 모멘트는 Fig. 5(a하)와 (b하)에 나타낸 바와 같다. 완전합성(fully composite)으로 설계될 경우, 개구부 휨모멘트에 의해 발생되는 압축력은 모두 콘크리트에 의해 저항하는 것(C1)으로 가정하며, 상부T에 의한 저항분(T0)은 0인 것으로 가정한다. 따라서, 식 (3)과 같이 축력을 계산할 수 있다.
| (3) |
| (4) |
여기서, T1 = 하부 T단면에 발생되는 축력, deffec-comp = C1과 T1 사이 거리로 식 (4)에 의해 결정, dg = 셀룰러 강재 보 전체 춤, = 하부 T 하단에서 도심까지 거리, hr = 데크 골의 높이, tc = 데크 골 위로 타설된 콘크리트 슬래브 두께를 각각 의미한다. 그리고 부분합성(partial composite)에 대한 사항은 본 논문의 연구 범위 이외 것으로 상세한 기술은 생략하도록 한다.
합성 셀룰러 보에서 비렌딜 모멘트는 전체 전단력의 크기(V)에서 콘크리트 슬래브가 부담하는 부분(Vc)을 제외하고 식 (2)를 이용하여 동일하게 계산할 수 있다(Fig. 5(b하)). 이때, 콘크리트 슬래브의 전단강도는 식 (5)로 결정할 수 있다. 여기서, f’c = 콘크리트 설계압축강도이다.
| (5) |
이후 결정된 임계 T단면에 발생되는 축력 및 비렌딜 모멘트의 크기와 단면의 축강도 및 휨강도를 함께 고려하여 조합력에 대한 안정성을 평가하는 것으로 비렌딜 휨에 대한 내력평가를 마무리 짓는다.
Fig. 5(c)에 나타낸 바와 같이, 인접한 개구부 중심의 상·하부 T에 발생되는 축력(C(i), C(i+1), T(i), T(i+1),)의 차이로 인해 웨브 포스트에 수평 전단력(Vh)이 발생된다. 이러한 수평력은 개구부 사이 웨브 중심부에 작용하여 휨에 의한 좌굴을 유도한다. 이때 좌굴을 유발하는 모멘트(Mh)의 크기는 식 (6)으로 산정할 수 있다. 해당 식에서 모멘트 팔거리는 0.9D0/2로 가정한다.
| (6) |
한편, 웨브 포스트의 좌굴에 대한 저항 성능(Mwpb)은 식 (7) – 식 (12)를 이용하여 결정할 수 있다. 여기서, Me= 0.9D0/2 떨어진 지점에서 발생되는 탄성 휨모멘트, S = 개구부 중심 사이 거리, Fy = 강재의 항복강도, tw = 웨브 두께이다.
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
웨브 포스트는 모멘트에 의한 좌굴 안전성 뿐만 아니라, 발생되는 수평 전단력에 대해 전단 저항 면적이 충분한지 그 안전성도 별도로 검토되어야 한다.
마지막으로 휨모멘트 및 전단력의 크기는 보의 길이에 따라 각기 변화하기 때문에, 상기 기술된 T단면에 대한 비렌딜 휨 및 축력 조합에 대한 검토와 웨브 포스트의 안전성 검토는 매 개구부마다 별도로 진행되어야 함을 유의해야 한다.
3. 실험 계획
3.1 실험체 형상
Fig. 6에 휨-전단 성능을 평가하기 위한 실험체 상세를 나타냈다. 먼저 콘크리트가 타설되기 전 시공 단계에서 거동을 확인하기 위한 목적으로 비합성 셀룰러 보 2개를 계획하였다. 보 전체 춤은 600 mm, 길이는 8,800 mm, 웨브 및 플랜지 두께는 각각 10 mm와 14 mm로 계획하였다. 강재 보의 지점 및 가력점에는 집중하중에 따른 국부 파괴를 제어하기 위해 웨브 측면에 10t 수직 스티프너를 설치하였다.
실험체 Steel-PB는 비렌딜 휨 거동을 제외한 순수 휨(pure bending) 상태에서의 개구부 존재에 따른 성능을 확인하기 위한 실험체로 개구부는 가력부 사이 중앙부에만 3개 형성하였다. 형성된 개구부의 크기는 지름이 400 mm, 개구부 중심 사이 간격은 600 mm로 설계하였다. 이는 식 (10) – 식 (12)에 제시된 계수 C1-3를 적용하기 위한 제한 조건인 1.08 ≤ S /D0 ≤ 1.50 그리고 1.25 ≤ dg /D0 ≤ 1.75를 고려하여 결정한 수치이다. 실험체 Steel-Vier는 휨과 전단에 동시에 노출되었을 때 거동을 확인하기 위한 실험체로, 보의 전 길이에 걸쳐 개구부를 일정하게 형성하였다.
실험체 Comp-PB와 Comp-Vier은 셀룰러 강재 보에 콘크리트 슬래브를 완전합성으로 설계한 실험체이다. 이를 위해 상부 플랜지 상단에 D19-100 mm 스터드를 2열, 350 mm 간격으로 배치하였다. 콘크리트 슬래브의 유효폭은 사용될 UTM의 기둥 사이 간격을 고려하여 1,000 mm로 설계하였으며, 두께는 311 mm의 솔리드 형상으로 제작하였다. 본래 개발된 합성보에는 춤이 깊은 데크 또는 중공형 PC가 적용될 계획이나, 1,000 mm 밖에 안되는 유효폭에 맞추어 양쪽에 해당 소재를 절단하여 부착해야 하는 제작상의 어려움 때문에, 일반 트러스 데크를 이용한 솔리드 슬래브로 대체 평가하였다. 비록 솔리드 슬래브로 대체 평가하였으나, 콘크리트 압축블록의 깊이를 데크 골 상단 위의 토핑 두께(또는 PC 중공 상부 콘크리트 두께)로 제한 설계하여 춤이 깊은 데크 또는 중공형 PC를 적용하였을 때와 유사한 효과를 거둘 수 있도록 고려하였다. 트러스 데크의 설치 위치는 강재 보 상단으로부터 140 mm 아래 위치한 웨브 측면에 고정하였으며, 이 때문에 원형 개구부의 상부 일부에 콘크리트가 채워지도록 하였다.
3.2 실험 셋업 및 가력 계획
실험체 가력은 중앙부 1,800 mm에 순수휨 구간이 형성되도록 2점 가력하였다. 지점 사이 거리는 7,800 mm로 실험체 두께에 대한 가력점까지의 거리 비(전단스팬비)는 강재 보의 경우 5.0, 합성보는 3.85를 나타냈다. 가력은 3,000 kN Universal Testing Machine(UTM)을 사용하여 0.02 mm/sec의 속도로 가력하였으며, 지점은 롤러를 사용하여 단순지지 하였다. 또한 실험체의 처짐을 계측하기 위해 중앙부와 가력부 하부플랜지 하단에 1,000 mm 용량의 변위계를 설치하였다. Fig. 7에 실험 셋업(Set-up)을 나타냈다.
4. 실험 결과
4.1 재료 실험
Table 1에 실험에 사용된 재료들의 특성을 정리하여 나타냈다. 강재 보 제작에 사용된 SM355 10 t와 14 t의 항복강도(Fy)는 3개 시편으로부터 평균 376.5 MPa과 369.5 MPa로 각각 나타났다. 합성보 슬래브에 사용된 콘크리트는 재령일 28일에 압축강도(fck)가 평균 27.9 MPa로 확인되었다.
4.2 하중-변위 곡선 및 파괴 모드
Fig. 8에 각 실험체별 하중-변위 곡선과 실험에서 관측된 최종 파괴 형상을 나타냈다. 하중-변위 곡선에서 항복하중(yield load, Py)의 위치는, Fig. 9에 나타낸 바와 같이, 초기탄성강성(initial elastic stiffness, Ki)의 연장선과 극한하중(ultimate load, Pu)을 지나는 할선의 교점으로 정의하였으며, 이때 두 직선과 응답 곡선 사이에 형성되는 두 면적 A1과 A2가 같은 값을 가지도록 설정하였다.
실험체 Steel-PB의 경우, Fig. 8(a)에서 볼 수 있듯이, 하중 512.3 kN에 이르러 항복이 진행되었으며, 극한하중은 598.4 kN을 나타냈다. 항복하중 작용 시 변위에 대한 극한하중 작용 시 변위의 비(δu /δy), 즉 연성비(μ)는 약 2.21을 나타냈다. 극한하중 이후, 가력점 사이의 순수 휨 영역에서 개구부의 상단T가 압축력에 의한 좌굴이 발생하면서 하중이 감소하였다.
실험체 Steel-Vier은 전 구간에 걸쳐 웨브 개구부가 형성된 보로, 항복하중과 극한하중은 각각 429.0 kN과 534.1 kN을 나타냈다. 극한하중 이후 전단스팬 내 가력점에 바로 인접한 개구부의 상부T에서 비렌딜 변형이 진행되면서 최종 파괴가 진행되었다. 해당 실험체의 연성비는 1.90으로, 실험체 Steel-PB에 비해, 전단력에 의한 비렌딜 휨이 상·하부 T에 가미되면서 항복 이후 더 빠른 파괴가 유도된 것을 확인할 수 있었다.
콘크리트 슬래브를 가지는 Comp 실험체에 대한 결과는 Fig. 8(b)에서 확인해 볼 수 있다. 순수 휨 파괴를 유도한 실험체 Comp-PB는 하중 728.4 kN에서 항복이 진행되었으며 이후 안정적인 비선형 거동을 나타냈다. 하중이 937.5 kN에 이르렀을 때, 콘크리트 슬래브 상단 일부에 압괴가 발생하며 하중 저감이 관찰되었다. 이후 실험 종료 시점까지 극한하중 대비 약 85 % 수준의 하중 저항 능력을 유지하는 특성을 나타냈다. 해당 실험체의 연성비는 약 2.92였다.
마지막으로, 본 연구의 타겟인, 실험체 Comp-Vier은 항복하중이 776.9 kN으로 나타났으며, 극한하중 1006.7 kN까지 매우 안정적인 연성 거동을 확인할 수 있었다. 최종 파괴는, 실험체 Comp-PB와 마찬가지로, 스팬 중앙부의 콘크리트 슬래브 상단에 압괴 발생으로 확인되었다. 연성비는 3.14로 실험을 수행한 실험체들 중 가장 높은 값을 나타냈다.
콘크리트 슬래브를 가지는 두 실험체의 거동을 비교하였을 때, 전단스팬 내 웨브 개구부가 없는 실험체 Comp-PB의 초기 강성(Ki)이 29.48 kN/mm로 실험체 Comp-Vier의 초기 강성 24.89 kN/mm에 비해 약 18.5 % 높게 형성된 것을 확인할 수 있다. 그러나 실험체 Comp-Vier의 전단스팬 내 비렌딜 파괴가 콘크리트 슬래브에 의해 제어되어, 실험체 Comp-PB와 동일한 파괴 모드가 관찰되었다. 이 때문에 초기 강성에는 차이가 있었으나, 항복 이후 가력된 하중은 항복이 진행된 가력점 사이 구간의 변형으로 대부분 집중되면서, Fig. 8(b)에 보여지듯이, 유사한 하중-변위 특성을 나타냈다. 다만, 실험체 Comp-PB의 콘크리트 슬래브 압괴가 빨리 진행되어 실험체 Comp-Vier보다 극한하중이 약 7.4 % 낮게 형성되었다. Table 1(c)의 콘크리트 공시체 시험 결과에서도 확인할 수 있듯이, 통상 동일하게 제작된 콘크리트 실험체들 사이에서도 5 % – 10 % 가량 성능 차이가 날 수 있음을 감안하면, 두 합성보의 내력 차이는 쉽게 이해될 수 있다.
4.3 내력 평가
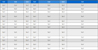
Table 2에 2.2절 내용에 근거하여 이론적으로 추정된 값과 실험으로부터 확인된 결과 값을 함께 비교하여 나타냈다. 해당 표에서 아래 첨자로 사용된 ‘t’는 이론값을, ‘e’는 실험값을 의미한다.
실험체 Steel-PB의 경우, 개구부를 동일한 크기의 휨모멘트가 발생하는 영역에만 형성하였기 때문에, 전단력에 따른 비렌딜 휨이나 인접 T단면 사이의 축력 차이에 따른 수평 전단력이 발생하지 않아, 개구부 중심 단면에서의 휨내력 성능만을 이론적으로 계산하면 된다. 이론적으로 확인된 해당 실험체의 극한하중 값(Put,pb)은 513.4 kN으로 실험값 598.4 kN 대비 약 17 % 정도 보수적인 값을 추정하는 것으로 확인되었다.
실험체 Steel-Vier은 가력점 사이 순수 휨 영역과 전단력이 동시에 작용하는 구간이 존재함으로, 보의 전 길이 개구부에 걸쳐 내력 검토를 진행하였다. 그 결과, 전단스팬 내 가력점 인접 개구부에서 비렌딜 거동에 의한 파괴 예상하중(Put,v)이 318.3 kN으로 가장 작았으며, 웨브 포스트 좌굴에 대한 파괴 예상하중(Put,wpb)은 600.3 kN, 웨브 포스트의 수평 전단에 대한 파괴 예상하중(Put,hs)은 832.0 kN으로 나타났다. 실제로 실험 결과 해당 위치에서 비렌딜 모멘트에 의한 파괴 모드가 관찰되었으며, 이론 대비 실험 결과값의 비율은 1.68로 다소 보수성이 높게 평가됨을 확인할 수 있었다. 해당 내력 평가 시, 비렌딜 휨에 의한 모멘트 강도비가 대략 0.46이었으며, T단면 축력에 의한 강도비가 0.54로 각각의 내력비에 있어서는 여유치가 많았으나, 이에 대한 조합력에서 1.0을 넘어 이론적으로 안정성이 결여되는 것으로 확인되었다.
콘크리트 슬래브를 가지는 실험체 Comp-PB의 경우, 순수 휨 파괴에 의한 내력(Put,pb)이 790.3 kN으로 예상되었으며, 실제 실험값 937.5 kN과 비교하여 약 19 %의 보수적인 결과를 산출하였다. 이를 통해, 이론식 접근에 있어서 합성보 및 비합성보에 대한 순수 휨에 의한 극한하중 예상은 17 % – 19 % 정도의 적절한 보수성을 가짐을 확인할 수 있었다.
반면, 실험체 Comp-Vier의 경우, 비렌딜 거동에 의한 극한하중(Put,v)이 969.6 kN, 웨브 포스트 좌굴에 의한 극한하중(Put,wpb)이 899.4 kN, 마지막으로 웨브 포스트 수평 전단에 의한 극한하중(Put,hs)이 1216.6 kN으로 각각 예상되어, 순수 휨 파괴에 의한 예상 극한하중(Put,pb)보다 더 높은 값을 나타냄을 확인할 수 있었다. 이는 콘크리트 슬래브의 전단력 저항 기여도가 강재 셀룰러 보에 부담되는 전단력을 감소시켜 비렌딜 휨 현상을 약화시키는 효과가 있었기 때문이며, 더불어 휨모멘트에 의한 축력 작용 역시, 콘크리트 슬래브가 압축력을 대신 저항하면서 상부T에 좌굴과 같은 파괴 모드를 제외시킬 수 있었던 점에서 큰 기여를 했기 때문인 것으로 판단된다. 특히, 본 실험체의 솔리드 슬래브 두께가 가력된 하중에 의한 전단력을 모두 지지할 수 있을 만큼 두꺼웠던 점도 큰 몫으로 작용하였다. 실험 결과에서 확인할 수 있듯이, 이러한 특이점 때문에 합성보 실험체 모두 스팬 중앙부에서 콘크리트 압괴에 의한 파괴모드로 극한하중이 형성되었다. 본 실험 결과를 통해서, 부분 매입된 셀룰러 보의 안정성이 순수 강재 보에 비해 매우 향상될 수 있음을 확인할 수 있다.
4.4 유효 단면2차모멘트(Ieffec) 평가
보의 전 구간에 개구부를 가지는 Vier 실험체들에 대해, 하중-변위 곡선으로부터 초기 형성된 강성 크기를 식 (13)을 활용하여 유효 단면2차모멘트를 유추하였다.
| (13) |
여기서, a = 전단스팬(shear span) 거리, L = 양단 지점 사이 거리, E = 강재의 탄성계수, 200,000 MPa, P = 가력 하중, δ = 처짐 변위이다. 본 연구에서는 AISC 기준에 기반한 이론 산정을 진행하였기에, 탄성계수 역시 200,000 MPa로 적용하였다. 유효 단면2차모멘트(Ieffec,t)의 이론값은, AISC Steel Desgn Guide 31에 근거하여, 개구부 중심 단면에 대해 산정한 단면2차모멘트 값의 90 %를 적용하여 결정하였다.
Table 2에 정리된 내용과 같이, 실험체 Steel-Vier의 이론 유효 단면2차모멘트는 약 6.333E+08 mm4으로 식 (13)을 이용해 실험 결과로부터 산정한 결과(Ieffec,e) 5.085E+08 mm4 보다 약 20 % 가량 높은 값이 산출되었다. 실험체 Comp-Vier도 마찬가지로, 실험값이 1.085E+09 mm4 으로 이론값 1.602E+09 mm4 대비 32 % 가량 낮게 관측되어 이론 추산이 고평가되는 것을 확인해 볼 수 있었다. 다만, 해당 이론적 추산 방식이 실험이라는 특수한 집중하중 요건보다 등분포 하중이라는 보다 실무적인 조건에서 보다 합당한 결과를 제시할 수 있음을 염두해 두어야 한다. 그러나 보의 정확한 강성 추론은 처짐 및 바닥진동 평가에도 영향을 미치는 주요한 사항으로 추후 해석적 연구를 통해 보다 정확한 검증이 필요할 것으로 사료되었다.
5. 결 론
본 연구에서는 층고절감 및 장스팬 구조에 효과가 탁월하고, 설비 배관을 자유롭게 관통형으로 설계할 수 있는 부분 매입형 셀룰러 합성보를 제안하였다. 해당 합성보의 휨-전단 성능을 규명하고자 실험적 평가를 수행하였으며, 그 결과 다음과 같은 결론을 도출하였다.
- (1) 부분 매입형 셀룰러 합성보의 경우, 콘크리트 슬래브의 휨 및 전단 저항 기여도 덕분에 셀룰러 강재보 T단면에 발생되는 비렌딜 휨과 압축에 의한 좌굴을 완화시킬 수 있었으며, 이로 인해 비합성 셀룰러 보 대비 하중 저항 및 연성 능력을 크게 향상시키는 결과를 거둘 수 있었다.
- (2) AISC Steel Desgn Guide 31 내용에 근거하여 이론적 접근 방법과 실제 실험 결과를 비교한 결과, 합성 셀룰러 보에 대해서는 27 % 수준의 합리적이고 보수적인 이론값을 추산하였다. 그러나, 비합성 셀룰러 보의 비렌딜 거동에 대한 이론적 저항 성능은 실험 대비 68 %까지 보수적인 결과를 산출하는 것으로 나타났다. 이는 T단면에 발생되는 비렌딜 휨과 축력에 의한 조합력 평가가 성능을 크게 과소평가할 수 있기 때문인 것으로 확인되었다.
- (3) 보 전 길이에 걸쳐 개구부가 형성된 비합성 및 합성 셀룰러 보의 유효 단면2차모멘트는 실험 결과, 이론값 대비 약 20 % – 30 % 가량 저감된 성능이 확인되었다. 해당 부분에 대해 보다 명확한 결론 도출을 위해 등분포 하중 및 기타 경계 조건에 대한 해석적 연구를 추가적으로 수행하는 것이 필요하다 판단되었다.
Acknowledgments
본 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단(No. RS-2023-00252521)의 지원과 ㈜포스코의 연구비 지원을 받아 수행된 연구임.
References
- Ju, Y.K., Chun, S.-C., and Kim, S.-D. (2009) Flexural Test of a Composite Beam Using Asymmetric Steel Section with Web Openings, Journal of Structural Engineering, American Society of Civil Engineers, Vol.135, No.4, pp.448-458.
- Hwang, H., and Baek, S. (2009) 비대칭 조립 H형강 합성보, SMARTBEAM 개발 및 적용사례 소개, 건축구조, Korean Structural Engineers Association, Vol.16, No.4, pp.48-52 (in Korean).
- Kim, S.S., Kim, S.M., Kim, S.B., Seo, D.G., and Kim, K.S. (2004) An Experimental Study on the Behavior of the T-Type Steel Composite Beam, Journal of Korean Society of Steel Construction, KSSC, Vol.16, No.2, pp.225-233 (in Korean).
- Heo, B.-W. (2008) Flexural Behavior of Profiled Steel Composite Beams with Partial Shear Interaction, Journal of the Architectural Institute of Korea Structure & Construction, AIK, Vol.24, No.10, pp.69-76 (in Korean).
- Lee, H. (2008) Introduction of Modularized Hybrid System, 건축구조, Korean Structural Engineers Association, Vol.15, No.1, pp.55-65 (in Korean).
- Mullett, D.L., and Lawson, R.M. (1993) Slim Floor Construction Using Deep Decking, The Steel Construction Institute, UK.
- Rackman, J.W., Hicks, S.J., and Newman, G.M. (2006) Design of Asymmetric Slimflor Beams with Precast Concrete Slabs, The Steel Construction Institute, UK.
- Ryu, J., Lee, C.-H., Oh, J., Yoon, S.-W., and Ju, Y.K. (2017) Shear Resistance of a Biaxial Hollow Composite Floor System with GFRP Plates, Journal of Structural Engineering, American Society of Civil Engineers, Vol.143, No.2, 04016180.
- Sehwail, M.M., and Celikag, M. (2022) Load Carrying Capacity of Hot-Rolled Hybrid Cellular Steel Beams: Experimental Investigations, Arabian Journal for Science and Engineering, King Fahd University of Petroleum and Minerals, Vol.47, No.10, pp.12633-12648.
- ArcelorMittal Europe (2021) ACB® and Angelina® Beams: A New Generation of Beams with Large Web Openings, ArcelorMittal Europe, Luxembourg.
- Kim, K.-J., and Eun, S.-W. (2006) Introduction of Cellular Beam Made of Rolled H Beam, Magazine of the Korean Society of Steel Construction, KSSC, Vol.18, No.1, pp.101-107 (in Korean).
- Fares, S.S., Coulson, J., and Dinehart, D.W. (2016) Steel Design Guide 31: Castellated and Cellular Beam Design, American Institute of Steel Construction, USA.
- Lawson, R.M., and Hicks, S.J. (2011) Design of Composite Beams with Large Web Openings, SCI P355, The Steel Construction Institute, UK.
- Bjorhovde, R. (2000) Design Outline for Vierendeel Bending of Cellular Beams, University of Arizona, USA.
- AISC (2022) Specification for Structural Steel Buildings, ANSI/AISC 360-22, American Institute of Steel Construction, USA.