다수의 T-단면 보강재로 보강된 압축판의 좌굴계수 평가
Copyright © 2024 by Korean Society of Steel Construction
초록
본 연구에서는 폭이 큰 압축판에서 다수의 T-단면 보강재로 보강된 판의 좌굴계수식을 제안하기 위한 연구를 수행하였다. AASHTO LRFD 교량설계기준의 해설부 C6.11.11.2에서 보강재 5개까지 갖는 판에 대해 좌굴계수식을 제시하고 있다. 이 식은 Timoshenko and Gere의 근사적인 좌굴계수식(kf)을 토대로 한 것이나, 형상비와 좌굴계수의 크기를 감안한 보강재의 제원을 결정할 수 없는 문제가 있다. 본 연구에서는 보강재 9개까지의 판에 대해 형상비와 폭-두께비 그리고 보강재 제원을 변수로 하여 고유치해석을 수행하였다. FE 해석에 의한 좌굴계수를 kf 식과 비교함으로써 수정계수(cc)를 보강재 개수(n)에 따라 n ≤ 3과 n > 3 에 대해 각각 도출하고 이를 반영한 좌굴계수식을 제안하였다. 한편, 좌굴계수 산정 시 보강재의 단면2차모멘트 산정 방안에 대해 제안하였다.
Abstract
A study was conducted to propose a buckling coefficient equation for a wide compression plate reinforced with multiple T-section stiffeners. The commentary C6.11.11.2 of AASHTO LRFD bridge design specifications presents a buckling coefficient equation for the plates with up to 5 stiffeners. This equation is based on the approximate buckling coefficient equation(kf) of Timoshenko and Gere, but it has the limitation of being unable to determine the size of stiffeners considering the aspect ratio and the magnitude of buckling coefficient. A series of eigenvalue analysis was performed for plates with up to 9 stiffeners, including the aspect ratio, width-to-thickness ratio and the size of stiffeners as variables. By comparing the buckling coefficient from FE analysis with the kf equation, correction factor(cc) was derived for n ≤ 3 and n > 3 (n : number of stiffeners) respectively and a buckling coefficient equation incorporating cc was proposed. In addition, a method for calculating the second moment of inertia of the stiffener was proposed when determining the buckling coefficient.
Keywords:
Compression plate, Multiple stiffeners, Buckling coefficient equation, Aspect ratio, Moment of inertia of stiffener키워드:
압축판, 다수 보강재, 좌굴계수식, 형상비, 보강재 단면2차모멘트1. 서 론
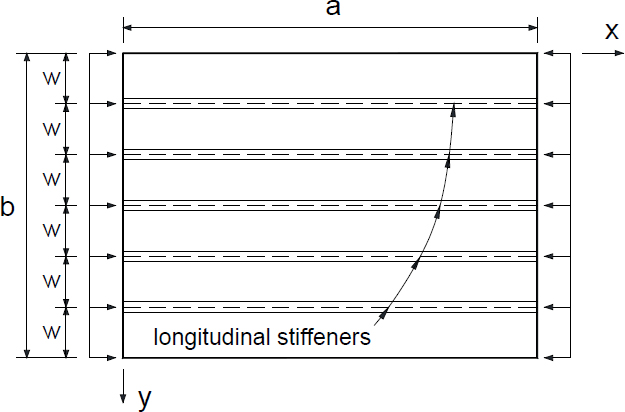
강박스 거더의 압축플랜지와 같은 압축판은 소정의 좌굴강도 확보를 위해 종방향보강재로 보강하게 된다(Fig. 1)[1]-[3]. 현재 AASHTO LRFD 교량설계기준(이하 AASHTO 기준)[4]과 국내 KDS 기준[5]에서는 좌굴계수로부터 정의한 판의 ‘조밀’ 및 ‘비조밀’ 한계세장비에 따라 보강판의 압축강도를 산정토록 하고 있어 좌굴계수의 정확한 평가가 중요하다.
AASHTO 기준의 본문 6.11.11.2에서는 보강재 개수(n) ≤ 2일 때 보강재의 단면2차모멘트(Is)에 따른 좌굴계수 산정식을 제시하고 있다. 보강재는 횡비틀림좌굴(lateral torsional buckling)에 유리한 T-단면을 전제로 하며, Is 값은 보강재의 하단에 대해 산정하도록 규정하고 있다. n ≤ 2로 제한한 이유는 본문 규정의 식은 종방향보강재가 매우 길다는 가정으로 인해 n이 증가할수록 보강재 제원이 과도하게 커지는 문제가 있기 때문이다[6].
한편, AASHTO 기준의 해설부 C6.11.11.2에서는 n ≤ 5까지의 판에 적용할 수 있는 좌굴계수식을 별도로 제시하고 있다. 이 식은 Timoshenko and Gere[7]가 에너지법으로 유도한 좌굴강도(Fcr) 식을 토대로 한 것이다. 단, 해설부의 좌굴계수식은 판의 형상비와 좌굴계수 크기에 따른 보강재의 제원을 유연하게 결정할 수 없는 제약이 있다. 또한 Timoshenko and Gere의 식은 좌굴 형상을 종방향 및 횡방향(Fig. 1의 x축 및 y축 방향)으로 각각 half-sine wave로 가정한 근사식에 해당된다. 이에 Wang et al.[8]은 Timoshenko and Gere 식의 적정성을 평가하기 위해 n ≤ 3에 대해 판의 형상비, 세장비(폭-두께비) 그리고 보강재의 제원 변화에 따른 좌굴계수 평가 해석을 수행하고 Timoshenko and Gere의 식에 보정계수(cf)를 적용한 좌굴계수식을 제안한 바 있다.
거더 폭이 큰 해상 교량과 같은 경우에는 다수의 종방향 보강재가 필요할 수 있다. 본 연구의 목적은 다수의 보강재가 적용되고 서브패널 형상비(a = a/w, Fig. 1 참조)가 큰 범위까지 Timoshenko and Gere의 좌굴계수식의 적용성을 평가하는 것이다. 이를 위해 n ≤ 9, 즉 서브패널 10개까지에 대해 판의 형상비, 세장비 및 보강재의 제원 변수를 고려한 좌굴고유치해석을 수행하고 보강재의 단면2차모멘트 산정 방안과 좌굴계수 산정식을 제안하였다.
2. 압축판의 좌굴계수식
2.1 AASHTO 기준
본문 6.11.11.2에서는 n = 1, 2에 대해 좌굴계수식을 다음 식 (1)로 제시하고 있다. 식 (1)은 종방향보강재가 매우 길다는 가정에 의한 것이어서 형상비 관련 변수가 포함되지 않는다.
| (1a) |
| (1b) |
여기서, 주목할 사항은 보강재는 T-단면으로 적용하되 단면2차모멘트(Is)는 압축판의 면(즉, T-단면 보강재의 하단)에 대해 산정하도록 규정하고 있다.
한편, 해설부에서는 n ≤ 5, β ≤ 3인 조건에서 다음 식 (2)의 적용을 허용하고 있다.
| (2) |
여기서 β (= a/b)는 압축판의 세장비이다. 단, 본 기준에서는 식 (2)의 적용 시 T-단면 보강재의 (tf: 판의 두께, w: 서브패널 폭)가 되도록 규정하고 있어 판의 형상비와 목표 좌굴계수 크기에 따른 보강재의 제원을 유연하게 결정할 수 없다.
식 (2)는 Timoshenko and Gere[7]가 에너지법으로 유도한 좌굴강도(Fcr) 식으로부터 최종 유도되는 다음 식 (3)을 토대로 한 것이다. 식 (3)은 형상비를 고려하고 목표 좌굴계수 값에 해당하는 보강재 제원의 선정이 가능하다.
| (3) |
여기서,
| (4a) |
| (4b) |
그리고, : 판의 휨강성, ν (= 0.3) : 포아송 비, Al : 보강재 1개의 단면적이며, γ와 δ는 각각 보강재 1개의 ‘휨강성비’와 ‘단면적비’이다.
2.2 Wang et al.의 좌굴계수식
Wang et al.[8]은 압축판의 형상비와 목표 좌굴계수 값에 따라 보강재 제원을 결정할 수 있도록 하기 위해 식 (3)의 적용성을 평가하였다. 이를 위해 판의 형상비, 서브패널의 폭-두께비(λf = w/tf), 그리고 보강재의 제원을 주요 변수로 하여 보강재 3개까지에 대해 좌굴고유치해석을 수행하였다. 수치해석 결과를 바탕으로 식 (3)에 수정계수(cf)를 도입하여 좌굴계수 산정식을 다음 식 (5a) 및 식 (5b)로 제안하였다.
• β / βcr ≤ 1.0일 때
| (5a) |
• β / βcr > 1.0일 때
| (5b) |
여기서, βcr은 식 (3)의 kf가 최소값을 보이는 한계 형상비로서 다음과 같다.
| (6) |
| (7) |
Wang et al. 역시 식 (4a)의 γ 산정 시 Is를 AASHTO 기준과 같이 보강재의 하단에 대한 단면2차모멘트로 고려하였다.
3. 전산 모델 및 예비 분석
3.1 전산 모델
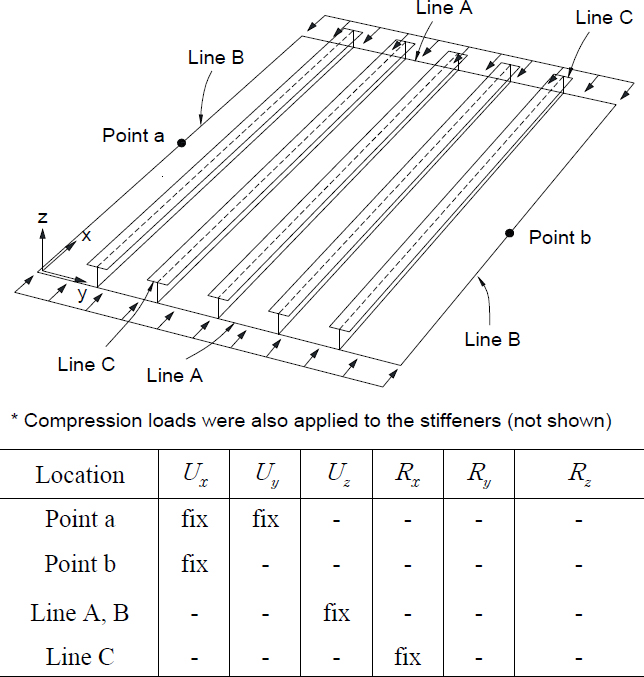
보강판의 좌굴고유치해석은 ABAQUS 프로그램[9]으로 수행하였다. 판과 T-단면 보강재는 모두 S4R 쉘요소로 모델링하였으며, 요소의 크기는 20 mm × 20 mm 내외로 충분히 세분화하였다. 경계조건은 Fig. 2에 n = 5의 예를 보였으며, 여기서 U는 이동변위, R은 회전변위이다. Line A에는 x축 방향 이동변위(Ux)를 동일하게 부여하기 위해 ‘coupling: kinematic’ 옵션을 적용하였다.
본 모델은 4변 모두 단순지지 조건에 해당하여 인접 패널에 의한 구속 효과(즉, continuity effect)를 고려하지 않으므로 안전측의 좌굴계수를 제공할 것이다. 한편 하중은 Fig. 2에 보인 바와 같이 압축플랜지와 보강재에 단위 압축응력(1 MPa)에 해당하는 선하중을 재하하였다.
한편, 보강재의 초기처짐을 고려하였으며 Fig. 3에 보인 바와 같이 종방향의 중앙선을 기준으로 횡방향으로는 중앙점에서 최대 1/50 rad 회전된 것으로 고려하였다.
3.2 단면2차모멘트 산정 방안 및 좌굴계수식 도출을 위한 예비 분석
좌굴계수식의 도출을 위한 본 해석에 앞서 예비 분석을 수행하였다. n = 5, tf = 32 mm, w = 600 mm로 하였으며 간격(a)과 보강재 제원은 Table 1에 제시하였다. Table 1에서 kFEA는 좌굴고유치해석에 의한 좌굴계수이며 a =1,500 mm와 a =9,000 mm의 좌굴형상을 Fig. 4에 예시하였다(Fig. 4는 좌굴형상을 명확히 보이기 위해 요소 크기를 (a) 45 mm × 45 mm와 (b) 60 mm × 60 mm로 크게 한 것임).
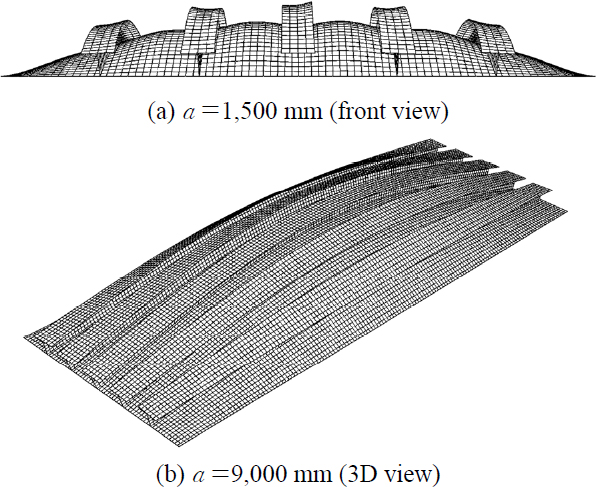
Buckling shapes : n = 5, tf =32 mm, (a) a = 1,500 mm, T-135×200×12×12, (b) a = 9,000 mm, T-265×400×22×22
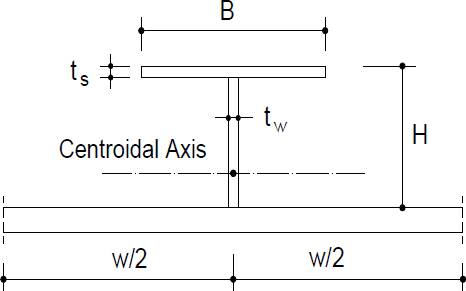
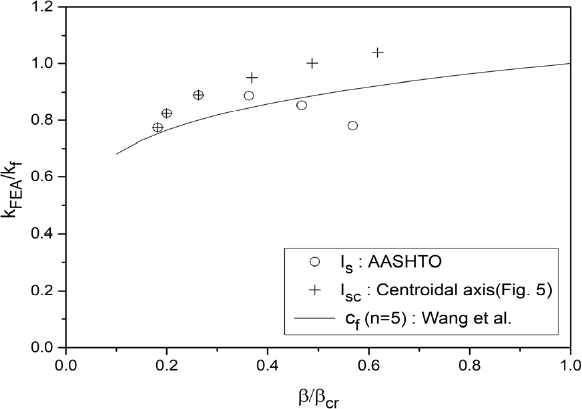
Table 1에서 Is는 AASHTO 기준에 따라 T-보강재 하단에 대해 산정한 단면2차모멘트이다. 반면 Isc는 압축판(총폭 b)과 보강재들이 이루는 총단면의 도심축에 대해 서브패널과 보강재가 이루는 단면(Fig. 5 참조)의 단면2차모멘트이다. 단, 도심축이 압축판의 면내에 있는 경우에는 Is와 같다고 고려하였다. 이로부터 각 경우별 βcr과 kf를 식 (6)과 식 (3)으로부터 산정하였다.
단면2차모멘트 산정 방식별 kFEA / kf 비를 Fig. 6에 도시하였다. 이로부터 AASHTO 방식으로 산정한 Is 적용 시 형상비 변수 β / βcr이 증가함에 따라 kFEA / kf 비가 다시 감소하는 결과를 보인다. 보강재 개수가 적은 경우 및 보강재 제원이 크지 않은 경우(일반적으로 형상비가 작을 때)에는 압축판과 보강재들이 이루는 총단면의 도심이 압축판 내 또는 보강재 하단 근처에 있게 된다. 이에 따라 Timoshenko and Gere는 압축판의 기여는 작으므로 무시하고 보강재의 단면2차모멘트를 보강재 하단에 대해 산정토록 규정하였으며[7], AASHTO 기준도 이를 따르고 있다. 그러나, 보강재 수가 많은 경우와 보강재의 제원이 커지면 도심은 보강재의 스템 내에 존재하게 된다. 이 경우 Is > Isc가 되며, 따라서 Fig. 6으로부터 단면2차모멘트를 Isc로 고려하는 것이 적절함을 알 수 있다.
한편, β / βcr이 작을수록 kFEA / kf 비가 감소하는 이유는 식 (3)의 kf가 좌굴모드를 종방향과 횡방향으로 half-sine wave로 가정하여 유도된 반면, Fig. 4(a)에서와 같이 횡방향으로 보강재 위치에서 국부변형의 발생으로 인한 차이가 발생하며 β / βcr이 작을수록 그 영향이 커지기 때문이다. 이를 고려하고자 Wang et al.[8]은 n ≤ 3에 대해 수정계수(cf)를 식 (7)로 제안하였다. 만약 n = 5인 경우에 적용하면 cf = (β / βcr)1/6이 되며 이를 Fig. 6에 도시하였다. 이로부터 Isc를 적용하더라도 보강재 개수가 많은 경우(n > 3)에는 보정계수를 새로이 도출하여야 함을 보여준다.
4. 고유치해석 및 좌굴계수식 제안
4.1 고유치해석 및 결과
보강재 개수(n)는 3, 5, 7 및 9, 서브패널의 폭-두께비(λf)는 18.8과 33.3, 그리고 서브패널의 폭(w)은 600 mm, 형상비(a)는 15까지 고려하였다. a = 15일 때 간격(a)은 9,000 mm가 되는데, 이는 Hall and Yoo[10]가 강박스거더교에서 뒤틀림응력(distortional stress)을 제한하기 위해 제안한 최대 간격 30 feet(=9.14 m)에 해당된다.
보강재의 제원은 형상비에 따라 식 (3)의 kf가 4.0에서 1.0의 값을 갖도록 선정하였다. 좌굴해석 경우와 결과를 Table 2에서 Table 5까지 제시하였다. 이들 Table에서 보강재의 단면2차모멘트(Is,min)은 다음과 같다.
• 총단면 도심이 압축판 내에 있는 경우 : 압축판의 기여는 무시하고 보강재의 압축판 면에 대한 단면2차모멘트(=Is)
• 총단면의 도심이 보강재 스템 내에 있는 경우(Fig. 5) : 도심축에 대한 보강재와 서브패널판의 단면2차모멘트(=Isc). 단, 도심이 보강재 스템 내에 있으나 압축판의 표면에 가까울 때 Isc가 Is보다 조금 크게 되는 경우가 있는데, 이 때는 Is를 적용한다.
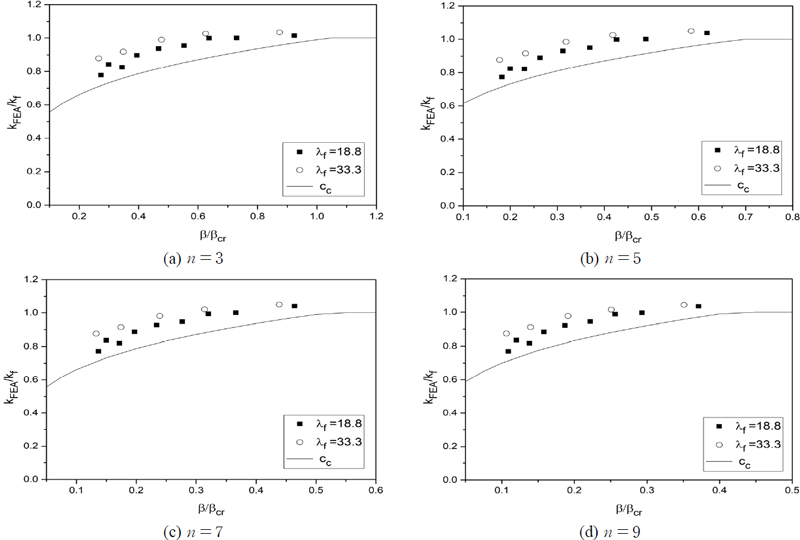
즉, 보강재의 단면2차모멘트는 Is와 Isc 중 작은 값을 적용하기로 한다. 이로부터 kFEA와 식 (3)에 따라 산정한 kf의 비를 Fig. 7에 도시하였다. Fig. 7로부터 β / βcr이 작을수록, 또한 판의 세장비(λf)가 작을수록 kFEA / kf 비가 더 작은 결과를 보인다.
4.2 좌굴계수식 제안
Fig. 7로부터 합리적인 좌굴계수식의 도출을 위해서는 식 (3)의 kf 식에 수정계수가 필요함을 보여준다. 곡선접합(curve fitting)으로부터 λf = 18.8과 λf = 33.3의 평균값에 해당하는 수정계수식을 도출한 후, 안전율을 감안하되 λf가 작을수록 kFEA / kf 비가 더 작은 값을 보이므로 λf = 18.8의 경우를 포괄하도록 최종 수정계수식(cc)을 도출하였다. 세장비 λf = 18.8은 항복강도 460 MPa까지의 강박스거더에서 최소 세장비 수준으로 생각된다.
β / βcr ≤ 1.0일 때 적용되는 보정계수 cc는 n ≤ 3과 n > 3으로 구분하여 도출하였으며, 이를 적용한 좌굴계수 kc는 다음 식 (8), 식 (9a) 및 식 (9b)와 같다.
| (8) |
| (9a) |
| (9b) |
| (10) |
Fig. 7(a)–(d)에 보정계수 cc를 도시하였다. 한편 β / βcr > 1.0일 때 식 (10)의 kf,min은 앞의 식 (5b)와 같다. Table 2–Table 5에 제시한 kFEA / kf 값으로부터 kc 식은 다수의 보강재가 설치된 압축판에서 좌굴계수를 합당하게 추정할 수 있을 것으로 판단된다.
본 연구에서 n = 1과 2에 대해 별도의 좌굴해석을 수행하지 않았으나, 식 (9a)의 cc는 Wang et al.[8]이 제안한 식 (7)의 cf와 단지 1 % 차이를 보인다. 따라서 cc는 n = 1과 2에서도 타당할 것이다.
5. 결 론
본 연구에서는 폭이 큰 압축판을 고려하기 위해 다수의 T-단면 보강재로 보강된 압축판의 좌굴계수식을 제안하기 위한 연구를 수행하였다. 주요 결론은 다음과 같다.
- (1) 광폭의 압축판을 고려하고 판의 형상비에 따른 합리적인 보강재 제원을 결정할 수 있도록 보강재 개수(n)는 9개까지, 서브패널의 형상비(a)는 15까지, 그리고 판의 폭-두께비(λf)는 18.8과 33.3의 조건에 대해 좌굴고유치해석을 수행하였다. 에너지법으로부터 유도된 식 (3)의 좌굴계수 kf와 FE 해석에 의한 좌굴계수 kFEA와의 차이를 보정하기 위한 보정계수 cc를 n ≤ 3과 n > 3에 대해 구분하여 식 (9a)와 식 (9b)로 제안하였다. 이로부터 좌굴계수(kc)는 β / βcr ≤ 1.0과 β / βcr > 1.0일 때 각각 식 (8)과 식 (10)으로부터 구한다.
- (2) 좌굴계수 산정 시 AASHTO 기준은 T-보강재의 단면2차모멘트(Is)를 보강재의 하단(즉, 압축플랜지의 면)에 대해 산정하도록 규정하고 있는데, 이는 압축판과 보강재들이 이루는 총단면의 도심이 압축판 내에 있다는 가정에 의한 것이다. 그러나, 보강재 개수가 많은 경우 및 보강재 제원이 커지는 경우(형상비 증가에 따라) 총단면의 도심이 T-보강재의 스템 내에 있게 된다. 이 경우, 도심이 압축판의 표면에 가까운 경우를 제외하면 도심에 대해 보강재와 서브패널이 이루는 단면의 단면2차모멘트 Isc(Fig. 5 참조)가 Is보다 통상 작게 된다. 이에 따라 kf 산정시 T-보강재의 단면2차모멘트는 Is와 Isc 중 작은 값을 적용하는 것이 타당한 것으로 나타났다.
- (3) 제안한 좌굴계수식(kc)이 AASHTO 기준에서 정의한 보강판의 압축강도를 합당하게 평가하는지 여부는 초기처짐과 잔류응력을 고려한 비선형해석으로부터 추후 검증할 예정이다.
References
-
Narayanan, R. (1983) Plated Structures: Stability and Strength, Applied Science Publishers, London and New York.
[https://doi.org/10.1201/9781482284980]
-
Yoo, C.H., Choi, B.H., and Ford, E.M. (2001) Stiffness Requirements for Longitudinally Stiffened Box-girder Flanges, Journal of Structural Engineering, American Society of Civil Engineers, Vol.127, No.6, pp.705-711.
[https://doi.org/10.1061/(ASCE)0733-9445(2001)127:6(705)]
-
Kim, K.S. (2019) In-Plane Compressive Strength of Hybrid Steel Stiffened Plate with Single Stiffener, Journal of Korean Society of Steel Construction, KSSC, Vol.31, No.1, pp.65-73 (in Korean).
[https://doi.org/10.7781/kjoss.2019.31.1.065]
- American Association of State Highway and Transportation Officials (2020) AASHTO LRFD Bridge Design Specifications (9th Ed.), AASHTO, USA.
- Korea Construction Standards Center (2024) Design Standards for Steel Members(Load and Resistance Factored Design), KDS 14 31 10, Ministry of Land, Infrastructure and Transport (in Korean).
- Choi, B.-H. (2002) Design Requirements for Longitudinal Stiffeners for Horizontally Curved Box Girders, Ph.D. Dissertation, Auburn University, USA.
- Timoshenko, S., and and Gere, J.M. (1961) Theory of Elastic Stability (2nd Ed.), McGraw-Hill, USA.
-
Wang, L., Park, Y.M., Liu, Y., and Choi, B.H. (2021) Proposal of Buckling Coefficient Equation Considering Aspect Ratio of Compression Plates Stiffened with Tees, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.5, pp.275-283 (in Korean).
[https://doi.org/10.7781/kjoss.2021.33.5.275]
- Dassault Systèmes Simulia (2022) Abaqus Analysis User’s Manual, DSS, USA.
- Hall, D.H., and Yoo, C.H. (1998) Improved Design Specifications for Horizontally Curved Steel Girder Highway Bridges, NCHRP Project 12-38, National Cooperative Highway Research Program, USA, Appendix D.