강구조 접합부 내진보강용 헌치형 에너지 흡수장치의 강도설계식 및 적정 설계범위 제안

1. 서 론

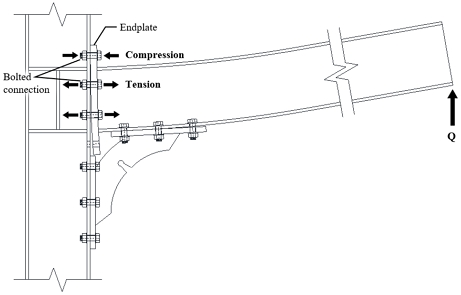
지진하중 작용 시 보-기둥 접합부는 강도 및 강성 손실을 최소화하기 위해 많은 에너지를 소산하며 전체 골조 성능에 크게 기여한다. 본 연구에서 다루고자 하는 엔드플레이트 접합은 공장용접으로 엔드플레이트와 보를 일체화하고 현장에서 볼트만으로 기둥 플랜지에 접합하는 방식으로, 현장용접을 필요로 하지 않아 화재 발생 위험을 방지하는 등 시공 안정성 확보가 가능하여 파이프랙(pipe-rack) 등 산업 플랜트 구조물의 접합부에 널리 적용되었다.

Northridge 지진(1994), Kobe 지진(1995)과 같은 대지진 발생 시 강구조 접합부의 취성파단이 발생하며 내진성능 개선 필요성이 제기되었으며, 모멘트, 전단력 모두를 견뎌야 하는 전체 골조에서 접합부의 강도, 강성의 증대 및 연성능력 확보를 통한 취성파단 방지는 필수적이다. 접합부의 성능향상 및 소성변형을 허용하는 설계방법으로 용접헌치(welded haunch)^[1],[2], 보 플랜지 절취형(Reduced Beam Section, 이하 RBS)^[3],[4], 보 플랜지 개량^[5],[6] 등이 제안되어 왔다. 이는 간편한 시공과정으로 내진성능 향상 효과를 가져왔으나, 접합부 보강 후 보 단부에서 보강재 끝단으로 소성힌지의 위치 변화는 기둥, 보 부재의 손상을 발생시켰으며, 슬래브 합성효과에 따른 보 하부 플랜지의 취성적 거동에 대응하지 못한다. 또한 대부분의 관련 연구들은 노스리지(Northridge) 지진 시 접합 상세인 용접 접합부를 가지는 신축 건축물 내진성능 향상에 관한 것으로 기존의 엔드플레이트형 접합부의 보강에 관한 연구는 미비한 실정이다.

앞서 언급한 대다수의 내진성능향상 기법은 주부재에 대한 용접작업이 수반되며, 이는 신규 구조물에는 적용이 용이하나 파이프랙 구조물과 같이 엔드플레이트 접합부를 가지는 경우 적용에 제약이 따른다. 대규모 산업시설에서 고압가스 및 석유, 화학물질 등을 수송하는 파이프랙 구조물은 인화성, 가연성 물질에 상시 노출되어 있어, 현장용접 시 발생하는 스파크와 고온 환경이 화재 위험을 증가시킨다. 화재 시 인명‧재산상의 피해를 초래할 뿐만 아니라 파이프랙과 같이 화기에 취약한 철골 구조물의 구조적 성능을 현저히 저하시키며 대규모 피해를 발생시킬 수 있어, 현장에서의 용접작업은 가급적 지양되어야 한다.

이에 대한 대안으로 Park and Oh^[7]의 연구에서는 무용접·무천공 보강공법을 제안하고 내진성능 평가를 위한 실험적 연구를 수행하였다. 실험결과 제안 공법 적용 시 국부좌굴 및 취성파단 등의 손상이 완화되며 그 효과가 입증되었다. 접합부 보강장치의 내력이 과도한 경우 기둥, 보 부재의 손상을 가중시키고, 부족한 경우 보강효과가 감소하는 문제가 발생한다. 이에 따라 효과적인 성능 발휘 및 보 부재의 손상 방지를 위해서는 보강장치의 적정 내력을 산정하는 것이 필수적이며, Oh and Park^[8]의 연구에서는 부재 재사용을 위해 지진 발생 시 부재가 손상되지 않는 적정 내력비를 0.6에서 0.8의 범위로 제시한 바 있다. 그러나 본 연구에서 다루고자 하는 엔드플레이트형 접합부에 대한 적정 설계범위 연구는 아직 미비한 실정이다.

본 연구에서는 엔드플레이트형 기존 철골 구조물에서 내진성능을 향상시키고, 부재 손상방지를 통한 재사용이 가능하도록 접합부 보강장치의 적정 내력 및 설계범위를 분석하고자 한다. 유한요소해석을 실시하여 보강장치 적용 시 엔드플레이트형 접합부의 중립축 변화에 따른 간극거리를 반영한 보강장치 강도설계식을 확립한다. 또한 보 부재 손상도를 고려하여 선행연구에서 제시된 적정 설계범위의 적용 가능성을 검증하고자 한다.

2. 선행연구 실험결과

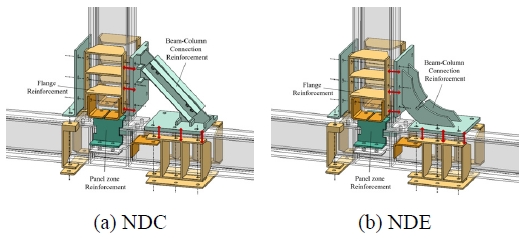
Park and Oh^[7]의 선행연구에서는 무용접‧무천공 접합상세를 적용한 보강 접합부의 내진성능평가를 위해 정적성능검증실험을 수행하였다. Fig. 1과 같이 실험체 NDC (ND: Non-driling, C: CSE_Channel Strength Enhancement)는 내진성능 향상을 기대할 수 있는 찬넬 강도 향상형 보강장치(Channel Strength Enhancement, CSE)를, 실험체 NDE (ND: Non-driling, E:EAS_Energy Absorption Stiffener)는 접합부의 손상방지를 위한 에너지 흡수형 스티프너(Energy Absorption Stiffener, EAS)를 적용하였다.

Fig. 1.

Bolt assembly details of specimens

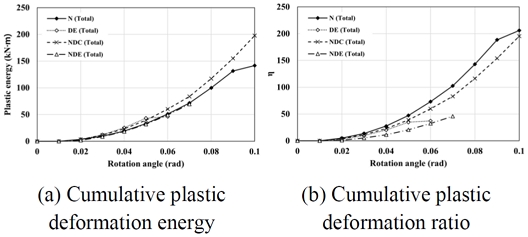
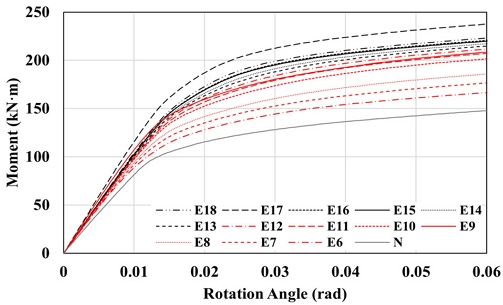
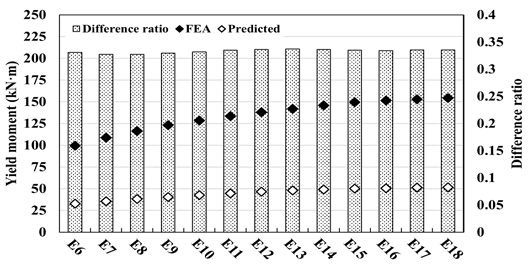
실험결과, 보강장치와 무관하게 해당 접합상세를 적용하여 보강하는 경우 내진성능향상 효과를 확인하였으며, 0.04 rad에서 최대모멘트 비교 시 실험체 NDC의 경우 실험체 NDE에 비해 약 4 %–7 % 개선된 성능을 보였다. CSE 보강안은 내력상승효과는 우수하였으나 변형률 측정값 결과 기존 부재의 손상을 초래하는 문제가 확인되었으며, 이는 보 춤이 증가할 경우 보 부재의 손상은 더욱 가중될 것으로 예상된다. 손상방지 측면에서 EAS 보강안을 적용할 수 있으나, CSE 대비 유효단면 크기가 작은 EAS의 특성으로 인해 실험에서는 조기 파단이 발생하였고, 그 결과 Fig. 2와 같이 내력 및 에너지 소산능력이 감소하는 한계가 확인되었다. 따라서 기존 구조물의 성능향상을 위해 보강장치를 적용하는 경우, 일정 수준 이상의 내력을 확보함과 동시에 주부재의 손상을 방지할 수 있는 보강안의 적정 내력 산정이 필요하다.

Fig. 2.

Cumulative energy dissipation capacity

3. 유한요소해석을 통한 구조성능 검토

3.1 보강장치 적용 시 접합부 거동

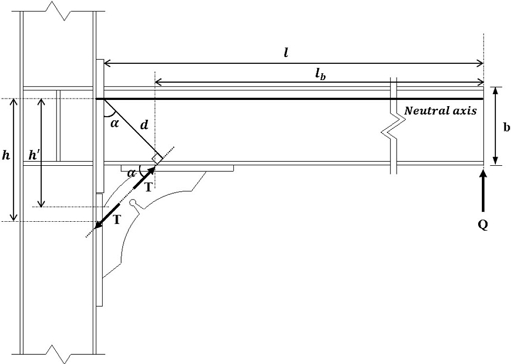
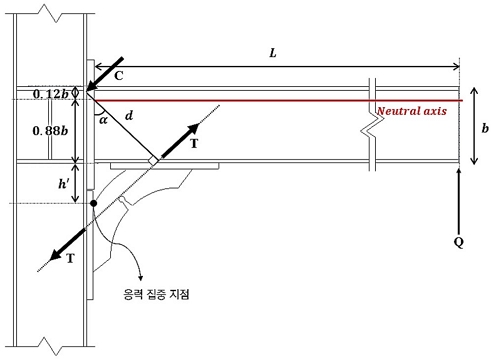
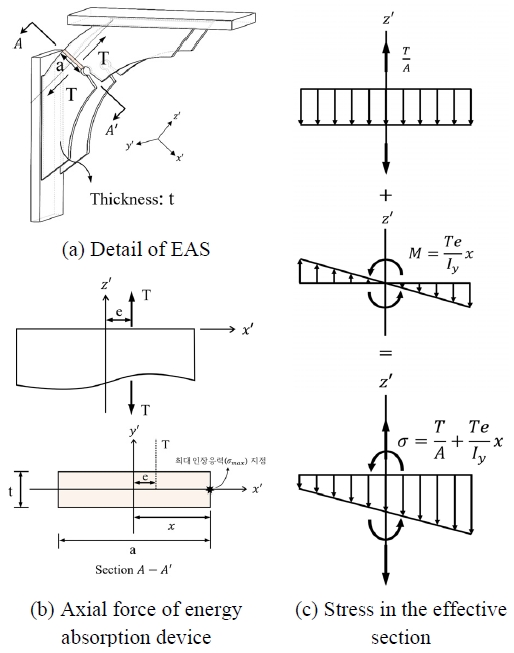
엔드플레이트 접합부에서 접합부 보강장치를 적용하는 경우 Fig. 3와 같이 나타낼 수 있다. 이는 Seol^[9]의 연구에서 스티프너형 에너지 흡수장치를 적용한 경우와 유사하다. 보강 접합부에서 보에 하중(Q) 작용 시 접합부에 대각으로 위치한 보강 스티프너에 축력(T)이 발생하며 스티프너 유효단면이 축력의 대부분을 분담한다. 스티프너를 항복시키는 힘은 작용하중(Q)의 보강 스티프너 끝단까지의 거리(l_b)에 대한 전도모멘트이며, 이때 스티프너에 인장‧압축력 작용 시 발생하는 모멘트가 이에 저항한다. 저항모멘트는 스티프너에 작용하는 축력과 간극거리(d)의 곱으로 산정할 수 있으며, 간극거리는 스티프너가 보 부재와 이루는 각도(α)와 중립축에서 기둥과 맞닿는 부분의 스티프너 끝단까지의 거리(h^′)를 통해 산정할 수 있다. 보 부재에서 최대응력의 발생위치는 보강 스티프너에 작용하는 축력과 맞닿는 지점이다. 접합부 보강 시 최대응력 발생 지점에서 보 부재의 손상도는 보강 스티프너 내력에 좌우되며 보강 스티프너로의 응력집중을 유도하기 위해서는 보강 스티프너의 내력이 보 부재보다 작게 설계되어야 한다. 따라서 보 항복모멘트(_bM_y)에 대한 보강장치의 항복모멘트(_EM_y) 비율인 항복내력비(λ)를 도출하는 것이 중요하다.

Fig. 3.

Behavior of reinforced connection under external load (Q)

3.2 해석방법 및 검증

보강 접합부에서 보강장치의 항복모멘트를 도출하는 경우 보강 접합부 모멘트 관계를 바탕으로 한다. 보강장치에 작용하는 축력과 축력 작용지점에서 보 단부의 중립축까지의 수직거리의 곱으로 산출하므로, 전체 접합부의 중립축 위치를 파악하는 것이 선행되어야 한다.

ABAQUS(2022) 상용유한요소해석 프로그램을 통해 해석모델에 대한 보강장치 인장방향인 정(+)방향 단조가력을 수행하였다. Mesh 크기는 20 mm로 부재별로 동일하게 적용하였으며 보강장치의 경우 정밀한 해석을 위해 10 mm로 조밀하게 설정하여 해석 정확성을 향상시켰다. 경계조건의 경우 기둥 양단부의 Z축 방향 회전을 구속하여 핀으로 고정하고, 실험 시 횡방향 좌굴방지 지그를 설치한 위치의 Z축 변위와 X, Y축 회전자유도를 구속하여 보 부재의 면외방향 좌굴과 비틀림을 방지하였다. 변위제어를 통한 가력을 위해 보 절취 단면에 대한 Y축 방향 변위를 부여하고, Z축 방향 변위는 0으로 설정하여 면외방향으로의 이동을 제한하였다. 변위에 필요한 진폭은 시간과 동일하게 하여 해석시간 당 1 mm 가력하도록 하였다. 볼트 접합을 구현하기 위해 M20 고장력 육각볼트의 모델링을 실시하였으며, 모델링 편의성을 위해 볼트머리와 너트는 원형으로 모델링하고 와셔와 몸통 나사부의 모델링은 생략하였다. 볼트 원통부 몸통의 중심 단면에 Bolt load 옵션으로 프리텐션을 가했으며, 가력 스텝에서는 볼트의 과도한 변형을 방지하기 위해 길이를 고정(Fix at current length)하였다. 접촉면에 대하여 Surface to Surface 옵션으로 접촉 조건을 부여하고, 접촉면 물성치는 Hard contact 조건에서 일반적인 강재 간 마찰계수인 0.25를 적용하였다.

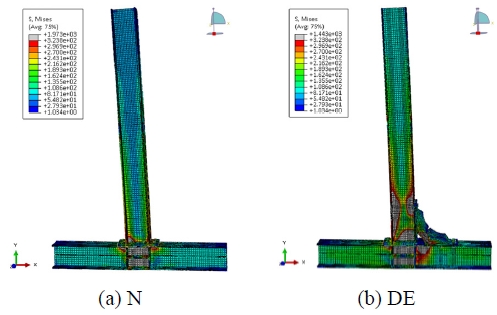
해석 모델링에 대한 신뢰성 검증을 위해, 보 춤 244 mm의 비보강 엔드플레이트 접합부(N)와 해당 접합부에 에너지 흡수형 보강장치(EAS, Energy Absorption Stiffener)를 적용한 모델(DE)의 유한요소해석 및 실험결과를 비교하였다. Fig. 4는 해석모델 항복 시 Von-Mises 응력분포이며, Table 1에서 초기강성, 항복변형각 및 항복모멘트에 대한 실험결과와 해석결과 간의 오차율 산정 시 해석모델 N의 경우 10 % 이내로, 해석모델 DE의 경우 5 % 이내로 나타나며 해석결과에 대한 신뢰성을 입증하였다.

Fig. 4.

Von-Mises contour of FEA models

Table 1.

Summary of specimen analysis results

3.3 해석결과

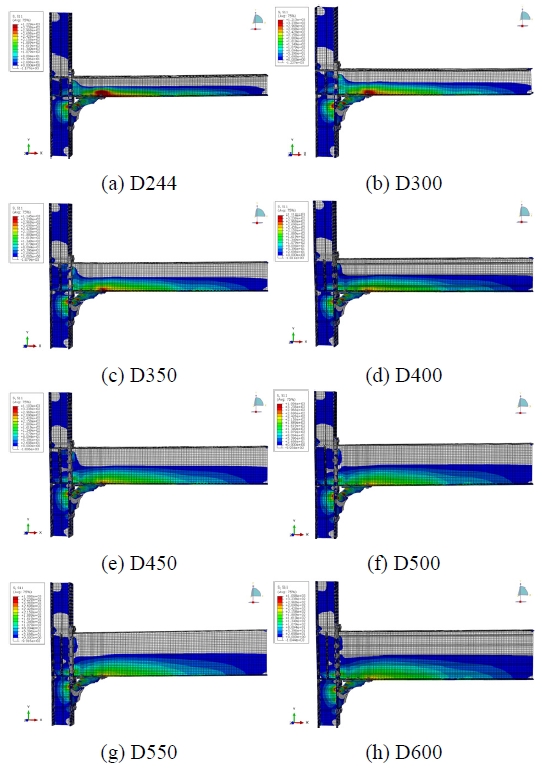
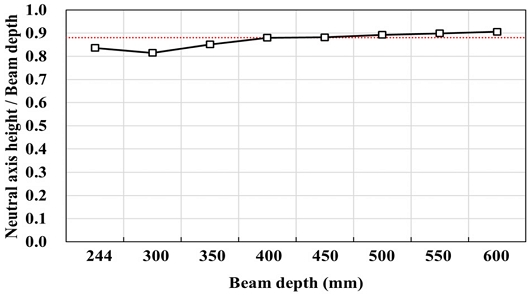
해석모델에서 접합부의 중립축 위치를 도출하고자, 실험에 적용된 것과 동일한 두께 15 mm, 유효폭 55 mm의 2개의 스티프너를 가지는 보강장치를 적용하였을 때 보 춤에 따른 중립축 위치 변화를 분석하였다. 해석모델의 변수는 보 춤으로, Table 2에 나타나듯이 244 mm에서 약 50 mm씩 증가시켜 최대 600 mm까지 해석을 진행하였다. 이때, 보와 기둥 부재의 길이는 각각 2,400 mm, 1,800 mm로 고정하고, 엔드플레이트와 기둥을 접합하기 위해 보강장치와 근접한 볼트 2개를 제외한 총 6개의 볼트만을 체결하여 보강장치로 응력을 집중시켰다.

Table. 2

Details of FEA models

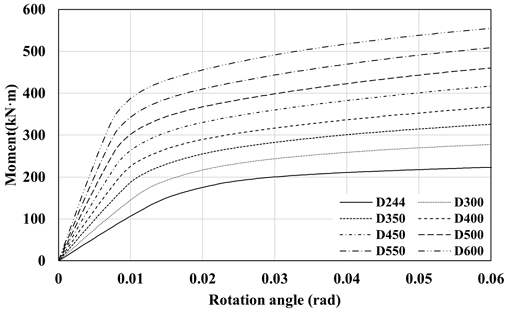
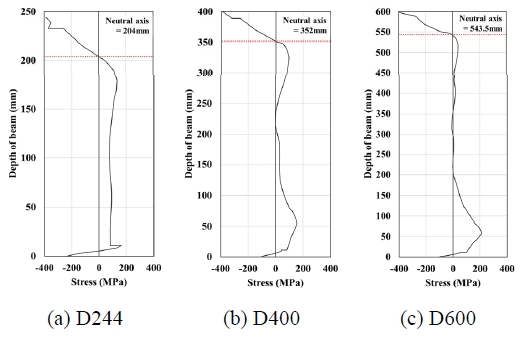
보강장치의 인장방향에 해당하는 가력방향의 축방향에 대한 응력분포를 Fig. 5에 나타내었다. 가장 진한 적색으로 표시된 부분은 인장 응력에 의한 항복 구간이며, 흰색으로 나타난 부분은 압축 응력이 작용하는 영역을 의미한다. Fig. 6는 해석모델의 모멘트-변형각 관계이며, Fig. 8은 응력분포를 바탕으로 Fig. 7과 같이 보 단부에서 보 춤에 대한 응력분포를 나타낸 그래프이다. 그래프의 세로축은 보강장치가 접합된 보 하부 플랜지를 기준(0 mm)으로 상부 플랜지까지의 보 춤이며 가로축은 단면의 응력을 의미한다. 중립축의 위치는 응력이 0 MPa인 지점으로, 이 지점에서 인장 응력과 압축응력이 발생하는 영역의 합이 0이 된다. 응력분포에서 0 MPa 미만은 압축응력이, 0 MPa 초과는 인장응력이 발생하는 영역을 나타낸다. 그래프의 적색 파선은 중립축 위치에 해당하며 보 춤이 증가할수록 중립축이 상승하는 것으로 확인되었다. 해석모델별로 항복모멘트(M_y), 중립축 높이(NA), 기둥 부재에서 스티프너와 맞닿는 응력집중 지점까지의 거리(h^′)를 산정하여 Table 3와 Fig. 9에 정리하였다. 분석 결과 산출된 값들은 항복모멘트와 비례하게 증가하였으며, 보강 후 중립 축의 위치는 보춤의 약 0.88배 지점으로 보강 전 보 춤 중심에 위치한 중립축에 비해 상승하는 것으로 나타났다.

Fig. 5.

Von-Mises contour at yield in FEA models

Fig. 6.

Monotonic loding curve of FEA models

Fig. 7.

Stress evaluation region in beam section

Fig. 8.

Neutral axis variation with beam height

Table 3.

Results for varying beam heights

Fig. 9.

Neutral axis to beam height ratio

또한 보강장치의 내력에 따른 보강 접합부의 구조성능을 파악하기 위해 보강장치 주요 영향인자를 변수로 하는 보강 접합부의 유한요소해석 결과를 비교하였다. 총 13개의 해석모델이 고려되었으며, 주요 변수는 스티프너 두께로 실험에서 적용된 15 mm를 기준으로 1 mm 단위로 증감하여 6 mm에서 18 mm 범위에 대하여 해석을 수행하였다. 기둥과 보 부재는 실험과 동일한 H-244 × 175 × 7 × 11 단면으로 모델링하였으며, 스티프너 두께를 제외한 나머지 설계 조건은 기존 실험과 동일하게 설정하였다. 해석결과 내력 및 구조적 성능은 Fig. 10 및 Table 4와 같다.

Fig. 10.

Skeleton curve of FEA models

Table 4.

Summary of FEA results

4. 엔드플레이트형 보강 접합부 내력식

4.1 접합부 내력 약산식

엔드플레이트형 보강 접합부 설계를 위해 앞서 분석한 접합부의 거동과 해석결과를 통해 내력식을 도출하고자 하며, 이때 설계의 간략화를 위해 약산식을 우선적으로 도출하고 보정계수를 적용하고자 한다. 본 연구에서 적용하는 접합부는 Fig. 11과 같이 두께 25 mm의 확장형 4-bolted 엔드플레이트를 적용하였으며, 볼트접합 시 하부 보강장치로의 응력집중을 유도하기 위해 엔드플레이트 최외각 하부 2개의 볼트는 미체결하였다. 이는 중립축 위치와 접합부 거동에도 영향을 미치는 요인으로 작용한다. 접합부에서 엔드플레이트 두께, 볼트 개수 등은 엔드플레이트 체결부의 볼트 축력과 이로 인해 발생하는 엔드플레이트의 인장 및 압축력에 변화를 유발하며, 이러한 변수들이 결과값 차이에 영향을 미친 것으로 판단된다. 그러나 예측식에서 접합부 거동에 영향을 미치는 모든 변수를 개별적으로 고려하는 데는 한계가 있다. 해당 거동을 간략화하여 예측식에 반영하기 위해 보정계수를 도입하고자 한다.

Fig. 11.

Behavior of end-plate reinforced connection

해석결과를 바탕으로 산정된 죽립축의 높이를 통해 보강장치에 작용하는 축력의 간극거리를 계산할 수 있다. Fig. 12에 나타난 바와 같이 보 단부에서 발생하는 응력은 보 상부 플랜지에 집중되며 해당 지점에서 발생하는 하중과 보강장치의 축력은 우력모멘트를 형성한다. 이때 우력모멘트를 발생시키는 하중 간의 거리를 간극거리(d)로 정의하며, 이는 편심거리와 보 상부 플랜지에 발생하는 하중지점까지의 거리를 합산한 값으로 식 (2)와 같다.

Fig. 12.

Moment relationship of reinforced connection under external force

또한 스티프너에 발생하는 응력분포는 Fig. 13에 제시되어 있으며, 곡률을 가지는 비정형 스티프너에서 축력(T)은 유효단면에 편심하중으로 작용한다. 보강장치에 작용하는 축력의 편심거리는 스티프너 상세와 작용축력의 크기에 따라 달라진다. 이에 따라 단면에 편심하중이 작용하는 경우의 응력분포를 고려하여 식 (3)을 통해 편심거리를 산정하였다. 유효단면에서의 응력은 중첩의 원리에 따라 중심 축하중이 작용할 때의 균일한 축력과 편심거리(e)에 의한 모멘트의 조합하중으로 산정하며, 식 (4) 및 식 (5)와 같이 나타낼 수 있다. 스티프너에서 최대 인장응력이 발생하는 위치는 노치 부근으로, 해당 지점에서 항복이 가장 먼저 발생한다. 스티프너의 항복축력은 스티프너 유효단면 특성을 적용하고 재료인장시험 결과를 통해 재료항복강도에 도달할 때의 하중으로 산정한다. 항복축력과 간극거리의 곱으로 나타내는 보강장치의 항복모멘트는 식 (6)과 같다.

$\[ M=Q\times L=T\times d \]$

(1)

$\[ d=\left\{\left(0.88b+h^{\prime }+\frac{2}{3}\times 0.12b\right)\times \mathrm{c}\mathrm{o}\mathrm{s}\alpha \right\}+\frac{a}{2}+e \]$

(2)

$\[ e=\frac{\left(a^2\times t\right)\times {\sigma }_y\times n}{6T}-\frac{a}{6} \]$

(3)

$\[ \sigma =\frac{T}{A}+\frac{Te}{I_y}x \]$

(4)

$\[ T_y=\frac{{\sigma }_y}{\frac{1}{A}+\frac{e}{I_y}x}\times n=\left(\frac{a^2\times t}{a+6e}\times {\sigma }_y\right)\times n \]$

(5)

$\[ {}_E{M}_y\begin{array}{l}=T_y\times d\hfill \\ =\frac{a^2\times t}{a+6e}\times {\sigma }_y\times n\times \hfill \\ \left\{\left(0.88b+h^{\prime }+\frac{2}{3}\times 0.12b\right)\times \text{cos}\alpha +\frac{a}{2}+e\right\}\hfill \end{array} \]$

(6)

• 여기서, Q: 작용하중                       L: 보 길이
•  　 　　T: 보강장치 작용 축력      d: 간극거리
•  　 　　A: 유효단면적                   e: 편심거리
•  　 　　I_y: 단면2차모멘트             t: 스티프너 두께
•  　 　　a: 스티프너 유효폭
•  　 　　σ_y: 스티프너 소재항복강도
•  　 　　n: 스티프너 개수
•  　 　　h^′: 보 하부플랜지부터 응력집중 지점까지 거리
•  　 　　b: 보 춤
•  　 　　α: 축력이 접합부와 이루는 각도

Fig. 13.

Effective section under eccentric axial load

4.2 접합부 내력식의 보정계수 적용

설계식을 통해 산정한 예측값과 FEA 결과값을 비교한 결과, Table 5 및 Fig. 14과 같이 해석모델별로 차이는 존재했으나 전체 해석모델에서 예측값은 해석값의 약 0.33배로 나타나며 유사한 경향을 보였다. 해석값이 예측값의 약 3배에 해당하므로 보정계수를 3으로 설정하고 이를 반영하여 보강장치의 항복모멘트 예측식을 식 (7)과 같이 수정하였다. 보강장치의 적정 내력비 산정을 위해 보강장치와 보의 항복내력비(λ)를 식 (8)에 따라 산정한다. 접합부의 항복내력은 스티프너 항복 시 발생 모멘트이며, 보의 항복내력에 대한 스티프너 항복내력의 비율로 항복내력비를 도출할 수 있다. 보의 항복내력은 재료인장실험 결과를 반영한 보의 항복모멘트에 해당한다.

$\[ {}_E{M}_y\begin{array}{l}=3T_y\times d\hfill \\ =3\times \frac{a^2\times t}{a+6e}\times {\sigma }_y\times n\times \hfill \\ \left\{\left(0.88b+h^{\prime }+\frac{2}{3}\times 0.12b\right)\times \text{cos}\alpha +\frac{a}{2}+e\right\}\hfill \end{array} \]$

(7)

$\[ \lambda =\frac{{}_E{M}_y}{{}_b{M}_y} \]$

(8)

• 여기서, T: 보강장치 작용 축력       d: 간극거리
•  　 　　a: 스티프너 유효폭            t: 스티프너 두께
•  　 　　e: 편심거리                        n: 스티프너 개수
•  　 　　b: 보 춤                              e: 편심거리
•  　 　　σ_y: 스티프너 소재항복강도
•  　 　　h^′: 보 하부플랜지부터 응력집중 지점까지 거리
•  　 　　α: 축력이 접합부와 이루는 각도
•  　 　　_bM_y: 보 항복모멘트

Table 5.

Difference in yield moment

Fig. 14.

Ratio of difference between FEA and predicted values

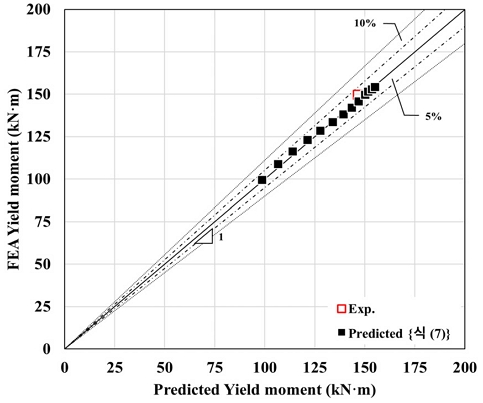
보정계수를 적용한 항복모멘트 예측값을 해석값과 비교하여 오차율을 산정하였다. 예측값은 식 (5)에 제시된 두께 변수 및 유효단면적의 영향인자를 대입해 도출한 보강장치 항복내력(T_y,Pred.)과 식 (7)을 통해 간극거리를 고려하여 산정한 보강장치 항복모멘트(M_y,Pred.)를 기반으로 하였다. 식 (8)에 따라 보강장치 항복모멘트 예측값을 보 항복모멘트 대비 비율로 계산한 항복내력비(λ)는 0.62부터 0.98의 범위를 보였다. Table 6에 요약된 결과를 바탕으로 보강장치 항복모멘트의 예측값과 해석값의 비율을 Fig. 15에 나타낸 결과, 기울기가 1에 수렴하여 두 값의 높은 일치성을 확인할 수 있었다. 또한, 스티프너 두께가 15 mm인 해석모델 E15를 기존 실험결과와 비교하였을 때 유사한 경향이 관찰되었으며, 해당 결과는 그래프상에서 5 % 이내의 오차율 구간에 포함되어 적절한 타당성을 입증하였다.

Table 6.

Calculation of yield moment following correction

Fig. 15.

Error ratio of yield moment between predicted and analysis values

5. 보강장치 설계범위 산정

철골 모멘트 저항골조에서 접합부는 구조적으로 응력이 집중되는 주요 영역으로, 기존 구조물의 내진보강을 위해 접합부 보강을 실시하는 경우 내력의 향상과 더불어 기존 부재의 손상을 방지할 수 있도록 설계되어야 한다. 앞서 6 mm에서 18 mm 두께의 스티프너 두 개로 구성된 해석모델을 대상으로 변수해석을 수행하였다. 그 결과, 해석모델의 항복내력비가 0.62에서 0.98 범위에 해당함을 확인하였으며, 이를 바탕으로 항복내력비에 따른 내력상승효과와 손상도를 평가하였다.

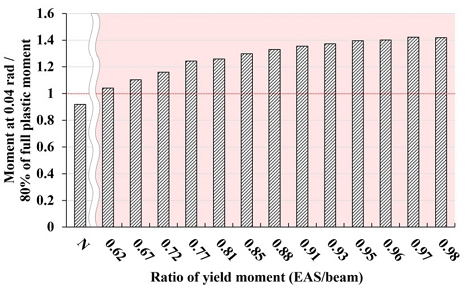
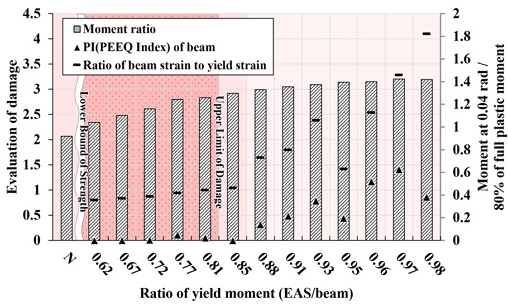
내력상승효과를 비교하기 위해 Fig. 16과 같이 설계기준에 따라 보수적인 측면에서 층간변형각 0.04 rad에서 보 전소성모멘트의 80 % 대비 성능을 분석하였다. 비보강 해석모델 N의 경우, 성능이 0.92배로 나타나 기준에 미치지 못하였다. 반면, 접합부 보강을 적용한 해석모델 중 항복내력비가 0.62인 모델 E6의 경우, 기준 대비 성능이 1.04배로 소폭 향상되었으며, 항복내력비가 더 높은 해석모델에서는 성능이 더욱 증가하여 특수모멘트골조 접합부의 요구성능을 충족함과 동시에 충분한 내력 상승효과를 보였다. 따라서 내력 측면에서의 적정 설계범위는 항복내력비 약 0.6 이상으로 판단된다.

Fig. 16.

Design range of strength

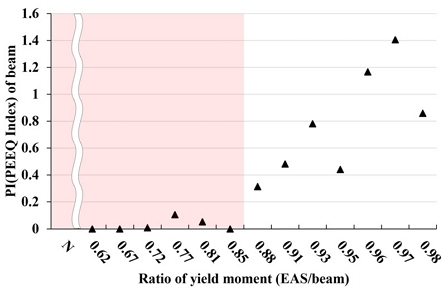
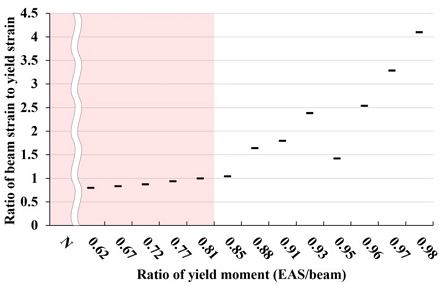
PEEQ Index와 부재별 변형률 비교를 통해 접합부 손상도를 평가한 결과, Fig. 17에서와 같이 항복내력비 0.85 이하에서 PI 지수가 0에 근접한 값을 나타냈다. 보 부재의 재사용을 고려할 때 보의 손상을 최소화시키는 것이 요구되며 이에 따라 PI 지수가 극히 작은 값을 나타나는 항복내력비 0.85 이하를 적정 PI 지수를 만족시키는 설계범위로 선정하였다. 또한 Fig. 18과 같이 0.02 rad에서 항복변형률 대비 응력집중이 예상되는 보 부재의 변형률 비율이 1 이상인 경우 부재가 항복하여 손상이 진행될 것으로 판단된다. 이에 따라 변형률 측면에서 약 0.81 이하의 항복내력비를 가지는 경우 손상을 저감시킬 수 있는 것으로 나타났다.

Fig. 17.

Design range of PI (PEEQ Index)

Fig. 18.

Design range of strain

해석모델의 내력상승효과 및 보 부재 손상도 분석결과를 Fig. 19에서 종합하면 항복내력비의 하한치는 내력을 고려한 0.62이며 상한치는 손상도를 고려한 0.81로 도출되었다. 즉 손상도 요구성능을 모두 만족시키기 위해서는 항복내력비가 약 0.6에서 약 0.8 사이의 범위가 타당할 것이다.

Fig. 19.

Optimal design range

엔드플레이트형 접합부는 반강접으로 분류되며, 손상 발생 시 보강장치뿐만 아니라 보-기둥 접합부가 함께 손상을 분담하는 특성을 보였다. 해석결과를 종합하였을 때 적정 항복내력비에 대한 설계범위는 약 0.6에서 약 0.8로 산출되었으며, 이는 기존의 Oh and Park(2017)^[8]의 연구에서 제시된 0.6에서 0.8의 범위와 유사하다. 이를 바탕으로 보강장치 항복모멘트에 대해 보강장치에 작용하는 축력으로 치환하면 식 (9)와 같이 나타낼 수 있다, 또한 보강장치 항복모멘트는 보 항복모멘트의 0.6에서 0.8배에 해당하므로. 보강장치 작용 축력의 적정 설계범위는 식 (10)과 같이 도출할 수 있다.

• 여기서, T_y: 보강장치 항복 시 작용 축력
•  　 　　d: 간극거리
•  　 　　_EM_y: 보강장치 항복모멘트
•  　 　　_bM_y: 보 항복모멘트

6. 결 론

본 연구에서는 엔드플레이트형 기존 강구조 접합부의 내진성능 향상 및 주요부재의 손상을 방지하기 위해 접합부 보강장치를 적용하고, 해당 장치의 적정내력을 산정을 위한 유한요소해석을 수행하였다. 연구결과는 다음과 같은 결론을 도출하였다.

• (1) 엔드플레이트형 보강 접합부에서 에너지 흡수장치의 강도설계식 도출을 위한 유한요소해석 결과 중립축은 보 춤의 약 0.88배 지점에 위치하였으며, 접합부 거동을 기반으로 한 약산식을 제시하였다. 보강장치 내력에 따른 해석 결과 예측값과 해석값 사이에 약 3배의 일정한 차이가 발생하였으며, 보정계수를 적용하여 약산식을 수정하였다. 보정계수를 반영한 예측값은 해석값 및 실험결과와 높은 일치도를 보이며 설계식의 타당성을 입증하였다.
• (2) 보강안의 적정 설계범위를 선정하기 위해 항복내력비에 따른 내력상승효과 및 보 부재 손상도를 분석한 결과, 항복내력비 0.62 이상의 해석모델은 설계기준을 만족하는 충분한 내력을 발휘하였다. 항복내력비 0.85 이하의 해석모델에서는 층간변형각 0.02 rad까지 PI (PEEQ Index) 지수가 0에 근접하였으며, 항복내력비 0.81 이하의 해석모델에서는 보 부재가 0.02 rad까지 탄성상태를 유지하는 것으로 나타났다. 이를 종합하였을 때 항복내력비의 적정 설계범위는 약 0.6에서 약 0.8로 판단된다.

Acknowledgments

이 연구는 2023년도 과학기술정보통신부 재원으로 한국연구재단 연구비 지원에 의한 결과임(RS-2023-00218875).

References

• Uang, C.-M., Bondad, D., and Lee, C.-H. (1998) Cyclic Performance of Haunch Repaired Steel Moment Connections: Experimental Testing and Analytical Modeling, Engineering Structures, Elsevier, Vol.20, No.4-6, pp.552-561. [https://doi.org/10.1016/S0141-0296(97)00093-X]
• Uang, C.-M., Yu, Q.-S. K., Noel, S., and Gross, J. (2000) Cyclic Testing of Steel Moment Connections Rehabilitated with RBS or Welded Haunch, Journal of Structural Engineering, American Society of Civil Engineers, Vol.126, No.1, pp.57-68. [https://doi.org/10.1061/(ASCE)0733-9445(2000)126:1(57)]
• Iwankiw, N.R., and Carter, C.J. (1996) The Dogbone: A New Idea to Chew on, Modern Steel Construction, American Institute of Steel Construction, Vol.36, No.1, pp.18-23.
• Lee, C.-H., Jung, J.-H., Oh, M.-H., and Koo, E.-S. (2003) Cyclic Seismic Testing of Steel Moment Connections Reinforced with Welded Straight Haunch, Engineering Structures, Elsevier, Vol.25, No.14, pp.1743-1753. [https://doi.org/10.1016/S0141-0296(03)00176-7]
• Tanaka, N. (2003) Evaluation of Maximum Strength and Optimum Haunch Length of Steel Beam-end with Horizontal Haunch, Engineering Structures, Elsevier, Vol.25, No.2, pp.229-239. [https://doi.org/10.1016/S0141-0296(02)00146-3]
• Oh, S.H., Kim, Y.J., and Moon, T.S. (2005) Deformation Capacity of Existing Moment Connections retrofitted with Horizontal Stiffeners, Proceedings of the Earthquake Engineering Society of Korea Conference, EESK, pp.220-227 (in Korean).
• Park, S.M., and Oh, S.H. (2024) Seismic Performance Evaluation of End-plate Type Non-welded Reinforced Joints for Major Member Damage Prevention, Journal of Korean Society of Steel Construction, KSSC, Vol.36, No.6, pp.345-355 (in Korean). [https://doi.org/10.7781/kjoss.2024.36.6.345]
• Oh, S.-H., and Park, H.-Y. (2017) Evaluation of Strength and Stiffness of the Damper Installed at Beam End for Damage-controlled Structures, Journal of the Architectural Institute of Korea Structure & Construction, AIK, Vol.33, No.2, pp.27–36 (in Korean). [https://doi.org/10.5659/JAIK_SC.2017.33.2.27]
• Seol, Y.H. (2024) Evaluation of Seismic Performance of Steel Structural Connections with Stiffner-type Energy Absorbtion Devices for Beam-ends, Master’s Thesis, Pusan National University (in Korean).