수평연결부재에 손상제어 전단패널을 적용한 멀티강관교각에 관한 연구

2.1 멀티강관교각의 거동 개요

멀티강관교각은 여러 개의 기성 강관을 이력형 댐퍼기능을 갖는 수평연결부재에 의해 하나의 기둥으로 만든 구조이며, 지진 발생 시에 주된 손상을 수평연결부재인 전단연결패널부에 집중시켜 주부재 역할을 하는 강관의 손상을 제어하는 매커니즘을 가지고 있다.

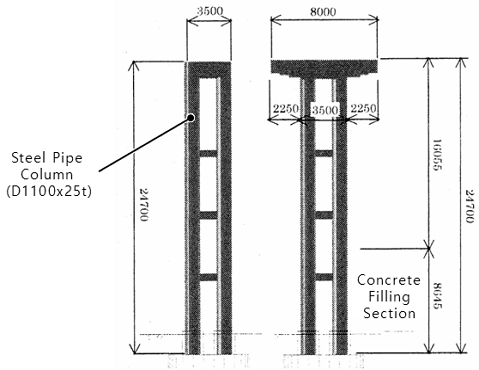
Kanaji et al.^[2]은 기존에 설치된 직사각형 단면의 RC 기둥을 Fig. 2와 같이 멀티강관기둥으로 환산하고, 그 특성을 실험적으로 분석하였다. 이 연구에서는 기존 기둥의 높이 24.7 m, 폭 3.5 m의 직사각형 단면을 직경 1100 mm, 두께 25 mm의 강관을 4개 배치하고, 높이 600 mm 수평연결부재의 전단연결패널을 3단으로 설치한 형상으로 제안하였다.

Fig. 2.

Proposed shape of multi steel pipe column[6]

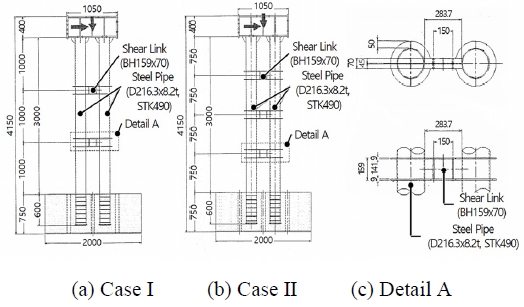
실험에 사용된 실험체는 Fig. 3와 같이 제안된 형상의 1/5 축소모형을 사용하였으며, 상부구조에 재료 항복하중의 약 10 %를 수직하중으로 재하한 상태에서 반복수평변위를 주었다. 실험체 높이는 실험환경 제약상 1/8.2로 하였고, 수평연결부재 전단패널의 경우 폭-두께 비를 소성좌굴이 발생하는 30 이상으로 제작하였다. 강관의 상부는 실험기와 힌지 구조가 되도록 강재 부재에 연결하였고, 강관 하부는 RC 기초에 매입하였다. 또한, 전단연결재의 단수를 2단(이하 CaseⅠ) 및 3단(이하 CaseⅡ)으로 구분하여 전단연결재 단수의 차이에 의한 영향을 검토하였다.

Fig. 3.

Reduction model applied to the experiment[6]

실험 전에 시험체의 내력은 Beam 요소를 이용한 골조계산에 의해 산정되었으며, 수평연결부재 전단패널의 복부가 전단 항복응력에 도달할 때의 수평하중에 대응하는 변위를 1δ_y로 설정하였다. 이 연구 결과에서는 Case Ⅰ의 실험체보다 Case Ⅱ의 내하력이 더 큰 것으로 나타났으며, 중단-하단-상단패널 순으로 전단좌굴이 발생하며 항복하는 것으로 나타났다.

2.2 실험자료 분석에 기초한 구조해석 타당성 검증

멀티강관교각의 국내 적용성 및 거동특성을 분석하기에 앞서 이 연구에서 적용하고자 하는 FE해석 모델방법의 타당성을 검증하고자 2.1절에서 기술한 Kanaji 연구의 실험 내용을 바탕으로 범용유한요소해석프로그램인 ABAQUS를 사용하여 구조해석을 수행하였다.

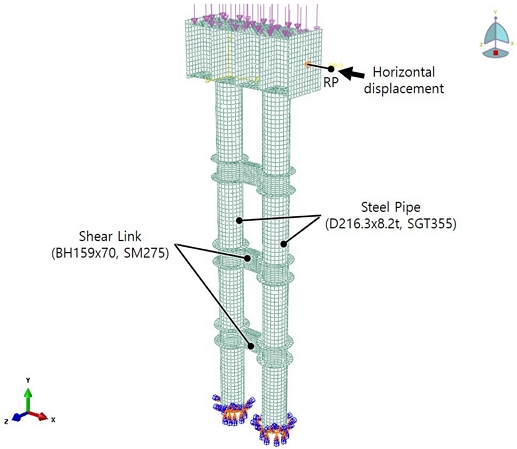
해석모델은 2.1절의 실험내용에 기초하여 전체구조물의 직경 및 두께를 고려하여 3차원 Shell 요소를 사용하였으며, FE해석에서의 강관과 전단연결패널 및 다이어프램 등의 단면 제원 및 강종은 Table 1에 나타낸 것과 같이 실험과 동일하게 설정하였다. Fig. 4에 FE해석 타당성 검증을 위해 이 연구에서 수행한 멀티강관교각에 대한 구조해석모델을 나타내었다.

Table 1.

Cross-sectional dimensions and steel type of the analysis model

Fig. 4.

FEA model of column specimenn in this study

강관과 전단패널은 실험에서 적용한 STK490 및 LYP225^[6]와 인장강도가 비슷하며 국내에서 생산이 가능한 강재인 SGT355 및 SM275를 사용하였다. 구조모델링에서는 전체 구조를 상부구조, 수평연결부재 전단패널 그리고 강관기둥의 3개 Part로 모델링 한 후, 1개의 Part로 Merge기능을 사용하여 연결하였다. 전단패널을 제외한 부재의 재료는 SGT355 강재를 적용하였으며, 전단패널의 스티프너 및 패널부는 저항복점 강재인 SM275를 적용하였다.

구조해석 모델의 상부는 Kanaji 연구에서의 실험장비 Actuator의 힌지거동을 묘사하기 위해 가상의 절점(Reference Point, RP)을 생성한 후, Kinematic-coupling을 사용하여 상부구조 측면 절점의 이동자유도 및 회전자유도를 모두 RP에 구속시키고, 수평변위를 작용시켰으며, 상부에는 항복하중의 약 10 %를 재하하였다. 실제 실험체는 하부를 콘크리트 푸팅에 매입하였으나, 해석모델에서는 하부 경계조건을 고정단으로 설정하였다. FE해석은 Pushover해석 및 Cyclic해석을 수행하였다.

Kanaji연구에서는 Case Ⅱ에 대한 실험 결과, 전단패널의 복부가 항복하는 하중인 약 60.5 kN에 대응하는 수평변위 9.5 mm를 1δ_y로 정의하여 17δ_y까지 반복 변위를 재현하였다. 그러나 이 연구의 Pushover해석 결과에서는 멀티강관기둥의 중단 전단연결패널부 항복이 수평변위 약 8.9 mm에서 발생하였다. 따라서 이때의 변위를 1δ로 정의하고, Kanaji 연구와 같이 양과 음의 수평변위를 각각 3회씩 반복하여 15δ까지 Cyclic 변위로 입력하였다.

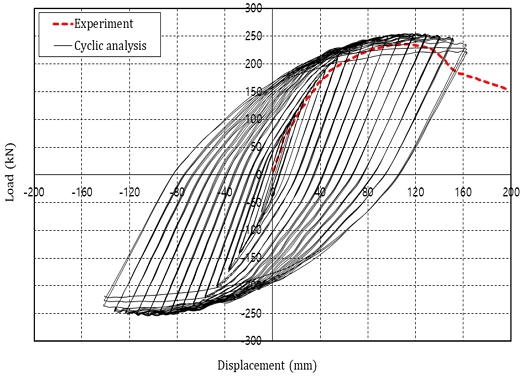
Fig. 5에 시험체 상부구조 도심 위치에 대해 Kanaji연구의 실험에서 얻어진 하중-변위이력곡선의 각 Peak-point를 이은 곡선(점선 표시) 및 이 연구의 FE해석결과로부터 얻어진 하중-변위곡선(실선 표시)을 나타내었다.

Fig. 5.

Load-displacement curve obtained from experiment and FEA at the center of the upper structure

이 연구의 Cyclic해석으로부터 얻어진 하중-변위곡선은 점선으로 나타낸 Kanaji연구의 실험곡선과 초기에는 유사한 거동을 나타냈으나, 전단패널의 항복하중을 넘어선 수평변위 8.9 mm 이후부터의 소성영역에서는 실험곡선과 차이가 발생하였다. 이는 해석에서는 강관교각 하부의 경계조건 6개의 자유도를 고정단 모델로 하였으나, 실험에서는 강관을 콘크리트에 매입시켜 이로 인한 강관의 경계조건 및 강성 차이에 의한 것으로 판단된다. 한편, Kanaji 실험에서의 최대하중 236.9 kN일때의 변위는 11δ=104.5 mm이며, 이 연구의 구조해석 결과의 하중은 239.2 kN으로 오차는 약 0.96 %로 나타났다. 이는 전체 내하력에 비해 매우 작은 값으로 판단되므로, 이 연구에서의 해석모델의 정합성을 확인할 수 있었다. 그러므로 이 연구에서는 멀티강관교각의 적용성 검토를 위해 이 연구에서 검증된 해석모델을 사용하기로 한다.

3.1 대상교각 선정 및 단면형상 제안

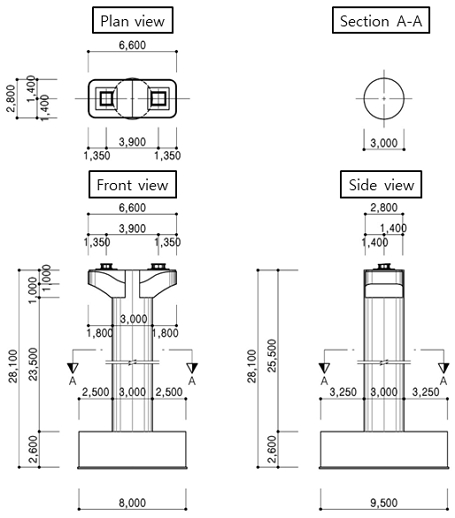
멀티강관교각의 국내 적용을 위해 ○○고속도로 건설공사의 교각 중 하나인 Fig. 6와 같은 대상교각을 선정하였다. 대상교각의 상부구조는 개량형 강합성거더, 하부구조는 높이 23.5 m, 폭 3 m의 직접기초형식의 콘크리트 교각이다.

Fig. 6.

Front view of domestic target column

대상교각을 멀티강관교각으로의 변환을 위해 상부자중인 1차 고정하중 및 포장, 방호벽 등의 2차 고정하중, 그리고 차량 주행으로 발생하는 활하중으로 구성된 상시하중 입력 시 부재의 항복 여부를 파악하기 위하여 범용구조해석프로그램인 MIDAS를 사용하여 골조해석을 수행하였다.

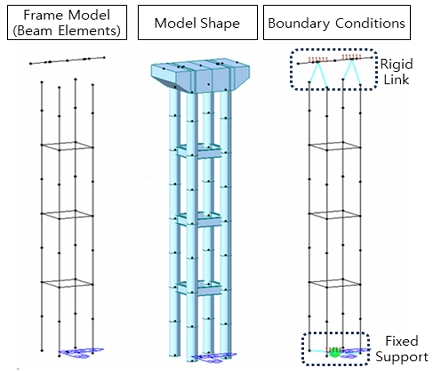
Fig. 7과 같이 대상교각의 폭과 높이를 고려하여 강관 4개를 대상교각의 둘레인 3 m 간격의 정사각형으로 배치하였으며, 각 강관 사이에 3단의 전단패널을 배치하였다. 강관과 전단패널에는 2.2절과 동일한 강재인 SGT355 및 SM275를 사용하였다. 코핑부는 절점 공유를 통해 연결하였으며, 하부 경계조건은 고정단으로 하였다.

Fig. 7.

Section conversion model

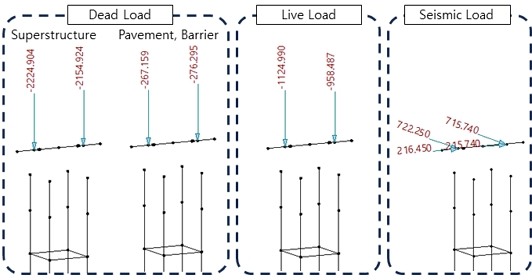
Fig. 8과 같이 교량받침 위치에 상시하중(고정하중, 활하중) 재하시, 강관 Φ914.4×t16 및 전단패널 H-700×300×14×14을 적용하면 전체 부재의 단면에서 항복이 발생하지 않는 것으로 나타났다. 이 부재규격을 바탕으로 단면 제원을 반복 수정하여 설계를 진행하는 것으로 하였다.

Fig. 8.

Design load of section conversion model

상세 응력검토 및 변위, 부재의 항복 여부 등을 보다 면밀하게 검토하기 위해 범용구조해석프로그램인 ABAQUS를 통한 구조해석을 재차 수행하였다. 해석모델은 3차원 Beam 요소인 B31 요소를 모든 부재에 사용하였고, 상부에는 Connector를 사용한 절점공유를 통해 기둥과 코핑부를 연결하였다. Fig. 8에 나타낸 지진하중을 포함하여 대상교각의 설계하중 입력시, Table 2와 같이 MIDAS에서의 해석결과와 거의 동일하게 나타나는 것을 확인하였다. 그러나, 전단패널의 양 끝 절점에서 부재가 항복을 일으키는 것으로 나타났기 때문에 뒤에서 기술하는 전단패널 및 다이어프램의 삽입 등의 고려가 필요한 것으로 판단하였다.

Table 2.

Reaction forces shell model and beam model

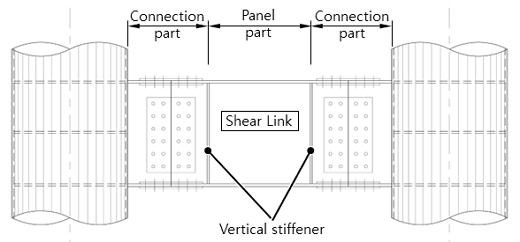
실제 단면형상을 보다 상세하게 제시하는 것과 각 부재의 단면력 및 응력검토의 용이성을 위해서는 Beam요소는 적절하지 않다고 판단하여 Shell요소(S4R: 4절점 감차적분 일반 판요소)를 사용하여 제안된 단면제원으로 모델링을 수정하였다. 교각 코핑부의 콘크리트를 모델링하기 위해 상부에는 Solid요소를 사용하였으며, 전단패널이 위치한 강관의 내부에 Ring 형태의 다이어프램을 삽입하여 강관 연결부의 강성 증대를 도모하였다. 또한 Fig. 9과 같이 전단패널의 손상 및 항복을 연결부로부터 먼 쪽인 중앙으로 유도하기 위해 수직보강재를 삽입하고 연결부(수직보강재 외측)와 패널부(수직보강재 내측)로 분류하였다.

Fig. 9.

Shear link with vertical stiffener inserted

Table 2에 Shell요소 모델 및 Beam요소 모델 해석결과로부터 얻어진 강관교각 하단부에서의 반력 및 코핑부에 발생한 수평변위를 나타내었다. 연직반력 및 모멘트반력은 코핑부의 형상과 강관의 길이가 증가함에 따라 증가하였다.

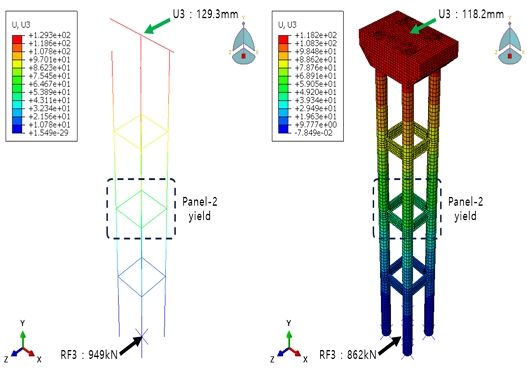
지진하중에 의한 수평반력이 크게 작용하는 3축방향을 기준으로 중단 전단패널인 Panel-2 접합부 항복시의 강관하부의 수평반력 및 수평변위는 Fig. 10과 같이 Beam 모델에서는 949 kN, Shell 모델에서는 862 kN으로 나타났다. 이때 각각의 콘크리트 코핑부에서의 3축방향 수평변위(U3)는 129.3 mm 및 118.2 mm로 나타났다.

Fig. 10.

Z-axis horizontal reaction and displacement when panel-2 stress exceeds yield stress

수직보강재 유무 및 다이어프램 연결부 수정으로 인해 수평하중 재하방향의 변위인 U3는 약 9 mm 정도 차이가 있었다. 이는 강관과 전단패널 접합부 모델시 Beam모델에서는 절점간 무한강성연결로 모델링하였으나, Shell모델에서는 강관내부에 다이아프램를 설치하여, 이에 따른 강성차이로 인한 차이로 판단된다. 이를 고려하면 두 해석모델의 반력 및 코핑부의 변위가 유사하게 나타난다고 판단되며, Shell요소를 사용한 모델의 합리성은 확보한 것으로 볼 수 있다.

3.2 강관의 강성이 부재의 항복 변위에 미치는 영향

Shinohara의 실험(2014)^[1]에 따르면 수평연결부재의 연결부와 패널부를 용접 또는 고장력볼트의 지압접합보다 마찰접합의 내하력이 더 큰 것으로 나타났다. 그러므로 후자의 방법을 사용하여 수평연결부재의 연결부(Connect) 및 패널부(Panel)를 접합하는 것을 고려하였다. 기둥 내부에 배치되는 링플레이트의 내부 다이어프램과 연결부의 플랜지, 패널부의 플랜지의 두께를 동일하게 설정하였다. Table 3에 사용부재의 단면제원 및 강종을 나타내었다. 사용강재는 Table 3에 나타낸 것과 같이 부재의 역할을 고려하여 정하였으며, 특히 패널부는 국내 건축용 저항복점 강재인 SN400을 사용함으로써 패널부 복부로의 손상유도를 고려하였다.

Table 3.

Temporary section specification

강관의 두께와 사용강재가 패널부의 항복유도에 미치는 영향을 조사하기 위해 전단패널의 형상을 Table 3의 단면제원에 대해 Pushover해석을 수행하였다.

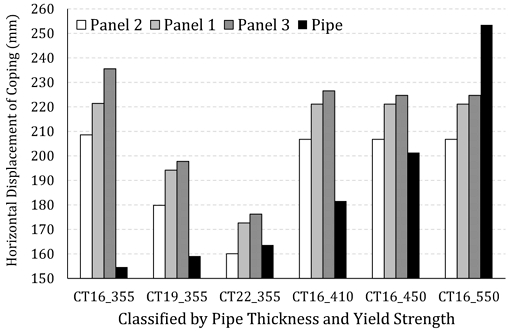
Fig. 11에 패널 및 강관이 항복하는 시점의 코핑부의 수평변위를 나타내었다. 강관두께와 사용강재에 따라 CT00_000와 같이 모델명을 구분하였다. CT 뒤의 숫자는 강관두께, 뒤의 3자리 숫자는 재질(SGT000)를 의미한다. 상단, 중단, 하단 패널 및 강관은 각각 Panel 1, Panel 2, Panel 3 및 Pipe로 표기 하였다.

Fig. 11.

Effect of pipe thickness and yield strength on the yield displacement of each member

Fig. 11에 나타낸 것과 같이 CT00_355의 경우, 강관의 두께가 증가할수록 패널의 항복변위가 감소하는 동시에 강관의 항복변위는 소폭 증가하는 양상이 나타났다. 한편, CT16의 경우 강관 두께가 동일한 상태에서 고강도강재를 사용할수록, 패널 항복시 코핑부 수평변위는 변화가 거의 없으며, 강관 항복시 코핑부 수평변위만 크게 증가하는 양상으로 나타났다. 이와 같이 강관을 고강도강재로 사용하는 경우, 강관기둥의 항복을 배제하면서 패널부 손상을 유도하려는 이 연구의 목적과 부합하는 것으로 나타났다.

이들로부터 강관두께 조정을 통한 단면강성 증대 방법은 각 패널과 강관의 항복 시 수평변위에 직접적인 영향을 미치는 것을 알 수 있었다. 그러나, 강관 내부 다이어프램의 용접시공성을 고려하면, 강관 두께는 작을수록, 사용강재는 SGT355를 사용하는 것이 적절하다고 판단하였다. 강관의 강종 변경을 통한 강도증대 방법보다 단면계수 변경을 통한 방법이 보다 효과적이므로, 다음 절에서 강관 직경 변화에 따른 거동 특성을 검토하였다. 따라서 사용강재는 SGT355로 적용하고, 강관 규격은 Fig. 11에서 검토한 단면 중 최대 단면2차모멘트(I)를 가지는 ∅914.4 t=22 (I=6.14×10⁹ mm⁴)보다 단면제원이 큰 ∅1016, t=18 (I=7.03×10⁹ mm⁴)로 정하였다.

3.3 패널 및 연결부의 단면 수정

강관의 단면을 ∅1016, t=18 (I=7.16×10⁹ mm⁴)로 사용하는 경우, 앞 절에서 사용된 Table 3의 단면제원은 전단패널 강성이 강관에 비해 매우 커서 패널부로 소성손상을 선행적으로 유도할 수 없다. 그러므로 패널부와 연결부의 단면 수정을 통해 이 연구의 목표인 설계하중 작용 시 강관 단부를 제외한 패널부 및 연결부로의 손상유도를 도모하였다.

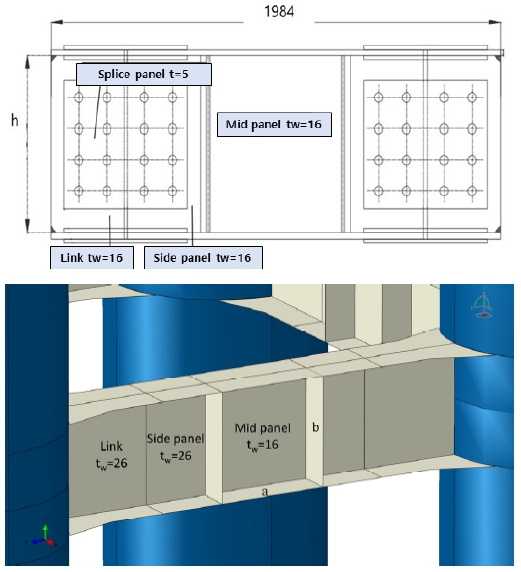
패널부와 연결부는 앞 절에서 기술한 것과 같이 Fig. 12의 연결판(Splice plate)을 덧대어 마찰접합시공을 한다는 가정 하에 단면산정을 실시하였다. 마찰접합방법을 이용하여 패널부와 연결부를 연결하는 경우, 패널부 및 연결부의 플랜지와 복부 두께는 동일하게 설정하는 것이 시공에 유리하므로 이들 두께는 동일한 것으로 가정하였다.

Fig. 12.

Example of Panel and Link part section

단면산정 과정의 변수를 줄이고자 ｢강구조 부재 설계기준(LRFD)｣^[7]을 참조하여 국부좌굴에 대해 비세장판 단면으로 가정하였다. 패널부 및 접합부의 플랜지는 자유돌출판, 복부는 양연지지판으로 하여 이들의 폭두께비 b/t가 한계 값 λ_r을 넘지 않는 범위에서 계산하였다. 계산과정에서 사용된 플랜지 폭은 국내 H형강 규격 중, 높이가 500 mm 이상의 규격을 참조하여 300 mm로 정하였다. 또한, ｢강구조 연결 설계기준(LRFD)｣^[8]에서는 토목구조물의 필릿용접의 최소치수를 6 mm로 규정하는데, 복부의 폭두께비 계산 시 사용되는 유효 간격(h_w)에 이것을 고려하여 계산하였다.

한편, Shinohara의 연구^[1]에 의하면 멀티강관교각의 전단패널은 형상비가 작을수록 면외 변형량이 작고, 전단좌굴의 발생가능성을 감소시키는 것으로 보고하고 있다. 그러나 패널의 형상비는 강관사이의 거리에 의해 직접적으로 제약을 받으므로 이 연구에서는 기존 선행연구의 형상비가 1.0을 넘지 않는 것을 참조하여 형상비를 1.0으로 정하였다.

기존 연구^[1]에 의하면 식 (1)을 사용하여 계산한 폭-두께비 R_tw에 대해서는 0.2 이상일 경우 전단좌굴에 의해 파괴가 되며, 0.4에 가까워질수록 전단연결패널의 복부 주위 필릿용접부의 저주기 피로에 수반되는 균열 진전에 의해 최종적으로 파괴되는 것으로 보고되었다. 또한, 전단연결패널의 대각선 길이가 1000 mm 이상인 대형 전단패널의 경우 R_tw가 0.2 이상이면, 면외변형이 먼저 발생하나, 큰 곡률을 가지고 있어서 균열을 발생시키는 변형까지 도달하지 못하는 것으로 보고되어 있다.

여기서 R_tw는 패널부의 폭-두께비, a와 b는 패널의 가로 및 세로 길이, α는 형상비(a/b), t_w는 패널 두께이며, k는 좌굴 파라메터로 식 (2)를 통해 산정된다.

Table 4에 한계 폭-두께비 검토를 통해 산정된 범위 내의 단면제원을 나타내었다. 전단패널의 대각선 길이는 모두 1000 mm 이하이므로 R_tw를 0.4에 가깝게 하는 것이 전단패널 복부 주위의 필릿용접부 저주기 피로파괴로 유도할 수 있는데, 제시된 단면제원은 모두 그 이하로 나타났다.

Table 4.

Section property of panel and link part used in analysis

4.1 변수해석에 사용된 해석모델 개요

멀티강관기둥 손상제어 전단패널 거동에 가장 크게 영향을 미치는 것은 전단패널 형상이므로 Table 4에 나타낸 전단패널의 패널부(Panel) 및 연결부(Connect) 단면제원을 변수로 하고, 사용강재 SN400을 적용하여 구조해석을 기반으로 멀티강관기둥 거동을 검토하였다.

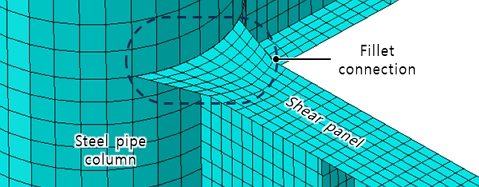
해석모델은 요소망 생성과정의 효율성을 위해 강관, 전단패널 그리고 코핑으로 재모델링하였으며, Fig. 13에 해석모델의 전체형상을 나타내었다. 코핑-강관의 구속조건, 하중조건, 경계조건은 3.1절의 Shell 요소 모델 해석결과의 타당성 검토과정과 동일하게 적용하였다. 추가적으로 전단패널 연결부-강관의 이음은 용접시공을 한다는 가정하에 Tie- constraint 조건을 부여하여 절점 자유도를 공유시켰으며, 연결부에서의 응력집중으로 인한 손상이 발생하지 않도록 Fig. 14과 같이 필릿형상으로 모델링하였다.

Fig. 13.

Example of entire multi-steel pipe pier analysis model

Fig. 14.

Fillet connection between steel pipe and shear connection panel

강관 단면은 3.3절에서 정한 ∅1016, t=18, SGT355로 모델링 하였고, 전단패널의 연결부가 위치하는 강관 내부에는 연결부의 전단력 저항성을 높이기 위해 두께 28 mm 강판으로 링플레이트의 내부다이어프램을 설치하였다.

사용요소는 General purpose conventional shell요소(S4R: 4절점 감차적분 판 요소)를 사용하였으며, 강관을 제외한 전단패널은 모두 중립면으로 모델링하였다. 이 해석에서는 부재의 항복여부를 판단하는 것에 중점을 두었으며, 계산시간의 효율을 위해 S4R요소를 사용하였다. 부재에 발생하는 응력 및 변형률은 두께방향 기준 최외측 단면점에서 가장 크게 나타나므로 응력결과는 모두 두께방향 최외측 단면점에서 계산하였다.

4.2 전단패널의 단면 형상별 구조해석 결과

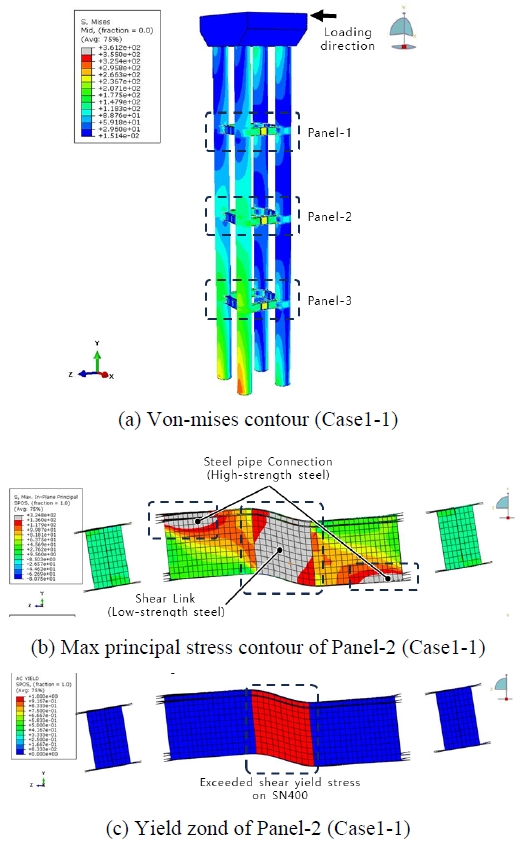
해석결과 일례로 Table 4의 Case1-1에 대한 Von-mises 응력의 Stress contour를 Fig. 15에 나타내었다.

Fig. 15.

Contour example of analysis result

Fig. 15(a) 및 Fig. 15(b)에 나타낸 것과 같이 모든 Case에서 최대 Von-mises 응력은 다른 부재에 비해 상대적으로 고강도강재를 사용한 전단패널 연결부에서 발생하였다. 그러나, 강관과의 연결부는 Fig. 14과 같이 응력저감용의 필릿형상에 의해 응력은 부재의 항복강도를 초과하지 않는 것으로 나타났다.

수평연결부재의 전체적인 거동은 지진하중 방향과 수직인 방향으로 전단패널에 전단변형이 발생하였으며, 이때 발생하는 면내 주응력이 전단 항복응력을 초과하는 경우, Fig. 15(c)와 같이 부재에 항복이 발생하는 것으로 나타났다.

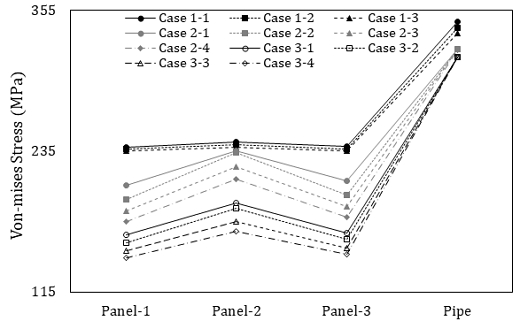
Table 5에 각 Case에서 수평연결부재 전단패널 및 강관에서 발생하는 최대 Von-mises응력을 나타내었으며, Fig. 16에 이를 나타내었다. 그림에서 Von-mises 응력은 패널 및 강관에 사용된 SN400강재 및 SGT355강재의 항복강도인 235 MPa, 355 MPa을 기준으로 나타내었다. 상단패널은 Panel-1, 중단패널은 Panel-2, 하단패널은 Panel-3, 강관은 Pipe로 표기하였다.

Table 5.

Von-mises stress ocurrred in panel and pipe

Fig. 16.

Von-mises stress Relationship between panel and pipe

전단패널의 가로 및 세로 길이가 500 mm × 500 mm인 Case 1 모델에서는 입력 지진하중의 방향과 평행한 전단연결패널의 모든 패널부가 모두 항복강도를 초과하였다. 고정단 경계조건을 적용한 강관 단부응력은 전단패널 강성이 가장 약한 모델인 Case1-1에서 약 346 MPa이며, Table 4의 Case1-2와 Case1-3과 같이 전단패널부 복부 두께가 1 mm씩 증가할수록, 약 5 MPa씩 감소하는 경향을 나타내었다. 또한, Case1-3의 Panel-1과 Panel-3, 그리고, Case2-1의 Panel-1 에서는 전체 단면 항복은 발생하지 않았다. 한편, Case3에서는 전단연결패널 패널부의 강성이 매우 커서 Panel-2에서 응력도 다른 Case에 비해 상대적으로 작게 나타났다.

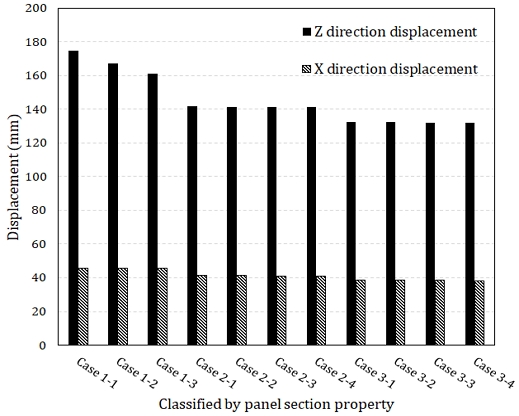
Fig. 17에 각 Case 별 설계하중 작용 시의 수평변위를 나타내었다. 수평변위는 x축과 z축으로 작용하는 지진하중에 의해 발생되며, 고정하중과 활하중의 연직하중에 의한 수평변위는 매우 미비하게 나타났다. 또한, z축 방향의 지진하중 이 x축 방향보다 약 3배 크게 작용하므로 부재의 항복이 없는 Case에서는 2가지 수평 변위 비율이 유사하게 나타났다. 모든 전단패널에서 항복이 발생되는 Case1 모델에서 x축과 z축으로의 수평변위가 가장 크게 나타났으며, 수평변위는 전단패널의 복부 두께가 증가함에 따라 선형적으로 감소하는 것으로 나타났다. 이는 전단패널부의 항복범위 영역에 따른 차이로 판단된다. 그러나, 전단패널이 일부만 항복하거나, 부재의 항복이 없는 모델인 Case2, Case3의 경우, 전단패널의 복부 두께가 증가함에 따라 수평변위 감소량이 매우 작거나 없는 것으로 나타났다.

Fig. 17.

Horizontal displacement of analysis result

고정하중, 활하중, 지진하중과 같은 설계하중 작용 시 전단패널이 항복하는 Case 중 강관의 발생응력이 가장 작은 Case1-3에 대해 고정하중과 활하중을 적재한 상태에서 Pushover 해석을 수행하였다. 2.2절의 Fig. 4와 같이 코핑부 옆면의 절점을 24.5 m 높이에 있는 가상의 절점(RP)에 회전변위를 제외한 이동변위 자유도를 구속시켜 추가 구속조건을 설정하여 실제 실험에서의 Actuator 힌지거동을 묘사하였다. RP점에는 수평변위가 가장 큰 Case1-1의 z축 방향 변위 175 mm를 넘어서는 300 mm까지 변위가 발행하도록 입력하여, 각 부재의 항복상태에 따른 수평변위, 반력을 검토하였다.

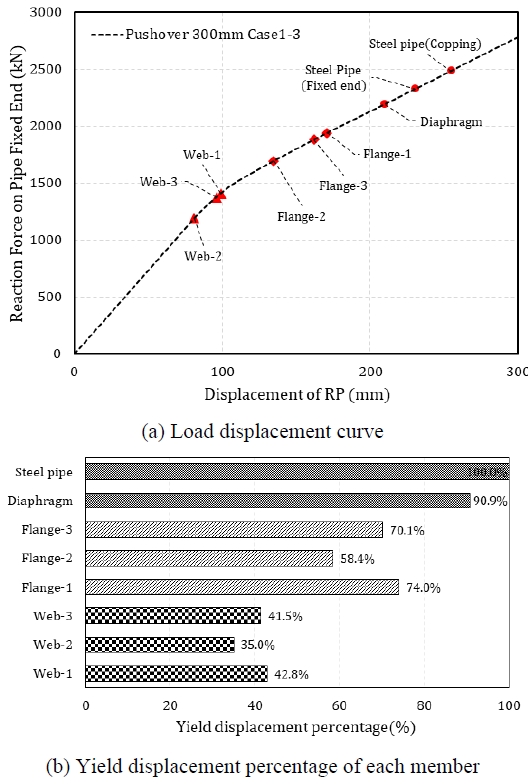
Fig. 18에 Pushover 해석 결과를 나타내었다. 항복해석 결과, Panel-2, Panel-3, Panel-1 순으로 전단패널 복부가 항복강도를 초과하였으며, 이때 RP점의 수평변위는 각각 81 mm, 96 mm, 99 mm로 나타났다. 그 이후 전단패널 플랜지가 항복하고 내부 다이어프램이 위치한 강관부, 강관단부, 그리고 강관상단 코핑부 순으로 항복하였다. 이는 전단패널의 플랜지도 강관 간의 전단연결 역할을 일부 부담하고 있으며, 강도와 단면제원이 강관보다 작아 먼저 항복한 것으로 판단된다.

Fig. 18.

Pushover analysis result

Fig. 18(a)의 Pushover해석 결과의 하중-변위곡선은 2개의 선형구간을 나타내는데, Web-2가 전체 단면항복 및 Web-3의 최초 항복시점에서 소성화 영역 증가와 함께 기울기 변화가 나타났다. Fig. 18(b)에는 고정단 경계조건을 부여한 강관단부가 항복할 때의 변위를 100 %으로 환산하여 각 부재가 항복하는 변위의 비율을 나타내었다. 전단패널부 복부 3개소가 모두 항복할 때의 비율은 42.8 %, 전단패널부 플랜지 3개소가 모두 항복할 때의 비율은 74.0 %로 강관이 항복하는 변위까지의 여유도가 각각 57.2 %, 26.0 %인 것을 알 수 있다.

Fig. 17의 Case1-3에 도시된 코핑부의 z축 방향 변위인 161 mm 위치에서 모든 전단패널 복부가 항복하고, 중단 전단패널의 플랜지만 항복한 상태이다. 그러므로 Case1-3의 전단패널 규격은 실제 설계지진력 재하조건에서 강관기둥의 항복없이 전단패널의 손상을 유도시키기에 적정한 것으로 확인되었다. 이로부터 설계지진력이 작용하는 경우에도 손상된 전단패널 교체만으로 실제 지진이후 교각기둥의 지속적인 사용이 가능하게 하여, 유지보수 측면에서 매우 유리할 것으로 판단된다.