내진설계변수와 설계요구조건에 따른 파이프랙 중심가새골조의 확률론적 내진성능
Copyright © 2024 by Korean Society of Steel Construction
초록
화학산업단지 내에 배관을 지지하기 위한 파이프랙은 지진과 같은 횡력에 충분한 저항능력을 확보해야한다. 국내 건설환경을 고려할 때, 배관길이방향 횡력저항시스템으로 역V형 철골가새골조를 일반적으로 적용한다. 국내 내진설계기준은 파이프랙을 건물과 유사한 건물외구조물로 분류하고, 건축물 OCBFs의 내진설계변수를 사용하며, 높이를 제한하지 않는다. 본 연구는 다양한 내진설계변수와 설계요구조건에 따라 설계된 파이프랙의 붕괴확률에 따른 내진성능을 파악하고 비교하기 위하여, 표본파이프랙을 선정하고, 다양한 내진설계변수에 따라 설계한 후 해석모델을 수립하였다. 비선형정적해석을 수행하여 파악한 표본 파이프랙의 밑면전단강도와 붕괴기구를 바탕으로 붕괴에 대한 지진취약도 분석을 수행하였다. 해석결과에 의하면, 국내 내진설계기준에서 허용하는 일반 강구조규정만을 만족하는 철골 파이프랙 가새골조는 목표 내진성능을 발휘하기 어려운 것으로 조사되었다.
Abstract
Piperacks are pipeline supporting structures in petrochemical complexes. Chevron-configured concentrically braced frames (CBFs) have been commonly used as the lateral-force-resisting systems for such piperacks in the longitudinal piping direction. The Korean Seismic Design Code (KSDC) classifies piperacks as non-building structures similar to buildings. KSDC prescribes that without specific height limitation, they should be designed to resist seismic loads calculated using seismic design parameters that are the same as those of CBFs employed in buildings. Based on their collapse probabilities, this study estimates the seismic performance of piperacks designed to various seismic design codes, parameters, requirements. To do this, archetype three- and six-tier piperacks were selected and designed using different design variables. Their analysis models were then constructed for nonlinear static analyses which were utilized to evaluate the base-shear strengths and the collapse mechanism. Finally, the seismic collapse fragility of the archetype piperacks were evaluated throughout the statistically manipulation of the nonlinear static analysis results. The seismic collapse fragility shows that CBFs in piperacks designed according to the Korean general steel structural provisions could not achieve the codified target seismic performance.
Keywords:
Piperack, Concentrically braced frames, Seismic design parameters, Design requirements, Seismic collapse performance키워드:
파이프랙, 중심가새골조, 내진설계변수, 내진설계요구조건, 지진붕괴성능1. 서 론
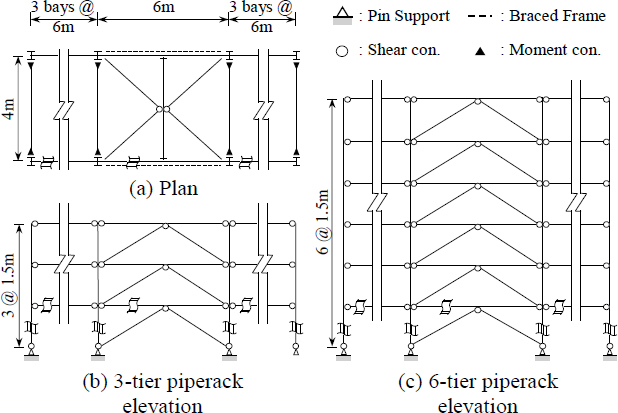
화학산업단지 내에 주로 설치되는 파이프랙(piperack)은 위험물을 운반하기 위한 배관을 지지하기 위한 구조물로, 지진에 의한 손상 또는 파단이 발생할 경우 사회·경제적 측면에서의 파급효과가 매우 큰 중요도가 높은 시설물이다. 이런 파이프랙의 중요성을 고려할 때 지진과 같은 횡력에 대해 충분한 구조적 안전성을 확보해야 한다. 일반적으로 파이프랙의 배관길이방향 횡력저항시스템으로 철골가새골조가 널리 사용된다. 역V형 가새 골조는 우수한 시공성과 개구부 확보의 용이성 등을 이유로 자주 채택되며[1] 일반적인 파이프랙의 형상은 Fig. 1과 같다. 접합상세와 설계지진력과 함께 기둥, 보 및 가새의 크기를 보면 국내에 건설되고 있는 일반적인 파이프랙 가새골조는 철골특수중심가새골조(steel special concentrically braced frames, SCBFs)보다는 철골보통중심가새골조(steel ordinary concentrically braced frames, OCBFs)로 분류된다.

General configuration of piperacks consisting of typical double angle bracing members, columns, and beams
파이프랙 내진설계 가이드라인[2]은 역량설계법[3]의 도입 시점인 1988년에 비해 늦은 1997년에 최초로 제시되었다. 이후 수 차례의 개정과 다양한 파이프랙 연구를 기반으로 현행 내진설계기준에 이르게 되었다. 국내 내진설계기준[4]에 의하면 파이프랙은 건물외구조물로 분류되며, Fig. 1과 같은 구조형상 및 구조형식을 가지는 건물외구조물은 건물과 유사한 건물외구조물로 세분된다. 건물외구조물로 분류되는 OCBFs의 내진설계변수(반응수정계수, R, 시스템초과강도계수, Ω0, 변위증폭계수, Cd)는 건축물의 지진력저항시스템과 같은 값이 할당된다. 현행 국내 기준에서는 명시되어 있지는 않으나 건축물 OCBFs의 내진설계변수를 사용할 경우, 동일한 내진설계요구조건을 적용하여 설계 및 시공되어야 하며 내진설계범주에 따라 높이를 제한하지 않는다. 논란의 여지가 있지만 다수의 파이프랙 설계경험이 있는 엔지니어는 파이프랙을 OCBFs가 아닌 일반 강구조규정만을 만족하는 건축물 철골중심가새골조(steel concentrically braced frames, CBFs)로 분류하고 이에 해당하는 내진설계변수를 적용하여 내진설계를 하기도 한다.
이와 반면 미국의 내진설계표준인 ASCE 7-22[5]는 국내 내진설계기준과 같이 파이프랙을 건물과 유사한 건물외구조물로 분류하며, 만일 건축물 OCBFs와 같은 내진설계변수로 파이프랙을 설계할 경우, 이에 해당하는 내진설계 요구조건(AISC 341[6])을 모두 만족하도록 명시하며 내진설계범주 D, E, F에 따라 높이를 제한한다. 만일 더 높은 파이프랙이 요구될 경우 더욱 엄격한 내진설계변수를 적용하여 해당 제한을 완화할 수 있다. 일반 강구조규정(AISC 360[7])만을 만족하는 CBFs의 경우, 별도의 내진설계변수를 적용하도록 규정하며 국내 기준보다 엄격한 내진설계변수를 적용한다. 이렇듯, 국내 파이프랙 내진설계기준은 미국에 비하여 덜 엄격하며 목표하는 내진성능의 명확한 확인없이 엔지니어가 골조 형식을 임의로 선택할 수 있는 여지도 있다. 국내 내진설계기준 및 해설[8]은 이를 국내 중약진 지진환경을 고려했기 때문으로 설명한다. 하지만, 자의적 선택에 의해 내진설계변수가 결정되고 이에 따라 부재 치수, 부재 및 접합 상세가 결정될 경우, 목표 수준의 내진성능이 발휘되지 않을 수 있다. 또한 파이프랙은 배관의 질량 분포, 슬래브에 의한 격막의 존재 유무, 마감재 및 외장재 미적용 등으로 인해 건축물과 현저히 다른 동적특성을 가질 수 있다. 그럼에도 불구하고, 국내 파이프랙 내진설계기준은 경험식에 의한 주기산정식을 배제하는 점을 제외하면 건축물과 같은 방식으로 내진설계를 할 수 있도록 허용하고 있다. 따라서 현행 국내 내진설계기준으로 설계된 파이프랙 CBFs가 목표 내진성능을 충분히 확보했는지 의구심이 생길 수 있다.
본 연구는 다양한 내진설계변수 및 요구조건에 따라 설계된 파이프랙의 내진성능을 파악하고 비교하기 위해 우선 표본파이프랙을 선정하고, 국내 내진설계기준과 미국 내진설계표준에서 제시하는 내진설계변수와 이에 따른 부재 및 접합 상세를 적용하여 표본파이프랙을 설계하였다. 검증된 다양한 선행연구에서 제시하는 방법을 따라 표본파이프랙을 모델링하였으며 비선형정적해석을 통해 강도 및 붕괴기구를 파악하였다. 최종적으로, 비선형정적해석 결과를 바탕으로 붕괴 손상도기준에 대한 지진취약도를 산정하고 누적붕괴확률을 활용하여 내진성능을 파악하였다. 최근 연구에 의하면 비선형정적해석보다는 비선형동적해석을 이용하여 지진취약도를 파악하는 것이 적절하다고 보고하고 있다. 하지만, 본 연구의 표본파이프랙은 구조적으로 정형이며, 강도저감영역도 포함하여 구한 성능점으로 지진취약도를 산정하여 비선형정적해석에 의한 지진취약도가 가지는 본질적인 문제점을 최소화·방지하고자 하였다.
2. 표본파이프랙 설계 및 해석모델 수립
2.1 표본파이프랙 선정과 내진설계
국내 내진설계기준[4]은 파이프랙을 건물과 유사한 건물외구조물로 분류하며 건축물의 지진력저항시스템 중 골조형식을 결정하여 시스템, 부재 및 접합 상세의 요구조건을 만족하도록 한다. 배관길이방향 파이프랙의 지진력저항시스템으로 OCBFs(R = 3.25, Ω0 = 2.0, Cd = 3.25)가 국내에 널리 사용되고 있다. 다만, OCBFs의 설계요구조건, 특히 역V형 가새골조의 불균형력에 대한 설계요구조건을 회피하기 위해 일반 강구조규정만을 만족하는 CBFs(R = 3.0, Ω0 = 3.0, Cd = 3.0)로 가정하여 내진설계하는 경우도 종종 있음은 주지의 사실이다.
앞서 언급한 바와 같이, 미국 내진설계표준[5]은 국내 내진설계기준[4]에 비해 파이프랙 OCBFs의 내진설계변수 및 설계요구조건을 보다 엄격하게 규정한다. 국내 기준과 같이 내진설계변수(R = 3.25, Ω0 = 2.0, Cd = 3.25)를 가지는 OCBFs를 파이프랙 구조물에 사용할 수 있지만, 내진설계범주 D, E에 해당할 경우 파이프랙의 높이를 약 19.8 m(65 ft)로 제한하며 내진설계범주 F에 속하는 경우 OCBFs를 사용할 수 없다. 만약, 파이프랙 OCBFs를 내진설계변수(R = 2.5, Ω0 = 2.0, Cd = 2.0)로 설계할 경우, 내진설계범주 D, E, F에 적용되는 높이 제한은 각각 약 48.5 m(160 ft), 48.5 m(160 ft)와 30.3 m (100 ft)로 완화된다. 이 두 종류의 OCBFs 모두 AISC 341[6]의 설계요구조건을 만족해야 한다. AISC 341은 가새의 좌굴로 인한 불균형력을 고려하여 역 V형 가새골조의 보를 설계하도록 하며, 이때 인장가새의 부재력은 증폭지진하중을 적용하여 산정하고 압축가새의 내력은 설계압축강도의 30 %로 결정한다. 접합부의 소요강도는 증폭지진하중을 통해 산정하나 가새의 최대 강도를 초과할 필요는 없으며, 이 밖에도 가새의 판폭두께비, 세장비 등을 요구조건으로 고려한다. 이와 반면, 내진설계변수(R = 1.5, Ω0 = 1.0, Cd = 1.5)와 일반 강구조규정에 해당하는 AISC 360[7]의 요구조건을 만족하는 CBFs는 내진설계범주와 관계없이 높이가 제한되지 않으며 불균형력을 고려하여 보를 설계하지 않는다. 또한, 증폭하지 않은 지진하중을 통해 접합부의 소요강도를 산정한다. 앞서 언급한 국내 내진설계기준 및 미국 내진설계표준의 파이프랙 내진설계변수, 설계요구조건 및 높이제한을 Table 1에 정리하였다.

Seismic design parameters, requirements, and height limitations for OCBFs designed according to KDS 41 17 00 : 2022 and ASCE 7-22
본 연구에서는 국내 국가화학산업단지 내에 위치하는 파이프랙을 실측조사하여 가장 많이 분포하는 3단(파이프랙 높이 = 4.5 m)과 6단(파이프랙 높이 = 9.0 m)을 표본 단수로 선정하였으며, 단별 높이 차이가 크지 않은 점을 반영하여 평균 높이인 1.5 m를 1단 높이로 결정하였다. 실측조사를 통해 결정한 표본파이프랙의 평면과 입면은 Fig. 2와 같으며, 선정된 표본파이프랙의 최대 높이는 9.0 m로, 미국 내진설계표준[5]에 따라 높이가 제한되지 않아 Table 1에 제시된 어떤 종류의 OCBF도 적용할 수 있다. 표본파이프랙에 대한 각 지진력저항시스템의 내진설계변수와 지반조건, 단주기와 1초주기의 설계가속도스펙트럼을 Table 2에 정리하였다.
내진설계변수와 설계요구조건에 따른 내진성능 및 지진취약도를 분석하기 위하여, 국내와 미국의 내진설계기준을 변수로 표본파이프랙의 CBFs를 4개의 지진력저항시스템으로 구분하였다.
- (1) N-KBC : 불균형력 요구조건이 도입되지 않은 과거의 건축물 기준(KBC 2005[9])으로 설계되어 비내진상세를 갖는 CBFs
- (2) G-KDS : 일반 강구조규정만을 만족하며 국내 기준을 따라 설계되어 일반상세를 갖는 CBFs
- (3) G-ASCE : 일반 강구조규정만을 만족하며 미국 기준을 따라 설계되어 일반상세를 갖는 CBFs
- (4) S-KDS : 불균형력 요구조건을 고려하여 국내 기준을 따라 설계되어 내진상세를 갖는 OCBFs.
표본파이프랙에 대한 지진력저항시스템의 명칭의 N, G, S는 적용 내진설계요구조건에 관한 것으로 각각 비내진(non-seismic), 일반규정(general), 내진규정(seismic)을 의미하며, “-”다음에 오는 KBC, KDS, ASCE는 적용기준의 명칭으로 각각 KBC 2005, KDS 41 17 00 : 2022, ASCE 7-22을 의미한다. “N-KBC”는 앞서 언급한 국내외 현행 기준에는 포함되지 않지만, 국내에 건설된 상당수의 파이프랙 설계에 사용된 내진설계기준으로 현재 파이프랙의 지진취약도를 평가한다는 측면에서 추가하였다.
파이프랙의 배관하중은 중력하중, 마찰하중, 정착하중(anchor) 하중으로 분류하는데, 일반적인 구조설계 관행에 따라 고정하중으로 취급하였다. 배관에 의한 중력하중은 12인치 직경의 배관에 물이 가득 찬 것으로 가정하여 구조물의 자중과 함께 지진에 의한 관성력을 발생시키는 지진중량으로 산정하였다. 마찰하중은 운송물질의 열영향으로 배관이 수축·팽창하며 유발되는 마찰력을 고려하며 중력하중의 10 %로 산정하였다. 파이프랙의 배관은 수직가새가 존재하는 경간에만 정착된다고 가정하였으며 4개 경간의 마찰하중과 40 kN 중 큰 값을 정착하중으로 산정하였다.
기존 시설물 내진성능 평가요령[10] 및 ASCE 41-13[11]는 외장재가 없는 건축물의 비선형정적해석 시 고유감쇠비를 2 %로 제한하고 있다. 파이프랙은 배관을 지지하기 위한 구조물로, 일반적으로 외장재가 없으며 주요 감쇠메커니즘은 배관과 파이프랙 구조부재와의 정착부와 구조부재 간의 접합부의 마찰에 의한 에너지소산이라 할 수 있다. 이런 건축물과 구분되는 특이성을 보수적으로 고려하기 위하여 파이프랙의 고유감쇠비를 1.5 %로 결정하였다. 지진 1구역과 지반등급 D에 대한 5 % 감쇠비의 설계스펙트럼을 파이프랙의 고유감쇠비로 조정하여 지진하중을 산정하였다. 또한, 파이프랙은 배관을 통해 운송하는 화학물질이 누출되면, 심각한 경제적, 인명 피해를 야기할 수 있다는 점을 고려하여 내진등급을 특등급으로 가정하였다.
산정한 중력하중 및 지진하중으로 부재 설계를 수행하였으며 설계한 부재 치수는 Table 3에 정리하였다. 가새는 파이프랙에서 널리 사용되는 쌍ㄱ형강으로 설계하였다. R값이 가장 작아 동일한 단수에서 설계밑면전단력이 가장 큰 G-ASCE의 가새 단면이 가장 크게 설계되었으며, 이와 반대로 가장 큰 R을 사용한 N-KBC에서 가새 단면이 가장 작았다. 기둥은 단수에 따라 달라지나 적용한 기준에 상관없이 일정한 크기로 설계하였다. 다만, S-KDS 표본구조물의 보 부재는 불균형력을 고려하여 보 부재를 설계하여 R값에 상관없이 같은 단수에서 단면성능이 가장 큰 부재가 사용되었다.
2.2 표본파이프랙의 해석모델
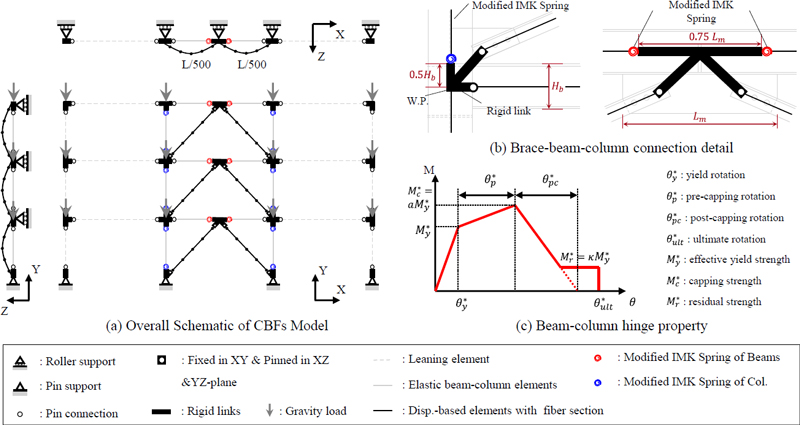
표본파이프랙의 붕괴확률과 이를 바탕으로 한 내진성능을 파악하기 위해 지진해석을 위한 해석 프로그램인 OpenSees[12]로 비선형 해석모델을 수립하였다. 해석모델은 Sen et al.[13]의 모델링 방법론을 참고하였으며 Fig. 3과 같다. 배관 길이방향의 CBFs는 2차원 골조로 모델링이 가능하나 국내 파이프랙에 가새부재로 널리 사용되는 쌍ㄱ형강의 면외방향 좌굴을 모사하기 위하여 3차원으로 모델링하였다. 가새 이외의 모든 절점은 면외방향으로 구속하였다. 재료모델은 Menegotto-Pinto 모델인 OpenSees[12]의 Steel02 모델을 적용하였다. 재료 특성은 SS275 강종의 탄성계수와 기대항복강도인 210 GPa, 358 MPa을 각각 적용하였으며 변형경화 기울기는 탄성계수의 2 %로 가정하였다.
기존 시설물 내진성능 평가요령[10]과 ASCE 41-13[11]은 기둥에 작용하는 압축력이 공칭압축강도의 50 %를 초과할 경우 기둥의 휨 거동을 힘지배거동으로 간주한다. 그러나, Elkady et al.[14]는 다수의 실험적인 연구를 통해 기둥의 소성변형 능력은 기둥의 축력비와 더불어 부재의 세장비, 단면특성에 크게 영향을 받는다고 보고하였으며, Bech et al.[15]는 ASCE 41-13의 비선형 파라메터가 과도하게 보수적이고 필요치 않은 보수 또는 보강을 야기할 수 있다고 보고하고 있다. Lignos et al. (2019)[16]는 기둥의 축력비, 부재의 세장비, 단면특성에 따른 영향을 반영하여 기둥 부재의 휨 이력모델을 제시하였다. 국내 건설환경을 고려할 때 대부분의 파이프랙은 역V형 가새골조로 시공되며, 보 부재는 압축가새의 좌굴 이전까지는 주로 축력을 받고 가새가 좌굴한 후에는 축력과 함께 불균형력으로 인한 휨을 동시에 받게 된다. 따라서, 보의 휨 성능이 인장가새의 축력과 전체 구조물의 연성도에 큰 영향을 줄 수 있다[17]. 따라서 표본파이프랙의 내진성능을 파악하기 위해 보 부재의 해석모델은 앞서 언급된 영향을 고려해야 하며, 이를 위해 Lignos et al.[16]의 방법론에 따라 수정된 IMK model을 적용하였다. 기둥의 축력비는 배관 중력하중으로 산정하였으며, 등가정적해석 시 보에 가해지는 축력을 통해 보의 축력비를 산정하였다. Fig. 3(c)는 수정된 IMK model의 보-기둥 이력모델의 예를 보여주며 축력이 가장 크게 도입되는 1단 기둥, 보의 모델링 파라메터를 정리하여 Table 4에 제시하였다.
가새는 섬유요소 단면으로 구성되며, 변위 기반 보-기둥 요소를 적용하였다. 가새는 4개의 개별 부재로 모델링하고 개별 부재별 곡률계산을 위한 가우스 적분점을 4개씩 할당하였다. 좌굴을 모사하기 위한 가새의 초기결함은 길이의 0.2 % 진폭을 갖는 조화함수 형상을 따라 면외방향으로 부가하였다. 가새의 양단의 경계조건은 거셋플레이트의 휨 저항 성능을 고려하여, 면내 방향으로는 강접합, 면외 방향으로는 핀접합으로 모델링하였다.
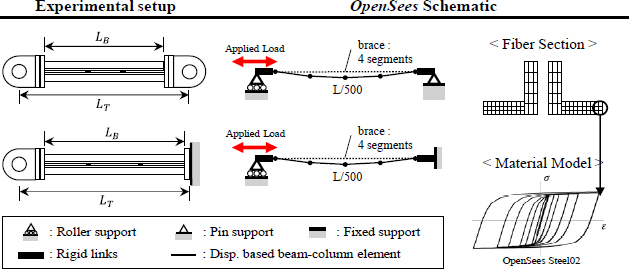
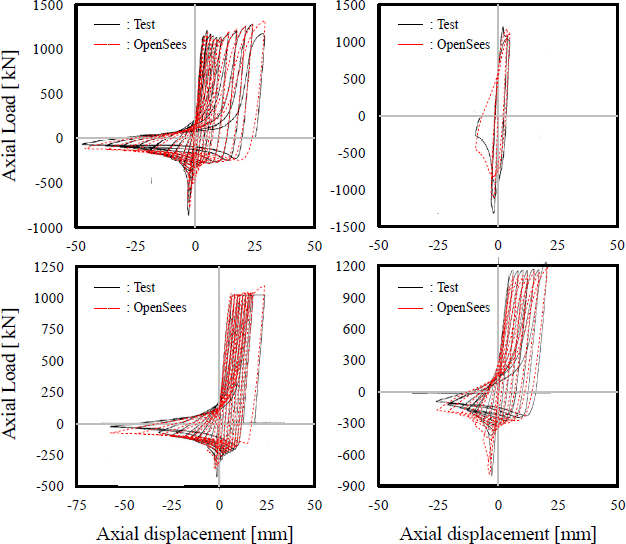
CBFs의 횡력저항성능은 가새의 이력거동에 크게 의존하며, 정밀한 내진성능을 파악하기 위해 실험 및 해석적 연구가 다수 수행되었다[18]-[22]. H형강과 HSS단면 가새의 실험 및 해석연구가 많으며 제한적이기는 하나 쌍ㄱ형강 가새의 실험적 연구[23]-[26]와 해석적 연구도 찾아볼 수 있다[27]. 기존 연구의 모델링 방식이 쌍ㄱ형강 가새에 유효한지 검토하고자 기존 실험 결과와 해석모델의 이력곡선을 비교하여 적용성을 검토하였다. Black et al.[23]은 쌍ㄱ형강을 포함한 다양한 단면 가새의 반복가력 실험을 수행하였으며, 그 중 쌍ㄱ형강 가새에 해당하는 Strut 8, 9, 10, 20 실험체와 비교를 수행하였다. 해당 실험체의 재료 및 부재 특성을 Table 5에 정리하였으며, 실험조건과 해석모델 구축방법은 Fig. 4에 제시하였다. Fig. 5의 실험과 해석 결과를 비교한 그래프를 통해 해석모델이 좌굴 후 급격한 강도저감, 사이클 진행에 따른 강도 및 강성열화 등 가새의 이력특징을 적절히 모사하는 것을 확인할 수 있다.
3. 표본파이프랙의 내진성능평가
3.1 비선형정적해석을 통한 표본파이프랙의 지진거동
표본파이프랙의 지진거동과 붕괴기구를 파악하기 위하여 비선형정적해석을 수행하였다. 횡하중패턴은 FEMA 356[28]에서 제시하는 바와 같이 질량 참여율이 75 % 이상인 1차 모드의 형상비율로 결정하였으며, 최상단 층간변위각이 2 %가 될 때까지 변위제어를 통해 하중을 가력하였다.
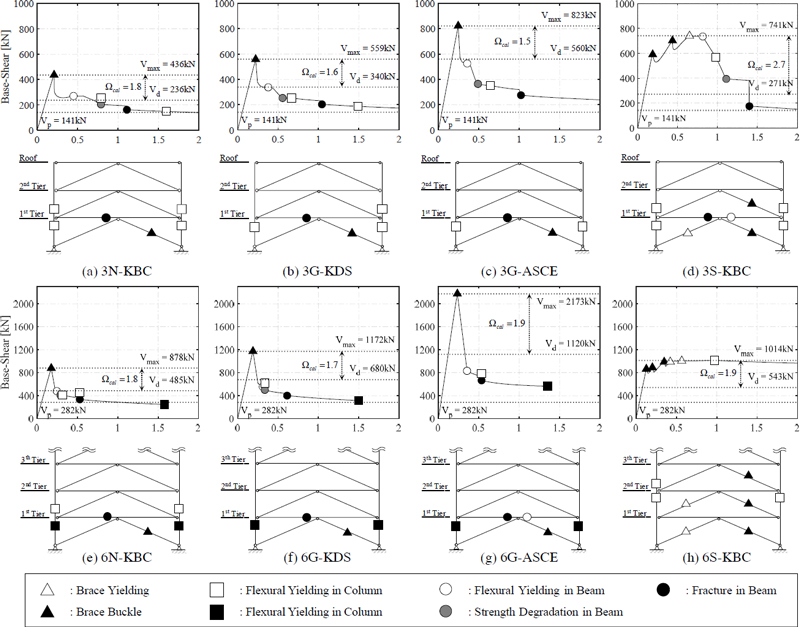
Fig. 6는 비선형정적해석을 통해 구한 각 표본파이프랙의 최상단 층간변위-밑면전단강도 관계곡선과 소성힌지분포를 보여준다. 그림에서 알파벳 앞의 수는 표본파이프랙의 단수를 의미한다. 내진상세를 갖지 않는 모든 파이프랙(N-KBC, G-KDS, G-ASCE)은 반응수정계수 등 내진설계변수에 차이가 있으며, 내진설계요구조건은 동일하다. 예상한 바와 같이, 각 표본파이프랙의 밑면전단강도는 R값이 감소함에 따라 증가하였다. 3N-KBC, 3G-KDS, 3G-ASCE의 3단 파이프랙 모델의 경우, 1단 압축가새의 좌굴 이후 급격한 강도 감소를 보이며 내력을 회복하지 못하는 취성적인 거동을 보였다. 이는 1단의 인장가새가 충분한 내력을 발휘하기 전에 압축가새의 좌굴에 의한 불균형력의 수직성분에 의한 요구휨모멘트가 증가하여 1단 상단 보에서 붕괴기구가 형성되었기 때문이다. 변형은 1단에 집중적으로 누적되며 1단 기둥 상부 혹은 2단 기둥 하부에 휨항복에 이은 휨파괴가 발생하였다. 이러한 거동은 6단 파이프랙(6N-KBC, 6G-KDS, 6G-ASCE)에서도 동일하게 나타났다. 6단 파이프랙의 최종 파괴모드는 1단 기둥의 휨파괴이며 이후 하중저항능력을 완전히 상실하여 해석이 종료되었다.
내진상세를 갖는 파이프랙(3S-KDS와 6S-KDS)은 비내진, 일반상세를 갖는 파이프랙(N-KBC, G-KDS, G-ASCE)과 달리, 가새의 불균형력을 고려하는 등 보다 엄격한 설계요구조건을 반영하여 설계된 구조물이다. 밑면전단강도는 1단 압축가새의 좌굴 이후 저감된 내력이 회복한 후 소성변형하는 제한적인 연성적인 거동을 보였다. 보다 엄격한 내진설계요구조건에 의해 1단 보는 인장가새가 항복하기까지 휨항복하지 않았으며 주요 변형은 1단에 집중되지 않고 상단으로 전파되는 경향을 보였다. 이는 가력종료 후 소성힌지의 분포를 통해 확인할 수 있다. 특히 6S-KDS는 3단 압축가새의 좌굴 이후 1단 인장가새가 항복하며 모든 주요 손상이 가새에 집중되었으며, 가력 종료 시점까지 보의 항복이 관찰되지 않았다. 이는 보의 불균형력에 대한 내진설계요구조건에 의해 OCBFs의 목표거동이 달성되었음을 의미한다. 다만, 3S-KDS는 6S-KDS 와 동일한 내진설계요구조건을 적용했음에도 불구하고 힘의 재분배 측면에서 일부 차이를 보였으며 상대적으로 변형능력이 떨어졌다. 3S-KDS는 2단 압축가새가 좌굴하고 1단 인장가새가 항복한 후, 최상단까지 소성변형이 전파되지 못하고 1단 상단보에 휨파괴가 발생했다. 이는 6S-KDS에 비하여 단수가 낮은 3S-KDS가 부정정차수를 충분히 확보하지 못하여 나타난 결과로 해석할 수 있다. 3S-KDS과 6S-KDS의 연성적 거동과 다른 표본파이프랙의 거동을 통해 내진설계요구조건이 파이프랙의 연성거동에 미치는 영향이 크다는 사실을 알 수 있다.
설계밑면전단력과 최대밑면전단강도의 비인 초과강도계수 Ω를 이용하여 표본파이프랙의 밑면전단강도를 비교하였다. 설계밑면전단력 Vd는 배관하중에 의한 횡력 Vp와 지진하중에 의한 횡력 Vs의 합으로 계산하고, 해석으로 구한 밑면전단강도 Vmax를 구하여 Table 6에 정리하였다. 또한 설계초과강도계수 Ω0, 해석으로 구한 초과강도계수 Ωcal, 이를 비교한 초과강도계수비 Ωcal/Ω0를 표에 같이 제시하고 있다. 모든 표본파이프랙의 Ωcal는 2 내외의 값을 보였으며, 보의 불균형력을 포함하는 엄격한 내진설계요구조건에 따라 설계된 3S-KDS가 가장 큰 초과강도를 보였다. 가장 작은 R값으로 설계한 G-ASCE 표본구조물의 Ωcal/Ω0이 약 1.5로 비교적 큰 값을 보였다. 반면, R = 3.0과 일반 강구조규정만을 만족하는 G-KDS 표본구조물은 약 0.5로 조사되었다. 다만, Ωcal/Ω0가 1.0보다 작은 표본구조물은 강도측면에서 지진에 대한 저항 여유분이 상대적으로 적지만 내진성능이 부족하다는 것은 아니다.
3.2 확률론적 지진취약도
표본파이프랙의 붕괴확률을 파악하기 위하여 앞선 비선형정적해석 결과를 활용해 붕괴에 대한 지진취약도 분석을 수행하였다. 지반운동강도의 중앙값은 설계스펙트럼을 사용하였으며 대수표준편차 βd는 Newmark et al.[29]의 중앙값과 중앙값+표준편차 관계식을 통해서 식 (1)과 같이 결정한다.
| (1) |
여기서, ξ0는 백분율로 표현된 고유감쇠비이다. 구조물 내진성능의 중앙값은 비선형정적해석 결과를 삼선형의 골격곡선으로 최대 강도와 잔류강도를 추정하도록 이상화하여 사용하였다. 지진취약도 분석에 사용한 각 표본파이프랙의 골격곡선을 Fig. 6에 굵은 점선으로 표시하였다. 건축물의 지진취약도곡선에서 사용하는 강도저감이 없는 골격곡선을 파이프랙 표본구조물의 지진취약도에 사용할 경우, 가새의 좌굴과 보의 불균형력에 의한 급격한 강도저감을 무시하여 지진에너지소산능력을 과대평가할 수 있다. 이러한 문제를 방지하기 위하여 본 연구에서는 성능점을 산정하는데 강도저감이 포함된 골격곡선을 사용하였다. 이러한 방법은 비선형거동하는 구조물의 성능점에서의 유효감쇠비 산정이 복잡해짐에 불구하고, 표본구조물의 붕괴에 대한 지진취약도를 보다 정확하게 평가할 수 있다. 역량스펙트럼의 대수표준편차 βc는 HAZUS[30]의 값을 적용하였으며 엄격한 내진설계요구조건을 적용한 S-KDS 표본구조물은 다양한 설계 및 해석과 실험결과가 제시되고 있는 점을 고려하여 0.25, 이외 표본파이프랙에는 0.30을 적용하였다.
지반운동강도는 총 60단계로 구분하였으며 증감의 크기는 파이프랙 붕괴확률의 경향을 적절히 예측하도록 시행착오법을 통해 결정하였다. 앞서 정의된 지반운동과 골격곡선으로부터 효과적인 분산 감소 기법으로 잘 알려진 라틴방격추출법을 통해 각각 10개의 표본을 추출하여 ATC-40[31] 방법론을 따라 단계별로 100개의 성능점을 산정하였다. ATC-40에서는 이력감쇠보정계수 χ를 통해 다양한 이력거동의 차이를 간접적으로 고려한다. 이력유형은 내진성능별로 type A, type B, type C로 구분하며, 유형별로 상이한 χ를 적용한다. 상대적으로 연성적인 거동을 보여주는 S-KDS 표본파이프랙은 full hysteretic 거동을 한다고 가정하여 type A로, 압축가새의 좌굴 이후 밑면전단력이 급격히 감소하는 취성적인 거동을 보이는 그 외 표본파이프랙은 type C로 가정하였다.
손상도기준은 건축물의 성능목표에 따라 다양하게 적용되는 것이 일반적이다. 그러나, 파이프랙은 배관을 지지하는 목적으로 사용되며 사람이 점유하지 않는 구조물로, 건축물의 성능목표(기능수행, 인명안전, 즉시복구)와 대응되는 손상도기준을 파이프랙에 적용할 수 없다. 더욱이 이에 대한 체계적인 연구가 현재까지 거의 없는 실정이다. 본 연구에서는 배관이 대규모 손상을 입을 수 있는 붕괴방지만을 손상도기준으로 고려하였으며, FEMA 356[23]에서 제시하는 가새골조의 붕괴방지 층간변위비인 2 %를 붕괴에 대한 손상도기준으로 적용하였다. 붕괴손상도기준의 불확실성을 나타내는 대수표준편차 βMds는 HAZUS[30]에서 제시하는 0.4를 적용하였다. 표본파이프랙의 높이가 낮고 횡하중패턴이 1차모드 형상비를 따르는 점을 고려하여, 기존 소방방재청[32]의 방법론과 같이 지붕층변위비를 붕괴손상도기준으로 적용하였다. 입력지반운동의 불확실성과 구조물의 불확실성의 중첩곱(convolution) Conv(βc, βd)과 붕괴손상도기준의 표준편차 βMds를 SRSS 조합하여 식 (2)와 같이 표본파이프랙의 총 불확실성 표준편차 βtot를 산정하였다.
| (2) |
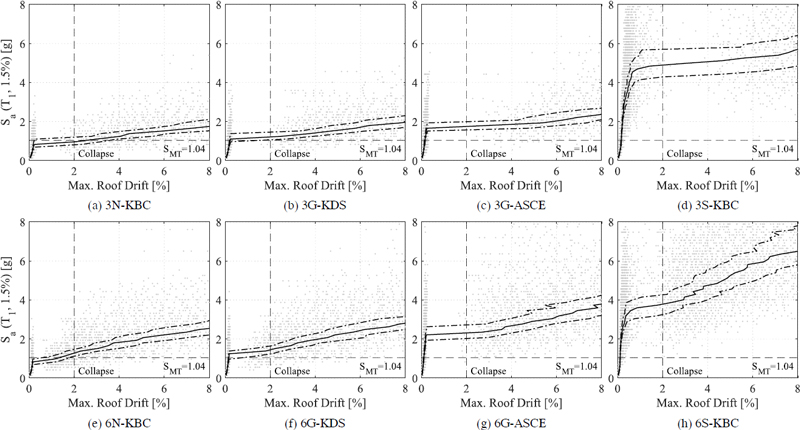
각 표본파이프랙의 βtot은 Table 7에 제시되어 있다. Fig. 7의 회색 원은 앞서 기술한 방법을 통해 구한 6,000개의 각 표본파이프랙의 성능점을 표시한 것이다. 그림에서 가로축은 성능점에서의 지붕층변위비를 뜻하며, 세로축은 표본파이프랙의 1차 주기 T1과 고유감쇠비 1.5 %에 대한 스펙트럴가속도를 의미한다. 또한 그림에서 검은 실선은 지반운동강도에 따른 지붕층변위비의 중앙값을 보여주며, 검은 일점쇄선은 중앙값±σ(표준편차)를 나타낸다. 모든 표본파이프랙은 지붕층변위비가 급격하게 증가하는 특정 지반운동강도가 존재하여, 이선형분포와 유사한 경향을 보인다. 아울러, 그림에서 S-KDS 표본파이프랙과 나머지 표본파이프랙의 성능점 분포를 비교하면, 적용한 R값에 상관없이 더 엄격한 내진설계요구조건을 따라 설계한 표본파이프랙의 밑면설계강도가 증가하고, 이에 따라 표준편차도 증가함을 알 수 있다.
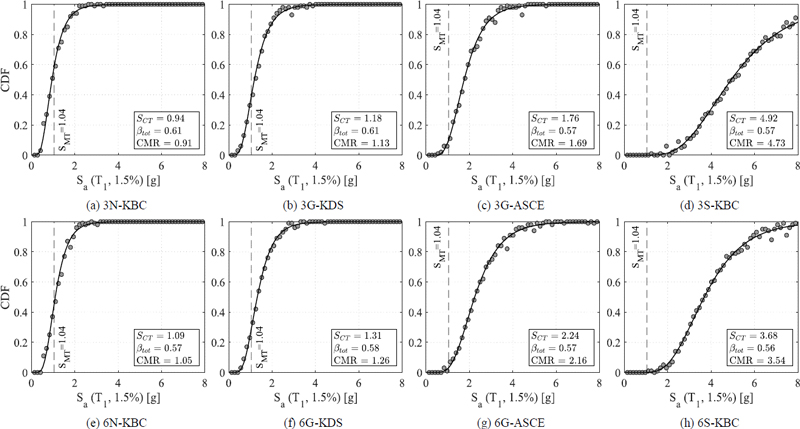
Fig. 8은 Fig. 7의 성능점 분포를 통하여 구한 누적붕괴확률분포를 보여준다. 붕괴확률분포는 성능점과 붕괴손상도기준을 비교하여 단계별 붕괴확률을 계산하고 60단계로 정의되는 붕괴확률함수에 최우도법을 적용하여 산정하였다. S-KDS를 제외하면 작은 R값을 사용할수록 붕괴확률분포의 중앙값 스펙트럴가속도 SCT가 증가하고, 특정 지붕층변위비 구간에서 누적붕괴확률이 급격하게 증가한다. S-KDS 표본파이프랙은 다른 표본파이프랙에 비하여 SCT값이 상대적으로 크게 평가되었다.
산정한 붕괴확률분포를 통해 구조물의 내진성능지표 중 하나인 붕괴여유비(collapse margin ratio, CMR)를 최대고려지진(maximum considered earthquake, MCE)의 스펙트럴가속도 SMT에 대한 SCT의 비로 계산하여 Table 7에 정리하였다. 각 표본파이프랙의 SMT는 Fig. 8에서 확인할 수 있다. N-KBC 표본파이프랙의 CMR은 1이하이며, MCE에 대한 붕괴확률 P(SMT)은 Table 7과 Fig. 8에서 보는 바와 같이 평균적으로 0.50보다 크게 평가되었다. 이는 과거 기준에 따라 설계된 비내진상세를 가지는 N-KBC 표본파이프랙은 MCE에 대해 충분한 붕괴방지성능을 확보하고 있지 못함을 보여준다. S-KDS 표본파이프랙의 CMR은 3보다 크며, P(SMT)는 0에 수렴함을 알 수 있다. 이는 해당 내진설계변수(R = 3.25, Ω0 = 2.0, Cd = 3.25)와 엄격한 내진설계요구조건을 통해 설계된 S-KDS 표본파이프랙이 다른 표본파이프랙에 비해 우수한 내진성능과 붕괴방지성능을 발휘함을 보여준다. 이와 반면, 일반 강구조규정만을 만족하는 표본파이프랙은 동등한 내진설계요구조건을 만족함에도 불구하고 적용한 R값에 따라 붕괴확률측면에서 큰 차이를 보인다. 특히, 미국 기준에서 허용하는 G-ASCE 표본파이프랙에 비해 국내에서 허용하는 G-KDS 표본파이프랙의 CMR은 3단의 경우 약 33 %, 6단의 경우 41 % 작으며, 누적붕괴확률 P(SMT)는 현저히 큼을 알 수 있다. 한정된 지면으로 인해 상세한 평가방법을 기술하지는 않지만, 내구연한(50년)동안 구조물의 누적붕괴확률에 관한 Luco et al.[33]의 연구결과를 적용하면, G-ASCE와 S-KDS 표본파이프랙은 목표 내진성능을 발휘하나, 내진설계변수(R = 3.0, Ω0 = 3.0, Cd = 3.0)로 설계된 G-KDS 표본파이프랙은 기준에서 제시하는 목표 내진성능을 발휘하지 못하였다.
4. 결 론
본 연구에서는 철골 파이프랙 가새골조의 붕괴취약도에 따른 내진성능을 파악하기 위하여 내진설계변수, 설계요구조건, 단수를 변수로 하여 표본파이프랙을 선정 및 내진설계하였다. 표본파이프랙의 해석모델을 수립하고 기존 실험과 해석결과를 비교하여 가새부재 해석모델이 적절함을 검토하였다. 해당 모델을 바탕으로 비선형정적해석을 수행하여 표본파이프랙의 밑면전단강도 및 붕괴기구를 파악하였으며, 최종적으로, 붕괴에 대한 지진취약도 분석을 통해 각 표본파이프랙의 확률론적 내진성능을 파악하였고 다음과 같은 결론을 얻었다.
- (1) 불균형력 요구조건을 고려하여 설계된 표본파이프랙은 가새의 좌굴 후 밑면전단력을 회복하는 비교적 연성적 거동을 보이며, 충분한 초과강도를 발휘한다.
- (2) 표본파이프랙의 지붕층변위비는 특정 지반운동강도에서 급격히 증가하는 이선형거동을 보이며, 더욱 엄격한 설계기준으로 설계될수록 우수한 붕괴취약도 곡선과 낮은 붕괴확률을 보인다.
- (3) 표본파이프랙은 설계변수 및 요구조건에 따라 상이한 내진성능을 보이며, 국내 내진설계기준의 일반 강구조규정만을 만족하는 철골가새골조는 목표 내진성능을 발휘하지 못할 수 있다.
Acknowledgments
이 연구는 2024년 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20017750).
References
-
Roeder, C.W., Sen, A.D., Terpstra, C., Ibarra, S.M., Liu, R., Lehman, D.E., and Berman, J.W. (2019) Effect of Beam Yielding on Chevron Braced Frames, Journal of Constructional Steel Research, Elsevier, Vol.159, pp.428-441.
[https://doi.org/10.1016/j.jcsr.2019.04.044]

- American Society of Civil Engineers (1997) Guidelines for Seismic Evaluation and Design of Petrochemical Facilities, ASCE, USA.
- International Conference of Building Officials (1988) Uniform Building Code, ICBO, USA.
- Ministry of Land, Infrastructure and Transport (2021). Seismic Building Design Code, MOLIT (in Korean).
- American Society of Civil Engineers (2022) Minimum Design Loads for Buildings and Other Structures, ASCE/SEI 7-22, ASCE, USA.
- American Institute of Steel Construction (2022) Seismic Provisions for Structural Steel Buildings, ANSI/AISC 341-10, AISC, USA.
- American Institute of Steel Construction (2022) Specification for Structural Steel Buildings, ANSI/AISC 360-10, AISC, USA.
- Architectural Institute of Korea (2019) Seismic Building Design Code and Commentary, Kimoondang (in Korean).
- Architectural Institute of Korea (2005). Korean Building Code, KBC 2005, Ministry of Construction & Transportation (in Korean).
- Ministry of Land, Infrastructure and Transport (2021) Guidelines for Seismic Evaluation of Existing Structures, 11-B552016-000035-14, Korea Authority of Land & Infrastructure Safety (in Korean).
- American Society of Civil Engineers (2014) Seismic Evaluation and Retrofit of Existing Buildings, ASCE/SEI 41-13, ASCE, USA.
-
McKenna, F., Scott, M.H., and Fenves, G.L. (2010) Nonlinear Finite-Element Analysis Software Architecture Using Object Composition, Journal of Computing in Civil Engineering, American Society of Civil Engineers, Vol.24, No.1, pp.95-107.
[https://doi.org/10.1061/(ASCE)CP.1943-5487.0000002]

-
Sen, A.D., Roeder, C.W., Lehman, D.E., and Berman, J.W. (2019) Nonlinear Modeling of Concentrically Braced Frames, Journal of Constructional Steel Research, Elsevier, Vol.157, pp.103-120.
[https://doi.org/10.1016/j.jcsr.2019.02.007]

-
Elkady, A., and Lignos, D.G. (2018) Full-Scale Testing of Deep Wide-Flange Steel Columns under Multiaxis Cyclic Loading: Loading Sequence, Boundary Effects, and Lateral Stability Bracing Force Demands, Journal of Structural Engineering, American Society of Civil Engineers, Vol.144, No.2, 04017189.
[https://doi.org/10.1061/(ASCE)ST.1943-541X.0001937]

-
Bech, D., Tremayne, B., and Houston, J. (2015) Proposed Changes to Steel Column Evaluation Criteria for Existing Buildings, Proceedings of the 2nd ATC & SEI Conference on Improving the Seismic Performance of Existing Buildings and Other Structures, American Society of Civil Engineers, USA, pp. 255-272.
[https://doi.org/10.1061/9780784479728.022]

-
Lignos, D.G., Hartloper, A.R., Elkady, A., Deierlein, G.G., and Hamburger, R. (2019) Proposed Updates to the ASCE 41 Nonlinear Modeling Parameters for Wide-Flange Steel Columns in Support of Performance-Based Seismic Engineering, Journal of Structural Engineering, American Society of Civil Engineers, Vol.145, No.9, 04019083.
[https://doi.org/10.1061/(ASCE)ST.1943-541X.0002353]

-
Choi, K.-S., Park, J.-Y., and Kim, H.-J. (2017) Numerical Investigation on Design Requirements for Steel Ordinary Braced Frames, Engineering Structures, Elsevier, Vol.137, pp.296-309.
[https://doi.org/10.1016/j.engstruct.2017.01.066]

- Uriz, P., and Mahin, S.A. (2004) Seismic Vulnerability Assessment of Concentrically Braced Steel Frames, Steel Structures, KSSC, Vol.4, No.4, pp.239-248.
-
Uriz, P., Filippou, F.C., and Mahin, S.A. (2008) Model for Cyclic Inelastic Buckling of Steel Braces, Journal of Structural Engineering, American Society of Civil Engineers, Vol.134, No.4, pp.619-628.
[https://doi.org/10.1061/(ASCE)0733-9445(2008)134:4(619)]

-
Hsiao, P.-C., Lehman, D.E., and Roeder, C.W. (2012) Improved Analytical Model for Special Concentrically Braced Frames, Journal of Constructional Steel Research, Elsevier, Vol.73, pp.80-94.
[https://doi.org/10.1016/j.jcsr.2012.01.010]

-
Hsiao, P.-C., Lehman, D.E., and Roeder, C.W. (2013) A Model to Simulate Special Concentrically Braced Frames Beyond Brace Fracture, Earthquake Engineering & Structural Dynamics, Wiley, Vol.42, No.2, pp.183-200.
[https://doi.org/10.1002/eqe.2202]

-
Tirca, L., and Chen, L. (2014) Numerical Simulation of Inelastic Cyclic Response of HSS Braces upon Fracture, Advanced Steel Construction, The Hong Kong Institute of Steel Construction, Vol.10, No.4, pp.442-462.
[https://doi.org/10.18057/IJASC.2014.10.4.5]

- Black, R.G., Wenger, W.A.B., and Popov, E.P. (1980) Inelastic Buckling of Steel Struts under Cyclic Load Reversals, Report No. UCB/EERC-80/40, University of California, USA.
-
Astaneh-Asl, A., and Goel, S.C. (1984) Cyclic in-Plane Buckling of Double Angle Bracing, Journal of Structural Engineering, American Society of Civil Engineers, Vol.110, No.9, pp.2036-2055.
[https://doi.org/10.1061/(ASCE)0733-9445(1984)110:9(2036)]

-
Astaneh-Asl, A., Goel, S.C., and Hanson, R.D. (1985) Cyclic Out-of-Plane Buckling of Double-Angle Bracing, Journal of Structural Engineering, American Society of Civil Engineers, Vol.111, No.5, pp.1135-1153.
[https://doi.org/10.1061/(ASCE)0733-9445(1985)111:5(1135)]

-
Aslani, F., and Goel, S.C. (1991) Stitch Spacing and Local Buckling in Seismic-Resistant Double-Angle Braces, Journal of Structural Engineering, American Society of Civil Engineers, Vol.117, No.8, pp.2442-2463.
[https://doi.org/10.1061/(ASCE)0733-9445(1991)117:8(2442)]

- Jiang, Y., Tremblay, R., and Tirca, L. (2012) Seismic Assessment of Deficient Steel Braced Frames with Built-up Back-to-Back Double Angle Brace Sections Using OpenSees Modelling, Proceedings of the 15WCEE, Sociedade Portuguesa de Engenharia Sismica, Portugal, pp.24663-24671.
- Federal Emergency Management Agency (2000) Prestandard and Commentary for the Seismic Rehabilitation of Buildings, FEMA 356, FEMA, USA.
- Newmark, N.M., and Hall, W.J. (1982) Earthquake Spectra and Design, Earthquake Engineering Research Institute, USA.
- Federal Emergency Management Agency (2022) Hazus Earthquake Model Technical Manual, Hazus 4.2 SP3, FEMA, USA.
- Applied Technology Council (1996) Seismic Evaluation and Retrofit of Concrete Buildings, ATC-40, ATC, USA.
- National Emergency Management Agency (2009) Development of Seismic Fragility Curves for Domestic Building Structures, NEMA (in Korean).
- Luco, N., Ellingwood, B.R., Hamburger, R.O., Hooper, J.D., Kimball, J.K., and Kircher, C.A. (2007) Risk-Targeted versus Current Seismic Design Maps for the Conterminous United States, SEAOC 2007 Convention Proceedings, Structural Engineers Association of California, USA.