한 방향 수직 다이어프램의 두께 및 간격 결정을 위한 단순인장 실험평가

1. 연구배경 및 목적

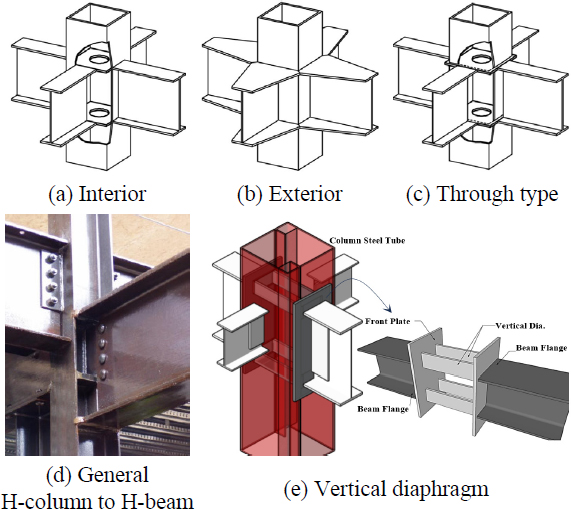
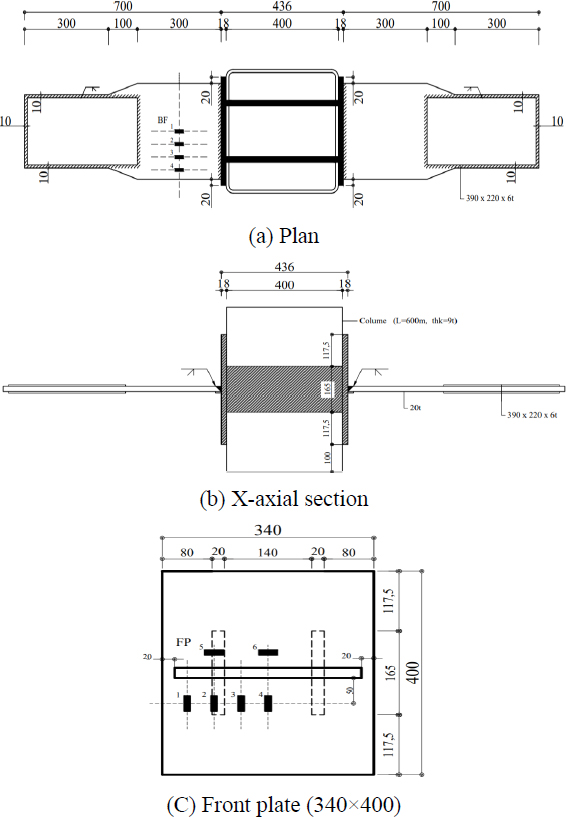
기둥 보 접합부의 하중전달을 위한 매개체로 다이어프램은 필수적인 요소이다. 다이어프램의 명쾌한 응력전달로 인해 수평부재(보 플랜지)에서 수직부재(기둥)로 힘은 분산되고 응력이 집중되지 않도록 유도된다. 대부분의 다이어프램은 플랜지의 휨 응력이 가장 크게 작용하는 부분과 직접 접합되는 형태로 나뉜다. 충전형 기둥인 경우, 다이어프램의 위치에 따라, 내, 외 다이어프램으로 나뉘고, 기둥을 관통하여 보 플랜지와 다이어프램이 직접 접하는 관통형으로 구분할 수 있다^[1]. H형 기둥에 H형 거더가 접합인 경우 기둥에서 플랜지와 맞닿는 위치에 수평형 다이어프램이 구성되는 경우가 대부분이다. 패널존이라고 불리는 기둥-보 접합 구간에는 축력, 휨력, 전단력의 힘이 존재한다. 즉, 명확한 응력전달로 설계가 명쾌할 필요가 있다. 보 춤이 다르거나, 양측 휨 모멘트가 상이할 경우, 설계자의 선택폭을 넓히는 방안으로 Fig. 1(e)와 같이 수직 다이어프램형 접합을 제안하고자 한다. 즉 정면판에는 보 플랜지가 직접 부착되며, 보 플랜지에서 전달되는 인장력은 정면판을 통해 수직 다이어프램으로 전달된다.

Fig. 1.

Column to beam connection type

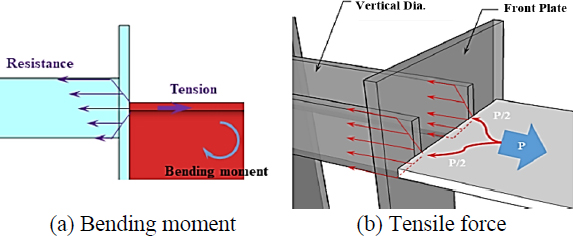
정면판은 모멘트 접합이 필요한 보의 춤 만큼 제작되기 때문에, 상·하부 모멘트 전달이 필요한 위치에 선택적으로 부착이 가능하다^[2]. 응력전달 메커니즘은 내 다이어프램과 유사하지만, 내부에 수평적으로 설치된 내다이어프램과는 달리 수직적으로 설치 될 경우 시공오차에 유리한 장점이 있다. 한 방향 수직 다이어프램은 수평 방향의 하중 전달 기구를 수직 방향으로 형성하여 수평적 공간 활용이 가능하므로 기둥내 주근이나 콘크리트와 간섭을 최소화 할 수 있다^[3],[4]. 일방향 수직 다이어프램의 하중전달 메커니즘은 Fig. 2와 같다. 정면판에 접합된 보에 휨모멘트가 발생함에 의해 인장력이 작용할 경우, 정면판을 통해 수직 다이어프램이 분담하여 하중을 전달한다. 수직 다이어프램에 작용하는 하중 분포는 Fig. 2(a)와 같다. 안정적인 하중전달을 위해서는 정면판에 충분한 강성이 필요할 것이다. 정면판의 두께가 얇아 수평방향으로 작용하는 보 플랜지의 인장력에 의해 정면판이 면외변형을 일으킬 경우, 수직 다이어프램으로 하중전달이 불안정할 것이기 때문이다. 따라서 보 플랜지가 항복 후 충분히 소성변형을 나타낼 때까지 정면판의 면외변형은 제어 되어야하며, 수직 다이어프램 또한 항복하지 않아야할 것이다. 따라서, 본 연구에서는 수직 다이어프램과 정면판의 관계를 변수로 한 단순인장 실험을 수행하였고, 각 요소에 대한 응력분포를 변형률를 통해 검토하였다. 기둥 타입은 콘크리트가 충전된 각형강관이며, 결과적으로 수직형 다이어프램의 합리적인 두께(크기)결정을 위한 설계안을 제시하는 것을 목표로 하고 있다.

Fig. 2.

Load transfer mechanism

2. 이론적 검토 및 국내외기준

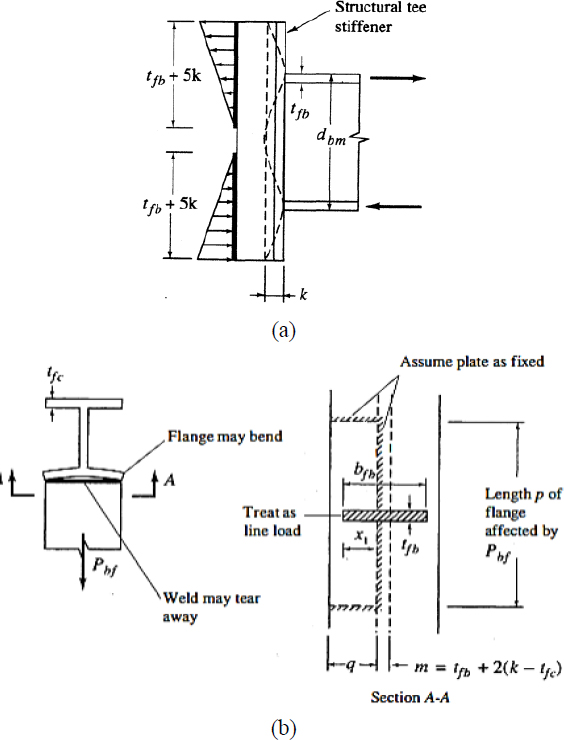
H형강 보가 기둥에 전이되는 인장응력을 산정할 때, 기둥에서 대응하는 유효춤에 대한 내용을 AISC 360-J10^[5]에서 확인할 수 있다. Fig. 3(a)와 같이 수평 다이어프램이 없는 H형강 기둥의 H형강이 접합된 상태에서 보 플랜지에 인장력을 발생시키는 결과를 토대로 제시되었다. 이때, H형강 기둥 웨브의 영향면적의 춤은 보 플랜지 두께(t_fb)와 H형강 기둥의 곡률(r)로 표현되는 용접부를 포함한 플랜지 두께(k)의 5배를 더한 값을 제시한다. 이때 제시된 5배는 보 플랜지가 접합되어 인장력이 발생할 때 인장응력의 분포가 보 플랜지 접합면 중앙을 기준으로 양방향으로 2.5배 씩 분포하는 것에 의한 결과이다.

Fig. 3.

Strength of column flange in tension region of connection[6]

일반적으로 기둥 강관은 접합되는 H형강 보의 플랜지 두께보다 얇은 판 두께를 가지며, 이에 따라 수직 내 다이아프램의 정면판 테두리의 필렛용접 사이즈는 기둥 강관 두께에 의해 결정된다. 그러므로 기둥의 강관 두께는 접합되는 보에서 전달되는 수직 전단력에 충분히 저항할 수 있는 필렛용접부의 사이즈를 고려하여 결정되어야 할 필요가 있을 것으로 판단된다. KDS 14 31 25^[7]에서는 완전용입 용접부의 설계에 대해 ‘모재와 동일’이라고 정하고 있으며 AISC 360의 경우 ‘모재의 의해 결정된다’고 정하고 있다. 이는 ‘모재의 공칭강도와 그루브 용접의 공칭강도 중 작은 값으로 한다.’는 내용으로 판단된다. 수직 내다이아프램 정면판과 보 플랜지의 용접은 완전용입 용접으로 설계된다. 일반적으로 용접재의 항복강도가 모재의 항복강도보다 큰 것을 고려했을 때, 용접부는 모재와 동등 이상의 강도를 갖을 것이다. 이외의 경우에 대해서는 추가적인 용접부 검토가 필요하다^[8].

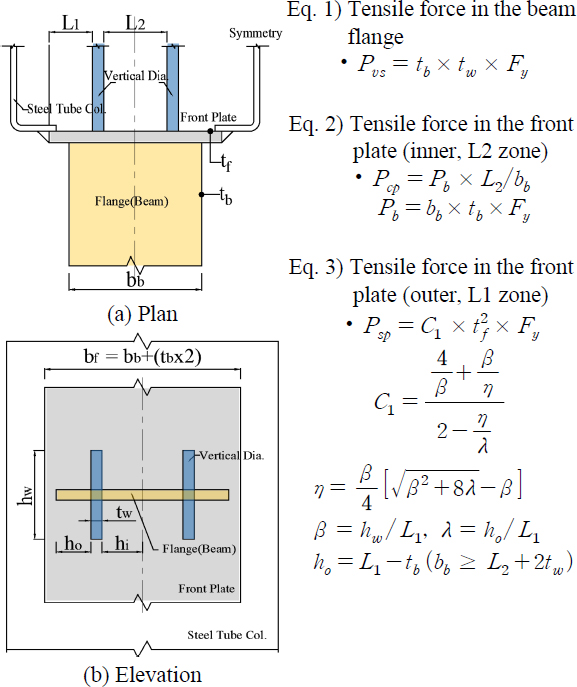
일방향 수직다이어프램의 하중흐름은 보 플랜지에서 정면판을 통해 수직 다이어프램으로 전달되며, 휨강도에 대해 구성 요소의 크기가 산정 된다. 따라서 정면판은 수평방향으로 작용하는 보 플랜지 인장력이 수직방향의 다이어프램으로 원활히 전달되도록 충분한 강성이 필요하다. 또한 정면판에는 면외변형에 대한 저항성능을 만족시키 위해 두께(t_f)를 충분히 확보해야 한다. 정면판은 보 플랜지가 용접 접합되며, 보의 소성휨강도가 발현될 때까지 용접부 파괴가 발생하지 않아야 한다^[9]. 이를 위해 보 플랜지의 용접성을 확보하기 위해 충분한 폭(b_f)이 필요하다. 내부의 수직 다이어프램은 보 플랜지의 인장력에 대응하는 충분한 단면적(A_v = t_w × h_w)이 필요하다. AISC-J10에서 제시하는 Fig 3(b)과 같이 보 플랜지의 인장력은 기둥 보 플랜지의 유효면적에서 대부분은 대응 될 것이다. 따라서 기둥 보 플랜지에 해당하는 정면판을 기준으로 수직 다이어프램 사이구간(L2)에 정면판은 고정지점으로 그 외 의 외측 구간(L1)은 단부가 자유단인 캔틸레버의 거동이 예상된다. Fig. 4와 같이 수직 다이어프램이 양측으로 나뉘어 힘이 분산될 때 각 요소에 대한 거동을 나타내었다. 동일한 보 플랜지의 인장력이 작용할 때, 수직 다이어프램 간격이 멀어지는 것은, 바깥쪽의 캔틸레버 길이가 짧아지는 것을 의미한다. 따라서 캔틸레버의 길이가 짧아지기 때문에, 면외변형이 작아진다. 그러나 중앙부, 즉 수직 다이어프램 사이는 양단고정보의 길이가 길어지며, 휨 변형이 증가한다. 따라서 수직 다이어프램의 간격이 변화됨에 따라, 단부와 중앙부의 주요 변형이 결정된다^[10]. 기존 H형강의 강도 평가식을 기초로 하여 Fig. 4와 같이 수직 다이어프램을 갖는 인장력을 정리 하였다. 일방향 수직 다이어프램의 거동은 웨브 역할의 수직 다이어프램이 2개로 나뉘서 구성하므로 기본 웨브 저항력보다는 다른 양상으로 두께 와 간격을 결정할 필요가 있다. 따라서, 두 수직 다이어프램에 의해 정면판이 외측, 내측으로 구분되어 저항력이 작용된다고 가정하였다. 따라서 수직다이어프램에서 받는 힘(P_vs), 정면판 내측(P_cp)과 외측 힘(P_sp)으로 나 뉠수 있으며, 이들의 총 합이 접합부 인장 저항성능으로 평가 할 수 있다. 정면판에 부착된 수직 다이어프램가 고정지점 기능을 하므로, 다이어프램 사이의 정면판은 양단고정보로 거동이 예상된다. 따라서 보 플랜지의 인장력에 대해 중앙부 정면판의 휨(M_cen) 거동을 양단고정보 조건으로 정면판의 두께를 산정 하였다. 정면판의 안정성을 고려하여 보 플랜지의 항복시까지, 정면판의 휨응력은 탄성상태를 유지하도록 하였다. 또한 정면판의 유효폭을 12t_f로 가정하였다(식 (4)).

Fig. 4.

Design concept

앞서 3가지 조건을 적용하여, 수직 다이어프램의 간격에 대한 각각 정면판의 두께를 비교해 보면, 수직 다이어프램의 간격(L2)이 증가 할수록 정면판 두께(t_f)도 비례적으로 필요 두께가 증가했다. 각 요소에 대한 힘을 검토 하기 위해 강재두께를 20 mm로 설정하고 보 플랜지 폭 300 mm, 수직다어프램 간격을 외부(L1) 80 mm, 안쪽 간격(L2) 140 mm 일 때, 각각의 내력을 검토하여 Table 1에 정리하였다. 강재의 항복강도(Fy)는 모두 355 MPa로 계산되었다. 그 결과, 보 플랜지에서 발생되는 인장력대비 정면판에서 상응하는 내력이 크게 나타났다.

Table 1.

Review of tensile stress ratio for each member

3. 단순인장 실험

3.1 실험 계획 및 개요

제안 상세에 대한 접합성능을 평가하기 위해 단순인장 실험을 계획하였다. 보 플랜지의 응력이 수직 다이어프램에 원활히 전달하는지를 평가하고자 한다. 실험체 기둥은 각형강관으로 크기는 400 mm × 400 mm이며, 강관의 두께는 9 mm이다. 수직 다이어프램의 간격과 정면판의 두께를 변수로 4개의 실험체를 제작하였으며, Table 2와 같다. 수직 다이어프램의 두께는 20 mm으로 동일하다. 실험체 상세는 Fig. 5와 같다. 실험은 3,000 kN 유압식 만능시험기(U.T.M)을 사용하였다. Fig. 6와 같이 반력바닥과 UTM에 설치된 인장지그에 보 플랜지를 맞물려 고정하고 인장력을 가하였다. 실험체의 최대내력과 파괴모드가 확인될 때까지 가력속도 0.05 mm/s의 변위제어로 진행되었으며, 보 플랜지와 정면판, 그리고 기둥 강판의 응력분포를 확인하기 위해 스트레인게이지를 부착하였다. 각 실험체의 보 플랜지는 동일하므로 플랜지의 인장내력(P_f)은 2,160 kN으로 실험결과의 기준이 될 수 있다(재료 결과 반영). 예상 내력(∑ P_{1 ~ 3})을 같이 정리하여 비교하였다.

Table 2.

Specimen list(Unit: mm, kN)

Fig. 5.

Specimen detail (D140-18)

Fig. 6.

Boundary condition

3.2 재료시험 결과

기둥내에 충전된 콘크리트 공칭 압축강도는 24 MPa이며 28일 평균 압축강도는 27.4 MPa로 평가되었다. 실험에 사용된 강재는 모두 SM355A 강종을 사용하여 제작하였고, 강재의 기계적 성질을 알아보기 위하여 KS B 0802기준^[9]에 따라 각각 3개씩 인장 시험편을 절취하여 인장 시험을 수행하였다^[6],[7]. 각 시편의 두께는 9 mm, 18 mm, 20 mm, 22 mm 그리고 24 mm이다. 각 재료 시험결과의 평균치를 Table 3에 정리하였다. 균일한 항복강도와 인장강도를 갖지 않는 것을 알 수 있다.

Table 3.

Material property of steel

특히, 두께 18 mm의 경우, 다른 강종대비 낮은 강도와 강도비를 갖는 것으로 평가되었다. 따라서 부재 전체 예상내력을 산정할 때, 각 요소에 사용된 강재의 항복강도를 각각 재료시험 결과를 적용하여 도출하였다.

3.3 최대내력 및 항복내력

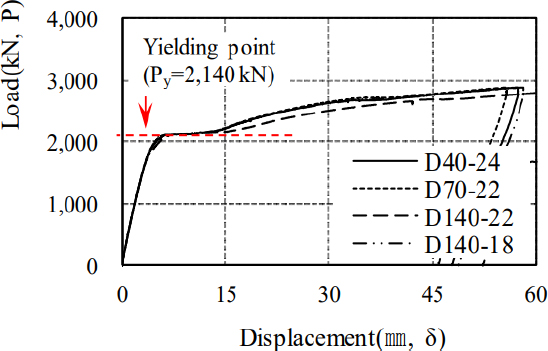
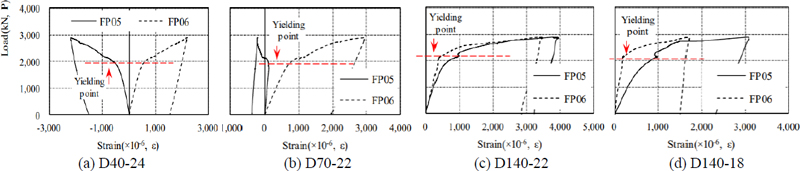
보 플랜지(20 mm)의 재료시험 강도를 적용한 항복강도(P_fl)는 2,160 kN (σ_y=360 MPa)이다. 전체 실험체의 하중-변위 관계를 Fig. 7에 나타내었다. 하중 변위 관계를 보면 거동이 매우 유사하게 나타났다. 공통적으로 변형경화 구간이 발생하였고, 그 지점은 보 플랜지의 양측부에 부착한 변형율 게이지의 측정값이 항복 변형율에 도달하였을 때와 일치 했다. 따라서, 하중-변위 관계에서 항복강도(P_y)를 산정해 보면 약 2,140 kN로 추정되며, 이 값은 보 플랜지의 단면 항복강도(P_fl) 대비 약 99 % 관계를 갖는다. 이때의 LVDT에서 측정한 변위값을 항복하중 시 변위(δ_y)로 산정하였다. 실험체의 파괴거동은 항복내력 이후 변형이 심화되었으며, 보 플랜지에서 네킹 현상이 발생되면서 내력저하가 발생되었다.

Fig. 7.

Load-displacement curve

4. 분석 및 고찰

4.1 하중-변형율 관계

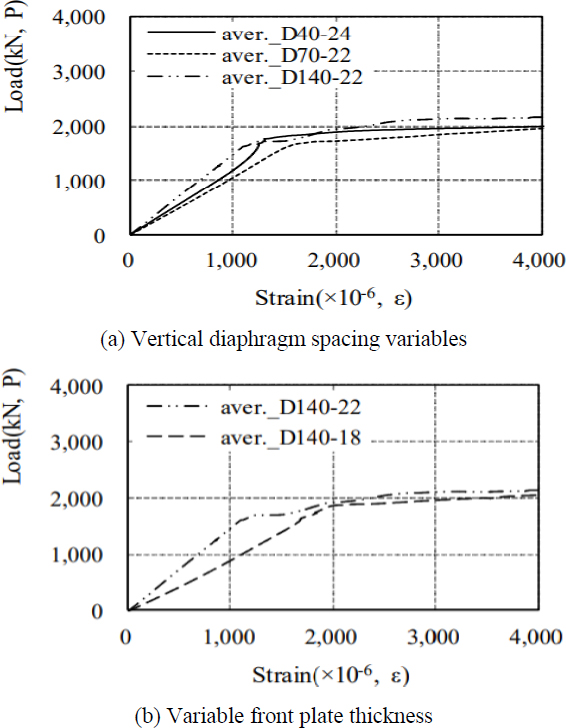
보 플랜지의 변형율은 매우 유사한 거동을 나타냈다. 모든 실험체의 보 플랜지는 약 2,000 kN에서 하중 증가 대비 변형율의 증가폭이 커졌다. 따라서 하중-변위 관계에서 나타낸 항복하중(2,140 kN)과 유사한 결과를 나타내고 있다. 변수별 비교결과, 정면판의 두께가 동일할 때 수직 다이어프램의 간격이 클수록 강성은 크게 나타났다(Fig. 8(a)). 수직 다이어프램의 간격이 크면 수직 다이어프램 외부의 구간이 작아지기 때문으로 판단된다. 또한, 수직 다이어프램이 동일한 간격일 때, 정면판의 두께가 두꺼울수록 강성이 크게 나타났다(Fig. 8(b)). 정면판의 두께가 두꺼울수록 수직 다이어프램으로 응력전달이 빠르게 전이되기 때문으로 판단된다. 수평으로 작용하는 보 플랜지 인장력이 수직방향 다이어프램으로의 전달은 앞서 2장에서 언급됐듯이 1:2.5의 비율로 분포하기 때문이다.

Fig. 8.

Comparison of strain distributions

4.2 보 플랜지의 변형률 분포

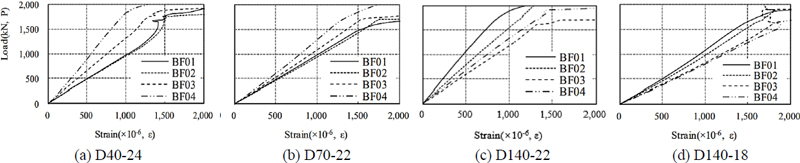
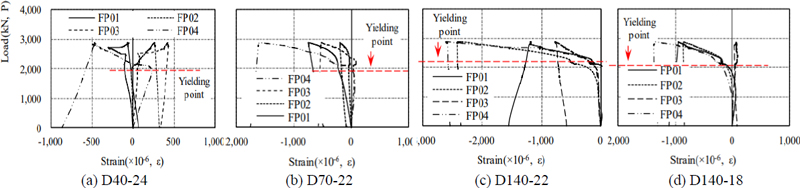
각 실험체별 보 플랜지의 변형률 분포를 Fig. 9에 나타내었다. 보 플랜지의 인장력은 수직 다이어프램 부착부위에서 가장 큰 응력을 나타냈으며, 상대적으로 수직 다이어프램과 멀어질수록 응력전달은 작게 나타났다. 실험체 D40-24에서 BF01과 BF02의 응력전달은 거의 동일하게 나타나는데 이는 수직 다이어프램의 간격이 작아 보 플랜지의 응력이 수직 다이어프램으로 유사하게 전달되기 때문으로 판단된다. 실험체 D70-22는 수직 다이어프램 부착 위치에서 가장 큰 응력을 나타냈으며, 동일 한 정면판 두께를 갖는 실험체 D140-22보다 응력분포가 밀집되어 나타났다. 실험체 D140-22는 같은 수직 다이어프램 간격을 갖는 실험체 D140-18보다 응력이 크고 넓게 분포되어 나타난다. 이를 통해 정면판이 두꺼울수록 정면판을 통해 전달되는 응력이 비례하는 것을 알 수 있다. Fig. 9(a)와 Fig. 9(b)에서 수직 다이어프램이 부착된 위치의 보 플랜지 변형율(BF-01, BF-02)은 약 1,000 kN 하중에서 0.001의 변형율을 나타냈으며, 이 외의 보 플랜지(BF-03, BF-04)는 상대적으로 작은 변형율을 나타내었다. 이는 보 플랜지의 응력을 정면판에 부착된 수직 다이어프램으로 전달함과 동시에, 정면판이 응력 저항하기 때문으로 판단된다. Fig. 9(c)에서 D140-22는 수직 다이어프램 부착위치에서의 보 플랜지 변형율이 Fig. 9(a), Fig. 9(b) 보다 작게 나타났으며, Fig. 9(d)의 D140-18은 Fig. 9(a), Fig. 9(b)보다 크게 나타났다.

Fig. 9.

Strain distribution of beam flange

4.3 정면판의 길이방향 거동

각 실험체별 정면판의 길이방향 변형율 분포를 Fig. 10에 나타냈다. 가력 초반부에 4개의 실험체 모두 변형이 나타나지 않았으나 보 플랜지 항복 후 정면판의 길이방향으로 변형이 심화하였다. 실험체 D40-24 정면판의 변형율 변화는 0.0005 이내로써 미미한 변형을 나타내었다. 이 중, FP04는 가력 초반부에 인장변형 을 보이나 보 플랜지 항복 후 압축변형을 나타내고 있다. 이는 수직다이어프램의 간격이 좁으므로, 보 플랜지의 인장력에 대해 하중 초반에는 면외방향으로 볼록한 변형을 보이다가, 보 플랜지 항복 이후하중 증가 때문에 면외방향으로 오목한 변형을 나타낸 것으로 판단된다. 실험체 D70-22은 가력 초반에 변형이 거의 나타나지 않았지만, 보 플랜지 항복 후 압축거동을 나타내고 있다. 실험체 D140-22도 정면판의 길이방향으로 압축변형을 나타내고 있으며 보 플랜지 측부에서 가장 큰 변화가 일어났다. 실험체 D140-18에서 수직 다이어프램 부착위치의 변형을 측정하는 FP03은 거의 변화가 일어나지 않고 있는 데 이는 정면판에 수직다이어프램이 부착되어 정면판의 변형을 제어하고 있는 것으로 판단된다. 실험체 D140-18의 나머지 FP01, 02, 04 부분에서는 유사한 압축변형을 나타내고 있다.

Fig. 10.

Strain in the longitudinal direction of the front plate

4.4 정면판의 폭 방향 거동

정면판의 폭방향 변형은 수직 다이어프램 간격과 정면판 두께 관계를 검증하는 중요한 요소이다. 당초 예상한 정면판의 폭방향 거동은 앞 절에 설명한 것과 같이 수직 다이어프램사이의 정면판은 보 플랜지 인장력에 대해 면외 방향으로 볼록한 혹은 오목한 휨변형이 발생할 것이다. 수직 다이어프램의 간격이 클수록 내부의 정 면판은 면외방향으로 볼록한 휨 변형을 나타내며, 인장측 변형이 발생하 였다. 수직 다이어프램 간격이 40 mm인 D40-24 실험체는 수직 다이어프램의 내부와 외부가 반대로 압축·인장 변형을 보였다. Fig. 11과 같이 간격이 70 mm인 D70-22 실험체는 정면판 외부가 인장변형을 보였으나, 내부는 보 플랜지 항복 시까지 미미한 변형만 나타냈으나 보 플랜지 항복 이후 크기는 작지만 압축측 변형을 나타내었다.

Fig. 11.

Strain in the width direction of the front plate

수직 다이어프램 사이의 정면 판에 발생한 압축측 변형은 보 플랜지 인장력에 의해 정면판이 면외방향으로 오목한 휨변형이 나타난 것이다. 따라서 수직 다이어프램의 간격이 70 mm 이하에서는 수직 다이어프램에 의한 정면판의 휨변형이 구속되는 것으로 판단할 수 있다. 수직 다이어프램의 간격이 140 mm인 D140-22, D140-18 실험체는 내·외부가 모두 인장측 변형이 발생하여 면외방향으로 볼록한 변형을 나타내었다. 두 실험체 중 상대적으로 정면판의 두께가 두꺼운 D140-22의 휨변형이 큰 것은 두꺼운 정면판이 응력저항에 더 많이 기여하였기 때문으로 판단된다. 정면판 외부를 자유단으로 가정하였기 때문에, 캔틸레버의 휨변형을 가정하였다. 그러나 실험체의 경우, 정면판의 가장자리를 기둥면에 모살용접하였기 때문에 고정지점으로 작용한 것으로 사료된다. 따라서 정면판은 양측 가장자리의 용접부와 내부의 수직 다이어프램이 부착된 2개소가 지점으로 작용하는 연속보의 휨변형을 나타낸 것으로 판단된다.

4.5 수직 다이어프램의 설계값 평가

수직 다이어프램의 강도 평가는 다이어프램에 대해서만 고려하였으나, 실험체는 다이어프램의 위치 고정을 위해 기둥의 강관과 다이어프램의 정면판을 용접하였다. 따라서 실험결과는 정면판의 양측부가 용접 기둥 강관을 통해, 하중 일부가 전달된 것으로 판단된다. 기둥 측면에 부착한 게이지의 측정값에서 작지만 하중 일부가 전달되었다. 기둥 강관을 통해 전달된 하중은 식 (5)와 같이 산정할 수 있다.

$\[ P_{col}=2\times \frac{\left(\frac{{ϵ}_{cen}+{ϵ}_{side }}{2}\right)}{{ϵ}_{y,col}}\times {\sigma }_{y,col}\times A_{col} \]$

(5)

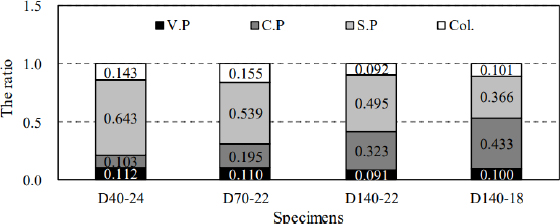
실험 결과와 각 요소에 따른 예상 결과치를 비교하면, 실험값을 상회하며 안정적인 값을 나타내었다. 일방향의 수직 다이어프램은 보 플랜지 인장력을 고려하여 정면판의 두께를 적절히 두껍게 적용하는 것이 보수적인 설계가 될 것으로 판단된다. 각 실험체별로 수직 다이아프램을 구성하는 수직 다이어프램, 중앙부 정면판, 양측 정면판, 기둥 강관으로 구분하여 하중 분담율을 Fig. 12와 Table 4에 정리하였다. 비교결과 수직 다이아프램을 구성하는 수직 다이어프램(0.09 ∼ 0.11)와 기둥 강관(0.10 ∼ 0.15)은 실험체별로 하중분담율이 유사한 분포를 나타났으나, 중앙 부 정면판과 양측 정면판은 시험체별로 다른 경향을 나타내었다. 수직다이어프램의 간격이 증가할수록(L₂가 증가할수록) 정면판의 하중분담은 눈에 띄게 증가하였으며, 반대로 양측 정면판은 하중분담이 작아졌다. 따라서 수직다이아프램 설계 시, L₂를 조절하여 가급적 중앙부와 양측부의 하중 분담율을 유사하게 할 때, 효율적인 정면판의 두께 선택이 가능할 것이다.

Fig. 12.

Comparison of load ratio by vertical diaphragm element

Table 4.

Comparison of experimental results with nominal strength

5. 결 론

일방향 수직 다이아프램을 개발하였으며, 단순인장실험을 통해 구조적 기초성능을 분석하였다. 각형기둥 단면을 대상으로 하였으며, 폭 300 mm, 두께 20 mm의 보 플랜지를 적용하였다. 실험을 통해 다음과 같은 결론을 얻었다.

• 1) 모든 실험체는 보 플랜지의 항복강도 이상으로 충분히 안정적인 인장거동을 발휘하였다. 수직 다이아프램을 구성하는 수직 다이어프램의 간격과 정면판 두께에 따른 다이아프램의 하중전달 양상, 수직 다이어프램의 위치에 따른 보 플랜지의 하중전달 양상을 검증하였다.
• 2) 수직 다이어프램과 정면판으로 보 플랜지의 인장력에 저항할 것으로 예상하였으나, 제작 및 시공을 위해정면판과 기둥 강관을 용접 부착하기 때문에 기둥 강관을 통해서도 일부 하중 전달이 이루어졌다. 전체 인장력에 약 10 %에 해당된다.
• 3) 정면판의 두께는 보 플랜지의 인장력에 저항하는 중요한 요소이다. 정면판의 두께가 두꺼워질수록 접합부의 강성은 향상되었고, 하중전달이 넓은 범위로 빠르 게 진행되었다. 따라서 수직다이어프램의 간격이 동일할 경우, 정면판의 두께가 두꺼울수록 보-기둥 접합부의 하중 저항성능은 향상될 가능성이 커짐을 의미한다.
• 4) 수직 다이어프램의 간격은 정면판의 두께와 같이 하중전달에 주요 인자이다. 보 플랜지의 인장력에 대해 수직다이어프램의 간격이 클수록 정면판 외부거리가 작기 때문에 높은 강성으로 하중전달이 가능하며, 정면판의 면외변형이 작게 나타났다. 또한 중앙부와 양측부의 강도가 균형을 이룰 때, 정면판의 두께를 효과적으로 설계할 수 있으며, 안정적인 접합부 거동을 유도할 수 있다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 인력지원을 받아 수행된 연구임(No. 2023 R1A2C1005591).

References

• Kim, K., Lee, H.-Y., Kim, Y.-K., Kim, T., and Kim, J.-H. (2017) Structural Strength of Beam-to-CFT Connections with Vertical Diaphragm, Journal of Korean Society of Steel Construction, KSSC, Vol.29, No.3, pp.237-247 (in Korean).
• Choi, I.R., Kim, Y.H., Chung, K.S., and Choi, H.S. (2019) Cyclic Loading Test for CFT Column Connection Using T-Type Exterior Diaphragm and Embeded H-Type Connection Detail, Journal of Korean Society of Steel Construction, KSSC, Vol.31, No.2, pp.​97-106 (in Korean). [https://doi.org/10.7781/kjoss.2019.31.2.097]
• Kim, S.H., Yom, K.S., and Choi, S.M. (2014) Seismic Performance of Built-up Concrete Filled Square Composite Column to Beam Connection with Through Diaphragm, Journal of Korean Society of Steel Construction, KSSC, Vol.26, No.5, pp.431-439 (in Korean). [https://doi.org/10.7781/kjoss.2014.26.5.431]
• Lee, B.-H., and Seo, S.-Y. (2022) Development and Structural Behaviors of New Vertical-Diaphragm Connections to CFT Column-H Beam Under Cyclic Loading, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.6, pp.363-372 (in Korean). [https://doi.org/10.7781/kjoss.2022.34.6.363]
• American Institute of Steel Construction (2016) Specification for Structural Steel Buildings, ANSI/AISC 360-16, USA.
• Salmon, C.G., Johnson, J.E., and Malhas, F.A. (2009) Steel Structures: Design and Behavior (5th Ed.), Prentice Hall, USA.
• Korean Agency for Technology and Standards (2010) Standard Test Method for Compressive Strength of Concrete, KS F 2405: 2010, Korea (in Korean).
• Ministry of Land, Infrastructure and Transport (2019) Steel Structures Design Standard, KDS 41 31 00: 2019, Korea (in Korean).
• Korean Agency for Technology and Standards (2007) Test Pieces for Tensile Test for Metallic Materials, KS B 0801: 2007, Korea (in Korean).
• Kim, J., Park, H.Y., Kim, T.H., & Kim, T.S. (2023). Experimental Study on the Tensile Behavior of Interlocks on U-Type Section Steel Piling. International Journal of Steel Structures, KSSC, Vol.23, No.5, pp.1368-1375. [https://doi.org/10.1007/s13296-023-00775-7]