이동하중이 작용하는 곡선보의 MIDAS를 이용한 동해석 기법

1. 서 론

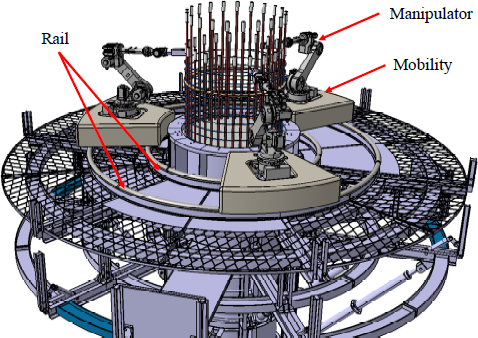
현재 국토교통부에서는 기술혁신 및 산업생태계를 조성하고자 스마트건설기술개발사업을 추진하고 있으며, 한국건설기술연구원은 이 사업에서 교량에 대한 무인·자동화 시공 및 품질관리 기술을 개발 중이다. 교각의 경우 원격 및 무인화 시공기술을 위해 시공용 모바일 매니퓰레이션 시스템(manipulation system) 기술 적용을 위한 원격·자동화 거푸집 시스템(remote-automated formwork system)을 개발하고 있다^[1],[2]. Fig. 1은 원격·자동화 거푸집 시스템과 매니퓰레이션 시스템을 보여주며, 매니퓰레이터가 교각의 주철근을 연결하는 모습을 보여준다. 원형 교각에 적용되는 모바일 매니퓰레이션 시스템은 매니퓰레이터와 이동체(mobility)로 구성되며, 거푸집 시스템 상부의 원형 레일 위를 이동하며 인력을 대신하여 철근망 조립과 콘크리트 바이브레이터 작업을 진행한다.

Fig. 1.

Remote-automated elevating formwork system and a manipulation system

무인화 시스템의 완성을 위해선 매니퓰레이터 시스템의 작업환경을 제공하는 다수의 교각에 재사용을 위해서 해체 및 조립이 용이한 강재만으로 이루어진 원격·자동화 거푸집 시스템의 안전성 검증이 필요하다. 안전성 검증으로서 원격·자동화 거푸집 시스템의 정적하중에 대한 구조부재의 안정성과 매니퓰레이터 시스템의 작업환경을 고려하여 매니퓰레이션 시스템의 이동하중에 대한 구조물 사용성의 검토가 필요하다. 이에 따라, 유한요소해석 프로그램으로 일반적으로 사용되는 MIDAS CIVIL을 통해, 원격·자동화 거푸집 시스템의 안전성을 검증하는 방법에 관한 연구가 진행 중이다.

Fig. 2는 MIDAS CIVIL을 통한 원격·자동화 거푸집 시스템의 유한요소모델을 보여준다. 원격·자동화 거푸집 시스템을 통해 교각을 무인화 시공하기 위해선 구조물에 다양한 장치들에 의한 하중이 발생한다. Choi et al.은 원격·자동화 거푸집 시스템의 유한요소해석을 통해 예상되는 정적하중에 대한 구조적 안전성을 분석하였다^[3]. 구조적 안전성 분석을 통해 구조물의 전체적인 사용성과 구조부재의 안정성에 대한 검증이 이루어졌다. 추가적으로 매니퓰레이션의 오차 범위 내의 수평을 유지하는 작업환경의 검증을 위해서 매니퓰레이션 시스템이 이동하는 레일의 사용성에 대한 검증이 필요하다.

Fig. 2.

Finite element model of the remote-automated formwork system using MIDAS CIVIL

매니퓰레이션 시스템이 이동하는 레일의 경우 원격·자동화 거푸집 시스템과 일체화하여 거동한다. 레일은 일정한 곡률을 갖는 원형 곡선보이며, 매니퓰래이션 시스템의 하중은 면내 방향(반경방향 및 접선방향)과 면외 방향(수직방향)으로 작용할 수 있다. 여기서, 면외 방향이란 곡선보가 존재하는 면에 수직인 방향을 뜻한다.

외력이 작용하는 곡선보에 대한 유한요소해석의 경우 분할된 부재의 인접한 두 노드 사이를 직선보 요소 또는 일정한 곡률을 갖는 곡선보 요소로 모델링할 수 있다. Yoon and Kang은 수평곡선 I형교의 자유진동을 직선보 요소를 활용한 유한요소해석을 수행하였다^[4]. Yang and Kuo는 휨과 전단효과를 고려한 여섯 가지 변형률을 통해 곡선보의 지배 미분 방정식을 유도하였으며, 직선보 요소 모델은 곡률 효과를 표현할 수 없다는 결과를 확인하였다^[5]. Lebeck and Knowlton은 면내외 힘을 받는 원형 링에 대하여 회전각에 따른 변위방정식을 유도하였다^[6]. 이를 활용하여, Wu and Chiang은 곡선보 요소를 활용한 유한요소모델을 제시^[7]하였으며, Yang et al.이 유도한 이동하중이 작용하는 곡선보의 이론적 해^[8]와 비교하였다.

본 연구에서는 원격·자동화 거푸집 시스템에 작용하는 연직하중의 가장 큰 비중을 차지하는 매니퓰레이션 시스템이 원형 레일 위에서 이동하중으로 작용할 때 시간이력해석을 수행하고자 한다. 이에 따라, 원형 레일을 곡선보로 간주하고 곡선보는 분할된 직선보 유한요소모델로 나누고, 직선보들은 양단의 절점으로 연결된 것으로 고려하였다. 분할된 직선보 위를 이동하는 하중은 양단의 절점에 곡률효과를 고려한 하중으로 치환하여 적용하였다. 이때, MIDAS CIVIL 프로그램을 사용하여 각 절점에 시간의 함수로 하중을 적용하여 이동하중의 효과를 구현하였다. 이를 통해, MIDAS CIVIL을 이용한 곡선보의 해석결과와 이론적 해석결과를 비교분석하고자 한다.

2. 곡선보의 유한요소 수치해석 모델

2.1 곡선보 요소의 변위와 회전각

Fig. 3는 x z 평면에 존재하는 곡선보 요소의 국부좌표계에서의 부재 변위(u_y, ψ_x, ψ_z)와 내력(F_y, M_x, M_z)을 보여준다. x, y, z는 전체좌표계이며 x, y, z는 요소의 국부좌표계를 나타낸다. 국부좌표계의 x축은 곡선보의 반경 방향이며 z축은 접선방향 그리고 y축은 면외 방향이다. 곡선보 요소는 접선방향에 따라 단면이 일정하며 x축에서 시계방향으로 θ₁만큼 회전한 노드 ①과 θ₂만큼 회전한 노드 ②를 연결한다. 여기서, 회전각 θ₂와 θ₁의 차이 α는 곡선보 요소의 분할각을 의미한다. 곡률 중심으로부터 반지름이 R인 곡선보는 접선방향으로 x축과 y축 대칭 단면이므로 Wu and Chiang^[7]이 제시한 회전각(θ)에 따른 변위(u_y, ψ_x, ψ_z)의 관계를 적용할 수 있다.

Fig. 3.

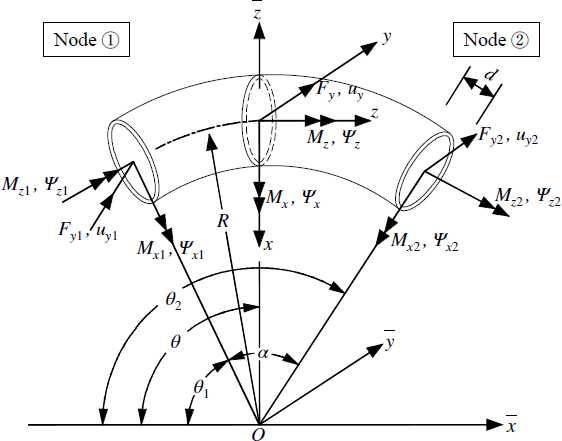
Element displacements(uy, ψx, ψz) and element forces(Fy, Mx, Mz) of curved beam element with local coordinate system

변위와 회전각의 관계식은 식 (1)과 같다.

$\[ \begin{array}{cc}{u}_y=& \begin{array}{l}{G}_1+G_2{C}_{so}\theta +G_3\sin \theta +G_4\cos \theta \\ +G_5\theta \sin \theta +G_6\theta \cos \theta \end{array}\end{array} \]$

(1a)

$\[ {\psi }_x=\frac{1}{R}\left[\begin{array}{l}{G}_2+G_3\cos \theta -G_4\sin \theta \\ +G_5\left(\theta \cos \theta +\sin \theta \right)\\ -G_6\left(\theta \sin \theta +\cos \theta \right)\end{array}\right] \]$

(1b)

$\[ {\psi }_z=\frac{1}{R}\left[\begin{array}{l}-G_3\sin \theta -G_4\cos \theta \\ -G_5\left(\theta \sin \theta -2C_o\cos \theta \right)\\ -G_6\left(\theta \cos \theta +2C_o\sin \theta \right)\end{array}\right] \]$

(1c)

여기서,

$\[ C_o={\Phi }_{bt}/\left(1+{\Phi }_{bt}\right) \]$

(2a)

$\[ C_{so}=1+\left[G{J}_{\theta }/\left(R^2{k}^{\text{'}}GA\right)\right] \]$

(2b)

$\[ {\Phi }_{bt}=E{I}_x/\left(G{J}_{\theta }\right) \]$

(2c)

$\[ I_x={\int }_A{y}^{2}dA \]$

(2d)

$\[ J_{\theta }={\int }_A\left(x^2+y^2\right)dA \]$

(2e)

식 (1a)–식 (1c)에서 G₁–G₆는 적분상수로서 곡선보 요소의 경계조건에 따라 결정된다. 식 (2a)–식 (2b)에서 C_o와 C_so는 곡선보 요소의 휨강성(EI_x)과 비틀림 강성(GJ_θ)의 비율(Φ_bt), 전단탄성계수(G), z축에 대한 단면적의 극 관성 모멘트(J_θ), 곡률 반경(R), 전단보정계수(k^′), 단면적(A)에 의해 결정된다. 또한, I_x는 x축에 대한 단면2차모멘트를 나타낸다.

식 (1a)–식 (1c)의 변위는 회전각에 따른 행렬과 적분상수 행렬의 곱으로 식 (3)과 같이 나타낼 수 있다.

$\[ \left\{u\right\}=\left[H\right]\left\{G\right\} \]$

(3)

여기서,

$\[ \left\{u\right\}=\left\{\begin{array}{ccc}{u}_y& {\psi }_x& {\psi }_z\end{array}\right\} \]$

(4a)

$\[ \left[H\right]=\left[\begin{array}{cccccc} 1 & C_{so}\theta & \sin \theta & \cos \theta & \theta \sin \theta & \theta \cos \theta \\ 0& 1/R& \cos \theta /R& -\sin \theta /R& \left(\theta \cos \theta +\sin \theta \right)/R& -\left(\theta \sin \theta -\cos \theta \right)/R\\ 0& 0& -\sin \theta /R& -\cos \theta /R& -\left(\theta \sin \theta -2C_o\cos \theta \right)/R& -\left(\theta \cos \theta +2C_o\sin \theta \right)/R\end{array}\right] \]$

(4b)

$\[ \left\{G\right\}=\left\{\begin{array}{cccccc}{G}_1& G_2& G_3& G_4& G_5& G_6\end{array}\right\} \]$

(4c)

식 (3)에서 θ = θ₁인 경우와 θ = θ₂인 경우를 고려하면 식 (5)와 같이 나타낼 수 있다.

$\[ \left\{\delta \right\}=\left[B\right]\left\{G\right\} \]$

(5)

여기서,

$\[ \left\{\delta \right\}=\left\{\begin{array}{cccccc}{u}_{y1}& {\psi }_{x1}& {\psi }_{z1}& u_{y2}& {\psi }_{x2}& {\psi }_{z2}\end{array}\right\} \]$

(6a)

$\[ \left[B\right]=\left[\begin{array}{cccccc} 1 & C_{so}{\theta }_1& \sin {\theta }_1& \cos {\theta }_1& {\theta }_1\sin {\theta }_1& {\theta }_1\cos {\theta }_1\\ 0& 1/R& \cos {\theta }_1/R& -\sin {\theta }_1/R& \left({\theta }_1\cos {\theta }_1+\sin {\theta }_1\right)/R& -\left({\theta }_1\sin {\theta }_1-\cos {\theta }_1\right)/R\\ 0& 0& -\sin {\theta }_1/R& -\cos {\theta }_1/R& -\left({\theta }_1\sin {\theta }_1-2C_o\cos {\theta }_1\right)/R& -\left({\theta }_1\cos {\theta }_1+2C_o\sin {\theta }_1\right)/R\\ 1& C_{so}{\theta }_2& \sin {\theta }_2& \cos {\theta }_2& {\theta }_2\sin {\theta }_2& {\theta }_2\cos {\theta }_2\\ 0& 1/R& \cos {\theta }_2/R& -\sin {\theta }_2/R& \left({\theta }_2\cos {\theta }_2+\sin {\theta }_2\right)/R& -\left({\theta }_2\sin {\theta }_2-\cos {\theta }_2\right)/R\\ 0& 0& -\sin {\theta }_2/R& -\cos {\theta }_2/R& -\left({\theta }_2\sin {\theta }_2-2C_o\cos {\theta }_2\right)/R& -\left({\theta }_2\cos {\theta }_2+2C_o\sin {\theta }_2\right)/R\end{array}\right] \]$

(6b)

식 (5)로부터 적분상수 행렬은

$\[ \left\{G\right\}={\left[B\right]}^{-1}\left\{\delta \right\} \]$

(7)

변위방정식 식 (3)에 적분상수 식 (7)을 대입하면

$\[ \left\{u\right\}=\left[H\right]{\left[B\right]}^{-1}\left\{\delta \right\} \]$

(8)

이에 따라, 곡선보의 형상함수 행렬 [a]는 θ의 함수이며 식 (9)와 같다.

$\[ \left[a\right]=\left[H\right]{\left[B\right]}^{-1}=\left[\begin{array}{cccccc}{a}_{y1}& a_{y2}& a_{y3}& a_{y4}& a_{y5}& a_{y6}\\ a_{x1}& a_{x2}& a_{x3}& a_{x4}& a_{x4}& a_{x6}\\ a_{z1}& a_{z2}& a_{z3}& a_{z4}& a_{z5}& a_{z6} \end{array}\right] \]$

(9)

3. 곡선보의 MIDAS CIVIL 모델

3.1 매니퓰레이터 레일 및 모델 형상

Fig. 4(a)는 길이(L)가 5.76 m인 곡선보를 보여준다. 레일은 n개의 요소를 가지며, 노드 N₁과 노드 N_n+1를 잇는 중심각이 120°이고, 반지름(R) 2.75 m인 부채꼴의 호 형태를 하고 있다. 즉, 중심각이 120°인 매니퓰레이터 레일을 분할각(α)에 따라 등간격으로 총 n개의 요소로 나누어 모델링을 진행하였다. 곡선보의 양단은 힌지로 고려하였고, 국부좌표계에서 x축·z축·y축의 처짐과 z축에 대한 처짐각을 구속하였다.

Fig. 4.

A curved beam

Fig. 4(b)는 MIDAS CIVIL을 이용하여 매니퓰레이터 레일을 분할각(α)은 6°로 가정하여 총 20개의 요소 및 21개의 노드를 가진 곡선보를 보여준다.

매니퓰레이터 레일은 강재 SS275를 사용하며 단면의 지름 89.1 mm, 두께 5.5 mm인 파이프를 사용한다. SS275의 탄성계수(E = 205 GPa)와 푸아송비(υ = 0.3)에 의해 전단탄성계수(G = 788.46 GPa)를 산정할 수 있으며, 비중(γ)과 전단보정계수(k^′)는 각각 76.98 kN/m², 0.833을 사용한다. 단면 형상에 의하여 단면적(A)은 1,444.504 mm²으로 산정된다. 이에 따라, 식 (2)에 정의된 변위방정식의 상수는 Table 1과 같다.

Table 1.

Constants of displacement equations

3.2 이동하중 적용

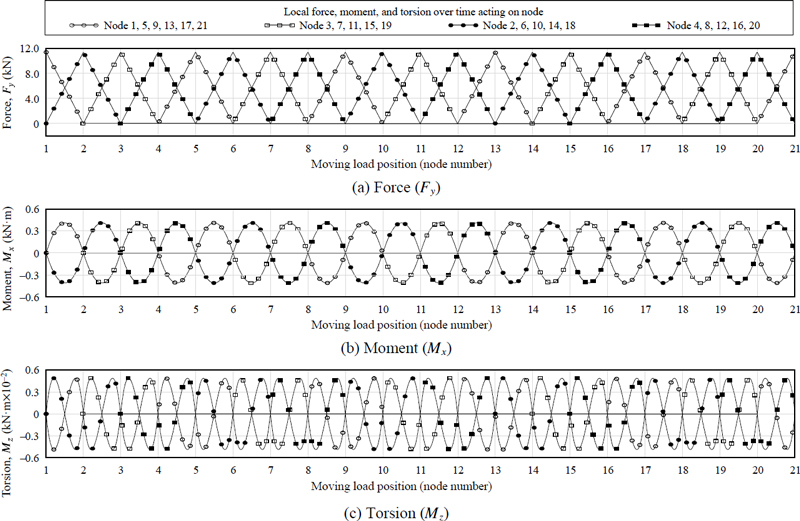
레일 위를 이동하는 연직하중의 크기(P_oy)는 11.4 kN이며, 첫 번째 노드에서 마지막 노드까지 이동한다고 가정하였다. Fig. 5는 이동하중이 첫 번째 노드에서 마지막 노드까지 이동할 때, 각 노드에 작용하는 국부 좌표계에서 외력(F_y, M_x, M_z)의 크기를 보여준다. 또한, 이동하중에 의해 각 노드에 발생하는 국부 좌표계에서의 외력을 MIDAS CIVIL 모델에 적용하기 위해선 전체 좌표계의 외력으로 식 (14)를 통해 변환시켜야 한다. Fig. 6는 이동하중의 위치에 따라 모든 노드에 발생하는 전체 좌표계에서 외력(F_y, M_x, M_z)의 크기를 보여준다. 이동하중의 속도(v) 효과는 이동하중이 한 개 요소(길이 l)를 통과하는 데 소요되는 시간(l/v)을 사용하였다.

Fig. 5.

External local forces acting on nodes

Fig. 6.

External global forces acting on nodes

4. 시간이력 해석결과

해석프로그램 MIDAS CIVIL을 통한 곡선보 해석결과와 이론적 해석결과를 비교분석하였다. Yang et al.^[8]이 제안한 시간에 따른 곡선보 중앙지점에서의 처짐에 대한 이론해에 곡선보 모델의 물성치를 적용하였으며, 곡선보의 감쇠효과는 없는 것으로 가정하였다. 이에 따라, Yang et al.^[8]의 이론해, 곡률효과를 고려한 하중분배(VMT)가 적용된 유한요소해석, 곡률효과를 고려하지 않은 하중분배(VM)가 적용된 유한요소해석을 비교하였다.

4.1 수직응답(u_y) 결과 비교

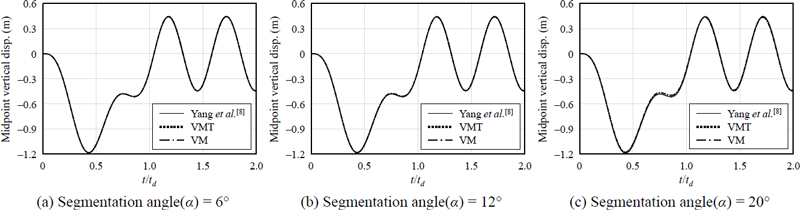
Figs. 7–9은 곡선보의 중앙지점(Fig. 4(b)의 절점 11)에서 시간이력에 따른 수직응답을 보여준다. 그래프의 x축은 경과된 시간을 이동하중이 곡선보를 통과하는 시간(t_d = L/v)으로 나눈 값을 나타내며, x축의 값이 1보다 클 때는 이동하중이 통과한 후 곡선보의 자유진동을 보여준다. 실선은 Yang et al.^[8]에 따른 곡선보의 이론해를 나타낸다. 또한, 유한요소해석으로서 점선은 VMT를 적용한 결과를, 일점쇄선은 VM을 적용한 결과를 나타낸다.

Fig. 7.

Time histories of midpoint vertical displacements with α = 6°, 12°, 20° at v = 1.0 m/s

Fig. 7은 곡선보의 중앙지점에서 수직응답을 이동하중의 속도(v)가 1.0 m/s일 때, 분할각(α)의 크기에 따라 그래프를 나타냈다. VMT와 VM을 적용한 유한요소모델의 응답은 분할각과는 상관없이 이론해와 유사하게 나타났다.

Fig. 8과 Fig. 9은 곡선보의 중앙지점에서 수직응답을 이동하중의 속도(v)가 각각 5.0 m/s, 10.0 m/s일 때, 분할각(α)의 크기에 따라 그래프를 나타냈다. VMT와 VM을 적용한 유한요소모델은 모두 이론적 해와 유사한 파형을 띄는 것으로 나타났다. 그러나 VMT와 VM을 적용한 유한요소모델의 응답은 분할각과는 상관없이 모두 이론적 해와 유사한 결과를 나타냈다.

Fig. 8.

Time histories of midpoint vertical displacements with α = 6°, 12°, 20° at v = 5.0 m/s

Fig. 9.

Time histories of midpoint vertical displacements with α = 6°, 12°, 20° at v = 10.0 m/s

Table 2는 곡선보에서 발생하는 최대 처짐의 크기와 첫 번째 모드의 고유주기 및 이론적 해석과 모델링의 오차율을 나타냈다. 1차 모드 고유주기의 경우 이동하중과 상관 없이 곡선보의 질량과 강성에 의해 결정된다. 분할각이 6°일 때, 이론해와 첫 번째 모드의 고유주기 오차(frequency error in the 1st mode)는 가장 작게 나타났으며 그 값은 약 0.041 %인 것으로 나타났다. 또한, 분할각이 12°, 20°인 경우 이론해와의 첫 번째 모드의 고유주기 오차는 각각 0.045 %, 0.059 %로 분할각이 커질수록 고유주기에 대한 오차율 역시 커지는 것을 확인하였다.

Table 2.

The maximum vertical displacement and occurrence time that occurs in curved beam

유한요소모델에서 곡선보의 중앙지점 최대 처짐은 VMT을 적용한 경우 분할각이 커질수록 값이 증가하는 것으로 나타났으며, VM을 적용한 경우 분할각이 커질수록 값이 감소하는 것으로 나타났다. 처짐 오차(displacement error)는 유한요소모델에서 나타난 최대 처짐과 이론해의 최대 처짐 간의 차이를 이론해의 최대처짐으로 나눈 값이다. 유한요소모델에 VMT을 적용할 경우 처짐 오차는 0.763 % 이내로 이론해와 유사한 값이 나타나는 것으로 확인되었다. 또한, VM을 적용하면 처짐 오차는 최대 2.086 %까지 나타났다.

5. 결 론

본 연구는 이동하중을 받는 곡선보에 MIDAS CIVIL을 활용한 동해석 결과와 이론해를 비교하여 MIDAS의 곡선보 동해석을 검증하였다. MIDAS CIVIL을 통한 유한요소해석결과는 다음과 같다.

• (1) 유한요소모델에 이동하중에 대하여 곡률효과를 고려한 하중분배(VMT)를 적용할 경우 곡률효과를 고려하지 않은 하중분배(VM)보다 이론해와 더 유사한 곡선보의 동적 응답이 나타났다.
• (2) 이론해와 유한요소모델의 처짐 오차는 VMT를 적용할 경우 0.763 % 이내로 나타났으며, VM을 적용하면 최대 2.086 %까지 확인되었다.
• (3) 유한요소모델에서 곡선보의 중앙지점 최대 처짐은 VMT를 적용한 경우 분할각이 커질수록 값이 증가하는 것으로 나타났으며, VM을 적용하면 분할각이 커질수록 값이 감소하는 것으로 나타났다.
• (4) 이론해와 유한요소모델 첫 번째 모드의 고유주기 오차는 분할각이 6°, 12°, 20°일 때, 각각 0.041 %, 0.045 %, 0.059 %로 분할각이 커질수록 고유주기에 대한 오차가 증가하는 것으로 확인되었다.

이에 따라, 본 연구를 기반으로 원격·자동화 거푸집 시스템의 MIDAS CIVIL을 통한 유한요소모델은 곡선보 위의 이동하중에 대한 동적 효과를 충분히 나타낼 수 있도록 곡률효과를 고려한 하중분배(VMT)를 적용하여 해석을 수행해야 할 것으로 보인다.

Acknowledgments

이 연구는 국토교통부/국토교통과학기술진흥원이 시행하고 한국도로공사가 총괄하는 “스마트건설기술개발 국가 R&D사업(과제번호 RS-2020-KA157074)”의 지원으로 수행하였습니다.

References

• Shim, C., Lee, S., and Sim, S.-H. (2020) Smart Construction Technologies for Roadway Structures, KSCE Magazine, Korean Society of Civil Engineers, Vol.68, No.8, pp.36–43 (in Korean).
• Lee, S. (2021) Developement and Application of Robotic Construction, KSCE Magazine, Korean Society of Civil Engineers, Vol.69, No.4, pp.34–42 (in Korean).
• Choi, D.-H., Lee, S.H., and Lee, H.J. (2022) Structural Safety of Unmanned Smart Form System for Piers, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.6, pp.411–418 (in Korean). [https://doi.org/10.7781/kjoss.2022.34.6.411]
• Yoon, K.Y., and Kang, Y.J. (1998) Free Vibration Analysis of Horizontally Curved I-Girder Bridges Using the Finite Element Method, Journal of Korean Society of Steel Construction, KSSC, Vol.10, No.1, pp.47–61 (in Korean).
• Yang, Y.-B., and Kuo, S.-R. (1987) Effect of Curvature on Stability of Curved Beams, Journal of Structural Engineering, American Society of Civil Engineers, Vol.113, No.6, pp.1185–1202. [https://doi.org/10.1061/(ASCE)0733-9445(1987)113:6(1185)]
• Lebeck, A.O., and Knowlton, J.S. (1985) A Finite Element for the Three-Dimensional Deformation of a Circular Ring, International Journal for Numerical Methods in Engineering, John Wiley & Sons, Vol.21, No.3, pp.421–435. [https://doi.org/10.1002/nme.1620210304]
• Wu, J.-S., and Chiang, L.-K. (2003) Out-of-Plane Responses of a Circular Curved Timoshenko Beam Due to a Moving Load, International Journal of Solids and Structures, Elsevier, Vol.40, No.26, pp.​7425–7448. [https://doi.org/10.1016/j.ijsolstr.2003.07.004]
• Yang, Y.-B., Wu, C.-M., and Yau, J.-D. (2001) Dynamic Response of a Horizontally Curved Beam Subjected to Vertical and Horizontal Moving Loads, Journal of Sound and Vibration, Elsevier, Vol.242, No.3, pp.519–537. [https://doi.org/10.1006/jsvi.2000.3355]
• Midas Information Technology, Co., Ltd., (2023) Midas Civil 2023 (v1.1), Korea.