축소모델을 이용한 대형 감쇠 구조물의 내진성능평가
Copyright © 2023 by Korean Society of Steel Construction
초록
대형구조물의 효율적인 내진성능평가를 위해 본 연구에서는 축소모델을 사용하였다. 원 구조물과 축소모델의 등가성을 확인하기 위해 감쇠장치가 설치된 구조물의 비선형정적해석을 이용한 등가감쇠비 비교를 진행하였다. 축소모델을 직접적분법과 모드중첩법을 통해 시간이력해석을 진행하여 결과의 유사성을 확인하였다. 이상의 결과를 통해 원 구조물과 축소모델의 등가성을 확인하였으며, 축소모델의 비선형시간이력해석을 통해 감쇠장치 설치 전/후로 내진성능의 변화를 비교하였다. 또한, 감쇠장치의 종류를 달리해 가며 내진성능을 비교하였다. 이상의 결과를 통해 축소모델을 통한 대형구조물의 내진성능평가 결과가 타당함을 확인하였다.
Abstract
A reduced model was used for efficient seismic performance evaluation of a large-scale structure. To confirm the equivalence of the original structure and the reduced model, a comparison of equivalent damping ratios was carried out using nonlinear static analysis of a structure equipped with dampers. The similarity of the results was confirmed by conducting time history analysis of the reduced model through direct integration and mode superposition methods. Through these results, the equivalence of the original structure and the reduced model was confirmed, and changes in seismic performance before and after damper installation were compared through nonlinear time history analysis of the reduced model. Additionally, seismic performance was compared by varying the type of dampers. Through these results, the validity of seismic performance evaluation of a large-scale structure using a reduced model was confirmed.
Keywords:
Reduced model, Seismic performance evaluation, Damping ratio, Time history analysis, Large-scale structure키워드:
축소모델, 내진성능평가, 감쇠비, 시간이력해석, 대형구조물1. 서 론
경주, 포항 지진 이후 내진성능평가에 대한 수요가 꾸준히 증가하고 있다. 더불어 내진성능평가에 대한 구조 기준이 개정되고 여러 가지 방법론과 각종 도구들이 널리 사용되고 있다. 여러 방법론 중에서 부재의 비선형성을 고려한 성능기반설계는 난이도가 높고 계산 시간이 오래 걸리는 단점이 있다. 이는 특히 대형 구조물에 적용할 때 문제가 된다. 이 연구에서는 대형 구조물을 대상으로 내진성능평가를 진행하였으며, 간편한 해석을 구현하기 위하여 축소모델을 사용하고 감쇠장치를 적용함으로써 내진성능이 향상된 정도를 평가하였다.
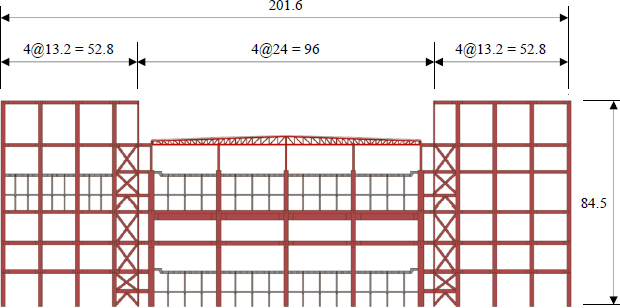
이 연구의 대상 구조물은 반도체 생산시설이며 x방향 길이 약 600 m, y방향 길이 약 200 m인 대형 구조물이다(Fig. 1 참조). 이러한 대형 구조물의 모든 부재에 비선형 속성을 적용하고 시간이력해석을 진행하면 지나치게 큰 계산 비용을 소모하게 된다. 따라서 단순화된 모델과 해석방법을 적절히 선정하여 원 구조물과의 등가성을 판단하였고, 이를 바탕으로 원 구조물의 내진성능을 평가하였다.
Facade of structure
2. 평가 절차
2.1 경계비선형해석
본 연구에서는 최대 고려 지진 하에서 대상 구조물의 비선형 거동을 정밀하게 평가하는 것이 아니고, 감쇠장치 설치 전·후의 성능변화를 평가하고자 한다. 따라서 부재 비선형 속성은 적용하지 않고 감쇠장치만 general link property를 사용, 비선형속성을 적용하여 경계비선형 해석방법을 사용하였다.
경계비선형해석에서는 구조물을 선형계와 비선형계로 나누고 비선형계에서 발생하는 비선형 부재력을 선형계에 가해지는 외부 동적하중으로 치환한다. 감쇠장치를 제외한 구조 부재들은 탄성을 유지한 상태에서 감쇠장치의 비선형성만을 고려하므로 이 해석방법의 적용은 타당하다고 할 수 있다.
2.2 모드중첩법
제진장치 이외의 구조 부재에도 비선형 속성을 적용하면 강성행렬의 변화를 고려하기 위해 직접적분법을 사용해야 하나, 대상 구조물과 같은 대형 구조물에서 이 방법은 사실상 불가능에 가까운 해석시간을 필요로 한다.
경계비선형해석을 사용하면 주요 구조체의 거동을 탄성으로 계산할 수 있다. 이는 시간이력해석 시 모드중첩법을 통해 주요 모드만을 고려한 효율적인 계산을 가능하게 해준다. 외부하중으로 치환된 감쇠장치의 비선형 부재력은 운동방정식의 우변에 위치한다. 구조물의 변위에 따라 감쇠장치의 부재력도 바뀌므로 반복계산을 통해 수렴시켜 나간다[1].
2.3 축소모델의 등가성
모드중첩법과 직접적분법의 차이를 확인하기 위하여 축소모델을 사용하였다. 전체 모델은 60개 스팬으로 이루어져 있으며 감쇠장치는 6개 스팬마다 설치되어 있다. 정적해석을 통해 전체 모델과 6-스팬 모델, 1-스팬 모델을 비교하여 등가의 관계가 있는지 확인하였다. 이후에 1-스팬 모델을 이용하여 모드중첩법과 직접적분법의 비교를 통해 두 해석방법의 등가성을 확인하였다.
3. 비선형정적해석을 통한 등가점성감쇠비 평가
비선형정적해석결과를 통해 등가점성감쇠비를 평가하였고 이를 통해 축소모델과 전체모델의 등가성을 확인하였다. 감쇠장치를 제외한 모든 구조부재는 탄성상태이므로 감쇠장치가 설치되지 않은 구조물은 비선형정적해석에서 탄성 응답이 나올 것이고 등가점성감쇠비도 0이 나온다. 따라서 감쇠장치가 설치된 모델을 대상으로 비교를 진행하였다.
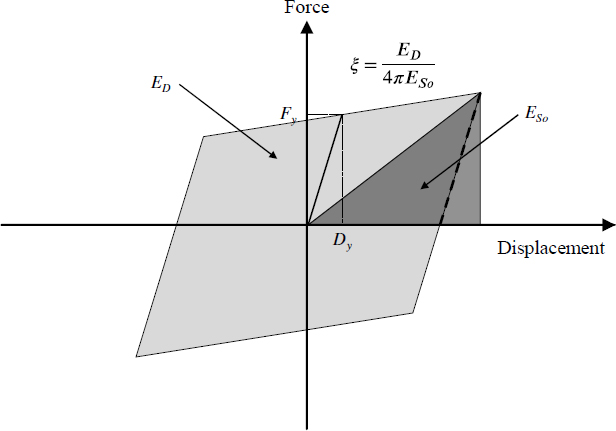
등가점성감쇠비는 이력거동에 의한 감쇠효과를 진동속도에 비례하는 점성감쇠로 나타내는 것으로 다음 Fig. 2와 같이 비선형이력거동에 의한 면적(ED)과 탄성 에너지(ESo)의 비율로 나타낸다[2],[3].
Equivalent damping ratio
3.1 모델링
원 구조물은 Fig. 1에 표현한 단면이 60개 스팬에 걸쳐 반복되는 구조로 되어 있다. 감쇠장치는 6개 스팬마다 설치되었으므로 전체 모델에서 좌측 6개 스팬을 이용하여 6-스팬 모델을 만들었고, 그 중 감쇠장치가 설치된 스팬만을 이용하여 1-스팬 모델을 만들었다.
1-스팬 모델의 경우 감쇠장치 초기강성과 항복강도를 1/6로 감소시켜 적용하여 6-스팬 모델과의 상관성을 비교하였다.
Whole model
6-span model
1-span model
3.2 비선형정적해석결과
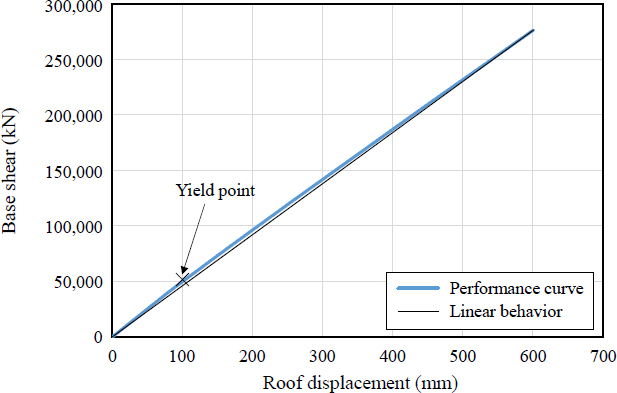
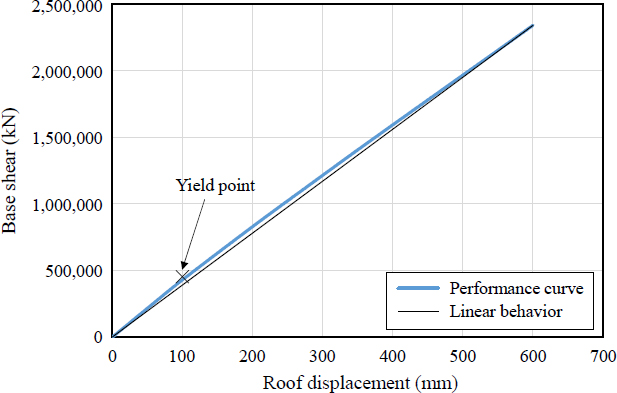
감쇠장치가 설치된 부분 중 최상층인 7층의 변위를 기준으로 600 mm를 가력하여 얻은 하중-변위 곡선으로 등가감쇠비를 계산하였고 이를 Fig. 6–Fig. 8에 그래프로 표현하였다. 각 그래프에서 파란색 곡선은 구조물의 역량곡선이며, ‘×’ 표시는 이선형 곡선을 위한 Fy점을 나타낸다. 검은색 실선은 선형을 가정한 직선이다.
Pushover result of 1-span model
Pushover result of 6-span model
Pushover result of whole model
3.3 등가점성감쇠비 비교
구조물의 역량곡선을 통해 계산된 수치들을 Table 1에 정리하였다. 감쇠장치의 성능은 동일하므로 역량곡선에서 1차 항복변위(Dy)는 동일하다고 가정하였다. 원점과 1차 항복점을 연결하여 1차강성(K1)을 구하고 항복점과 최대변위점을 연결하여 2차강성(K2)을 구하였다. 최대변위는 높이의 1 % 정도에 해당하는 600 mm로 정하였다.
Results of pushover analysis
1-스팬 모델과 6-스팬 모델을 비교하면 등가점성감쇠비가 각각 1.41 %와 1.30 %로 유사한 값이 나왔다. 반면 6-스팬 모델과 전체 모델을 비교하면 각각 1.30 %와 1.68 %로 약간의 차이가 있다. 전체 모델은 60개 스팬을 포함하고 감쇠장치는 12곳에 설치되었다. 따라서 6-스팬 모델에 비해 약간의 등가점성감쇠비 증가를 확인할 수 있다.
등가점성감쇠비를 계산할 때, 최대 변위의 설정이나 감쇠장치와 기존 골조 간의 강성비 등에 따라 값이 다르게 계산될 수 있다. 하지만 위의 결과를 살펴보면 전체 모델과 축소 모델의 등가점성감쇠비가 유사한 경향을 확인할 수 있다. 이는 감쇠장치의 비선형 거동이 각 모델에서 유사함을 의미한다. 따라서 축소 모델의 감쇠장치 거동 특성을 통해 전체 모델에 대한 감쇠장치의 효과를 확인하는 것은 타당하다고 할 수 있다.
4. 직접적분법과 모드중첩법
시간이력해석을 진행할 때 시간에 따른 하중과 강성의 변화를 고려하여 미분방정식을 통해 변위를 계산하게 된다. 탄성해석에서는 구조체 강성이 변화하지 않으므로 강성행렬의 수정이 필요하지 않고 시간의 증분에 따른 하중의 변화만 고려하므로 빠른 계산이 가능하다. 반면, 비선형해석에서는 강성행렬이 바뀌고 시간의 증분 사이에 반복계산을 통한 수렴의 과정이 필요하므로 탄성해석에 비해 많은 계산 시간이 필요하다.
상기한 대로 감쇠장치를 제외한 모든 구조체는 탄성으로 가정할 수 있다. 탄성해석의 경우 각 모드별 변위를 중첩하는 모드중첩법으로 더욱 효율적인 계산이 가능하다. 전체 모델의 모드중첩법을 통한 시간이력해석에 앞서 축소 모델을 통해 모드중첩법이 직접적분법과 얼마나 유사한 결과를 도출하는지 검토해 보았다.
Tables 2–3는 감쇠장치를 미설치/설치한 1-스팬 모델의 시간이력해석 결과를 비교한 것이다. 7개 지진파에 대해 감쇠장치가 설치된 최상층 변위를 비교하였다.
Roof displacements of 1-span model without damper
Roof displacements of 1-span model with damper
결과를 살펴보면 감쇠장치가 미설치된 구조물에서는 거의 같은 값이 나온 반면, 비선형거동이 포함된 감쇠장치 설치 구조물에서는 8 % 정도의 차이가 났다. 감쇠장치가 설치된 구조물의 경우 모드중첩법에서 약간 더 큰 변위가 계산되는 것을 알 수 있다. 이 연구에서는 감쇠장치가 설치된 구조물의 정확한 변위를 평가하는 것이 아니고 감쇠장치의 효율성을 주목하므로, 이 정도의 오차를 감안하고 판단하면 큰 무리는 없을 것으로 보인다.
5. 시간이력해석을 통한 내진성능평가
상기한 바와 같이 전체 구조물에 대해 경계비선형을 사용하고 모드중첩법을 이용한 시간이력해석의 결과는 충분한 신뢰성을 확보할 수 있다. 따라서 전체 구조물에 대해 비선형시간이력해석을 진행하고 그 결과로 질량중심점에서의 층간변위를 평가한다. 이 평가 결과를 감쇠장치 설치 전·후로 비교하여 감쇠장치의 효용성을 판단하고자 한다.
5.1 적용 지진파
구조물에 지진하중 작용 시 동적효과를 고려하여 비선형동적해석(nonlinear time history analysis)을 수행하여 지진에 대한 구조물의 거동을 확인하였다. 본 연구의 비선형동적해석에 사용된 지진파로는 50개의 부지응답해석을 통해 지진의 거리, 규모, 목표스펙트럼과의 편차를 고려하여 총 7개의 지진파를 선정하여 적용하였다. 선정된 7개의 지진에 대해 평균 응답스펙트럼을 산정하고, 해당 구조물에 해당하는 주파수대역에서의 평균응답스펙트럼과 목표스펙트럼의 scale-factor를 산정하였다. 주파수별로 산정된 scale-factor는 7개 지진의 주파수별로 동일하게 적용하여, 각 주파수별 지진 사이의 편차를 유지하였다.
50쌍 지진의 부지응답해석결과로부터 MCE 수준으로 선정된 7쌍의 지반운동은 Fig. 9 및 Table 4와 같으며, 본 연구에서는 1,000년 재현주기로 scale-factor를 적용하여 동해석을 실시하였다.
Earthquake wave spectrum
Earthquake records
5.2 최대변위 비교
감쇠장치가 설치된 최상층인 7층에서 y방향 변위의 시간이력 데이터 중 최댓값·최솟값을 각 지진파 별로 Table 5에 정리하였다. 지진파의 종류는 총 7개이며, 각 지진파 별로 x방향·y방향 지진파 한 쌍으로 이루어져 있다. 관련 기준(KDS 41 17의 7.3.4.1)에 의하면 2방향의 성분이 대상 구조물의 평면상에 교대로 2회 해석되어야 하므로 해석결과는 표와 같이 14개가 된다. 각 지진파 별 절대변위의 평균값을 비교하면 감쇠장치를 설치한 후에 약 9.8 %의 변위 감소 효과가 있는 것으로 나타났다.
Max. displacements
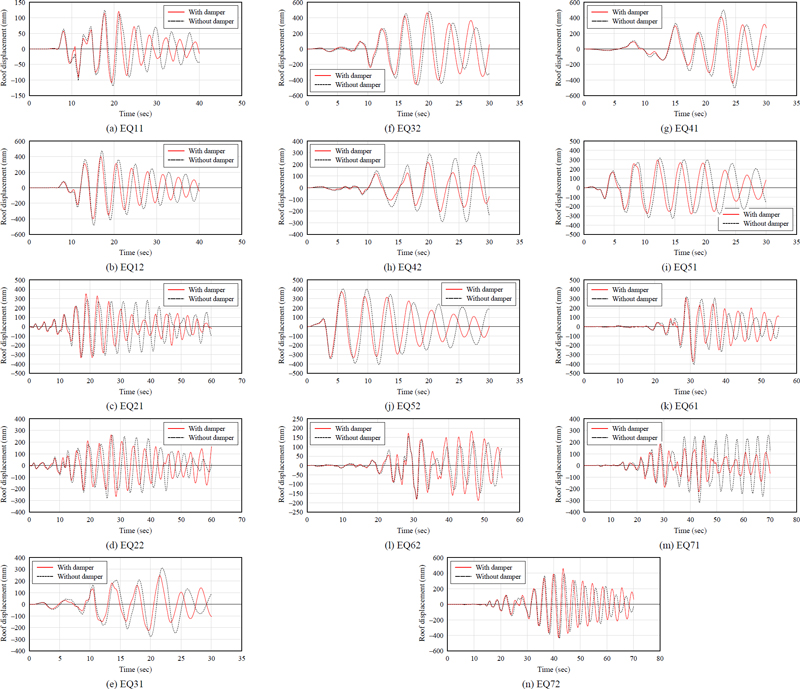
5.3 각 지진파 별 감쇠장치 설치 전·후 최상층 변위 시간이력 그래프 비교
Fig. 10은 x축에는 시간, y축에는 7층의 y방향 변위를 나타낸 시간이력 그래프이다. 이들 시간이력 그래프를 살펴보면 감쇠장치를 설치한 후에는 일반적으로 최대 변위가 감소하는 것을 알 수 있다. 하지만 일부 지진파에서는 최대 진동 이후에 감쇠장치를 설치한 경우 더 큰 변위가 발생하고 있다. 이는 강재이력형 감쇠장치의 특성에서 기인한 것이다. 강재의 특성상 감쇠장치가 일종의 스프링 역할을 하며 특정 주파수에서는 오히려 진동을 증폭시키는 효과가 있다.
Time history results of roof displacement
5.4 감쇠장치 종류에 따른 변위 및 가속도 비교
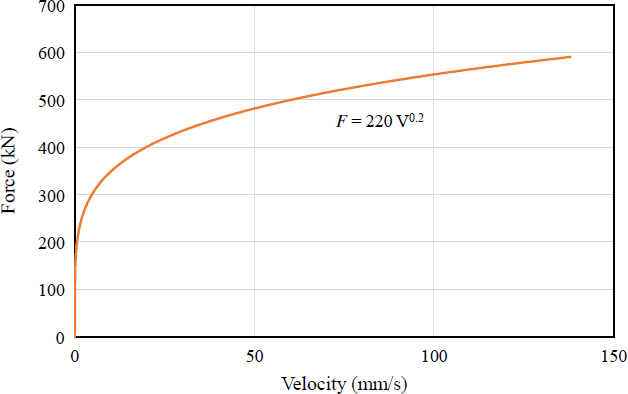
위의 모델에 사용된 강재이력형 감쇠장치의 물성치는 Fig. 11과 같다. Fig. 5의 1-스팬 모델을 대상으로 점성 감쇠장치(Fig. 12 참조)를 적용하여 결과를 비교하였다.
Steel damper property
Viscous damper property
감쇠장치 설치 유무 및 장치 종류를 달리하여 결과를 비교하여 Table 6에 정리하였다. 장치를 설치하지 않은 구조물에 비해 강재이력형 감쇠장치는 약 14 %의 최대 변위 감소 효과가 있다. 점성 감쇠장치를 설치한 경우에는 15.7 %의 최대 변위 감소 효과가 있어 강재이력형 감쇠장치와 비슷한 성능을 보였다.
Max. displacements of 1-span model
반면에 최대가속도를 비교하면 점성 감쇠장치의 최대가속도 감소 효과를 확인할 수 있다.(Table 7 참조) 강재이력형 감쇠장치의 경우에는 가속도 감소 효과가 적은 것을 알 수 있다. 따라서 강재이력형 감쇠장치를 설치할 때에는 구조물과 장치의 특성을 잘 이해하고 진행 하여야 한다.
Maximum accelerations of 1-span model
Fig. 13은 감쇠장치 종류에 따른 구조물의 최상층 변위를 비교한 그래프이다. Table 6에서 확인한 것처럼 최대 변위는 비슷한 수준을 보이나, 점성 감쇠장치를 사용한 경우에는 변위 감소 속도가 빠르며 지진파의 최대 변위 시점 이후 잔류 진동이 빠르게 감소되는 것을 확인할 수 있다.
Time history results of roof displacement
6. 결 론
본 연구는 대형 구조물에 강재이력형 감쇠장치와 점성 감쇠장치를 설치하여 내진성능의 변화를 살펴보았다. 축소모델을 통한 검증 결과 전체 모델에 경계비선형과 모드중첩법을 이용한 비선형시간이력해석의 결과가 신뢰성이 있음을 확인하였다. 다만, 이 결과는 본 연구에 사용된 것과 같이 정형이며 비틀림 거동이 거의 없는 구조물에 제한된다.
비선형시간이력해석을 통해 감쇠장치가 설치된 최상부층의 횡변위를 비교하였다. 비선형시간이력해석에는 1,000년 재현주기로 크기가 조정된 7종류의 지진파가 사용되었다. 지진파는 x방향 및 y방향 교대로 해석하여 총 14번의 해석을 수행하였다. 각각의 해석결과에서 최대 변위를 평균하여 최종 내진성능 지표로 활용하였다.
장치 설치 전에는 347.9 mm의 변위가 발생하였고 장치 설치 후에는 9.8 % 감소한 313.8 mm의 변위가 발생하였다. 이를 통해 강재이력형 감쇠장치의 설치 후 내진성능의 증가를 확인할 수 있다.
한편, 점성감쇠장치는 최대변위 제어 효과는 강재이력형 장치와 동등한 성능을 보였다. 하지만 최대가속도의 감소 측면에서는 더 뛰어난 성능을 보여주었다.
이상과 같이 감쇠장치 설치에 따른 내진성능의 향상을 확인하였고, 감쇠장치의 특성에 따른 내진성능의 변화를 통해 구조물의 응답 특성이 달라지는 것도 확인하였다. 따라서 적절한 해석방법을 사용하면 축소모델을 통한 내진성능평가가 가능함을 확인하였다.
Acknowledgments
이 연구는 삼성물산 건설부문의 지원으로 수행되었으며 이에 감사드립니다.
References
- Kim, H.J., and Choi, K.-S. (2014) Performance-Based Seismic Design Using Nonlinear Static/Dynamic Analysis, Magazine of the Korean Society of Steel Construction, KSSC, Vol.26, No.4, pp.43–49 (in Korean).
- Kim, H.-J. (2019) Rapid Seismic Evaluation for Regular Steel Moment Frames Based on Collapse Probabilities, Magazine of the Korean Society of Steel Construction, KSSC, Vol.31, No.1, pp.27–30 (in Korean).
- Yoon, B.-I., Shin, D.-H., and Park, J.-Y. (2015) Evaluation of Influence of Hysteretic Damping Device Property’s Change on Seismic Performance, Magazine of the Korean Society of Steel Construction, Vol.27, No.2, pp.35–41 (in Korean).
- Kim, T., Chu, Y., Ha, S., Shin, J., and Lee, C.-H. (2022) PART I Guidelines for Performance-Based Design and Seismic Evaluation of Steel Structures, Magazine of the Korean Society of Steel Construction, KSSC, Vol.34, No.4, pp.7–12 (in Korean).
- Lee, D.-K., Kim, S.-Y., Lee, K.-K., Choi, I.-R., Lee, K.-M., Lee, C.-H. (2022) PART II Modeling Guide for Performance-Based Design and Seismic Evaluation of Steel Structures: Guidelines on Structural Members, Magazine of the Korean Society of Steel Construction, KSSC, Vol.34, No.4, pp.19–30 (in Korean).