CFD를 활용한 이중 패널 벽체구조 무도류벽 원형 물탱크의 흐름특성 분석

1. 서 론

수원에서 취수한 상수는 병원성 미생물을 제거하기 위해 소독공정을 필수로 거쳐 소비자에게 공급된다. 염소는 소량으로도 세균 제거에 탁월한 성능을 갖기 때문에 소독공정에 일반적으로 많이 사용된다. 이러한 염소 소독공정은 정수지뿐만 아니라, 공급과정에서의 재오염을 방지하기 위해 약 0.2 ppm의 일정 잔류염소가 유지되도록 한다. 만일 소독제가 물탱크 내에서 충분한 체류시간을 갖지 않고 빠르게 유출되는 단락류가 발생할 경우 상수에서 병원균 및 미생물이 검출될 수 있으며, 소독제가 정체되는 사수부가 발생할 경우 물탱크의 부식을 발생시켜 위생 및 구조적 문제가 발생할 수 있다. 따라서 일반적인 물탱크 내부에는 일정한 흐름을 유도하여 단락류와 사수부를 방지하기 위해 도류벽이 설치된다.

도류벽은 물탱크 내부에 설치되는 간벽으로, 물탱크 내부에 수로를 형성하여 일정 구역에 정체되지 않고 충분한 체류시간을 갖도록 한다. 하지만, 도류벽 설치 상세에 따라 물탱크의 흐름 및 소독성능이 달라지기 때문에 도류벽 형태에 따른 소독능 분석 및 최적 도류벽 형태에 대한 연구가 활발히 수행되고 있다^[1]-[3]. 이처럼 도류벽 물탱크는 도류벽 설치 상세에 따라 균일한 소독성능을 발휘하지 못한다는 한계가 있다.

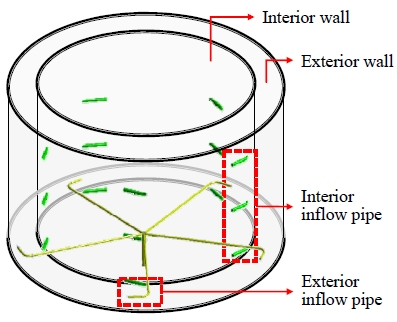
한편, 무도류벽 물탱크는 도류벽이 설치되지 않고 내부 배관 시스템에 의해 자체적 수류를 형성하도록 고안되어(Fig. 1 참조) 균일한 소독성능과 함께 기존 도류벽 물탱크 대비 시공·관리 비용 감소의 장점이 있다^[4].

Fig. 1.

Example of water tank with double panel wall[4]

무도류벽 물탱크의 자체 수류 형성을 위한 내부 배관 시스템은 두 종류의 배관(외통/내통 유입 배관)으로 나뉜다. 외통 유입 배관은 수조 중심에 수직으로 설치된 입수관과 연결되어 복수 개의 측방향 유도관으로 구성된다. 용수는 수조 중심에서 유입된 뒤 측방향 외통 유입 배관을 따라 외통부로 유입된다. 이후 내통 유입 배관을 통해 외통부의 용수가 내통부로 유입된 뒤, 물탱크 중심부 출수관을 통해 유출된다. 이렇게 무도류벽 물탱크는 자체적으로 수류 형성이 가능한 배관 구조를 갖지만, 유입 용수의 수압에 의존하여 수류 형성이 이루어지므로 배관 및 구조 시스템 변화에 따른 내부 유속 변화와 내부 수류 형성 성능에 대한 연구가 필요하다.

이 연구에서는 0.2톤 규모의 무도류벽 원형 물탱크를 대상으로 추적자 시험(tracer test)을 수행하였으며, 이를 모사하는 해석을 기반으로 CFD(computational fluid dynamics) 해석모델의 타당성을 검증하였다. 나아가, 배관 개수와 내외벽 직경비를 변수로 추가 해석을 수행함으로써 설계변수의 영향으로 유속과 내외통부의 면적 변화가 무도류벽 원형 물탱크 수류 형성 성능에 미치는 영향을 분석하였다. 이 연구는 지진파와 유체 압력의 상호작용 및 내진설계에 대한 선행연구들^[5],[6]의 정보를 기반으로 향후 추가 연구를 통해 무도류벽 원형 물탱크의 수류 형성 성능을 고려한 상세 설계기준 마련에 기여할 수 있을 것으로 기대된다.

2. 무도류벽 원형 물탱크의 CFD 모델

2.1 무도류벽 원형 물탱크의 추적자 시험

추적자 시험은 일정 농도의 추적 물질을 주입한 뒤 유출되는 농도를 측정함으로써 분산, 확산, 유출 경향을 파악하고 이를 기반으로 흐름특성을 분석하기 위하여 수행된다. 이 연구에서는 0.2톤 규모의 소형 무도류벽 원형 물탱크를 대상으로 추적자 시험을 수행하였으며, 시험 데이터를 기반으로 실제 무도류벽 원형 물탱크의 내부 흐름을 모사하는 CFD 해석모델의 타당성 검증을 수행하고자 하였다.

시험체는 외경 800 mm, 내경 600 mm의 이중 패널 벽체구조를 갖는 원형 물탱크로, 아크릴 소재를 사용하여 제작되었다. 외통 유입 배관은 수조 중심부에서 다섯 방향으로 나뉘어 외통부로 이어진다. 내통 유입 배관은 한 높이에 5개의 배관이 125 mm 간격으로 4단 설치되었으며, 설치 상세는 Fig. 2와 같다.

Fig. 2.

Details of tracer test specimen

추적자 시험은 출구에서 유출되는 추적 물질이 일정한 농도를 나타낼 때까지 일정하게 주입하는 step input test 방법과 순간적으로 많은 추적 물질을 주입하여 시간에 따라 유출되는 농도를 측정하는 pulse input test 방법이 있다^[7]. 이 연구에서는 다량의 추적 물질 주입 시 최대 농도 유출 시간을 통해 목표 수조의 처리 능력을 확인할 수 있어 일반적으로 많이 사용되는 pulse input test 방법으로 시험하였다. 시험 조건은 유량 5 L/min, 비반응성 불소 수용액을 추적 물질로 사용하였으며, 주입량은 ‘정수장 기술진단 매뉴얼’^[7]을 따라 Table 1과 같이 산정하였다.

Table 1.

Conditions of the tracer test

2.2 무도류벽 원형 물탱크의 CFD 해석모델 구축

2.2.1 추적자 모의해석

이 연구에서는 상용프로그램인 ANSYS^[8]를 사용하여 수치해석을 수행하였다. 0.2톤 규모 무도류벽 원형 물탱크 시험체는 Fig. 2와 같이 외통과 내통의 높이가 각각 650 mm, 470 mm로 상이하다. 물이 없는 빈 수조에 물이 채워지는 과정을 모사할 경우, 공기압의 영향이 크기 때문에 실제 내·외통의 상이한 높이를 반영해야 한다. 하지만 담수의 높이가 내통의 높이를 초과하지 않도록 물이 채워진 상태에서 추적자 시험이 수행되었으므로, 해석 시간 단축을 위해 CFD 모델의 높이는 내통 높이로 통일하여 단순화하였다. 이외의 규격은 시험체와 동일 조건으로 모델링하였다.

입구의 경계조건은 유량 5 L/min 시험 조건과 10 mm의 유입관 직경을 고려하여 1.061 m/s 속도 조건을 적용하였다. CFD 해석은 유체의 운동을 기술하기 위해 질량보존법칙을 기반으로 한 연속방정식을 따르는데, 입구와 출구의 경계조건을 모두 속도 조건으로 적용할 경우, 전체 질량의 균형을 위해 정밀한 값이 요구된다. 이 연구에서는 출구에 압력 조건을 지정함으로써 해석의 수렴성 향상 및 역류 등의 문제를 방지하고자 하였다.

출구의 상세 압력 조건은 시험에서 출구의 압력 조절을 위한 추가 장치가 사용되지 않으므로, 기본 대기압 조건을 적용하였다. 수조 내에 위치한 배관의 출구면은 격자 Matching 조건을 적용하여 유체의 이동이 가능하도록 하였다. 이외의 경계면은 No-slip의 벽 조건을 적용하였는데, 교반기와 같이 움직이는 면의 경우 정확한 해석을 위하여 벽면에서의 유체 속도를 지정해주지만, 대상 모델의 벽면은 모두 고정면으로 벽면에서 유체 속도를 0으로 가정하는 No-slip 조건을 지정하였다^[8].

정확한 CFD 모사에는 난류모델의 선정이 중요하며, 대상 해석모델은 내부 배관 시스템으로 인해 다소 복잡한 형상을 갖는다. 따라서 복잡한 난류 흐름 예측에 적합하며 선행 연구자들이 적용한 Realizable 난류운동에너지(k)-에너지소산율(ϵ) 난류모델을 사용하였다^[9],[10].

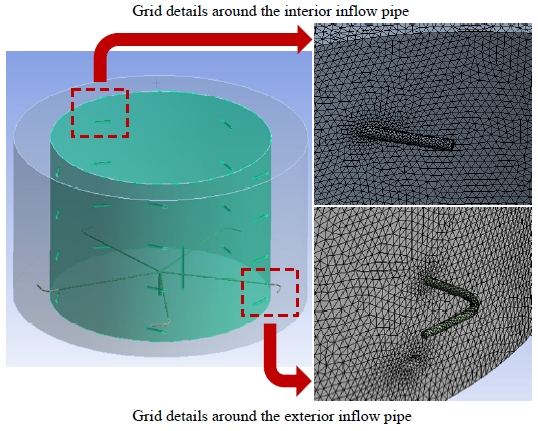
Fig. 3는 해석모델의 격자 형상을 나타내며, 상세 정보는 Table 2와 같이 1,071,813개 노드, 5,736,766개 요소를 생성하였다. 해석의 정확성을 높이기 위해 배관과 벽면 경계는 더 조밀하게 격자를 생성하였으며, 무도류벽 원형 물탱크는 수조 내에 배관이 위치함에 따라 곡선 및 곡면에 대해 격자 형성이 유리한 사면체 요소를 사용하였다. 수학적으로 유체 흐름을 모사하는 CFD 해석에서 격자 품질은 해석의 수렴성뿐만 아니라 유체 흐름 모사의 정확성에도 영향을 미치므로, 격자 품질에 대한 평가가 요구된다. 격자의 기하학적 특성을 평가하는 중요한 지표인 직교 품질(orthogonal quality)은 격자의 직교성을 나타내며, 최소 0.1 이상의 값이 요구되고, 1에 가까울수록 좋은 격자 품질을 의미한다^[8]. 격자 생성 결과, 해석모델의 직교 품질은 0.7 이상으로 나타났다.

Fig. 3.

Details of grid around the inflow pipe

Table 2.

Information on the grid in the model

Pulse input test로 수행된 추적자 시험의 일시 투입 조건을 모사하기 위해 추적 물질이 1.5초 동안 주입되도록 지정해주었다.

2.2.2 추적자 시험 및 모의해석결과

추적자 시험 및 모의해석 결과 시간별 불소 유출 농도는 Fig. 4와 같다. 초기 불소 유출량이 점차 증가하고, 약 20분 시점을 기준으로 유출량이 감소하는 경향이 유사하게 나타났으며, 최대 유출 농도는 약 96.3 %의 정확도로 나타났다.

Fig. 4.

C-curves, C(t)

시험 대비 해석결과에서 불소의 초기 유출량이 많은 것으로 나타나는데, 이는 입수관과 외통 유입 배관에서 이루어지는 초기 확산 과정이 해석에서 빠르게 진행된 것으로 판단된다. 무도류벽 물탱크에서 추적 물질의 초기 확산 과정은 입수관과 외통 유입 배관에서 이루어지는데, 고농도의 물질이 외통부까지 도달하는 시간을 정확히 모사하기 위해서는 1차 확산 과정을 거치는 입수관과 외통 유입 배관의 격자가 상당히 조밀해야 한다. 하지만, 배관의 격자만 조밀하게 형성하는 경우에는 격자 품질의 저하로 해석 수렴성과 정확성이 저하될 수 있으며, 배관을 기준으로 전체 격자를 조밀하게 형성하는 경우에는 비효율적인 해석 시간 증가로 이어진다.

이 연구에서는 무도류벽 물탱크의 전체 흐름 경향 파악을 목표로 함에 따라 수렴성과 해석 시간의 효율을 고려하여 해석모델을 구축하였으며, 추적 물질의 초기 주입 과정이 시험 대비 빠르게 수행됨에 따라 해석의 초기 유출량이 많게 나타났으나, 전체적인 유출 경향과 최대 유출 농도에서 높은 정확도를 보인다. 따라서 전체적인 혼화·분산 경향을 충분히 모사하고 있다고 판단하였다.

3. 매개변수에 따른 흐름특성 분석

3.2 배관 개수에 따른 흐름특성 분석

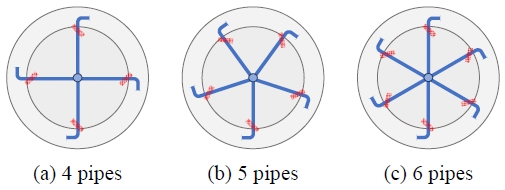
내외통 유입 배관 개수 증감에 따른 수류 형성 성능을 확인하기 위하여 Fig. 5와 같이 3개의 모델을 대상으로 흐름특성을 분석하였다. Fig. 5(b)는 앞서 타당성을 검증한 0.2톤 규모의 무도류벽 원형 물탱크 모델로 외통 및 내통 유입 배관은 원주 방향으로 5개 설치된다. 타당성 검증 모델에서 외통 유입 배관 개수를 4개, 6개로 증감하여 추가 해석을 수행하였으며, Fig. 5(a) 및 Fig. 5(c)와 같이 내통 유입 배관은 외통 유입 배관과 동일 위치에 설치되므로 한 높이에 설치되는 내통 유입 배관의 수는 외통 유입 배관과 동일하게 증감한다.

Fig. 5.

Details according to number of exterior inflow pipe

3.2.1 배관 개수에 따른 흐름특성

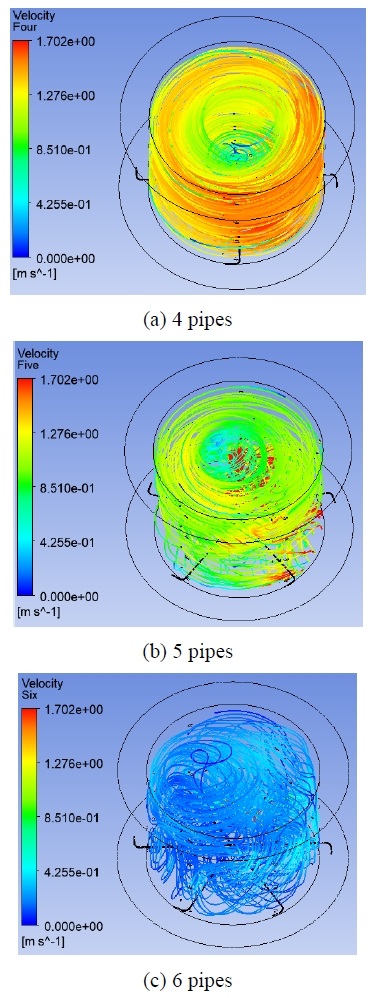
무도류벽 원형 물탱크에서 외통부는 내통부 대비 면적이 작아 내외벽이 도류벽과 같은 역할을 하며 원활한 수류 형성이 가능하다. 하지만 내통부는 비교적 넓은 면적을 가지며, 중심에 출수관이 위치하므로 무도류벽 원형 물탱크 내통부의 수류는 내부 용수 위생에 지배적 영향을 미친다. 따라서 이 연구에서는 내통부의 유속 분포를 대상으로 흐름특성을 분석하였으며, 외통 유입 배관 개수에 따른 내통부 유속 분포는 Fig. 6와 같다.

Fig. 6.

Velocity contour of internal tank according to number of the inflow pipe

무도류벽 원형 물탱크는 수조 외곽부터 원주 방향의 수류가 형성되어 수조 중심부에서 유출되는 배관 시스템을 갖는다. Fig. 6(a)과 Fig. 6(b)에서는 원주 방향 수류가 내통부 외곽부터 형성되는 것을 확인할 수 있지만, 배관 개수가 6개로 가장 많은 모델의 경우 Fig. 6(c)와 같이 계획한 수류가 형성되지 않는 것으로 나타났다. 또한 배관 개수가 4개로 가장 적은 Fig. 6(a)에서는 수조 중심부까지 원주 방향의 수류가 확인되나, Fig. 6(b)에서는 외통 유입 배관 개수의 증가함에 따라 1차 수류가 형성되는 외통부 유입 용수의 유속이 감소하기 때문에 내통부의 수류 형성 성능이 저하됨을 알 수 있다.

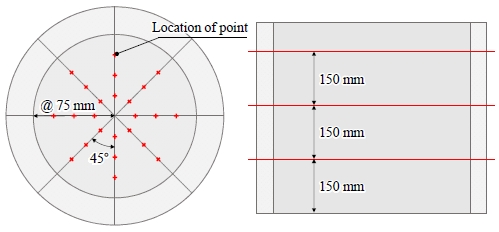
Fig. 6(a)과 Fig. 6(b)에서 확인한 바와 같이 내통부의 외곽은 내통 유입 배관과 근접하므로 비교적 수류 형성이 원활하다. 하지만 물탱크 중심부 및 높이별 흐름이 균일하지 않을 경우, 소독제가 특정 구간에 오래 체류함에 따라 스테인리스의 부식, 용수의 위생성 저하의 문제가 발생할 수 있다. 따라서 Fig. 7과 같이 물탱크 중심부터 외곽까지의 거리와 물탱크 높이에 따른 총 72개 지점의 유속을 확인하였다. 중심에서 75 mm, 150 mm, 225 mm 거리 지점의 유속을 확인하였으며, 각 거리의 유속 데이터는 원주 방향으로 45°씩 8개 지점의 평균값을 사용하였다. 한 높이에서 총 24개 지점의 데이터를 추출하였으며, 150 mm, 300 mm, 450 mm 높이의 유속을 확인하였다.

Fig. 7.

Details of velocity data extraction points

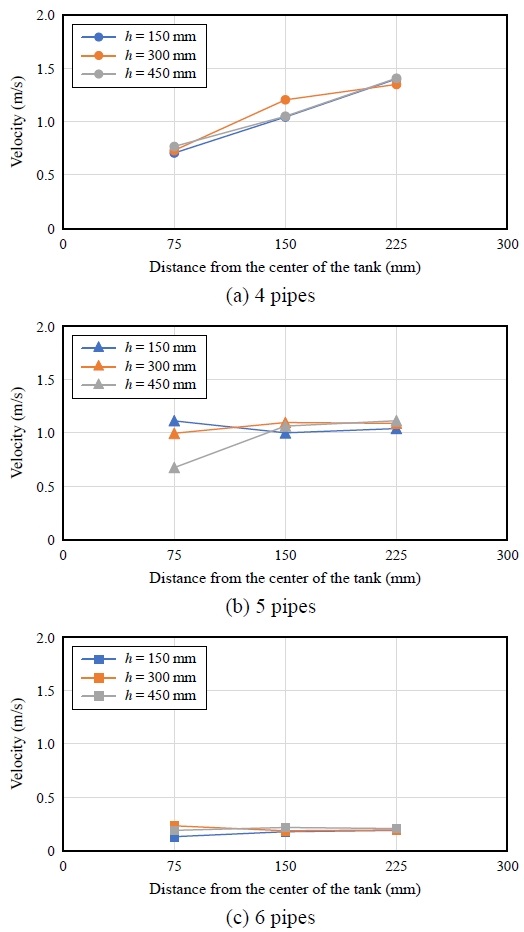
배관이 4개인 경우, Fig. 8(a)과 같이 높이별 유속 분포가 유사하며, 중심으로부터 225 mm 거리의 유속은 약 1.39 m/s, 75 mm 거리의 유속은 약 0.73 m/s로 외곽의 유속이 가장 빠르게 형성되었다. 즉, 동일 유량에서 배관 개수 감소로 용수가 빠르게 유입될 경우 내통부 외곽부터 원주 방향 수류가 강하게 형성되나, 중심부와 가까워질수록 유속이 느려진다. 따라서 수조 규모가 증가할 경우, 내통부 외곽에서 소독제의 체류시간이 길어질 수 있으므로 용량과 유량을 고려한 검토가 필요하다고 판단된다. 배관이 1개 증가하자 Fig. 8(b)과 같이 담수 높이와 근접한 450 mm 높이의 중심부 유속이 약 0.38 m/s 낮게 나타났으나, 이를 제외한 모든 지점의 유속은 최대 약 0.11 m/s 차이로 유사하게 나타났다.

Fig. 8.

Velocity according to distance from the center of the tank

무도류벽 원형 물탱크의 내통부 수류는 내통 유입 배관에 의해 외곽에 형성되는 원주 방향 수류와 중심부 출수관에서 유출되는 용수에 의해 형성되는 수류로 구분할 수 있다. Fig. 8(b)은 배관 4개 모델 대비 유입 용수의 유속이 일부 감소함에 따라 내통부 외곽과 중심부의 수류의 조합으로 내통부 유속 분포가 전체적으로 균일한 것으로 나타났다. 배관 6개로 용수가 가장 느린 속도로 유입될 경우 Fig. 8(c)와 같이 내통부 유속은 최대 0.23 m/s로 느리게 나타남에 따라 Fig. 6(c)에서 확인한 바와 같이 계획된 수류가 원활하게 형성되지 않음을 알 수 있다.

내외통 유입 배관 개수에 따른 해석 결과, 무도류벽 원형 물탱크는 배관 시스템에 의해 수류 형성이 가능하나, 안정적 수류 형성을 위해선 유속의 최소 기준이 요구된다. 따라서 무도류벽 원형 물탱크의 배관 구조의 상세를 결정하기 위해선 용량 및 유량 조건을 고려한 수류 형성 성능의 평가가 선행되어야 함을 알 수 있다.

3.2.2 추적자 모의해석결과

배관 개수에 따른 세 모델의 추적자 모의해석을 수행하고 이를 기반으로 수리학적 지표를 통해 흐름특성을 비교하였다. 수리학적 평가 방법은 대표적으로 Index 법과 Reghun & Argaman 법이 있다^[11],[12]. 각 방법에서 제시하는 지표를 통해 수조 내의 교반 정도, plug flow, 단락류 정도 등의 흐름특성을 평가할 수 있다. Rebhun & Argaman 법은 시간별 추적자의 누적 농도 곡선, F(t)를 변형한 1 – F(t) 곡선을 작도한 뒤 그래프에 선을 그어 도식적으로 지표를 산정하는 방법으로, 주관적 경향이 있고 음의 값이 나오는 등의 한계가 있다. 반면 Index 법은 수리학적 분석 방법으로 이론적 체류시간과 일정 농도가 유출될 때의 시간의 비율로 지표를 산정하며, 상대적 비율을 통해 효율을 비교할 수 있어 일반적으로 많이 사용된다. 이 연구에서는 배관 개수에 따른 세 모델에 대한 추적자 모의해석을 수행하였으며, Index 법의 지표를 활용하여 수리학적 효율을 비교하였다.

배관 개수에 따른 세 모델의 추적자 모의해석 결과, 시간별 추적자의 유출 농도 및 누적 농도는 Fig. 9 그래프와 같으며, Table 3는 Fig. 9의 추적자 모의 해석결과를 기반으로 산정한 일정 농도의 추적자가 유출될 때의 시간을 나타낸다. Fig. 9에서 확인할 수 있듯 세 모델의 추적자 유출 경향은 유사했으나, 최대 농도 유출량이 배관 4개 모델에서 최대 약 4.86 %p 높게 나타났다.

Fig. 9.

Results of tracer simulation

Table 3.

Results of the tracer simulation

Table 4는 Table 3의 결과로부터 산정한 Index 법의 지표를 나타낸다. β 값은 1에 가까울수록 plow flow(압축형 유동)에 가까움을 의미하며, Morrill index는 교반 정도를 나타내는 지표로서 이상적인 plug flow에서는 1, 완전혼합 반응조에서는 1보다 매우 큰 값을 나타낸다. modal index는 plug flow 정도를 나타내는 지표로 1에 가까울수록 plug flow에 가까움을 의미하며, short circuiting index는 값이 작을수록 단락류가 높음을 의미한다. 여기서, plug flow는 유체 흐름에 의한 이동 이외의 운동이 일어나지 않는 이상적 흐름이며, 완전혼합 반응조는 유입 유체가 짧은 시간 동안 완벽히 혼합되는 특성을 갖는다. 따라서 plug flow에 가까울수록 유입 순서대로 인접한 유체 간 혼합 없이 유입량만큼 유출되는 특성을 갖기 때문에, 짧은 시간에 높은 농도의 유체가 유입될 경우 유출 시 높은 잔류농도를 가지며 소독공정에 어려움이 있을 수 있다. 반면 완전혼합 반응조에 가까울 경우 시약이 유입 즉시 전체적으로 균등하게 분산됨에 따라 유입한 유체의 일부가 즉시 유출되기 때문에 동일 처리효율에서 비교적 큰 용량이 요구된다.

Table 4.

Index value of the tracer simulation

세 모델의 β 값과 modal index는 최대 약 0.03 차이로 유사하며 1보다 작은 값으로 나타났다. 또한 Morrill index는 최대 약 0.02 차이로 유사하며 1보다 매우 큰 값으로 나타났다. 즉, 세 모델 모두 교반정도가 높으며, plug flow보다 완전혼합 반응조에 가까운 것으로 나타났다. 한편, 배관 4개 모델의 단락류 정도가 가장 높게 나타났다. 이는 모든 모델의 규모가 0.2톤으로 비교적 작으며, 앞서 확인한 바와 같이 배관 4개 모델의 수류 형성 성능이 가장 높기 때문에 유출되기까지의 시간이 세 모델 중 가장 짧은 것으로 판단된다.

3.3 내외벽 직경비(d/D)에 따른 흐름특성 분석

무도류벽 원형 물탱크는 외통부에 이어서 내통부로 두 단계의 수류가 계획된다. 설계변수인 내외벽 직경비(d/D)에 따라 내외통부 면적이 달라지며, 이는 무도류벽 원형 물탱크 수류 형성에 영향을 미칠 수 있다. 따라서 동일 유량에서 내외벽 직경비의 영향을 확인하기 위하여 외통부 직경(D)은 800 mm로 고정하였으며, 내통부 직경(d)을 500 mm, 600 mm, 700 mm로 나누어 세 모델에 대해 추가 해석을 수행하였다. 세 모델의 배관 개수는 5개로 설정하고, 해석조건은 2.2.1과 같이 적용하였다. 앞서 배관 개수를 변수로 유동해석을 수행한 결과, 유속 분포를 통해 수류 형성 성능을 비교하였으나 수조의 용량이 0.2톤으로 작기 때문에 추적자 모의해석결과는 모두 유사하게 나타났다. 따라서 내외벽 직경비에 따른 세 모델은 내부 유선 및 유속 분포를 통해 흐름특성을 분석하였다.

Fig. 10은 내외벽 직경비에 따른 해석결과로 유선 및 유속 분포를 나타낸다. 모든 모델에서 외통부는 계획된 수류가 비교적 원활하게 형성되지만, 내통부의 경우 내외벽 직경비가 증가함에 따라 유속이 감소하는 것을 확인할 수 있다. 앞서 배관 개수가 변수인 경우에서 확인한 바와 같이 내부 유속의 감소는 무도류벽 원형 물탱크의 수류 형성 성능 감소로 이어질 수 있다. 즉, 무도류벽 원형 물탱크에서 외통부는 내외벽 직경비가 증감하여도 내외벽이 도류벽 역할을 하기 때문에 수류 형성 성능에 변화가 크지 않은 것으로 나타났다. 하지만 내통부는 내외벽 직경비 증가로 내통부 면적이 증가할 경우, 동일 유량에서 수조 용량 증가와 같은 효과를 보인다.

Fig. 10.

Velocity contour according to diameter ratio of interior and exterior wall

4. 결 론

이 연구에서는 자체 수류 형성을 목표로 고안된 무도류벽 원형 물탱크의 설계변수에 따른 수류 형성 성능을 분석하였다. 0.2톤 규모 소형 무도류벽 원형 물탱크의 추적자 시험 및 모의해석을 수행하여 CFD 모델의 타당성을 검증하였다. 나아가, 동일 유량에서 배관 개수에 따른 유입 용수의 유속 변화와 내외벽 직경비를 변수로 흐름특성을 분석하였다.

• (1) 0.2톤 무도류벽 원형 물탱크 CFD 모델의 추적자 모의해석 결과, 투입 초기 배관에서 추적자의 확산 과정이 시험 대비 빠르게 수행되어 해석의 초기 유출량이 많게 나타났으나, 약 20분 시점을 기준으로 최고 농도가 유출된 뒤 유출량이 감소하는 경향과 최대 유출 농도가 시험과 약 96.3 %의 정확도를 보이므로 CFD 모델이 실제 무도류벽 원형 물탱크의 교반 및 분산 경향을 충분히 모사하고 있다고 판단된다.
• (2) 내외통 유입 배관 개수를 변수로 해석한 결과, 무도류벽 원형 물탱크는 유입 용수의 수압에 의해 자체 수류가 형성되는 배관 시스템을 갖기 때문에 동일 유량 조건에서 배관 개수가 증가는 내부 유입 용수의 유속 감소로 이어지며 수류 형성 성능이 저하되는 것으로 나타났다.
• (3) 용수의 유입 속도가 빠를 경우, 내통부 외곽의 원주 방향 수류가 강하게 형성되어 내통부 중심 대비 외곽의 유속이 빠른 흐름을 갖기 때문에 물탱크의 용량이 증가할 경우 외곽에서 소독제의 체류시간이 길어질 것으로 판단된다.
• (4) 0.2톤 규모 무도류벽 원형 물탱크 수리학적 지표를 산정한 결과, β 값과 modal index가 1 이하, Morrill index는 1보다 매우 큰 값을 가지며 완전혼합 반응조에 가까운 흐름특성을 갖는 것으로 나타났다.
• (5) 0.2톤 무도류벽 원형 물탱크에서 외통부는 내통부 대비 면적이 작고, 내외벽이 도류벽의 역할을 함에 따라 내외벽 직경비 변화에 따른 수류 형성의 변화는 미소한 것으로 확인되나, 내통부의 경우 내외벽 직경비의 증가로 면적이 증가함으로 인해 내부 유속 저하로 수류 형성 성능이 저하되는 것으로 나타났다.
• (6) 이 연구에서는 추적자 시험을 모사하여 무도류벽 원형 물탱크 CFD 모델의 타당성 검증을 기반으로 하여 확장 해석을 수행함에 따라 0.2톤의 용량과 5 L/min의 유량을 고정하였으나, 향후 대용량 및 다양한 유량 조건을 변수로 추가 연구를 수행함으로써 안정적 수류 형성을 위한 무도류벽 원형 물탱크의 설계 상세기준이 정립될 수 있을 것으로 사료된다.

Acknowledgments

본 연구는 중소벤처기업부와 중소기업기술정보진흥원의 “지역특화산업육성+(R&D, S3090747)”사업과 ㈜포스코의 지원을 받아 수행된 연구결과임.

References

• Cho, Y., Roh, J., Bin, J., Kim, T.K., and Choi, Y.J. (2011) Evaluation of Economic L/W Ratio and the Best Shape of Baffle in Clearwell by Using CFD, Journal of Korean Society of Environmental Engineers, KSEE, Vol.33, No.6, pp.432-438 (in Korean). [https://doi.org/10.4491/KSEE.2011.33.6.432]
• Foukrach, M., Bouzit, M., Ameur, H., and Kamla, Y. (2019) Influence of the Vessel Shape on the Performance of a Mechanically Agitated System, Chemical Papers, Springer, Vol.73, pp.469-480. [https://doi.org/10.1007/s11696-018-0606-4]
• Zhou, S., Yang, Q., Lu, L., Xia, D., Zhang, W., and Yan, H. (2022) CFD Analysis of Sine Baffles on Flow Mixing and Power Consumption in Stirred Tank, Applied Sciences, MDPI, Vol.12, No.11, 5743. [https://doi.org/10.3390/app12115743]
• Heo, S.J., Yoh, K.Y., and Kim, J.K. (2023) Analysis of Behavior Characteristics According to Structural Details of Circular Water Tank with Double Panel Wall, Journal of Korean Society of Steel Construction, KSSC, Vol.35, No.2, pp.56-69 (in Korean). [https://doi.org/10.7781/kjoss.2023.35.2.059]
• Heo, S.J., Yoh, K.Y., and Kim, J.K. (2022) Design of Large Capacity Water Tank with Stainless Corrugated Panel Wall, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.1, pp.55-66 (in Korean). [https://doi.org/10.7781/kjoss.2022.34.1.055]
• Kang, T.-W., Yun, J.-H., Yang, H.-I., and Jeon, J.-S. (2020) Fluid Pressure Response of Steel Water Tanks Accounting for the Effect of Vertical Ground Motion, Journal of Korean Society of Steel Construction, KSSC, Vol.32, No.3, pp.149-159 (in Korean). [https://doi.org/10.7781/kjoss.2020.32.3.149]
• Ministry of Environment (2021) Technical Treatment Manual for Water-Purification Plants, Korea (in Korean).
• ANSYS Inc. (2021) ANSYS Fluent User’s Guide, USA.
• Shih, T.-H., Liou, W.W., Shabbir, A., Yang, Z., and Zhu, J. (1994) A New k-ϵ Eddy Viscosity Model for High Reynolds Number Turbulent Flow, Computers & Fluids, Elsevier, Vol.24, No.3, pp.227-238. [https://doi.org/10.1016/0045-7930(94)00032-T]
• Shaneed, R., Mohammadian, A., and Gildeh, H.K. (2019) A Comparison of Standard k-ϵ and Realizable k-ϵ Turbulence Models in Curved and Confluent Channels, Environmental Fluid Mechanics, Springer, Vol.19, pp.​543-568. [https://doi.org/10.1007/s10652-018-9637-1]
• Hart, F.L., and Gupta, S.K. (1978) Hydraulic Analysis of Model Treatment Units, Journal of the Environmental Engineering Division, American Society of Civil Engineers, Vol.104, No.4, pp.785-798. [https://doi.org/10.1061/JEEGAV.0000798]
• Rebhun, M., and Argaman, Y. (1965) Evaluation of Hydraulic Efficiency of Sedimentation Basins, Journal of the Sanitary Engineering Division, American Society of Civil Engineers, Vol.91, No.5, pp.37-48. [https://doi.org/10.1061/JSEDAI.0000576]