[ Article ]

Journal of Korean Society of Steel Construction - Vol. 35, No. 4, pp.169-177

ISSN: 1226-363X (Print) 2287-4054 (Online)

Print publication date 27 Aug 2023

Received 17 May 2023 Revised 25 May 2023 Accepted 25 May 2023

DOI: https://doi.org/10.7781/kjoss.2023.35.4.169

보강플레이트를 갖는 파형웨브 보의 전단접합부 설계법 제안

김대경¹^{, *}

1교수, 울산대학교, 건축학부

Design Method for Shear Joints of Sinusoidally Corrugated Web Beams with Reinforcing Plates

Kim, Dae Kyung¹^{, *}

1Professor, College of Architecture and Design, University of Ulsan, Ulsan, 44610, Korea

Correspondence to: ^* Tel. +82-52-259-2271 Fax. +82-52-259-1690 E-mail. dkkim13@ulsan.ac.kr

초록

이 논문에서는 보강플레이트를 활용한 정현파형 주름웨브 보(파형웨브 보)의 볼트 전단접합부의 설계법을 제안하였다. 선행연구의 실험 및 해석결과를 바탕으로 엄격한 제한을 두어 안전한 접합설계를 도모하였다. 실제 PEB 골조 설계예제에 제안방법을 적용하여 전단접합부를 설계하는 방법을 자세히 소개하였으며, 설계예제를 부분골조로 모델링하여 유한요소해석을 통해 제안방법의 타당성을 검토하였다. 해석결과는 제안방법으로 설계한 보강플레이트를 갖는 파형웨브 보의 전단접합부가 충분히 탄성거동함을 보여주었다.

Abstract

This paper presented a design method for bolted shear joints of sinusoidal corrugated web beams utilizing reinforcing plates. Based on the experimental and analytical results of previous study, a safe shear joint design was achieved by imposing strict limitations. The method of designing shear joints by applying the proposed method to an PEB frame design example was introduced in detail. And the feasibility of the proposed method was examined through finite element analysis by modeling the design example as a partial frame. The analysis results show that the shear joint of the corrugated web beam with the reinforcing plate designed by the proposed method has sufficient elastic behavior.

Keywords:

Sinusoidally corrugated web beams, Bolted connections, Shear connections, PEB, Design methods

키워드:

파형웨브 보, 볼트접합, 전단접합, 설계법

1. 서 론

정현파 주름웨브를 갖는 보(이하 파형웨브 보)는 플랜지를 휨모멘트, 파형웨브를 전단력만 담당하도록 설계를 단순화할 수 있고, 파형웨브의 기하학적 형상으로 인해 수직보강재 없이 대형단면을 구성하기 쉬워 공업화박판강구조물(pre-engineered metal building system, 일명 PEB 구조)에 주로 활용되고 있다.

일반적인 PEB 골조의 이음은 마찰접합보다는 현장시공이 단순한 단부강판 접합을 사용하며, 국외에서는 파형웨브를 적용한 PEB 골조뿐 아니라 파형웨브 보와 일반 압연형강 기둥 또는 보의 접합에 대해서도 단부강판 접합을 주로 적용하고 있다^[1],[2]. 이에 웨브 주름판재로 구성된 공업화박판강구조 설계지침^[3]에서는 파형웨브 보를 적용한 PEB 골조의 접합 및 파형웨브 보와 타(他) 부재를 접합 또는 병행하는 경우에 대해서도 단부강판 접합을 기본 원칙으로 명시하고 있다. 그러나 파형웨브 보에 타 부재를 접합할 경우 파형웨브 굴곡형상으로 인해 파형웨브에서 접합부를 구성하기가 다소 불편한 문제가 있다.

국내에서는 파형웨브 강판 간의 볼트접합 성능 검증이 이루어졌으나^[4]-[6], 보의 전단연결과 관련한 연구는 수행된 바 없다. 국내 철골조는 전단탭을 이용하여 전단접합으로 처리하는 것이 보편적이므로 선행연구^[7]를 통하여 파형웨브로 구성된 큰보와 작은보의 전단접합상세를 제안한 바 있다. 선행연구에서 제안한 볼트 전단이음 상세는 기존 상세보다 제작 및 시공의 편의를 향상시키면서도 단순보 전단접합성능이 충분히 발휘됨을 실험적, 해석적으로 검증하였다.

이 논문에서는 선행연구에서 제안한 상세에 대하여 설계법을 상세히 제안하고 설계예제를 작성하였다. 이후 설계예제에 대한 부분골조 유한요소해석을 수행하여 제안한 설계법의 타당성을 입증하였다.

2. 파형웨브 보 전단접합 설계법 제안

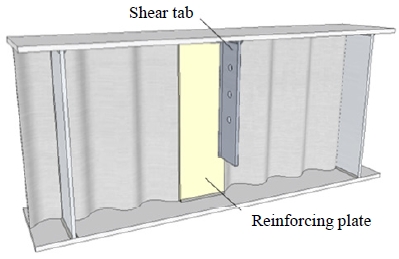
Fig. 1은 선행연구에서 제안한 보강플레이트와 전단탭으로 구성된 파형웨브 보의 모습을 보여준다. 제안상세는 보강플레이트를 적용을 통해 볼트접합부를 파형웨브의 굴곡과 무관하게 구성할 수 있는 장점이 있다.

Fig. 1.

Configuration of corrugated web beam with reinforcing plate and shear tab

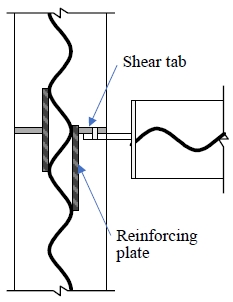
일반적인 큰보와 작은보를 단순 전단접합한 경우, 국내외 많은 설계예제집에서 볼트접합부와 용접접합부의 다양한 한계상태를 상세히 검토하고 있으나, 편심하중을 받는 큰보에 대해서는 발생 가능한 비틀림에 대해 큰보가 저항할 수 있어야 한다는 점을 간단히 언급만 하고 있다^[8]-[10]. Singapore Structural Steel Society ^[11]는 Fig. 2와 같이 웨브 한 면에만 볼트 전단접합하게 될 때 큰보의 편심하중이 작용하여 비틀림과 좌굴이 유발할 수 있음에 주의할 것을 언급하였다. 이 경우도 비틀림이나 웨브의 좌굴을 방지하기 위해서는 접합부 반대편에도 플레이트를 보강할 것을 권고하는 정도이다.

Fig. 2.

Girder web buckling shape in one-side shear connection under large shear force[11]

파형웨브 보는 파형웨브의 특성상 얇은 두께를 적용하더라도 면외방향의 비틀림강성이 평웨브 보의 그것보다 높다. 그러나 동일한 부분높이를 갖는 보강플레이트와 전단탭의 조합을 적용하는 경우 전단탭 단부의 지압력이 큰보 파형웨브의 골에 직접적으로 가해져 파형웨브 골에 국부변형이 발생하고 비틀림이 유발되는 것을 선행연구의 실험과 해석을 통해 관측하였다. 따라서 파형웨브 보는 큰 편심하중에 대한 비틀림 저항 검토가 요구되며, 제안 상세에 제한을 두어 보수적으로 설계할 필요가 있다.

이 논문에서는 선행연구^[7]의 실험결과와 유한요소해석결과를 바탕으로 다음과 같은 제한 조건에서 보강플레이트를 갖는 파형웨브 보의 전단접합 설계법을 제안하고자 한다.

큰보의 파형웨브 춤이 750 mm 이하인 경우에는 전높이 또는 부분높이를 갖는 보강플레이트와 전단탭의 조합을 적용해도 무방하다. 고하중을 받는 테두리 보와 같이 비틀림이 크게 유발될 가능성이 높을 경우에는 보강플레이트와 전단탭을 가급적 전높이로 제작하여야 한다.

큰보의 파형웨브 춤이 1,000 mm 이상인 대단면일 경우 작은보는 웨브 높이 500 mm 이하를 적용하며, 작은보의 하중은 항복모멘트의 50 % 이하로 제한한다.

큰보 양측에 작은보가 위치하여 양방향의 편심 모멘트를 받는 경우와 같이 비틀림이 유발될 가능성이 낮다면 큰보의 제작성을 고려하여 부분높이를 갖는 보강플레이트와 전단탭을 적용하여도 무방하다. 단, 동일한 부분높이를 갖는 보강플레이트와 전단탭의 조합은 강성저하의 요인으로 작용하기 때문에 보강플레이트의 보강효과를 기대하기 어려우므로 접합상세로 적절하지 않다. 부분높이 보강플레이트는 작은보 춤의 1.5배 이상의 높이를 확보하고, 부분높이 전단탭은 작은보 춤 이하로 적용해 파형웨브의 국부적 변형을 제어한다. 국내의 제작가능한 파형웨브의 최대 춤은 1,500 mm로, 여기에 연결되는 작은보의 춤이 약 300 mm - 500 mm일 것임을 감안하면 전술한 제한조건은 충분한 보강효과를 보여줄 것으로 판단된다.

큰보에 비틀림이 유발될 가능성이 있으나 부분높이의 전단탭을 사용하는 경우, 큰보 파형웨브의 국부적인 변형을 제어하기 위해 필요한 보강플레이트의 비틀림 저항을 식 (1)을 통해 검토한다.

I w + I p l a 3 / 2 × min ⁡ F y, w, F y, p l ≥ R × e

(1)

여기서, I_w와 I_pl은 각각 큰보 파형웨브와 보강플레이트의 유효 단면2차모멘트, a₃는 큰보 파형웨브의 정현파고, F_y_,_w와 F_y_,_pl은 각각 큰보 파형웨브와 보강플레이트의 공칭항복강도이다.

아래의 경우에 따라 식 (1)의 유효 단면2차모멘트 I_w와 I_pl를 각각 산정한다.

큰보의 양쪽 면에 전높이 보강플레이트를 적용한 경우에는 약산식으로 유효 단면2차모멘트 I_w와 I_pl의 값을 산정한다(식 (2) 참고). 이때 큰보 파형웨브의 유효폭은 정현파 반파장 w의 3배이다(Fig. 3 참조).

Fig. 3.

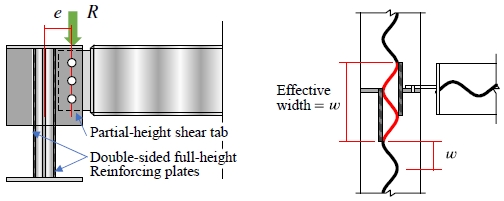
Definition of effective width of corrugate web when joining partial-height shear tab and double-sided full-height reinforcing plates

작은보 춤의 1.5배 이상 높이를 갖는 부분높이 보강플레이트와 작은보 춤 이하의 부분높이 전단탭을 적용한 경우, I_w는 식 (2a)와 동일하며 I_pl은 식 (2b)의 절반을 적용한다.

I w = 3 w × t w × a 32 8

(2a)

I p l = w × t p l × a 3 + t p l 2

(2b)

여기서, w는 큰보 파형웨브의 반파장 너비, t_w와 t_pl은 각각 큰보 파형웨브와 보강플레이트의 두께이다.

다음은 작은보의 단부플레이트에 요구되는 두께를 결정하는 과정이다. Fig. 4와 같이 작은보의 단부플레이트를 단순보로 가정하고, 전단탭에 작용하는 편심 모멘트를 선형분포로 치환하여 단순보에 재하한다. 식 (3a)의 분포하중에 의한 최대 모멘트와 식 (3b)의 단부플레이트의 소성강도를 동일하게 두어 식 (3c)와 같이 단부플레이트의 두께를 산정할 수 있다. 여기서 파형웨브는 골의 직각방향으로 축강성이 크지 않고, 단부플레이트와 맞닿는 파형웨브 골의 위치가 각 부재마다 다르므로 파형웨브의 기여는 계산과정에서 제외한다.

Fig. 4.

Assumed linearly distributed load acting on a beam end plate

더불어 볼트접합부의 일반적인 다양한 한계상태(지압강도, 볼트전단파단, 블록전단파단 등)와 용접부에 대한 검토가 수반되어야 하며, 그 설계는 KDS 14 31 25^[12]를 따른다.

M m a x = R × e h w 14 - h t 6 h w h w - 23 h t

(3a)

M p = Z × F y = B t r e q 2 4 × F y

(3b)

t r e q = 4 R × e B × F y × 12 - h t / h w 3

(3c)

여기서 R은 볼트군에 작용하는 전단력, e는 볼트군 도심과 큰보 중심라인까지의 거리, h_w는 단부플레이트의 높이, h_t는 전단탭의 너비, B는 작은보의 너비, F_y는 단부플레이트의 공칭항복강도이다.

3. 설계예제

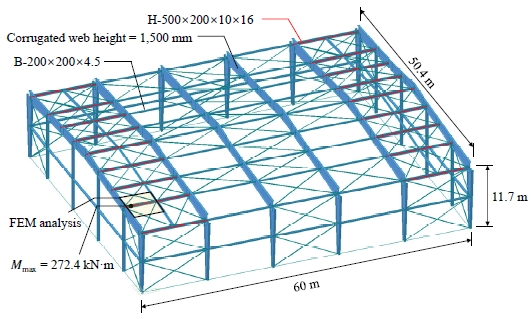
Fig. 5는 실제 PEB 구조물의 설계사례를 보여준다. 이 예제에서는 춤 1,500 mm의 대형 파형웨브를 갖는 PEB 골조의 면외방향 볼트 전단접합부에 대해 앞에서 제안한 설계법에 따라 검토하였다. 예제의 목적상 접합부 설계법의 과정을 명료하게 보여주기 위하여 하중조건, 해석결과, 기둥 및 가새 등의 부재 조건 등에 대한 설명은 생략한다.

Fig. 5.

Design example of PEB system and maximum bending moment acting on small beam

3.1 설계예제 제원

PEB 서까래(이하 큰보)에 적용된 파형웨브 보의 크기는 1,528×300×3×14이며, 플랜지는 SM355, 파형웨브는 SS275이다. PEB 건물 모서리에서 발생하는 부풍압을 제어하기 위하여 골조 양단의 갖도리와 중도리(이하 작은보)에 길이 12 m의 SS275강 H-500×200×10×16를 적용하였다. 이 중도리의 공칭항복모멘트인 M_y의 크기는 525.8 kN·m이다. 내부 스팬에는 B-200×200×4.5의 스트럿을 적용했다. 여러 하중조합 조건 검토를 통해 찾은 작은보에 작용하는 가장 큰 휨모멘트 크기는 272.4 kN·m로 공칭항복강도의 50 % 수준이다.

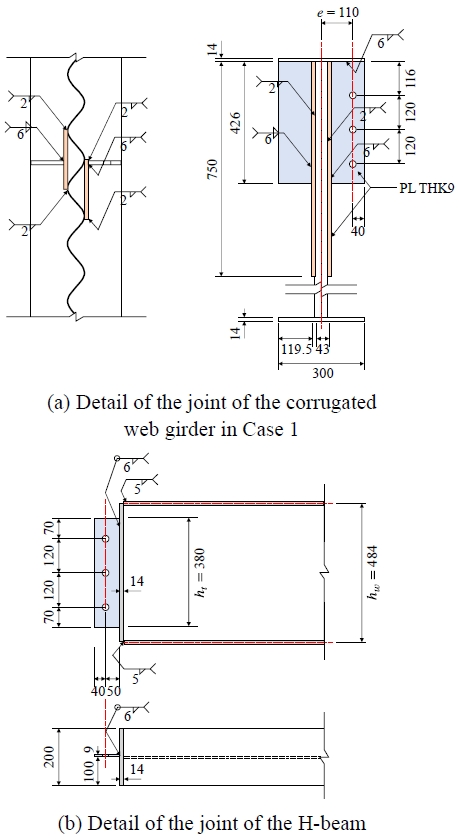
이 설계예제에서 큰보에 적용되는 파형웨브 두께를 두 가지로 검토하였다. Case 1은 파형웨브 두께를 3 mm로 적용한 경우로서, 이때의 정현파고 a₃는 43 mm이다. Case 2는 파형웨브의 생산규격 두께 중 가장 얇은 2 mm가 가장 큰 웨브 춤인 1,500 mm에 적용된 경우로, 주로 PEB 구조물에 적용되는 제원이며 국내에서 제작 가능한 파형웨브 중 가장 세장한 경우이다. 두께 2 mm인 파형강판의 파고는 40 mm이다. 두 경우 모두 파형웨브의 한 파장의 길이(즉, 2w)는 155 mm로 동일하다.

Fig. 6는 설계예제 접합부의 상세도이다. 큰보의 부분높이 보강플레이트는 작은보 춤의 1.5배인 750 mm이며, 너비는 200 mm, 두께는 14 mm를 적용하였다. 큰보의 전단탭은 높이 440 mm, 두께 9 mm를 갖는다. 너비는 Case 1에 대해 119.5 mm, Case 2에 대해 121 mm이다. 두께 14 mm인 작은보 단부보강플레이트의 너비는 보의 너비와 동일한 200 mm이며, 높이는 작은보 상/하 플랜지 간 중심거리인 484 mm이다. 작은보의 전단탭은 높이 380 mm, 너비 90 mm, 두께 9 mm이다. 각 플레이트의 소재는 모두 SS275강이다. 볼트는 1열의 F10T-M20의 3@120 mm를 적용하였다. 용접재의 강도 F_uw는 420 MPa이며, 모살용접의 크기는 파형웨브에 접합되는 플레이트에 2 mm, 그 외의 경우에는 5 mm 또는 6 mm를 적용하였다.

Fig. 6.

Detail of the shear joint in the design example of PEB frame

3.2 접합부의 요구강도 산정

이 설계예제는 파형웨브 춤이 1,000 mm 이상이고, 작은보 춤은 500 mm, 부분높이 웨브보강플레이트의 높이는 750 mm(작은보 춤의 1.5배)인 경우이다. 따라서 작은보에 작용하는 최대휨모멘트강도 262.4 kN·m(즉, 작은보의 공칭항복모멘트강도 M_y = 525.8 kN·m의 50 %) 이상을 전단접합부가 지지할 수 있도록 설계한다. 접합부의 전단하중 R_u는 식 (4)와 같다.

R u = w u L 2 = 8 0.5 M y L 2 × L 2 = 87.6 k N

(4)

3.2.1 볼트 강도 검토

F10T-M20 볼트 1개의 전단파단강도 검토는 식 (5)와 같이 나사부가 전단면에 포함되는 경우로 하였다. 편심하중을 받는 경우이므로 탄성해석으로 볼트에 작용하는 최대 힘을 식 (6)과 같이 검토하였다. 식 (5)의 전단파단강도보다 최대 작용 힘(식 (6d))이 작으므로 F10T-M20 볼트의 3개 배열은 적절하다.

ϕ R n, 1 = ϕ F u b A b n s = 94.2 k N

(5)

M u = R u × e = 9,636 k N · m m

(6a)

r m x = M u 120 m m = 80.3 k N

(6b)

r m y = R u 3 = 29.2 k N

(6c)

R m a x = r m x 2 + r m y 2 = 85.5 k N

(6d)

3.2.2 작은보의 접합부 강도 검토

작은보의 볼트접합부 검토는 다음과 같다. 식 (7)은 전단탭 가장 윗 열 볼트의 수평연단부에 대한 지압강도로, 식 (6b)를 통해 구한 수평방향의 볼트 힘보다 크므로 안전하다. 식 (8)은 수직방향 지압강도이며, 식 (9) - 식 (11)은 각각 전단면 항복, 순단면 파단과 블록전단파단을 검토한 것이다. 검토 결과 작용하중에 대해 각 한계상태는 안전한 것으로 나타났다.

1.2 F u L c t = 1.2 × 275 × 40 - 11 × 9 = 175.2 k N

(7a)

2.4 F u d t = 2.4 × 275 × 20 × 9 = 118.8 k N

(7b)

ϕ R n, 3 = ϕ Σ min ⁡ 1.2 F u L c t, 2.4 F u d t = 64.6 k N

(7c)

1.2 F u L c, 1 t = 1.2 × 275 × 70 - 11 × 9 = 175.2 k N

(8a)

1.2 F u L c, 23 t = 1.2 × 275 × 120 - 22 × 9 = 291.1 k N

(8b)

2.4 F u d t = 2.4 × 275 × 20 × 9 = 118.8 k N

(8c)

ϕ R n, 3 = ϕ Σ min ⁡ 1.2 F u L c, i t, 2.4 F u d t = 267.3 k N

(8d)

ϕ R n, 4 = ϕ F y A g = 0.9 275 × 3,420 = 846.5 k N

(9)

ϕ R n, 5 = ϕ F u A e = 0.75 410 × 2,826 = 869.0 k N

(10)

A n t = 9 40 - 11 = 2,826 m m 2

(11a)

A n v = 9 2 × 120 - 2.5 × 22 = 2,295 m m 2

(11b)

A g v = 9 2 × 120 + 70 = 2,790 m m 2

(11c)

ϕ R n, 6 = ϕ min ⁡ 0.6 F u A n v, 0.6 A g v + F u A n t = 655.7 k N

(11d)

이 설계예제의 작은보는 파형웨브 보가 아닌 일반 압연 H형강이지만, 식 (3)에 따라 파형웨브 작은보와 동일한 절차로 단부플레이트의 두께를 아래와 같이 검토하였다. 그 결과, 요구되는 두께가 12.9 mm로 나타났다. 예제에 적용된 두께는 14 mm이므로 충분히 안전하다.

t r e q = 4 R × e B × F y × 12 - h t / h w 3 = 4 × 87.6 × 110 200 × 275 × 12 - 380 / 484 3 = 12.9 m m

(12)

용접재의 단위면적 당 설계강도는 식 (13)과 같이 계산된다. 식 (14)와 식 (15)는 각각 작은보의 전단탭과 단부플레이트, 단부플레이트-작은보 플랜지 간에 적용한 모살용접의 최대 인장-전단응력 조합강도를 나타낸다. 식 (14b)와 식 (15b)는 편심 모멘트에 의한 축방향 응력, 식 (14c)와 식 (15c)는 전단력에 의한 전단응력이다. 두 모살용접부에 작용하는 조합응력은 모두 설계강도보다 작으므로 용접부는 안전하다.

ϕ f w = 0.75 0.6 × 420 = 189 M P a

(13)

a = 0.7 s = 0.7 × 6 = 4.2 m m

(14a)

σ u = M S w = R u e 1 2 a h t 2 / 6 = 87.6 × 50 2 × 4.2 × 3802 / 6 = 137.2 M P a

(14b)

v u = V A w = R u 2 a h t = 87.6 2 × 4.2 × 380 = 137.2 M P a

(14c)

f u = σ u 2 + v u 2 = 140 M P a

(14d)

a = 0.7 s = 0.7 × 5 = 3.5 m m

(15a)

σ u = M S w = R u e 2 a B - 2 s h w / 2 = 87.6 × 50 + 14 23.5 200 - 2 × 10 242 = 34.8 M P a

(15b)

v u = V A w = R u 2 a B - 2 s = 87.6 7 200 - 20 = 69.5 M P a

(15c)

f u = σ u 2 + v u 2 = 77.8 M P a

(15d)

큰보의 접합부 검토는 생략하였다.

3.2.3 큰보와 보강플레이트의 비틀림 저항 검토

큰보 파형웨브의 유효 단면2차모멘트 I_w는 식 (2a)를 적용하였고, 보강플레이트의 I_pl은 식 (2b)의 절반을 적용하였다.

I w, 1 = 3 × 77.5 × 3 × 432 8 = 161,209 m m 4

(16a)

I p l, 1 = 77.5 × 9 × 43 + 9 2 2 = 719,723 m m 4

(16b)

I w, 1 + I p l, 1 a 3 / 2 × min ⁡ F y, w, F y, p l = 11.27 k N · m

(16c)

Case 1의 경우 식 (16)에서 볼 수 있듯, 두께 3 mm의 파형웨브의 유효 단면2차모멘트 I_w,₁는 두께 9 mm의 보강플레이트 두 장의 유효 단면2차모멘트 I_pl,₁의 1/5 수준이다. Case 1은 식 (6a)의 편심모멘트에 충분히 저항 가능하다(식 (1) 참고).

I w, 2 = 3 × 77.5 × 2 × 402 8 = 93,000 m m 4

(17a)

I p l, 2 = 77.5 × 9 × 40 + 9 2 2 = 622,800 m m 4

(17b)

I w, 2 + I p l, 2 a 3 / 2 × min ⁡ F y, w, F y, p l = 9.16 k N · m

(17c)

Case 2는 파형웨브의 두께가 2 mm, 파고가 40 mm인 경우이다. 식 (17)에서 보듯 두께 2 mm의 파형웨브의 유효 단면2차모멘트 I_w,₂는 두께 9 mm의 보강플레이트 두 장의 유효 단면2차모멘트 I_pl,₂의 1/7 수준으로, 편심모멘트에서의 비틀림에 충분히 안전하다.

설계예제의 전단접합부는 다양한 한계상태에 모두 안전한 것으로 나타났다. 가장 세장한 파형웨브 제원의 경우에도 편심모멘트에 의해 발생하는 비틀림에 대하여 본 설계예제의 두께 9 mm의 보강플레이트 정도로도 저항할 수 있는 것으로 나타났다. 이는 다음 4장의 유한요소해석결과와 일치함을 알 수 있다.

4. 설계예제 전단접합부의 수치해석결과

Fig. 5에서 최대 모멘트를 받는 작은보의 전단접합부를 부분골조로 모델링하여 유한요소해석을 수행하였다.

큰보와 작은보의 길이는 해당 스팬 길이의 절반(변곡점에 해당)으로 하였다. 큰보의 양단의 경계조건은 약축방향 및 수직방향의 병진운동에 대해 구속하였으며, 강축방향에 대한 회전운동과 약축방향으로의 비틀림을 구속하지 않도록 하였다. 레퍼런스 포인트를 작은보의 끝단면의 도심에 두어 단면을 커플링시켰으며, 대칭조건을 갖도록 경계조건을 부여하고 변위제어 방식의 하중을 도입하였다.

각 F10T 볼트에는 하중해석 전에 볼트 프리텐션 옵션을 통해 설계장력을 도입하였다. 볼트 접합부의 계면은 Contact 조건을 부여하였고, 보수적인 평가를 위하여 마찰계수 0.3을 적용하였다.

해석에서 모든 강재의 재료모델은 이선형으로 가정하여 각 재료의 공칭항복응력에 도달한 이후 항복참이 일정하게 유지되는 것으로 적용하였다.

큰보의 플랜지, 작은보는 C3D8R요소를 적용하였으며, 메쉬 크기는 10 mm, 각 부재요소의 두께별 레이어는 4겹으로 적용하였다. F10T 볼트는 C3D8R 요소이며 메쉬 크기는 5 mm를 적용하였다. 큰보의 파형웨브와 보강플레이트, 전단탭은 C3D20R요소를 적용하였고, 메쉬 크기는 2 mm, 두께방향 레이어를 4개로 매우 세밀하게 적용하여 전단탭에 의한 파형웨브 골의 국부지압에 의한 응력분포를 면밀히 살펴보고자 하였다.

Case 1과 Case 2를 보수적으로 평가하기 위하여 전단탭이 보강플레이트의 편측에 접합된 상황을 가정하였다(Fig. 7 참조).

Fig. 7.

Bolt connection located at the end of the reinforcing plate[2]

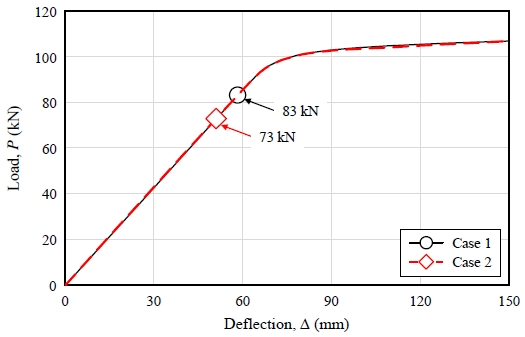
Fig. 8과 Fig. 9은 두 해석결과에서 작은보에 비슷한 수준의 모멘트가 작용하고 있을 때 응력분포도를 나타낸 것이다. 파형웨브 두께가 2 mm인 Case 2의 경우 두께 3 mm가 적용된 Case 1보다 파형웨브에 더 큰 응력이 작용하였다. 단, Fig. 9(b)에서 보듯 보강플레이트의 높이를 충분히 키움으로써 편측에 위치한 부분높이 전단탭 단부의 지압력이 파형웨브 골에 의도한 대로 분산되어 전달되었음을 알 수 있다.

Fig. 8.

Finite element analysis results of partial framing joint in Case 1

Fig. 9.

Finite element analysis results of partial framing joint in Case 2

Case 1의 경우, 하중 83 kN에서 작은보에 휨모멘트가 376.2 kN·m 작용하였는데, 이는 작은보 공칭항복모멘트 강도의 약 72 % 정도 수준이다. Case 2의 경우, 하중 73 kN에서 작은보에 공칭항복모멘트 강도의 약 67.6 % 수준인 354.9 kN·m의 휨모멘트가 작용하였다.

Fig. 10에는 두 경우에 대한 작은보의 하중과 처짐의 관계도를 함께 도시하였다. 강성 및 강도 측면에서 파형웨브 두께와 무관하게 동일한 거동을 나타냈으며, 항복모멘트의 약 70 % 수준에서도 접합부 거동은 탄성상태임을 알 수 있다. 이것은 파형웨브의 구성원리와 제안한 보강플레이트의 접합부 작동 메커니즘을 고려한다면 충분히 예상되었던 거동이며, 큰보에 유발된 변형이 두 경우에 차이 없음을 의미한다. 또한 3.2절의 설계예제와 함께 2장에서 제안한 큰보 파형웨브의 비틀림 저항검토식이 충분히 보수적임을 시사한다.

Fig. 10.

Comparison of load vs. deflection relationships for the beam in Case 1 and 2

두 해석결과는 춤이 1,500 mm인 대형 파형웨브 보의 볼트 전단접합부에 대해 2장의 설계조건이었던 작은보의 작용하중을 항복모멘트의 50 % 이하로 하고 작은보 춤의 1.5배 이상인 보강플레이트를 사용해야 하는 제한사항을 적용하면 충분히 탄성거동을 한다는 것을 보여준다.

5. 결 론

이 논문에서는 선행연구에서 제안한 파형웨브 보의 볼트 전단접합상세에 대해 다소 보수적인 제한조건 하에서의 설계법을 제안하고 실제 PEB 구조 예제의 접합부를 제안 방법으로 검토하였다. 더불어 설계예제에 대한 부분골조 수치해석을 수행하여 제안방법으로 안전한 설계가 가능함을 입증하였다.

(1) 선행연구의 결과를 바탕으로 보강플레이트와 전단탭을 갖는 파형웨브 보의 설계 조건을 엄격하게 제한하였다. 부분높이 보강플레이트의 적용높이는 작은보 춤의 1.5배 이상으로 하고 부분높이 전단탭은 작은보 춤 이하의 높이로 제작하여 파형웨브 골에 발생 가능한 국부적 변형을 제어하였다. 큰보의 파형웨브 춤이 1,000 mm 이상, 1,500 mm 이하일 경우에는 웨브 높이 500 mm 이하의 작은보를 적용하며, 작은보의 하중은 항복모멘트의 50 % 이하로 제한하였다.
(2) 보강플레이트가 적용된 파형웨브 큰보의 비틀림저항에 대한 검토식과 작은보의 단부플레이트 두께 검토식을 제안하였다. 큰보 파형웨브의 국부적 변형을 방지하기 위한 보강플레이트 설계식을 전단탭의 높이에 따라 제시하였다.
(3) 제안식을 춤이 1,500 mm인 대형 파형웨브 보로 조립한 PEB 골조의 전단접합부에 적용하여 설계하는 과정을 소개하였다. 이 설계예제는 큰보에 적용 가능한 파형웨브 제원 중 가장 세장한 경우를 갖는 경우를 포함한다.
(4) 큰보의 파형웨브 두께가 2 mm 및 3 mm인 경우에 강도 및 강성 측면에서 거동 차이가 거의 없음을 유한요소해석결과를 통해 확인하였다. 제안식을 통해 산정한 전높이 보강플레이트를 파형웨브 양면에 적용할 경우, 제한조건 하에서 전단접합부가 충분히 탄성상태임을 확인하였다.

Acknowledgments

이 연구는 ㈜반석중공업과 ㈜포스코의 지원사업으로 이루어진 것으로 이에 감사드립니다.

References

Aydın, R., Yuksel, E., Yardımcı, N., and Gokce, T. (2016) Cyclic Behaviour of Diagonally-Stiffened Beam-to-Column Connections of Corrugated-Web I Sections, Engineering Structures, Elsevier, Vol.121, pp.120-135. [https://doi.org/10.1016/j.engstruct.2016.04.036]
Jiang, Z.-Q., Li, S.-H., Liu, X.-C., Ping, Q., and Niu, Z.-Y. (2020) Influence of Bolts on Seismic Performance of Earthquake-Resilient Prefabricated Sinusoidal Corrugated Web Steel Beam-Column Joints, Journal of Constructional Steel Research, Elsevier, Vol.172, 106214. [https://doi.org/10.1016/j.jcsr.2020.106214]
KSSC (2015) Guidelines for Design and Construction of Pre-Engineered Metal Building System, Korea (in Korean).
Park, Y.-S., Cui, G., and Park, Y.-C. (2018) Experimental Study on Compressive Seam Strength of Bolted Connections in Extra-Deep Corrugated Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.30, No.5, pp.309-316 (in Korean). [https://doi.org/10.7781/kjoss.2018.30.5.309]
Park, Y.-S., Cui, G., and Park, Y.-C. (2018) Experimental Study on Flexural Strength of Bolted Connection in Extra-Deep Corrugated Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.30, No.5, pp.317-323 (in Korean). [https://doi.org/10.7781/kjoss.2018.30.5.317]
Shin, J.H., Sim, H.-B., and Park, Y.C. (2023) Modeling Bolted Connection in Corrugated Beams to Simulate Bending Test, Journal of Korean Society of Steel Construction, KSSC, Vol.35, No.1, pp.31-39 (in Korean). [https://doi.org/10.7781/kjoss.2023.35.1.031]
Kim, D.K. (2023) Evaluation of Shear Connections in Sinusoidally Corrugated Web Beams with Reinforcing Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.35, No.3, pp.137-147 (in Korean). [https://doi.org/10.7781/kjoss.2023.35.3.137]
The Steel Construction Institute, and the British Constructional Steelwork Association Ltd. (2002) Joints in Steel Construction – Simple Connections (Publication P212), UK.
Building Research Establishment Ltd. (2003) Design of Structural Connections to Eurocode 3 – Frequently Asked Questions, UK.
Park, Y.H., and Chung, K.R. (2019) Steel Structure Design for Practical Engineers: KBC 2016 Design Examples of Steel Connection Design, Koomiseogwan, Korea (in Korean).
Singapore Structural Steel Society (2019) Design Guide for Buildable Steel Connections – Bolted and Welded Connection to SS EN1993-1-8, Singapore.
Ministry of Land, Infrastructure and Transport (2017) Design Standards for Steel Structure Connection (Load and Resistance Factored Design) (KDS 14 31 25: 2017), Korea (in Korean).