유한요소해석 기반 그라운드 앵커 긴장재의 국부 부식에 따른 자기이력 변화 분석
Copyright © 2023 by Korean Society of Steel Construction
초록
본 논문에서는 전자기장 유한요소해석을 통해 그라운드 앵커 긴장재의 국부 부식 발생에 따른 자기적 특성의 변화를 분석하였다. 그라운드 앵커 긴장재가 부식되면서 나타나는 자기적 특성을 관찰하기 위해 부식 깊이를 실험변수로 설정하였으며, 5가지 case의 긴장재와 EM(elasto-magnetic) 센서를 3차원 모델링하였다. 또한 유한요소해석결과를 바탕으로 작도한 자기이력곡선으로부터 특정 인덱스를 추출하였다. 시뮬레이션 결과, 부식으로 인해 긴장재의 유효단면적이 감소할수록 자기이력곡선의 초기 곡선 포화점이 감소하는 것으로 나타났으며, 이로 인해 투자율 또한 감소하는 것으로 나타났다.
Abstract
In this paper, the change in magnetic hysteresis due to the occurrence of a localized corrosion of ground anchor tendon was analyzed through electromagnetic field FEM(finite elements method). To observe the change in the magnetic hysteresis that appear as the ground anchor tendon corrosion, 3-D modelings of corroded steel bars for 5 cases and an EM(elasto-magnetic) sensor were conducted by setting the depth of corrosion as a experiment variable. Magnetic hysteresis curves were plotted based on the results of FEM, and specific indexes were extracted from them. The simulation results show that the virgin curve saturation point of the virgin curve decreased with the decrease in the effective cross-section area due to corrosion of tendon. As a result, the permeability also decreased.
Keywords:
Ground anchor, Tendon, Finite element method, Elasto-magnetic sensor, Non-destructive testing, Sectional damage, Corrosion damage키워드:
그라운드 앵커, 긴장재, 유한요소해석, EM 센서, 비파괴검사, 단면 손상, 부식 손상1. 서 론
그라운드 앵커(ground anchor)는 선단부를 양질의 지반에 정착시키고, 이를 반력으로 하여 흙막이벽 등의 구조물을 지지하기 위한 구조체로, PS 강연선, PS 강봉 등과 같은 긴장재(tendon)를 사용하고 지반에 시멘트풀을 주입하여 정착시킴으로써 긴장력 전달을 통해 지반의 과도한 변위 및 붕괴를 방지한다. 1912년 Albert Bishop에 의해 최초로 발명된 그라운드 앵커는 1934년 Algeria의 CheurfasDam에 제방 보강에 사용된 이후로 90여년의 역사를 가지고 있으며 1980년대 이후에는 비탈면 보강 및 흙막이벽 지지 등에 효과적인 대책공법으로 인식되어 그 사용이 급속히 확산되었다.
하지만 매년 그라운드 앵커 관련 사고사례가 잇따라 발생하고 있으며, 기(旣)시공된 그라운드 앵커 중 공용수명에 다다른 노후화된 그라운드 앵커의 파손, 부식 및 기타 기능 저하 사례가 계속해서 보고되고 있다. 그라운드 앵커 긴장재에 발생하는 부식은 앵커가 지지하는 구조물의 내구성을 저하시키며 안정성에 심각한 문제를 야기할 수 있다.
이에 따라서 국제 프리스트레스 콘크리트 연맹 FIP(International Federation for Pre-stressing)에서는 앵커 사고 유형 및 원인 분석을 통해 그라운드 앵커를 영구적으로 사용하기 위한 대책 마련을 강구하고 앵커 관리 규정을 제정했으나 실질적인 대안을 제시하지 못하고 있는 실정이다. 우리나라의 경우 국토교통부에서 제시하는 ‘그라운드 앵커 설계·시공 및 유지관리 매뉴얼’을 바탕으로 앵커 공용수명에 대한 전반적인 관리를 하고 있으나 앵커 내구성에 큰 영향을 미치는 긴장재 부식에 대한 고려가 미비한 실정이다.
금속은 보통 산화물 또는 황화물의 형태로 자연계에 존재하며, 통상 건설재료로 사용되는 철근, 강봉과 같은 금속은 자연계 금속의 광석이 제련의 과정을 거쳐서 생산된 것으로 화학적으로 불안정한 상태로 존재한다. 우리가 사용하는 금속은 그 환경 속에서 가장 안정된 상태로 돌아가려는 성질을 갖는다. 부식(corrosion)은 금속이 그 외부환경과의 물질과 화학적, 전기적 반응에 의해 소모되어 가는 현상으로, 부식으로 인해 발생한 금속의 녹은 물과 공기가 공존하는 환경에서 가장 안정된 상태로 변화한 결과로 볼 수 있다.
그라운드 앵커는 비탈면과 같은 시설물을 보강하기 위한 구조체로 강선, 강봉과 같은 금속재료의 긴장재가 공용기간 동안 시설물의 하중에 저항하기 위한 긴장력을 유지하게 된다. 그라운드 앵커의 앵커 두부에는 낙석과 같은 외력에 의한 손상과 강우, 눈 등에 의한 부식으로부터 정착구를 보호하기 위한 보호캡을 설치한다. 이러한 그라운드 앵커 긴장재에 강우를 포함한 유해물질이 침투하게 되면 부식이 발생해 긴장력이 감소하게 되어 긴장재의 파단으로 이어질 수 있으므로, 그라운드 앵커의 유지관리는 공용기간 중에 앵커의 역할을 유지하고 앵커가 보강하는 구조체의 안정성을 확보하기 위한 중요한 과정이다.
또한, 그라운드 앵커 긴장재는 온천, 폐기물 처리장, 해수, 지하수의 영향을 받는 지반 등과 같이 지반 내에 물이나 산 등의 물질이 침투 가능한 부식환경에 노출될 수 있다. 이러한 부식환경에 노출된 그라운드 앵커 긴장재는 내구성이 약한 주름관의 국부파손 부위나 정착구의 배면 등을 통해 침투한 유해물질로 인해 부식이 발생하게 되는데, 긴장재 부식은 긴장재의 유효단면적이 감소함에 따라 그라운드 앵커의 역학적 성능 저하를 유발하게 되고 이는 곧 그라운드 앵커가 지지하는 구조물의 안정성을 저하시킨다.
특히, 앵커 긴장재에 발생하는 국부 부식(localized corrosion)은 한번 발생하기 시작하면 그 성장 속도를 예측하기 힘들 뿐만 아니라, 예기치 못한 외력에 의한 취성파괴(brittle fracture)가 발생할 위험이 존재한다. 따라서, 그라운드 앵커가 지지하는 구조물의 구조 건전성을 확보하기 위해서는 그라운드 앵커 긴장재에서 발생하는 부식량을 정량화함으로써 부식을 선제적으로 검출하는 과정이 필수 불가결하다.
영구앵커의 경우 지반에 매립된 후 앵커 자유장에서 발생하는 부식을 육안으로 검사하는 것이 불가능할뿐더러 앵커 설치 이후 유지관리 없이 방치하는 경우가 대부분인 실정이며, 현재로서는 내부 긴장재 부식 검출에 대한 효과적인 기술이 부재한 실정이다. 따라서, 본 논문에서는 극소한 양의 부식에서부터 인장파괴 발생 가능성이 있는 수준까지의 부식량을 설정하여 분석하였다.
앵커 및 기타 긴장재를 사용하는 구조물의 건전성 모니터링을 위한 연구는 대부분 긴장력 모니터링에 관한 것으로, 현재 긴장재 부식 검출을 위한 국내외적 연구 사례는 미비한 실정이다.
본 논문에서는 기존 그라운드 앵커의 국부 부식 검출 방법의 대안을 마련하고자 EM(elasto-magnetic) 센서의 그라운드 앵커 부식 검출 가능성을 검증하기 위해 전자기장 유한요소해석을 실시하였다.
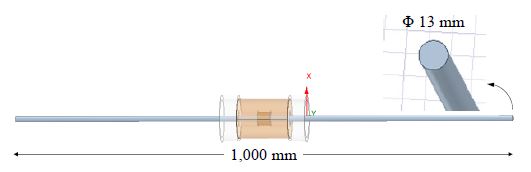
그라운드 앵커의 긴장재 부식에 따라 발생하는 긴장재 유효단면적 손실과 이에 따른 자기특성 변화를 관찰하기 위해, 여러 형태의 부식을 갖는 그라운드 앵커 긴장재에 대하여 유한요소해석을 진행한 다음 그 결과를 분석하였다. 그라운드 앵커 긴장재의 부식 발생 깊이를 변수로 설정하고, 부식 발생 깊이 별로 긴장재 및 EM(elasto-magnetic) 센서를 3D로 모델링하였다. 유한요소해석은 ANSYS MAXWELL의 Transient Solution Type을 적용해 EM 센서를 통한 긴장재 부식 계측을 모사하였다. 유한요소해석을 통해 설정 시간 동안의 EM 센서 2차 코일로 인가된 전압(induced voltage)값을 추출하였으며, 이를 바탕으로 자기이력곡선(magnetic hysteresis curve)을 작도하여 긴장재 유효단면적 변화에 따른 자기이력 변화를 분석하였다.
2. EM(elasto-magnetic) 센서 계측 원리
2.1 전자기유도 현상(Faraday’s law of induction)
본 논문에서는 그라운드 앵커 긴장재의 국부 부식으로 인한 유효단면적 변화에 따른 자기이력을 관찰하고자 하였다. EM 센서를 통한 계측 시뮬레이션을 위해 전자기장 유한요소해석 프로그램인 ANSYS MAXWELL을 활용하였으며, 이를 이해하기 위해서는 먼저 EM 센서 계측 원리의 가장 중요한 이론 중 하나인 전자기 유도현상에 대한 이해가 필요하다. 아래 Fig. 1은 전자기 유도현상을 나타내는 간단한 예이다.
Fig. 1과 같이 1차 코일에 교류 전류가 흐르면 자성체 재료가 자화되어 재료 내에 전위차가 발생하고 이로 인해 2차 코일에 유도 기전력이 발생하는데 이러한 현상을 전자기 유도현상이라고 한다. 유도된 전위차는 시간에 대한 자기 선속의 변화 및 코일 권선 수에 비례하며 2차 코일에 유도된 기전력은 아래 식 (1)과 같이 나타난다.
| (1) |
여기서, ϵ(t),2는 2차 코일에 유도된 기전력(electromotive force), N2은 1차 코일 권선 수, Φ(t),2는 2차 코일의 자기 선속(magnetic flux)을 나타낸다.
2.2 자기변형과 역자기변형 효과
자기변형(magnetostriction)은 자성체가 외부 자기장에 의해 자화(magnetization)될 때 물리적 변형이 발생하는 현상을 말한다. 자연상태의 자성체 재료는 자구(magnetic domain)가 무질서한 분포를 나타내지만, 외부 자기장에 의해 자화됨에 따라 자구가 서서히 자기장 방향으로 정렬하여 자화가 최대치에 이르러 포화(saturation)하게 된다.
이와 반대로, 자성체에 물리적 변화가 발생했을 때 자기특성이 변화하는 현상을 역자기변형(inverse magnetostriction)이라고 한다. 자성체 재료에 부식(corrosion), 긴장(tension) 등의 물리적 변화가 발생하게 되면 역자기변형 현상으로 인해 자기특성이 변화하게 되는데, 이러한 자기특성을 EM 센서를 통해 측정함으로써 물리적 변화를 추정할 수 있다.
2.3 EM(elasto-magnetic) 센서 계측 원리
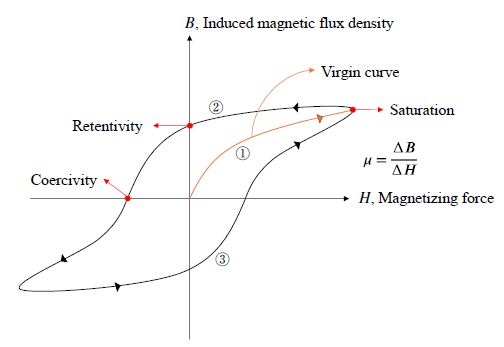
자성체 재료에 자화력 H가 작용하게 되면 자속밀도 B가 발생하며, 강자성체의 경우 아래 그림과 같이 비선형 형태를 나타낸다. Fig. 2는 자기장 세기와 자속밀도의 관계를 나타내는 자기이력곡선(magnetic hysteresis curve)으로 EM 센서를 통해 측정한 자기이력을 바탕으로 작도할 수 있다.
본 논문에서는 앞서 언급한 역자기변형 현상으로 인해 부식 정도에 따라 변화하는 긴장재의 자기이력을 전자기장 유한요소해석 시뮬레이션을 통해 추출하였으며, 이를 기반으로 자기이력곡선을 작도하였다. 이후 각 부식 case 별 초기 곡선(virgin curve)의 포화점(saturation point) 및 투자율(permeability)를 추출하였으며, 여기서 투자율 μ는 아래 식 (2)와 같이 자속밀도 B와 자화력 H의 비율로, 외부 자기장에 의한 자성체 재료의 자화 정도를 나타내는 정량적 지표이다. 또한, 자기 포화(magnetic saturation) 현상은 자화력을 증가시켜도 더 이상 자속밀도가 증가하지 않는 현상을 의미한다.
| (2) |
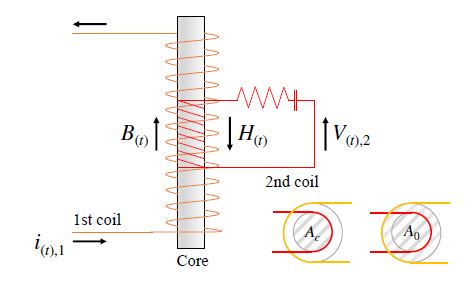
Fig. 4는 EM 센서의 계측 원리를 나타낸 모식도로, 그 원리는 다음과 같다. 먼저 1차 코일에 교류 전류를 가하면 자기장이 형성되어 자성체가 포화하게 되고, 자성체의 자속에 의해 2차 코일에 인가되는 전압이 계측된다.
패러데이 전자기 유도법칙을 따라 2차 코일에 인가되는 출력전압 V(t),2는 전자기 유도법칙을 따라, 아래 식 (3)과 같이 표현할 수 있다.
| (3) |
여기서, Φ는 자속으로 긴장재에 흐르는 자속 Φcore와 에어 갭(air gap)에 흐르는 자속 Φair로 나눌 수 있고, 자속 Φ는 자기력선과 자기장 방향이 수직일 때 자속밀도 B와 자기력선이 지나는 단면적 A의 곱으로 아래 식 (4)와 같이 표현할 수 있다.
| (4) |
따라서, 2차 코일에 인가되는 출력전압 V(t),2는 아래의 식 (5)와 같이 표현할 수 있다. 여기서, μ0는 진공 투자율(space permeability)로 에어 갭 부분의 투자율을 나타내며, 약 4π × 10-7 H/m의 값을 갖는다. 또한, Fig. 4에서 볼 수 있듯 Ac는 긴장재의 단면적을, A0는 2차 코일 내부 면적을 의미한다.
| (5) |
자화력(magnetizing force, H(A/m))은 자성체를 자화시키는 힘으로 아래 식 (6)과 같이 나타낼 수 있다.
| (6) |
여기서, F(A)는 기자력(magnetomotive force), l(m)은 자로의 길이, N은 코일의 권선 수, 그리고 I는 코일에 걸리는 전류를 의미한다.
전압 V(t),2를 계측시간 t1 - t2 동안 시간에 대해 적분하면 해당 시간 동안 2차 코일에 인가된 평균 전압 Vaverage를 얻을 수 있으며 아래 식 (7)과 같이 표현할 수 있다.
| (7) |
| (8) |
또한, 긴장재가 없는 경우 Ac = 0이므로 2차 코일에 인가되는 평균 전압은 아래 식 (9)와 같이 표현할 수 있다.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
여기서, μc는 긴장재의 투자율이며 μr는 진공 투자율과의 비율을 나타내는 상대 투자율(relative permeability)로 아래 식 (14)와 같다.
| (14) |
3. 유한요소해석 시뮬레이션(ANSYS MAXWELL)
3.1 ANSYS MAXWELL
본 절에서는 EM 센서의 긴장재 부식 계측을 모사하기 위해 ANSYS 기반 전자기 유한요소해석을 수행하였다. EM 센서는 앞서 언급한 바와 같이 패러데이 전기유도 법칙, 자기탄성 등의 원리에 의해 긴장재의 유효단면적 감소에 따른 자기이력의 변화를 검출할 수 있다.
본 논문 전반부에 기재된 EM 센서 계측 원리는 패러데이 전자기 유도법칙(Faraday’s law of electromagnetic induction)으로 설명할 수 있다. 본 논문에서 유한요소해석을 위해 사용한 ANSYS MAXWELL은 Maxwell 방정식(Maxwell’s equations)을 기반으로 만들어진 전자기 유한요소해석 프로그램이다. 네 가지 맥스웰 방정식 중 맥스웰 패러데이 방정식(Maxwell-Faraday’s equation)은 켈빈-스토크스 정리(Kelvin-Stokes theorem)를 따라 아래 식 (15), 식 (16)과 같이 표현할 수 있으며, 이를 기반으로 EM 센서의 계측 시뮬레이션을 수행할 수 있다.
| (15) |
| (16) |
여기서, ∇×는 컬 연산자(curl operator), E는 전기장, B는 자기장을 의미한다. 또한, 스토크스의 정리(Stokes’ theorem)에 따라 Ʃ는 미분 가능 다양체(differentiable manifold)의 표면을, σƩ는 폐경로를 의미한다.
본 장에서는 ANSYS MAXWELL 유한요소해석 프로그램을 통해 EM 센서 및 긴장재를 모델링하였으며, EM 센서 계측 시뮬레이션을 실시함으로써 국부 부식 검출기술 적용성을 검증하였다.
3.2 실험변수 설정
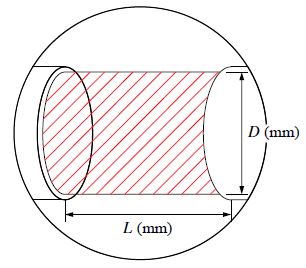
본 절에서는 그라운드 앵커 긴장재가 부식함에 따라 나타나는 자기이력을 관찰하기 위해 부식의 깊이를 변수로 설정해 총 5가지 case에 대한 부식을 모사하였다. 실제 긴장재의 부식은 다양한 형상으로 발생하나, 본 논문에서는 긴장재 부식으로 인해 발생하는 단면적 손실에 따른 자기이력 변화를 분석하고자 하였다. 따라서, 사방으로 균일하게 부식이 발생한다는 가정하에 긴장재의 국부 부식을 모사하였으며, 실험에 사용된 총 5가지 가공된 실험체 실험변수는 Fig. 5, Table 1과 같다.
3.3 유한요소해석을 위한 긴장재 및 EM 센서 3D 모델링
Fig. 6 및 Fig. 7은 본 연구진이 제작한 EM 센서 및 부식량 측정 실험을 위한 구성으로, 1·2차 코일, 센서 헤드, DAQ(data acquisition system) 그리고 데이터 무선 송수신을 위한 안테나로 구성된다. EM 센서의 경우 추후 현장에 설치할 것을 고려해 실제 그라운드 앵커 7구 인장판의 제원을 바탕으로 제작하였으며, 센서 제작에 사용된 코일 특성치 및 권선에 관한 내용은 Table 2와 같다.
본 절에서는 ANSYS MAXWELL Transient Analysis를 기반으로 실제 EM 센서의 계측을 시뮬레이션하여 각 부식 case에 대한 유한요소해석을 수행하였다. 3D 해석은 2D 해석에 비해 많은 수의 mesh elements를 분석하기 때문에 많은 시간이 소요되는 단점이 있지만, 2D 해석에 비해 훨씬 정밀한 해석이 가능하다. 먼저, Figs. 8-9과 같이 Maxwell 3D design을 통해 긴장재, 1차 코일, 2차 코일 그리고 센서 헤드를 모델링하였다.
1차 및 2차 코일의 상대 투자율(relative permeability), 전기 전도도(electrical conductivity), 밀도(mass density)는 ANSYS의 Materials 중 Copper의 물성값을 적용하였다. 센서 헤드의 경우 긴장재 자화에 영향을 미치지 않는 PVC 재질로 모델링하였다. 우리나라 PC 긴장재의 경우 SWPC1AN ~ SWPC19L(KS D 7002)를 주로 사용하나 ANSYS MAXWELL 프로그램 내에 존재하지 않아, 이와 유사한 물성치를 갖는 실린더 형태의 Steel_1008(AISI, UNS G10080)를 적용하였으며 Table 3는 Steel_1008의 재료 특성치를 나타낸다. 또한, Table 4는 코일 재료 특성치 및 권선에 관한 내용이다.
Fig. 10은 ANSYS MAXWELL의 Eddy Current Solution Type을 적용한 시뮬레이션 결과로, EM 센서 계측 시 지정된 구역 내에서 phase에 따른 자기장의 거동을 시각적으로 확인할 수 있다. Fig. 10에서 볼 수 있듯 1차 코일에 AC(alternating current) 전압을 인가하면 코일 주변에 자기장이 형성되고, 이로 인해 긴장재가 자화되면 2차 코일에 유도전압이 인가된다.
본 연구진이 보유한 EM 센서의 경우, 1차 코일에 –4 V - 4 V까지의 진폭을 갖는 AC 전압을 인가하고, 자화된 긴장재로 인해 2차 코일에 인가되는 AC 전압을 수신하게 된다. 초기 ANSYS 시뮬레이션에서는 실제 계측과 동일한 크기와 형태를 갖는 AC 전압을 적용하여 3초(1 cycle) 동안 0.01초 step으로 자기이력을 추출하였으나 Fig. 11에서 볼 수 있듯 Case 2에서의 자기이력 변화가 뚜렷하게 나타나지 않아, 1차 코일 input voltage를 –10 V - 10 V로 증가시켜 시뮬레이션을 수행하였다.
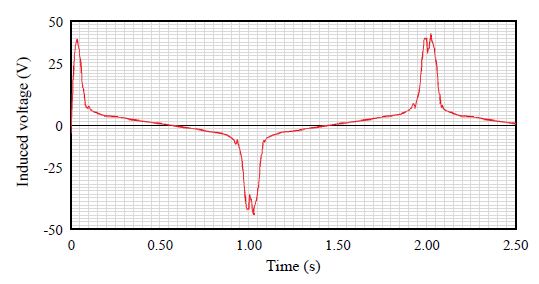
Figs. 12-13은 Transient Solution Type을 적용해 시뮬레이션 시작 후 3초 간 1차 코일을 통해 인가한 전압과 2차 코일에 유도된 전압의 이력을 추출한 그래프이다.
3.4 ANSYS 전자기장 시뮬레이션 결과
본 절에서는 EM 센서의 계측 신뢰성을 평가하기 위해 transient analysis를 이용해 각 부식 case에 대한 시뮬레이션을 수행하였다.
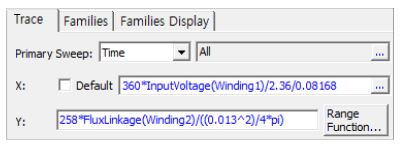
시뮬레이션으로 얻은 전압 이력 데이터를 통해 앞서 언급한 전자기 유도현상 이론을 바탕으로 Fig. 14과 같이 수식을 입력하여 자기이력곡선(magnetic hysteresis curve)을 작도할 수 있다.
Fig. 14에서 y축의 입력변수 중 하나인 flux linkage(Φ)는 자속 쇄교수(flux linkage)로, 코일을 구성하고 있는 각 권선과 쇄교(link)하는 자속의 총합을 의미하며, 아래 식 (17)과 같이 자속밀도와 자속이 통과하는 센서 내부 단면적의 곱으로 나타낼 수 있다.
| (17) |
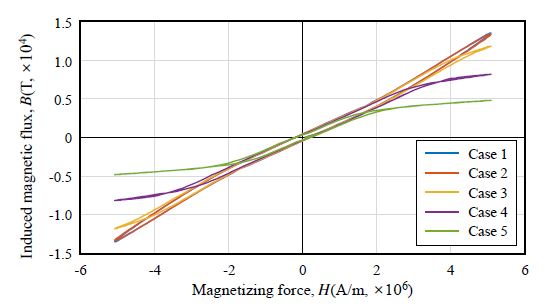
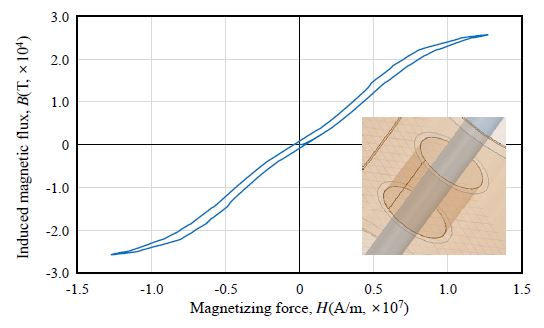
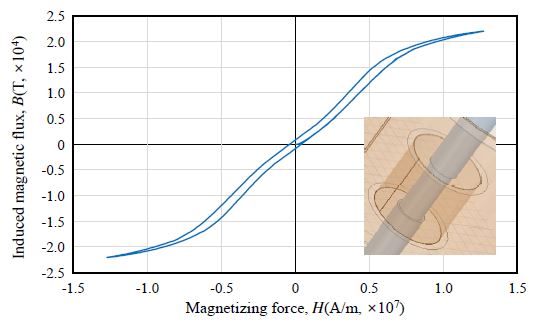
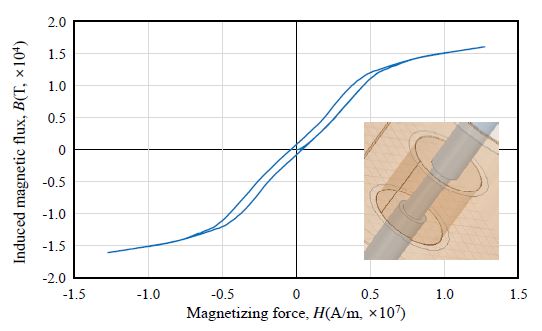
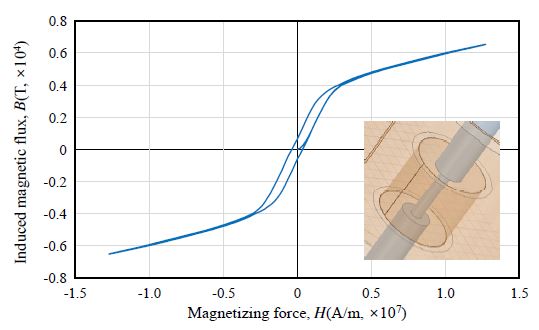
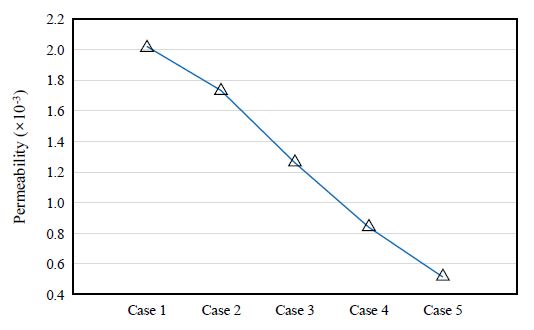
Figs. 15-19는 각 부식 case 별 자기이력곡선을 작도한 결과이다. 각 case 별 자기이력곡선으로부터 초기 곡선 포화점(virgin curve saturation point)과 투자율을 추출하였으며, 그 결과는 Fig. 20, Fig. 21과 같이 나타났다. 본 논문에서 말하는 투자율은 자기이력곡선의 최댓값과 최솟값을 연결한 직선의 기울기를 의미한다.
Case 1 - Case 5의 자기이력곡선의 초기 곡선 포화점은 각각 25723T, 22058T, 16042T, 10680T, 6534T로 아래 Fig. 20와 같이 유효단면적이 감소함에 따라 감소하는 경향을 나타냈다.
Fig. 21은 case 별 투자율을 추출한 결과이다. 각 case 별 입력 전압 값이 일정한 상태에서 초기 곡선의 포화점이 감소하였기 때문에 투자율 역시 각각 0.0020, 0.0017, 0.0013, 0.00084, 0.00051로, 자기이력곡선의 초기 곡선 포화점과 거의 유사한 형태를 나타냈다.
시뮬레이션 결과, 긴장재의 부식으로 유효단면적이 감소할수록 자기이력곡선의 초기 곡선 포화점이 감소하였으며, 이에 따라 투자율 역시 감소하는 것으로 나타났다.
앞서 언급한 바와 같이, 계측 시 센서 내부에 발생하는 자속은 식 (15)와 같이 긴장재에 흐르는 자속 Φcore와 에어 갭에 흐르는 자속 Φair로 나눌 수 있다.
| (18) |
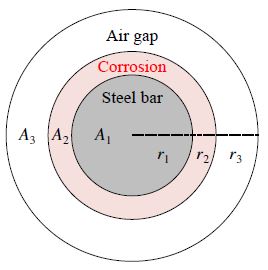
Fig. 22와 같이 A1 + A2의 단면적을 갖는 긴장재에 A2 만큼의 부식이 발생하게 되면 긴장재의 유효단면적은 A1으로 감소하게 된다.
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
부식이 발생하지 않은 Case 1을 기준으로 한 Case 2, Case 3, Case 4, Case 5의 단면 손실률은 각각 85.20 %, 71.00 %, 52.07 %, 28.40 %로, 이에 따른 초기 곡선 포화점 및 투자율의 변화율은 Table 5와 같이 나타났다. 포화점 및 투자율 모두 단면적 감소율에 비례하여 그 값이 줄어드는 것을 확인할 수 있었다.
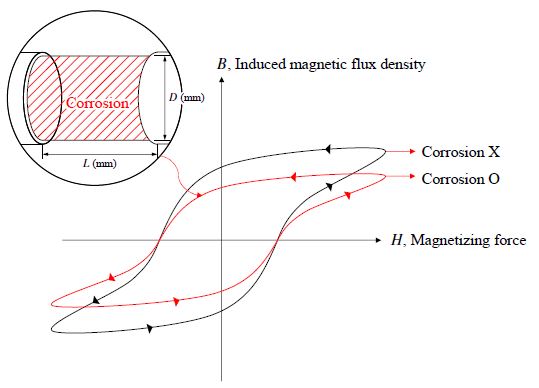
부식이 발생하게 되면 식 (20)과 같이 2차 코일에 인가되는 전압에 변화가 발생하고, 이로 인해 Figs. 11-15과 같이 자기이력곡선의 형태가 부식 case 별로 다르게 나타난다. 부식 깊이가 증가할수록 자기이력곡선의 초기 곡선 포화점, 투자율이 감소하는 경향은 부식 발생으로 인해 긴장재의 유효단면적이 줄어들어, 긴장재를 통과하는 자속이 감소함에 따라 나타나는 결과로 사료된다.
4. 결 론
본 논문에서는 기존 그라운드 앵커 긴장재의 부식 검출법의 대안으로 EM 센서를 활용한 비파괴 검사법을 제안하였으며, 이에 대한 적용 가능성을 검토하기 위해 전자기장 유한요소해석을 수행하였다. 부식 깊이를 실험변수로 설정하여 시뮬레이션을 수행한 결과는 다음과 같다.
- (1) 부식의 깊이를 실험변수로 설정해 총 5가지 case에 대한 부식을 모사해 전자기 유한요소해석을 실시한 결과, 부식으로 인한 긴장재 단면변화가 발생함에 따라 자기이력이 변화함을 확인하였다.
- (2) –4 V - 4 V 크기의 AC 전압을 입력 전압으로 설정하여 시뮬레이션을 수행했을 때, Case 2에서 자기이력의 변화가 뚜렷하게 나타나지 않았다. 이후, –10 V - 10 V로 입력 전압의 크기를 증가시켜 시뮬레이션을 수행한 결과, 모든 case에서 자기이력의 변화가 뚜렷이 나타났다. 따라서, 계측하고자 하는 긴장재의 전자기적 특성 및 물리적 특성에 따라 입력 전압의 적정 크기를 산정할 필요가 있다.
- (3) 각 case 별 자기이력곡선에서 초기 곡선 포화점과 투자율을 각각 추출하였으며, 두 값 모두 긴장재 단면적 감소율에 비례해 감소하는 것으로 나타났다.
- (4) 이는 긴장재에 부식이 발생하여 긴장재의 유효단면적이 줄어들고, 이에 따라 긴장재를 통과하는 자속이 감소함에 따라 나타나는 현상으로 사료된다.
본 논문에서는 부식으로 인한 긴장재의 유효단면적이 감소함에 따라 자기이력곡선의 변화가 나타났으며, 따라서 EM 센서를 통한 그라운드 앵커 긴장재의 국부 부식 검출 가능성을 입증하였다.
향후 연구에서는 실제 현장에서 쉽게 발생할 수 있는 소규모의 부식 검출이 가능한 EM 센서를 설계하고 제작하여 이에 관한 연구를 진행하고자 한다. 또한, EM 센서를 현실적으로 설치하고 운영할 수 있는 방법을 모색하고, 실제 계측을 통해 긴장재 부식 검출에 대한 현장 적용성을 검토하고자 한다.
Acknowledgments
본 연구는 국토교통부의 스마트시티 혁신인재육성사업과 2021년도 중소벤처기업부의 기술개발사업(S3174912)의 지원으로 수행되었습니다.
References
- Jang, B.S., Yu, D.W., Kim, T.H., Cha, G.S., and Nam, H.G. (2008) Domestic and International Case Analysis Research on Corrosion of Ground Anchors, Proceedings of Annual Spring Conference of Korean Society for Rock Mechanics and Rock Engineering, KSRM, pp.257-266 (in Korean).
-
Cappello, C., Zonta, D., Laasri, H.A., Glisic, B., and Wang, M. (2018) Calibration of Elasto-Magnetic Sensors on In-Service Cable-Stayed Bridges for Stress Monitoring, Sensors, MDPI, Vol.18, No.2, 466.
[https://doi.org/10.3390/s18020466]

-
Zhang, S., Zhou, J., Zhou, Y., Zhang, H., and Chen, J. (2019) Cable Tension Monitoring Based on the Elasto-Magnetic Effect and the Self-Induction Phenomenon, Materials, MDPI, Vol.12, No.14, 2230.
[https://doi.org/10.3390/ma12142230]

-
Park, J., Kim, J., Eum, K.-Y., and Park, S. (2019) Low-Voltage EM(Elasto-Magnetic) Sensing Technique for Tensile Force Management of PSC(Prestressed Concrete) Internal Tendon, Journal of Computational Structural Engineering Institute of Korea, COSEIK, Vol.32, No.2, pp.87-92 (in Korean).
[https://doi.org/10.7734/COSEIK.2019.32.2.87]

-
Cao, Y., Yim, J., Zhao, Y., and Wang, M.L. (2010) Temperature Effects on Cable Stayed Bridge Using Health Monitoring System: A Case Study, Journal of Structural Health Monitoring, Sage, Vol.10, No.5, pp.523-537.
[https://doi.org/10.1177/1475921710388970]

-
Liu, X., Wu, D., He, C., Feng, H., and Wu, B. (2018) Comparison of AC and Pulsed Magnetization-Based Elasto-Magnetic Methods for Tensile Force Measurement in Steel Strand, Measurement, Elsevier, Vol.117, pp.410-418.
[https://doi.org/10.1016/j.measurement.2017.12.033]

-
Wang, M.L., and Wang, G. (2022) Sensor Technologies for Civil Infrastructures, Vol. 1: Sensing Hardware and Data Collection Methods for Performance Assessment (2nd Ed.), Chapter 8: Electromagnetic Sensors for Assessing and Monitoring Civil Infrastructures, Elsevier, USA., pp.211-236.
[https://doi.org/10.1016/B978-0-08-102696-0.00015-4]