
전단탭이 없는 상·하부 스플릿 티 접합부를 적용한 강구조물의 설계
Copyright ⓒ 2015 by Korean Society of Steel Construction
초록
금상․하부 스플릿 티 접합부는 접합부를 구성하는 T-stub 플랜지의 두께, 고장력볼트의 게이지 거리, 고장력볼트의 개수 및 직경 등의 변화에 따라서 상이한 강도, 강성, 에너지소산능력 등을 발현한다. 이러한 상․하부 스플릿 티 접합부가 중․저층 강구조물에 적용될 경우에 전단력을 지탱하는 전단탭을 적용할 수 없는 상황이 발생한다. 이 때문에 충분한 휨모멘트지지능력뿐만 아니라 전단력도 지탱할 수 있는 개선된 상․하부 스플릿 티 접합부상세의 제안이 필요하다. 이 연구는 양재근 등이 해석적 연구와 실험적 연구를 수행하여 얻은 전단탭이 없는 상․하부 스플릿 티 접합부가 중․저층의 강구조물에 적용되었을 때 충분한 회전강성을 발현하는 가를 평가하기 위하여 진행하였다. 또한, 전단탭이 없는 상․하부 스플릿 티 접합부를 적용한 중․저층 강구조물이 안전한 구조적거동양상을 나타냄과 동시에 무차원화 된 초기회전강성을 구조해석에 적용하여 재료적 물량저감 효과도 나타낼 수 있는 가를 평가하기 위하여 진행하였다.
Abstract
Double split tee connection has various strength, stiffness, and energy dissipation capacity according to changes of thickness of T-stub flange and gauge distance, number, and diameter of high-strength bolt. If the double split tee connection is applied to a low- or medium-rise steel structure, a shear tab can't be applied for supporting shear force because of geometrical limitation. So it is required to propose details of improved double split tee connection to support shear force as well as flexural force. This research was performed to see if enough rotational stiffness is found when the double split tee connection without shear tab which was obtained through analytic and experimental researches by Yang et al. is applied to a low- or medium-rise steel structure. Also, it was seen if the low- or medium-rise steel structure having double split tee connection without shear tab has safe structural behavior, as well as material saving effect.
키워드:
상·하부 스플릿 티 접합부, 회전강성, 전단텝, 중·저층 규모의 강구조물, 안전한 구조적 거동Keywords:
Double split tee connection, Rotational stiffness, Shear tab, Low and medium steel structures, Stable structural behavior1. 서 론
상․하부 스플릿 티 접합부는 대표적인 모멘트 접합부의 한 형태로 T-stub 플랜지의 두께, 고장력볼트의 게이지 거리, 고장력볼트의 개수 및 직경, 보 부재와 기둥 부재의 규격 등의 조합에 따라서 보통모멘트골조 혹은 특수모멘트골조 등에 적용된다[1],[2],[3]. 상․하부 스플릿 티 접합부의 설계에 있어서 접합부에 작용하는 휨모멘트는 T-stub, 전단력은 전단탭이 지지하는 것으로 이상화된다[4],[5],[6],[7],[8],[9]. 그러나 중․저층 규모의 강구조물에 상․하부 스플릿 티 접합부가 적용될 경우에는 기하학적 형상 제한에 의하여 전단탭을 적용할 수 없는 상황이 발생할 수 있다. 이러한 경우에는 전단력을 지지하는 전단탭을 대체할 수 있는 접합부상세의 제안이 필요하다. 양재근 등은 해석적 연구와 실험적 연구를 수행하여 전단탭이 없는 상․하부 스플릿 티 접합부에 대한 접합부상세를 제안하였다. 이러한 Yang et al.[10],[11]의 연구를 통하여 전단탭이 없는 상․하부 스플릿 티 접합부도 기존의 전단탭이 있는 상․하부 스플릿 티 접합부와 비교하였을 때 충분한 강도, 강성, 에너지소산능력 등을 발현하는 것을 파악하였다[12],[13]. 또한, 제안한 전단탭이 없는 상․하부 스플릿 티 접합부는 T-stub 필릿부의 전단파단 및 하부 T-stub 플랜지에 추가적으로 체결된 고장력볼트의 전단파단 등이 발생하지 않았기 때문에 충분한 전단력 지지능력도 갖는 것을 파악하였다.
이 연구는 전단탭이 없는 상․하부 스플릿 티 접합부가 중․저층의 강구조물에 적용되었을 때 충분한 하중지지 능력과 안전한 구조적 거동을 하는 가를 파악하기 위하여 진행하였다. 아울러 무차원화 된 전단탭이 없는 상․하부 스플릿 티 접합부의 초기회전강성을 적용하여 중․저층 강구조물의 구조해석을 수행하였을 때 접합부에 발생하는 부모멘트의 감소와 응력재분배를 통하여 부재의 재료적 물량저감 효과를 평가하기 위하여 수행하였다.
2. 전단탭이 없는 상․하부 스플릿 티 접합부의 회전강성 평가
2.1 전단탭이 없는 상․하부 스플릿 티 접합부의 초기회전강성
전단탭이 없는 상․하부 스플릿 티 접합부에 대한 실험체 계획은 Table 1과 Fig. 1에 정리한 것과 같다. 각 실험체를 구성하는데 사용한 보 부재, 기둥 부재, T-stub 등의 재료적 물성값은 Table 2에 정리하였다. 접합부실험은 동일한 기하학적 형상을 갖는 각각의 접합부에 대하여 실험체 A 및 실험체 B를 제작하여 수행하였다. 작용하중은 FEMA350에서 정의한 재하조건을 따랐다. 하중작용에 따른 접합부 변형과 변위는 Fig. 2에 나타낸 것과 같이 스트레인게이지 부착 및 LVDT 설치를 통하여 얻었다. 각 실험체의 모멘트-회전각 관계 이력곡선은 Fig. 3과 같다. 전단탭이 없는 상․하부 스플릿 티 접합부의 회전강성은 모멘트-회전각 관계 이력곡선 각 싸이클의 당 최대 모멘트-회전각 이력곡선에 해당하는 포락선에 대한 회귀분석을 수행하여 얻었다. 각 접합부의 포락선에 대한 회귀분석은 식 (1)로 정의되는 Richard 해석모델을 적용하였다. 회귀분석을 통하여 얻은 새로운 포락선은 점선의 형태로 Fig. 4에 나타내었다. 회귀분석을 통하여 얻은 각 접합부 실험체의 초기회전강성과 소성회전강성 등은 Table 3에 정리하였다.
Richard 회귀분석 식:
 (1)
(1)
2.2 전단탭이 없는 상․하부 스플릿 티 접합부의 초기회전강성 무차원화
각 접합부의 모멘트-회전각 관계 이력곡선의 포락선에 대한 회귀분석을 통하여 얻은 초기회전강성은 Table 3과 같다. Table 3과 나타난 것과 같이 전단탭이 있는 G210-T21- B300-SI 모델의 실험체 A와 실험체 B의 초기회전강성 값은 전단탭에 체결된 고장력볼트의 슬립 및 지압 등의 현상에 의하여 초기회전강성 값의 차이가 나타났다. 반면에 전단탭이 없는 G210-T21-B300-SO 모델의 실험체 A와 실험체 B의 초기회전강성 값은 전단탭에 체결된 고장력볼트의 슬립 및 지압 등의 현상이 없기 때문에 초기회전강성 값의 차이가 발생하지 않았다.
상․하부 스플릿 티 접합부의 초기회전강성을 예측하기 위하여 그동안 많은 연구가 진행되었다. 이 연구에서는 양재근 등이 제안한 식 (2)와 같은 상․하부 스플릿 티 접합부의 초기회전강성 예측모델을 적용하여 얻은 초기회전강성 값과 접합부 실험을 통하여 얻은 초기회전강성 값과 비교하였다. Table 4에 정리한 것과 같이 양재근 등이 제안한 예측모델을 적용하여 얻은 접합부의 초기회전강성 값은 전단탭이 있는 G210-T21-B300-SI 모델의 실험체 A와 실험체 B의 초기회전강성 값과 비교하면 각각 26.33%, 23.57%의 초기회전강성 값 차이를 나타낸다. 반면에 전단탭이 없는 G210-T21- B300-SO 모델의 실험체 A와 실험체 B의 초기회전강성 값과 비교하면 각각 8.10%, 11.53%의 차이를 나타낸다. 이와 같이 초기회전강성 값의 차이를 나타내는 것은 Yang 해석모델은 전단탭이 없는 상․하부 스플릿 티 접합부에 대한 초기회전강성 값의 예측을 위한 해석모델이기 때문이다. 그러므로 전단탭의 영향을 포함한 접합부의 초기회전강성 예측모델의 제안이 필요하다. 또한, 비록 전단탭이 없는 접합부의 경우에 Yang 해석모델이 전단탭이 있는 접합부보다 초기회전강성 값의 예측에 더 근사적인 초기회전강성 값을 제공하나 추가적인 연구를 통한 해석모델의 개선은 필요할 것으로 판단한다.
구조해석 프로그램을 적용하여 강구조물에 대한 구조해석을 수행하기 위해서는 접합부의 초기회전강성 값에 대한 무차원화 작업이 선행되어야 한다. 일반적으로 접합부의 회전강성은 모멘트-회전각 관계 곡선의 기울기에 해당한다. Fig. 4에 정리한 모멘트-회전각 관계 곡선에 대한 접합부의 초기회전강성은 아래의 식 (3)을 적용하여 무차원화 할 수 있다. 식 (3)을 적용하면 Table 5에 나타난 것과 같이 접합부 실험을 통하여 얻은 무차원화 된 초기회전강성 값은 G210-T21-B300-SI A,B 모델의 경우 각각 0.45, 0.76이고, G210-T21-B300-SO A,B 모델의 경우 각각 0.57, 0.55 이다. 따라서 이 연구에서 고찰한 전단탭이 없는 상․하부 스플릿 티 접합부는 부분강접접합부로 판단할 수 있다.
양재근 등의 초기회전강성 예측모델:

 (2)
(2)
접합부 초기회전강성 무차원화 식:
 (3)
(3)
3. 전단탭이 없는 상․하부 스플릿 티 접합부를 적용한 강구조물의 구조안전성 평가
3.1 구조계획 및 구조해석결과
전단탭이 없는 상․하부 스플릿 티 접합부의 적용 가능성을 검토하기 위하여 지상 4층 규모의 업무시설에 대한 구조해석을 수행하여 구조안전성을 검토하였다. 설계개요, 건물개요, 하중적용, 구조계획은 Table 6~Table 8에 정리하였다. 대상구조물의 구조평면도 및 입면도는 Fig. 5와 같다. 전단탭이 없는 상․하부 스플릿 티 접합부가 적용된 위치는 적용부재의 응력재분배를 위하여 Fig. 5의 구조평면도의 표시된 기둥과 직접 접합되는 부재인 SG1, SG2의 양단에 설치되었으며 2층~지붕 층까지 전 층에 동일하게 설치되는 것으로 계획하였다. 설계적용기준은 건축구조기준(대한건축학회, 2009) 및 하중저항계수설계법에 의한 강구조설계기준(한국강구조학회, 2014)를 적용하였다.
지진하중 계획은 Table 9와 같으며 지진하중에 의한 층간변위는 Table 10에 정리하였다. 층간변위에 대한 검토는 다음과 같다.
이 구조물은 내진등급 II에 속하는 구조물이며, 허용층간변위는 식 (4)와 같다.
X-directional horizontal displacement
≤

Y-directional horizontal displacement
≤
 (4)
(4)
풍하중에 의한 X방향 및 Y방향 수평변위는 Table 11에 정리하였다. 풍하중에 의한 수평변위 검토는 식 (5)와 같다.
X-directional horizontal displacement
≤

Y-directional horizontal displacement
≤
 (5)
(5)
3.2 접합부의 회전강성 변화에 따른 구조안전성 평가
Table 5에 정리한 것과 같이 접합부실험을 통하여 얻은 각 접합부의 무차원화 된 회전강성비(
 =0.45,0.76,0.57, 0.55) 값을 갖는 강골조의 부재 응력과 층간변위를 구조해석 프로그램을 적용하여 검토하였다. Fig. 6에 나타난 것과 같이 전단탭이 없는 상․하부 스플릿 접합부로 구성된 강골조의 부모멘트 값이 강접된 접합부로 구성된 강골조의 부모멘트 값보다 감소되는 것을 확인 할 수 있었다. 접합부 1개당 사용되는 접합부 소요부재 물량 예측은 Table 12과 같다.
=0.45,0.76,0.57, 0.55) 값을 갖는 강골조의 부재 응력과 층간변위를 구조해석 프로그램을 적용하여 검토하였다. Fig. 6에 나타난 것과 같이 전단탭이 없는 상․하부 스플릿 접합부로 구성된 강골조의 부모멘트 값이 강접된 접합부로 구성된 강골조의 부모멘트 값보다 감소되는 것을 확인 할 수 있었다. 접합부 1개당 사용되는 접합부 소요부재 물량 예측은 Table 12과 같다.
이 경우에 Table 13에정리한 것과 같이 전단탭이 없는 상․하부 스플릿 티 접합부로 구성된 강골조가 강접된 접합부로 구성된 강골조보다 약 20% 정도의 물량감소 효과가 나타나는 것을 확인 할 수 있다.
보-기둥 접합부 회전강성을 조절한 Y방향 부재는 2층에서 지붕 층까지의 SG1, SG2 부재이다. 4개의 해석모델은 Table 14에 나타난 것과 같이 모두 충분한 하중지지 능력과 적합한 구조적 안전성을 보였다. 또한 변경 후 부재의 응력비가 0.8 내외로 설계되며 층간변위도 만족하는 것으로 확인되었다. 실시 설계단계에서의 보다 효과적인 경제성을 확보하기 위하여 위치별로 3가지 정도의
 값을 적용하되 적용 위치를 층간변위 제어에 보다 효과적인 위치로 변화시켜 시도를 한다면 이 연구에서 검토한 예제보다 효과적인 물량 절감효과를 기대할 수 있을 것으로 판단한다.
값을 적용하되 적용 위치를 층간변위 제어에 보다 효과적인 위치로 변화시켜 시도를 한다면 이 연구에서 검토한 예제보다 효과적인 물량 절감효과를 기대할 수 있을 것으로 판단한다.
4. 결 론
이 연구는 전단탭이 없는 상․하부 스플릿 티 접합부가 중․저층의 강구조물에 적용되었을 때 충분한 회전강성을 갖고 하중지지 능력 및 재료적 물량감소 효과를 발현하는 것을 평가하기 위하여 진행하였다. 이 연구를 통하여 얻은 결론은 다음과 같다.
(1)Yang 해석모델을 적용하여 산정한 전단탭이 없는 상․하부 스플릿 티 접합부의 초기회전강성 값은 접합부 실험을 통하여 얻은 초기회전강성 값과 각각 8.10%, 11.53%의 오차를 나타내었다. 따라서, Yang 해석모델은 추후 보완이 필요하며, 보완 후 전단탭이 없는 상․하부 스플릿 티 접합부의 초기회전강성 값 예측에 적절하게 활용될 수 있을 것으로 판단한다.
(2)접합부 실험결과에 근거하면 전단탭이 없는 상․하부 스플릿 티 접합부는 하부 T-stub 필릿부의 전단파단뿐만 아니라 하부 T-stub 플랜지에 체결된 고장력볼트의 전단파단도 발생하지 않았다. 따라서 제안한 전단탭이 없는 상․하부 스플릿 티 접합부는 충분한 전단력 지지능력을 갖고 있는 것으로 판단한다.
(3)전단탭이 없는 상․하부 스플릿 티 접합부를 적용한 강구조물은 충분한 하중지지 능력과 구조적 안전성을 발현함과 동시에 충분한 재료적 물량절감 효과도 나타내는 것으로 판단한다. 따라서 제안한 전단탭이 없는 상․하부 스플릿 티 접합부는 강구조물에 적용하기에 합당한 것으로 판단한다.
Acknowledgments
이 연구는 한국연구재단의 지원(과제번호: NRF-2013-R1A1A2008363)에 의하여 수행된 과제의 일부입니다. 이에 논문의 저자들은 깊은 감사의 말씀을 전합니다.
기 호(Notation)
 :고장력볼트의 공칭단면적(mm2)
:고장력볼트의 공칭단면적(mm2)
 :전단면의 총 단면적(mm2)
:전단면의 총 단면적(mm2)
 :전단면의 순단면적(mm2)
:전단면의 순단면적(mm2)
 :인장면의 순단면적(mm2)
:인장면의 순단면적(mm2)
 :고장력볼트 중심축과 T-stub 플랜지 끝 단 사이의 거리(mm)
:고장력볼트 중심축과 T-stub 플랜지 끝 단 사이의 거리(mm)
 :고장력볼트 볼트구멍 끝단과 T-stub 스템 면 사이 의 거리(mm)
:고장력볼트 볼트구멍 끝단과 T-stub 스템 면 사이 의 거리(mm)
 :T-stub 플랜지 폭(mm)
:T-stub 플랜지 폭(mm)
 :T-stub 플랜지 분절의 길이(mm)
:T-stub 플랜지 분절의 길이(mm)
 :보의 춤(mm)
:보의 춤(mm)
 :고장력볼트의 직경(mm)
:고장력볼트의 직경(mm)
 :기둥의 폭(mm)
:기둥의 폭(mm)
 :강재의 탄성계수(N/mm2)
:강재의 탄성계수(N/mm2)
 :강재의 할선계수(N/mm2)
:강재의 할선계수(N/mm2)
 :강재의 인장강도(N/mm2)
:강재의 인장강도(N/mm2)
 :고장력볼트의 공칭인장강도(N/mm2)
:고장력볼트의 공칭인장강도(N/mm2)
 :강재의 항복강도(N/mm2)
:강재의 항복강도(N/mm2)
 :고장력볼트의 공칭항복강도(N/mm2)
:고장력볼트의 공칭항복강도(N/mm2)
 :고장력볼트의 전단강도(N/mm2)
:고장력볼트의 전단강도(N/mm2)
 :T-stub의 고장력볼트 게이지 거리(mm)
:T-stub의 고장력볼트 게이지 거리(mm)
 :볼트구멍을 제외한 T-stub의 고장력볼트 게이지 거리(mm)
:볼트구멍을 제외한 T-stub의 고장력볼트 게이지 거리(mm)
 :인장볼트의 총 개수
:인장볼트의 총 개수
 :최단 고장력볼트의 순 거리(mm)
:최단 고장력볼트의 순 거리(mm)
 :고장력볼트의 피치(mm)
:고장력볼트의 피치(mm)
 :필릿 반경(mm)
:필릿 반경(mm)
 :기둥 외면으로부터 T-stub 스템 첫 번째 고장력볼트 중심간 거리(mm)
:기둥 외면으로부터 T-stub 스템 첫 번째 고장력볼트 중심간 거리(mm)
 :T-stub 스템 고장력볼트 사이 거리(mm)
:T-stub 스템 고장력볼트 사이 거리(mm)
 :T-stub 스템 양끝단 고장력볼트 사이 거리(mm)
:T-stub 스템 양끝단 고장력볼트 사이 거리(mm)
 :부재의 두께(mm)
:부재의 두께(mm)
 :기둥 웨브의 두께(mm)
:기둥 웨브의 두께(mm)
 :T-stub 플랜지의 두께(mm)
:T-stub 플랜지의 두께(mm)
 :T-stub 스템의 두께(mm)
:T-stub 스템의 두께(mm)
 :강재의 인장 변형률
:강재의 인장 변형률
 :강재의 항복 변형률
:강재의 항복 변형률
References
-
김희동, 양재근, 이재윤, 이형동(2014) 상·하부 T-Stub 접합부의 초기회전강성 평가, 한국강구조학회논문집, 한국강구조학회, 제26권, 제2호, pp.133-142.
Kim, H.D., Yang, J.G., Lee, J.Y., and Lee, H.D. (2014) Evaluation of the Initial Rotational Stiffness of a Double Split Tee Connection, Journal of Korean Society of Steel Construction, KSSC, Vol.26, No.2, pp.133-142 (in Korean). [https://doi.org/10.7781/kjoss.2014.26.2.133]
- Faella, C., Piluso, V., and Rizzano, G. (2000) Structural Steel Semirigid Connections: Theory, Design and Software, CRC Press, UK.
-
양재근, 최정환, 김현광, 박재호(2011) 무보강 상·하부 ㄱ형강 접합부의 소성휨모멘트 저항능력 예측을 위한 실험 및 해석적 연구, 한국강구조학회논문집, 한국강구조학회, 제23권, 제5호, pp.547-555.
Yang, J.G., Choi, J.H., Kim, H.K., and Park, J.H. (2011) Experimental Tests and Analytical Study for the Prediction of the Plastic Moment Capacity of an Unstiffened Top and Seat Angle Connection, Journal of Korean Society of Steel Construction, KSSC, Vol.23, No.5, pp.547-555 (in Korean). - SAC Joint Venture (2000) Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings (FEMA-350), Federal Emergency Management Agency, USA.
-
Piluso, V., Faella, C., and Rizzano, G. (2001) Ultimate Behavior of Bolted T-Stubs, I: Theoretical Model, Journal of Structural Engineering, American Society of Civil Engineers, Vol.127, No.6, pp.686-693.
[https://doi.org/10.1061/(ASCE)0733-9445(2001)127:6(686)]

-
Piluso, V., Faella, C., and Rizzano, G. (2001) Ultimate Behavior of Bolted T-Stubs, II: Model Validation, Journal of Structural Engineering, American Society of Civil Engineers, Vol.127, No.6, pp.694-704.
[https://doi.org/10.1061/(ASCE)0733-9445(2001)127:6(694)]

-
Swanson, J.A., Kokan, D.S., and Leon, R.T. (2002) Advanced Finite Element Modeling of Bolted T-Stub Connection Components, Journal of Constructional Steel Research, Elsevier, Vol.58, pp.1015-1031.
[https://doi.org/10.1016/S0143-974X(01)00098-0]

- Thornton, W.A. (1985) Prying Action: A General Treatment, Engineering Journal, American Institute of Steel Construction, Vol.22, No.2, pp.67-75.
-
양재근, 이형동, 김용범, 배다솔(2015) 전단탭이 없는 상·하부 스플릿 티 접합부의 접합부상세 제안, 한국강구조학회논문집, 한국강구조학회, 제27권, 제5호, pp.423-433.
Yang, J.G., Lee, H.D., Kim, Y.B., and Pae, D.S. (2015) Proposal of Connection Details for a Double Split Tee Connection Without a Shear Tap, Journal of Korean Society of Steel Construction, KSSC, Vol.27, No.5, pp.423-433 (in Korean). [https://doi.org/10.7781/kjoss.2015.27.5.423]
-
Coelho, A.M.G., da Silva, L.S., and Bijlaard, F.S.K. (2006) Finite-Element Modeling of the Nonlinear Behavior of Bolted T-Stub Connections, Journal of Structural Engineering, American Society of Civil Engineers, Vol.132, No.6, pp.918-928.
[https://doi.org/10.1061/(ASCE)0733-9445(2006)132:6(918)]

-
Lemonis, M.E., and Gantes, C.J. (2006) Incremental Modeling of T-Stub Connections, Journal of Mechanics of Materials and Structures, Mathematical Sciences Publishers, Vol.1, No.7, pp.1135-1159.
[https://doi.org/10.2140/jomms.2006.1.1135]

- Stankiewicz, B. (2002) Experimental Tests of T-Stub Joints and Refined Finite Element Method Computer Model, Proceedings of EUROSTEEL 2002: The 3rd European Conference on Steel Structures (Vol. 2), European Convention for Constructional Steel, Portugal, pp.927-936.
-
Richard, R.M., Hsia, W.-K., and Chmielowiec, M. (1988) Derived Moment Rotation Curves for Double Framing Angles, Computers and Structures, Elsevier, Vol.3, No.3, pp.485-494.
[https://doi.org/10.1016/0045-7949(88)90281-7]








 (N/mm2)
(N/mm2) (N/mm2)
(N/mm2) (N/mm2)
(N/mm2)
























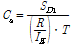


 =0.55)
=0.55) =0.55)
=0.55) =0.55)
=0.55)

 = 0.57
= 0.57 )
)