강섬유 콘크리트 혼입율에 따른 내부앵커형 콘크리트 충전기둥 내화성능에 관한 해석적 연구

1. 연구 배경 및 목적

콘크리트 충전강관(Concrete Filled steel tube, 이하 CFT)기둥의 내화성능의 연구는 유럽에서 1970년대 전반부터 1980년대 걸쳐서 합성구조 연구의 일환으로 시작되었으며^[1], 일본에서는 1977년에 최초의 CFT기둥에 대한 가열시험 및 온도해석이 실시되었다^[2]. 이후 지금까지 CFT기둥의 화재성능에 대한 국외 연구는 Kodur and MacKinnon(2000)^[3], Han et al.​(2003)^[4]등 중심이 되어 연구결과가 발표되었으며, 연구 대부분 CFT기둥의 내화성능을 평가하는데 그 목적이 있었다. 이후, CFT기둥의 내화성능 평가뿐만 아니라 CFT기둥의 내화성능을 향상시키기 위한 연구가 Cheng et al.^[5]에 의해 수행되었는데, 그의 연구는 CFT기둥의 내부 콘크리트에 철근 또는 강섬유를 삽입함으로써 내화성능을 향상시킬 수 있음을 제안하였다. 한편 중국에서는(Muhamed et al., 2011^[6]) 이중강관 충전형(Double-Skin)기둥의 연구를 수행하며 고온에 의한 열 변형을 억제하는데 상당히 효과적임을 검증하였다. 이러한 연구 결과 끝에 CFT기둥은 중국, 일본, 미국 등을 중심으로 내화 구조부재로 인정되며, 기둥의 실제 내화성능을 고려하여 내화 피복량을 절감한 성능설계가 이루어지고 있다. 국내의 경우도 무피복 CFT기둥을 사용하기 위한 연구가 지속적으로 소개되고 있다^[7],[8]. 그 중 일반 CFT기둥에 비해 내부 앵커형 용접조립각형(Advanced Construction Technology, 이하 ACT)기둥은 제작과정에서 자연스럽게 생성되는 리브가 콘크리트와 함께 앵커역할을 하여 일반 CFT기둥에 비해 경제적인 단면설계가 가능하다는 장점을 갖고 있다^[9]. ACT기둥 내화성능 연구는 CFT기둥과 마찬가지로 콘크리트가 충전되어 있는 구조체이므로 순수 강관기둥에 비해 내화성능 확보가 가능했다. 또한 강섬유 콘크리트(Steel Fibers Reinforced Concrete, 이하 SFRC)를 충전한 ACT기둥(이하, SF-ACT)의 경우 리브와 합성작용에 의해 열 변형이 지연되는 실험연구가 소개되었다^[10],[11]. 충전형 기둥의 내화성능에 영향을 미치는 주요 영향인자 중 하나는 하중비이다. SF-ACT의 재하가열 시험결과, 하중비가 약 0.5로 무피복 상태에서 약 50분 이상의 내화성능이 발휘되어 무피복 합성기둥의 가능성을 보여주고 있다. 따라서 본 연구에선행된 유사 실험자료를 통해 해석모델을 교정하고 신뢰성을 검증하고자 한다. 최종적으로 완성된 해석모델을 통해 하중비 조건에 따른 SF-ACT기둥의 열 변형, 열응력을 검토하고 강섬유 혼입율과 내화성능 관계를 정량적으로 분석하고자 한다.

2. 선행 연구

2.1 강섬유 콘크리트 재료의 열적특성

국내에 생산되는 강섬유의 크기는 일반적으로 12.7∼63.5mm의 길이와 0.45∼1mm의 직경이 사용되고 있다. 제조과정에 따라라 Fig. 1과 같이 형상이 달라지며, 강섬유 혼입율 만큼 내력행상에 주요 변수가 되고 있다. 그 중 트위스트형에 속하는 Fig. 2(b),(c)와 양단에 절곡된 후크형(Fig. 1(d))이 뽑힘강도에 유리한 조건을 갖고 있어 많이 사용되고 있는 형태라 할 수 있다.

Lie and Kodur(1996, 1997)^[12],[13]의 연구에 의하면 SFRC의 열적 특성을 분석하기 위해 골재타입(Siliceous, Carbonate)과 배합을 변수로 하여 재료적 성질을 분석하였다. 사용된 강섬유는 길이( 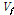)은 1.7%이며 시험체의 콘크리트 배합과 타입을 Table 1에 정리하였다. 온도변화에 따른 SFRC의 열적 특성(비열, 열팽창율, 열전도율, 부피손실율)을 Fig. 2에 표현하였다. 세 가지 콘크리트 타입의 비열은 100℃와 425℃에서 최대점을 나타내고 있다. 이는 시멘트 페이스트에 있는 수분이 증발되면서 발생되는 현상으로 분석되었다. 또한, Siliceous 시험체의 경우 550℃부근에서의 비열증가는 골재에 존재하는 석영(quartz)의 열 변형으로 인한 것으로 평가하고 있다. 마찬가지로 750℃의 가파른 비열 증가는 Carbonate 골재에 종속된 백운석(dolomite)으로 인해 나타난 현상인 것으로 분석되었다. 열팽창율에 대해 분석 결과 Siliceous 골재 시험체의 경우 600℃ 이후 열팽창율이 일정하게 유지되고, Carbonate 골재의 경우 550℃부터 상당한 열팽창 변화를 갖고 있으며 약 800℃ 이후부터 SFRC의 시험체는 가파른 증가 속도로 계속 확장되고 있다.

온도에 따른 콘크리트의 부피 손실량을 Fig. 2(d)를 통해 보면, 모든 타입의 시험체는 상온시 부피의 약 3% 손실량을 약 600℃ 까지 유지하는 것을 알 수 있다. 그 이후 600∼800℃ 사이의 Carbonate 골재의 경우 콘크리트의 질량은 온도 상승에 따라 상당히 떨어지는데 이는 콘크리트 백운석의 분리에 기인 된 것으로 보고되고 있으며 800℃부터 부피 손실율은 다시 서서히 감소한다. 콘크리트의 질량 손실은 0∼1,000℃의 조사 온도 범위에서 강섬유 보강에 의한 영향을 받지 않고 있다. 전반적으로, Carbonate 골재를 사용한 SFRC는 일반 콘크리트의 열적 특성과 유사한 경향을 보이고 있음을 알 수 있다.

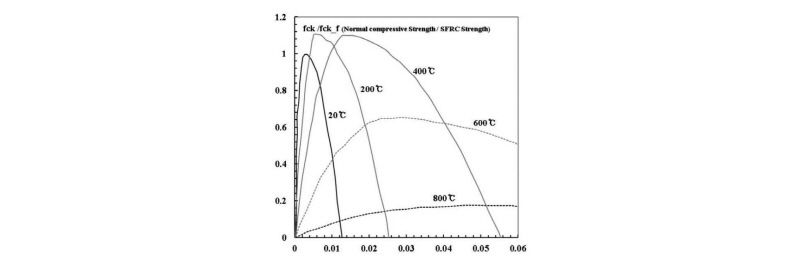
Kodur and Lie(1996)^[14]의 선행연구에서는 온도에 따른 SFRC의 응력-변형율 관계를 Fig. 3과 같이 제시하였고 식 (1),(2)와 같이 정의했다. SFRC의 압축 강도는 일반 콘크리트에 비해 상온(20℃)시 큰 차이를 나타내고 있지 않지만 200℃와 400℃상태에서는 약 1.3배 높이 평가되는 것으로 나타났다. 요약하면, 강섬유의 존재는 최대내력을 증가시키고 콘크리트의 연성을 향상시키는 것으로 분석되었다. 이때, T는 온도(℃), 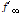는 상온상태의 콘크리트 공시체 압축강도를 뜻한다. 고온에서 SFRC의 압축 강도는 일반 콘크리트에 비해 높은 것으로 나타났다. 강섬유의 존재는 최대내력을 증가시키고 콘크리트의 연성을 향상시키는 것으로 분석되었다. 고온에서 SFRC에 대한 응력- 변형 곡선은 최대응력 위치가 높게 평가되는 차이점을 제외하고 일반 콘크리트와 재하구간의 비선형성 그리고 하강 구간의 기울기가 유사한 관계에 있음을 알 수 있다.

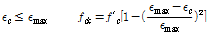 (1)

 (2)

여기서, 

 (3)

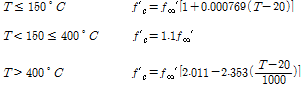
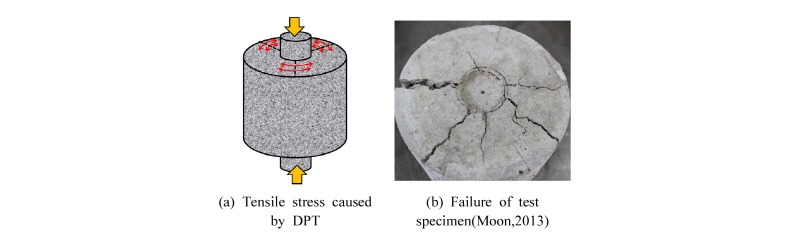
Moon(2013)^[15]연구자는 강섬유의 혼입량, 형상 그리고 형상비를 변수로 DPT(Double Punch Test)를 이용한 인장강도 실험을 수행하였다. 여기서 DTP인장강도 실험은 Barcelona test로 알려져 있으며, Fig. 4와 같이 공시체 인장응력이 가해지며 휨 공시체에 비해 파괴면적이 4배 이상 갖게된다. Chao(2012)연구자의 실험결과에 의하면 DPT실험방법은 변동계수가 12%이하로 정밀도가 우수한 것으로 보고되고 있다. 실험에 사용된 콘크리트 28일 압축강도는 31.1MPa이며 실험체의 일람은 Table 2에 정리했다.

인장강도 결과를 분석한 결과, 고온노출로 인하여 급격한 인장강도의 감소를 확인하였다. 강섬유 혼입량과 형상비에 따라 다소의 차이는 있지만, 300℃에서는 30∼40%, 500℃에서는 40∼55%, 700℃에서는 60∼70%의 강도 감소가 각각 나타났다.

각 영향인자에 대한 고찰 결과, 고온노출 시 섬유의 혼입률이 높을수록, 형상비가 클수록 인장강도가 큰 것으로 나타났다. 실험결과의 분석을 통하여 식 (3)과 같이 SFRC의 DPT(Double Punch Test) 인장강도를 예측할 수 있는 일반식을 제안하였다. 비록 제안된 식은 형상비 60과 80의 후크형 강섬유 실험결과에만 근거하였기 때문에 제한적이지만 본 연구와 동일한 형상의 강섬유를 사용했으므로 직접적인 비교가 가능하다. 식 (3) 함수에 사용된 는 상온상태의 인장강도(MPa)를 말한다.

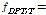
 (4)

강섬유 콘크리트의 가장 큰 특징은 균열 후 인장강도를 갖고 있다는 것이다. 균열 후 인장강도를 구하는 방법은 독일 콘크리트 위원회^[16], 일본 토목학회(JSCE-SF4)^[17]등 계산식을 제안하고 있다. 그 중 본 연구에서는 Fig. 5와 같이 균열 폭과 인장강도를 설정하였다.

2.2 SFRC를 충전한 합성기둥의 내화성능

필자(2013, 2014)는 강섬유 혼입량(Vf) 과 하중비(C/C'r)를 변수로 하여 실대 기둥크기의 재하가열 실험을 수행하였다. 그에따른 연구개요와 결과를 정리하면 Table 3과 같다. 여기서 C는 실험시 재하 하중량을 말하며, C'r은 콘크리트 단면에서 받을수 있는 압축력, Crc는 전 단면이 받을 수 있는 압축력을 계산하였다. 재하량(C)에서 콘크리트 단면이 받을 수 있는 압축력(C'r)을 나눈것을 하중비라 하며 하중비가 커질수록 내화성능이 저하되는것은 기둥 재하가열 선행연구를 통해 많이 알려져 왔다. 연구의 중점은 강섬유 혼입량에 비례적으로 내화성능이 향상되는 경향이 있지만 정비례적이지 않다는 점이다. 그 원인은 강섬유의 뭉침현상(시공상 문제)에 원인이 있었다.

무보강 콘크리트 대비 SFRC( : 0.375%) 적용 시 내화성능은 약 1.1∼1.3배 증가되었다. 콘크리트 내 강섬유는 균열을 억제 하며 그로 인한 열 변형을 완화시킨 결과로 평가되었다. 또한 Fig. 6과 같이 축 변형-시간관계를 볼 때 초기 30분 내외로 최대 강관 팽창구간을 갖고 있는 것으로 평가되었다. 강섬유 혼입량이 커질수록 콘크리트 하중전이 구간 (b)기울기가 완만하여 강재의 강도 손실 이후 콘크리트 하중 저항력이 향상되었음을 검증하였다.

3. 유한요소 해석

내화구조의 해석과정은 온도변화에 따른 요소별의 온도분포 및 상호작용, 재료의 기계적 변화, 하중과 구속조건에 따른 영향이 다양한 관계로 복합적으로 영향을 미치기 때문에 해석과정이 복잡하다. 해석과정은 비선형 열전달해석과 비선형 열응력해석의 연속하는 단계해석으로 구성된다. 비선형 열전달 해석은 열전도를 통한 단면 내 온도 평가 및 비선형 열응력 해석을 위한 열하중을 제공하기 위해 해석이 수행된다. 이어서 적용된 하중과 앞서 결정된 열하중 하에 의한 재료 손상 영향, 재료특성의 변화 그리고 구조부재의 하중능력 등 복합적인 구조적 반응을 결정하며, 본 연구에서는 구조 성능 평가에 사용된 범용 유한요소 해석 프로그램인 ABAQUS(Ver 6.10)을 동일하게 사용하여 해석적 접근을 수행하였다. 선행연구에서는 콘크리트 충전형 기둥의 열 해석 절차와 방법론에 대해 다양한 시각에서 소개(Lie and Irwin, 1995^[18], Ding and Wang, 2008^[19], Hong and Varma, 2009^[20])되고 있어 해석수행 시 고려할 요소와 경계조건을 반영하였다.

3.1 요소결정

열전달 해석(heat transfer analysis)시 사용된 표준가열 곡선은 실험과 동일한 KS F 2257-1을 적용하고, 초기온도는 20℃로 하였다. 강재의 재료에 대한 열적 특성을 나타내는 밀도, 비열 및 열전도율은 Eurocode 4^[21]에서 제시한 값을 적용하였다. 강재의 항복강도(Fy)는 325MPa로 그에 해당하는 고온에 따른 강도 저감율을 참고하여 Eurocode 4에서 제시된 온도에 따른 강재의 응력-변형률 선도를 입력하였다. 강섬유 콘크리트의 경우 각국규준에서 열적, 역학적 특성을 제시되고 있지 않으므로 Kodur and Lie(1996)^[14]가 제시한 강섬유 규산염 콘크리트의 온도에 따른 기계적(응력-변형률), 열적 함수를 인용하였다. 탄산염의 경우 비열과 열팽창율 구간에 급격한 변화가 있어 보다 안전적이고 보수적인 결과를 유도하기 위해 규산염 열적특성을 인용하여 해석을 수행했다. 이때 강섬유 콘크리트의 상온시 압축강도( 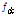)와 인장강도는 재료시험 결과를 근거로 계산되었다(Table 3). 열전달 해석은 기둥의 4면이 화재에 동일하게 노출되어 있다는 가정 하에 부재 전체를 모델링을 한 후 열전달 해석을 수행하였다.

8절점 열전달 해석요소(DC3D8)를 사용하여 모델링하였다. DC3D8은 온도에 대한 자유도를 가진 8개의 절점으로 이루어진 3차원 입방체 요소로서 등질성(homogeneous)과 등방성(isotropic)으로 정한 강재와 콘크리트의 구성요소로 적용하였다. SD4 는 3차원 입방체 요소의 표면에 정의되며 추가적인 절점(extra node)을 이용하여 가열로 내부 고온가스에서 부재까지의 대류열전달을 나타낸다.

열복사 효과를 위해 RSM(radiositysolver method)을 사용하였다. 비선형 열전달 해석의 풀이 과정으로 Newton- Raphson-method을 적용하였다. 온도별 SFRC 재료의 열적상수(비열, 열전도율, 밀도)는 앞서 2장에서 언급한 특성값을 적용하였다. 그 밖의 Eurocode 1-Part1-2^[22]에서 제시된 값을 적용하였는데 대류 열유속(qc)은 식 (5) 그리고 복사 열 유속(qr)은 식 (6)에 나타내고 있다.

 (5)

 (6)

3.2 비선형 열 해석 방법

비선형 열응력 해석은 온도증가에 의한 재료의 지속적인 역학적 특성변화의 고려가 필요하다. 열응력 해석 시 가장 중점을 둔 사항은 강재와 콘크리트와의 마찰력에 대한 부분이다. 일반 강관의 경우 고온에 도달할 경우 각 재료의 Slip이 발생되어 마찰력은 없는 것으로 간주되고 있다. 하지만. ACT기둥의 특성상 내부 리브는 콘크리트와 겹쳐있으므로 강관 축 팽창시 마찰력이 발생된다. 이러한 특성은 무피복 재하가열 실험을 통해 밝혀졌으며 해석상에 구현할 방법을 모색했다. 강관의 팽창에 의해 콘크리트가 파괴가능한 영역에 마찰계수 0.25를 추가 반영하여 모델을 수행하기로 했다. Wang(2008)연구에 의하면, 마찰계수를 0.2에서 0.8까지 상이하게 적용했을 때 해석결과는 1%미만의 결과를 갖는 것으로 평가되었다. 따라서 본 해석상에는 0.5의 마찰계수를 적용하였다.

비선형 열응력 해석시, 열전달 해석 모델과 같은 요소분할을 사용하였다. 등질성 및 등방성으로 가정한 강재와 콘크리트의 구성요소로 MISO(multi linear isotropic hardening) 모델을 적용하였다. 비선형 해석의 수렴을 위해 뉴턴-랩슨법을 사용 하였으며 LSM(line search method)으로 해의 안전성 및 수렴성을 높였다. 비선형 열응력 해석에서는 비선형 열전달 해석결과인 단면 내 온도분포 를 시간 순으로 불러들여 열하중으로 적용한다. 해석 모델의 지지조건은 양단 힌지 상태로 설정하였으며, 해석 시 가열면 이외 주위온도는 20℃로 설정하였다. 열응력 해석 시에는 온도상승에 따른 연속적인 재료의 역학적 특성변화의 고려가 요구된다.

4. 해석모델 결과 및 신뢰성 검증

4.1 일반각형 SFRC충전 기둥의 해석검증

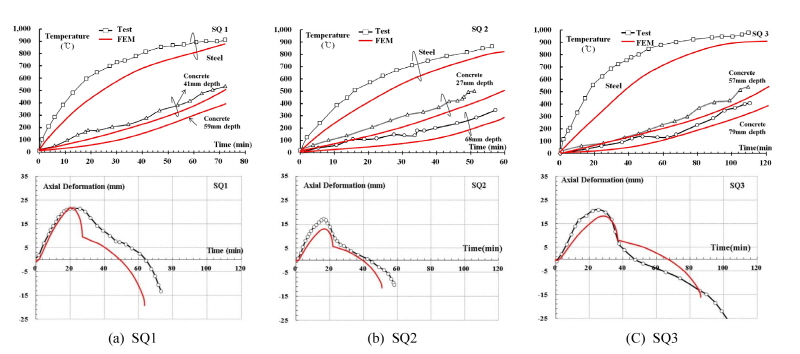
SFRC가 충전된 합성기둥의 모델을 대상으로 선행연구 Kodur and Lie(1997)^[13]와 해석결과를 비교함으로써 열전달 및 열 응력해석의 신뢰성을 검증하고자 한다. 예비 해석대상을 Table 4에 정리 하였다. 강섬유는 약 1.7% 혼입되었으며 적용된 강섬유 길이는 50mm, 직경 0.9mm로 섬유보강지수는 96이다. 콘크리트 압축강도는 SQ1～3부재 각각 49.5, 49.8 그리고 39.6MPa으로 측정되었다. 표준가열곡선은 식 (7)과 같은 KS F2258을 적용했으며 ‘t’는 시간(분)을 의미한다.

 (7)

열 전달 해석과 열 응력해석 결과를 실험결과와 중첩하여 Fig. 7에 정리하였다. 단면 내 온도 분포를 보면 전반적으로 열 분포 추세를 예측하고 있으며 다소 실험 결과에 비해 과소평가되어 평가되었다. 축 변형-시간관계의 경우 상당부분 유사성을 갖고 있다. 실험에 의한 내화성능 시간은 73, 60, 110분으로 평가 되었고, 해석에 의한 내화성능 시간은 강관의 팽창구간과 하중전이 구간이 매우 일치하게 추정되어 강섬유 콘크리트를 충전한 기둥부재의 내화성능 평가에 정량적 접근이 가능하다고 판단된다.

4.2 내부앵커형 SFRC 충전기둥의 해석검증

4.2.1 열 분포 및 확산 검토

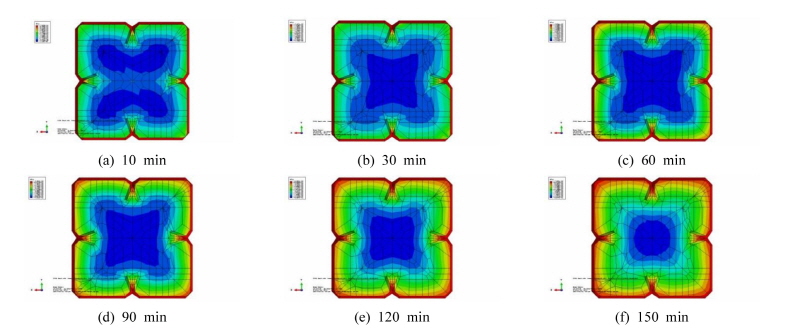
열전달 해석을 통해 시간에 따른 단면 내 온도를 확인할 수 있었다. Fig. 8은 가열 10분부터 150분까지 고온에 노출됐을 때 단면 온도분포를 나타내고 있다. 강관 경계면에서 열전도가 낮은 콘크리트의 열 특성에 의해 중앙부는 외부 온도변화에 대해 크게 영향을 받지 않음을 알 수 있다. 초기10분 이후 강재온도는 약 180℃를 육박하며 가파르게 상승하는 것으로 나타났다. 한편 콘크리트 단면의 경우 서서히 증가되며 가열 150분이 지났음에도 단면 중심부의 온도는 약 100℃미만을 유지하고 있다. 내부 리브로 인한 열 확산 범위를 보면 열전도율이 큰 콘크리트에 매립되어 온도상승 영향은 크지 않았다.

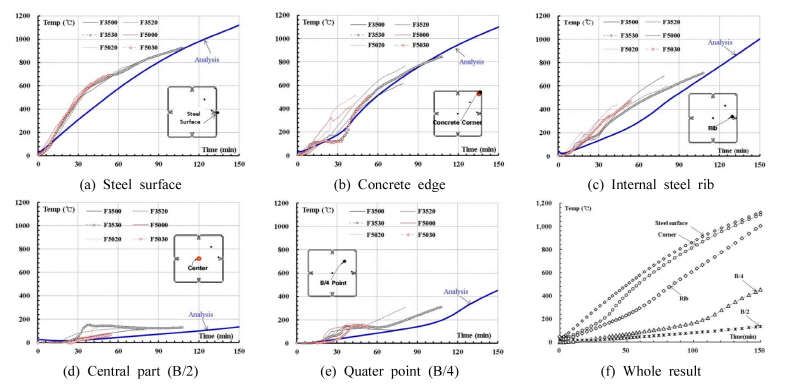
실험을 통해 측정된 단면 내 온도 분포를 해석결과와 검토하고자 Fig. 9와 같이 중첩하여 나타냈다. 실험 과정 중 발생되는 부재의 축 변형은 열전대 측정 값을 불안정하게 평가되지만 해석상에서는 매우 안정적으로 온도분포를 예측하고 있다. 강관에 표면에 측정된 초기 온도분포는 해석치가 다소 보수적으로 평가되고 있다. 이러한 원인을 선행연구를 통해 밝혀진 바에 의하면 열원에서 강관 표면까지 대류열전달로 전달되는 영향을 구하기 위해 표면의 기하학 형상, 유동의 성질 및 유체의 열역학적 특성과 열전달 특성 치들의 영향이 고려된 대류전달계수(Convection heat Transfer Coefficient)를 산정해야 하는데 이를 정확하게 구현하는 것은 현실적으로 불가능하므로 안전 측으로 설정값을 선택한 결과로 보인다. 그럼에도 단면 내 온도 분포의 전반적인 흐름은 비교적 일치하는 것으로 평가된다. 따라서 화재 발생 시 SF-ACT기둥의 온도분포 예측은 본 해석에서 예측 가능함을 알 수 있다.

가열 30분이 경과하면 강관은 온도가 700℃이상으로 급격히 증가하나, 강관 경계면에서 열전도가 낮은 콘크리트의 열특성에 의해 중앙부는 외부 온도변화에 크게 영향을 받지 않음을 알 수 있다. 또한, 열 부하(Heat Flux)는 Fig. 10과 같이 기둥 모서리와 중앙부 리브 부위에서 열 유입량이 크게 나타남을 알 수 있다. 따라서 콘크리트 단면 내부의 온도상승은 단면 중심에서 외측 면까지의 거리 변화에 따라 변화됨을 알 수 있다. 단면 중앙로 갈수록 방사형에 가깝게 온도분포가 나타났다. 측정된 온도와 해석결과의 온도분포는 전체적으로 거동이 유사하게 나타났지만 해석 시 열 환경의 변화, 가열에 의한 공간발생에 대한 실제 상황을 고려할 수 없으므로 실험결과보다는 다소 낮게 예측하고 있다. 하지만 그 오차범위는 10%미만이므로 전체 단면온도 분포 예측에 해석모델은 충분한 거동예측이 가능한 것으로 평가된다.

4.2.2 열 응력 및 변형 검토

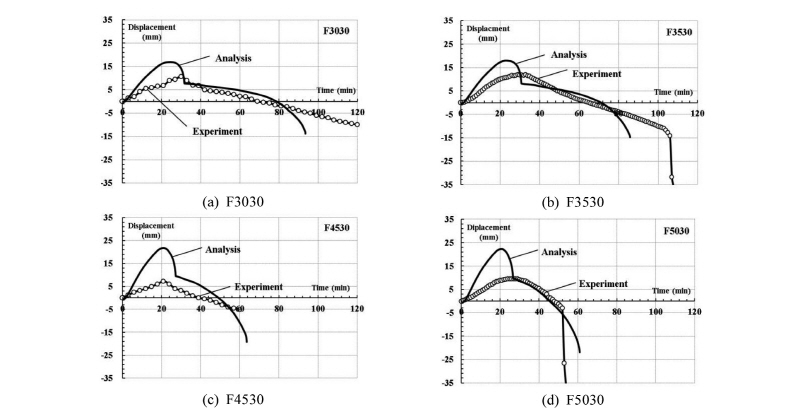
열응력 해석을 통해 고온시간에 따른 축 변형 관계를 유추할 수 있다. 시간에 따른 기둥부재의 열적 거동을 살펴보면 초기 20분부터 강재 팽창으로 인해 강재와 콘크리트간의 이격이 발생되는 것을 알 수 있다.

강재 팽창 시점 이후 전체 하중이 콘크리트로 전이되면서 강관의 좌굴 형상과 전체 열응력이 콘크리트에 집중되는 것을 확인할 수 있었다. 실험결과와의 검증을 위해 Fig. 11과 같이 중첩하여 표현하였다.

강관의 팽창 길이가 차이를 보이고 있는데 이러한 원인은 실제 고온에 노출된 이후부터는 두 재료는 이격되어 슬립현상만 발생되는 반면, 실제 ACT기둥은 내부의 리브가 콘크리트와 링크되어 있으므로 그 슬립차이가 비교적 작게 평가되고 있다. 그 외의 전반적인 거동은 실험결과와 매우 유사하게 예측되고 있다. 강섬유 혼입 유무에 따른 해석모델의 축변형-시간관계를 Fig. 12에 정리하였다. 재하 상태를 유지한 뒤에 가열을 하므로 시작상태에서는 이미 일정 하중을 저항하게 된다. 이후 고온에 직접적으로 노출된 강재는 면외로 팽창되며 이때 강재와 콘크리트는 슬립이 발생된다. 강재가 600℃이상 고온에 노출이 되면 강도가 급속도로 저감되면서 팽창된 강관은 수축하게 된다. 이때 늘어난 강관은 축 직각방향으로 많은 좌굴 형태를 나타나게 되며 이후 하중은 내부 콘크리트로 전이된다. 콘크리트는 축열효과로 인해 일정 하중상태에서 내화성능 발휘가 가능하지만 하중비가 클수록 매우 급격한 수축량을 보인다. 하지만. SFRC의 경우 가열시간 30분 이후부터 콘크리트 하중 전이 구간기울기가 매우 완만한 것을 알 수 있다. 동일한 경계조건을 갖는 해석모델이 다른 양상을 나타내는 원인은 콘크리트 물성치로 판단된다. SFRC의 경우 앞서 언급된 균열 후 인장강도(2장 참고)가 발휘되어 열 변형을 억제하는 역할을 하게 된다. 즉 하중이 내부 콘크리트로 전이되는 구간이 매우 안정적으로 거동되어 목표 내화성능 확보가 가능하게 된다고 보인다.

5. SFRC 충전 합성기둥의 내화성능 평가

5.1 해석개요

유한요석해석 모델을 활용하여 실험으로 분석되지 못한 변수를 통해 SF-ACT기둥의 열적 거동 특성의 영향인자를 고찰해 보고자 한다. 재하가열 실험을 통해 하중비는 내화성능에 주요 영향인자 임을 알 수 있었다. 하중비(C/C’_r)에 변화에 따른 열적 거동과 내화성능을 분석하고자 한다. Table 5와 같이 해석모델을 설정하여 총 9개의 하중비 변수를 갖도록 설정하였다. 해석방법과 경계조건은 앞서 수행된 절차와 동일하게 적용하였다. 우선 단면 내 온도해석을 수행하여 각 단면의 온도 분포 데이터를 정립 한 뒤 각 하중비에 따른 목표 재하량을 가력하여 좌굴해석을 수행한다. 이후 앞의 두 모델을 링크하여 열응력 해석을 수행하였다. 강재의 열적 특성은 Eurocode3에서 제시한 열적상수를 반영하였으며, SFRC의 경우 0.375% 혼입한 재료시험 결과를 토대로 실시하였다.

5.2 혼입율 변화에 따른 내화성능

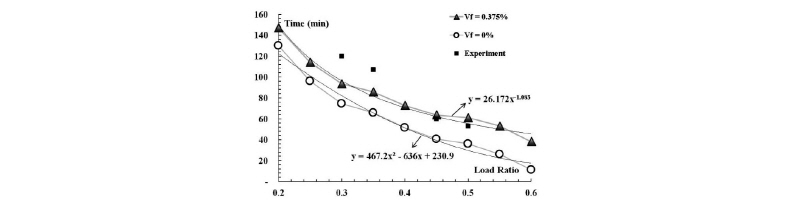
해석결과의 축 변형-시간관계를 Fig. 13에 정리하였다. 하중비가 커질수록 강관팽창 지속시간이 단축되고 있다. 전반적으로 고온에 노출된 30분 이내에 강관팽창 구간이 발생되며 하중비가 커짐에 따라 급격한 축방향 수축량을 보이고 있다. 하중비가 0.20인 경우 120분 내화성능 확보가 가능하며, 하중비 0.4이하부터는 60분 내화성능 확보가 가능한 것으로 평가되고 있다.

Table 6은 각 해석결과를 정리하였다. 강섬유 혼입율이 0.375%인 해석모델을 기준으로 혼입율이 0%인 해석 결과를 무차원하여 비교하였다. 하중비가 0.2～0.35사이에서는 약 1.2배 내화성능이 향상되는 것으로 평가 되었다. 실험 결과에서도 강섬유 혼입유무에 따라 약 1.2배 내화성능이 향상된 결과와 일치하였다. 한편 실험에서 측정하지 못한 하중비 0.4～0.5 사이에서는 내화성능이 약 1.6배 증폭되는 것으로 평가되었으며, 그 이상의 하중비 0.5∼0.6에서는 2배 이상 증가되어 나타났다. 즉 하중비가 커질수록 강섬유 콘크리트의 역할이 합리적으로 작용하는 것을 알 수 있었다. 이러한 원인은 콘크리트 전이 구간의 기울기(E)가 완만해지며, 내화성능까지 도달시점 목표에 매우 큰 영향을 미치는 것으로 판단된다. Fig. 14와 같이 강섬유 혼입 유무에 따라 비교해 보면 내화성능 시간과 하중비는 반비례적 관계에 있으며 하중비가 커질수록 강섬유 콘크리트가 유리하게 작용되는 것을 알 수 있다.

6. 결 론

비정상 열전달 해석과 열응력 해석을 통해 단면내 온도 분포와 하중비에 변화에 따른 내화성능을 검토 하였다. 선행연구(Kodur(1997), Kim(2014))를 대상으로 예비 해석을 수행하였으며 실험결과와 해석결과를 비교했을 때 단면 내 온도 분포와 내화하중 저항 구간 등 전반적인 거동예측이 가능한 것으로 평가되었다. 따라서 검증된 해석모델을 통해 SF-ACT 기둥의 구조 및 내화성능의 정량적 평가에 사용하고자 한다.

(1)예비해석을 통해 일반 CFT기둥의 열 전달 및 열응력상태를 분석한 결과, 전반적으로 열 분포 추세와 축 변형 기울기가 매우 유사한 경향을 갖고 있었다. 즉, 강섬유 콘크리트를 충전한 기둥부재의 내화성능 평가에 정량적 접근이 가능하다고 판단된다.

(2)혼입율 0.375%미만의 강섬유 콘크리트의 해석모델을 구현할 때, 내화성능에 영향을 끼치는 변수는 균열 후 인장강도에 따라 크게 상이하며, 강재와의 마찰계수 변화는 내화성능에 큰 영향을 미치지 않았다. 이러한 원인은 고온상태에서는 재료의 부착강도가 상실됨에 따라 마찰조건이 없는 상태가 되기 때문이라 판단된다.

(3)유한요소해석을 통해 SF-ACT기둥의 단면 내 온도분포를 살펴보면, 내부 리브(강관)보다 기둥 모서리부분의 온도가 오히려 상승되는 것을 확인하였다. 이는 강관표면에서 흐르는 열 유입량은 동일하지만, 리브의 경우 콘크리트 내에 충전되어 있으므로 열확산 범위가 확대되지 않은 것으로 보인다. 즉 내부 리브는 단면 내 온도 확산에 큰 영향이 없음을 알 수 있다.

(4)하중비에 따른 내화성능을 검토한 결과, SF-ACT기둥의 경우 하중비가 커질수록 콘크리트 전이구간 기울기가 매우 가파르게 형성되어, 하중비 0.6인 경우 30분 내화성능 확보되어 나타났다. 하중비가 0.20인 경우 120분 내화성능 확보가 가능하며, 하중비 0.4이하부터는 60분 내화성능 확보가 가능한 것으로 평가되고 있다.

(5)열 응력 해석을 통해 하중비에 따른 내화성능을 분석한 결과 강섬유 콘크리트 사용으로 1.2～2.0배 이상의 내화성능 발휘가 가능한 것으로 분석되었다. 결과적으로 온도 상승에 따른 내력관계를 비교하면 내부 콘크리트에서 대부분의 하중을 분담하므로 콘크리트의 열하중을 저항하기에 강섬유 콘크리트는 내화성능 확보에 효과적으로 작용된다.

Acknowledgments

본 연구는 2015년 국토교통부 창의도전 연구개발사업의 연구비지원(창조형 모험-442)에 의해 수행되었습니다.

References

• 대한건축학회(2004) 콘크리트 충전강관구조 요설, 기문당.
  Architectural Institute of Korea (2004) Commentary for Concrete Filled Tube (CFT) Steel Structures, Kimoondang, Korea (in Korean).
• 한국강구조학회(1999) 충전강관기둥의 내화성능평가 및 설계법에 관한 연구 보고서, 한국강구조학회.
  KSSC (1999) Research Report on Fire Performance Evaluation and Design of Filled Steel tube Columns, KSSC, Korea (in Korean).
• Kodur, V.K.R., and MacKinnon, D.H. (2000) Design of Concrete-Filled Hollow Structural Steel Column for Fire Endurance, Engineering Journal, American Institute of Steel Construction, Vol.37, No.1, pp.13-24.
• Han, H.-H., Xhao, X.-L., Yang, Y.-F., and Feng, J.-B. (2003) Experimental Study and Calculation of Fire Resistance of Concrete-Filled Hollow Steel Columns, Journal of Structural Engineering, American Society of Civil Engineers, Vol.129, No.3, pp.346-356. [https://doi.org/10.1061/(ASCE)0733-9445(2003)129:3(346)]
• Cheng, F.-P., Kodur, V.K.R., and Wang, T.-C. (2004) Stress-Strain Curve for High Strength Concrete at Elevated Temperature, Journal of Materials in Civil Engineering, American Society of Civil Engineers, Vol.16, No.​1, pp.84-90. [https://doi.org/10.1061/(ASCE)0899-1561(2004)16:1(84)]
• Muhamed, N.B., Fan, J., and Nei, J. (2011) Effects of Hollowness on Strength of Double Skinned Concrete Filled Steel Tubular Columns of Different Geometries Under Axial Loading, Applied Mechanics and Materials, Trans Tech Publications, Vol.94-96, pp.1746-1751. [https://doi.org/10.4028/www.scientific.net/AMM.94-96.1746]
• 구철회, 이철호, 안재권(2013) 화재 시 무피복 CFT 기둥의 축강도 평가를 위한 단면온도분포 예측기법의 개발, 한국강구조학회논문집, 한국강구조학회, 제25권, 제6호, pp.​587-​599.Koo, C.H., Lee, C.H., and Ahn, J.K. (2013) Prediction of Temperature Distribution to Evaluate Axial Strength of Unprotected Concrete-Filled Steel Tubular Columns Under Fire, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.6, pp.587-599 (in Korean). [https://doi.org/10.7781/kjoss.2013.25.6.587]
• 김해수, 이치형(2010) 내화피복종류에 따른 각형 CFT기둥의 온도분포에 관한 실험적 연구, 한국강구조학회논문집, 한국강구조학회, 제22권, 제6호, pp.523-532.
  Kim, H.S., and Lee, C.H. (2010) An Experimental Study on the Temperature Distribution of Square CFT Columns According to the Types of Fire Protection, Journal of Korean Society of Steel Construction, KSSC, Vol.22, No.​6, pp.523-532 (in Korean).
• 김선희, 염경수, 최성모(2013) 내부앵커형 콘크리트 충전 기둥의 내력 및 변형 능력에 관한 연구, 한국강구조학회논문집, 한국강구조학회, 제25권, 제4호, pp.347-357.
  Kim, S.H., Yom, K.S., and Choi, S.M. (2013) A Study on the Load Carrying Capacity and Deformation Capacity of the Internal Anchors Welded Cold Formed Concrete Filled Columns, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.4, pp.347-357 (in Korean). [https://doi.org/10.7781/kjoss.2013.25.4.347]
• Kim, S.-H., Choi, S.-M., and Yom, K.-S. (2014) Improving Fire Performance with Steel Fibers for Internally Anchored Square Composite Columns, Journal of Constructional Steel Research, Elsevier, Vol.103, pp.264-274. [https://doi.org/10.1016/j.jcsr.2014.09.003]
• 김선희, 염경수, 김용환, 최성모(2014) 내화성능 개선을 위한 강섬유 보강 내부 앵커형 각형강관 합성기둥의 실험연구, 한국강구조학회논문집, 한국강구조학회, Vol.26, No.​6, pp.499-509.
  Kim, S.H., Yom, K.S., Kim, Y.H., and Choi, S.M. (2014) An Experimental Study of Improving Fire Performance with Steel-Fibers for Internally Anchored Square Composite Columns, Journal of Korean Society of Steel Construction, KSSC, Vol.26, No.6, pp.499-509 (in Korean). [https://doi.org/10.7781/kjoss.2014.26.6.499]
• Lie, T.T., and Kodur, V.K.R. (1996) Thermal and Mechanical Properties of Steel-Fiber-Reinforced Concrete at Elevated Temperatures, Canada Journal Civil Engineering, Canadian Science Publishing (NRC Research Press), Vol.23, No.2, pp.511-517. [https://doi.org/10.1139/l96-055]
• Kodur, V.K.R., and Lie, T.T. (1997) Evaluation of Fire Resistance of Rectangular Steel Columns Filled with Fiber-​Reinforced Concrete, Canadian Journal of Civil Engineering, Canadian Science Publishing (NRC Research Press), Vol.24, No.3, pp.339-349. [https://doi.org/10.1139/l96-114]
• Kodur, V.K.R., and Lie, T.T. (1996) Fire Resistance of Circular Steel Columns Filled with Fiber-Reinforced Concrete, Journal of Structural Engineering, American Society of Civil Engineers, Vol.122, No.7, pp.776-782. [https://doi.org/10.1061/(ASCE)0733-9445(1996)122:7(776)]
• 문도영(2013) 고온노출된 강섬유보강 콘크리트 인장성능에 대한 실험적 연구, 한국방재학회논문집, 한국방재학회, 제13권, 제1호, pp.63-71.
  Moon, D.Y. (2013) Experimental Study on Tensile Strength of Steel Fiber-Reinforced Concrete Subjected to High Temperature, Journal of the Korean Society of Hazard Mitigation, KOSHAM, Vol.13, No.1, pp.63-71 (in Korean). [https://doi.org/10.9798/KOSHAM.2013.13.1.063]
• Deutsches Institut für Normung e.V. (1988) Beton und Stahlbeton - Bemessung und Ausführung (Structural Use of Concrete - Design and construction, DIN 1045: 1988-​07), Germany (in German).
• JSCE Concrete Committee (1984) Method of Tests for Flexural Strength and Flexural Toughness of Steel Fiber Reinforced Concrete (JSCE-SF4), Concrete Library International, Japan Society of Civil Engineers, Vol.3, pp.58-​61.
• Lie, T.T., and Irwin, R.J. (1995) Fire Resistance of Rectangular Steel Columns Filled with Bar-Reinforced Concrete, Journal of Structural Engineering, American Society of Civil Engineers, Vol.121, No.5, pp.797-805. [https://doi.org/10.1061/(ASCE)0733-9445(1995)121:5(797)]
• Ding, J., and Wang, Y.C. (2008) Realistic Modelling of Thermal and Structural Behavior of Unprotected Concrete Filled Tubular Columns in Fire, Journal of Construction Steel Research, Elsevier, Vol.64, No.10, pp.1086-1102. [https://doi.org/10.1016/j.jcsr.2007.09.014]
• Hong, S., and Varma, A.H. (2009) Analytical Modeling of the Standard Fire Behavior of Loaded CFT Columns, Journal of Constructional Steel Research, Elsevier, Vol.​65, No.1, pp.54-69. [https://doi.org/10.1016/j.jcsr.2008.04.008]
• European Committee for Standardization (1992) Eurocode 4: Design of Composite Steel and Concrete Structures, Part 1-1: General Rules and Rules for Building (ENV 1994-​1-1), Belgium.
• European Committee for Standardization (2002) Eurocode 1: Actions on Structures, Part 1-2: General Actions – Actions on Structures Exposed to Fire (EN 1991-1-2), Belgium.