
새로운 형태의 강바닥판 리브에 대한 연구
Copyright ⓒ 2014 by Korean Society of Steel Construction
초록
본 연구의 목적은 파형 복부판과 허니컴 샌드위치 패널에 사용된 강판 보강 방법을 강바닥판에 적용하고, 새로운 리브와 기존 개단면 및 폐단면 리브와의 비교를 통하여 경제적인 새로운 형태의 리브를 제안하는데 있다. 새로운 리브 형태로 사다리꼴 파형, ㄹ형, 벌집형, ㅁ형 리브를 고려하고, 개단면 및 폐단면 리브와 리브 강재량을 비교한 결과, 경제성 측면에서 벌집형과 ㅁ형 리브가 좋은 결과를 나타내었으며, ㅁ형 리브가 벌집형보다 좀 더 좋음을 알 수 있었다. 실제 강바닥판에 적용 가능한 ㅁ형 리브를 만들기 위하여, 민감도 분석과 매개변수 연구를 수행하였으며, 특정 응력 조건하에서 적정한 단면을 선택할 수 있는 시스템을 구축하였다. 실 교량의 폐단면 리브와 제안한 시스템의 ㅁ형 리브의 강재량을 비교한 결과, 새로운 형태의 리브가 더 경제적임을 알 수 있었다. 따라서, ㅁ형 리브를 갖는 보강판에 대하여 본 연구에서 제안한 시스템을 이용하면 보다 더 경제적인 강바닥판을 얻을 수 있을 것으로 판단된다.
Abstract
The purpose of this study is to propose an economic new type rib by applying plate stiffening methods of the corrugated plate and the honey-comb sandwich panel to the steel deck plate and comparing the new type rib with existing open and closed ribs. The trapezoidal corrugated type, ㄹ type, honey-comb type and ㅁ type ribs are considered as new type ribs and the moment and the steel volume are compared with that of open ribs and closed ribs. The results shows that the honey-comb type and ㅁ type ribs are good in aspects of economic feasibility and the ㅁ type is better than the honey-comb type. To make the ㅁ type rib applicable to the steel deck plate, the sensitivity analysis and parametric study are performed and the system to select the proper section under the particular stress condition is established. The closed rib of real bridges is compared with the ㅁ type rib of the proposed system and it is known that the new type rib is more economic. Therefore, more economic steel deck plates can be achieved by using the system proposed in this study for the plate stiffened with the new ㅁ type rib.
키워드:
강바닥판, 경제적, 새로운 형태의 리브, ㅁ형 리브, 벌집형 리브, 특정 응력 조건Keywords:
Steel deck plate, Economic, New type rib, ㅁ type rib, Honey-Comb type rib, Particular stress condition1. 서 론
교량, 터널, 항공기, 선박, 건축 구조물 등에 다양하게 사용되고 있는 강판은, 큰 강도로 소요단면이 작아져 자중을 줄일 수 있다는 장점을 갖고 있지만, 단면이 박판 형태로 좌굴에 취약하다는 단점을 가지고 있어 이를 보완하기 위하여 다양한 보강 방법이 사용되고 있다.
먼저, 개단면 리브와 폐단면 리브로 보강된 강바닥판은 토목 및 건축 구조물 등에 많이 쓰이고 있으며, 개단면 리브는 제작이 쉽고, 폐단면 리브는 큰 비틀림 강성으로 효율적인 구조를 갖는다는 장점을 갖고 있다[1],[2],[3],[4],[5].
다른 보강 형태인 파형 강판은 아치 형태를 적용하여 터널이나, 격납고 같은 시설물에 쓰이고 있으며[6], 최근에는 높은 전단 저항력과 아코디온 효과를 이용하여 PSC의 복부판으로 사용되고 있다[7].
또 다른 보강 형태인 허니컴 샌드위치 패널 구조는 철도차량, 항공기, 선박 등에 사용되고 있으며, 최근에는 충돌에너지 흡수장치로도 활발히 연구되고 있다[8],[9].
본 연구에서는 PSC의 복부판으로 사용되는 파형과 허니컴 샌드위치 패널에 사용되는 벌집 형태의 보강재를 적용하여 새로운 형태의 리브를 구성하고, 기존의 개단면 및 폐단면 리브와의 응력 및 강재량 비교를 통하여, 강바닥판에 적용 가능한 경제적인 새로운 형태의 리브를 찾고자 한다.
2. 새로운 형태 리브의 거동 분석
본 장에서는 보강판의 거동 분석시 한 패널에 국부 거동이 함께 발생하도록 하중을 재하하는 것이 안전성 측면에서 더욱 좋으며, 보강재에 하부 플랜지가 있는 경우가 더 효율적이라는 기존 연구[10]를 반영하여, 한 패널의 보강판에 국부 거동이 발생하도록 하중을 재하하고 하부 플랜지를 갖는 새로운 형태의 리브와 기존의 개단면 및 폐단면 리브의 결과를 비교하여, 새로운 형태의 리브 중 더 경제성과 효율성을 가진 리브를 선택하고자 한다.
2.1 예제 제원 및 하중 Case
Fig. 1과 같이 개단면과 폐단면 리브로는 국내에서 제작되는 L형을 기준으로 같은 단면을 갖는 역T형, ㄷ형 리브를, 새로운 형태의 리브로는 실제 PSC 교량에 사용된 파형강판의 비율을 기준으로 파형 및 벌집형 리브를 구성하고 이를 응용한 ㄹ형, ㅁ형 리브를 고려하였으며, 각 리브의 제원은 Table 1 및 Fig. 2와 같다. Table 1에서 a, b, c 는 리브 간격을 나타내며, 각 리브 간격에서 Case 1은 기본 제원, Case 2, 3은 리브 높이가 변화하는 경우, Case 4, 5는 리브 두께가 변화하는 경우를 나타낸다.
국부 거동이 발생하도록 Fig. 3과 같이 2변 단순 지지된 판의 중앙에 위치한 100mm×100mm의 정사각형에 100kN을 재하 하였으며, 리브 형태 및 보강판 중앙의 리브 배치에 따라 최대 3가지 하중 Case를 고려하였다.
2.2 해석 결과 비교
각각의 리브 형태마다 Fig. 3에 나타낸 하중 케이스에 대하여 요소 크기 12.5×12.5mm의 4절점 판 요소로 모델링하고 범용프로그램인 MIDAS를 이용하여 해석하였다.
Fig. 3의 하중 Case에 대하여 각각의 리브 형태별로 보강판 중앙점에서 발생하는 X축에 대한 모멘트 Mxx 및 Y축에 대한 모멘트 Myy와 리브의 강재량을 구하고, 그 중 가장 큰 모멘트를 대표 값으로 하여 나타내면 Fig. 4와 같다.
Fig. 4를 살펴보면, 기존의 리브는 Myy보다 Mxx가 더 크게 나타나고, 개단면 리브가 폐단면 리브보다 약간 큰 결과를 나타냄을 알 수 있다. 새로운 리브를 살펴보면, 파형 리브는 개단면 리브보다 약간 작은 모멘트를, ㄷ형 리브와 비교하여 유사하거나 약간 작은 결과를 나타내나, 강재량은 기존 리브와 유사하거나 약간 큰 결과를 나타내어 효율성 부분에서 개단면 리브와 거의 유사할 것으로 예측된다. 또한 새로운 리브 형태 중 ㄹ형, 벌집형, ㅁ형 리브는 기존의 개단면 및 폐단면 리브와 비교하여 Mxx, Myy 모두 훨씬 작은 결과를 나타내었으나, 리브 강재량은 더 큰 값을 가짐에 따라 그 경제성과 효율성을 판단하기 어려움을 알 수 있다.
새로운 리브에 대한 효율성을 명확하게 살펴보기 위하여, 각 제원 Case별로 ㄷ형 리브의 강재량과 동일하도록 새로운 형태 리브의 두께를 조절한 뒤, 새로운 보강판을 재해석하고 그 결과를 폐단면 ㄷ형 리브의 결과 값으로 나누어 그 비율로 나타내면 Fig. 5와 같다.
ㄷ형과 동일 강재량일 때의 모멘트 결과를 나타낸 Fig. 5를 살펴보면, 파형 리브는 Mxx, Myy 모두 폐단면 리브보다 더 큰 결과를 나타내어 효율성이 떨어짐을 알 수 있으며, ㄹ형 리브는 Mxx에서는 가장 좋은 결과를 나타내었으나, Myy에서는 폐단면 리브와 유사한 결과를 나타냄을 알 수 있다. 또한, 벌집형과 ㅁ형 리브는 Mxx, Myy 모두 기존의 리브보다 더 작은 모멘트를 가짐을 알 수 있으며, Myy의 경우에는 서로 비슷한 결과를, 더 큰 모멘트를 나타내는 Mxx의 경우에는 벌집형(80.6~87.6%)보다 ㅁ형 리브(76.4~83.8%)가 약 4% 정도 더 좋은 결과를 나타냄을 알 수 있다.
따라서, 기존의 리브보다 벌집형, ㅁ형 리브가 더 효율적임을 알 수 있으며, 이 중 ㅁ형 리브가 더 큰 모멘트가 발생하는 Mxx에서 4% 정도 더 좋은 결과를 나타냄에 따라 본 연구에서는 ㅁ형 리브를 중심으로 연구를 수행하고자 한다.
3. ㅁ형 리브 보강판의 민감도 분석
본 장에서는 박스 크기가 일정한 경우와 박스 크기가 변하는 경우에 대한 민감도 분석을 통하여, 제원에 따른 ㅁ형 리브 강바닥판의 거동을 살펴보고, 적정 단면 산정에 가장 큰 영향을 미치는 제원을 결정하고자 한다.
3.1 ㅁ형의 박스 크기가 일정한 경우
본 절에서는 Fig. 6과 같이 일정한 박스 크기를 갖는 판 두께 14mm인 강바닥판에 대하여 ㅁ형 리브 제원 변화가 강바닥판의 거동에 미치는 영향을 분석하였으며, 각각의 제원 변화와 그 해석 결과를 나타내면 Table 2와 같다.
Table 2를 살펴보면, ㅁ형 리브의 제원 변화와 상관없이 모든 경우에
 보다 더 큰 값을 나타내며, 제원 변화에 따라 강재량이 작은 구조에서는 큰 응력이 발생하고, 반대로 강재량이 큰 경우에는 응력이 작아짐을 알 수 있다.
보다 더 큰 값을 나타내며, 제원 변화에 따라 강재량이 작은 구조에서는 큰 응력이 발생하고, 반대로 강재량이 큰 경우에는 응력이 작아짐을 알 수 있다.
각 제원의 영향을 살펴보면, 리브 간격이 응력에 미치는 영향이 가장 크며, 이에 따라 강재량의 변화도 가장 크다는 것을 알 수 있으며, 리브 두께와 높이가 응력에 미치는 영향은 비슷하고, 리브 간격보다 상대적으로 작음을 알 수 있다.
그러나 Table 2의 결과는 각각의 제원 변화량이 다르다는 문제를 갖고 있으므로, 각 제원에 따른 영향을 명확하게 비교하기 위하여 최대 응력
 를 기준 응력으로, 각각의 제원 1% 변화당 응력의 변화율, 강재량의 변화율 및 단위 강재량 당 발생하는 응력 변화율을 나타내면 Table 3과 같다.
를 기준 응력으로, 각각의 제원 1% 변화당 응력의 변화율, 강재량의 변화율 및 단위 강재량 당 발생하는 응력 변화율을 나타내면 Table 3과 같다.
제원 1%당 변화율을 나타낸 Table 3을 살펴보면, 모든 변화율에서 리브 간격의 영향이 가장 크게 나타나 ㅁ형 리브 보강판의 거동에 가장 큰 영향을 주는 제원임을 알 수 있으며, 리브 두께와 리브 높이 변화는 응력에 미치는 영향에 비하여 강재량 변화에 미치는 영향이 훨씬 크게 나타남에 따라 경제적인 단면을 만들기 위해서 리브 두께와 리브 높이는 가능한 작은 제원을 사용하는 것이 효율적임을 알 수 있다.
이상으로부터, 리브 간격이 ㅁ형 리브 보강판의 거동에 가장 큰 영향을 주는 제원이며, 리브 두께와 리브 높이는 가능한 작은 제원을 사용하는 것이 경제적임을 알 수 있다.
3.2 ㅁ형의 박스 크기가 변하는 경우
본 절에서는 ㅁ형 리브 보강판의 거동에 가장 큰 영향을 주는 리브 간격을 중심으로 박스 크기 및 나머지 제원 변화가 미치는 영향을 살펴보기 위하여, Fig. 7 및 Table 4와 같이 ㅁ형 박스의 폭 w는 s/6, 2s/6, 3s/6, 박스 깊이 d는 0.5w, 1.0w, 1.5w의 형식으로 리브 간격에 비례하는 형태의 박스 단면을 구성하고, 두께 t는 6, 8, 10mm, 리브 높이는 200, 250, 300mm를 고려하였으며, 이때 판 두께는 14mm를, 리브 간격은 300mm, 450mm, 600mm를 사용하였다.
폭 w는 2s/6, 박스 깊이 d는 1.0w, 두께 t는 8mm, 리브 높이는 250mm를 갖는 ㅁ형 박스를 기본 단면으로 Table 4에 나타낸 제원 및 박스 크기 변화에 따른 해석 결과를 리브 간격별로 정리하여 나타내면 Table 5와 같다.
Table 5를 살펴보면, 모든 경우에
 보다 크고, 리브 간격이 커지면 발생하는 응력은 커지나 강재량은 줄어드는 것을 알 수 있으며, 박스 깊이 d를 제외한 모든 제원에서 제원이 증가하면 응력은 감소하고 강재량은 증가하는 경향을 나타내며, 박스 깊이 d는 그 반대임을 알 수 있다.
보다 크고, 리브 간격이 커지면 발생하는 응력은 커지나 강재량은 줄어드는 것을 알 수 있으며, 박스 깊이 d를 제외한 모든 제원에서 제원이 증가하면 응력은 감소하고 강재량은 증가하는 경향을 나타내며, 박스 깊이 d는 그 반대임을 알 수 있다.
박스 폭 2s/6인 기본 단면 중 리브 간격 300mm 일 때 0.378이던 응력
 가 리브 간격이 450mm로 50% 증가하면 0.467로, 박스 폭이 s/6으로 50% 감소하면 0.471로 증가하여 리브 간격과 박스 폭이 미치는 영향이 비슷함을 알 수 있다.
가 리브 간격이 450mm로 50% 증가하면 0.467로, 박스 폭이 s/6으로 50% 감소하면 0.471로 증가하여 리브 간격과 박스 폭이 미치는 영향이 비슷함을 알 수 있다.
제원 변화에 따른 결과를 비교하기 위하여 Table 5의 결과 중 응력
 와 강재량에 대하여 기본 단면에 대한 변화율로 바꾸어 나타내면 Fig. 8과 같으며, 이를 다시 각 제원 1% 변화에 따른 변화율로 나타내면 Fig. 9와 같다.
와 강재량에 대하여 기본 단면에 대한 변화율로 바꾸어 나타내면 Fig. 8과 같으며, 이를 다시 각 제원 1% 변화에 따른 변화율로 나타내면 Fig. 9와 같다.
Fig. 8 및 9를 살펴보면, 응력
 측면에서 박스 폭 w가 미치는 영향이 가장 크므로, 응력을 감소시키기 위해서는 박스 폭 w를 증가시키는 것이 가장 효과적임을 알 수 있다.
측면에서 박스 폭 w가 미치는 영향이 가장 크므로, 응력을 감소시키기 위해서는 박스 폭 w를 증가시키는 것이 가장 효과적임을 알 수 있다.
또한, 강재량 측면에서 살펴보면, 박스 깊이 d는 다른 제원에 비하여 증감에 따른 리브 강재량 변화율에 큰 차이가 발생함을 알 수 있으며, 강재량을 줄이기 위해서 리브 두께와 리브 높이를 줄이는 것이 효과적임을 알 수 있다.
각 제원의 영향을 종합적으로 살펴보기 위하여 Fig. 9에 나타낸
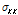 의 변화율을 강재량 변화율로 나누고 그 결과를 표로 나타내면 Table 6과 같다.
의 변화율을 강재량 변화율로 나누고 그 결과를 표로 나타내면 Table 6과 같다.
Table 6을 살펴보면, 박스 폭(w)은 리브 간격이 커짐에 따라 응력 변화량이 작아지기는 하나, 다른 제원들에 비하여 응력 변화량이 가장 크게 나타나 일정한 리브 간격에서 박스 폭이 응력에 영향을 주는 가장 중요한 제원임을 알 수 있다. 박스 깊이(d)는 제원을 작게 하는 경우 응력에 가장 영향을 적게 미치는 것으로 나타났으나, 크게 하는 경우 리브 간격 증가에 따라 더 큰 영향을 미치는 것으로 나타났으며, 이는 박스 깊이 자체가 리브 간격에 따라 제원이 변하는 변수이기 때문에 나타난 현상으로 풀이된다. 또한 리브 높이와 리브 두께는 리브 간격이 커짐에 따라 응력 변화에 미치는 영향이 점점 작아지며, 제원 변화에 따른 응력 변화가 매우 작은 값을 나타내므로, 좀 더 경제적인 ㅁ형 리브 단면을 얻기 위해서는 가능한 작은 제원의 리브 높이와 리브 두께를 사용하는 것이 효과적일 것으로 판단된다.
이상으로부터, 리브 간격이 ㅁ형 리브 보강판의 거동에 큰 영향을 주는 제원임을 알 수 있으며, 같은 리브 간격에서는 박스 폭이 미치는 영향이 가장 크고, 리브 두께와 리브 높이는 가능한 작은 제원을 사용하는 것이 경제적임을 알 수 있다.
4. ㅁ형 리브 보강판의 적정 단면 산정
본 장에서는 제원 및 박스 형태에 따른 매개변수 연구를 통하여 ㅁ형 리브 보강판의 적정 단면을 산정하는 시스템을 구축하고, 실교량의 폐단면 리브 보강판과 비교함으로써 ㅁ형 리브 보강판의 효율성을 살펴보고자 한다.
4.1 적정 단면 산정 시스템의 구축
리브 두께와 높이는 가능한 작은 것이 경제적이므로, 리브 높이는 200mm와 250mm, 리브 두께는 6mm와 8mm를, 모든 판 두께는 14mm를 사용하였으며, Fig. 7과 같이 박스 폭과 깊이가 다른 9가지 박스 형태에 대한 해석 결과를 정리하여 각각의 리브 높이와 두께 별로 X축에는 리브 간격, Y축에는 발생 응력으로 하여 나타내면 Fig. 10과 같다.
Fig. 10을 살펴보면, 같은 리브 간격이라도 박스 형태에 따라 발생하는 응력이 서로 다르고, 같은 박스 형태라 할지라도 (a) 리브 높이 200mm, 리브 두께 6mm인 경우에 가장 큰 응력이 발생하고, (d) 리브 높이 250mm, 리브 두께 8mm인 경우에 가장 작은 응력이 발생함을 알 수 있다.
또한, 각각의 박스 형태별로 리브 간격 300, 450, 600mm에 대한 응력 결과가 일정한 양상을 나타냄을 알 수 있으며, 이를 Hermite 2차 다항식을 이용하여 식 (1)과 같이 리브 간격의 함수로 표현하고, 각 박스 형태별 추세선에 대한 식 (1)의 계수값
 를 나타내면 Table 7과 같다.
를 나타내면 Table 7과 같다.
 (1)
(1)
Fig. 10을 살펴보면, 특정한 응력에 대하여 여러 형태의 단면을 가지며, 식 (1)과 Table 7을 이용하면 각각의 박스 형태별로 해당 응력에 맞는 리브 간격을 구할 수 있음을 알 수 있으므로, 이 시스템을 이용하면 특정 응력에 대한 단면을 간편하게 산정할 수 있을 것으로 판단된다.
4.2 단면 산정 시스템의 활용
본 절에서는 실 교량에서 발생하는 응력을 기준으로 ㅁ형 리브 단면을 구성하고 각 단면별 리브 강재량을 비교함으로써 구축한 시스템의 타당성을 확인하고, ㅁ형 리브 보강판이 강바닥판에 적용가능한지 살펴보고자 한다.
ㅁ형 리브의 적용성을 살펴보기 위하여, 총 5개의 실 교량을 모델링하고, 판 중앙에 위치한 100×100mm의 정사각형에 100kN을 작용시킨 뒤, 그 결과를 정리하여 나타내면 Table 8과 같다.
앞서 구축한 시스템(Fig. 10과 Table 7 참조)에 실 교량들의 응력을 대입하여 새로운 ㅁ형 리브의 적정 간격을 산정하고, 해당 단면에 대한 단위 길이당 리브 강재량을 산출한 뒤 실 교량의 단위 길이당 리브 강재량으로 나누어 비율로 표현하면 Table 9와 같으며, 이때 실 교량보다 작은 강재량을 갖는 경우는 진하게 나타내었다.
Table 9에서 먼저, 리브 높이 250mm, 리브 두께 8 mm인 단면을 기준으로 실 교량보다 작은 강재량을 갖는 단면을 살펴보면, 리브 두께를 6mm로 줄인 경우 14가지, 리브 높이를 200mm로 줄였을 경우 8가지, 리브 높이를 200mm로 리브 두께를 6mm로 줄인 경우 만족하는 단면이 28가지로 리브 높이보다 리브 두께를 줄이는 것이 더 경제적이며, 리브 두께와 리브 높이를 동시에 줄이는 것이 가장 효과적임을 알 수 있다. 또한, 박스 형태를 살펴보면, 박스 폭 w=2s/6, 박스 깊이 d=1.5w인 경우와 박스 폭 w=3s/6, 박스 깊이 d=0.5w인 경우에 만족하는 단면이 가장 많은 것으로 파악되었으며, 특히 리브 높이 200mm, 리브 두께 6 mm, 박스 폭 w=3s/6, 박스 깊이 d=0.5w 인 경우에는 최대 30%까지 강재량을 줄일 수 있음을 알 수 있다.
이상의 결과로부터, 매개변수 연구를 통해 구축한 시스템을 이용하면 특정 응력 조건에 대한 새로운 ㅁ형 리브의 단면을 구성할 수 있으며, 실 교량과 리브 강재량을 비교하였을 때 보다 더 경제적인 단면을 얻을 수 있음을 확인하였다.
따라서 리브 높이 200mm, 리브 두께 6mm인 경우에 대한 단면 산정 시스템을 사용하여 새로운 ㅁ형 리브 보강판을 구성하면, 기존의 폐단면 리브 보강판에 비하여 좀 더 경제적인 단면을 얻을 수 있을 것으로 판단된다.
5. 적용성 검토
본 장에서는 실 교량의 강바닥판 설계시 사용하는 DB 하중에 대한 ㅁ형 리브 강바닥판의 적용성을 살펴보고자, 하중은 DB-24의 후륜하중 96kN을, 접지면적은 500×200mm를 사용하여 실 교량의 사다리꼴 리브와 새로운 ㅁ형 리브를 해석한 뒤 그 결과를 비교하고자 한다.
앞서 살펴본 바와 같이 가장 경제적인 단면을 얻을 수 있는 리브 높이 200mm, 리브 두께 6mm를 갖는 경우에 대하여 Fig. 7과 같이 박스 형태에 따라 총 9가지 경우를 해석하였으며, 그 결과를 그림으로 나타내면 Fig. 11과 같다.
판의 중심에 위치한 500×200mm의 사각형에 96kN을 작용시켰을 때 발생하는 실 교량의 응력을 산정하고, Fig. 11에 적용하여 박스 형태별로 ㅁ형 리브의 적정 간격을 구하고, 리브 강재량을 산출한 뒤, 그 결과를 실 교량의 강재량에 대한 비율로 나타내면 Table 10과 같다. 이때, 실 교량보다 작은 강재량을 갖는 경우는 진하게 나타내었다.
Table 10에서 강재량이 가장 작은 경우를 살펴보면, 제2진도대교는 74%, 나머지 교량은 85% 내외의 강재량을 나타내어 새로운 ㅁ형 리브 강바닥판을 사용하는 경우 최대 26%가량 더 경제적인 설계를 할 수 있음을 알 수 있다.
100×100mm의 정사각형에 하중을 작용시킨 Table 9와 함께 살펴보면, 발생 응력이 클수록 새로운 ㅁ형 리브 강바닥판의 경제성이 더 커지고 만족하는 단면도 더 많아짐을 알 수 있다. 또한, 리브 높이 200mm, 두께 6mm인 경우에 박스 폭 w=2s/6, 박스 깊이 d=1.5w인 형태와 박스 폭 w= 3s/6, 박스 깊이 d=0.5w 및 1.0w인 형태에서 폐단면 리브를 갖는 모든 교량보다 경제적인 단면이 구성됨을 알 수 있으며, 이 중 박스 폭 w=3s/6, 박스 깊이 d=0.5w인 형태가 가장 경제적인 ㅁ형 리브 단면을 가짐을 알 수 있다.
따라서 리브 높이 200mm, 두께 6mm를 갖고, 박스 폭 w=2s/6, 박스 깊이 d=1.5w인 형태 또는 박스 폭 w= 3s/6이고, 박스 깊이 d=0.5w 또는 1.0w인 형태를 갖는 ㅁ형 리브 단면을 구성하면, 기존의 사다리꼴 폐단면 리브에 비하여 더 경제적인 단면을 얻을 수 있을 것으로 판단된다.
6. 결 론
본 연구에서는 파형 복부판과 허니컴 샌드위치 패널에 사용된 강판 보강 방법을 적용하여 새로운 형태의 리브를 구성하고, 기존 개단면 및 폐단면 리브와의 비교․분석을 통하여 강바닥판에 적합한 새로운 리브 형태를 찾고자 하였으며, 그 결과를 정리하여 나타내면 다음과 같다.
(1)파형을 기준으로 ㄹ형, 벌집형, ㅁ형 리브를 구성하여, 기존의 L형, 역T형, ㄷ형 리브와 모멘트 및 리브 강재량을 비교한 결과, 경제성면에서 ㅁ형 리브가 가장 좋은 결과를 나타내어, 이를 새로운 리브 형태로 선택하였다.
(2)강바닥판에 적용 가능한 ㅁ형 리브 보강판을 구성하기 위하여, 각 제원이 응력과 리브 강재량에 미치는 영향을 살펴본 결과, 리브 간격에 따른 영향이 가장 크며, 리브 간격이 일정한 경우 박스 폭의 영향이 가장 크다는 것을 알 수 있었다.
(3)ㅁ형 리브 보강판에서 리브 간격에 비례하는 박스 형태를 구성하여 매개변수 연구를 수행한 결과, 각각의 박스 형태별 발생 응력은 리브 간격에 따른 함수로 표현됨을 알 수 있었으며, 이를 이용하여 특정 응력에 해당하는 ㅁ형 리브 단면을 구성하는 시스템을 구축할 수 있었다.
(4)여러 가지 실 교량에서 발생하는 응력을 구축한 시스템에 적용한 결과, 기존의 실 교량보다 더 적은 강재량을 나타내는 새로운 ㅁ형 리브 보강판을 구성할 수 있었다.
따라서 본 연구에서 제안한 시스템을 이용하여 새로운 ㅁ형 리브 보강판을 구성하면 기존의 폐단면 리브 보강판과 비교하여 보다 경제적인 설계를 할 수 있을 것으로 판단된다.
Acknowledgments
본 논문은 2013학년도 세명대학교 교내학술연구비 지원으로 수행되었기에 이에 감사드립니다.
References
-
국토해양부(2010) 도로교설계기준.
Ministry of Land, Transport and Maritime Affairs (2010) Highway Bridge Design Standard, Korea (in Korean). -
방명석(1993) 강교설계의 기초, 건설도서.
Bang, M.S. (1993) Basic of the Steel Bridge Design, Geonseoldoseo, Korea. -
주석범(2012) 보강판 제원에 따른 개단면 리브 보강판의 국부 처짐과 국부 모멘트의 정형화, 한국강구조학회논문집, 한국강구조학회, 제24권, 제6호, pp.659-670.
Chu, S.B. (2012) Formulating the Local Displacement and Local Moments of a Plate Stiffened with Open Ribs According to the Dimensions of Stiffened Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.6, pp.659-670 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.6.659 ]
-
박호상, 서상정, 권영봉(2010) 국부좌굴과 뒤틀림좌굴이 발생하는 종방향 보강재로 보강된 강판의 압축강도, 한국강구조학회논문집, 한국강구조학회, 제22권, 제3호, pp.219-228.
Park, H.S., Seo, S.J., and Kwon, Y.B. (2010) The Compressive Strength of Longitudinally Stiffened Plates Undergoing Local and Distortional Buckling, Journal of Korean Society of Steel Construction, KSSC, Vol.22, No.3, pp.219-228 (in Korean). - Troitsky, M.S. (1992) Orthotropic Bridges: Theory and Design, The James F. Lincoln Arc Welding Foundation, USA.
-
마호성, 조광일, 유성흠(2012) 구조물 경계조건에 따른 파형강판 터널라이닝의 풍하중에 대한 동적거동, 한국강구조학회논문집, 한국강구조학회, 제24권, 제1호, pp.47-58.
Mha, H.S., Cho, K.I., and Yoo, S.H. (2012) Dynamic Behaviors of a Corrugated Steel Tunnel Lining System Due to Wind Loads by Passing Vehicles According to the Boundary Conditions, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.1, pp.47-58 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.1.047 ]
-
이종원, 길홍배, 이학은(2005) 제형파형강판 복부판의 탄성 연성전단좌굴 거동, 한국강구조학회논문집, 한국강구조학회, 제17권, 제6호, pp.707-715.
Yi, J.W., Gill, H.B., and Lee, H.E. (2005) Elastic Interactive Shear Buckling Behavior of Trapezoidally Corrugated Steel Webs, Journal of Korean Society of Steel Construction, KSSC, Vol.17, No.6, pp.707-715 (in Korean). -
권순철, 임철문, 최병근, 이세원, 한중원, 김윤해(2001) 항공기용 복합재료 샌드위치 구조물의 오토클레이브 성형시 발생되는 결함 원인 분석과 그 최소화 방안, 한국복합재료학회지, 한국복합재료학회, 제14권, 제1호, pp.22-29.
Kwon, S.-C., Im, C.-M., Choi, B.-K., Lee, S.-W., Han, J.-W., and Kim, Y.-H. (2001) A Study on the Analysis of Causes & Minimizing of Defects at Composite Materials Sandwich Aircraft Structure in Autoclave Processing, Journal of the Korean Society for Composite Materials, KSCM, Vol.14, No.1, pp.22-29 (in Korean). -
Heimbs, S. (2009) Virtual Testing of Sandwich Core Structures Using Dynamic Finite Element Simulations, Computational Materials Science, Elsevier, Vol.45, No.2, pp.205-216.
[https://doi.org/10.1016/j.commatsci.2008.09.017]

-
주석범, 박종해(2013) 새로운 형태의 강바닥판 리브에 대한 거동분석, 한국토목학회 2013년 학술대회논문집, 대한토목학회, pp.1077-1080.
Chu, S.B., and Park, J.H. (2013) Analyzing the Behavior of New Type Ribs of the Steel Deck Plate, Proceedings of Annual Conference of Korean Society of Civil Engineers, KSCE, pp.1077-1080 (in Korean).




















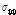








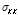 per unit volume rate
per unit volume rate
















 (MPa)
(MPa)