반원형 스프링으로 횡지지된 건식형 좌굴방지가새의 개발

1. 서 론

횡력 저항 요소인 좌굴방지가새(Buckling Restrained Braces, 이하 BRB)는 신축 및 내진 보강에 사용되어 왔다. 내진 보강용 이력 댐퍼로 활용하기 위해 동경기술연구소의 Akira Wada 교수가 일본제철(주)과 공동 개발하여 상용화한 Unbonded Brace^TM가 BRB의 최초로 1988년 건물에 실제 적용되었으며, 실험적 검증을 통해 2000년 미국 대학에도 설치되었다^[1].

BRB에 대한 연구로 Watanabe et al.^[2]은 심재와 강관의 강도비가 1.5 이상일 때 안정적인 거동을 한다는 점을 실험적으로 규명하였고 2000년대 들어서 Clark, Iwata, Kamura 등이 다양한 BRB에 대한 비선형 반복 거동 실험을 보고하였다^[3]. 이후 FRP, 강섬유콘크리트, 이중강관, 원형강관 등을 이용한 BRB에 대한 연구도 진행되었다. 국내에서도 Han et al.^[4]은 각형강관을 이용한 BRB에서 강관의 판폭두깨비가 클수록 국부좌굴 억제 효과가 작아지고 판폭두께비가 20 이상일 때 에너지 소산능력이 향상됨을 실험적으로 규명하였다. 또한 Park et al.^[5]은 BRB 전체 길이에 대한 무보강 구간의 길이는 16～24%가 적절하다는 연구 결과를 보고하였다.

대다수의 BRB는 심재와 강관 사이에 콘크리트나 모르타르 등을 채워 넣는 습식 방식으로 심재와 콘크리트의 비부착 처리와 타설 공정으로 인한 제작 효율이 떨어질 수 있다. 이런 단점을 극복하기 위해 최근 건식형 BRB에 대한 개발도 시도되고 있다. 대표적으로 Park and Kim^[6]은 콘크리트 대신 각형강봉으로 심재를 구속한 BRB의 실험을 통해 심재와 강관의 강도비를 3.5 이상으로 계획할 것을 제시하였다. Pham and Kim^[7]은 샌드위치 비좌굴가새에 대해 콘크리트의 채움이 없이도 적절한 거동을 확보할 수 있음을 해석적으로 입증하였다. Zhan et al.^[8]은 이중 원형강관 사이에 일정 간격으로 강재 링을 끼워 구속한 BRB의 유한 요소 해석을 통해 이력 거동이 향상될 수 있음을 보였다.

이 연구에서는 판형 심재를 반원형 스프링으로 구속되도록 구성한 건식형 BRB를 고안하였다. 이 건식형 BRB의 설계를 위해 먼저 횡방향 구속을 담당하고 있는 반원형 스프링의 상세를 결정하고자 이론 및 해석적 평가를 실시하였다. 건물 내에서 활용될 조건을 가정하여 소요 강성과 강도를 이론적으로 결정하였으며, 이 조건에 적절한 형상을 해석적으로 추적하여 그 결과를 제시하였다.

2. 건식형 BRB의 개발

2.1 건식형 BRB의 형상

BRB의 개념은 압축 요소를 횡방향으로 규칙적인 간격으로 지지하여 압축 요소의 비지지 거리를 작게 함에 따라 좌굴 내력이 상승하고 에너지 소산이 큰 안정적인 이력 거동을 보인 다는 것으로 개념 자체에 특허권이 설정되어 있지는 않다.

Fig. 1(a)에 나타낸 것과 같이 강재 골조로 구성되는 코어 부분을 BRB로 보강하여 자중을 줄이면서 강성을 확보하고자 Fig. 1(b)에 나타낸 건식형 BRB를 고안하였다.

2.2 건식형 BRB의 설계 조건

건식형 BRB는 판형 심재를 반원형 스프링이 일정 간격으로 횡지지 하도록 외부 보강재에 접촉면 주위를 모살 용접한다. 반원형 스프링이 용접되는 외부 보강재로 판재가 사용될 경우 볼트로 연결되고, C형강이 사용될 경우 만나는 가운데 부분을 용접하게 된다. 길이에 따라 반원형 스프링은 추가될 수 있고, 판형 심재와 반원형 스프링 사이에는 마찰력을 최소화할 수 있는 완충재나 윤활제 등이 첨가될 수 있다.

제안한 건식형 BRB는 현재 개발 단계로 반원형 스프링의 적절한 형상과 내력 등을 설계하기 위해 Fig. 1(a)의 평면을 갖는 12층 규모 건물의 코어에 대각 방향으로 설치된 건식형 BRB에 작용하는 하중을 해석하였다. 대각 방향의 길이는 6,730mm이며, 작용하는 하중은 245kN임을 확인하였다. 기존 연구에서 제안한 16～24%의 무보강 길이비를 2배 정도 강화하여 반원형 스프링의 간격을 500mm로 결정하였고 이를 바탕으로 설계한 272kN의 공칭설계강도를 갖는 90×20mm의 심재 단면을 Fig. 2와 같이 결정하였다.

3. 반원형 스프링의 소요 강성 및 강도

3.1 반원형 스프링의 이론적 강성 및 강도

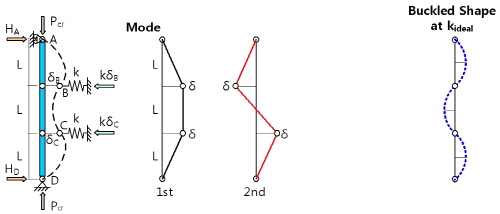
반원형 스프링이 적절한 강성( 으로 쉽게 유도된다. 그러나 3개 이상의 스프링이 등간격으로 배치된 경우는 다소 복잡한 계산 과정이 필요하다.

Fig. 3(c)와 같이 스프링이 3개인 경우 A점과 E점에서 모멘트의 평형 원리를 통해 반력 를 구할 수 있다. 마찬가지로 B점, C점, D점에서 모멘트 평형을 통해 다음 식을 얻을 수 있다.

 (1)

 (2)

 (3)

식 (3), 식 (4), 식 (5)를 연립하여 정리하고, 라 가정하면 식 (4)와 같은 3차 방정식을 얻을 수 있다.

 (4)

이 3차 방정식의 해는 이며, 이를 다시 식 (1)～식 (3)에 대입하면 각 스프링의 변위를 미지수로 한 연립방정식이 세워지며 그 해는 다음과 같다.

ⅰ)

ⅱ)

ⅲ)

이 결과는 각각의 고유치에 대한 고유벡터로 Fig. 3(c)에 순차적으로 나타낸 1차, 2차, 3차 모드의 변형을 의미하게 되고 식 (4)의 해의 역수로부터 좌굴모드별 스프링의 소요강성을 평가할 수 있다.

먼저 각 모드에서 스프링의 강성이 0이라면 좌굴길이는 각각 )에 해당할 것이다. 따라서 각 모드에서 스프링의 강성이 0인 경우와 이상적인 경우에 대해 결정된 2개의 위치를 직선으로 연결하여 나타낼 수 있다.

스프링의 강성이 증가함에 따라 고차 모드가 지배하여 좌굴하중이 결정되기 때문에 Fig. 4에 나타낸 것과 같이 스프링의 강성과 좌굴하중의 관계는 각 점선의 교차점을 연결한 실선으로 결정된다.

스프링의 개수가 증가되더라도 동일한 방법으로 스프링의 강성을 평가할 수 있다. 스프링의 개수만큼의 식 (4)에 나타낸 특성방정식의 차수가 증가하게 되어 풀이 과정이 다소 복잡해진다. 일반적으로 스프링의 개수가 증가함에 따라 스프링의 강성은 에 수렴한다는 뜻이다. 따라서 Fig. 4에서 가로축이 4이상이면 실선은 수평선으로 표현될 수 있다.

결과적으로 심재를 등간격으로 지지하여 고차모드의 좌굴 형상을 기대할 수 있는 이상적인 스프링의 강성( )는 다음과 같이 평가된다.

) (5)

=스프링의변위) (6)

3.2 반원형 스프링의 소요강성 및 소요강도

반원형 스프링의 실제 소요강성과 소요강도는 압축 요소에 실제 있을 수 있는 초기변형( )는 식 (8)과 같이 평가될 수 있다.

 (7)

 (8)

The AISC Code of Standard Practice에서 초기변형은 전체길이의 1/500로 제시하였고, Winter는 초기변형을 전체길이의 1/250～1/500으로 제안하였으며, 실용적인 설계를 위해 좌굴변형( )을 동일한 것으로 간주할 것을 제안하였다^[9]. 따라서 실용적 소요강성은 이상적인 강성의 2배로 평가될 수 있다.

Fig. 2에 나타낸 건식 BRB의 경우 좌굴길이가 500mm로 14쌍의 반원형 스프링이 설치되어 는 3～4 사이의 값에 해당되지만 최대 수렴값인 4로 간주하였다. 이를 이용해 계산한 실용적 소요강성은 7,769N/mm, 소요강도는 7,769～15,539N이었으며, 이 값을 비교 기준으로 활용할 것이다.

4. 반원형 스프링의 해석

4.1 반원형 스프링의 모델링

Fig. 2에 나타낸 건식형 BRB에 적용할 반원형 스프링의 적정한 형상을 찾기 위해 높이를 변수로 유한요소 해석을 실시하여 실용적 소요강성과 소요강도를 비교하였다.

해석 대상 반원형 스프링의 형상과 치수는 Table 1에 정리하였다. 주요 변수는 스프링의 높이로 50, 40, 30, 20, 10mm로 변하지만 곡률은 일정하게 유지하였다. 반원형 스프링의 최적화된 조건을 찾기 위해 두께 10mm에 대해 강종을 SM490과 SS400에 비교하였고, 강종 SS400에 대해 추가로 두께 8mm와 6mm의 모델에 대해 해석을 계획하였다.

해석 프로그램은 Ansys를 사용하였고, Beam23 2D 요소를 이용하여 선으로 모델링하였고 폭은 10mm를 기준하여 단면 성능을 입력하였다. 재료의 거동은 완전탄소성으로 가정하였고 반원형 스프링의 중앙 상부에 집중하중을 작용시켜 고유치(eigenvalue) 좌굴하중과 비선형(nonlinear) 좌굴해석을 실시하였다.

4.2 해석 모델링의 검증

4.1에서 설명한 반원형 스프링의 해석 모델에 대한 검증을 위해 이론적인 탄성좌굴하중과 해석을 통해 얻은 고유치 좌굴하중을 비교하였다. 반원형 스프링의 이론적인 탄성좌굴하중은 Schmidt and DaDeppo^[10]에 제시된 원형 아치의 탄성좌굴하중 도표를 이용하여 평가하였다. Fig. 5에 아치의 각도 및 반경에 따른 탄성좌굴하중을 계산할 수 있는 도표를 그대로 옮겨 나타내었다. 해석에 사용된 반원형 스프링은 양쪽에 곡선부가 있어 각도( )을 Table 2에 정리하였다.

도표에서 세로축을 읽을 수 없었던 H10의 경우를 배제하고 비교한 결과 이론적인 탄성좌굴하중과 해석적 고유치 좌굴하중의 차이는 1～9% 정도로 나타났다.

이론적으로 계산된 탄성좌굴하중이 도표에서 세로축에 해당하는 값을 소수점 이하까지 정확히 읽어낼 수 없었다는 점과 곡선부에 따른 영향이 반영되지 못했다는 점을 고려한다면 해석에 사용된 모델링은 비교적 타당한 것으로 보여 진다.

4.3 반원형 스프링의 비선형 좌굴해석

4.3.1 강종에 따른 해석 결과

반원형 스프링의 적절한 강종을 선택하기 위해 두께를 10mm로 유지한 상태에서 강종을 SM490과 SS400으로 달리하여 비선형 좌굴해석을 실시하였다. 해석을 통해 얻은 반원형 스프링의 하중-변형 관계는 Fig. 7에 강종별로 각각 나타내었고, 강성과 강도를 수치적으로 비교할 수 있도록 Table 3에 정리하였다.

두 강종에 대한 해석 결과에서 공통적으로 H30과 H20이 다른 형상에 비해 상대적으로 우수한 강성과 강도를 발휘하고 있음을 확인할 수 있다. 반원형 스프링의 높이 변화에 따른 강도 변화는 두 강종에서 유사한 경향을 보이고 있다. 강종 차이에 따른 비선형 좌굴하중비는 약 1.38로 항복강도비 1.38과 거의 일치하고 있다. 이 사실은 원형 아치에 가까운 형상을 갖는 스프링의 내부 각도가 135° 이하로 좌굴모드가 스냅-스루(snap-through)로 결정되기 때문으로 판단된다.

반면에 강성은 반원형 스프링의 높이가 낮아질수록 증가하지만, 좌굴이 시작되는 변위도 작아지는 경향이 있다. H50～H30은 강성은 상대적으로 작지만 좌굴이 시작되는 변위는 약 0.2～0.4mm로 큰 반면 H20과 H10은 강성이 비교적 높지만, 좌굴이 시작되는 변위는 0.05～0.1mm로 매우 작아 순간적으로 좌굴이 발생한다는 것을 추정할 수 있다.

von Mises 응력분포를 나타낸 Fig. 8에서 H50~H20의 경우 스냅-스루(snap-through) 좌굴에 의해 응력이 집중될 수 있는 중앙부와 방사상 45° 위치가 두께 전체에 걸쳐 항복강도에 도달하는 것으로 나타났다. 이와 달리 H10의 경우 중앙부는 두께 전체에 걸쳐 항복에 도달하지만 그 이외의 구간은 밑면 부분만 항복하는 응력 분포를 보이고 있다. 한편 H50의 양쪽 곡선부는 다른 것보다 항복 범위가 깊어 구조적으로 불리한 형상임을 알 수 있다.

이와 같은 결과에 비추어 볼 때 건식형 BRB에 적용하기 위한 두께 10mm의 반원형 스프링의 형상은 중요 구조 성능인 강성 측면에서 H10이 가장 적합하나 강도, 좌굴 시작 변위, 응력분포 등을 함께 고려했을 때 H30의 형상이 가장 적합할 것으로 분석된다.

한편, Table 3에 정리한 강도와 강성은 반원형 스프링의 폭이 10mm인 경우로 Fig. 2에 나타낸 심재 단면을 지지하기 위해서 스프링의 폭을 동일하게 할 필요가 있을 것이다. 만약 이를 위해 반원형 스프링의 폭을 90mm로 확대한다면 해석 결과에서 강성은 그대로 유지되지만 강도는 9배가 증가하게 될 것이다.

Fig. 2에 나타낸 건식형 BRB를 대상으로 3.2에서 이론적으로 평가한 반원형 스프링의 실용적 소요강성과 소요강도를 Table 3에 정리한 강성과 강도를 비교했을 때 반원형 스프링의 폭을 조정하지 않더라도 모두 만족하고 있음을 확인할 수 있다. 따라서 반원형 스프링을 최적화하기 위해 강종은 SS400으로 낮추고 두께를 감소시킬 수 있는 여지가 있음을 알 수 있다.

4.3.2 두께에 따른 해석 결과

반원형 스프링의 적절한 두께를 찾기 위해 SS400 강종의 8mm와 6mm에 대해 비선형 좌굴해석을 추가로 실시하였다. 두께 6mm의 경우 모살용접의 실용적 한계로 두께가 얇으면 반원형 스프링의 제작은 쉬워지지만 용접에 의한 변형 및 결함이 발생할 가능성이 높아져 6mm를 최소 두께로 간주하였다.

두께 8mm와 6mm인 반원형 스프링의 하중-변형 관계는 Fig. 9에 두께별로 각각 나타내었고, 강성과 강도를 수치적으로 비교할 수 있도록 Table 4에 정리하였다.

두께 8mm의 해석 결과는 두께 10mm인 해석 결과와 형상 변화에 따른 강성과 강도의 변화 경향이 유사하나, 두께 6mm의 경우 반원형 스프링의 높이가 작아질수록 강성과 강도는 상승하는 경향을 보이고 있다. 두께 10mm에서는 H30과 H20의 하중-변형 관계가 거의 겹치는 양상을 보였으나, 두께 8mm에서 H30의 하중-변형 관계가 H20과 구분되기 시작하면서 두께 6mm에서 H20과 H10의 하중-변위 관계가 겹치는 양상을 Fig. 9에서 확인할 수 있다.

Fig. 10의 von Mises 응력분포에서 두께 8mm의 높이별 항복 범위는 두께 10mm의 항복 범위와 유사하다. 이에 반해 두께 6mm의 경우 항복 범위가 두께 8mm의 경우보다 넓고 깊게 나타나고 있다. 두께 6mm H50의 경우 양쪽 곡선부의 항복 범위가 두께 전체에 걸쳐 발생하고, 두께 6mm H10의 경우 방사상 45° 위치도 다른 두께에서와는 달리 두께 전체에 걸쳐 항복이 발생하는 것으로 나타나고 있다.

Table 4에 정리한 강성은 실용적 소요강성을 모두 만족하고 있다. 강도의 경우 실용적 소요강도를 만족시키기 위해 반원형 스프링의 폭을 확대시킬 필요가 있다. 일례로 SS400 8mm의 H30 형상을 적용할 경우 반원형 스프링의 폭은 20mm 정도면 만족되고, SS400 6mm의 H30 형상을 적용할 경우 폭은 약 30mm가 되어야 할 것이다.

이상의 해석결과를 비교해 보았을 때 반원형 스프링의 강종은 SS400, 두께는 6mm, 형상은 H30으로 제작하는 것이 상대적으로 유리할 것으로 분석되었다.

4.4 반원형 스프링의 강성이 반영된 건식형 BRB의 해석

두께 6mm인 SS400 강재의 H30 형상의 반원형 스프링을 Fig. 2에 나타낸 건식형 BRB에 적용했을 때 건식형 BRB의 거동을 해석적으로 평가하였다. 해석 프로그램은 Ansys를 이용하였고, Fig.11과 같이 2D 선 요소로 반원형 스프링이 약 500mm 간격으로 14개가 배치되도록 모델링하여 비선형 좌굴해석을 실시하였다. 심재의 강종은 SM490으로 응력-변형도의 관계는 완전탄소성으로 가정하여 Beam23 요소를 적용하였다. 반원형 스프링의 경우 비선형 스프링 요소인 Combin39를 이용해 강성을 4등분하여 입력하였다.

경계조건은 한 쪽 단부의 이동은 구속하고 회전은 구속하지 않은 상태에서 다른 쪽 단부에서 수평하중을 작용시켰다. 스프링 요소의 지점은 수직방향만 구속하는 것이 정확한 경계조건일 것이다. 그러나 이와 같이 경계조건을 부여하게 되면 Combin39 요소 가운데 일부가 Beam23 요소와 만나는 절점에서 큰 변형이 발생하여 수렴하지 못하는 결과를 보였다. 그래서 Combin39의 지점은 수직 및 수평방향을 구속하는 경계조건을 부여하였다. 건식형 BRB에 설치되는 반원형 스프링은 압축에만 저항하고 인장에는 저항할 수 없지만, 해석 모델에는 한쪽 측면에만 모델링 되는 관계로 압축과 인장에서 동일한 강성을 갖는 하중-변위 관계를 입력하였다.

건식형 BRB의 비선형 해석을 수행하기 위해 먼저 고유치 좌굴해석을 실시하여 Fig. 12와 같은 변형 분포를 얻었다. 고유치 좌굴해석의 변형은 양 단부에서 중앙부로 가면서 변위가 증폭되는 형태로 나타나며 최대변위는 약 1mm으로 비선형 좌굴해석에 필요한 초기 결함이 이 변위의 5%를 입력하였다. 반원형 스프링이 없는 양단 힌지 조건에서 고유치 좌굴해석을 통해 얻은 하중은 2.7kN으로 이론적으로 계산한 하중과 일치한다. 14쌍의 반원형 스프링이 배치된 건식형 BRB의 고유치 좌굴해석으로 얻은 하중은 498.4kN이며, 건식형 BRB의 좌굴길이가 500mm로 보았을 때 이론식을 통해 얻은 하중은 485.1kN으로 해석결과가 약 3% 큰 것으로 평가되었다. 또한 양단 힌지 조건인 6,730mm인 기둥이 13번의 파형이 발생할 때 좌굴하중은 452.5kN이고, 14번의 파형이 발생할 때 좌굴하중은 524.8kN으로 해석에 사용된 모델링은 타당할 것으로 판단된다.

선 요소가 사용된 해석 결과를 확인하기 쉽도록 요소의 크기와 변형을 과장하여 Fig. 13에 나타내었다. 심재의 변형은 중앙부에서 최대가 되는 형태를 보이고 있으며, 비선형 좌굴이 발생하는 시점에서 von Mise 응력은 항복강도에 도달하는 것을 확인할 수 있다.

Fig. 14에 심재의 비선형 좌굴하중과 최대 횡변위 관계를 나타내었으며 최대 횡변위 발생 위치에서 제일 가까운 반원형 스프링의 변위도 함께 나타내었다. 비선형 좌굴은 횡변위가 1.67mm에 도달했을 때 시작되며 하중은 383kN에 해당한다. 이 시점에서 반원형 스프링의 변위는 0.012mm이고, 심재의 횡변위가 최대인 2.48mm에 도달했을 때 반원형 스프링의 변위는 0.025mm로 모두 첫 번째 강성 구간에 해당하여 반원형 스프링은 여전히 탄성구간에 머물고 있는 것으로 확인되었다.

한편, KBC2009에서 좌굴길이가 500mm인 심재의 공칭압축강도는 354kN으로 계산되며, 해석 결과인 383kN과 약 8%의 오차가 있다. 물론, 여기서 반원형 스프링을 지지하는 커버 플레이트에 대한 고려가 없었기 때문에 실제 건식형 BRB의 거동과 차이가 있을 수 있음을 감안해야 한다. 그러나 이번 연구를 통해 건식형 BRB를 구성하는 반원형 스프링의 적절한 형상 범위를 찾았고 건식형 BRB의 구현 가능성을 확인한 의미가 크다.

5. 결 론

이 연구는 새롭게 개발한 형상의 건식형 BRB를 실용화하기 위해 적절한 성능을 발휘하는 반원형 스프링의 형상을 해석적으로 선정하였다. 또한 이를 반영하여 건식형 BRB의 비선형 좌굴해석을 통해 실용화의 가능성을 확인하였다. 이상의 연구를 통해 다음과 같은 결론을 얻었다.

(1)새롭게 개발한 건식형 BRB의 실용화를 위해 내부에 설치되는 반원형 스프링의 실용적 소요 강성은 이론적 최대 값인 로 평가하는 것이 안전상 바람직하다.

(2)길이가 6730mm이고 단면이 90×20mm인 SM490 심재를 갖는 건식형 BRB에서 약 500mm 간격으로 설치될 반원형 스프링의 실용적 소요 강성은 7,769N/mm, 소요강도는 7,769～15,539N로 평가되었다.

(3)곡률 반경은 50mm로 일정하지만 높이를 50, 40, 30, 20, 10mm로 변화시킨 반원형 스프링의 비선형 좌굴해석 결과 높이가 30mm일 때 가장 바람직한 거동을 보이는 것으로 나타났다.

(4)길이가 6730mm이고 단면이 90×20mm인 SM490 심재를 갖는 건식형 BRB에 약 500mm 간격으로 설치될 반원형 스프링은 비선형 좌굴해석과 용접을 고려했을 때 강종은 SS400, 두께는 6mm가 적절할 것이다.

(5)강종은 SS400이고, 두께가 6mm이며, 높이 30mm인 반원형 스프링을 갖는 건식형 BRB의 비선형 좌굴하중은 반원형 스프링의 배치 간격을 좌굴길이로 가정한 이론적 좌굴하중과 유사하게 나타나 건식형 BRB의 내력 발현은 충분한 것으로 확인되었다.

(6)충전 각형강관 BRB의 안정적 거동을 위해 심재와 강관의 강도비가 1.5 이상으로 제시된 것과 같이 건식형 BRB의 전체 좌굴를 방지하기 위해 심재와 외부 보강재의 강도(또는 강성)비의 제시가 필요하다.

Acknowledgments

연구는 한국건설기술연구원 주요사업(탈현장 초고속 주택 구조안전성 기술 개발)과 국토교통과학기술진흥원의 도시건축연구사업(13AUDP-C068788-01)의 지원에 의해 수행되었습니다.

References

• Hussain, S., Benschoten, P.V., Al Satari, M., and Lin, S. (2006) Buckling Restrained Braced Frame (BRBF) Structures: Analysis, Design and Approvals Issues, Proceedings of the 75th SEAOC Convention, Structural Engineers Association of California, USA, pp.87-98.
• Watanabe, A., Hitomi, Y., Saeki, E., Wada, A., and Fujimoto, M. (1988) Properties of Brace Encased in Buckling-Restraining Concrete and Steel Tube, Proceedings of the 9th World Conference on Earthquake Engineering, Japan Association for Earthquake Disaster Prevention, Japan, pp.IV.719-IV.724.
• Sabelli, R., Mahin, S., and Chang, C. (2003) Seismic Demands on Steel Braced Frame Buildings with Buckling-​Restrained Braces, Engineering Structures, Elsevier, Vol.​25, No.5, pp.655-666. [https://doi.org/10.1016/S0141-0296(02)00175-X]
• 한상환, 유호원, 김욱태, 이리형(2004) 냉간성형 HSS가새부재의 판폭두께비에 따른 구조성능 평가, 대한건축학회논문집 – 구조계, 대한건축학회, 제20권, 제9호, pp.45-53.
  Han, S.-W., Ryu, H.-W., Kim, W.-T., and Lee, L.-H. (2004) Structural Performance of Cold-Formed HSS Bracing Members According to Width-Thickness Ratio, Journal of Architectural Institute of Korea – Structure & Construction, AIK, Vol.20, No.9, pp.45-53 (in Korean).
• 박대진, 주영규, 김명한, 김도현, 김상대(2006) 비좌굴 가새의 무보강 길이에 따른 이력거동 평가, 대한건축학회논문집 – 구조계, 대한건축학회, 제22권, 제12호, pp.37-46.
  Park, D.-J., Ju, Y.-K., Kim, M.-H., Kim, D.-H., and Kim, S.-D. (2006) Evaluation of Hysteretic Behaviors of the Buckling Restrained Braces According to the Unconstrained Length, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.22, No.12, pp.37-46 (in Korean).
• 박준희, 김진구(2008) 각형강봉으로 충전된 좌굴방지가새의 반복하중실험, 대한건축학회논문집 – 구조계, 대한건축학회, 제24권, 제10호, pp.53-60.
  Park, J.-H., and Kim, J.-K. (2008) Cyclic Test of Buckling Restrained Braces Filled with Square Bars, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.24, No.10, pp.53-60 (in Korean).
• 팜 타이 호안, 김승억(2013) 샌드위치 비좌굴가새의 거동 에 대한 수치해석적 연구, 한국강구조학회 2013년도 학술발표대회 논문집, 한국강구조학회, pp.89-90.
  Pham, T.H., and Kim, S.E. (2013) Numerical Study on the Behavior of Sandwiched Buckling-Restrained Braces, Journal of the Architectural Institute of Korea – Structure & Construction, KSSC, pp.89-90 (in Korean).
• Zhan, Z.Y., and Xiu, L.W. (2011) Force Analysis of Double-Tube Buckling Restrained Braces with Contact-​Ring, The Open Civil Engineering Journal, Bentham Open, Vol.5, pp.46-51. [https://doi.org/10.2174/1874149501105010046]
• Salmon, C.G., and Johnson, J.E. (1996) Steel Structures: Design and Behavior, Harper Collins College, USA, pp.​547-548.
• Schmidt, R., and DaDeppo, D.A. (1972) Buckling of Clamped Circular Arches Subjected to a Point Load, Journal of Applied Mathematics and Physics, Springer, Vol.23, No.1, pp.146-148. [https://doi.org/10.1007/BF01593212]