
다양한 기하학적 인자를 고려한 고무받침의 압축 및 전단 내력
Copyright ⓒ 2014 by Korean Society of Steel Construction
초록
본 논문에서는 적층탄성받침과 납 고무받침을 대상으로 재료 및 기하비선형을 고려한 3차원 유한요소로 모델링하고 다양한 파라미터에 대한 압축 및 전단특성을 비교 분석하여 적층고무받침의 해석적 데이터베이스를 구축하였다. 유한요소해석에서 적층고무받침을 모델링하기 위해서 고무시편시험을 통해 고무의 응력-변형률 관계를 얻어내고 커브피팅을 이용하여 고무재료상수를 구하였다. 고무재료상수를 검증하기 위하여 실제 적층탄성받침 제품 시험과 유한요소해석을 비교함으로서 고무재료상수의 유효성을 확인하였다. 적층탄성받침과 납 고무받침의 압축거동은 1차 형상계수에 따라서 가장 큰 영향을 받았으며, 전단거동은 2차 형상계수에 따라 크게 달라지는 것을 알 수 있었다. 또한 납의 직경이 증가할수록 납 고무받침의 수평강성과 에너지 소산능력이 증가하였다.
Abstract
In this study, compression and shear characteristics of laminated rubber bearings and lead rubber bearings with various parameters are investigated by using material and geometric nonlinear three-dimensional finite element analysis. Rubber coupon tests are performed to make a model of the laminated rubber bearings. In addition, the material constants of the rubber are calculated by the curve fitting process of stress-strain relationship. The finite element analysis and experimental tests of the laminate rubber bearings are used to verify the validity of the rubber material constants. It is seen that the compression behavior of the laminated rubber bearings and lead rubber bearings mainly varies depending on the first shape factors and their shear behavior significantly varies depending on the second shape factors. In addition, the horizontal stiffness and energy dissipation capacity of lead rubber bearing are increased when the diameter of a lead bar is increased.
키워드:
적층고무받침, 납 고무받침, 3차원 비선형 유한요소해석, 1차 형상계수, 2차 형상계수, 고무재료상수Keywords:
Laminated rubber bearing, Lead rubber bearing, 3D nonlinear finite element analysis, Shape factors, Rubber material constant1. 서 론
20세기 이후 기술 및 산업의 발달로 인하여 구조물이 고층화 대공간화 되어가고 있다. 따라서 대규모 지진이 발생하게 되면 인명 피해 및 국가 산업 기반시설 등의 피해가 막대하게 발생된다. 이러한 지진으로부터 구조물을 보호하기 위한 방법으로는 보강(strengthening)과 격리(isolation)라는 두 가지 공학적 기법이 있다. 이 두 가지의 방법은 근본적으로 다른 원리를 가지고 있으며, 보강은 부가적인 구조재료나 구조요소 등을 이용하여 구조물의 설계강도를 증가시키는 반면에, 격리는 구조물의 기초에 설치되어서 상부구조물의 주기를 지진하중의 탁월주기(predominant period)범위 밖으로 이동시킴으로서 상부 구조물의 동적응답을 감소시킨다[1],[2],[3].
지진격리장치 중에서 널리 알리진 것은 가황고무층과 강판의 반복된 적층으로 구성된 적층탄성받침(Laminated Rubber Bearing)과 중심에 납을 삽입한 납 고무받침(Lead Rubber Bearing)이며, 이미 미국, 일본, 유럽 등을 비롯하여 전 세계적으로 많이 사용되고 있는 실정이다. 우리나라에서도 다수의 교량과, 인천 LNG 저장탱크, 트리움하우스, 예천동 주민복지센터, 김포 고촌 현대아파트, 등 다양한 시설물에 적층탄성받침과 납 고무받침의 적용이 이루어졌으며 지속적으로 설치 사례가 증가하고 있는 추세이다. 그러나 이에 대한 국내의 연구 활동은 매우 미비한 실정이다.
본 연구에서는 국내에서 가장 많이 사용되고 있는 적층탄성받침과 납 고무받침을 대상으로 재료 및 기하학적 비선형을 고려한 3차원 유한요소모델을 제시하고자 한다. 또한 실험 결과와의 비교를 통한 검증이 이루어진 후, 다양한 형상비를 갖는 적층탄성받침과 납 고무받침의 압축과 전단 특성에 대한 데이터베이스를 구축하고자 한다.
2. 초탄성재료의 특성
2.1 고무시편시험 및 재료상수 결정
적층고무받침에 사용되는 주요 재료는 고무와 금속이다. 이중에서 고무는 다른 재료에 비하여 강성이 낮고 변형회복 성능이 뛰어나며 에너지 흡수성이 우수한 재료로 평가되어 차음이나 방진의 목적으로 많이 사용하고 있다. 특히 적층고무받침과 같은 지진격리장치에서는 외부로부터 전달되어진 진동을 저감하고 에너지를 소산시키는 역할을 담당하기 때문에 기능적 측면에서 가장 큰 역할을 하고 있다. 하지만 이런 고무는 제작과정에서 여러 가지 변수가 작용할 수 있기 때문에 그 특성을 보편화하기가 매우 어렵다. 따라서 고무의 경우 반드시 엄밀한 재료시험을 거쳐서 그 특성을 파악하는 것이 중요하다[4],[5],[6].
고무는 초탄성(hyperelastic) 재료로서 비선형 및 대변형 거동이 나타나는 재료특성을 갖고 있다. FE(finite element) 해석 시, 초탄성재료 모델은 변형률 에너지 함수를 이용해서 나타낼 수 있다. 이때, 변형률 에너지 함수의 상수는 고무의 시편시험을 통하여 결정될 수 있음을 주지해야 한다.
시편 시험의 종류에는 단축 인장, 단축 압축, 2축 인장, 2축 압축, 평면 인장, 평면 압축, 단순 전단 시험 등이 있다. 본 연구에서는 고무시편의 단축 인장시험, 단축 압축시험, 순수전단시험 등 세 가지 고무시편시험을 수행 하였으며, 시험을 통해 구해진 응력-변형률 관계를 이용하여 고무의 재료특성을 나타내는 변형률 에너지 함수의 상수를 구하였다.
일반적으로, 변형률 에너지 함수는 Neo-Hookean 모델, Mooney-Rivlin 모델, Ogden 모델 등으로 표현될 수 있다[7].고무의 재료특성을 나타내는 가장 간단한 형태는 Neo- Hookean 모델이며 단축인장시험의 40%, 단순전단시험의 90% 변형률까지는 비교적 잘 맞는 것으로 알려져 있다. Mooney-Rivlin모델의 경우 인장시험의 100%변형률까지 잘 맞으나 압축변형과 대변형률에서의 강성 증가효과를 묘사하는 데 부적절하다고 알려져 있다. Ogden 모델의 경우 2∼3항으로 시험자료를 묘사할 수 있으며 인장시험의 700%까지도 잘 맞는 것으로 알려져 다방면의 산업현장에서 고무부품의 구조해석에 매우 성공적으로 적용되고 있다[8].
본 연구에서는 고무의 재료특성을 가장 잘 묘사하는 것으로 알려진 Ogden 모델을 이용하였으며, 변형률 에너지 함수는 식 (1)과 같다. 시편시험의 응력-변형률 관계를 이용한 커브피팅(curve fitting)을 통해 Ogden 3항의 변형률 에너지 함수의 상수 값을 구했으며 Table 1과 같다.
 (1)
(1)
여기서
 는 연신율이다.
는 연신율이다.
2.2 고무재료상수의 유효성 검토
앞 절에서는 고무시편의 인장, 압축, 전단 시험 결과와 Ogden 변형률에너지 함수를 이용하여 고무의 재료상수를 구하였으며, 본 절에서는 이러한 고무재료상수의 유효성을 검증하기 위하여 실제 적층탄성받침과 납 고무받침에 대한 실험을 수행하였다. 또한, FE 해석을 수행하여 실험결과와 비교하였다.
2.2.1 적층탄성받침의 압축거동
압축에 대한 검증을 위하여 사용된 적층탄성받침 시험체는 Fig. 1과 같이 가로 300mm × 세로 200mm × 높이 60mm의 직육면체로 되어 있으며, 이 받침의 수직설계하중은 550kN으로 산정되었다.
Fig. 1의 적층탄성받침은 두께가 8mm인 고무판을 이용한 3개 층과 두께가 3mm인 강판을 이용한 2개 층으로 구성되어있다. 하중을 직접 받는 커버플레이트의 두께는 상・하부 동일하게 15mm이다. 시험체의 압축시험은 Fig. 2와 같은 30,000kN 압축전단시험기를 이용하여 적층탄성받침이 압축파괴가 일어 날 때 까지 가력하였으며, 압축하중에 따른 받침의 수직변위는 시험체 양쪽에 설치된 2개의 전자식변위계(LVDT)를 이용하여 측정하였다.
적층탄성받침의 실험 결과에 대한 검증을 위하여 범용 유한요소해석 소프트웨어인 ANSYS(ver. 13)를 사용하였다. 적층탄성받침의 고무층의 FE 모델은 초탄성재료의 특성을 지원하는 3차원 Solid185 요소를 이용하였으며 2.1절에서 언급된 고무재료상수(Table 1 참조)를 적용하였다. 보강판은 적층탄성에서 가장 많이 쓰이는 SS400 강재의 물성치를 이용하였다. Fig. 2의 압축실험과 동일한 경계조건을 묘사하기 위하여 하부의 지지조건은 고정으로 처리하였으며, 상부는 상호연계(coupling)하여 압축하중을 적용시켰다. 적층탄성받침의 전형적인 FE 모델은 Fig. 3과 같다.
Fig. 4는 적층탄성받침의 압축하중과 변위 관계에 대한 실험과 FE 해석 결과를 나타내고 있으며, 여기서 실험과 해석 결과가 매우 근접함을 볼 수 있다. Fig. 4로부터 받침의 변형 초기 단계에서는 선형적 거동을 보이다가 하중이 증가할수록 점점 경화(hardening) 현상이 발생하는 것을 알 수 있다. 또한, 약 3,000kN의 압축하중에서 고무층 사이의 강판에서 소성화가 일어나기 시작하며, 하중이 지속적으로 증가하여 수직설계하중(550kN)의 10배인 5,500kN에 도달하게 되면 적층탄성받침의 파괴가 발생하게 된다.
적층탄성받침이 압축하중을 받을 때 프와송의 효과로 고무판과 강판은 서로 다른 크기를 가지고 수평방향으로 늘어나게 되며, 상대적으로 변형률이 큰 고무판에 의해 강판은 인장응력을 받게 된다. 따라서 고무판과 밀착되어 있는 강판은 커다란 인장 변형에 의해 소성거동을 진행하게 되며 이는 Fig. 5에서와 같이 배불림 현상으로 나타나게 된다. Fig. 5로부터 실험과 FE 해석을 통한 적층탄성받침의 변형 모드는 거의 유사한 것을 알 수 있다.
2.2.2 납 고무받침의 전단거동
전단거동을 위해 사용된 납 고무받침의 형태는 Fig. 6과 같이 외경이 800mm이고, 납의 직경이 180mm인 원통형이다. 6mm 두께인 고무판은 로 총 26개 층으로 적층되어 있으며, 4.5mm 두께인 강판은 총 25개 층으로 적층되어 있다. 가력을 위한 상・하부 커버플레이트의 두께는 40mm이다. 전단거동에 대해서 납 고무받침을 선택한 이유는 FE 해석 시 고무뿐만 아니라 납의 재료특성도 함께 적용함으로써 실험 결과와의 근접성을 알아보고자 하는 것이다.
납 고무받침의 전단실험은 적층탄성받침과 동일한 시험기를 사용하였으며, 납 고무받침의 설계압축하중 5,000kN을 유지한 상태에서 ±150mm의 수평변위를 3회 반복가력하여 이루어졌으며, 또한 실험과 동일한 조건하에서 FE 해석이 수행되었다. Fig. 7은 납 고무받침의 전단실험과 해석으로부터 얻어낸 수평하중과 변위에 대한 이력곡선을 나타내고 있다.
Fig. 7의 실험 결과로부터 수평하중 초기에는 납의 탄성거동으로 인해 상당히 큰 강성이 나타남을 알 수 있으며, 이후 약 250kN에서 납이 소성거동을 시작하여 150mm 변위에서 약 930kN의 수평하중을 나타내었다. 하지만 두 번째와 세 번째 사이클에서는 고무가 안정화되면서 동일한 150mm의 변위에 대해 130kN이 감소한 약 800kN의 결과를 나타내는 것을 알 수 있다.
Fig. 7의 FE 해석 결과에서는 약 320kN까지 탄성거동이 나타나며, 이후 납의 소성으로 150mm 변위에 대해 800kN의 수평하중 결과를 나타내었다. 이러한 해석 결과는 실험 결과와 매우 유사함 나타낸 것이다. 따라서 적층탄성받침의 압축시험, 납 고무받침의 전단시험을 유한요소해석으로 각각 비교한 결과, FE 해석에서 적용한 고무재료상수와 납의 재료특성이 실제 받침의 거동을 잘 묘사해 내는 것을 알 수 있다.
Fig. 8로부터 실험과 FE 해석을 통한 납 고무받침의 전단변형 모드가 거의 유사한 것을 알 수 있으며, 매우 큰 수평방향의 변형으로 인한 유연한 거동이 일어남을 확인 할 수 있다.
3. 고무받침의 형상계수와 구조 특성
3.1 형상계수
최근에는 건축물의 대형화로 인해 매우 커다란 수직하중과 수평하중을 견딜 수 있는 대형 크기의 적층고무받침의 사용이 증가하고 있는 실정이며, 이 절에서는 800mm의 직경을 갖는 원통형의 적층탄성받침과 납 고무받침의 구조특성을 위한 변수연구(parametric study)를 해석적 접근방법으로 수행하였다.
적층탄성받침과 납 고무받침은 1차 형상계수와 2차 형상계수, 그리고 중공직경과 납 직경의 크기에 따라 분류되며, 변수에 따라서 달라지는 수직하중과 변위, 수평하중과 변위의 관계 등을 파악하여 압축 및 전단특성을 알아보았다.
1차 형상계수(
 는 적층 고무판의 직경과 총 두께의 비로 정의된다.
는 적층 고무판의 직경과 총 두께의 비로 정의된다.
고무받침이 Fig. 9와 같이 원형 단면인 경우 1차 형상계수와 2차 형상계수는 다음 식 (1)과 (2)와 같이 나타낼 수 있다.
 (2)
(2)
 (3)
(3)
여기서,
 은 고무 층의 수이다.
은 고무 층의 수이다.
 가 커질수록 고무는 편평하게 되어 좌굴을 일으키기 어려운 형상으로 된다.
가 커질수록 고무는 편평하게 되어 좌굴을 일으키기 어려운 형상으로 된다.
3.2 고무받침의 FE 모델
본 연구의 FE 해석은 2.2절에서 언급된 범용소프트웨어인 ANSYS(ver.13)를 이용하여 수행하였으며, 적층고무받침과 납 고무받침의 3차원 FE 모델은 Fig. 10과 같다. 수렴 테스트를 진행하여 적절한 요소 수와 크기를 결정하였으며, 변수연구를 위한 요소 수는 약 30,000개, 절점 수는 약 65,000개를 이용하였다.
2.2절에서 수행된 FE 해석과 마찬가지로 고무판은 초탄성재료를 지원하는 3차원 요소 Solid 185요소를 사용하여 모델링 하였다. 고무판의 재료특성에 대해서 Table 1의 상수값을 이용하였으며, 강판에 대해서는 SS490의 재료특성을 사용하였다.
Fig. 10의 두 받침의 구속조건 및 하중조건은 동일하게 적용되었다. 받침의 하부에는 실제 실험에서와 동일하도록 x, y, z축으로 모두 구속하였으며, 상단은 상호연계(coupling)하여 하중을 적용하였다. 고무받침의 원형 단면과 작용 하중의 대칭성을 이용하여 전체 형상의 절반만을 모델링하였고, 절단면에는 대칭 경계조건을 적용하였다. 압축해석에서는 5,000kN의 압축하중을 적용하여 변수에 대한 받침의 압축거동특성을 살펴보았고, 전단해석에는 5,000kN의 압축하중 재하 상태에서 ±150mm의 수평변위를 3회의 사이클 하중으로 가하여 받침의 전단거동 특성을 알아보았다.
3.3 적층탄성받침의 변수해석
이 절에서는 다양한 형상계수(즉,
 ) 및 중공직경을 갖는 적층탄성받침의 압축 및 전단 특성을 알아보고자 한다. Table 2는 적층탄성받침의 해석모델 제원을 나타내고 있다.
) 및 중공직경을 갖는 적층탄성받침의 압축 및 전단 특성을 알아보고자 한다. Table 2는 적층탄성받침의 해석모델 제원을 나타내고 있다.
3.3.1 적층탄성받침의 압축특성
Fig. 11은 5,000kN의 압축하중이 작용할 때 적층탄성받침(RB_F_1)의 수직변위 및 von Mises 응력의 분포를 나타내고 있다. Fig. 11(a)로부터 수직하중에 대한 압축변위의 크기가 매우 작게 나타나 매우 큰 수직강성을 유지하는 것을 알 수 있으며, Fig. 11(b)에서는 받침의 강판 단면의 중심부에서 최대응력(약 33.6MPa)이 발생하는 것으로 나타났다.
적층탄성받침의 변수에 따라서 달라지는 압축하중과 변위의 관계를 Fig. 12에 나타내었다. Fig. 12(a)는
 의 크기가 커지면 수직변위가 감소하게 되며, 압축강성이 증가하게 된다.
의 크기가 커지면 수직변위가 감소하게 되며, 압축강성이 증가하게 된다.
Fig. 12(b)는
 의 변화에 따른 압축하중-변위의 관계를 나타내고 있으며, 여기서 RB_S_1부터 RB_S_4까지 최대 압축변위가 각각 0.52mm, 0.44mm, 0.36mm, 0.28mm로 나타났다. 1차 형상계수에 따른 해석결과와 동일하게 2차 형상계수가 증가할수록 압축변위는 줄어드는 경향을 보였다. 이와 같은 결과는 적층수의 감소가 적층된 고무의 총 두께의 감소를 초래하고, 동시에 압축 변형량도 함께 감소하게 된다는 것을 의미한다.
의 변화에 따른 압축하중-변위의 관계를 나타내고 있으며, 여기서 RB_S_1부터 RB_S_4까지 최대 압축변위가 각각 0.52mm, 0.44mm, 0.36mm, 0.28mm로 나타났다. 1차 형상계수에 따른 해석결과와 동일하게 2차 형상계수가 증가할수록 압축변위는 줄어드는 경향을 보였다. 이와 같은 결과는 적층수의 감소가 적층된 고무의 총 두께의 감소를 초래하고, 동시에 압축 변형량도 함께 감소하게 된다는 것을 의미한다.
Fig. 12(c)는
 의 크기에 따른 압축하중-변위의 관계를 나타내고 있으며, 예상한데로 중공직경이 커질수록 압축변위가 증가하는 것으로 나타났다. Fig. 12(d)로부터 2차 형상계수와 중공직경의 변화보다 1차형상계수의 변화가 적층탄성받침의 압축거동에 미치는 영향이 더 크다는 것을 알 수 있다.
의 크기에 따른 압축하중-변위의 관계를 나타내고 있으며, 예상한데로 중공직경이 커질수록 압축변위가 증가하는 것으로 나타났다. Fig. 12(d)로부터 2차 형상계수와 중공직경의 변화보다 1차형상계수의 변화가 적층탄성받침의 압축거동에 미치는 영향이 더 크다는 것을 알 수 있다.
3.3.2 적층탄성받침의 전단특성
Fig. 13은 적층탄성받침(RB_F_1)에 압축하중 5,000kN을 재하한 상태에서 수평 변위하중 150mm를 반복가력한 결과로서의 변형형상과 von Mises 응력분포를 나타낸다. Fig. 13(a)와 같이 적층탄성받침의 전단거동이 수평변위 150mm에 대해서 유연하게 일어남을 볼 수 있으며, Fig. 13(b)로부터 중공에 인접해있는 강판에서 185.0MPa의 최대응력이 나타난 것을 볼 수 있다.
적층탄성받침의 변수에 따라서 달라지는 수평하중과 변위의 관계를 Fig. 14에 나타내었다. Fig. 14(a)는
 의 변화가 받침의 전단거동에 큰 영향이 미치지 않는 것을 알 수 있다.
의 변화가 받침의 전단거동에 큰 영향이 미치지 않는 것을 알 수 있다.
Fig. 14(b)는
 가 증가하게 되면 적층탄성받침의 고무 층의 총 두께가 감소하여 수평강성 증가하게 됨을 주지해야 한다.
가 증가하게 되면 적층탄성받침의 고무 층의 총 두께가 감소하여 수평강성 증가하게 됨을 주지해야 한다.
Fig. 14(c)는
 의 크기에 따른 수평하중-변위의 관계를 나타내고 있으며, 예상한데로 중공직경이 커질수록 수평반력이 감소하는 것으로 나타났으며, 이에 대한 영향이 크지 않은 것을 알 수 있다. Fig. 14(d)로부터 1차 형상계수와 중공직경의 변화보다, 2차 형상계수의 변화가 적층탄성받침의 전단거동에 미치는 영향이 더 크다는 것을 알 수 있다.
의 크기에 따른 수평하중-변위의 관계를 나타내고 있으며, 예상한데로 중공직경이 커질수록 수평반력이 감소하는 것으로 나타났으며, 이에 대한 영향이 크지 않은 것을 알 수 있다. Fig. 14(d)로부터 1차 형상계수와 중공직경의 변화보다, 2차 형상계수의 변화가 적층탄성받침의 전단거동에 미치는 영향이 더 크다는 것을 알 수 있다.
3.4 납 고무받침의 변수해석
이 절에서는 다양한 형상계수(
 )을 갖는 납 고무받침의 압축 및 전단 특성을 알아보고자 한다, Table 3는 납 구무받침의 해석모델 제원을 나타내고 있다.
)을 갖는 납 고무받침의 압축 및 전단 특성을 알아보고자 한다, Table 3는 납 구무받침의 해석모델 제원을 나타내고 있다.
3.4.1 납 고무받침의 압축특성
Fig. 15는 5,000kN의 압축하중이 작용할 때 납 고무받침 (LRB_F_1)의 수직변위 및 von Mises응력분포를 나타내고 있다. Fig. 15(a)로부터 적층탄성받침에서와 같이 압축하중에 대한 수직변위가 매우 작게 일어나 큰 수직강성이 유지되는 것을 볼 수 있다. Fig. 15(b)에서는 납봉과 인접해있는 강판에서 최대응력(64.0MPa)이 발생하는 것으로 나타났다.
납 고무받침의 변수에 따라서 달라지는 압축하중과 변위의 관계를 Fig. 16에 나타내었다. Fig. 16(a)는
 이 증가할 때 수직변위는 감소하며, 납 고무받침의 수직변위가 적층탄성받침의 수직변위보다 절반정도 작게 나타났다.
이 증가할 때 수직변위는 감소하며, 납 고무받침의 수직변위가 적층탄성받침의 수직변위보다 절반정도 작게 나타났다.
Fig. 16(b)는
 과 마찬가지로 납 고무받침의 수직변위가 적층탄성받침의 수직변위(Fig. 12(b)보다 절반정도 작게 나타났다.
과 마찬가지로 납 고무받침의 수직변위가 적층탄성받침의 수직변위(Fig. 12(b)보다 절반정도 작게 나타났다.
Fig. 16(c)는
 의 변화에 따른 압축하중-변위 관계를 나타내고 있으며, 납봉의 직경이 커질수록 수직변위가 증가하나 크게 영향이 미치지 않는 것으로 나타났다. Fig. 16(d)로부터 2차 형상계수와 납봉 직경의 변화보다 1차 형상계수의 변화가 적층탄성받침과 마찬가지로 납 고무받침의 압축거동에 미치는 영향이 더 크다는 것을 알 수 있다.
의 변화에 따른 압축하중-변위 관계를 나타내고 있으며, 납봉의 직경이 커질수록 수직변위가 증가하나 크게 영향이 미치지 않는 것으로 나타났다. Fig. 16(d)로부터 2차 형상계수와 납봉 직경의 변화보다 1차 형상계수의 변화가 적층탄성받침과 마찬가지로 납 고무받침의 압축거동에 미치는 영향이 더 크다는 것을 알 수 있다.
3.4.2 납 고무받침의 전단특성
Fig. 17은 납 고무받침(LRB_F_1)에 압축하중 5,000kN을 재하한 상태에서 수평 변위하중 150mm를 반복가력한 결과로서의 변형형상과 및 von Mises 응력분포를 나타낸다. Fig. 17(a)와 같이 납 고무받침의 전단거동이 수평변위 150mm에 대해서 유연하게 일어남을 볼 수 있으며, Fig. 17(b)로부터 납봉에 접해있는 강판에서 161.9MPa의 최대응력이 나타나는 것을 알 수 있다.
납 고무받침의 변수에 따라서 달라지는 수평하중과 변위 관계를 Fig. 18에 나타내었다. Fig. 18(a)는
 이 납 고무받침의 수평거동의 변화에 큰 영향이 없는 것으로 나타났다. 적층탄성받침(Fig. 14(a) 참조)과 비교해볼 때 납 고무받침(Fig. 18(a) 참조)에서 더 큰 수평반력을 얻었으며, 또한 에너지소산능력이 크게 증가되었다.
이 납 고무받침의 수평거동의 변화에 큰 영향이 없는 것으로 나타났다. 적층탄성받침(Fig. 14(a) 참조)과 비교해볼 때 납 고무받침(Fig. 18(a) 참조)에서 더 큰 수평반력을 얻었으며, 또한 에너지소산능력이 크게 증가되었다.
Fig. 18(b)
 의 변화에 따른 수평하중-변위의 관계를 나타내고 있으며, 여기서 LRB_S_1부터 LRB_S_4까지 수평반력이 각각 791.8kN, 874.3kN, 990.9kN, 1171.1kN으로 나타났다.
의 변화에 따른 수평하중-변위의 관계를 나타내고 있으며, 여기서 LRB_S_1부터 LRB_S_4까지 수평반력이 각각 791.8kN, 874.3kN, 990.9kN, 1171.1kN으로 나타났다.
Fig. 18(c) 납봉의 직경에 따른 수평하중-변위 관계를 나타내고 있으며, 여기서 LRB_D_1부터 LRB_D_4까지 수평반력이 각각 678.0kN, 791.8kN, 925.8kN, 1080.3kN으로 나타났다. 적층탄성받침의 중공직경의 변화(Fig. 14(c) 참조)와는 상대적으로 납봉의 직경이 커질수록 전단변형이 감소하며, 예상한데로 에너지 소산능력이 향상되는 것을 알 수 있다. Fig. 18(d)로부터 1차 형상계수의 변화보다, 2차 형상계수와 납봉 직경의 변화가 납 고무받침의 전단거동에 미치는 영향이 더 크다는 것을 알 수 있다.
4. 결 론
본 연구에서는 적층탄성받침과 납 고무받침의 재료 및 기하비선형을 고려한 3차원 유한요소해석을 수행하기 위하여 고무시편의 재료시험을 통해 고무재료 상수를 획득하였고, 실제 제품과 비교하여 고무재료상수의 유효함을 알아보았다. 이를 근거로 1차 형상계수, 2차 형상계수, 납봉의 직경 등에 따른 적층고무받침의 압축특성 및 전단특성을 분석하였으며 또한 적층탄성받침과 납 고무받침의 압축 및 전단 변형에 따라 달라지는 보강철판의 최대 von Mises 응력분포 형태를 알아보았다.
본 연구의 해석결과를 분석하고 평가하여 다음과 같은 결론을 제시한다.
(1)고무시편의 인장, 압축, 전단 시험을 통한 응력-변형률 관계를 이용하여 유한요소해석에 필요한 고무재료상수를 구하였으며, 적층탄성받침과 납 고무받침에 대한 실험과 FE 해석 결과를 비교하여 고무재료상수의 유효성을 검증하였다.
(2)적층탄성받침과 납 고무받침의 압축거동에 대하여 2차 형상계수와 중공 및 납봉 직경의 변화는 큰 영향을 미치지 못하였으나, 1차 형상계수의 변화에 따라 크게 달라지는 것을 알 수 있었다.
(3)적층탄성받침과 납 고무받침의 전단거동에 대하여 1차 형상계수와 중공직경의 변화는 받침의 전단 거동에 큰 영향을 미치지 못하였으나, 2차 형상계수의 변화에 따라 크게 달라졌다.
(4)납 고무받침의 납봉은 작은 하중에 대해서 비교적 높은 강성을 유지하도록 하며, 큰 하중에 대해서는 납의 소성거동으로 인해 에너지 소산능력을 증가시키는 것을 알 수 있다. 여기서 납봉의 직경이 커질수록 에너지 소산능력이 증가하게 된다.
(5)압축하중이 작용할 때 적층탄성받침의 강판은 외경과 내경의 사이에서 최대 응력이 나타났으며, 납 고무받침의 강판은 납봉과 강판의 경계부근에서 최대 응력이 나타났다. 전단하중에 대해서는 적층탄성받침과 납 고무받침의 응력분포는 동일한 양상을 보였다.
이상의 결론에서 1차 형상계수의 변화는 받침의 압축특성에, 2차 형상계수는 받침의 전단특성에 큰 영향을 미치는 것을 알 수 있으며, 납 고무받침의 납봉의 직경은 받침의 초기강성과 에너지 소산능력을 결정하는 중요한 변수임을 알 수 있다.
Acknowledgments
이 논문은 2013년도 세명대학교 교내학술연구비의 지원을 받아 수행된 연구임.
References
-
정우정(1998) 지진격리장치를 이용한 구조물의 내진성능 향상에 대한 실험적 연구, 박사학위논문, 한국과학기술원.
Chung, W.J. (1998) Experimental Study on Seismic Performance Improvement of Structures Using Base Isolation Techniques, Ph.D. Dissertation, Korea Advanced Institute of Science and Technology, Korea (in Korean). -
오주(2011) 교량용 적층고무받침의 물리적 특성 및 내진성능평가, 박사학위논문, 서울시립대학교.
Oh, J. (2011) An Evaluation of Physical Characteristics and Seismic Performance of Laminated Rubber Bearings Being Used in Bridges, Ph.D. Dissertation, University of Seoul, Korea (in Korean). -
김현수, 강주원(2012) 중약진지역에 대한 MR 감쇠기로 구성된 스마트 면진시스템의 특성연구, 한국강구조학회논문집, 한국강구조학회, 제24권, 제3호, pp.325-336.
Kim, H.S., and Kang, J.W. (2012) Study of Characteristics of Smart Base Isolation System with MR Damper for Regions of Low-to-Moderate Seismicity, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.3, pp.325-336 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.3.325 ]
-
Robinson, W.H. (1982) Lead-Rubber Hysteretic Bearings Suitable for Protecting Structures During Earthquakes, Earthquake Engineering Structural Dynamics, John Wiley & Sons, Vol.10, No.4, pp.593-604 .
[https://doi.org/10.1002/eqe.4290100408]

-
구경회, 이재한, 유봉(1997) 면진용 적층고무베어링의 기계적 역학 특성, 한국지진공학회논문집, 한국지진공학회, 제1권, 제2호, pp.79-89.
Koo, G.H., Lee, J.H., and Yoo, B. (1997) Mechanical Characteristics of Laminated Rubber Bearings, Journal of the Earthquake Engineering Society of Korea, EESK, Vol.1, No.2, pp.79-89 (in Korean). - ANSYS (2011) ANSYS Multiphysics, Ver. 13.0, ANSYS Inc., USA.
-
김완두, 김완수, 김동진, 우창수, 이학주(2004) 고무부품의 유한요소해석을 위한 재료시험 및 비선형 재료물성에 관한 연구, 대한기계학회논문집 A, 대한기계학회, 제28권, 제6호, pp.848-859.
Kim, W.-D., Kim, W.-S., Kim, D.-J., Woo, C.-S., and Lee, H.-J. (2004) Mechanical Testing and Nonlinear Material Properties for Finite Element Analysis of Rubber Components, Transactions of the Korean Society of Mechanical Engineers A, KSME, Vol.28, No.6, pp.848-859 (in Korean). [ https://doi.org/10.3795/KSME-A.2004.28.6.848 ]
-
엄성우(2002) 고무부시의 유한요소 해석에 필요한 물성치 측정과 형상계수에 관한 연구, 석사학위논문, 울산대학교.
Uhm, S.W. (2002) A Study on Form Factor and Property Measurement for FEM Analysis of Rubber Bush, Master’s Thesis, University of Ulsan, Korea (in Korean).


 (MPa)
(MPa)






















 )
)
 )
)
 )
) 



 )
)
 )
)
 )
) 










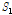 )
)
 )
)
 )
) 



 )
)
 )
)
 )
) 