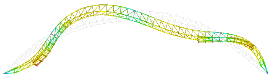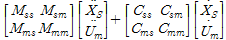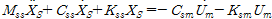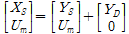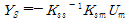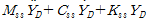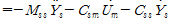다중지점 지진하중을 고려한 대공간구조물의 지진응답 분석

1. 서  론

경기장의 지붕구조와 같은 장경간 대공간구조물의 동적거동은 일반적인 라멘구조와는 상이하게 나타나고 있다. 특히, 지진하중에 의한 대공간구조물의 지진응답은 수평지진하중에 의하여 연직방향 응답이 크게 나타나는 등 일반구조물의 지진응답과는 다른 응답특성을 보이고 있다[1],[2],[3],[4],[5],[6]. 그리고 구조물이 위치하는 지점부의 지반조건, 하부구조의 형태와 같은 하부구조의 조건에 따라서 상부 지붕구조의 지진응답이 매우 다양하게 나타난다. 또한 대공간구조물은 장경간의 특성으로 인하여 하나의 대공간구조물에서 멀리 떨어져 있는 지점부에 도달하는 지진하중의 특성이 서로 다를 수가 있다.

대공간구조물의 내진설계 및 사용성 평가 등을 위해서는 대공간구조물의 지진응답 특성에 대한 정확한 분석이 요구된다. 대공간구조물의 지진하중 적용방법은 일반적으로 지점에 상관없이 모든 지점에 동일한 지진하중이 가해지는 것으로 가정하여 해석을 하게 된다. 그러나 대공간구조물은 장경간의 특성으로 인하여 지점 지반조건, 지진하중 도달시간, 위상차 등이 각각의 지점에 따라서 다르게 작용할 수 있다. 따라서 장경간의 대공간구조물의 지진응답 분석을 위해서는 다중지점 지진하중을 적용한 대공간구조물의 동적해석이 필요하다. 다중지점 지진하중 효과를 고려하기 위하여 지진파가 한 지점에서 다른 지점으로 형상의 변화 없이 이동한다고 가정한다. 구조물에 대한 다중지점 지진하중 적용에 대한 연구는 주로 장견간 교량구조물 위주로 연구가 수행되어 왔다[7],[8],[9], [10],[11],[12]. 그러나 대공간구조물의 경우에도 경간이 상대적으로 길어 하부구조가 위치하는 지반의 물성치가 달라 지점에 작용하는 지진하중이 서로 상이할 수 있다. 또한 대공간구조물의 장경간 특성으로 인하여 지진의 전파속도에 따라서 지점간에 시간지연된 지진하중이 가진될 수 있다.

본 연구에서는 대공간구조물의 다중지점 지진하중의 적용을 통한 지진응답 특성을 분석하고자 한다. 다중지점 지진하중은 두 가지 방법으로 지점의 지반조건이 다른 경우 그리고 시간지연을 갖는 지진하중이 가진되는 경우로 하여 상용프로그램인 MIDAS/Gen을 사용하여 수치해석을 수행하였다.

2. 예제 구조물의 고유치해석 및 지진하중

2.1 예제 구조물

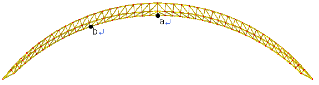
다중지점 지진하중을 적용한 대공간구조물 예제 구조물은 Fig. 1과 같다. 예제 구조물은 두 개의 킬 아치(Keel Arch)가 나란히 구성된 대공간구조물로 지점과 지점 거리가 392M, 높이가 97M, 두 킬 아치이 사이는 84M이다. 예제 구조물의 하중은 두 개의 킬 아치에 의하여 지점으로 전달된다. 대공간아치구조물은 대공간구조물의 기본적인 동적특성을 내재하고 있어 대공간구조물의 거동 분석에 많이 사용된다.

예제 구조물의 킬 아치 형상은 압축력에 유리한 삼각형 형태의 입체 트러스로 재질은 강관으로 되어 있다. 대다수의 대공간구조물의 경우에 풍하중에 의하여 부재의 단면이 결정된다. 따라서 본 예제 구조물의 주요부재 단면은 고정하중, 적재하중 및 풍하중에 의하여 예비 설계되었으며 상현재, 하현재 및 중간재는 같은 직경을 가지고 있으며 부재력에 따라서 단면의 두께가 다르게 설계되었다. 예제 구조물의 주요 부재 단면은 Table 1과 같다.

2.2 예제 구조물의 고유치해석

킬 아치(Keel Arch) 구조물은 대공간구조물에 대한 기본적인 동적특성을 내재하고 있다. 따라서 다중지점 지진하중을 적용한 대공간구조물의 지진응답 분석에 앞서 예제 구조물에 대한 고유치해석을 수행하여 예제 구조물에 대한 동적특성을 분석하고자 한다.

킬 아치 구조물의 진동모드 및 고유진동수와 같은 동적특성 그리고 변위, 속도 및 가속도와 같은 동적응답은 구조물의 형상을 결정하는 개각 및 겉보기 세장비 등에 의하여 좌우되며 일반적으로 진동모드는 대칭모드와 역대칭 모드가 순차적으로 나타난다.

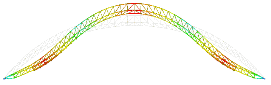
예제 구조물의 진동모드 양상은 Fig. 2(a)와 Fig. 2(c)와 같은 역대칭 모드 그리고 Fig. 2(b)와 Fig. 2(d)와 같은 대칭 모드로 나타나고 있다. 역대칭 모드는 수평방향 지진하중에 반응하여 수평방향 및 연직방향의 지진응답에 기여하며 대칭 모드는 연직방향 지진하중에 의하여 연직방향 지진응답을 크게 일어나게 한다. 킬 아치 구조물과 같은 대공간구조물에서는 수평지진에 의하여 수평응답은 물론 연직응답도 나타나고 있다. 또한 주요 저차모드의 진동주기가 지진하중의 가속도스펙트럼의 탁월한 주기영역에 존재하는 것을 알 수 있다.

2.3 지진하중

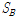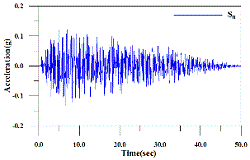
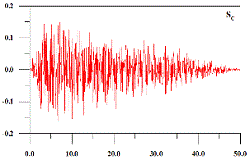
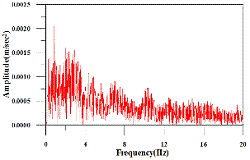
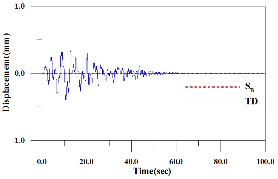
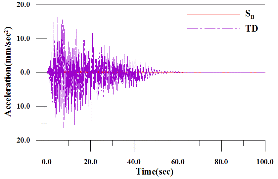
예제 구조물에 적용한 지진하중은 KBC2009의 설계응답스펙트럼에 따른 인공지진하중으로 지역계수는 0.22, 지반종류는 와 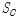로 가정하여 두 개의 지진하중을 생성하여 예제 구조물에 적용하였다. 두 지반에 따른 인공지진하중의 가속도시간이력과 가속도스펙트럼을 Fig. 3에 나타내었다. 두 인공지진의 형상은 유사하나 지반의 특성으로 인하여 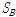지반보다 지반의 지반가속도가 큰 것을 볼 수 있다. 대공간구조물 지점의 지반특성으로 인하여 하나의 대공간구조물에 서로 다른 두 개의 지진하중이 작용할 수 있다.

3. 다중지점 지진하중을 적용한 구조물의 운동 방정식

예제 대공간구조물과 같이 지점이 상당한 거리를 두고 있는 경우에 각각의 지점에 도달하는 지진하중이 시간 지연되어 기초에 도달할 수 있으며 또한 지진하중이 가해지는 기초의 지반조건이 다를 수 있다. 이러한 경우에는 각각의 지점에 가해지는 지진하중이 다를 수가 있으며 대공간구조물의 정확한 지진응답 분석 및 내진설계를 위해서는 지점에 이러한 조건을 반영한 다중지점 지진하중을 적용해야 할 것이다.

다중지점 지진하중을 받는 구조물에 대한 자유도를 지점부분과 구조물부분으로 구분하여 이에 대한 동적운동방정식을 식 (1)과 같이 나타낸다.

여기서, 와 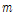는 구조물부분과 지점부분의 자유도를 의미한다. 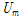는 지점부분에 대한 변위, 는 지점 이외의 부분에 대한 변위를 의미한다. 그리고 , , 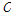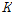는 질량, 감쇠, 강성행렬을 의미한다. 은 지점 변위를 구조물에 가하기 위해 필요한 유사정적 지점하중을 의미한다.

질량행렬은 집중질량행렬이므로 식 (1)의 첫 번째 행은 다음 식 (2)와 같다.

여기서, 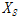는 유사정적 변위( 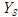)와 동적변위( 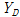)로 구분하여 식 (3)과 같이 나타낼 수 있다.

다중지점 지진하중을 받는 구조물에 대한 운동방정식, 식(1)에서 동적항을 무시할 경우에 유사정적 변위( 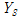)는 다음 식 (4)와 같이 나타낼 수 있다.

식 (4)를 식 (2)에 넣어 정리하면 식 (5)와 같다.

식 (5)의 오른쪽에서 감쇠항이 질량항에 비하여 매우 작으므로 이를 제거하면 식 (6)과 같이 나타낼 수 있다.

4. 다중지점 지진하중을 적용한 대공간구조물의 지진응답

4.1 상이한 지반조건에 따른 지진응답

지진하중에 의한 대공간구조물의 변위응답은 비구조재의 손상, 구조부재의 추가적인 응력 발생, 사용성의 문제 등을 일으키므로 가속도응답은 물론 변위응답에 대한 분석이 필요하다. 대공간구조물의 변위응답이 비교적 크게 나타날 것으로 예상되는 경간의 1/4지점(점 b)과 1/2지점(점 a)에서 단일 지진하중( 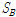와 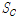)과 다중지점 지진하중( 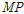)에 의한 변위응답을 비교분석하고자 한다.

본 논문의 수치해석에 사용한 예제 구조물은 정적하중에 의한 처짐과 풍하중에 의한 변위 제한조건을 만족시키도록 주요 부재가 설계되었다. 따라서 예제 구조물의 전체적인 강성이 크게 되어 지진하중에 의한 예제 구조물의 변위응답이 매우 작게 나타나고 있다. 예제 구조물의 고유진동모드의 영향으로 인하여 변위응답의 경우에 응답의 위치에 관계없이 수평변위응답이 연직변위응답보다 크게 나타나고 있다. 그리고 지진하중에 의한 지점변위를 반영하였기 때문에 수평방향 변위응답의 경우에 시간이 경과해도 변위가 복원되지 않은 것을 볼 수 있다.

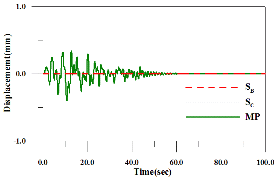
Fig. 4는 지반조건에 따른 1/4지점에서의 수평방향과 연직방향 변위응답을 나타낸 것이다. 수평방향 변위응답은 단일 지진하중에 의한 변위응답과 다중지점 지진하중에 의한 변위응답의 양상이 유사한 것을 볼 수 있으나 SC 지반조건의 단일 지진하중에 의한 변위응답이 약간 크게 나타나고 있다. 이는 SC 지반의 지반가속도가 가장 크기 때문이다. 그리고 두 지점의 지반조건이 상이한 경우에 변위응답이 중간 값을 유지하고 있다. 연직방향의 변위응답의 경우에 단일 지진하중의 변위응답 양상과 다중지점 지진하중의 변위응답 양상이 약간 다른 것을 볼 수 있다.

Fig. 5는 지반조건에 따른 1/2지점에서의 수평방향과 연직방향의 변위응답을 나타낸 것이다. 1/2지점의 수평방향 변위응답은 1/4지점의 수평방향 변위응답과 마찬가지로 SC 지반조건의 단일 지진하중에 의한 변위응답이 가장 크게 나타나고 있다. 연직방향의 변위응답의 경우에 단일 지진하중의 변위응답 양상과 다중지점 지진하중의 변위응답 양상이 매우 다른 것을 볼 수 있으며 단일 지진하중에 의한 변위응답보다 다중지점 지진하중에 의한 변위응답이 현저하게 크게 나타나고 있다. 이는 두 지점에 가진되는 지진하중이 다르기 때문에 지진하중의 위상차에 의한 것으로 사료된다.

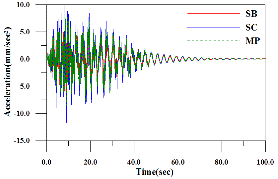
Fig. 6는 지반조건에 따른 1/4지점에서의 수평방향과 연직방향 가속도응답을 나타낸 것으로 가속도응답의 양상은 유사하게 나타나고 있다. 이는 지진하중의 양상이 유사하기 때문이다. 그러나 연직방향의 가속도응답은 SC 지반조건에서 가장 크게 나타나고 있다. 이는 변위응답과 마찬가지로 SC 지반의 지반가속도가 가장 크기 때문이다.

Fig. 7은 지반조건에 따른 1/2지점에서의 수평방향과 연직방향의 가속도응답을 나타낸 것으로 수평방향 가속도응답은 응답의 양상과 크기가 유사하게 나타나고 있다. 그러나 연직방향의 가속도응답의 경우에 연직방향의 변위응답과 마찬가지로 단일 지진하중의 변위응답 양상과 다중지점 지진하중의 변위응답 양상이 매우 다른 것을 볼 수 있다. 그리고 두 지점에 서로 다른 지진하중이 적용되는 다중지점 지진하중을 적용한 예제 구조물의 1/2지점 연직방향 가속도응답이 현저하게 크게 나타나고 있다.

대공간구조물 지점의 지반조건이 상이할 경우에 단일 지진하중을 적용한 구조물의 지진응답과 다중지점 지진하중을 적용한 예제 구조물의 지진응답이 다르게 나타나는 것을 볼 수 있다. 따라서 장경간을 갖는 대공간구조물의 정확한 지진응답 분석을 위해서는 각각의 지점에 대한 지반조건을 정확하게 고려하여 동적해석을 수행하는 것이 바람직할 것이다.

4.2 시간지연 지진하중에 따른 지진응답

장경간의 대공간구조물은 지진의 전파속도에 따라 지점에 도달하는 지진하중의 시각이 다를 수가 있다. 따라서 대공간구조물의 정확한 지진응답 분석을 위해서는 대공간구조물의 지점간 거리와 지진 전파속도를 고려에 의한 시간지연을 갖는 지진하중을 적용해야 할 것이다.

예제 구조물의 지점간 거리(약 400m)와 지진의 전단파속도(800m/sec)를 고려하여 지연 시간을 산정하고 이를 예제 구조물의 동적해석에 반영하여 수치해석을 수행하였다. 지연 시간은 전파속도를 지점간 거리로 나눈 것으로 두 지점간 지진하중의 지연시간은 0.5초로 하였다.

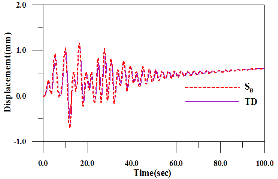
Fig. 8은 1/4지점에서의 지점에 지진이 도달하는 시간이 같은 경우와 지점에 지진이 도달하는 시간이 다른 경우의 수평방향과 연직방향 변위응답을 나타낸 것이다. 두 경우의 변위응답의 양상이 유사하게 나타나고 있다. 수평방향 변위응답의 크기는 시간지연을 갖지 않은 경우( )의 변위응답이 시간지연을 갖는 경우( 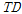)의 변위응답보다 약간 크게 나타나고 있으며 연직방향의 변위응답은 시간지연을 갖는 경우의 변위응답이 시간지연을 갖지 않는 경우의 변위응답보다 약간 크게 나타나고 있다. 그러나 지점에 도달하는 지진파의 시각차가 매우 작기 때문에 변위응답의 차이도 미비한 것을 볼 수 있다.

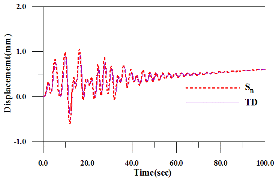
예제 구조물의 1/2지점에서의 수평방향 및 연직방향 변위응답을 Fig. 9에 나타내었다. 1/2지점의 수평방향 변위응답은 1/4지점의 수평방향 변위응답과 마찬가지로 수평방향 변위응답의 양상은 매우 유사하게 나타나고 있으나 시간지연을 갖지 않은 경우( 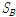)이 시간지연을 갖는 경우( 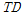)의 변위응답보다 미소하게 큰 것을 볼 수 있다. 그러나 연직방향의 변위응답은 시간지연을 갖는 경우의 변위응답이 시간지연을 갖지 않는 경우의 변위응답보다 매우 크게 나타나는 것을 볼 수 있다. 시간지연을 갖는 경우의 1/2지점 연직방향 변위응답 양상과 시간지연을 갖지 않는 경우의 1/2지점 연직방향 변위응답 양상을 나타낸 것으로 변위응답 양상이 매우 다르게 나타는 것을 볼 수 있다.

Fig. 10은 1/4지점에서의 수평방향과 연직방향 가속도응답을 나타낸 것이다. 수평방향 가속도응답의 양상은 매우 유사하게 나타나고 있으나 시간지연을 갖지 않은 경우( 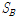)이 시간지연을 갖는 경우( 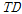)의 가속도응답보다 약간 크게 나타나고 있다. 그러나 연직방향의 가속도응답의 양상은 다르게 나타나고 있으며 시간지연을 갖는 경우의 변위응답이 시간지연을 갖지 않는 경우의 변위응답보다 크게 나타나는 것을 볼 수 있다.

Fig. 11은 1/2지점에서의 수평방향과 연직방향 가속도응답을 나타낸 것이다. 그림 10과 마찬가지로 수평방향 가속도응답의 양상은 매우 유사하게 나타나고 있으나 시간지연을 갖지 않은 경우( 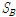)이 시간지연을 갖는 경우( 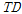)의 가속도응답보다 약간 크게 나타나고 있다. 그러나 연직방향의 가속도응답은 응답의 양상이 다르게 나타나고 있으며 시간지연을 갖는 경우의 변위응답이 시간지연을 갖지 않는 경우의 가속도응답보다 크게 나타나는 것을 볼 수 있다.

장경간의 대공간구조물은 지진의 전파속도에 따라서 지점에 전달되는 지진하중의 도달 시각이 다를 수 있다. 따라서 장경간을 갖는 대공간구조물의 정확한 지진응답 분석을 위해서는 각각의 지점에 대한 지진파의 도달시각을 고려한 동적해석을 수행하는 것이 바람직할 것이다.

4.3 지진하중 조건에 따른 부재력

대공간구조물의 변위 및 가속도 응답 분석과 함께 구조 부재의 설계를 위해서는 모멘트 및 축력과 같은 부재력에 대한 분석이 필요하다. Fig. 9는 지진하중 조건에 따른 예제 구조물의 축력분포를 나타냈으며 Table 2는 하현재의 최대 축력을 나타낸 것이다.

예제 구조물에 동일한 지진하중이 가진되는 SB와 SC의 경우에 부재력 분포가 대칭적으로 나타나는 것을 볼 수 있다. 그러나 지점의 좌우 지반조건이 다르거나 지진전단파 속도에 따라서 지연된 지진하중이 가해지는 경우에 예제 구조물의 부재력 분포가 비대칭적으로 나타나는 것을 볼 수 있다. 따라서 대공간 구조물의 구조 설계를 위해서는 다양한 지진하중 조건에 따른 부재력 분석이 요구된다.

5. 결  론

본 논문에서는 장경간의 대공간구조물의 다중지점 지진하중 적용성에 대하여 알아보았다. 대공간구조물의 정확한 지진응답 분석을 위해서 약 400m의 킬 아치 구조물을 대상으로 수치해석을 수행하였다. 상이한 지반조건 및 시간지연을 갖는 대공간구조물의 수치해석에 의한 지진응답 분석을 통하여 다음과 같은 결론을 얻을 수 있었다.

첫째, 대공간구조물의 경우에 기초가 놓이는 각각의 지점에서 지반조간이 다를 수가 있으며 단일 지진하중을 적용한 경우의 지진응답과 다중지점 지진하중 적용한 경우의 지진응답이 다르게 나타나고 있다. 따라서 장경간의 대공간구조물에 대한 정확한 지진응답 분석을 위해서는 다중지점 지진하중을 적용하여 각각의 지점에 대하여 상이한 지반조건을 고려한 수치해석을 해야 한다.

대공간구조물은 지진의 전단파속도와 경간 거리에 따라서 각각의 지점에 도달하는 지진하중의 시각이 다를 수가 있으며 시간지연을 갖지 않는 경우의 지진응답과 시간지연을 갖는 경우의 지진응답이 다르게 나타나고 있다. 따라서 장경간의 대공간구조물에 대한 정확한 지진응답 분석을 위해서는 시간지연을 갖는 지진하중을 고려한 수치해석이 요구된다.

그리고 대공간 구조물의 사용성 평가 및 구조 설계를 위해서는 다양한 지진하중 조건에 따른 진동응답 및 부재력에 대한 분석이 필요하다.

본 연구에서는 아치구조물로 대상으로 수치해석을 수행하였으나 대공간구조물의 전반적인 지진응답 분석을 위해서는 돔 구조물과 같은 대공간구조물에 대한 수치해석이 필요할 것이다. 또한 지진의 전파속도가 다양하므로 지진의 전파속도의 변화에 따른 대공간구조물의 지진응답 분석이 필요할 것이다.

Acknowledgments

이 논문은 2012년도 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2012043503)

References

• Sadeghi, A. (2004) Horizontal earthquake loading and linear/nonlinear seismic behavior of double layer barrel vaults, International Journal of Space Structure, Vol. 19. No. 1, pp.21-37. [https://doi.org/10.1260/026635104322988344]
• Hassan, A.M. (2000) Seismic behavior of space structures, International Journal of Space Structure, Vol. 15, No. 2, pp.119-135. [https://doi.org/10.1260/0266351001495026]
• Kang, J.W. and Jeong, C.W. (2008) Seismic behavior according to type of large spatial structures, Magazine of the Korean Association for Spatial Structures, Vol. 8, No. 1, pp.5-12.
• Lee, K.S. and Han, S.E. (2009) A Development of analytical strategies for elastic bifurcation buckling of the spatial structures, Journal of the Korean Society of Steel Construction, KSSC, Vol. 21, No. 6, pp.563-574 (in Korean).
• Han, S.E., Lee, S.J., and Gang, E.K. (2006) Evaluation of performance point of the spatial structures using the ESDOF system, Proceeding of the Korean Society of Steel Construction, KSSC, pp.200-205.
• Kim, G.C. and Kang, J.W. (2012) Performance evaluation of vibration control of adjacent buildings according to installation location of MR damper, Journal of the Korean Society of Steel Construction, KSSC, Vol. 24, No. 1, pp.91-99 (in Korean). [https://doi.org/10.7781/kjoss.2012.24.1.091]
• Kang, K.D. (1990) Application of response spectrum method to a bridge subjected to multiple support excitation, Journal of Korean Societe Civil Engineering, Vol. 10, No. 3, pp.1-6.
• Kim, H.K. and Suh, J.I. (1997) Nonlinear earthquake response analysis of a multi-supported self-anchored suspension bridge, Earthquake Engineering Society of Korea, Vol. 1, No. 3, pp.45-58.
• Kwon, J.S., Paik, I.Y., and Chang, S.P. (2004) Dynamic analysis of floating bridge subjected to earthquake load considering multi-support excitation, Earthquake Engineering Society of Korea, Vol. 8, No. 2, pp.27-33. [https://doi.org/10.5000/EESK.2004.8.2.027]
• Su, L., Dong, S., and Kato, S. (2007) Seismic design for steel trussed arch to multi-support excitations, Journal of Constructional Steel Research 63, pp.725-734. [https://doi.org/10.1016/j.jcsr.2006.09.009]
• Jihong, Y., Zhiqiang, Z., and Ye, C. (2011) Strength failure of spatial reticulated structures under multi-support excitation, Earthquake Engineering and Engineering Vibration, Vol. 10, No. 1, pp.21 -36. [https://doi.org/10.1007/s11803-011-0044-6]
• Sextos, A., Kappos, A.J., and Mergos, P. (2004) Effect of Soil-Structure Interaction and Spatial Variability of Ground Motion on Irregular Bridge: The Case of The Krystallopigi Bridge, Proceedings of 13th World Conference on Earthquake Engineering, 1-6, Paper No. 2298.