
재하 크기에 따른 개단면 리브 보강판의 국부 처짐과 국부 모멘트의 정형화
ⓒ KSSC 2013
초록
본 연구에서는 개단면 리브를 갖는 보강판에서 발생하는 국부처짐과 모멘트가 정사각형 재하크기에 따라 어떻게 변화하는지 분석하여 이를 정형화 하고자 하였다. 평강 리브와 역T형 리브를 갖는 보강판에 대하여 각각의 재하크기별로 여러 가지 제원 변화에 따른 비율 함수를 구하여 분석한 결과, 재하크기에 따라 기준 보강판의 값에는 차이가 있으나 리브 간격을 제외하고, 각 제원별 비율 함수에는 큰 차이가 없어 재하크기를 통합하여 표현 가능함을 알 수 있었다. 또한, 평강 리브와 역T형 리브의 차이도 크지 않아 리브 형태와 상관없이 통합한 하나의 함수로 사용 가능함을 알 수 있었으며, 이러한 통합된 하나의 비율함수식을 적용한 결과 상당한 정확도를 나타내었다. 본 연구에서 제안한 통합 함수를 L형 리브와 직사각형 재하에 적용한 결과, 타당한 결과를 나타내어 통합 함수의 적용성을 확인할 수 있었다. 따라서 본 연구에서 제안한 통합 비율함수식을 이용하면, 개단면 리브를 갖는 보강판에서 발생하는 국부처짐과 국부 모멘트 결과를 간편하게 얻을 수 있을 것으로 판단된다.
Abstract
In this study, stiffened plates with open ribs are analyzed to estimate and formulate the local displacement and local moments according to square loading sizes. For the local behaviors of plates stiffened with rectangular and reverse T ribs, the ratio functions according to the dimensions of stiffened plates are obtained at each square loading size. Analytical results show that values of the basic stiffened plates are different but the ratio functions of each square loading size are similar and the difference of the ratio functions between rectangular ribs and reverse T ribs are small, so the ratio functions can be unified by integrating the loading sizes regardless of the rib type. The application of the unioned ratio functions to L type ribs and rectangular loading shows good accuracies. Therefore, the local behaviors of plates stiffened with open ribs can easily be obtained by using the unioned ratio functions proposed in this study.
키워드:
개단면 리브 보강판, 국부 처짐, 국부 모멘트, 국부 거동, 비율 함수, 재하크기Keywords:
plate stiffened with open ribs, local displacement, local moment, local behavior, ratio function, loading size1. 서 론
사하중 감소 효과를 위해 많이 사용되는 강바닥판은 효율적인 구조를 갖고 있으나, 설계를 위한 거동 분석이 어려워 간단하게 격자 구조 또는 직교이방성 판으로 해석하는 방법이 널리 사용되고 있다[1],[2].
그러나 이러한 해석 방법은 강판 자체에서 발생하는 국부 거동을 고려할 수 없다는 문제점을 갖고 있으며, 이러한 문제를 해결하기 위하여 여러 가지 연구가 진행되었으나[3],[4],[5],[6], 국부 거동에 대하여 재하크기와 제원을 동시에 고려한 종합적인 연구는 미흡한 실정이다.
본 연구에서는 제원에 따라 다르게 발생하는 국부거동을 정형화한 기존 연구를[5] 바탕으로, 재하크기가 다른 경우에도 보강판의 국부처짐과 국부 모멘트가 제원에 대한 비율 함수로 표현 가능한지, 재하크기까지 고려한 함수로 표현 가능한지 분석하여 이를 정형화 하고자 한다.
또한, 정형화된 함수의 적용성을 확인하기 위하여 L형 리브와 같이 다른 형태의 리브를 갖는 경우에 대한 적용 방법과 도로교 설계기준[7]의 DB 하중과 같이 직사각형 분포하중이 작용하는 경우에 대한 적용 방법을 살펴보고자 한다.
2. 해석 예제
개단면 리브로는 평강 리브와 역T형 리브를 고려하였으며, Table 1 및 Fig 1에 나타낸 바와 같이 여러 가지 제원을 갖는 보강판에 대하여 분석하고자 한다[5].
기존의 연구 결과를[5],[6] 토대로 Fig 2와 같이 2변 단순지지된 폭 6m, 길이 1m인 보강판의 중앙에 위치한 mm 의 정사각형에 400kN의 하중을 작용시켰으며, m 은 50, 100, 150, 200, 250, 300(mm) 의 6가지 경우를 고려하였다. 여러 제원을 갖는 보강판은 12.5mm12.5mm 크기의 4절점 판요소로 모델링 한 뒤[8],[9], MIDAS 프로그램을 이용하여 재하크기(m)에 따른 거동 분석을 수행하고자 한다.
3. 국부 거동의 정형화
제원에 따른 국부 거동을 정형화하기 위하여 기존 연구[5]와 마찬가지로, Table 1에서 역T형 리브의 중간값인 판 두께 12mm, 리브 간격 400mm, 복부 높이 250mm, 복부 두께 10mm와 플랜지 두께 15mm, 플랜지 길이 100mm를 기준 제원으로, 다른 제원은 동일한 상태에서 식 (1)~(4)와 같이 각각의 제원 변화에 따른 결과를 각 기준 제원의 결과로 나눈 비율 함수를 재하크기별로 구하여 사용하고자 한다.
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
3.1 국부처짐
본 연구에서는 먼저 각 재하크기별 보강판의 국부처짐에 대하여 식 (5)와 같이 기준 보강판의 결과에 각각의 제원 변화에 따른 비율 함수를 곱하여 구할 수 있는지 살펴보고, 재하크기 변화에 따른 경향을 분석하여 개단면 리브 보강판의 국부처짐을 재하크기까지 고려하여 정형화 하고자 한다.
 (5)
(5)
3.1.1 재하크기별 개별 국부처짐 함수
Table 1의 역T형 리브의 중간값, 판 두께 12mm, 리브 간격 400mm, 복부 높이 250mm, 복부 두께 10mm와 플랜지 두께 15mm, 플랜지 길이 100mm를 갖는 경우를 기준 보강판으로 하여, 재하크기(m×m)별 기준 보강판의 값을 초기값
 라 하고 리브 형태별로 나타내면 Table 2와 같다.
라 하고 리브 형태별로 나타내면 Table 2와 같다.
기존 연구[5]에 따르면 역T형 리브의 플랜지 두께와 플랜지 길이가 국부 거동에 미치는 영향은 매우 작으므로 플랜지 두께와 플랜지 길이를 제외하고, 각 제원별 비율의 대푯값을 산정한 뒤, 평강 리브와 역T형 리브 각각에 대하여 재하크기별로 리브 간격(
 ), 판 두께(
), 판 두께(
 ), 복부 두께(
), 복부 두께(
 ) 및 복부 높이(
) 및 복부 높이(
 )에 대한 비율 함수만을 구하여 나타내면 Fig 3 및 4와 같다.
)에 대한 비율 함수만을 구하여 나타내면 Fig 3 및 4와 같다.
Fig 3과 4를 살펴보면 리브 간격과 판 두께는 제원 변화에 따른 비율 차이가 크며, 리브 간격은 재하크기에 따라 비율 차이가 발생하는 반면 판 두께는 재하크기에 따른 차이가 없음을 알 수 있으며, 복부 두께, 복부 높이는 제원 변화 및 재하크기에 따른 차이가 크지 않음을 알 수 있다.
평강 리브와 역T형 리브 각각에 대하여 재하크기별로 Table 2의 초기값과 Fig 3과 4에 나타낸 비율함수를 식 (5)에 대입하고, 실제 계산된 국부처짐과의 오차율을 구한 결과, 평강 리브의 경우 전체 오차율이 -3.68%~+3.74% 의 범위를 나타내고, 역T형 리브의 경우 전체 오차율이 -1.66%~+3.38% 의 범위를 나타내어 각각의 재하크기별 국부처짐은 제원에 따른 비율함수로 표현 가능하며, 이를 이용하면 간편하게 타당한 결과를 얻을 수 있음을 알 수 있다.
3.1.2 재하크기 통합 국부처짐 함수
Table 2에 나타낸 초기값의 경우 리브별로 재하크기에 따른 하나의 함수로 표현 가능하며, 리브 간격을 제외하고 Fig 3 및 4에 나타낸 재하크기별 비율 함수가 거의 유사한 점을 고려하여 재하크기별 비율 함수를 통합하고자 하였다.
이를 위해 리브 간격의 비율함수는 재하크기별 함수 형태로, 다른 제원은 재하크기 150의 함수를 기본으로 판 두께와 복부 두께는 재하크기를 사용하여 보정하는 형태로 표현하여 각각의 리브별로 나타내면 Table 3 및 4와 같다.
평강 리브와 역T형 리브 각각에 대하여 Table 3 및 4에 나타낸 재하크기 통합 초기값과 비율함수를 이용하여 구한 국부처짐과 실제 계산된 국부처짐을 비교하면, 평강 리브의 경우 오차율이 -3.75%~+3.82%, 역T형 리브의 경우 오차율이 -2.40%~+2.44% 의 범위를 나타내어 재하크기별 개별 함수를 사용한 경우에 비하여 최대 오차율 증가가 크지 않아 재하크기 통합 비율함수를 사용하여도 타당함을 알 수 있다.
3.1.3 개단면 리브 통합 국부처짐 함수
Fig 3 및 4를 살펴보면 평강 리브와 역T형 리브 모두 비슷한 양상을 나타내므로, 제원이 다른 복부 두께만 따로 통합하고, 나머지 제원은 평강 리브의 재하크기 통합 비율함수를 기준값으로 비율함수를 통합하여 나타내면 Table 5와 같다.
Table 5에 나타낸 리브 통합 비율함수와 초기값을 식 (5)에 대입하고, 실제 국부처짐과 비교하여 오차율을 구한 뒤, 개별 함수, 재하크기 통합 함수를 사용한 경우와 비교하여 재하크기별 오차율 범위를 정리하여 나타내면 Table 6과 같다.
Table 6을 살펴보면, 재하크기별 개별 함수의 경우, 재하크기 통합함수의 경우와 비교하여 리브를 통합한 함수의 경우 최대 오차율 증가가 크지 않음을 알 수 있다.
따라서, 개단면 리브 보강판의 국부처짐은 Table 5에 나타낸 리브통합 비율함수를 이용하여 간편하게 계산할 수 있으며, 결과 또한 타당함을 확인할 수 있다.
3.2 국부 모멘트

국부처짐과 마찬가지로 보강판의 국부 모멘트
 가 식 (6)과 같이 기준 보강판의 국부 모멘트 에 제원 변화에 따른 비율 함수
가 식 (6)과 같이 기준 보강판의 국부 모멘트 에 제원 변화에 따른 비율 함수
 를 곱하여 간편히 구할 수 있는지 살펴보고, 그 경향을 분석하여 정형화 하고자 하였다.
를 곱하여 간편히 구할 수 있는지 살펴보고, 그 경향을 분석하여 정형화 하고자 하였다.
 (6)
(6)
3.2.1 재하크기별 개별
 함수
함수
각 재하크기별로 판 두께 12mm, 복부 높이 250mm, 리브 간격 400mm, 복부 두께 10mm와 플랜지 두께 15mm, 플랜지 길이 100mm를 갖는 기준 보강판의 국부 모멘트
 값을 초기값
값을 초기값
 로 하여 리브형태별로 나타내면 Table 7과 같으며, 각각의 리브에 대하여 재하크기별로 리브 간격(
로 하여 리브형태별로 나타내면 Table 7과 같으며, 각각의 리브에 대하여 재하크기별로 리브 간격(
 ), 판 두께(
), 판 두께(
 ), 복부 두께(
), 복부 두께(
 ) 및 높이(
) 및 높이(
 )에 대한 비율 함수를 나타내면 Fig 5 및 6과 같다.
)에 대한 비율 함수를 나타내면 Fig 5 및 6과 같다.
Fig 5와 6을 살펴보면 Fig 3과 4의 국부처짐에 비하여 리브 간격 및 판 두께의 제원 변화에 따른 비율 차이가 크지 않으며, 판 두께와 복부 두께가 국부모멘트에 미치는 영향은 재하크기에 따라 약간의 차이가 나타나나 복부 높이의 비율 함수는 재하크기와 상관없이 거의 유사함을 알 수 있다.
각 리브에 대하여 Table 7의 초기값과 Fig 5와 6에 나타낸 비율함수를 식 (6)에 대입하여 계산한 뒤, 실제 국부 모멘트와의 오차율을 구하면 평강 리브는 –1.69%~+2.68%, 역T형 리브는 –1.81 %~+1.00% 의 오차율 범위를 나타내어 재하크기별 국부 모멘트
 는 제원에 따른 비율함수를 이용하여 간편하게 타당한 결과를 구할 수 있음을 알 수 있다.
는 제원에 따른 비율함수를 이용하여 간편하게 타당한 결과를 구할 수 있음을 알 수 있다.
3.2.2 재하크기 통합
 함수
함수
Table 7에 나타낸 초기값은 재하크기에 따른 하나의 함수로, 리브 간격의 비율함수는 재하크기별 함수 형태로, 다른 제원은 재하크기 150의 함수를 기본으로 판 두께와 복부 두께는 재하크기를 사용하여 보정하는 형태로 표현하여 각각의 리브별로 나타내면 Table 8 및 9와 같다.
각각의 리브에 대하여 Table 8 및 9에 나타낸 재하크기 통합 초기값과 비율함수를 식 (6)에 적용하고, 실제 국부 모멘트
 와 비교하면, 평강 리브의 경우 오차율이 -2.27%~+2.42% 의 범위를 나타내고, 역T형 리브의 경우 오차율이 -2.09%~+1.93% 의 범위를 나타내어 재하크기별 개별 함수를 사용한 경우에 비하여 최대 오차율 증가가 크지 않으므로, 국부 모멘트
와 비교하면, 평강 리브의 경우 오차율이 -2.27%~+2.42% 의 범위를 나타내고, 역T형 리브의 경우 오차율이 -2.09%~+1.93% 의 범위를 나타내어 재하크기별 개별 함수를 사용한 경우에 비하여 최대 오차율 증가가 크지 않으므로, 국부 모멘트
 는 재하크기 통합 비율함수를 사용하여도 타당한 결과를 제공함을 알 수 있다.
는 재하크기 통합 비율함수를 사용하여도 타당한 결과를 제공함을 알 수 있다.
3.2.3 개단면 리브 통합
 함수
함수
Fig 5 및 6에 나타낸 비율 함수를 살펴보면 국부처짐과 마찬가지로 평강 리브와 역T형 리브 모두 비슷한 양상을 나타내므로, 복부 두께를 제외하고 평강 리브의 국부 모멘트
 통합 비율함수를 기준값으로 하여 개단면 리브의 비율함수를 통합하여 나타내면 Table 10과 같다.
통합 비율함수를 기준값으로 하여 개단면 리브의 비율함수를 통합하여 나타내면 Table 10과 같다.
Table 10의 리브 통합 비율함수와 초기값을 식 (6)에 대입하고, 실제 국부 모멘트
 와 비교하여 오차율을 구한 뒤, 개별 함수, 재하크기 통합 함수를 사용한 경우와 비교하여 재하크기별로 정리하여 나타내면 Table 11과 같다.
와 비교하여 오차율을 구한 뒤, 개별 함수, 재하크기 통합 함수를 사용한 경우와 비교하여 재하크기별로 정리하여 나타내면 Table 11과 같다.
Table 11을 살펴보면, 국부처짐에 비하여 그 오차율이 작음을 알 수 있으며, 재하크기별 개별 함수 및 재하크기 통합 함수를 사용한 경우와 비교하여 리브 통합 함수의 경우에 발생하는 오차율 증가가 크지 않아 개단면 리브 보강판의 국부 모멘트
 는 Table 10에 나타낸 식을 이용하면 간편하게 타당한 결과를 얻을 수 있음을 확인할 수 있다.
는 Table 10에 나타낸 식을 이용하면 간편하게 타당한 결과를 얻을 수 있음을 확인할 수 있다.
3.3 국부 모멘트

앞서의 연구와 마찬가지로 재하크기별 보강판의 국부 모멘트
 가 식 (7)과 같이 기준 보강판의 국부 모멘트
가 식 (7)과 같이 기준 보강판의 국부 모멘트
 에 각 제원 변화에 따른 비율 함수를 곱하여 구할 수 있는지 살펴보고, 그 경향을 분석하여 정형화 하고자 하였다
에 각 제원 변화에 따른 비율 함수를 곱하여 구할 수 있는지 살펴보고, 그 경향을 분석하여 정형화 하고자 하였다
 (7)
(7)
3.3.1 재하크기별 개별
 함수
함수
각 재하크기별로 기준 보강판의 값을 초기값
 로 하여 나타내면 Table 12와 같으며, 각각의 리브에 대하여 재하크기별 리브 간격(
로 하여 나타내면 Table 12와 같으며, 각각의 리브에 대하여 재하크기별 리브 간격(
 ), 판 두께(
), 판 두께(
 ), 복부 두께(
), 복부 두께(
 ) 및 복부 높이(
) 및 복부 높이(
 )에 대한 비율 함수는 Fig 7 및 8과 같다.
)에 대한 비율 함수는 Fig 7 및 8과 같다.
각각의 리브에 대하여 Table 12의 초기값과 Fig 7과 8에 나타낸 비율함수를 식 (7)에 대입하여 국부 모멘트
 를 산정하고, 실제 계산된 국부 모멘트
를 산정하고, 실제 계산된 국부 모멘트
 와의 오차율을 살펴보면 평강 리브의 경우 -2.23%~+1.72% 의 범위를, 역T형 리브의 경우 오차율이 -1.76%~+1.03% 의 범위를 나타내어 앞서 살펴본 국부처짐과 국부 모멘트
와의 오차율을 살펴보면 평강 리브의 경우 -2.23%~+1.72% 의 범위를, 역T형 리브의 경우 오차율이 -1.76%~+1.03% 의 범위를 나타내어 앞서 살펴본 국부처짐과 국부 모멘트
 와 마찬가지로 재하크기별 국부 모멘트
와 마찬가지로 재하크기별 국부 모멘트
 는 제원에 따른 비율함수를 사용하여 간편하게 계산할 수 있음을 확인 할 수 있었다.
는 제원에 따른 비율함수를 사용하여 간편하게 계산할 수 있음을 확인 할 수 있었다.
3.3.2 재하크기 통합
 함수
함수
앞서와 마찬가지로 Table 12에 나타낸 초기값은 리브마다 재하크기에 따른 하나의 함수로, 리브 간격의 비율함수는 재하크기별 함수 형태로, 다른 제원은 재하크기 150의 함수를 기본으로 판 두께와 복부 두께는 재하크기에 따라 보정하는 형태로 표현하여 나타내면 Table 13 및 14와 같다.
평강 리브 및 역T형 리브 각각에 대하여 Table 13과 14에 나타낸 초기값과 비율함수를 식 (7)에 적용한 뒤, 실제 계산된 국부 모멘트
 와 비교하면 평강 리브의 경우 오차율이 -2.21%~+2.25% 의 범위를, 역T형 리브의 경우 오차율이 -1.60%~+1.63% 의 범위를 나타내어 재하크기별 개별 함수를 사용한 경우에 비하여 최대 오차율 증가가 크지 않으므로 국부처짐 및 국부 모멘트
와 비교하면 평강 리브의 경우 오차율이 -2.21%~+2.25% 의 범위를, 역T형 리브의 경우 오차율이 -1.60%~+1.63% 의 범위를 나타내어 재하크기별 개별 함수를 사용한 경우에 비하여 최대 오차율 증가가 크지 않으므로 국부처짐 및 국부 모멘트
 와 마찬가지로 국부 모멘트
와 마찬가지로 국부 모멘트
 또한 재하크기 통합 비율함수를 사용하여도 타당한 결과를 제공해줌을 알 수 있다.
또한 재하크기 통합 비율함수를 사용하여도 타당한 결과를 제공해줌을 알 수 있다.
3.3.3 개단면 리브 통합
 함수
함수
Fig 7과 8에서 국부 모멘트
 도 역시 평강 리브와 역T형 리브 모두 비슷한 양상을 나타내므로, 평강 리브의 국부처짐 통합 비율함수를 기준값으로 하여 개단면 리브의 비율함수를 통합하여 나타내면 Table 15와 같다.
도 역시 평강 리브와 역T형 리브 모두 비슷한 양상을 나타내므로, 평강 리브의 국부처짐 통합 비율함수를 기준값으로 하여 개단면 리브의 비율함수를 통합하여 나타내면 Table 15와 같다.
Table 15의 리브 통합 비율함수와 초기값을 식 (7)에 대입하고, 실제 국부 모멘트
 와 비교하여 오차율을 구한 뒤, 개별 함수, 재하크기 통합 함수를 사용한 경우와 비교하여 재하크기별 오차율 범위를 나타내면 Table 16과 같다.
와 비교하여 오차율을 구한 뒤, 개별 함수, 재하크기 통합 함수를 사용한 경우와 비교하여 재하크기별 오차율 범위를 나타내면 Table 16과 같다.
Table 16을 살펴보면, 국부처짐 및 국부 모멘트
 와 마찬가지로 리브를 통합한 함수를 사용한 경우 재하크기별 개별 함수를 사용한 경우 및 재하크기 통합함수를 사용한 경우와 비교하여 최대 오차율 증가가 크지 않음을 알 수 있다.
와 마찬가지로 리브를 통합한 함수를 사용한 경우 재하크기별 개별 함수를 사용한 경우 및 재하크기 통합함수를 사용한 경우와 비교하여 최대 오차율 증가가 크지 않음을 알 수 있다.
이상의 결과들로부터, 개단면 리브 보강판의 국부처짐, 국부 모멘트
 , 국부 모멘트
, 국부 모멘트
 모두 리브까지 통합한 비율 함수를 사용하여 간편하게 값을 계산할 수 있으며, 결과 또한 타당함을 확인할 수 있었다.
모두 리브까지 통합한 비율 함수를 사용하여 간편하게 값을 계산할 수 있으며, 결과 또한 타당함을 확인할 수 있었다.
4. 적용성 검토
4.1 L형 리브 보강판에 대한 적용
해석예제에서 고려하지 않았던 보강판 및 재하크기에 대한 적용성을 살펴보기 위하여, 판 두께 10mm, 리브 간격 300mm, 복부 높이 200mm, 복부 두께 10mm, 플랜지 길이 90mm, 플랜지 두께 14mm를 갖는 L형 리브 보강판에 m = 50, 100, 125, 150, 200, 250, 275, 300 (mm)인 하중이 작용하는 경우에 대하여 제안한 통합 함수를 적용하고 그 결과를 실제 해석 결과와 비교하고자 하였다.
플랜지를 갖는 L형 리브는 본 연구의 역T형 리브와 같은 거동을 나타낸다고 가정하여 역T형 리브의 초기값 함수를 적용하였으며, Table 5, 10, 15의 리브 통합 비율 함수를 적용한 뒤 실제 결과와 비교하여 나타내면 Table 17과 같다.
Table 17을 살펴보면, 국부처짐의 경우 –2.88%∼-1.50 %, 국부 모멘트
 의 경우 -1.34∼+0.85%, 국부 모멘트
의 경우 -1.34∼+0.85%, 국부 모멘트
 의 경우 -1.02%∼+1.68%의 오차율을 나타내어 본 연구의 예제 결과와 마찬가지로 국부처짐의 오차율이 국부 모멘트보다 약간 크게 나타났으며, 본 연구 예제 결과와 유사한 정확도를 나타내어 제안한 리브 통합 비율 함수가 L형 리브 및 다른 재하크기에도 적용 가능함을 확인할 수 있었다.
의 경우 -1.02%∼+1.68%의 오차율을 나타내어 본 연구의 예제 결과와 마찬가지로 국부처짐의 오차율이 국부 모멘트보다 약간 크게 나타났으며, 본 연구 예제 결과와 유사한 정확도를 나타내어 제안한 리브 통합 비율 함수가 L형 리브 및 다른 재하크기에도 적용 가능함을 확인할 수 있었다.
4.2 직사각형 재하크기를 갖는 경우
본 연구에서는 정사각형 형태의 재하크기를 갖는 경우에 대한 국부 거동에 대하여 정형화 하였으며, DB 하중과 같이 본 연구에서 고려하지 않았던 직사각형 형태에 분포하중이 작용하는 경우에 대하여 그 적용 방법을 살펴보고자 한다.
Fig 1 및 Table 1에 나타낸 여러 가지 제원의 평강 리브 보강판 중 Table 18과 같이 10가지 경우를 고려하였다.
보강판 폭방향(
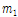 )×길이방향(
)×길이방향(
 )으로 표시하였을 때 직사각형 재하크기는 500×200, 200×500, 300×100, 100× 300(mm) 크기를 갖는 4가지 경우를 고려하였다.
)으로 표시하였을 때 직사각형 재하크기는 500×200, 200×500, 300×100, 100× 300(mm) 크기를 갖는 4가지 경우를 고려하였다.
재하크기가 달라지면 초기값에 차이가 있다는 점을 고려하여, 각 리브 형태별 기준 보강판에 대하여 직사각형 형태의 재하시 결과를 초기값으로 나타내면 별첨 Table 22-27와 같다.
Table 5, 10, 15에 나타낸 통합 비율함수를 적용하려면 정사각형 형태의 재하크기(
 )가 필요하게 되는데, 이때 재하크기(
)가 필요하게 되는데, 이때 재하크기(
 )은 재하 강도와 재하 폭이 동시에 고려된 것으로, 직사각형 재하크기(
)은 재하 강도와 재하 폭이 동시에 고려된 것으로, 직사각형 재하크기(
 ) 를 갖는 경우에는 양쪽 방향의 값이 다르게 되어 곧바로 적용할 수 없게 된다.
) 를 갖는 경우에는 양쪽 방향의 값이 다르게 되어 곧바로 적용할 수 없게 된다.
이러한 문제를 해결하기 위하여, 본 연구에서는 직사각형 재하크기 (
 )를 갖는 경우에 먼저, 재하 강도가 고려되도록 식 (8)과 같이 (
)를 갖는 경우에 먼저, 재하 강도가 고려되도록 식 (8)과 같이 (
 )의 기하 평균값
)의 기하 평균값
 를 구한 뒤, 보강판 폭 방향의 재하크기 (
를 구한 뒤, 보강판 폭 방향의 재하크기 (
 )가 고려되도록 식 (9)와 같이 재하 강도를 고려한
)가 고려되도록 식 (9)와 같이 재하 강도를 고려한
 와 보강판 폭 방향의 재하크기
와 보강판 폭 방향의 재하크기
 의 산술 평균값을 구하여 Table 5, 10, 15에 나타낸 통합 비율함수에 적용할 재하크기(
의 산술 평균값을 구하여 Table 5, 10, 15에 나타낸 통합 비율함수에 적용할 재하크기(
 )으로 사용하였다.
)으로 사용하였다.
 (8)
(8)
 (9)
(9)
직사각형 형태의 하중을 받는 경우에 대하여 별첨 Tables 22-24의 초기값과 Table 5, 10, 15의 통합 비율함수를 이용하여 계산한 결과와 실제 값을 비교하여 오차율로 나타내면 Table 19-21과 같다.
Table 19부터 21까지의 결과를 살펴보면, 본 연구의 예제보다는 오차율이 다소 커지는 경향이 있으나, 최대 오차율 ±10% 내외로 비교적 타당한 결과를 제공해줌을 알 수 있다.
5. 결 론
본 연구에서는 개단면 리브를 갖는 보강판에 대하여 재하크기에 따른 국부거동 양상을 정형화하여 비율함수로 나타내었으며, 그 결과를 정리하여 나타내면 다음과 같다.
(1)각각의 리브 형태에 대한 재하크기별 국부거동은 제원에 따른 비율함수로 표현 가능하고, 재하크기별 각 제원에 대한 비율함수는 통합하여 나타낼 수 있었으며, 이 비율함수를 적용한 결과 처짐은 오차율 ±3% 내외, 모멘트는 오차율 ±2% 내외의 결과를 얻을 수 있었다.
(2)평강 리브와 역T형 리브의 경우 각 제원에 대한 비율함수가 유사한 경향을 나타내어 리브 형태와 상관없이 하나의 통합함수로 표현 가능함을 알 수 있었으며, 재하크기별 개별함수, 재하크기 통합함수와 비교하여 오차율이 ±1% 정도 차이를 나타내나, 최종적으로 처짐은 ±3% 내외, 모멘트는 ±2% 내외의 오차율 결과를 나타내어 개단면 리브 통합함수의 타당성을 확인할 수 있었다.
(3)예제에서 고려하지 않았던 재하크기와 L형 리브 보강판에 역T형 리브의 값을 적용한 결과 최대 오차율이 국부처짐은 2.88%, 국부 모멘트
 는 1.34%, 국부 모멘트
는 1.34%, 국부 모멘트
 는 1.68%로 해석예제와 유사한 결과를 나타내어 본 연구의 적용성을 확인할 수 있었다.
는 1.68%로 해석예제와 유사한 결과를 나타내어 본 연구의 적용성을 확인할 수 있었다.
(4)DB 하중과 같이 직사각형 재하에 대한 적용 방법을 마련하여 계산한 결과, 예제보다 오차율이 다소 증가하였으나, 최대 오차율 ±10% 내외로 비교적 타당한 결과를 나타내어 본 연구의 활용성을 확인할 수 있었다.
이상의 결과들로부터, 개단면 리브를 갖는 보강판에 대하여 본 연구에서 제안한 통합 비율함수를 이용하면 간편하게 실제 거동과 유사한 국부거동 결과를 얻을 것으로 판단된다.
부 록
References
- Hambly, E.C., Bridge Deck Behaviour, 2nd Ed. , (1991), U.S.A., E & FN SPON An Imprint of Cha- pman & Hall.
- Troitsky, M.S., Orthotropic Bridges : Theory and Design , (1992), U.S.A., The James F. Lincoln Arc Welding Foundation.
- Chu, S.B., The Local Behavior of Stiffened Plates with Open Ribs Subject to a Concentrated Load , Journal of Korean Society of Steel Construction, (2005), 17(5), p593-604.
- Chu, S.B., The Effect of the Loading Size on Displacements of Stiffened Plates with Open Ribs , Journal of Korean Society of Steel Construction, (2006), 18(5), p563-574.
- Chu, S.B., Formulating the Local Displacement and Local Moments of a Plate Stiffened with Open Ribs According to the Dimensions of Stiffened Plates , 10.7781/kjoss.2012.24.6.659Journal of Korean Society of Steel Construction, (2012), 24(6), p659-670.
- Chu, S.B., Park, J.H., Model for Analyzing the Local Behavior of Plates Stiffened with Open Ribs , Proceedings of Annual KSSC Conference, (2011), 22(1), p229-230.
- K. R. T. A. (Korea Road & Transportation Association), Design Code for Road Bridges , (2010), Construction Information.
- MIDAS I.T., Structural Analysis by Midas, , (2006), Korea, Kimoondang.
- Finite Element Method , (2002), Techno-Press.










 ) of local displacements (mm)
) of local displacements (mm)

 )
) )
)

 )
) )
)

 )
) )
)

 )
) )
)







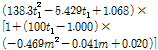

























 ) of local
) of local
 (kN․mm/mm)
(kN․mm/mm)

 )
) )
)

 )
) )
) for each loading size (Rectangular)
for each loading size (Rectangular)

 )
) )
)

 )
) )
) for each loading size (Reverse T)
for each loading size (Reverse T) ratio functions integrating loading sizes (Rectangular)
ratio functions integrating loading sizes (Rectangular)










 ratio functions integrating loading sizes (Reverse T)
ratio functions integrating loading sizes (Reverse T)

























 )
) )
)

 )
) )
) for each loading size (Rectangular)
for each loading size (Rectangular)
 ) of local
) of local
 (kN․mm/mm)
(kN․mm/mm)

 )
) )
)

 )
) )
) for each loading size (Reverse T)
for each loading size (Reverse T) ratio functions integrating loading sizes (Rectangular)
ratio functions integrating loading sizes (Rectangular)










 ratio functions integrating loading sizes (Reverse T)
ratio functions integrating loading sizes (Reverse T)
























 (kN·mm/mm)
(kN·mm/mm) (kN·mm/mm)
(kN·mm/mm)





 ) of local displacements (mm)
) of local displacements (mm)

 ) of local
) of local
 (kN·mm/mm)
(kN·mm/mm)

 ) of local
) of local
 (kN·mm/mm)
(kN·mm/mm)

 ) of local displacements (mm)
) of local displacements (mm)

 ) of local
) of local
 (kN·mm/mm)
(kN·mm/mm)

 ) of local
) of local
 (kN·mm/mm)
(kN·mm/mm)
