다경간 연속스트링거로 구성된 이중바닥 시스템의 강성기반 내진설계
Copyright © 2024 by Korean Society of Steel Construction
초록
이 연구에서는 이중바닥 시스템의 내진설계를 위한 구조시스템을 개발하였으며, 이에 대한 수치해석을 통해 적용 예제를 제시하며 구조성능평가를 수행하였다. 이중바닥 시스템의 스트링거를 다경간 연속으로 설계하여 길이 방향으로 모멘트 접합의 효과를 얻었다. 다경간 연속스트링거로 설계된 이중바닥 시스템에 대한 지배방정식을 유도하였으며, 일반적인 이중바닥 시스템 대비 강성의 증가정도를 정량화 하였다. 성능평가 결과, 다경간 연속스트링거 이중바닥 시스템으로 설계된 시스템은 기존대비 주기가 감소하였다. 또한 기존의 페데스탈 부재에 집중되어 있던 모멘트를 스트링거로 분산이 가능해진다.
Abstract
In this study, a structural system for earthquake-resistant design of a access floor system was developed, and application examples were presented through numerical analysis and structural performance evaluation was performed. The stringers of the access floor system were designed as multi-span continuous to obtain the effect of moment joint in the longitudinal direction. The governing equations for a access floor system designed with multi-span continuous stringers were derived, and the degree of increase in stiffness compared to a general access floor system was quantified. As a result of the performance evaluation, the cycle time of the system designed as a multi-span continuous stringer access floor system was reduced compared to the existing system. Additionally, the moment concentrated in the existing pedestal member can be distributed to the stringer.
Keywords:
Seismic design, Access floor, Nonstructural components, Structural performance, Numerical analysis키워드:
내진설계, 이중바닥시스템, 비구조요소, 구조성능, 수치해석1. 서 론
최근 경주지진과 포항지진 이후 지진에 대한 피해가 가시적으로 나타나면서, 지진에 대한 대비에 관심이 지속적으로 증가하고 있다. 특히 지진 피해사례로 비구조요소의 파손에 따른 인명, 재산피해에 대한 조사가 보고되면서, 비구조요소의 내진성능 만족을 위한 실효적 요구 역시 증대되었다[1]-[4]. 한편 최근 사무실, 학교, 공공 시설, 의료 시설 등 다양한 장소에서 컴퓨터 및 다양한 통신 장비의 사용이 확대되고 보편화되면서, 각종 통신 및 전기 배선은 종종 미관상의 문제뿐만 아니라 운영 및 안전상의 문제를 유발하고 있다. 이러한 문제를 해결하고 보행의 편의성 및 안전성을 향상시키기 위해 이중바닥 시스템이 널리 적용되고 있으며, 현재에는 전산실을 포함한 사무실뿐만 아니라 최근에는 일반 가정에서도 사용되고 있다. 정보통신 시스템은 컴퓨터 사용 환경을 유지하기 위해 이중바닥 시스템 상단에 설치되어 흔들림이 더 커지고, 설치된 장비의 하중은 관성력으로 작용하게 된다. 따라서 이중바닥 시스템 패널의 강도와 함께 지지 구조에 강한 전단력으로 작용하여 지주에 전달된다.
이중바닥 시스템의 내진성능과 관련된 실험 및 해석 연구가 여러 차례 있었다. Choi et al.[5]는 전력, 통신, 신호 등 주요 기간설비의 운영에 필수적인 배전반의 이중바닥 시스템의 내진성능개선을 위하여 정적하중 실험을 통하여 내진보강 이중바닥시스템을 개발 및 평가하였다. Choi et al.[6]는 비구조요소에 대한 지반가속도, 증폭, 중요도 등의 요소를 고려한 등가정적하중의 변화를 나타내는 관련기준을 분석하였다. Chang et al.[7]는 건물 내 비구조요소의 내진설계기준을 비교하고, 각 기준에서의 수평하중을 설치위치에 따라 비교하여 국내 기준에서 규정하는 비구조요소의 설계하중 수준을 조사하였으며, 시간이력해석에 의한 비구조요소의 해석결과와 비교하여 설계하중의 적정성을 검토하였다. Hwang et al.[8]는 정보통신시설에서 건물 내 바닥구조로 사용되는 이중바닥재의 내진성능 평가를 위한 평가절차를 국내 및 국외 관련기준들을 검토하여 정리하였다. Chang et al.[9]는 건물의 기능유지를 위해 중요한 정보통신기기의 안전성을 평가하였다. Park[10]은 엑세스플로어의 내진성능을 평가하고 강성기반 내진설계절차를 제안하였다.
한편, 다경간 연속보로 구성된 건축 구조물의 횡방향 강성에 대한 이론해는 널리 알려져 있으며 실무적으로도 일반적으로 활용되고 있으나, 보와 동일한 개념인 스트링거가 연속으로 설치되는 이중바닥 시스템에 대한 해석적 연구는 수행된 바가 없다. 특히나 프로젝트마다 다양한 층고와 경간을 가지는 일반 건축물의 구조설계와 비교하여, 이중바닥 시스템의 경우 경간이 규격화되어 있으며(국내에선 400 mm, 450 mm, 500 mm, 600 mm), 페데스탈의 높이는 공간의 사용용도에 따라 결정되는데, 예컨대 일반 사무용 건물의 경우 200 mm 내외이며, 복잡한 배선 및 냉방과 환기설비가 요구되는 데이터 센터의 경우 1,000 mm 이상인 경우도 있는 상황이다. 다만 이중바닥 시스템의 구조시스템 형태에 따로 내진설계와 내진성능평가가수행된 바가 없다. 특히 이중바닥 시스템의 경우 여러 관련 연구는 각 페데스탈 헤드에 각각의 스트링거를 걸어서 단순보 형태의 기본적인 형태를 취하는 이중바닥 시스템에 대한 연구가 대부분이다.
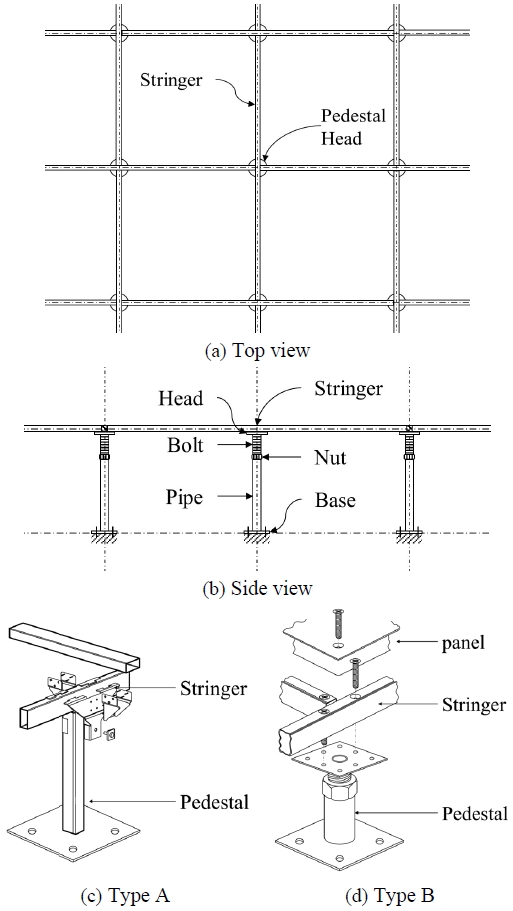
이 연구에서는 이중바닥 시스템의 내진성능을 확보하기 위한 방안으로써 다경간 연속스트링거로 구성된 이중바닥 시스템을 구상하였다. 이러한 형태는 Fig. 1과 같이 몇몇 해외 사례[11],[12]에서 찾아볼 수 있었지만, 국내에는 아직 도입되지 않았다. 이 시스템은 스트링거를 연속보의 형태로 설계하여 연속 지점에서 길이 방향으로 모멘트 접합의 효과를 얻고자 하였다. 이러한 형태를 가진 스트링거를 아래의 Fig. 2의 Type A 또는 Type B와 같이 배열함으로써 내진성능의 증가를 기대한다.
2. 이중바닥 시스템 관련 현행 기준 분석
건축물 내진설계기준 KDS 41 17 00:2022(Ministry of Land, Infrastructure and Transport, 2022)[13]에 따르면 비구조요소의 등가정적해석을 위한 수평설계지진력 Fp는 다음과 같이 산정한다.
| (1) |
여기서 ap는 비구조요소의 증폭계수, SDS는 단주기 설계스펙트럼가속도, Wp는 비구조요소의 작동상태를 고려한 중량, Rp는 비구조요소의 반응수정계수, Ip는 비구조요소의 중요도계수, z는 구조물의 밑면으로부터 비구조요소가 부착된 높이, h는 구조물의 밑면으로부터 지붕층의 평균높이를 의미한다. 또한 식 (1)에서 계산된 Fp는 다음 식(2)에서 제시하는 최댓값과 최솟값의 범위를 만족해야 한다.
| (2) |
위 변수들 중 비구조요소 증폭계수 ap는 기준의 건축비구조요소의 설계계수 표에 제시되어 있으며, 이중바닥의 경우 1.0으로 규정되어 있다. 이는 기존의 일반적인 이중바닥의 경우 공진의 가능성이 없다고 판단되어 결정된 값이였으나, 최근에는 요구 성능의 증가로 인해 일반적인 이중바닥도 고유주기가 길어짐에 따라 공진의 가능성이 높아져 경우에 따라서는 1.0보다 큰 값을 적용해야 한다. 비구조요소가 강체요소이거나 단단히 부착된 요소의 경우 ap = 1.0이며 유연한요소이거나 유연하게 부착된 요소의 경우 ap= 2.5이다. 이 값은 비구조요소의 고유주기에 대한 데이터가 있을 때 사용할 수 있으며, 여기서 강체요소란 고유주기가 0.06초 미만인 경우를 뜻한다. 또한, 상세한 동적해석에 의해 증명되는 경우 표에 규정된 값보다 더 낮은 ap를 사용할 수 있되, 이 때 ap의 값은 1보다 작아서는 안된다. 이는 동적해석을 통해 공진 발생의 여부를 엔지니어가 판단하여 ap를 산정할 수 있도록 규정되어 있다.
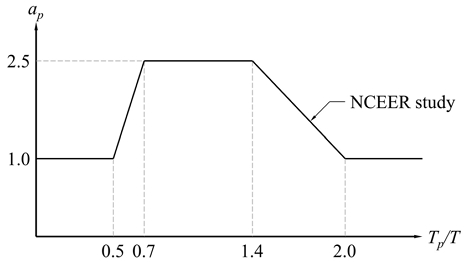
이 공진의 판단에 대해서 ASCE 7-16[14]에서는 구조물과 비구조요소의 고유주기비 Tp/T를 통해 NCEER[15]에서 제시하는 함수인 식 (3)가 사용될 수 있다고 제시한다.
| (3) |
여기서, Tp는 비구조요소의 주기, T는 구조물의 주기이다(Fig. 3 참조).
ASCE 7-22[16]에 따르면 공진 가능성의 결정은 비구조요소의 주기와 구조물 주기의 비가 비교적 작거나 클 때 공진이 발생할 가능성이 낮으며, NIST[17]에서 제안된 Tp/Ta < 0.5 또는 Tp/Ta > 1.5 기준을 사용할 수 있다.
현행 관련 기준 분석 결과, 비구조요소의 공진에 의해 비구조요소의 증폭계수 ap는 비구조요소의 고유주기와 구조물의 고유주기의 비에 의해 결정될 수 있다.
3. 다경간 연속스트링거 이중바닥 시스템 모델
3.1 지배방정식
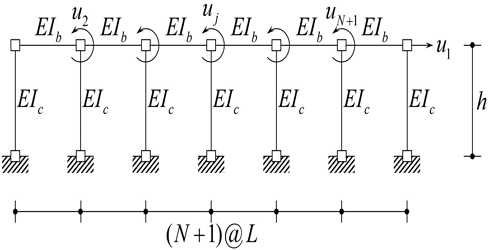
이 절에서는 다경간 연속스트링거 이중바닥 시스템에 대한 지배방정식을 유도한다. Fig. 4는 N개 연속접합부를 가진 형태의 다경간 연속스트링거 이중바닥 시스템에 대한 개념도를 나타낸 것으로, 다경간 연속스트링거란 이중바닥 시스템에서 양 끝의 페데스탈과 스트링거가 결합되는 부분을 제외한 N개 연속접합부를 가진 연속보 형태를 가진 시스템이다(j=(1, 2, ..., N)). 이 시스템의 너비는 L, 높이는 h이며, 탄성계수는 E, 보와 기둥의 중심축에 대한 단면 2차 모멘트는 각각 Ib, Ic이다. 이 시스템은 N+1개의 자유도로 나타낼 수 있다. 감쇠를 포함하지 않는 다경간 연속스트링거 시스템에 대한 운동방정식은 분할된 형식으로 다음과 같이 나타낼 수 있다.[18]
| (4) |
여기서, pt는 수평방향에 대한 외력이다. m00는 회전 관성력에 관한 질량으로 실제적인 구조물의 동역학에 무시할 만한 영향을 미치므로 영(0)의 질량을 나타내며, mtt는 동적자유도로 불리는 질량을 나타낸다. u0은 영(0)의 질량을 갖는 자유도 즉 회전자유도의 변위를, ut는 동적자유도로 불리는 질량을 가진 동적자유도의 변위를 나타낸다. k00는 u0에 대해 회전자유도의 변위형상을 유지하기 위하여 필요한 힘이다. 마찬가지로 ktt,kt0,k0t는 u0,ut에 의한 각각 자유도의 변위형상을 유지하기 위한 강성을 나타낸다. 이다. 두 개의 분할된 방정식은 다음과 같다.
| (5a) |
| (5b) |
어떠한 관성항이나 외부 하중도 u0과 연관되어 있지 않으므로 식 (5)b는 u0와 ut사이의 정적 관계식을 허용한다.
| (6) |
식 (6)를 식 (5)a에 대입하면 다음 방정식이 성립한다.
| (7) |
여기서, 는 응축된 강성행렬로 다음과 같이 쓸 수 있다.
| (8) |
응축된 강성행렬을 활용하여 다경간 연속스트링거 이중바닥 시스템의 횡강성을 구할 수 있다. 횡력 fS가 가해진 이 골조에 대해 평형방정식을 부록 1에 정리하였다.
이 연구에서는 계산과정을 줄이기 위해 강성저감항을 효율적으로 계산하는 알고리즘을 제안하였다. 이는 식 (8)에 포함된 가 삼중대각행렬(tridiagonal matrix)이며, 고유치와 관련된 특성을 활용해 계산량을 최소화한 방법으로, 부록 2에 정리하였다. 예를 들어, 4연속이라고 하자. 그러면 강성저감항에 대한 행렬식은 다음과 같은 형태로 나타난다.
| (9) |
여기서, β는 4α-1이고, P4는 4연속 길이에 해당하는 고유벡터, A4′는 4연속 길이에 해당하는 고유치를 뜻한다. P4와 (A4′)는 각각 다음과 같다.
| (10) |
| (11) |
λi는 상수행렬의 고유치이며, 여기서 λ1 ... λ4는 각각 4.4384, 6.0, 8.5616, 11.0이다.
3.2 시스템 강성식 분석
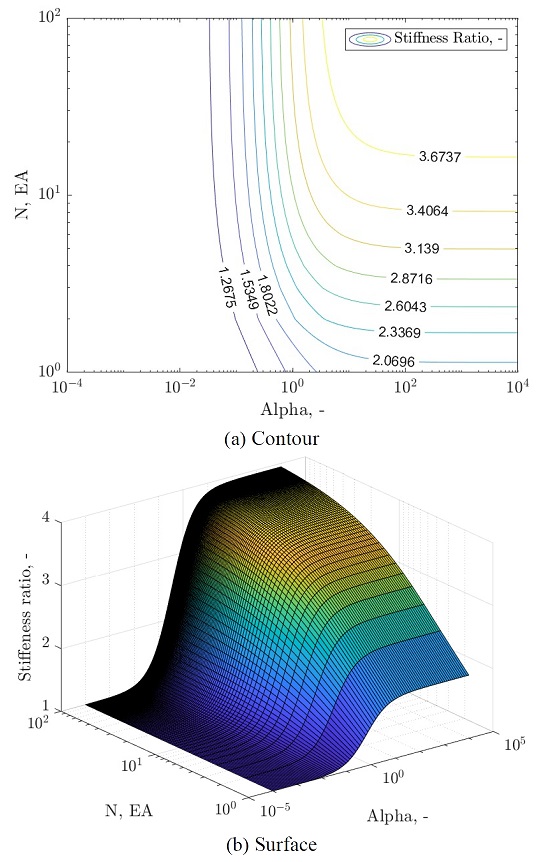
이 절에서는 결정된 다경간 연속스트링거 이중바닥 시스템의 횡방향 변위에 대한 횡강성에 대해서 분석한다. 부록 1에서 구한 강성행렬을 통해 보-기둥 강성비 α에 대한 정규화된 강성비를 Fig. 5와 같이 나타낼 수 있다. 여기서, 정규화된 강성비는 다경간 연속스트링거 이중바닥 시스템의 횡강성을 단순보 시스템의 횡강성으로 나눈 값이다. 그로인해 기존 일반적인 시스템 대비 변화의 형상을 한눈에 알 수 있는데, 이를 통해 설계 및 보강에서 Fig. 5를 활용할 수 있다. 예를들어 몇의 강성 증가가 필요한 경우 Fig. 5를 통해 필요한 값에 대한 적절한 α와 N을 선택하기만 하면 된다. 하지만 현실적으로 α와 N은 선택할 수 있는 폭에 한계가 있어 제약된 α와 N의 구간을 산정하여 선택해야 한다.
Fig. 5의 횡강성비는 α와 N에 대한 함수로 도시되어 있고, α가 증가함에 따라 증가하며, N이 증가함에 따라 증가한다. 강성증가의 최대 기댓값은 α와 N의 극한값에 의해 결정되며, 그래프로 나타내면 다음 Fig. 6와 같다.
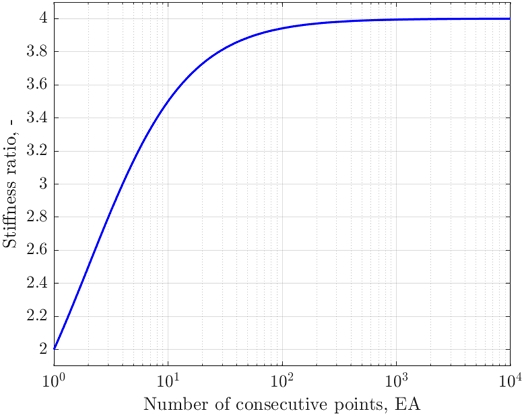
Maximum/minimum lateral stiffness ratio of beam-column stiffness ratio α according to the number of consecutive points
Fig. 6에 따르면 N에 따라 횡강성비가 2배에서부터 최대 4배까지 증가한다. 비교적 연속 지점의 개수가 작은 구간에서의 증가폭이 가파르며 연속 지점의 개수가 증가함에 따라 증가폭이 완만해져 4.0에 수렴한다. 시스템의 고유주기는 질량과 강성의 제곱근에 의해 결정되는데, 그렇다면 다경간 연속스트링거 이중바닥 시스템을 적용하면 강성이 2배에서 4배까지 증가함으로 고유주기의 경우 약 0.7배에서 0.5배까지 감소한다.
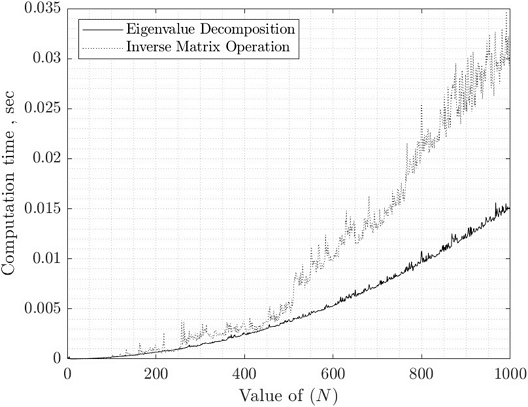
이 연구에서는 식 (8)의 강성저감항을 계산함에 있어 역행렬을 통해 계산하는 과정(이하 역행렬 방법) 부록 1과 고유치 분해를 통해 계산하는 과정(이하 고유치 분해 방법) 부록 2의 연산시간을 비교하였다. 강성저감항의 행렬의 크기는 N에 의해 결정되는데, 행렬의 크기에 의한 역행렬과 고유치 분해의 연산시간을 비교하였으며 이는 Fig. 7과 같다. 이 때, β는 영(0)이며 각 N에 의한 연산시간을 나타내었다. 그 결과 두 가지 방법 모두 N이 증가함에 따라 증가하는 곡선을 보여주는데 N이 작은 구간에서는 큰 차이를 보이지 않지만 N이 커질수록 역행렬 연산 그래프의 기울기가 더 가파르게 상승하여 두 연산 방법의 격차가 벌어진다.
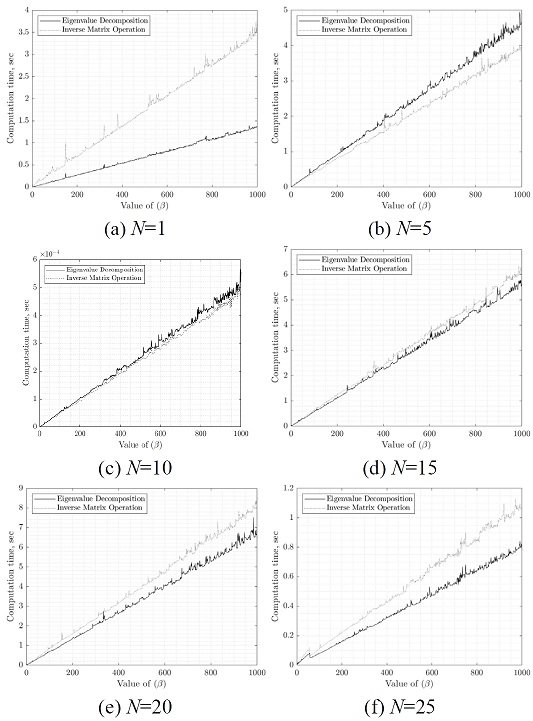
Fig. 8은 연속인 스트링거의 개수를 늘려가며, 각 경우에 고려하는 β개수를 늘려갔을 때의 요구되는 연산량을 도시한 것이다. 기존 방식은 주어진 β에 대해 각각 역행렬을 연산해야 하는 반면, 이 연구에서 유도한 방식에 따르면 β=0에 대해 상수행렬의 고유치를 미리 구하고 이로부터 고려하고자 하는 β를 합산하여 각 원소를 역수로 취하는 부록 2의 과정을 반복하였다. Fig. 8은 N이 연산시간에 미치는 영향도 보여주고 있으며, 그래프상에서 N이 1인 경우 고유치 분해 방법이 역행렬 방법보다 기울기가 작은 모습을 보인다. N이 5와 10인 경우 고유치 분해 방법이 역행렬 방법보다 기울기가 크며, N이 15, 20과 25인 경우 기울기가 작은 모습을 보인다. 기존 방식인 역행렬 방법은 간단한 과정에서 효율적인 모습을 보이며, 이 연구에서 제안하는 고유치 분해 방법은 복잡한 과정에서 효율적인 양상을 보인다. 또한, 고유치 분해 방법이 효율적인 구간에 들어서는 N은 약 10–15이며 그 이후로 N이 증가할수록 고유치 분해 방법의 효율이 높아진다.
4. 사례연구를 통한 해석모델 검증
4.1 해석개요
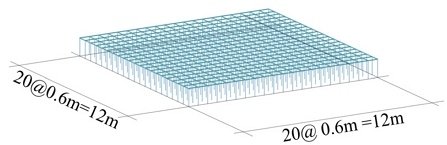
이하에서는 수치해석을 통해 사례연구를 진행하였으며, 이로부터 강성에 기반하여 이중바닥의 내진설계를 수행하기 위한 절차를 제시한다. 예제 구조물은 지진구역은 Ⅰ, 지반조건은 S4로 가정하였다. 이중바닥의 상세는 일반적으로 쓰이고 있는 이중바닥 시스템으로 가정한다. 대상 이중바닥 시스템의 모델은 Fig. 9과 같으며, 연구를 위한 설계변수를 Table 1에 정리하였다. 대상 이중바닥 시스템의 스트링거 경간은 600 mm이며, 이중바닥 시스템의 높이는 일반적으로 200 mm 내외로 다양하게 분포되어 있으나 이 연구에선는 최근 높아지는 요구성능을 반영하여 1,000 mm로 산정한다. 이중바닥 시스템의 위치는 건물 내부의 전산실 또는 서버룸으로 이 때 실의 위치는 지하층에 위치하는 것으로 가정하였다. 이중바닥 시스템의 상부 판넬은 면내방향의 강체거동을 한다고 가정하여, Rigid Floor Rigid Diaphragm을 고려하였다. 또한 중량의 장비가 상부에 재하되는 특성을 고려하기 위해 해석과정에서 P-Delta 효과를 고려하였다. 고정하중은 이중바닥 시스템 판넬의 무게로 판넬 하나의 무게는 0.2 kN로 산정하며, 활하중은 이중바닥 시스템 상부에 설치되는 장비하중으로 10 kN/m2로 고려하였다. 지진하중은 건축물 내진설계기준 KDS 41 17 00:2022에 제시된 비구조요소 설계지진력의 등가정적하중 수평설계지진력을 산정하였다. 이 연구에서는 이중바닥 시스템의 패널의 강성이 크기 때문에 스트링거가 수직하중에 대한 영향을 받지 않는다고 판단하여, 수직하중은 페데스탈 헤드에 해당하는 절점에 집중하중으로 입력하였다.
수평설계지진력의 계수는 Table 2와 같다. 여기서 비구조요소의 증폭계수 ap는 이중바닥에 대한 값인 1.0으로 가정하였으며, 반응수정계수 Rp는 이중바닥 시스템의 경우 중량의 구조물이 재하됨에 따라 연성능력이 제한적이라고 판단하여 1.0으로 가정한다.
4.2 다경간 연속스트링거 이중바닥 시스템 설계
이하에서는 비교분석을 위해 연속되는 스트링거의 경간수와 스트링거의 단면크기를 변수로 설정하였으며 아래의 Table 3에 이를 요약하였다. 이 연구에서는 네 가지의 구성에 대한 설계를 진행하였다(Fig. 10 참조). 페데스탈과 스트링거 간의 접합은 연속 스트링거의 양단부 지점은 핀접합으로 연속구간은 모멘트접합으로 모델링을 실시하였다. 또한 스트링거 단면에 따른 거동의 차이를 분석하기 위해 CS19 구성을 기초로 네 가지 스트링거 단면을 변수로 설정하였다.
수치해석을 통해 얻은 대상 모델의 고유주기는 Table 4와 같다. 연속길이가 증가함에 따라 고유주기가 감소하는 것을 확인할 수 있으며, 그 감소폭은 연속길이가 짧은 구간에서 크게 나타나고 길이가 길어질수록 감소폭이 감소하는 것으로 나타났다. 해석 결과 이 연구에서 제시한 식이 높은 정확도를 가지고 있음을 확인하였다.
Table 5는 지진하중에 의해 각 부재에 발생하는 모멘트의 최댓값을 정규화하여 정리한 것이다. 스트링거 부재의 경우 CS0 모델에서 스트링거가 지진하중에 대한 거동에 참여하지 않아 모멘트가 발생하지 않기 때문에 CS1을 기준으로 정규화하였다. CS1의 경우 CS0의 페데스탈에 발생하는 모멘트 최댓값의 27%가량의 모멘트가 발생한다. CS4의 경우 모멘트가 증가한다. 그 이후 연속길이가 늘어남에 따라 모멘트 최댓값은 감소한다. 비교적 연속길이가 짧은 구간에서 감소폭이 크게 나타나며 연속길이가 길어질수록 감소폭이 작아진다. 이에 따르면 페데스탈 부재의 경우 연속되는 스트링거의 갯수가 늘어남에 따라 모멘트 접합의 개소가 추가되면서, 연속되는 스트링거가 모멘트의 일부를 분담하게 되며, 결과적으로 모멘트 최댓값은 감소하게 된다. 특히 비교적 연속되는 스트링거의 개수가 적은 구간에서도 부재모멘트의 감소폭이 크게 나타나며 스트링거의 연속 개소가 많아질수록 감소폭이 작아지는 것을 확인하였다. CS19의 실험군을 살펴보면, 스트링거의 단면이 증가함에 따라 스트링거 자체 강성의 증가로 페데스탈 모멘트 최댓값은 감소하는 것으로 나타났다.
이 연구의 해석 단계에서 대상 모델과 비교하기 위해 지점을 강접합으로 설정하였으나, 일반적으로 사용되는 이중바닥 시스템은 바닥 접합을 위한 방법으로 접착제를 선호하며 사용하고 있다. 접착제는 접합성능이 낮으며, 그 성능 또한 기대하기 어렵다. 또한 일반적인 이중바닥 시스템의 상부 구조의 접합은 핀접합으로 이루어지는데 이는 횡력에 취약하다. 이중바닥 시스템의 요구성능이 높아지고 있는 현재 특수 이중바닥 시스템 뿐만 아니라 일반적인 이중바닥 시스템 또한 어느정도 높이나 하중을 초과하는 경우 지점 접합 과 상부구조의 접합 등 조건이 제시되어야 한다.
5. 요약 및 결론
이 연구에서는 이중바닥 시스템을 다경간 연속스트링거로 설계하였을 때 구조물의 횡강성 및 부재력에 대해 분석하였다. 이 연구를 통해 도출해 낸 결과는 다음과 같다.
- (1) 현행 건축물 내진설계기준 KDS 41 17 00:2022에 따르면 일반적인 이중바닥의 비구조요소 증폭계수는 1.0으로 제시되고 있다. 이는 이중바닥의 요구 성능이 증가하고 고유주기가 길어지면 더 이상 타당하지 않을 수 있다. 그렇다고 비구조요소 증폭계수를 크게 산정하면 자칫 비효율적인 설계를 할 수 있기 때문에 상세한 동적해석을 바탕으로 공진 발생의 판단을 엔지니어가 내려 적절한 비구조요소 증폭계수를 산정해야 한다. 다경간 연속스트링거 이중바닥 시스템을 적용하면 강성의 증가로 주기 감소의 효과를 볼 수 있는데, 이는 공진 발생에 대한 비구조요소 증폭계수 ap를 산정하는 단계에서 효율적인 설계를 할 수 있다.
- (2) 다경간 연속스트링거를 가지는 이중바닥 시스템에 대한 시스템 횡강성식을 유도하고 이를 연속지점 수 N과 보-기둥 강성비 α에 대해 분석하였다. 보-기둥 강성비 α와 연속지점 수 N이 증가함에 따라 시스템의 횡강성이 증가한다. 또한, 이 연구에서는 횡강성 산정식을 계산함에 있어 고유치 분해를 사용하는 방법을 제시하였으며, 기존 역행렬 접근 방식과 비교하여 효율을 분석했다. 그 결과 N의 값이 크거나 연산되는 β의 양이 많을수록 고유치 분해 방법으로 연산하는 방법이 효율적인 모습을 보였다.
- (3) 이 연구에서는 다경간 연속스트링거 이중바닥 시스템에 대한 사례연구를 수치해석을 통해 수행하였고, 그 성능을 비교 및 분석하였다. 그 결과 α와 N의 증가함에 따라 주기가 감소하였다. 분석 결과 N의 변화에 따라 페데스탈의 모멘트 최댓값이 크게 감소하여 구조적 안정성이 향상되는 모습을 보였다. 또한, 스트링거가 핀접합에서 모멘트 접합으로 전환되면서 지진거동에 참여하게 되는데 이를 통해 시스템의 발생하는 모멘트를 분산시켜 구조적 효율성을 보였다.
- (4) 이 연구의 해석 단계에서 대상 모델과 비교하기 위해 지점을 강접합으로 설정하였으나, 일반적으로 사용되는 이중바닥 시스템은 바닥 접합을 위한 방법으로 접착제를 선호하며 사용하고 있다. 접착제는 접합성능이 낮으며, 그 성능 또한 기대하기 어렵다. 또한 일반적인 이중바닥 시스템의 상부 구조의 접합은 핀접합으로 이루어지는데 이는 횡력에 취약하다. 이중바닥 시스템의 요구성능이 높아지고 있는 현재 특수 이중바닥 시스템 뿐만 아니라 일반적인 이중바닥 시스템 또한 어느정도 높이나 하중을 초과하는 경우 지점 접합 과 상부구조의 접합 등 조건이 제시되어야 한다.
Acknowledgments
이 논문은 2023년도 창원대학교 강사-대학원생-교원 간 융합연구 지원 사업으로 수행된 연구결과임.
References
-
Jun, S.C., Lee, C.H., and Bae, C.J. (2022) Development of Seismic Ceiling System Based on Shake Table Test of Full-Scale 2-Story Steel Moment Frame, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.6, pp.341-352 (in Korean).
[https://doi.org/10.7781/kjoss.2022.34.6.341]

-
Jun, S.C., Lee, C.H., and Bae, C.J. (2021) Analysis of Dynamic Behavior of Seismic and Non-Seismic Suspended Ceiling Systems Based on Shake-Table Testing, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.2, pp.63-74 (in Korean).
[https://doi.org/10.7781/kjoss.2021.33.2.063]

-
Oh, S.H., Park, H.Y., and Park, J.H. (2020) Connection Detail of Cladding Support System for Seismic Performance Improvement, Journal of Korean Society of Steel Construction, KSSC, Vol.32, No.5, pp.285-295 (in Korean).
[https://doi.org/10.7781/kjoss.2020.32.5.285]

-
Choi, E., Kim, J., Yoo, W.-D., and Lee, S.-Y. (2012) Developing Techniques for Increasing Seismic Performance of Existing Electronic Panel on Access Floor, Journal of the Korean Society of Hazard Mitigation, KOSHAM, Vol.12, No.2, pp.31-39 (in Korean).
[https://doi.org/10.9798/KOSHAM.2012.12.2.031]

- Choi, I., Lee, J.-H., Sohn, J.-H., and Kim, J.H. (2019) Investigation on Seismic Design Component and Load for Nonstructural Element, Journal of the Architectural Institute of Korea Structure & Construction, AIK, Vol.35, No.5, pp.117-124 (in Korean).
- Chang, K.-K., Lim, Y.-C., and Seo, D.-W. (2013) Comparison of Building Code for Design of Non-structural Elements for Buildings, Journal of the Architectural Institute of Korea Structure & Construction, AIK, Vol.29, No.1, pp.23-30 (in Korean).
- Hwang, K.-T., Chang, K.-K., and Seo, D.-W. (2012) Seismic Performance Evaluation of Seismic Resistant Access Floor for IT Facility Equipment, Journal of the Architectural Institute of Korea Structure & Construction, AIK, Vol.28, No.7, pp.11-18 (in Korean).
- Chang, K.-K., Im, H.-C., Hwang, K.-T., and Seo, D.-W. (2012) Safety Evaluation of Telecommunication Facilities with Earthquake Loading, Journal of the Architectural Institute of Korea Structure & Construction, AIK, Vol.28, No.6, pp.11-18 (in Korean).
- Park, S.B. (2016) Experimental Study on Seismic Performance of Access Floors and Seismic Design Procedure Based on Stiffness, Master’s thesis, Soongsil University (in Korean).
- Access Floor Systems (n.d.) Raised Floor Stringer, https://www.accessfloorsystems.com/raised-floor-stringer.html
- Applied Technology Council (2012) Reducing the Risks of Nonstructural Earthquake Damage - A Practical Guide, FEMA E-74, Federal Emergency Management Agency, USA.
- Chopra, A.K. (2018) Dynamics of Structures (Translated by Kang, H.K., Kim, J.K., Park, J.H., Lee, D.G., and Lee, J.H.), Protec Media (in Korean).
- Architectural Institute of Korea (2022) Seismic Design Standard for Buildings, KDS 41 17 00 : 2022, Ministry of Land, Infrastructure and Transport (in Korean).
- American Society of Civil Engineers (2017) Minimum Design Loads and Associated Criteria for Buildings and Other Structures, ASCE/SEI 7-16, ASCE, USA.
-
Drake, R.M., and Bachman, R.E. (1996) NEHRP Provisions for 1994 for Nonstructural Components, Journal of Architectural Engineering, American Society of Civil Engineers, Vol.2, No.1, pp.26-31.
[https://doi.org/10.1061/(ASCE)1076-0431(1996)2:1(26)]

- Soong, T.T., Chen, G., Wu, Z., Zhang, R.-H., and Grigoriu, M. (1993) Assessment of the 1991 NEHRP Provisions for Nonstructural Components and Recommended Revisions, Technical Report NCEER-93-0003, National Center for Earthquake Engineering Research, USA.
- American Society of Civil Engineers (2022) Minimum Design Loads and Associated Criteria for Buildings and Other Structures, ASCE/SEI 7-22, ASCE, USA.
- Applied Technology Council (2018) Recommendations for Improved Seismic Performance of Nonstructural Components, NIST GCR 18-917-43, National Institute of Standards and Technology, USA.
Appendix
부록 1. 다경간 연속스트링거 이중바닥 시스템의 횡변위에 대한 강성식 유도
다경간 연속스트링거 이중바닥 시스템에 대해 각 요소는 축방향으로 강체라고 가정하고 골조의 횡강성을 계산한다. 응축된 강성행렬인 식 (8)을 활용하여 각 N에 대하여 계산해보면, N의 값이 2 이상일 때부터 횡력에 대한 시스템의 평형방정식은 일정한 규칙을 가진다. 이 시스템은 Fig. 4에 표시된 것처럼 N+1개의 자유도를 가지고 있다. 따라서 시스템의 (N+1)×(N+1) 강성행렬을 결정할 수 있고, 결정된 강성행렬계수를 이용하면 강성행렬은 다음과 같다.
| (A-1) |
여기서 를 결정하기 위해서 결정된 (N+1)×(N+1) 강성행렬을 분할한다.
| (A-2) |
이들 부분행렬을 식 (8)에 대입하면 응축된 강성행렬이 얻어진다. 이것은 자유도가 층의 횡방향 변위이므로 횡강성행렬이라고 불린다. 이것은 건물의 지진해석의 한 구성요소가 된다. 부분행렬을 대입했을 때 식을 다음과 같이 정리할 수 있다.
| (A-3) |
여기서, 최우측 항은 보-기둥 강성비에 따라 강성을 저감시키는 항이다.
Appendix
부록 2. 강성저감항 계산방법
k00는 삼중대각행렬(Tridiagonal matrix)이며, 다음과 같이 분리된다.
| (B-1) |
여기서, 는 상수부행렬이며, I는 항등행렬, β = 4α-1이다. k00는 자명하게 실수 고유치를 가지며, 다음과 같이 고유치행렬로 분해될 수 있다.
| (B-2) |
즉, k00는 와 동일한 고유치 벡터를 가지며, 의 각 고유치에 β만큼 저감된 고유치를 가진다. 이러한 고유치로 구성된 행렬을 A'라 하자. 그러면 식 (15)는 다음과 같다.
| (B-3) |
이에 대한 역행렬은 다음과 같다.
| (B-4) |
한편, A'는 대각행렬로써, 그 역행렬은 각 대각원소의 역수를 구성원소로 한다. 식 (B-4)를 식 (A-3)에 대입하면 다음과 같이 정리된다.
| (B-5) |
여기서, (A')-1은 다음과 같으며
| (B-6) |
이 때, λi는 상수행렬의 고유치 벡터로 미리 구할 수 있다.