폭발하중에 대한 철골모멘트골조의 전체 거동 및 국부 거동 평가

1. 서 론

폭발사고, 군사무기 및 테러 등에 의해 폭발하중이 작용할 때 구조물의 안전성을 확보하기 위한 많은 연구가 진행되었다. 또한, 플랜트나 국방시설물의 경우 방호시설물의 방폭설계가 요구되고 있고, 국외에서는 테러 폭발물에 의한 일부 구조물의 연쇄붕괴방지설계가 요구되고 있다.

강구조물에 대한 폭발관련 국내 연구는 폭발하중을 받는 기둥 부재의 거동, 변형성능, 잔여저항성능에 대한 유한요소해석이 주로 수행되었다^[1]-[6]. 또한, 국외에서는 폭발하중을 받는 강구조물 골조의 층간변형 및 접합부 형식에 따른 모멘트골조의 거동에 대하여 연구가 수행되었다^[7]-[9]. 그러나 강구조 건축물이 폭발하중을 받으면, 하중을 직접 받는 수직부재의 변형과 같은 국부 거동과 구조물의 층간변형과 같은 골조 거동이 동시에 발생할 수 있는데, 이에 대한 연구는 미흡하다.

이 연구에서는 폭발하중을 변수로 철골모멘트골조의 전체 거동과 1층 기둥의 국부 거동을 해석적으로 평가하였다. 이를 위하여 골조모델과 부재모델에 대하여 각각 해석을 수행하여 기둥의 변형을 비교·분석하였다. 또한 폭발하중과 골조의 층간변형과의 관계를 도출하였다.

2. 유한요소해석

유한요소해석을 위해 미국 내진 연구 SAC Project^[10]에서 사용한 대표적인 강구조 건축물인 LA의 3층 철골모멘트골조를 선정하였다(Fig. 1 참조). 이 구조물에는 지진력저항시스템인 철골모멘트골조시스템이 평면 외곽에 x방향과 y방향으로 배치되어 있다. 이 연구에서는 Y1열에 배치된 3 bay의 철골모멘트골조를 모델링하였다. Fig. 1에 모사된 폭발하중의 1/2에 이 철골모멘트골조가 저항하고, 구조물 전체 질량의 1/2이 폭발하중에 대한 동적응답에 관여한다고 가정하였다. 다만, 폭발해석에서는 중력하중과 폭발하중을 동시에 고려하는 대신, 폭발하중에 대해서만 평가하는 방법이 일반적으로 사용되고 있다. 따라서 이 논문에서는 동적해석에서 질량만 고려하였고, 중력하중을 미리 작용하지 않았으며 P-Delta 효과를 고려하지 않았다.

Fig. 1.

Plan of steel structure

X1열의 외부 기둥은 단면 W14×257로, X2~X4열의 내부 기둥은 단면 W14×311로 설계되었다. 모든 층의 보 단면은 W33×118로 설계되었다(Table 1 참조).

Table 1.

Section dimensions of beams and columns

이 연구에서는 Fig. 2와 같이 철골모멘트골조 전체를 모사한 골조모델과 Fig. 3와 같이 X1열 1층의 외부 기둥을 모사한 부재모델을 구축하였다. 모델의 폭발 거동을 평가하기 위하여 범용 유한요소해석 프로그램인 LS-DYNA^[11]를 사용하여 명시적(explicit) 비선형 시간이력해석을 수행하였다.

Fig. 2.

Steel moment frame model under blast load

Fig. 3.

The first floor column model under blast load

Fig. 2에서와 같이 골조모델은 기둥의 경간이 9 m이고, 층고가 4 m이다. X1열의 모든 층 외부 기둥에 동일한 크기의 폭발하중을 등분포로 작용시켰다. 1층 기둥 하단의 경계조건을 고정단으로 가정하여, 기둥모델 하단의 모든 절점을 변위구속 및 회전구속하였다. 또한 보-기둥 접합부 패널존의 면외방향(모델 y방향)에 대한 변위를 구속하였다.

Fig. 3에서와 같이 기둥 부재모델은 높이가 3.16 m이고 양단고정단의 경계조건을 갖는다, 모델 높이는 층고 4 m에서 보의 춤을 제외한 기둥 순 높이이다. 고정단 경계조건을 위하여 기둥 상단과 하단에 강성이 매우 큰 판을 모델링하고 판의 모든 절점을 변위구속 및 회전구속하였다.

각 모델의 보와 기둥은 모두 4절점의 셸(shell) 요소로 모델링하였다. Fig. 4와 같이 골조모델의 보-기둥 접합부 인근의 요소는 20 mm × 20 mm 크기로 세밀하게 구성하여 정밀도를 높였고, 해석 소요시간을 효율적으로 운용하기 위하여 그 외 요소는 40 mm × 20 mm 크기로 구성하였다. 기둥 부재모델도 골조모델의 기둥과 동일한 크기와 구성의 요소로 모델링하였다.

Fig. 4.

Meshes of finite element model

강재의 재료모델은 부분선형소성(piecewise linear plasticity)모델^[12]을 사용하였고, 응력-변형률 곡선은 탄소성(elasto-plastic) 삼선형(trilinear) 곡선으로 간략화하였다. 기둥의 강재는 A572 Gr.50^[13]으로 정적항복강도 F_y = 345 MPa, 정적인장강도 F_u = 450 MPa이고, 보의 강재는 A36^[14]으로 정적항복강도 F_y = 250 MPa, 정적인장강도 F_u = 400 MPa이다. 강재의 탄성계수 E = 2.0×10⁵ MPa이다(Table 2 참조).

Table 2.

Material properties for beams and columns

폭발해석에서는 폭발하중의 빠른 재하속도로 인해 강재의 항복강도와 인장강도가 증가하는 변형률속도효과(strain rate effect)를 고려할 필요가 있다. 부분선형소성 모델은 변형률속도효과를 포함하는 재료모델로 Cowper-Symonds 모델^[12] 기반으로 변형률속도에 따라 각각 다른 응력-변형도 관계를 적용한다.

여기서, σ_dy = 동적항복강도, $$ \dot{ϵ}$$ = 변형률속도, C,p = 변형률속도 매개변수이다.

Table 2에 나타낸 C, p 값을 포함하여 이 논문에서 사용한 재료모델과 해석기법은 실험결과와 해석결과를 비교한 기존 연구^[15]에서 신뢰성을 검증하였다.

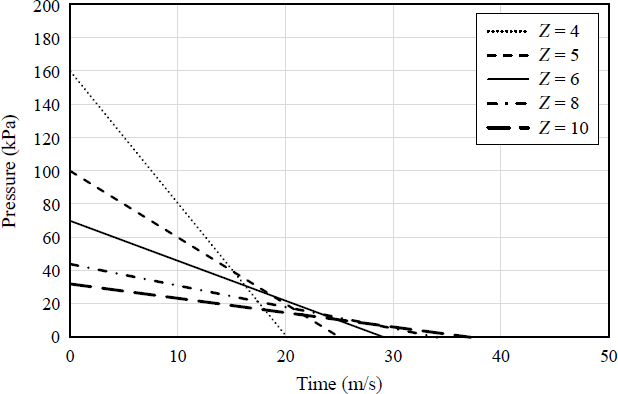
UFC-3-340-02^[16]는 다수의 실험데이터를 기반으로 환산거리, Z(= R/W^1/3; 여기서, R: 폭발 중심으로부터의 거리, W: 폭발물의 무게)에 따른 반사압력, 충격량 등을 차트로 제공하고 있다. 이 연구에서는 테러에 의한 차량폭발 중 큰 폭발물 무게인 1,000 kg의 TNT 폭발물에 대해 Table 3와 같이 폭발 중심으로부터의 거리를 변수로 하여 골조모델과 기둥모델에 폭발하중을 작용시켰다. 폭발하중은 지면폭발을 가정하였고, 구조물에 작용한 단순화된 폭발압력 시간이력곡선은 Fig. 5와 같다.

Table 3.

Scaled distance variables for parametric studies

Fig. 5.

Simplified blast pressure-time history for each scaled distance

3. 해석결과

3.1 부재의 소성변형분포

골조모델 폭발해석 결과, 환산거리(Z)에 따른 구조부재들(보 및 기둥)의 소성변형분포를 Fig. 6에 나타냈다. 폭발하중이 큰 Z = 4 m/kg^1/3와 Z = 5 m/kg^1/3의 경우, 외부기둥과 그 접합부, 연결된 보에 소성변형이 크게 발생하고, 골조 전체의 다른 부재에는 소성변형이 나타나지 않았다. 폭발하중이 클수록 하중을 직접 받는 부재 및 인근 보와 접합부의 국부적 변형이 크게 나타나지만, 이러한 부재들의 국부적 손상(변형)이 커지는 만큼 골조 내 다른 부재에는 소성변형이 발생하지 않음을 알 수 있다. 이러한 결과는 지진하중에 의한 골조 전체의 소성변형 또는 일부 부재의 소성변형이 커지면서 다른 부재들의 소성변형분포가 증가하는 것과 대조되는 결과이다^[17]-[19].

Fig. 6.

Effective plastic strain distribution of frame model

Fig. 7에서와 같이 부재모델에서도 폭발하중이 클수록 국부적 변형이 크게 나타남을 알 수 있다. 그러나 동일한 폭발하중(환산거리)을 받았을 때, 골조모델의 1층 기둥의 소성변형분포와 부재모델의 소성변형분포가 약간 다르게 나타났다. 골조모델의 경우, 접합부와 연결된 보의 소성변형과 골조 전체의 횡이동이 기둥의 소성변형 정도에 영향을 준 것으로 판단된다.

Fig. 7.

Effective plastic strain distribution of member model

3.2 기둥의 지점회전각

골조모델의 경우, Fig. 8에서와 같이 구조물의 층간변위를 고려하여 부재의 횡변위를 산정해야 한다^[16]. 골조모델에서 기둥의 횡변위 및 지점회전각 산정 시, 층간변위를 제외한 기둥의 상대변형을 고려하여야 한다. 즉 기둥 중간높이에서의 횡변위에서 층간변위의 1/2에 해당하는 변위(d₁)를 제외한 상대적 횡변위(d₂)를 부재의 횡변위로 정의한다. 기둥의 지점회전각 tanθ는 d₂를 기둥의 중간높이(H/2)로 나눈 값으로 산정할 수 있다. 부재모델의 경우, 기둥의 지점회전각 tanθ는 기둥 중간높이에서의 횡변위(d)를 기둥 중간높이(H/2)로 나눈 값으로 산정한다.

Fig. 8.

Definition of lateral displacement and support rotation

Fig. 9은 골조모델과 부재모델의 해석결과, 기둥의 횡변위 또는 지점회전각과 환산거리와의 관계를 나타낸다. 먼저 골조모델과 부재모델의 해석결과는 매우 유사함을 알 수 있다. 환산거리가 5 m/kg^1/3보다 작을 경우 기둥의 횡변위(또는 지점회전각)이 급격하게 커지고, 6 m/kg^1/3 이상이면 기둥의 횡변위(또는 지점회전각)이 거의 동일하게 매우 작은 것으로 나타났다.

Fig. 9.

Relation between scaled distance and support rotation

3.3 골조의 층간변위

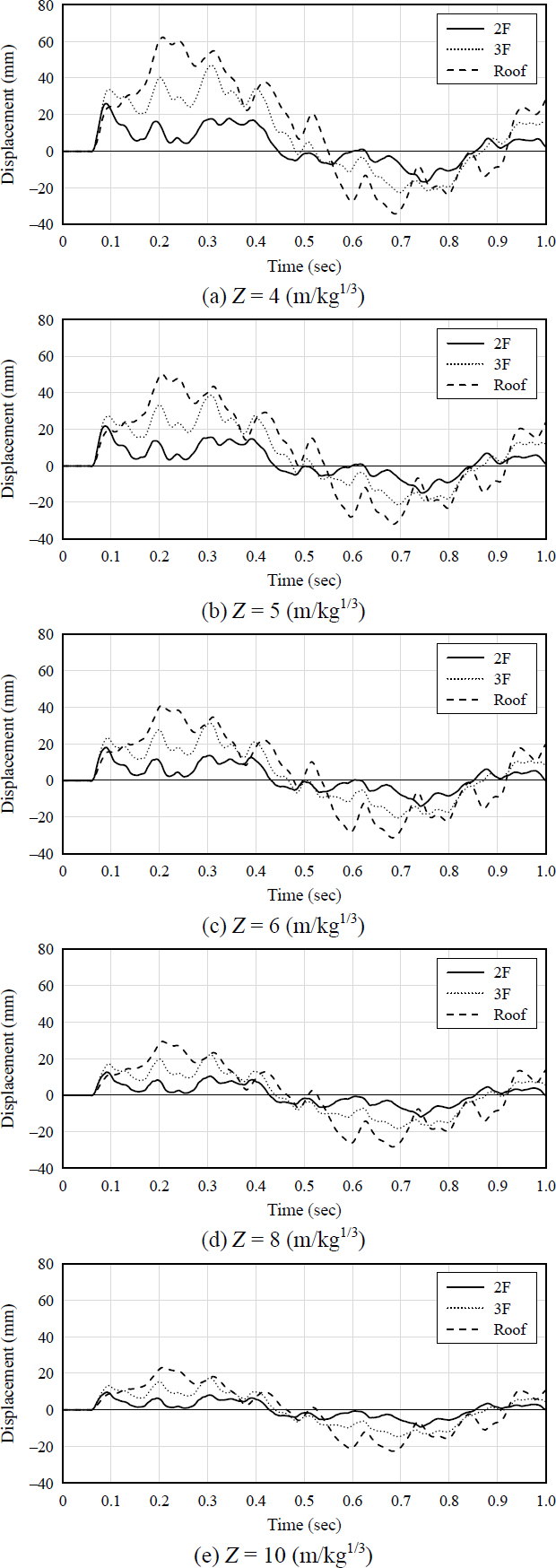
Fig. 10은 골조모델에서 각 층의 총 변위 시간이력곡선을 환산거리별로 나타낸 것이다. 층의 총 변위가 크게 sine 곡선 형상을 보이고, 기둥의 국부적 응답으로 인해 작은 주기로 진동하는 곡선을 보여준다.

Fig. 10.

Total displacement time history of each floor

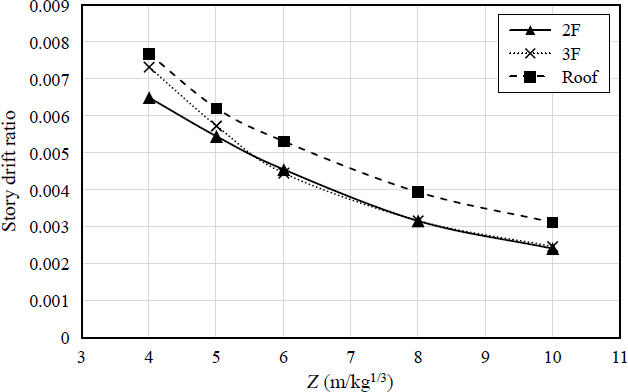
각 층의 총 변위 시간이력곡선에서 동일 시점에서의 층간변위를 산정한 후, 최대층간변위를 산정하였다. 최대층간변위를 층 높이로 나누어 층간변위비로 정의하고, 이를 환산거리와 층을 기준으로 Table 4에 정리하였다. Table 4에 따르면 모든 환산거리에서 층간변위비가 0.01 rad. 미만으로 철골모멘트골조가 안전한 것으로 나타났지만, 환산거리가 4 m/kg^1/3인 경우, 기둥 부재의 지점회전각이 3.5˚–4˚로 부재의 국부적 손상이 매우 크다. 따라서 골조 전체 응답과 부재의 국부 응답을 동시에 고려하여 구조물의 안전을 판단해야 한다.

Table 4.

Maximum story drift ratios of each floor

Fig. 11은 층간변위비와 환산거리 간의 관계를 그린 것이다. 폭발하중이 매우 크면 하중을 받는 기둥의 지점회전각(국부 거동)이 급속히 증가하는 반면, 골조의 층간변위비(골조 거동)는 크게 영향을 받지 않는 것으로 나타났다. 각 층의 층간변위는 환산거리와 반비례하며, 거의 선형관계를 보여준다. 층별 층간변위 크기는 크게 차이나지 않으며, 모든 층의 층간변위-환산거리 관계 기울기가 매우 일치함을 알 수 있다.

Fig. 11.

Relations between story drift ratio and scaled distance

4. 결 론

폭발하중을 받는 구조물은 하중에 직접적으로 영향을 받는 수직부재의 국부적 손상과 구조물의 층간변형과 같은 골조 변형이 동시에 발생할 수 있다. 이 연구에서는 폭발하중을 변수로 3층 철골모멘트골조의 전체 골조 거동과 1층 기둥의 국부 거동을 해석적으로 평가하였다. 이를 위하여 유한요소모델로 골조모델과 부재모델을 구축하고 비선형 시간이력해석을 수행하였다. 1,000 kg TNT 폭발물의 폭발하중에 대해 구조물로부터 이격거리를 달리하여 환산거리 4, 5, 6, 8, 10(m/kg^1/3)을 변수로 하였다. 연구결과는 다음과 같다.

• (1) 폭발하중이 클수록 하중을 직접 받는 기둥과 인근 보, 접합부의 국부적 소성변형이 급속히 증가하지만, 골조 내 다른 부재의 소성변형은 크게 증가하지 않는다. 이러한 결과는 지진하중에 의한 골조 전체의 소성변형 또는 일부 부재의 소성변형이 커지면서 다른 부재들의 소성변형분포가 증가하는 것과 다르다.
• (2) 기존의 많은 방폭설계 기준과 지침서에서 제시된 바와 같이, 골조모델에서의 부재응답을 평가할 때 상대회전각으로 평가해야 함을 유한요소해석으로 검증하였다. 즉, 골조모델에서 산정한 기둥의 상대 지점회전각이 부재모델을 통해 산정한 지점회전각과 매우 유사함을 확인하였다.
• (3) 폭발하중이 매우 크면 하중을 받는 기둥의 지점회전각(국부 거동)이 급속히 증가하는 반면, 골조의 층간변위비(골조 거동)는 크게 영향을 받지 않는다. 환산거리가 작을수록 부재의 국부 손상이 매우 커질 수 있으므로, 골조의 전체 거동과 부재의 국부 거동을 동시에 고려하여 골조의 안전성을 평가하여야 한다. 한편, 이 연구에서는 환산거리와 골조의 층간변위 관계가 선형관계와 가깝게 나타났다. 다만 이러한 환산거리와 층간변위의 관계를 일반화하기 위하여 보다 심화된 연구가 필요하다.

향후 연구에서는 중력하중과 폭발하중을 동시에 고려하였을 때의 철골모멘트 골조의 거동을 평가할 계획이다.

Acknowledgments

본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 RS-2021-KA163162).

References

• Lee, K.-K., Kim, T.-J., Kim, E.-S., and Kim, J.-K. (2007) Behavior of Steel Columns Subjected to Blast Loads, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.23, No.7, pp.​37–44 (in Korean).
• Lee, K.-K., Kim, T.-J., and Kim, J.-K. (2007) Blast Response Evaluation of Steel Structures Due to the Boundary Conditions, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.23, No.12, pp.43–50 (in Korean).
• Lee, K.-K. (2010) Evaluation of Residual Capacity of Steel Compressive Members Under Blast Load, Journal of the Architectural Institute of Korea – Structure & Construction, AIK, Vol.26, No.10, pp.​37–44 (in Korean).
• Lee, K., Rho, J., and Kim, S. (2013) Analytical Evaluation of Blast Resistance of H-Shaped Columns Considering Gravity Load, Journal of the Korean Society of Hazard Mitigation, KOSHAM, Vol.13, No.2, pp.31–36 (in Korean). [https://doi.org/10.9798/KOSHAM.2013.13.2.031]
• Lee, K., and Lee, M.C. (2015) Analytical Study on Effects of Gravity Load on Blast Resistance of Steel Compressive Members, Journal of Korean Society of Steel Construction, KSSC, Vol.27, No.3, pp.273–280 (in Korean). [https://doi.org/10.7781/kjoss.2015.27.3.273]
• Shin, J., and Lee, K. (2016) A Numerical Analysis for Blast Pressure and Impulse from Free-Air Burst, Journal of Korean Society of Steel Construction, KSSC, Vol.28, No.4, pp.271–280 (in Korean). [https://doi.org/10.7781/kjoss.2016.28.4.271]
• Bahrami, A., and Matinrad, S. (2020) Resistance of Blast-Loaded Steel and Reinforced Concrete Beam-​to-Column Connections, International Journal of Engineering Research and Technology, International Research Publication House, Vol.13, No.1, pp.12–27. [https://doi.org/10.37624/IJERT/13.1.2020.12-27]
• Yossof, M.M., Silalahi, J.H., Kamarudin, M.K., Chen, P.-S., and Parke, G.A.R. (2020) Numerical Evaluation of Dynamic Response of Steel Frame Structures with Different Types of Haunch Connection Under Blast Load, Applied Sciences, MDPI, Vol.10, No.5, 1815. [https://doi.org/10.3390/app10051815]
• Kou, S., Zhang, X., Li, W., and Song, C. (2022) Dynamic Response Parameter Analysis of Steel Frame Joints Under Blast Loading, Buildings, MDPI, Vol.12, No.4, 433. [https://doi.org/10.3390/buildings12040433]
• Gupta, A., and Krawinkler H. (1999) Seismic Demands for Performance Evaluation of Steel Moment Resisting Frame Structures (SAC Task 5.4.3), Report No. 132, The John A. Blume Earthquake Engineering Center, USA.
• Livermore Software Technology Corp. (2017) LS-DYNA Keyword User’s Manual, Ver. R10.0, USA.
• Livermore Software Technology Corp. (2023) LS-DYNA Theory Manual, Ver. R14, USA.
• American Society for Testing and Materials (2021) Standard Specification for High-Strength Low-Alloy Columbium-Vanadium Structural Steel (A572/A572M-​21e1), USA.
• American Society for Testing and Materials (2019) Standard Specification for Carbon Structural Steel (A36/A36M-19), USA.
• Lee, K., Shin, J., Lee, J., and Kim, K. (2022) Numerical Study on Steel Plate-Concrete Composite Walls Subjected to Projectile Impacts, Steel and Composite Structures, Techno-Press, Vol.44, No.2, pp.225–240.
• Department of Defense (2008) Unified Facilities Criteria: Structures to Resist the Effects of Accidental Explosions (UFC 3-340-02), USA.
• Kim, J., Lee, K., Kim, W., and Yoon, S. (2021) Experimental Seismic Performance Evaluation of DK Seismic Angle Connection for Exterior Stone Cladding, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.4, pp.257–264 (in Korean). [https://doi.org/10.7781/kjoss.2021.33.4.257]
• Jin, J., Lee, K., Park, K., Kim, D., and Seo, H. (2021) Seismic Performance Evaluation of Non-Welded Moment Connection (KONNECTION) Between Rectangular Tubular Section Column and H-​Shaped Beam, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.6, pp.355–362 (in Korean). [https://doi.org/10.7781/kjoss.2021.33.6.355]
• Kim, J., Kim, D., and Lee, K. (2022) Seismic Performance Evaluation of Connection with New Inner Diaphragm Between Steel Composite Column (POSCO-Column) and Built-up H-Beam, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.6, pp.401–410 (in Korean). [https://doi.org/10.7781/kjoss.2022.34.6.401]