저항복강 강판전단벽 골조의 구조거동에 관한 해석적 연구

2.1 해석모델 계획

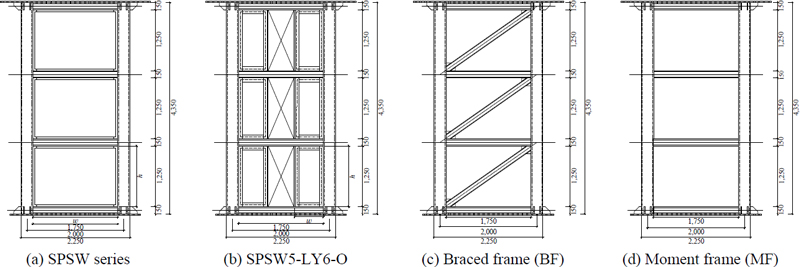
저항복강 강판전단벽 골조 및 비교 골조실험체의 사전 해석결과에 의한 구조거동을 비교하기 위해 해석모델을 계획하였다. 해석모델은 1경간 3층 1/2 축소모델로 제작한다. 주요 해석모델의 구성과 치수는 Fig. 1에, 해석모델의 주요변수는 Table 1에 정리하였다. 해석모델은 기존 연구를 참조하여 저항복강과 일반 탄소강 강판전단벽골조(SPSW series), 강판중간부 개구부를 갖는 골조(SPSW5-LY6-O), 가새골조(braced frame)와 모멘트저항골조(moment frame)로 구성하였다^[6],[7].

Fig. 1.

Shape and geometry of frame specimens (Unit: mm)

Table 1.

List of specimens

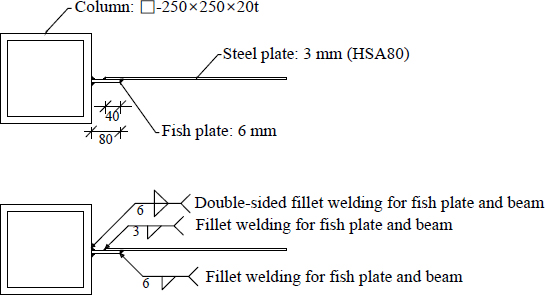
Fig. 1(a)의 해석모델은 Table 1에서 SPSW1-LY3, SPSW2-LY4, SPSW3-LY6, SPSW4-CS3이고 강판전단벽의 강종 및 두께에 따른 강판전단벽의 강성·강도·파괴형태를 비교하기 위하여 각각 적용강판은 저항복강 HSA80의 평판두께 3 mm, 4 mm, 6 mm, 일반구조용 압연강재 SS275의 평판두께 3 mm를 사용하였다. 골조 한 층의 상하 보 중심 간 높이는 1,750 mm, 좌우 기둥 중심 간 길이는 1,250 mm로 설정하였다. 강판전단벽 실험체의 경우 강판전단벽과 보 및 기둥과의 용접접합 및 하중전달을 원활하게 하기 위해 Fig. 2와 같이 피쉬플레이트(fish plate)를 설치한다^[8].

Fig. 2.

Welding between fish plates and steel plate shear wall (SPSW1-LY3)

Fig. 1(b)는 실험체 SPSW5-LY6-O를 나타내며 건축계획상 필요에 의해 강판의 중앙에 개구부가 있는 경우의 구조거동을 비교하기 위해 계획하였다. 개구부는 중앙부에 폭 570 mm의 크기로 설정하였으며 개구부 주위를 평판두께 20 mm 스티프너로 보강하였다.

Fig. 1(c)와 Fig. 1(d)는 비교용 해석모델으로 기존의 고층건물에서 횡력저항시스템으로 사용되고 있는 대각가새골조(braced frame)와 모멘트저항골조(moment frame)를 나타낸다.

2.2 해석모델 모델링

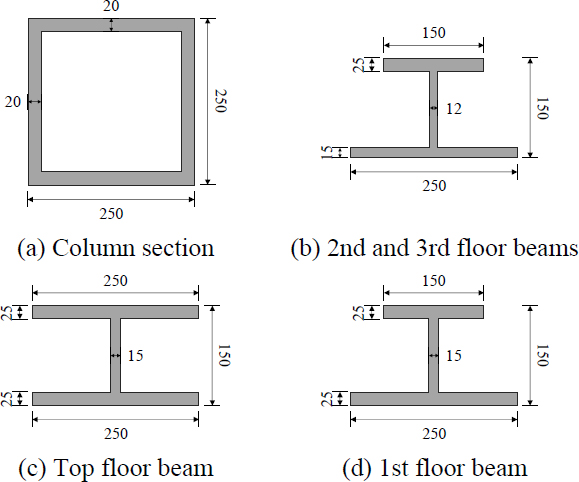
반복하중을 받는 Table 1의 골조 해석모델의 이력거동을 고찰하기 위하여 정적·동적 해석에 널리 사용되는 비선형 유한요소해석 프로그램 ABAQUS를 사용하여 수치해석을 수행하였다. 해석모델의 기둥과 보는 용접구조용 압연강재 SM355를 사용하여 용접조립(built-up)으로 제작하였다. Fig. 3(a)와 같이 기둥단면은 □-250×250×20이다. 보의 형상은 설치 위치에 따라 다음과 같이 다양한 단면을 적용하였다. 보 단면의 경우는 콘크리트 슬래브 내에 매입되어 목표 높이와 구조적 성능을 확보하기 위해 계획되었으며, 기본 단면으로 Fig. 3(b)와 같이 2층 및 3층 보는 비대칭용접 H형강 단면인 PH-150×250×150×12×25×15로 선정하였다. Fig. 3(c)와 같이 최상부 보는 최상부 가력용 프레임을 고정하기 위해 높은 휨강성을 갖는 H형강 단면 PH-150×250×15×25로 하였고, Fig. 3(d)에 나타낸 1층의 최하부 보는 2층 및 3층 보와 동일한 비대칭 단면이지만 하부면 지그와의 접합과 보웨브의 국부좌굴을 방지하기 위해 보 웨브 두께를 증가시킨 비대칭 H형강 단면 PH-150×250×150×15×25×25로 선정하였다.

Fig. 3.

Shape and geometry of column and beam (Unit: mm)

해석모델의 해석시간을 단축하기 위하여 솔리드 요소가 아닌 기존 연구에서 채택한 4절점 쉘(shell) 요소인 S4R 요소를 적용하였다^[9],[10]. Fig. 4에는 유한요소해석모델과 사용된 경계 및 하중조건을 나타냈다.

Fig. 4.

Numerical model of SPSW series

골조의 용접부분은 기둥, 보, 기초판, LHS(lengthened horizontal stiffeners) 및 rib plate는 Instance에서 ‘Merge’ 기능으로 합병하였고 이를 제외한 모든 요소는 ‘Tie’로 연결하여 모델링하였다. 해석모델의 상부에는 보의 중심에 임의의 절점 ‘reference point(RP점)’을 생성하여 윗면과 절점을 ‘Tie’로 구속한 후 z 방향으로 변위제어 방법으로 반복가력하였다. 골조하부는 고정단(U_x = U_y = U_z = 0)으로 가정하였다. 또한, 바닥 및 골조의 자중에 의한 영향을 고려하기 위해 y축 방향(중력방향)으로 기둥의 항복내력의 10 %에 해당하는 축력을 집중하중(1,438.6 kN)으로 입력하였다.

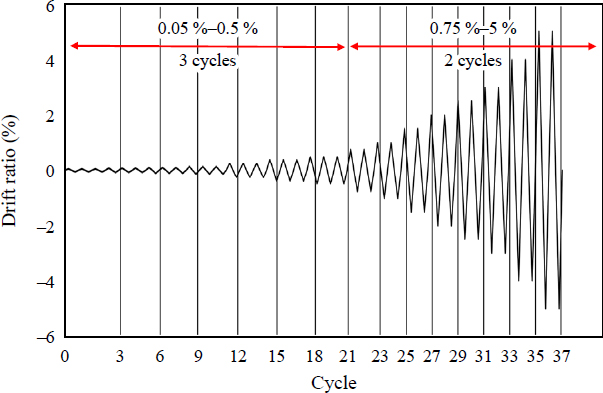
가력계획은 ATC-24의 ‘Guidelines for Cyclic Seismic Testing of Components of Steel Structures’^[11]에 따라 Fig. 5에 나타낸 바와 같이 설정하였다. 실험체 총 높이인 4,200 mm를 기준으로 층간변위비(drift ratio)를 정의하여 반복가력을 수행하였다. Fig. 1에서 우측방향 가력을 ‘+(positive)’, 좌측방향 가력을‘–(negative)’로 가력프로토콜을 설정하였다.

Fig. 5.

Loading protocol

해석모델의 신뢰성을 확보하기 위해 실험계획과 동일한 경계조건 및 부재 크기를 적용하였다. 실제 강판의 운반 중 변형, 용접으로 인한 잔류응력과 시공 시 오차로 인한 영향을 반영하기 위하여 강판의 초기 변형(initial imperfection)을 해석모델에 입력하였다. 강판전단벽 한 변 길이(h)의 1/1,000를 초기변형으로 입력하여 좌굴해석을 수행하였다. 면외방향으로 발생한 1차 좌굴모드형상을 초기 불완전성으로 고려하였다. 1차로 탄성좌굴해석(buckling analysis)을 수행하여 전체 좌굴모드와 국부좌굴모드를 확인하고, 이를 통해 얻어진 고유치(eigenvalue)를 이용하여 비선형 준정적 2차해석을 수행하였다.

강판의 좌굴과 하중이 제하(unloading) 후 가력방향이 바뀌어 재하(reloading) 시에 발생하는 snap-through를 고려하기 위해 외연적 적분법(explicit integration method)을 활용하여 준정적해석(quasi-static analysis)을 적용하였다.

2.3 재료모델

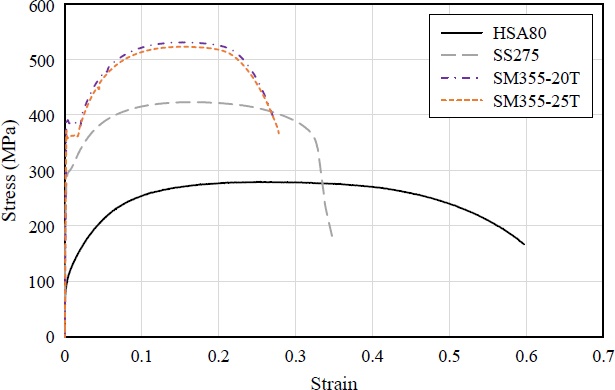
해석모델에 사용된 강종의 재료 데이터는 기존 연구자 Shin and Kim^[12]의 재료시험결과를 참조하였다. 강판전단벽 강판은 저항복강(HSA80)과 일반구조용 압연강재(SS275)를, 기둥과 보는 SM355를 적용하였고, 적용강판의 항복강도 및 인장강도를 Table 2에 정리하였다. 또한 미세스 항복조건 및 등방경화법칙이 적용되는 탄소성 재료모델을 채택하였다. 인장시험결과로부터 얻어진 Fig. 6와 같이 강재의 공칭응력-공칭변형률 선도(nominal stress-strain curve: σ_n – ε_n)를 식 (1)과 식 (2)를 이용하여 인장시편의 단면적 변화가 고려된 진응력-진변형률 곡선(true stress-true strain curve: σ_t – ε_t)으로 변환하고, 탄성영역 이후의 소성영역 거동은 식 (3)에 따라 전체 변형률(ε_e)에서 탄성변형률(σ_e/E)을 공제한 소성변형률(ε_p)을 입력하였다.

Table 2.

Mechanical properties of materials

Fig. 6.

Nominal stress-strain curve

여기서, σ_t는 진응력, σ_e는 공칭응력, ε_e는 공칭변형률, ε_t는 진변형률, E는 탄성계수이다.

강재에 대한 비탄성 해석을 수행하기 위해서 등방경화(isotropic hardening)모델을 사용하였다.

3.1 하중-변위 관계

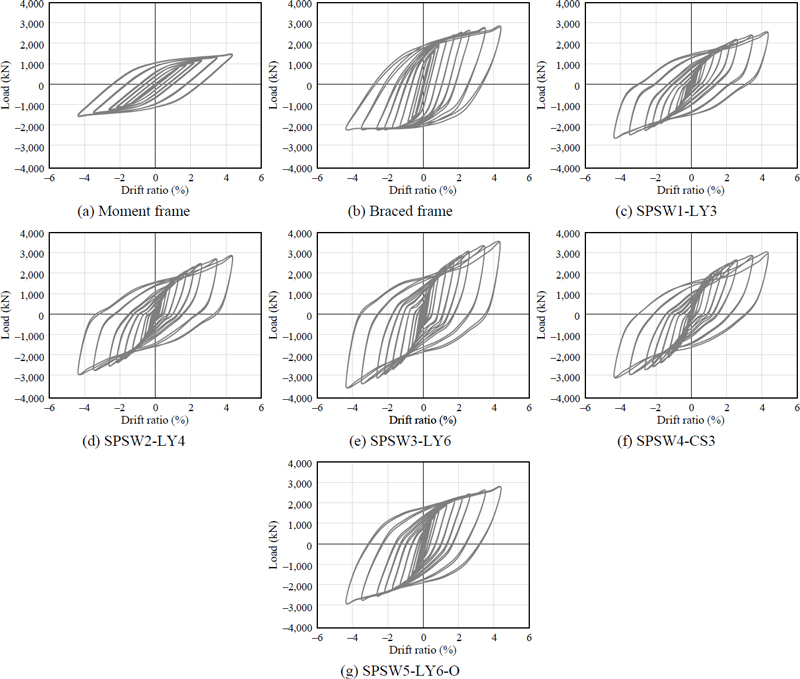
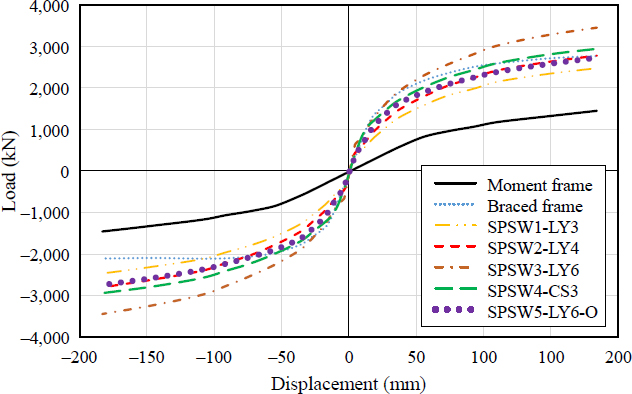
해석결과로부터 얻은 각 실험체의 하중-횡변위(drift ratio) 관계를 Fig. 7에 나타냈다. 각 해석모델별 최대내력($$ {\mathit{P}}_{ua}^{+}$$, $$ {\mathit{P}}_{ua}^{-}$$)과 초기강성($$ {\mathit{K}}_1^{+}$$, $$ {\mathit{K}}_1^{-}$$)은 Table 3에 정리하였다. 강판전단벽을 포함하는 SPSW1-LY3, SPSW2-LY4, SPSW3-LY6, SPSW4-CS3, SPSW5-LY6-O는 Fig. 9에나타난 바와 같이 강판 부분은 대각선 방향으로 명료한 인장응력장(tension field)이 형성되었다. 강판전단벽골조(SPSW series)는 모멘트저항골조(MF)에 비해 동일변위 기준 최대내력과 초기강성이 높게 나타났고, 가새골조(BF) 실험체의 ‘+’ 최대강도 및 초기강성에 비해 강판전단벽골조가 유사하거나 높은 성능을 확보하는 것으로 확인되었다.

Fig. 7.

Load-drift ratio curve of specimens

Table 3.

Analysis results

최대강도와 초기강성을 골조별로 비교하기 위해 모멘트골조(MF)를 기준으로 최대내력비(P_ua/P_ua,MF) 및 초기강성비($$ {\mathit{K}}_1^{+}/{\mathit{K}}_{1,MF}^{+}$$)를 산정하였다. 저항복강 6 mm 강판전단벽인 SPSW3-LY6이 최대강도 및 초기강도가 가장 높게 나타났고, 모멘트골조(MF)를 기준으로 최대강도비는 1.43–2.32, 초기강성비는 5.16–10.27 범위로 나타났다. 가새골조(BF)는 Fig. 1(c)와 같이 한 방향으로만 가새가 설치되어 ‘+’ 가력 시 가새는 인장력이, ‘–’ 가력 시에는 압축력이 작용하였다. 압축력이 작용하는 경우 좌굴이 발생하여 Table 3에서 알 수 있듯이 ‘–’ 가력의 최대강도와 초기강성이 ‘+’ 가력보다 낮았다.

SPSW1-LY3, SPSW2-LY4, SPSW5-LY6-O와 가새골조(BF)의 ‘+’ 영역에서의 최대강도는 유사하게 나타났다. 탄소강 3 mm 강판전단벽 SPSW4-CS3 해석모델의 최대강도는 저항복강 4 mm SPSW2-LY4에 비해 최대내력이 약 6 % 높게 나타났지만, Table 2에서 탄소강 SS275의 항복강도는 HSA80보다 3.05배 높은 것에 비해 면외좌굴 발생에 따라 내력상승 정도는 높지 않은 것을 알 수 있다. 이 결과로부터 가새골조(BF)에서는 가새설치로 마감을 고려해 총 벽두께가 강판전단벽에 비해 증가하며 탄소강 3 mm 강판전단벽골조와 저항복강 4 mm 강판전단벽 골조로 가새골조 이상의 골조의 수평전단강도와 초기강성을 확보할 수 있음을 확인하였다.

3.2 파괴양상

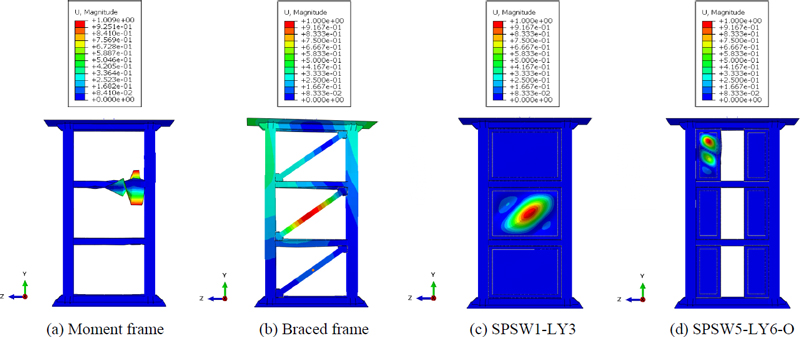
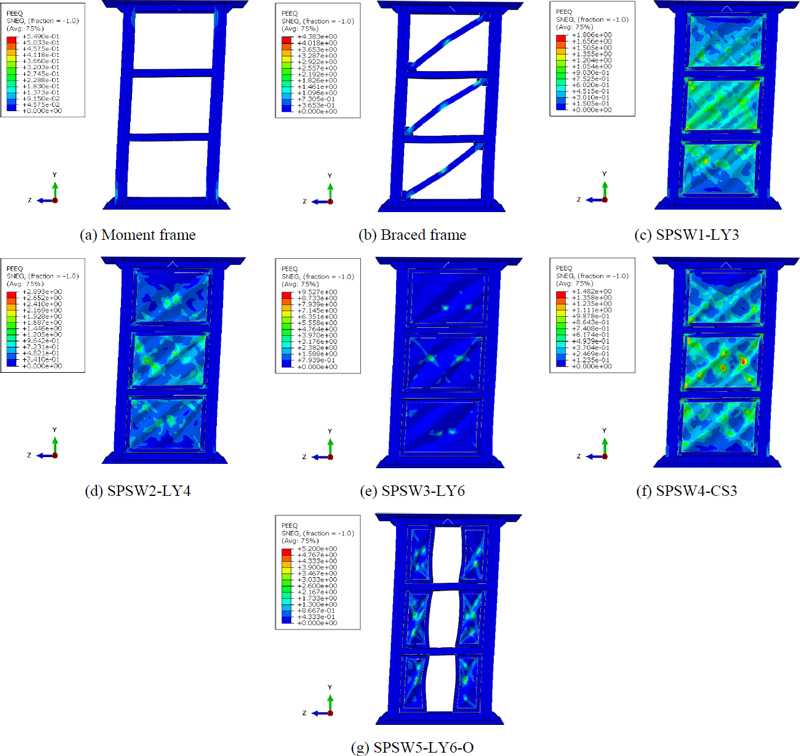
해석모델에 대한 고유치 해석을 통해 얻은 1차 좌굴모드 형상을 Fig. 8에 나타냈다. 해석결과로 얻어지는 등가소성변형률(equivalent plastic strain, PEEQ)은 재료의 비탄성변형분포로부터 파단 및 손상 가능 위치를 확일할 수 있는 스칼라 변수이다.

Fig. 8.

Buckling modes of specimens by Eigenvalue analysis

Fig. 9에 최대내력 시점에서 각 해석모델의 등가소성변형률 분포를 나타내었다. Fig. 9(a) 및 Fig. 9(b)와 같이 모멘트골조(MF)의 PEEQ는 주로 기둥의 하단부와 상단부에 집중분포하였으며 가새골조(BF)의 PEEQ는 주로 가새 중앙부에 분포하였다. Fig. 9(c), Fig. 9(e), Fig. 9(f)에서 SPSW2-LY4, SPSW4-CS3, SPSW5-LY6-​O의 주요 PEEQ는 강판전단벽과 피쉬플레이트(fish plate)에 집중되었다. 반면에 SPSW1-LY3와 SPSW3-​LY6는 Fig. 9(d)에서와 같이 PEEQ는 강판전단벽에만 집중분포하는 것으로 나타났다.

Fig. 9.

PEEQ distributions at ultimate state

3.3 포락곡선

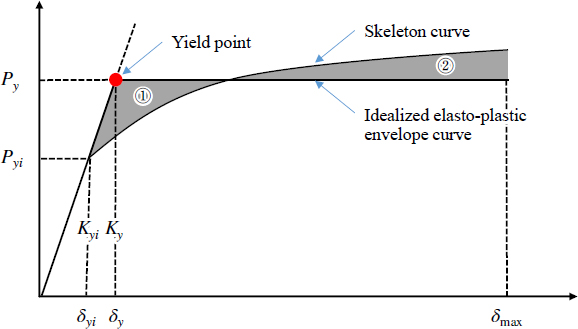
Fig. 7에서 각 하중단계의 첫 번째 사이클 동안의 최대강도를 연결하여 포락곡선(skeleton curve)을 구하였다. Fig. 10에서는 각 실험체의 포락곡선을 비교하였다. 각 해석모델의 곡선에서 뚜렷한 항복점이 관찰되지 않았으며, 항복 이후 소성영역에서 변위가 증가함에 따라 강성이 감소하였고, 골조형태에 따라 감소 정도가 상이했다^[13]. 항복점에서의 항복변위와 항복내력(δ_ya, P_ya)은 Fig. 11과 같이 각 실험체의 포락곡선으로 둘러싸인 부분의 면적 ①과 이상화된 탄소성곡선으로 둘러싸인 부분의 면적 ②가 동일하도록 등가에너지 방법으로 정의하였다^[8],[13] .

Fig. 10.

Skeleton curve of the specimens

Fig. 11.

Definition of yield point

각 해석모델의 항복내력(P_ya), 항복변위(δ_ya), 항복내력에 대한 최대내력의 강도비(P_ua/P_ya) 및 연성비(δ_max/δ_ya)를 Table 4에 정리하였다.

Table 4.

Energy dissipation comparison

강판전단벽골조(SPSW series)는 전반적으로 가새골조 및 모멘트저항골조보다 높은 항복내력을 나타냈다. 저항복강 6 mm 강판전단벽 골조인 SPSW3-LY6가 4.1절의 Table 3에서 언급한 바와 같이 내력과 강성이 가장 높았다. 이 연구의 기준모델이 되는 저항복강 4 mm 강판전단벽인 SPSW2-LY4는 SPSW3-LY6보다 정방향 항복내력은 25 % 낮았지만, 탄소강 3 mm 강판전단벽 SPSW4-CS3에 비해 정방향 항복내력이 12 % 증가하였다. 3.0 mm로 두께가 동일한 저항복강 강판전단벽인 SPSW1-LY3는 SPSW4-CS3보다 정방향 항복내력은 16 % 낮았다. 중앙부 개구부를 갖는 SPSW5-​LY6-O는 강판전단벽의 중앙에 전체 폭의 1/3의 개구부가 있음에도 불구하고 SPSW2-LY4보다 약 3 % 항복내력이 증가했고 SPSW3-LY6에 비하여 항복내력이 약 18 % 감소하였다.

3.4 에너지소산능력

에너지소산능력(energy dissipation capacity)은 내진성능 평가에 사용할 수 있다. 누적에너지소산능력(cumulative energy dissipation, CED)은 동일 목표 변위비(drift ratio)에 대해 Fig. 7의 사이클별 이력곡선에 둘러싸인 면적을 누적 합산한 에너지소산능력으로 정의된다^{[5],[6],[14],[17]}. Fig. 12는 각 해석모델의 전체 변위비와 누적에너지소산능력의 관계곡선이다.

Fig. 12.

Comparison of energy dissipation capacity

Table 4에 각 실험체별 누적에너지흡수능력(CED)과 모멘트골조(MF)를 기준으로 한 에너지소산능력(CED/​CED_MF)을 비교하였다. 모멘트 골조에 비해 가새골조 및 강판전단벽 골조는 2.19~3.09배 높은 누적에너지흡수능력을 보였다. 가새골조와 개구부가 있는 SPSW3-​LY6가 Table 3에 나타난 바와 같이 최대강도와 초기강성이 가장 높았기 때문에 누적에너지흡수능력도 다른 실험체에 비해 가장 높았다. 가새골조와 강판전단벽에 중앙 개구부를 갖는 SPSW5-LY6-O는 최대강도와 초기강성은 개구부가 없는 강판전단벽골조(SPSW2-LY4와 SPSW4-CS3)보다 낮았지만, SPSW1-LY3보다 높았고, 누적에너지흡수능력은 높은 것으로 확인되었다. 이는 Fig. 7에 나타난 바와 같이 가새골조와 SPSW5-​LY6-O는 각 사이클에서 항복 이후 2차 강성이 높은 것을 확인할 수 있다. 또한, 개구부가 없고 6 mm보다 얇은 강판전단벽골조(SPSW1-LY3과 SPSW2-LY4와 SPSW4-CS3)는 항복 이후 강판전단벽 내부에서 면외변형이 발생하여 최대변위비 도달 전까지 강성저하 및 일시적인 내력저하가 발생하여 누적에너지흡수능력이 낮게 나타난 것으로 판단된다.

3.5 강성저하(stiffness degradation)

골조해석모델이 탄성소성 단계로 들어간 후 변위가 증가함에 따라 강성이 점차 저하되며, 이러한 강성저하 특성은 구조의 누적손상을 반영한다. 해석모델의 2차 강성은 할선강성(secant stiffness) K_si로 나타낼 수 있다. 할선강성 K_si는 다음 식 (4)를 이용하여 산정한다^[15],[16].

여기서, K_si는 할선강성(2차강성), +P_i는 i사이클 정방향의 최대하중, –P_i는 i사이클 부방향의 최대하중, +δ_i는 i사이클 정방향의 최대변위, –δ_i는 i사이클 부방향의 최대변위이다.

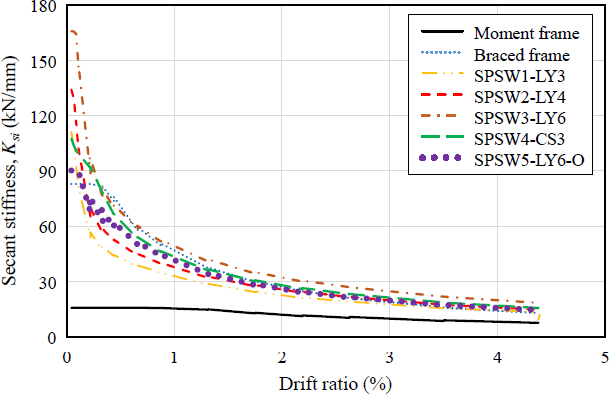
Fig. 13은 각 골조의 해석결과로부터 추출된 할선강성과 횡변위(drift ratio)와의 관계를 나타낸다. 가새골조 및 강판전단벽 골조의 해석모델은 전체 횡변위가 증가함에 따라 2차강성인 할선강성은 점차 감소하였으며, 초기에는 할선강성의 감소 정도가 급속하게 나타났고 횡변위가 1 % 이후에는 강성저하 정도가 완만하게 나타났다. 모멘트골조의 경우는 별도의 횡력저항 시스템이 없어 가력 초기부터 강성이 낮았고 강판전단벽이 6 mm로 가장 두꺼운 SPSW3-LY6가 할선강성이 전 구간에 대해 높았다. 가새골조는 초기에는 할선강성이 낮았지만 횡변위가 증가함에 따라 SPSW3-LY6를 제외한 강판전단벽 골조보다 할선강성이 높았고. 4.4절에서 언급한 바와 같이 항복 이후 누적손상이 작어 누적에너지흡수능력이 큰 것으로 판단된다.

Fig. 13.

Stiffness degradation curves of specimens