중공코어를 갖는 프리스트레스트 콘크리트 매입 강합성보의 휨거동
Copyright © 2023 by Korean Society of Steel Construction
초록
이 연구에서는 중공부를 갖는 프리스트레스트 매입형 합성보(PSC보)의 휨거동을 조사하였다. PSC보는 기존 PC보 내부에 각형강관 및 H형강이 매입되어 있는 형태로 웨브 중공부로 무게가 줄고, 강연선 긴장을 통해 균열 저항성을 키울 수 있다. 6개의 실스케일 휨실험체를 제작하였으며 CIP 콘크리트 슬래브 유·무에 따른 휨거동을 함께 분석하였다. 실험 결과 초기 긴장력 도입에 따른 철근 및 강재의 변형률 분포는 기존 PSC설계 이론과 잘 일치하였으며 모든 실험체는 압축측 콘크리트의 압괴와 함께 파괴되었다. PSC합성보의 강성 및 강도는 AISC 360-16에 따른 유효강성 및 소성모멘트와 잘 일치하였다. PSC보와 CIP 콘크리트 슬래브 사이 미끌림은 매입 수직 스터럽과 강재 용접 스터드를 통한 합성작용으로 나타나지 않았다.
Abstract
This study investigated the flexural behavior of prestressed concrete-encased steel composite beams (PSC composite beam) with hollow core. The PSC composite section consisted of the precast composite element, made of a steel section (H or box section) and U-shaped concrete encasement, and the cast-in-place concrete slab. By prestressing strands at the bottom of the precast element, the cracking resistance was enhanced. In addition, a void was formed in the web to reduce the beam weight. Six full-scale PSC composite beams were tested under positive bending and their flexural behaviors before and after casting the cast-in-place slab were investigated. The test results have shown that the initial strains of the steel section and reinforcing bars that occurred at the prestressing stage agreed well with the predictions by the existing PSC design theory. During the subsequent flexural testing, all beams were failed by concrete crushing at the compression end or slab. The stiffness and strength of the PSC composite beams agreed well with the effective stiffness and plastic moment strength for encased composite members, respectively, calculated in accordance with AISC 360-16. At the interface across the cast-in-place slab, relative slip did not occur and the interface shear resistance was contributed by both the vertical stirrups of the precast concrete encasement and headed studs of the steel element engaged or embedded within the slab.
Keywords:
Composite beam, Flexural behavior, Encased composite member, Prestressed concrete, Precast construction키워드:
합성보, 휨거동, 매입형 합성부재, 프리스트레스트 콘크리트, 프리캐스트 시공1. 서 론
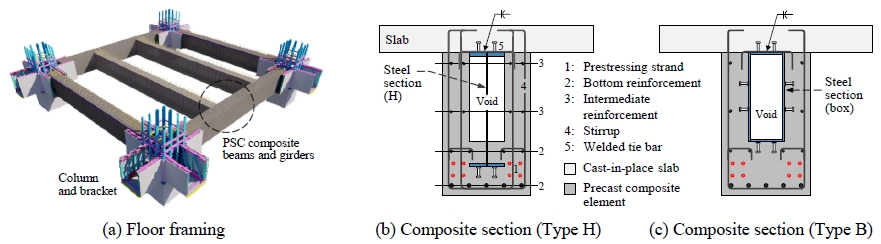
강구조 건물에는 Fig. 1(a)와 같이 콘크리트 슬래브를 H형강으로 지지하는 노출형 합성보가 널리 사용되어 왔다[1]–[3]. Fig. 1(b) 및 Fig. 1(c)처럼 강재보를 콘크리트로 감싼 매입형 합성공법이 일부 사용되지만 그 적용 사례는 많지 않다. 최근에는 시공성 및 구조성능을 개선한 대안공법으로 Fig. 1(d)와 같이 U단면 강합성보로 대체한 충전형 합성보가 오히려 더 많이 사용된다[4]–[6]. 이들 노출형 및 충전형 합성보에서는 주보강재인 강재가 외부에 노출되므로 내화피복이 필요하다. 내화비용 측면에서는 Fig. 1(c)와 같이 강재를 철근콘크리트로 완전히 감싸 내화피복이 불필요한 매입형 합성보가 유리하다. 하지만, 동일한 강재량이 사용된 충전형 합성보와 비교하여 매입형 합성보는 주보강재로 사용되는 강재단면이 단면 내부에 존재하므로 휨균열에 취약하고 휨성능(강도 및 강성)이 상대적으로 작을 수 있다.
이 연구에서는 기존 매입형 합성보의 단점을 극복하기 위하여 강재단면을 감싸는 콘크리트에 긴장력을 가한 프리스트레스트 콘크리트 매입 강합성보(prestressed concrete-encased steel composite beam, 이하 PSC합성보)를 개발하였다. Fig. 2에서 보듯이, PSC합성보 단면은 공장에서 사전제작되는 프리캐스트요소(precast composite element)와 현장에서 시공되는 현장타설요소(cast-in-place slab)로 구성된다. 프리캐스트요소는 H형 또는 박스형 강재단면을 U단면 콘크리트로 둘러싼 형태의 합성단면으로 제작되며, 강재와 콘크리트 사이 접합면에 스터드 전단연결재가 설치된다. PSC합성보는 다음 특징을 갖는다(Fig. 2(b) 및 Fig. 2(c) 참조) 첫째, 단면 하부에 배치되는 강선(prestressing strand) 긴장을 통해 균열·처짐에 대한 사용성능을 높인다. 둘째, 내부 강재는 PSC합성보의 휨성능 및 전단성능에 모두 기여한다. 셋째, 단면 내부에 중공을 두어 자중을 줄인다.
프리스트레스트 콘크리트와 강재가 합성된 매입형 합성보에 대한 대표적인 연구는 다음과 같다. Yao et al.[7]은 고강도 콘크리트를 사용한 PSC합성보의 전단성능을 연구하였다. 일반 PSC보와 비교하여, 콘크리트 내부에 강재단면이 매입된 PSC합성보는 우수한 잔류전단강도 및 연성을 보였고, 균열 이후 강성 또한 더 컸다. Weng et al.[8]은 매입형 합성보에서 H형강 플랜지와 콘크리트 접합면을 따라 발생하는 수평균열파괴를 연구하였다. 접합면의 수평전단강도는 콘크리트 내부 스터럽과 플랜지에 용접된 스터드에 의해 지지되었으며, 이 중 스터럽에 의한 전단강도 예측을 위해 전단마찰이론이 사용되었다. Kim et al.[9]은 파형강판웨브를 갖는 PSC합성보의 휨성능을 연구하였다. 프리스트레싱에 의해 PSC합성보의 강성 및 강도는 각각 20 % 및 25 % 증가하였고, PSC합성보의 휨성능은 일반 PSC보의 설계이론을 사용하여 평가되었다. 플랜지에 스터드가 설치되지 않았으며, 그 결과 PSC합성보는 슬래브 접합면에서 수평전단파괴를 보였다. Ayyub et al.[10],[11]은 콘크리트 슬래브가 있는 강재보의 하부에 강선을 설치하여 긴장력을 가한 외부 긴장 합성보의 휨거동을 연구하였다. 정방향 및 부방향 휨에 대한 보실험을 통해 프리스트레싱에 의한 합성보의 휨성능 향상 효과가 확인되었고, 이를 위한 해석방법이 제안되었다.
이 연구에서는 Fig. 2와 같이 중공코어를 갖는 PSC합성보의 구조성능을 평가하였다. 실험을 통해 긴장단계 및 합성단계에서 PSC합성보의 휨거동과 파괴모드를 조사하였다. PSC합보의 긴장단계 거동은 일반 PSC보 설계이론에 따라 분석되었으며, PSC합성보의 유효강성, 휨강도 및 슬래브 접합면 수평전단강도는 AISC 360-16의 설계규정에 따라 평가되었으며, PSC합성보의 설계방법이 검토되었다.
2. 실험계획
2.1 실험체 상세
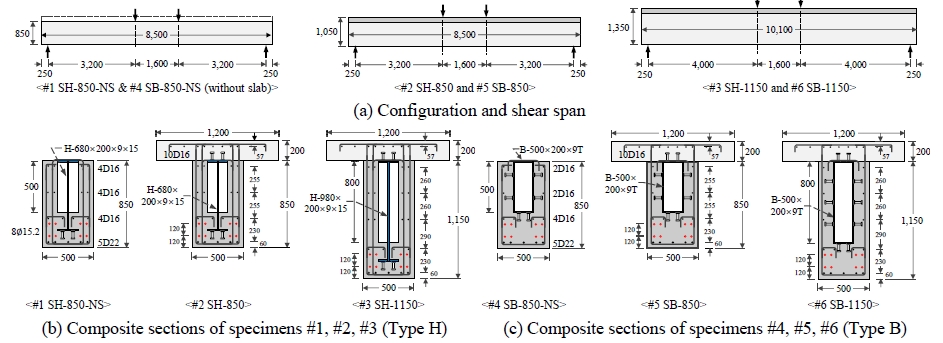
Fig. 3 및 Table 1은 PSC합성보 실험체 6개의 치수, 단면형상 및 주요 실험변수를 보여준다. #1 SH-850-NS, #2 SH-850, #3 SH-1150은 H형강을 강재단면으로 사용한 Type H 실험체이고, #4 SB-850-NS, #5 SB-850, #6 SB-1150은 각형강관을 강재단면으로 사용한 Type B 실험체이다. 실험체명에서 #1–#6은 일련번호, SH 및 SB는 각각 Type H 및 Type B, 850 및 1150은 각각 합성보 춤 850 mm 및 1,150 mm, NS는 슬래브가 사용되지 않았음을 가리킨다. Table 1에서 PSC합성보의 구조상세는 프리캐스트 부분과 현장타설 부분으로 구분된다. 다만, 실험체 #1 및 #4는 슬래브 없이 프리캐스트 부분만으로 제작되었다. 콘크리트 내부에는 ∅19 강선(단면적 138.7 mm2)과 D22(단면적 387 mm2), D16(단면적 198 mm2), D13(단면적 127 mm2) 철근이 보강재로 사용되었다. 실험체별 구조상세 및 보강재 종류는 Figs. 2–3와 Table 2를 참고한다.
강재단면과 콘크리트 사이 접합면에는 ∅19 스터드 앵커를 H형강 플랜지 및 각형강관 표면에 용접하였다. 실험체 #2 및 #3에는 H형강 상부 및 하부 플랜지 표면에 스터드 앵커 2∅19가 130 mm 간격으로 설치되었다. 실험체 #4 및 #5에는 슬래브 접합면에 위치하는 각형강관 상부 플랜지 표면에 대하여 스터드 앵커가 2∅19@110 mm으로 설치되었고 그 외 각형강관 하부 플랜지 및 웨브 표면에는 스터드 앵커가 3∅19@300 mm 간격으로 설치되었다.
2.2 제작 및 재료강도
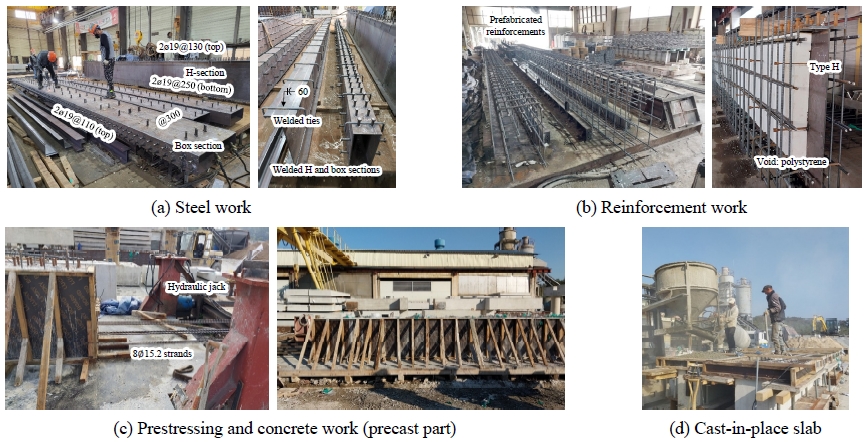
Fig. 4는 실험체 제작과정을 보여준다. 강판을 재단/용접하여 H형강 및 각형강관을 제작하였으며, H형강은 웨브와 플랜지 간 양면 모살용접(용접치수 5 mm)으로, 각형강관은 개선용접(45°, 개선깊이 6 mm)으로 제작하였다. 강재 표면에는 스터드 앵커를 설치하였다(Fig. 4(a) 참조). 강재단면의 상부 플랜지에 용접타이(D13@400)를 설치하고, 이후 종방향 및 횡방향 선조립 철근케이지와 강재단면을 조립하였다(Fig. 4(b) 참조). 그 다음 거푸집을 설치하고 긴장용 강선인 ∅15.2 강선 8개를 하부에 직선으로 배치하였으며, Fig. 4(c)와 같이 유압장비를 사용하여 강선을 긴장하였다(잭킹응력 0.8fpu 및 fpu = 1,860 MPa). 이후 콘크리트를 타설하고 24시간 동안 증기양생을 하였고, 그 다음 유압잭을 풀어 합성단면에 초기응력을 도입하였다. 실험체 #1 및 #4는 슬래브 없이 실험체 제작을 완료하였고, 반면 실험체 #2, #3, #5, #6의 경우 이후 상부에 현장타설 슬래브를 추가로 시공하였다(Fig. 4(e) 및 Fig. 4(f) 참조).
Table 3는 콘크리트·강재·철근의 재료강도를 보여준다. H형강 및 각형강관에 사용된 9T 및 15T 강판의 항복강도는 각각 Fy = 408 MPa 및 434 MPa였고, U단면의 휨철근으로 사용된 D16 및 D22 철근의 항복강도는 각각 fy = 463 MPa 및 458 MPa였다. U단면 스터럽 및 슬래브 횡철근으로 사용된 D13 철근의 항복강도는 fy = 472 MPa였으며, 전단연결재로 사용된 ∅19 스터드의 극한강도는 Fu = 484 MPa였다. 프리캐스트 및 현장타설 콘크리트의 압축강도는 각각 fck = 42.0 MPa 및 25.0 MPa(목표강도 40 MPa 및 21 MPa)였다.
2.3 재하 및 계측
휨실험은 Fig. 5와 같이 경간 중앙부를 수직으로 누르며 진행하였다. 실험에는 최대용량 5,000 kN 가력기를 사용했고, 가력속도는 0.05 mm/sec로 일정하게 유지했다. 경간 중앙의 두 가력점 사이 거리는 lm = 1,600 mm 였고, 가력점과 단부 지점 사이의 거리로 정의되는 전단경간은 ls = 3,200 mm 또는 4,000 mm였다. 보 하부의 수직처짐은 오른쪽 가력점으로부터 d = 800 mm 위치에 설치된 LVDT를 사용하여 계측하였다. 외부하중 P 및 수직처짐 δA, δB로부터 경간 중앙의 휨모멘트(M)와 평균 곡률(ϕ)은 다음과 같다.
| (1) |
| (2) |
| (3) |
식 (1)은 자중의 영향을 제외한 외부하중(P)만에 의한 경간 중앙의 모멘트이다. 실험체별 자중에 의한 초기모멘트 Mw는 Fig. 5를 참고한다. 식 (2)의 ϕAB는 수직처짐이 계측된 구간 AB에 발생하는 평균곡률이며, 균일한 곡률 분포를 가정한 값이다. 이와 달리, Fig. 5(b)과 같이 모멘트가 일정하지 않은 AB구간에서는 곡률 분포가 균일하지 않으며, 경간 중앙의 곡률(ϕ, 가력점 사이의 곡률)은 식 (2)에 의한 평균곡률 ϕAB보다 크다. 이를 보정하기 위해 식 (3)에 보정계수 1/(1 – 5d/[12ls])가 곱해진다. 이 보정계수는 항복 이전 선형탄성거동에 대하여 유효하다. 휨항복 이후 소성변형이 발생하는 경우에는 곡률 분포가 Fig. 5(b)의 모멘트 분포와 다르므로 식 (3)의 보정계수는 더 이상 유효하지 않다.
3. 실험결과
3.1 긴장에 의한 초기변형률 측정
강선 긴장에 의한 PSC합성보의 초기거동을 조사하기 위하여, H형강이 사용된 실험체 #2와 각형강관이 사용된 실험체 #4–실험체 #6에 대하여 긴장 직후 강재 및 철근의 변형률 변화를 계측하였다. Fig. 6는 실험체 #4 SB-850-NS에서 긴장 직후부터 약 160초 동안 계측된 결과를 보여준다. Fig. 6(a)는 부재 중앙으로부터 a–e 위치에서 U단면 하부 철근, 하부 플랜지 및 상부 플랜지로부터 계측된 변형률이며, Fig. 6(b)는 긴장 후 60초 시점에서 부재 중앙(line a)에서의 계측된 합성단면 높이에 걸친 변형률 분포이다. PSC합성보는 긴장에 의해 다음과 같은 초기 변형률 분포를 보였다.
- • Fig. 6(a)에서 각형강관의 상하 플랜지에는 긴장에 의해 부재 전체길이에 걸쳐 비교적 일정한 초기변형률이 발생하였다. 이와 달리, U단면 하부 철근의 초기변형률은 위치에 따라 그 크기가 변하였으며 보 단부에 가까울수록 변형률이 감소하였다. 이는 보 단부 정착구간에서 강선의 긴장응력이 손실되기 때문으로 판단된다.
- • Fig. 6(b)에서 긴장에 의한 합성단면 변형률 분포는 거의 선형을 나타냈다. U단면 하부철근 및 각형강관의 상부 플랜지에는 각각 압축변형률 240 με 및 인장변형률 50 με이 발생하였다. 상부 플랜지 주변에서는 인장변형률로 인해 코어강재와 접하는 콘크리트 내부 표면에 미세한 균열이 관찰되었다.
- • H형강이 사용된 실험체에서도 Fig. 6와 유사한 경향의 초기변형률이 계측되었다. U단면 하부철근의 압축변형률은 약 50 με 정도 더 작았고 상단의 인장변형률은 거의 동일하였다. 모든 실험체에서 강재코어와 접하는 콘크리트 내부에 미세한 표면균열이 발생하였다.
3.2 휨실험
휨실험에 의한 PSC합성보의 파괴모드를 Fig. 7에 나타냈다. Fig. 7은 실험체별 파괴모드로서, 경간 중앙에서 콘크리트 균열과 압축파괴를 중심으로 나타냈다. Fig. 7(a)에는 사진 3개를 이어붙여 실험체 #1 SH-850-NS의 파괴모드를 나타냈다. Fig. 7에서는 다음과 같은 균열양상 및 파괴모드가 확인되었다. 첫째, Fig. 7(a)에서 보듯이 경간 중앙부에서 휨균열(수직균열)이 지배적으로 발생하였고, 지점 주변에서는 경사균열이 발생하였다. 일부 실험체에서는 지점에서 45도 전단균열이 발생했지만 지배적인 파괴모드로 발전하지는 않았다(Fig. 7(b) 우측 참조) 둘째, 모든 실험체는 상부의 콘크리트 압축파괴에 의해 최종 파괴되었다. 슬래브가 없는 실험체 #1 및 #4에서는 강재단면을 감싸는 콘크리트 U단면의 좌우 측벽이 파괴되었고(Fig. 7(a) 및 Fig. 7(d) 참조), 현장타설 슬래브가 있는 나머지 실험체들은 모두 슬래브 콘크리트가 파괴되었다. 셋째, 실험체 #1을 제외하고 모든 PSC합성보에서는 최종파괴시까지 콘크리트와 코어강재 사이 분리 없이 온전한 합성거동을 보였다(Fig. 7(a) 우측 참조)
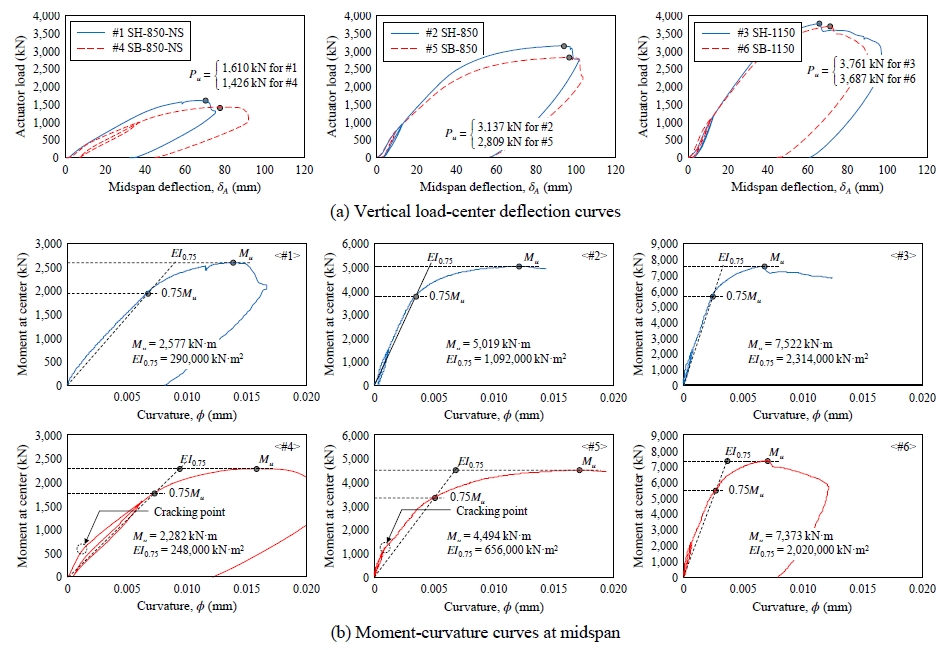
Fig. 8(a)는 액추에이터 하중(P)-중앙 처짐(δA, Fig. 5(b) 참조) 곡선을 보여주는데, 비교를 위하여 H형강이 사용된 Type H와 각형강관이 사용된 Type B 실험체의 실험결과를 동일 평면에 나타냈다. Fig. 8(b)는 식 (1) 및 식 (2)로부터 계산된 경간 중앙의 모멘트(M)-곡률(ϕ) 관계이며, 최대하중(Mu)과 유효강성(EI0.75)을 구하여 표시하였다. EI0.75는 원점과 최대하중의 75 %에 대응하는 점을 잇는 할선의 기울기로 구하였다.
Fig. 8(a)에서 Type H 및 Type B PSC합성보의 하중-변형 곡선 형태는 대체로 유사하였다. 항복 이전의 초기거동에서는 균열로 인한 강성 감소가 발생하였고, 항복 이후에는 변형경화거동을 보이며 최대하중에 도달하였다. 최종적으로는 슬래브에서 콘크리트 압축파괴가 발생하여 강도가 급격히 감소되었다. 전체적으로 Type H 실험체는 Type B 실험체보다 약간 더 큰 강성과 강도를 보였고, 슬래브가 없는 실험체 #1 및 #4 대비 현장타설 슬래브가 설치된 실험체 #2 및 #5에서 강성 및 강도가 약 2배 증가하였다.
Fig. 8(b)의 모멘트-곡률 관계에서는 구조상세에 따른 Type H 및 Type B 실험체의 거동 차이가 다음과 같이 보다 명확히 나타났다. 첫째, Type H 실험체 #1–#3에서는 초기 균열점이 뚜렷하지는 않았다. 이는 Fig. 2(b)에서 보듯이 H형강 하부 플랜지가 철근 및 강선과 함께 균열에 저항하기 때문으로 판단된다(Fig. 9(a) 변형률 참조). 둘째, Type B 실험체 #4–#6에서 균열점 및 이후 강성저하가 더 뚜렷하게 확인되었다. Type B의 경우 Fig. 2(c)에서 보듯이 위쪽에 위치한 강재단면이 U단면 콘크리트 바닥에서 시작되는 균열에 대하여 효과적으로 저항하기 어려우며, 그 결과 균열 이후 강성저하가 더 크게 나타난 것으로 판단된다.
Fig. 9은 경간 중앙에서 계측된 합성단면 깊이에 걸친 변형률 분포를 보여준다. 각 실험체마다 최대하중의 30 %, 60 %, 90 % 수준에서 발생한 변형률을 표시하였으며, 강재단면과 콘크리트 내부 철근으로부터 계측된 변형률을 각각 실선 및 점선으로 구분하였다. Fig. 9의 변형률은 사전긴장에 의한 초기변형률을 포함하지 않은 값이다.
모든 실험체에서 강재와 철근의 변형률 분포는 서로 유사하였으며, 전체 합성단면에 걸쳐 거의 선형의 변형률 분포를 보였다. 이는 강재코어와 U단면 콘크리트가 일체화된 합성거동을 하였음을 의미한다. 또한 Fig. 9 변형률 분포에 따른 중립축 위치는 강재단면의 중앙 높이(슬래브가 없는 실험체 #1 및 #4), 슬래브 접합면(실험체 #2 및 #5), 슬래브 접합면으로부터 약 250 mm 아래로 내려간 지점(실험체 #3 및 #6)이었다. 이러한 중립축 위치는 Fig. 7에서 관찰된 실제 콘크리트 파괴깊이와 대체로 일치하였다.
4. PSC합성보 거동 평가
4.1 긴장 단계 초기거동
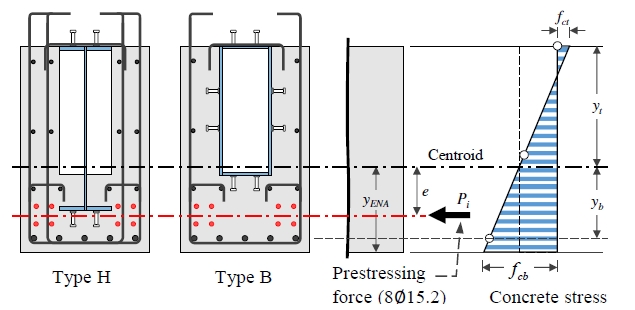
긴장에 의해 PSC합성보에 도입되는 콘크리트 초기응력(fci) 및 초기변형률(εci)은 다음과 같다(Fig. 10 참조).
| (4) |
| (5) |
| (6) |
여기서, Pi = 강선에 도입된 초기 긴장력, e = 합성단면 도심과 긴장력 중심 사이 편심거리, Agtr 및 Igtr = 강재, 철근의 영향을 포함한 비균열합성단면의 환산단면적 및 환산단면2차모멘트, y = 합성단면 도심으로부터 떨어진 거리, Eci = 콘크리트 초기탄성계수(= 1.18Ec)[12],[13], Ec = 콘크리트 탄성계수(= 4,700)[14], np = 긴장된 강선 개수, fpi = 강선의 초기응력, Ap = 강선 1가닥의 단면적, fpj = 강선의 잭킹응력(= 0.8fpu), fpu = 강선의 인장강도(= 1,860 MPa), ∆fpE = 탄성수축에 의한 긴장응력 즉시손실이다. 긴장 즉시 발생한 탄성수축에 의한 긴장력 손실 ∆fpE는 근사적으로 다음과 같이 구할 수 있다[13].
| (7) |
여기서, Ep = 강선 탄성계수(= 200,000 MPa), Ac = 합성단면의 콘크리트 면적, As = 합성단면의 강재 면적, r = 합성단면의 단면회전반경(= )이다. 식 (7)은 긴장 시 자중에 의한 휨모멘트가 없는 경우 사용할 수 있다.
식 (4)–식 (7)을 사용하여 계산한 각 실험체의 초기응력 및 초기변형률을 Table 4에 나타냈다(측정 재료강도 사용). 표에서 fct 및 εct는 단면 상단(즉, 상부 플랜지 표면)에서의 응력 및 변형률을 가리키며, fcb 및 εcb는 바닥철근(D22) 위치에서의 응력 및 변형률을 가리킨다. 압축응력 및 인장응력을 각각 + 및 – 부호로 표기하였다. Table 4에서 긴장에 의해 합성단면 상단 및 바닥철근에는 각각 –51 με– –74 με 및 +202 με– +245 με의 초기변형률이 발생하는 것으로 예측하였다(1 με = 10-6 mm/mm). 이러한 초기변형률은 Fig. 6(b)에 나타낸 실제 계측값과 잘 일치하였다. 이는 일반 PSC보 설계이론을 사용하여 PSC합성보의 긴장단계 초기거동을 합리적으로 예측할 수 있음을 보여준다.
4.2 휨강성 및 균열강도
AISC 360-16[1]에서 매입형 합성부재의 유효 휨강성은 다음과 같이 구할 수 있다.
| (8) |
| (9) |
여기서, Es = 강재 및 철근의 탄성계수(= 200,000 MPa), Ec = 콘크리트 탄성계수(= 4,700), Is = 합성단면의 탄성중립축에 대한 강재단면의 단면2차모멘트, Isr = 합성단면의 탄성중립축에 대한 철근의 단면2차모멘트, Isp = 합성단면의 탄성중립축에 대한 강선의 단면2차모멘트, Ic = 합성단면의 탄성중립축에 대한 콘크리트단면의 단면2차모멘트, As = 강재 단면적, Asr = 철근 단면적, Asp = 강선 단면적, Ag = 합성단면의 총단면적이다. 식 (8)에서 아래첨자 PC 및 CIP는 각각 프리캐스트 및 현장타설 콘크리트를 가리킨다. 식 (8)–식 (9)는 강선의 영향(Isp 및 Asp)을 고려하여 AISC 360-16의 식 (I2-6) 및 식 (I2-7)을 수정한 것이다.
식 (8)과 식 (9)로부터 계산된 PSC합성보의 유효강성을 Table 5에 나타냈다(측정 재료강도 사용). 표에서 EIeff 및 EI0.75는 각각 유효강성의 계산값 및 실험값을 가리킨다. 유효강성은 슬래브 유무에 따라 다음과 같은 차이를 보였다.
첫째, 슬래브가 없는 #1 SH-850-NS 및 #4 SB-850-NS에서는 EI0.75/EIeff가 각각 0.6 및 0.56으로 유효강성 계산값이 실험값보다 더 컸다. 그 이유는 다음과 같다. Table 5에서 보듯이 실험체 #1 및 #4에서 탄성중립축은 바닥 콘크리트 표면으로부터 각각 yENA = 389 mm 및 402 mm 높이에 위치하며 따라서 코어강재 대부분은 압축대에 존재한다. 이 경우 코어강재는 보 하단에서 발생하는 휨균열과 그로 인한 강성 저하를 효과적으로 억제하지 못한다.
둘째, 슬래브가 있는 실험체의 경우 유효강성 실험값(EI0.75)과 계산값(EIeff)이 잘 일치하였다(#5 SB-850 제외). 이는 슬래브가 합성된 이후 탄성중립축의 높이가 상부로 이동하여 H형강 또는 각형강관 하부 플랜지가 보 하부 인장대의 한가운데에 위치하게 되었기 때문이다. 이 경우 인장대에서 휨균열 이후 코어강재가 균열폭 증가를 효과적으로 억제할 수 있다. 이처럼 PSC합성보에서 균열 이후 강재코어에 의한 강성 향상 효과를 기대하기 위해서는 강재단면을 인장측의 강선 및 철근에 가능한 가깝게 배치해야 할 것으로 판단된다.
4.3 휨강도 및 슬래브 접합면 전단강도
PSC합성보의 휨강도는 AISC 360-16[1]의 소성응력분포법에 따라 계산하였다. 강도 산정에 사용한 가정은 다음과 같다(Fig. 11 참조).
- • 긴장력은 자기평형(self-equilibrium) 하중이므로, 강선 긴장이 극한강도에 미치는 영향은 통상 제한적이다. 따라서 PSC합성보의 휨강도는 일반 합성보에 사용하는 것과 동일한 소성응력분포를 적용한다.
- • 콘크리트 압축응력은 0.85로 가정하며, 인장응력은 무시한다. 프리캐스트 및 현장타설 콘크리트는 재료강도가 다르므로 각각 별도의 압축강도()를 적용한다.
- • 인장철근의 소성응력은 항복강도 fy를 적용한다. 슬래브 등 압축대에 배치된 철근의 압축응력은 무시한다.
- • 강재단면의 소성응력은 인장 및 압축에 대하여 모두 항복강도 Fy를 적용한다.
- • 인장대에 배치된 강선의 소성응력은 극한강도 fpu(= 1,860 MPa)를 적용한다.
소성응력분포법으로 계산한 이론 휨강도(Mn)와 실험 최대하중(Mu)을 Table 6에 나타냈다. 현장타설 슬래브가 시공된 실험체 #2, #3, #5, #6에서는 실험강도(Mu+Mw, 자중 모멘트 포함)가 이론강도(Mn)보다 약 12 %–18 % 정도 더 컸다. 이는 소성응력분포법이 PSC합성보의 휨강도 설계에 사용될 수 있음을 보여준다. 반면, 슬래브가 없는 실험체 #1 및 #4의 경우 실험강도(Mu+Mw)가 이론강도(Mn)보다 각각 7.7 % 및 2.7 % 더 작았다. 슬래브가 없는 실험체 #1 및 #2에서는 강재코어에 의해 콘크리트 압축대가 갈라져 폭이 150 mm로 얇아진다 (Fig. 8(a) 가운데 그래프 참조). 이 경우 콘크리트 소성압축응력 0.85에 도달하기 전에 압축연단에서 콘크리트 압괴가 일찍 발생할 수 있다. 그 결과 실험강도가 소성응력 이론강도보다 조금 작았던 것으로 판단된다.
현장타설 슬래브 접합면에서는 강재 플랜지에 용접된 스터드와 U단면 콘크리트에 매입된 스터럽에 의해 미끄럼이 방지된다. 스터드(강재앵커) 및 스터럽(전단마찰)은 접합면에 미끄럼변형이 발생하더라도 일정한 전단강도가 유지되는 연성전단연결재이다. 따라서 슬래브 접합면의 전수평전단강도는 스터드의 강재앵커강도와 스터럽의 전단마찰강도를 합산하여 다음과 같이 평가할 수 있다.
| (10) |
| (11) |
| (12) |
여기서, Ahs = 스터드의 몸체 단면적, = 스터드가 매입된 현장타설 슬래브의 콘크리트 압축강도, Fu = 스터드 앵커의 극한강도, μ = 콘크리트 표면처리상태에 따른 마찰계수(= 0.6), fyt = 스터럽 항복강도, Asb = 스터럽 1가닥의 단면적이다. 식 (10)에서 접합면의 수평전단강도(Vn)는 가력점과 가까운 지점 사이(즉, 전단경간 ls)에 배치된 모든 스터드와 스터럽의 기여를 합산하여 구한다.
실험체 #2, #3, #5 및 #6에 대하여 슬래브 접합면의 소요전단력(Vu)와 식 (10)–식 (11)로부터 계산되는 수평전단강도(Vn)를 Table 6에 나타냈다. 모든 실험체에서 소요전단력은 공칭강도(ΣQn+ΣVsf)의 55 %–67 % 수준이었고, 그 결과 슬래브 접합면에서는 육안상으로 상대슬립이 거의 없었다. 참고로, 모든 실험체에서 스터드 앵커만의 전단강도(ΣQn)가 슬래브 접합면의 소요전단력(Vu)보다 컸지만(1.07 ≤ ΣQn/Vu ≤ 1.58), 이것이 슬래브 접합면의 전단력이 스터드 앵커에 의해서만 전달되었음을 의미하지는 않는다. Fig. 8(b)의 실험체 #2 그래프에서 보듯이 U단면 콘크리트의 측벽에서 대각 전단균열이 발생하였는데, 이는 U단면 콘크리트에 매입된 스터럽 또한 슬래브 접합면에서 전단저항에 기여하였음을 보여주는 균열 양상이다.
5. 결 론
이 연구에서는 강재코어(H형강 또는 각형강관)를 사용한 PSC합성보의 정방향 휨거동을 조사하였다. 실험을 통해 초기거동, 강성 및 강도를 조사하고, 현행기준의 설계규정 적용 가능 여부를 조사하였다. 결론은 다음과 같다.
스터드 앵커에 의해 강재코어가 콘크리트 U단면 및 슬래브에 연결된 PSC합성보는 긴장단계 및 완전합성단계에서 모두 ‘완전합성’에 가까운 휨거동을 보였다. 실험에서 계측된 합성단면의 변형률 분포는 선형에 가까웠고, 탄성 휨이론에 근거하여 예측된 초기응력(변형률), 균열강도, 유효강성은 실험값과 잘 일치하였다. 프리스트레싱에 의한 초기거동은 일반 PSC보의 설계이론에 의한 예측에 부합하였고, 사용하중에 의한 균열강성과 극한하중에 의한 휨강도는 AISC 360-16에 제시된 매입형 합성보의 유효강성 및 소성휨강도와 잘 일치하였다. 콘크리트 내부에 강선에 가깝게 배치된 강재코어는 균열 이후 유효강성 향상에 기여하였으며, 또한 전체 합성단면 휨강도의 약 30 %를 강재코어가 기여하였다. H형강이 강재코어로 사용된 PSC합성보의 휨성능은 각형강관을 사용한 것보다 더 우수하였다.
프리스트레싱에 의한 PSC합성보의 초기거동은 강재코어 구조상세(형상, 면적, 배치 등)에 따라 다르고, 균열강도 및 유효강성은 크리프 등 장기변형의 영향을 받을 수 있다. 따라서 이에 대한 추가 연구가 필요하다.
Acknowledgments
이 연구는 삼성엔지니어링 및 한국연구재단 연구비지원(NRF-2022R1A2C1005211)에 의해 수행되었음.
References
- American Institute of Steel Construction (2016) Specification for Structural Steel Buildings (ANSI/AISC 360-16), USA.
- Architectural Institute of Korea (2016) Korean Building Code – Structural (KBC 2016), Korea (in Korean).
- European Committee for Standardization (2004) Eurocode 4: Design of Composite Steel and Concrete Structures, Part 1-1: General Rules and Rules for Building (EN 1994-1-1: 2004), Belgium.
- Turetta, M. (2019) Development of an Innovative U-Shaped Steel-Concrete Composite Beam Solution: Experimental and Numerical Studies on the Mechanical Behaviour, Ph.D. Dissertation, Universit de Lorraine; Universit du Luxembourg, France.
-
Liu, J., Zhao, Y., Chen, Y.F., Xu, S., and Yang, Y. (2018) Flexural Behavior of Rebar Truss Stiffened Cold-Formed U-Shaped Steel-Concrete Composite Beams, Journal of Constructional Steel Research, Elsevier, Vol.150, pp.175–185.
[https://doi.org/10.1016/j.jcsr.2018.08.011]

-
Eom, T.-S., and Lim, J.-J. (2022) Flexural Behavior of Noncompact and Slender Concrete-Filled U-Section Beams Under Negative Bending, Journal of Structural Engineering, American Society of Civil Engineers, Vol.148, No.10, 04022157.
[https://doi.org/10.1061/(ASCE)ST.1943-541X.0003468]

-
Yao, D., Jia, J., Wu, F., and Yu, F. (2014) Shear Performance of Prestressed Ultra High Strength Concrete Encased Steel Beams, Construction and Building Materials, Elsevier, Vol.52, pp.194–201.
[https://doi.org/10.1016/j.conbuildmat.2013.11.006]

-
Weng, C.C., Yen, S.I., and Jiang, M.H. (2002) Experimental Study on Shear Splitting Failure of Full-Scale Composite Concrete Encased Steel Beams, Journal of Structural Engineering, American Society of Civil Engineers, Vol.128, No.9, pp.1186–1194.
[https://doi.org/10.1061/(ASCE)0733-9445(2002)128:9(1186)]

-
Kim, K.S., Lee, D.H., Choi, S.M., Choi, Y.H., and Jung, S.H. (2011) Flexural Behavior of Prestressed Composite Beams with Corrugated Web: Part I. Development and Analysis, Composites Part B: Engineering, Elsevier, Vol.42, No.6, pp.1603–1616.
[https://doi.org/10.1016/j.compositesb.2011.04.020]

-
Ayyub, B.M., Sohn, Y.G., and Saadatmanesh, H. (1990) Prestressed Composite Girders Under Positive Moment, Journal of Structural Engineering, American Society of Civil Engineers, Vol.116, No.11, pp.2931–2951.
[https://doi.org/10.1061/(ASCE)0733-9445(1990)116:11(2931)]

-
Ayyub, B.M., Sohn, Y.G., and Saadatmanesh, H. (1992) Prestressed Composite Girders, I: Experimental Study for Negative Moment, Journal of Structural Engineering, American Society of Civil Engineers, Vol.118, No.10, pp.2743–2762.
[https://doi.org/10.1061/(ASCE)0733-9445(1992)118:10(2743)]

- Korea Concrete Institute (2012) Concrete Structure Design Code, Kimoondang, Korea (in Korean).
- Lee, J.H. (2015) Prestressed Concrete: Ultimate Strength Design and Limit State Design, Dongmyeong, Korea, p.858, (in Korean).
- American Concrete Institute (2019) Building Code Requirements for Structural Concrete and Commentary (ACI 318-19), USA.