성능설계법을 사용한 방탄문 설계 및 성능점검 프로세스

1. 서 론

현재 방탄문은 군부대, 경찰서, 구치소, 통신시설, 은행, 법원, 원자력발전소 등 많은 곳에 사용되고 있다. 방탄문 같은 특수문은 성능이 매우 중요하므로 수많은 연구와 실험 끝에 개발되어야 한다. 하지만 방탄문의 성능실험은 국방기술품질원에서 진행되며 환경적·경제적 제약 때문에 여러 번 실험하는 데 한계가 있다. 따라서 방탄문을 실증시험하는 방법 외에 전산구조해석을 활용하여 제품의 안전성을 평가하는 기술이 필요하다.

본 연구에서는 원자력발전소에서 사용하는 방탄문을 설계하고 품질을 점검한다. 이를 위하여 건축구조기준에서 제시하고 있는 성능시험법^[1]을 적용하여 방탄문을 설계하고 성능시험법의 요구사항인 제3자 검토에서 점검하는 설계검증항목을 검토하면서 방탄문 설계의 안정성을 평가하고자 한다. 이를 통해서 경제적이고 안전한 방탄문을 설계, 제작하고 품질을 확보할 수 있는 체계를 정립하고자 한다.

성능시험법에서 적용하는 제3자 검토의 검증사항 및 항목에는 KDS 41 17 00(건축물 내진설계기준 및 해설)에서 제시한 항목을 도입한다^[2]. 방탄문 설계 및 해석 과정에서 ① 성능목표 ② 성능설계전략 ③ 파괴 메커니즘 ④ 부재와 장치의 비탄성변형능력 및 관련 연성 상세 ⑤ 프로그램의 선택 ⑥ 비선형 해석방법 ⑦ 해석모델 ⑧ 경계조건 ⑨ 입력자료, 결과분석의 적절성 ⑩ 구조물 및 각 부재의 비탄성 거동의 적절성 ⑪ 강도, 변형능력, 초과강도 검증 ⑫ 안전성, 경제성의 검증 등을 적용하여 방탄문 설계의 타당성을 입증하고 이러한 점검과정을 방탄문 설계 프로세스로 제안하고자 한다.

2. 본 론

본론에서는 성능시험법의 검증항목에 따라 본 연구에서 제안하는 방탄문 설계과정의 적합성을 판단한다.

2.1 성능 목표

방탄문 제조업체에서 설계하여 원자력발전소에 납품하는 방탄문의 성능은 UL 752 Level 4를 만족해야 한다^[3]. Table 1에 나타낸 바와 같이 Level 4는 방탄문으로부터 4.6 m 떨어진 거리에서 총탄을 발사하여 총탄이 방탄문을 관통하지 않는 조건의 등급이다. UL 752는 각 level에 따라서 총탄의 질량, 속도, 충돌 에너지를 정의하고 있다.

Table 1.

US military bulletproof test standards

2.2 성능설계전략

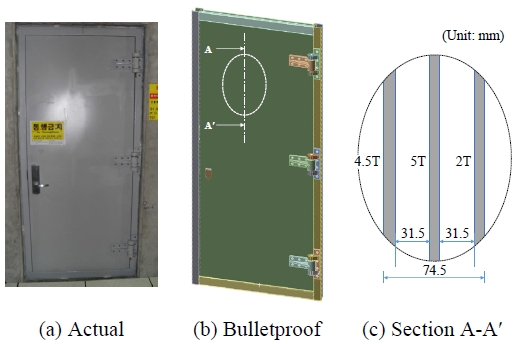
원자력발전소에서 사용하는 방탄문은 테두리 부분을 제외하면 높이 2,158 mm, 폭 911 mm, 깊이 74.5 mm의 3개의 강판으로 구성된다. 3개의 강판을 구조물에 결합시키고 3개의 경첩을 사용하여 방탄문이 개폐되도록 벽의 두께와 동일하게 방탄문의 테두리를 설계한다. 총탄의 관통을 방지하기 위해서 방탄문을 구성하는 강판의 두께와 개수를 여러 조합으로 설계할 수 있다. 강판의 두께는 방탄문의 안전성과 관련이 있고, 강판 사이의 간격은 방탄문의 사용성과 관련이 있다.

본 연구에서는 Fig. 1(c)와 같이 3개의 강판으로 방탄문을 구성할 것을 제안한다. 전면강판(skin plate)과 후면강판(cover plate)은 방탄문의 사용성 측면에서 방탄문의 외관을 담당한다. 전면강판의 두께를 후면강판의 두께보다 두껍게 하는 것이 일반적이다. 본 연구의 경우 전면강판의 두께는 4.5 mm로, 후면강판의 두께는 2 mm로 설계한다. 재질은 일반적으로 구조강을 적용하며 본 연구에서는 SS275를 사용한다.

Fig. 1.

Bulletproof door

방탄문의 중간에 설치하는 저항강판(resistant plate)은 방탄문의 안정성을 담당하는 강판으로 강판의 두께는 5 mm이고, 재질은 AR400를 사용한다. 특수 내마모 강판인 AR400은 저탄소 보론(B)을 함유한 합금강으로서 920 ˚C로 가열한 후 급랭시킨 열처리 강판이다. 강판 표면부와 내부의 경도가 균일하여 마모가 진행되더라도 초기의 경도 및 인성이 동일하여 내마모성이 크며, 다른 열처리 강판에 비하여 4~10배 이상의 내마모 성능을 보유한다. 강판 사이의 거리는 31.5 mm로 설계하는데 이것은 방탄문의 두께와 관련이 있을 뿐 안정성에는 영향을 주지 않고 있다.

2.3 방탄문의 파괴시험^[4]

방탄문의 실증시험은 방탄문 전체를 대상으로 시험하지 않고 방탄문을 구성하는 강판으로 시험편을 제작하여 수행한다. 시험편의 크기는 UL 752 Level 4에서 12×12 inch로 규정하고 있으며, 본 연구에서는 300×​300×74.5 mm의 시험판을 사용한다. 시험편의 강판은 방탄문과 같은 재질을 사용하고 강판을 고정하기 위하여 전면강판과 동일한 재질로 2개의 측면 보강재(reinforcement)를 사용한다.

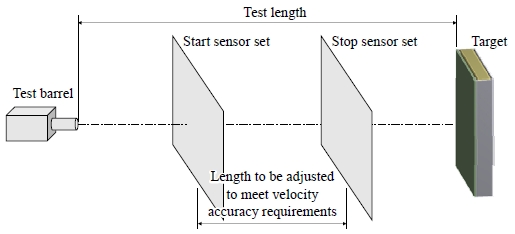
Fig. 2는 방탄 시험편에 대한 구성도로, Fig. 2(a)는 구조해석에 사용하는 모델링이고 Fig. 2(b)는 실증시험에 사용하는 시험편이다. 본 연구에서 방탄문의 실증시험은 육군사관학교 시험장에서 실시하였다. Fig. 3는 방탄문 실증시험 개념도로 시험편 고정대(target holder)와 총탄 발사대(test barrel) 사이 거리(test length)는 4.6 m이다. 총탄 발사대에서 총탄이 발사되면 두 개의 속도 감지기를 지나 총탄이 시험편에 충돌하게 된다. 이 과정에서 속도 감지기는 총탄의 속도를 계측한다.

Fig. 2.

Bulletproof test specimen

Fig. 3.

Experiment test schematic plan

UL 752 Level 4에서는 총탄의 속도를 774.19 m/s - 851.61 m/s, 충격에너지를 3,498 J - 4,929 J로 규정하고 있으나, 육군사관학교 시험장에서 발사되는 총탄의 속도는 935 m/s로 기준보다 빠르다. 시험편이 받는 충격에너지를 기준과 동일하게 맞추기 위하여 육군사관학교 시험장에서는 기준에서 제시하는 총탄의 무게보다 가벼운 9.6 g의 총탄을 사용한다. 방탄문 실증시험은 총탄 1발로 수행한다.

2.5 비선형 해석방법

동적하중을 받는 재료의 응답은 정적하중과 다르다. 방탄문에 작용하는 충격 하중은 매우 짧은 시간에 작용하므로 짧은 시간에 변형하는 재료의 응답특성을 고려해야 한다.

Fig. 4와 같이 총탄의 충격 하중은 10² s^–1 - 10⁴ s^–1 정도의 매우 높은 변형률 속도(strain rate)를 발생시킨다. 변형률 속도는 구조 재료의 기계적인 성질을 변화시키고 구조 요소의 파괴 거동에 영향을 준다.

Fig. 4.

Strain relation with various loads

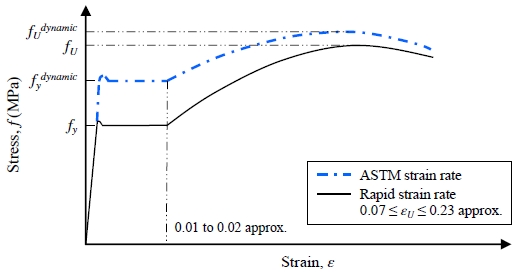
Fig. 5는 동적하중을 받는 부재의 강도증가 효과를 나타내고 있다. 높은 변형률 속도가 재료의 강도를 증가시키고, 동적 파괴에 대한 저항성을 증가시킨다^[5]. 변형률 속도를 고려하지 않으면 재료 강도를 과소평가하게 되므로 반드시 변형률 속도를 고려하여 구조해석의 정확성을 높여야 한다.

Fig. 5.

Stress-strain curves of steel under dynamic loading

Fig. 6는 5×10^-5 s^–1의 변형률 속도에서 온도가 다른 P92 강철 시험편의 응력-변형 곡선이다. 재료의 온도에 따라 동일 변형률에 대한 강도가 다름을 알 수 있다^[6].

Fig. 6.

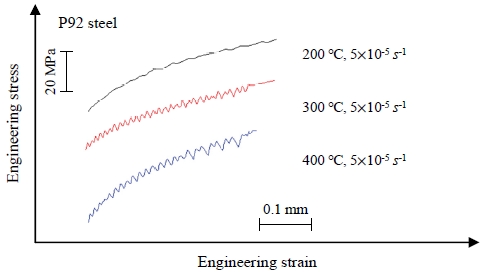
Segments of engineering stress-strain curves of P92 steel obtained from tensile tests at three different temperatures and the strain rate of 5×10−5 s−1.

본 연구의 전산구조해석에서는 방탄문을 구성하는 강판에 이중 선형 등방성 경도(bilinear isotropic hardness)를 적용하지 않고, 재료의 변형률 속도와 온도변화를 반영하는 응력과 변형률 관계를 적용한 재료 물성을 사용한다^[7],[8]. 동적구조해석 검증엔 Johnson-Cook strength를 적용하는 강판의 물성을 사용한다.

2.6 전산구조해석모델

2.6.1 탄환 모델링

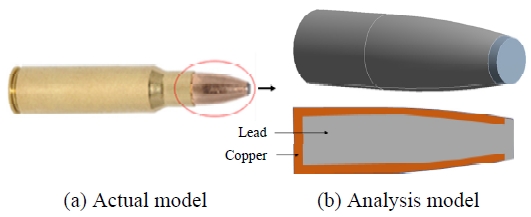
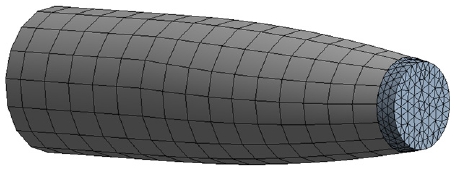
방탄문 실증시험에 사용하는 탄환은 Fig. 7과 같이 지름 7.85 mm로 모델링하였다. 탄피(bullet case)는 전산구조해석 시 필요하지 않으므로 탄두만 모델링하였다. Fig. 7(c)에서 보듯이 납(Pb)으로 된 탄자를 구리(Cu)가 감싸고 있는 형태로 탄두는 관통이 쉽게 뾰족하게 다듬어져 있다.

Fig. 7.

Bullet modeling

구리껍질은 총탄이 표적에 명중하면서 운동에너지가 급격히 감소하며, 총탄 내부의 무르고 밀도가 높은 납(Pb)이 관성에 의해 튀어 나간다. 30 caliber rifle lead bullet의 구조해석모델은 상용 CAD 프로그램인 솔리드웍스(Solidworks)로 3D 모델링하고 STP 파일형태로 변환하여 ANSYS workbench에서 동적구조해석모델 데이터로 사용한다. 총탄을 모델링한 결과를 검토하면, 실증시험에 사용한 총탄의 질량은 9.7 g인 반면 전산구조해석에서 사용한 총탄의 질량은 9.85 g으로 1.5 % 오차가 있다.

2.6.2 Target modeling

방탄문의 실증시험은 높이 300 mm, 폭 300 mm, 깊이 74.5 mm의 모형을 사용한다. 구조해석모델에는 Fig. 8과 같이 시험편을 구성하는 3개의 plate를 모델링하여 사용한다.

Fig. 8.

Analysis model of target

2.8 부재의 비탄성변형능력 및 관련 연성 상세

전산구조해석에서 방탄문을 구성하는 부재의 기본적인 재질 특성은 Table 2와 같다. 방탄문에 사용하는 재질은 강판을 구성하고 있는 SS275와 AR400과 총알을 구성하는 copper, lead로 구분할 수 있으며, 이 재료들은 비선형 물성치(bilinear isotropic hardness)를 사용하지 않고 Johnson-Cook strength를 적용한다.

Table 2.

Material properties

Johnson-Cook 모델은 재료의 변형률 속도와 온도를 반영하는 응력과 변형률에 관한 재료 물성을 식 (1)과 같이 정의한 것으로 동적구조해석에 적용한다^[9].

$\[ \sigma =\left(A+B{ϵ}^n\right)\left(1+C\ln {\dot{ϵ}}^{\mathrm{*}}\right)\left(1-T^{\mathrm{*}m}\right) \]$

(1)

여기서,

$\[ \begin{array}{l}{\dot{ϵ}}^{\mathrm{*}}=\dot{ϵ}/{\dot{ϵ}}_{ref}\hfill \\ T^{\mathrm{*}}=\left(T-T_{ref}\right)/\left(T_m-T_{ref}\right)\hfill \end{array} \]$

(2)

이며, $$ {\dot{ϵ}}^{\mathrm{*}}$$은 무차원 변형률 속도, $$ \dot{ϵ}$$은 변형률 속도(strain rate), $$ {\dot{ϵ}}_{ref}$$은 기준 변형률 속도(reference strain rate), T^*은 균질온도(homogeneous temperature), T는 변형온도, T_ref는 기준 변형온도(reference deformation temperature)이다.

식 (1)에 적용되는 방탄문 재료의 Johnson-​Cook 모델 재료 상수(A, B, C, n, m)를 Table 3에 제시하였다^[10],[11]. SS275와 lead의 파괴 모드는 Table 4와 같이 소성변형률 파손을 사용하고, AR400와 copper는 Table 5와 같이 Johnson-Cook failure를 사용한다.

Table 3.

Material properties of Johnson-Cook model

Table 4.

Material properties of plastic strain failure

Table 5.

Material properties of Johnson-Cook failure

2.9 전산구조해석 입력자료 및 결과분석의 적절성

2.9.1 구조물 간 접촉 정의

3개의 강판(plate)은 각각 독립되어 있어서 접촉에 대한 정의가 없고 측면 보강 대와는 완전결합(bonded)으로 설정하였다. 총탄이 방탄 시험편에 고속 충돌함으로써 마찰력에 대한 효과가 미세하므로, 부재 상호작용(body interaction)은 마찰 없음(frictionless)으로 설정하였다.

2.9.2 전산구조해석모델의 요소 크기 설정

전면강판의 메쉬(mesh) 크기는 1.5 mm로, 저항강판의 메시 크기는 Fig. 8(b)와 같이 1.6 mm로 설정하였다. 총탄이 강판과 충돌하는 영역은 Fig. 8(c)와 같이 구형 내부 요소 크기 조절방법을 사용하여 메쉬 크기를 1 mm로 정의하여 사면체 메쉬를 설정하였다. Fig. 9과 같이 총탄 구리 부분의 메쉬는 1.5 mm 크기의 육면체 형상으로 설정하고, 총탄 납부분의 메쉬는 0.5 mm 크기의 사면체 형상으로 설정하였다. 이와 같은 방법으로 전체 요소가 2,600개인 메쉬 모형을 설계하였다.

Fig. 9.

Analysis model of bullet

2.9.3 초기조건(initial condition) 정의

총탄 모델은 시험편의 전면강판에 접촉하도록 모델링하였다. 전산구조해석 조건으로 총탄의 초기속도를 방탄실증시험에서의 총탄속도와 동일한 935 m/s로 설정하였다.

2.9.4 전산구조해석 분석조건 설정

최소 종료시간(end time)은 총탄이 방탄 시험편을 뚫고 나갈 수 있는 시간으로 설정하였다. 총탄 길이와 방탄문 폭 길이를 합한 92.99 mm에 초기속도로 나누어서 산정한 1.0s^-4s를 총탄이 강판을 뚫는 시간으로 추정하여 최소 종료시간을 설정하였다. 본 연구에서 수행한 전산구조해석에서는 최소 종료시간에 2배의 여유시간을 두어 최소 종료시간을 2×10^-4s로 설정하였다.

해석모델의 전체 운동에너지(kinetic energy)가 0일 때 총알이 멈춘 것으로 판정하였다. 본 연구에서는 Automatic Mass Scaling을 Yes로 설정하고 Minimum CFL Time Step을 1×10^-4s로 설정하였다.

각 재료의 물성에서 소성변형률파손 값을 지정했기 때문에 On Geometric Strain Limit은 No로 설정하였다. 총알이 전면강판과 충돌하면서 파편이 발생할 수 있는데, 전면강판의 파편이 저항강판에 미치는 영향이 미미할 것으로 판단하여 Retain Inertia of Eroded Material은 No로 설정하였다. 따라서 강판이 파괴되어 날아간 파편에 관성을 주지 않는다. Step Control은 0.00075 sec으로 설정하였고, Output Control에서 Result Number of Points를 200으로 설정한다.

2.11 구조해석으로 산출된 강도, 변형능력, 초과강도 검증

2.3절의 실증시험결과와 2.4절 - 2.10절에서 기술한 구조해석 조건을 적용한 해석결과를 비교하여 안정성을 점검한다.

2.11.1 전체 운동에너지(kinetic energy)의 분석

Fig. 10은 전산구조해석 중에 발생한 운동에너지를 도시한 것이다. 해석에서 산정된 4,243 J의 운동에너지가 UL 752 Level 4에서 규정한 충격에너지인 3,498 J - 4,929 J에 해당하므로 전산구조해석의 입력조건은 타당하다고 할 수 있다.

Fig. 10.

Kinetic energy plot over time

2.11.2 시간의 변화에 따른 방탄문 저항 강도 분석

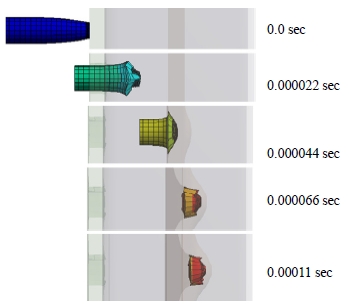
Fig. 11은 총탄과 강판의 전체 변형(total deformation)을 시간에 따라 도시한 것이다. 총탄이 1차 전면강판을 관통하고 2차 저항강판에 박히는 것을 시간에 따라서 관찰할 수 있다. 총알이 방탄문에 충돌하여 운동에너지가 완전 소멸할 때까지의 시간은 0.09661 msec로 해석된다.

Fig. 11.

Total deformation of bullet

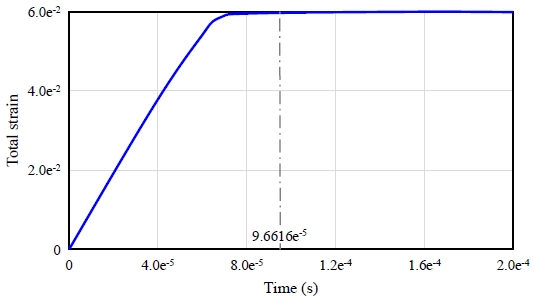
Fig. 12의 변형률 선도는 전체 구조물의 변형률 변화를 도시한 것인데, 0.09661 msec 이후 변형률의 변화가 없으므로 총탄 및 강판의 거동이 없는 것으로 해석한다.

Fig. 12.

Strain plot over time

2.11.3 전면강판의 파괴형상

Fig. 13은 전면강판의 파괴형상을 실증시험과 전산구조해석결과와 비교한 것이다. 전산구조해석에서 요소의 삼각형 한 변 길이는 1 mm이다. 총탄이 전면강판을 관통하면서 전면강판에 형성된 bur의 크기를 비교하면 전산구조해석에서는 1.14 mm로 산정되었고, 실증시험에서는 2 mm로 측정되었다. 이들 값의 차이를 비교하면 43 %의 오차가 발생한다. 전면강판의 관통 구멍 크기의 경우 구조해석에서는 9 mm로 산정되었고, 실증시험에서는 8.3 mm로 측정되어 7.8 %의 오차가 발생하였으며 따라서 구조해석결과와 실증시험의 결과가 근사한다.

Fig. 13.

Skin plate deformation

2.11.4 저항강판의 파괴형상

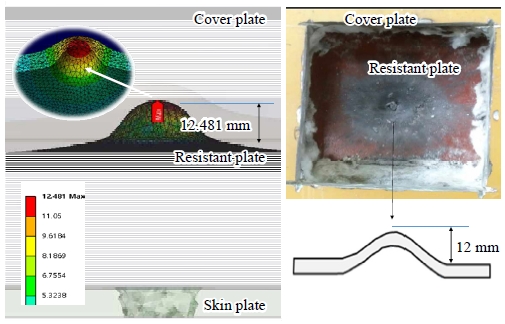
총탄이 전면강판을 관통한 후 저항강판에 충돌하여 Fig. 14와 같이 돔형으로 소성 변화한다. 돔 형상의 최댓값은 전산구조해석에서 12.48 mm로 산정되었고, 실증시험에서 12 mm로 측정되어 4 %의 오차가 발생하여 매우 근사한 결과를 얻었다.

Fig. 14.

Analysis model of plate

2.11.5 총탄의 파괴형상

Fig. 15은 총탄이 저항강판에 박힌 모습을 구조해석으로 산정한 변형 결과이다. 구조해석결과에서 변형된 총탄의 모습과 실증시험에서 총탄의 실제 모습을 비교한 것으로, 심하게 소성변형된 것을 관찰할 수 있다.

Fig. 15.

Analysis model of bullet

3. 결 론

원자력발전소에 사용되는 방탄문을 설계하고 검증하는 연구를 통하여 다음과 같은 결론을 얻었다.

• (1) 방탄문 설계 방법 및 성능점검 방법에 내진설계 구조기준에서 제시한 성능설계법의 제3자 성능점검 항목을 확대 적용할 수 있다.
• (2) 방판문 실증시험을 실시할 때 총탄발사대의 조건에 따라서 UL 752에 규정된 충돌에너지 수준을 맞추기 위해 총탄의 무게를 조정한다. 본 연구의 총탄속도가 935 m/s이므로 총탄의 무게를 규정된 11.7 g에서 9.6 g로 조정하여 시험을 수행하였다.
• (3) 전산구조해석 방법으로 상용소프트웨어 ANSYS Explicit Dynamics를 사용하여 구조해석한 결과는 UL 752 Level 4에서 규정한 충격에너지 조건을 만족한다.
• (4) ANSYS Explicit Dynamics를 사용하여 해석한 결과 중 전면강판과 저항강판의 변형은 실증시험한 방탄문의 파손 결과와 변형 형태가 일치하고, 변형 값도 일치한다. 전면강판의 총탄 관통지름은 7.8 %의 차이가 있고, 저항강판의 돌출량의 경우 4 %의 차이가 있다.
• (5) 방탄문의 전산구조해석에서 구조물의 거동을 정확히 해석하기 위해서는 재료의 고속 변형률 속도와 온도변화에 따른 재료거동을 묘사할 수 있는 모형을 사용하여 구조해석을 해야 한다. 본 연구에서는 Johnson-Cook 모델을 적용하였다.
• (6) 방탄문의 전산구조해석에서 구조물의 파괴모드를 정확히 해석하기 위해서는 소성변형률파손 모형이나 Johnson-Cook failure 모형을 사용해야 한다. 본 연구에서는 SS275와 lead에 소성변형률파손 모형을 사용하였고, AR400와 copper에 Johnson-Cook failure 모형을 사용하였다.
• (7) 두께가 4.5 mm인 SS275 강판과 두께가 5 mm인 AR400으로 제작된 방탄문은 UL 752 Level 4를 만족한다.

References

• Ministry of Land, Infrastructure and Transport (2019) General Rules for Korean Building Code (KDS 41 10 05: 2019), Korea, Chapter 4.2.3: Performance Design, p.9 (in Korean).
• Ministry of Land, Infrastructure and Transport (2019) Seismic Design Standard for Buildings (KDS 41 17 00: 2019), Korea, Chapter 15.7: Verification of Performance-Based Design Results, p.56 (in Korean).
• Underwriters Laboratories Inc. (2006) UL Standard for Safety Bullet-Resisting Equipment (UL 752), Test and Classification for Ballistic Resistant Materials, USA.
• Lee, J.-G., Kim, S., Kim, G., and Cho, M. (2012) Study on Bullet-Proof Performance of Multi-Layered Hybrid Armor Against 9mm FMJ Projectile, Journal of the Computational Structural Engineering Institute of Korea, COSEIK, Vol.25, No.6, pp.487-495 (in Korean). [https://doi.org/10.7734/COSEIK.2012.25.6.487]
• Department of Defense (2008) Unified Facilities Criteria: Structures to Resist the Effects of Accidental Explosions (UFC 3-340-02), USA, pp.409-418, pp.​1447-1448.
• Guo, X., Weng, X., Jiang, Y., and Gong, J. (2017) Effects of Temperature and Strain Rate on Tensile Deformation Behavior of 9Cr-0.5Mo-1.8W-VNb Ferritic Heat-Resistant Steel, High Temperature Materials and Process, De Gruyter, Vol.36, No.9, pp.913-920. [https://doi.org/10.1515/htmp-2016-0065]
• Shim, K.B., and Lee, T.S. (2020) Design of Frame Type Blast Door Reflecting Explosion Proof Test, Journal of Korean Society of Steel Construction, KSSC, Vol.32, No.2, pp.67-74 (in Korean). [https://doi.org/10.7781/kjoss.2020.32.2.067]
• Lee, J.-S., and Lim, H.-K. (2016) On the Derivation of Material Constants Associated with Dynamic Behavior of Heat Formed Plates, Journal of the Computational Structural Engineering Institute of Korea, COSEIK, Vol.29, No.2, pp.105-114 (in Korean). [https://doi.org/10.7734/COSEIK.2016.29.2.105]
• Johnson, G.R., and Cook, W.F. (1983) A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures, Proceedings of 7th International Symposium on Ballistics, American Defense Preparedness Association, USA, pp.541-547.
• Rahman, N.A., Abdullah, S., Abdullah, M.F., Omar, M.Z., Sajuri, Z., and Zamri, W.F.H. (2018) Ballistic Limit of Laminated Panels with Different Joining Materials Subjected to Steel-Hardened Core Projectile, International Journal of Integrated Engineering, Penebit UTHM, Vol.10, No.5, pp.8-14. [https://doi.org/10.30880/ijie.2018.10.05.002]
• Gomah, M., and Demiral, M. (2020) An Experimental and Numerical Investigation of an Improved Shearing Process with Different Punch Characteristics, Strojniški vestnik – Journal of Mechanical Engineering, University of Ljubljana (Faculty of Mechanical Engineering), Vol.66, No.6, pp.375-384. [https://doi.org/10.5545/sv-jme.2020.6583]