비확장 단부판 접합부의 헌치 형태에 따른 내력 평가

2.1 실험체 계획

본 실험에서는 비확장형 단부판으로 구성된 보-기둥 접합부의 내진성능을 평가하고자 반복가력실험이 가능한 총 3가지 실험체를 제작하였다. 실험체는 Fig. 2와 같이 기둥과 보로 구성하였으며 90° 회전하여 가력부를 보 중앙부에 위치하였다.

Fig. 2.

Detail of test set-up

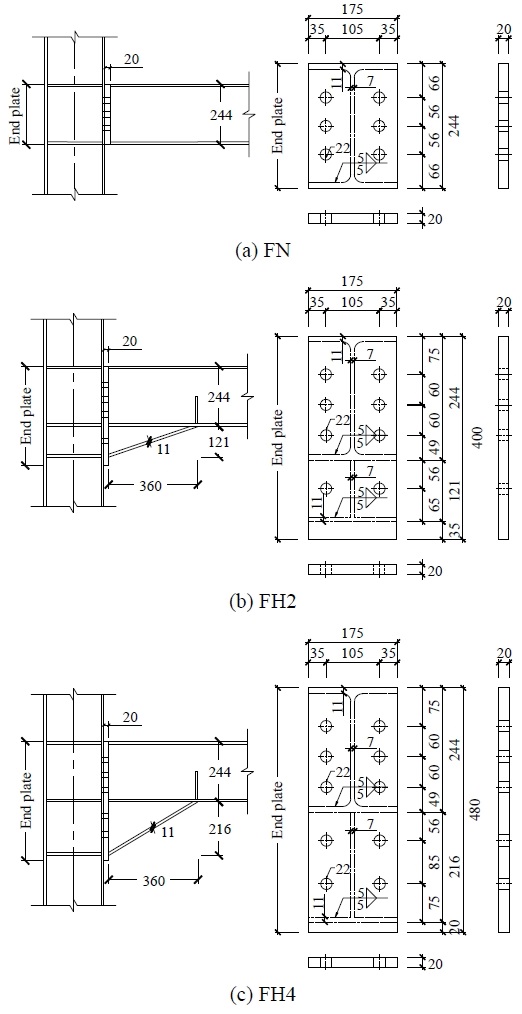
기둥과 보 단면은 모두 H-244​×175×7×11로 동일하게 설계하였다. 기둥 중심부에서 가력 지점까지 보의 길이는 1,860 mm이며, 보와 기둥은 20 mm 엔드플레이트를 사이에 두고 고장력볼트 6개를 이용하여 접합하였다. 헌치의 경우 H형강과 같은 웨브 7 mm, 플랜지 11 mm로 설계하여 보 단부 하단에 용접접합하였다. 이때 용접접합되는 헌치 너비는 실험체별 경간비가 동일하도록 모두 360 mm로 설계하였지만, 기둥 플랜지와 볼트 접합되는 헌치 높이는 각 2개, 4개의 볼트가 추가로 체결되도록 121 mm, 216 mm로 설계하였다.

따라서 헌치 보강을 하지 않은 FN 실험체를 바탕으로 삼각헌치를 활용하여 보단부 면적을 증가시킨 FH2와 FH4 실험체의 규격을 Table 1과 같이 정리하였으며 각 실험체별 접합부 상세는 Fig. 3와 같다. 실험체명의 ‘N’은 무보강, ‘H’는 헌치 보강을 나타내며 ‘H’ 뒤의 숫자는 헌치에 체결되는 볼트의 개수를 의미한다.

Table 1.

Test specimens

Fig. 3.

Details of end plate (Unit: mm)

2.2 재료성질

본 연구를 위해 실험에 사용된 실험체를 구성함에 있어 보와 기둥을 F10T(M20) 볼트를 사용하여 체결하였다. 각 실험체별로 6개, 8개, 10개의 볼트를 이용하였으며 F10T(M20) 볼트의 설계볼트장력인 182 kN을 도입해 체결하였다. 실험체를 구성한 강재에 대하여 동일한 강종 및 두께에 따라 금속인장시험편(KS B 0801)^[6] 기준을 만족하는 정형 시험편을 제작하였으며, 만능재료시험기를 이용하여 재료인장시험을 수행하였다. H형강과 헌치는 SS275로 제작하여 웨브 7 mm, 플랜지와 스티프너 11 mm에 대한 시험을 수행하였으며, 단부판은 SM355로 제작하여 20 mm에 대해 시험을 수행했다. 시험결과를 바탕으로 항복강도, 인장강도, 연신율을 산정한 결과는 Table 2와 같다.

Table 2.

Coupon test results

2.3 실험계획

접합부 내력평가를 위해 최대 500 mm, 250 kN 용량의 액추에이터(actuator)를 이용하여 반복가력실험을 수행할 수 있도록 Fig. 4와 같이 실험체를 설치하였다. 해당 실험체는 FH4이며, 이와 같은 헌치로 보강한 실험체의 경우 보강면을 액추에이터가 설치된 반대측에 위치시켜 실험을 진행하였다.

Fig. 4.

A front view of test set-up

FEMA350(2000)^[7]의 특수모멘트골조에 해당하는 가력 프로토콜 Table 3를 따라 변위를 제어해 각 step별로 6, 4, 2 cycle씩 반복가력하였다. 반복가력 중 지점의 이격으로 발생하는 변위차를 측정하기 위해 Fig. 2와 같이 기둥 양 끝단부와 가력지점 등 4개 지점에 LVDT를 설치해 실험의 신뢰도를 높였으며 횡좌굴 방지를 위해 횡지지대를 설치하였다.

Table 3.

Loading protocol according to FEMA350

또한 변형률 측정이 가능한 일축방향 스트레인 게이지(strain gauge)를 각 실험체의 웨브, 플랜지, 헌치 등에 부착하였으며 패널 존에는 전단 변형률 산정을 위한 삼축 방향의 로젯 게이지(rosette gauge)를 부착하였다. 모든 실험 데이터는 정적데이터로거(TDS)를 이용해 측정하였다. 실험 중 실험체 파손 또는 실험체 강도 변화 추이에 따라 실험 종료 후 실험을 통해 얻은 데이터를 그래프와 표로 제시한다.

2.4 이론검토

헌치를 활용해 보강함으로써 나타나는 실험체 보 단면의 넓이 변화에 따른 내력을 이론적으로 검토해보고자 Fig. 5와 같이 실험체 각 지점의 내력을 계산하여 Table 4에 정리하였다.

Fig. 5.

Theoretical calculation point

Table 4.

Theoretical value

모든 실험체는 일정한 단면을 가진 H형강으로 설계되었기 때문에 보 단면 넓이 A_d는 5,624 mm²로 같다. 하지만 헌치로 인해 변단면 형상을 보이는 실험체 FH2와 FH4의 보 단부 단면 A_f는 A_d에 비하여 각각 44 %, 56 % 증가하였다. 또한 각 단면의 형상에 따른 항복모멘트를 산정하였다. 이때 항복강도는 SS275의 공칭강도를 사용하였으며 그에 따른 보 중앙부의 공칭모멘트(M_pd)는 모든 실험체에서 153.45 kN·m로 산정되었다. 하지만 면적 증가에 따른 보 단부의 공칭모멘트(M_pf)는 FN 대비 FH2는 73 %, FH4는 93 % 증가하였다.

또한 기둥의 공칭모멘트(M_pc)는 153.45 kN·m로 산정되었다. 산정 과정에 따르면 단순 H형강과는 달리 단면의 중립축이 H형강의 중심에서부터 하단부에 위치한 것으로 파악되었다. 이로 인해 기존의 응력전달 메커니즘에 영향을 끼쳤을 것으로 판단된다.

더불어 헌치 보강 실험체의 강역이 넓어졌으며, 그에 따라 소성 힌지가 접합부에서 발생하지 않고 보다 약한 Fig. 5의 B 지점과 같은 헌치의 끝에서 선(先) 항복될 것으로 예상하였다. 이로 인해 헌치 보강이 전체적인 실험체의 강도 산정에 영향을 미칠 것으로 판단되며 상대적으로 내력이 강한 기둥으로 설계되어 안정적으로 에너지를 소산할 것으로 보인다.

3.1 접합부 회전능력

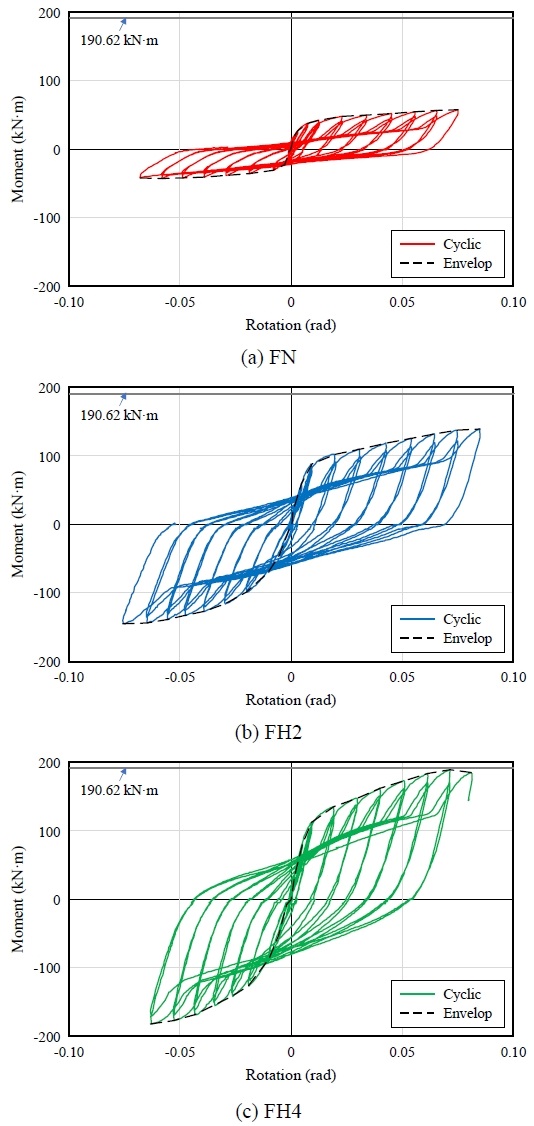
실험체의 회전능력에 따른 모멘트를 비교하기 위해 Fig. 6에 나타낸 것과 같이 실험결과를 정리하였다. 가력지점의 LVDT로 측정한 값은 보정을 통해 회전각(θ = ∆/l) 산정 시 변위 값으로 이용했으며, 액추에이터의 로드셀(load cell)을 이용하여 측정한 하중은 모멘트(M = Pl)값 산정에 이용하였다. 접합부 내력을 평가하기 위하여 보 부재의 소성모멘트(M_p = F_yZ)를 기준으로 항복상태를 유추하였으며, 사용된 강재의 인장시험을 통해 산정된 강도의 평균인 341.61 MPa에 따른 모멘트값 190.62 kN·m를 기준으로 하여 다음과 같이 실험결과를 분석하였다.

Fig. 6.

Moment-rotation curve

FN 실험체는 대칭 단면으로 반복가력 시 양측에서 같은 양상의 거동을 보였다. 회전각 최대 0.08 rad까지 가력했으며 초기 항복 이후 회전각이 커져도 강도가 거의 증가하지 않는 거동을 보였다. 0.075 rad에서 최대강도는 57.11 kN·m로 나타났으며 보 소성모멘트 대비 최대강도 30 %로 산정되었다. 회전각이 커질수록 Fig. 7(a)와 같이 단부판과 체결된 기둥 플랜지의 면내좌굴이 발생하였고, 가력 방향에 따라 면내좌굴 방향이 교차되었다. 반면 플랜지에 비해 두께가 두꺼운 단부판의 경우 육안으로는 거의 변형이 없는 것으로 파악되었다.

Fig. 7.

Failure mode of each specimen

FH2 실험체는 회전각 최대 0.09 rad까지 가력하였으며 보 소성모멘트 대비 최대강도는 약 76 %로 0.085 rad에서 144.38 kN·m로 측정되었다. 해당 실험체는 가력 중 Fig. 7(b), Fig. 7(c)와 같은 형태로 기둥 플랜지에서 파손이 발생하여 실험을 종료하였다. 또한 FN 실험체와 동일한 형상으로 기둥 플랜지의 면내좌굴을 확인할 수 있다.

FH4 실험체의 경우 회전각 0.076 rad에서 최대강도 188.06 kN·m에 도달하였으며 이는 보 소성모멘트의 약 99 %로 나타났다. FH2 실험체와 같이 패널 존 및 헌치 패널 존의 기둥 플랜지에서 파손이 발생하여 0.09 rad 가력 중 실험을 종료하였다. 실험 종료 형상은 Fig. 7(d), Fig. 7(e)와 같으며 해당 실험체의 경우 패널 존 변형으로 인해 기둥의 양측 중심선이 일치하지 않은 것을 확인할 수 있다. 또한 실험 종료 후 실험체를 해체한 결과 보와 기둥을 연결하는 볼트의 와셔도 파손되었음이 확인되었다.

3.2 데이터 분석

앞선 실험결과에서 모멘트-회전각 그래프의 포락곡선은 가력 변위에 따른 최대 모멘트의 집합으로 Fig. 8과 같이 나타난다. 특수모멘트골조는 0.04 rad에서 보 소성모멘트의 80 % 이상 나타나야 하며 세 가지 실험체 중에서는 FH4가 도달한 것으로 나타났다.

Fig. 8.

Envelop curve of specimens

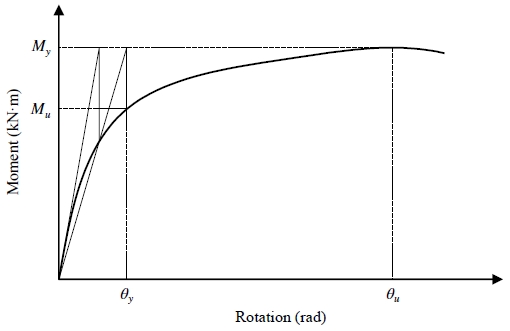
선행연구^[8]를 참고하여 Fig. 9과 같은 방법으로 항복점을 산정하였다. 초기강성(K_y), 항복점에서의 회전각​(θ_y) 대비 최대 회전각(θ_u)의 비, 보 소성모멘트 대비 최대모멘트의 비(M_u/M_pd), 기둥 플랜지의 소요모멘트(M_cf) 등을 비교하고자 가력 방향에 따라 헌치의 내력을 정모멘트(+)와 부모멘트(–)로 구분하여 Table 5와 같이 정리하였다. 이때 무보강 FN 실험체는 보 단부가 대칭 단면이기 때문에 양방향의 거동 형태가 비교적 같으므로 상대적으로 낮게 측정된 결과를 대상으로 분석하였다.

Fig. 9.

Method of calculating yield point

Table 5.

Test results(Unit: kN·m)

보의 소성모멘트($$ M_{pd}^{\mathrm{*}}$$, $$ M_{pf}^{\mathrm{*}}$$), 기둥의 소성모멘트($$ M_{pc}^{\mathrm{*}}$$)는 재료시험을 통해 나타난 강재의 항복강도를 적용해 산정하였다. 초기강성의 경우 헌치가 기둥 플랜지에 접합되는 면적이 커져 보 단부가 넓어질수록 높게 측정되었으며, 헌치 방향에 따라 부모멘트(–)를 받을 때보다 정모멘트(+)를 받을 때 상대적으로 높게 측정되었다. 초기 항복점에서의 양방향 최대 모멘트값이 약 20 kN·m로 다소 차이가 나지만 최대 항복점에서는 약 6 kN·m로 감소한 것을 통해 양방향의 항복 이후 강도의 차는 크지 않다고 판단할 수 있다.

SCI P207(The Steel Construction Institute)^[9]에 따른 식 (1)을 이용해 산정한 기둥 플랜지의 소요모멘트(M_cf)는 각 실험체의 최대 항복점에서의 모멘트와 비슷한 수준으로 나타났다. 이는 기둥 플랜지의 파괴 및 면내좌굴로 인해 강도 저하가 발생한 실험체의 최종 파괴 형상과 같은 양상임을 알 수 있다.

• 여기서, M_cf: 기둥 플랜지의 소요모멘트,
• 　　　  l_eff: 유효 항복선,
• 　　　  m: 볼트 중심부터 웨브까지의 길이,
• 　　　  h_r: 접합부 끝단부터 해당 열의 높이.

부모멘트를 받을 때 초기항복점의 회전각에 대한 최대 회전각의 비는 무보강의 경우 8.10이지만 헌치 보강을 할 경우 2.78, 2.26으로 줄어드는 것을 볼 수 있다. 따라서 헌치 보강 시 실험체의 연성능력은 줄어들며 헌치 크기에 따라 연성능력에 미세한 차이가 있다고 판단된다. 또한 헌치 보강 전 보의 소성모멘트에 대한 최대모멘트 비가 약 0.23에 해당하였지만 보강 후 최대 0.99로 늘어난 것으로 보아 헌치 보강이 강도에 미치는 영향이 크다고 판단할 수 있다.

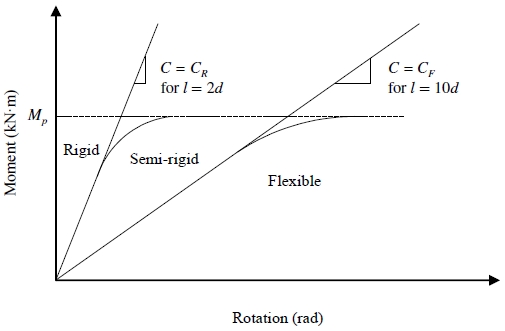
선행연구^[10]에 따르면 실험결과에 따른 회전각-모멘트 관계를 통해 알 수 있는 초기강성(C)에 따라 강접합 또는 힌지 등과 같은 접합부 형태를 Fig. 10의 기준에 따라 유추할 수 있다. 이에 따른 접합부의 초기강성은 식 (2)와 같이 산정할 수 있으며, 계산식에 사용된 길이(l)는 보의 높이(d)에 따라 2d ≤ l ≤ 10d일 때 접합부를 반강접이라 간주한다.

• 여기서, C: 접합부의 초기강성.

Fig. 10.

Dimensional classification of initial stiffness

본 연구에서 수행한 실험체를 대상으로 적용해 보았을 때 모두 반강접으로 분류되었다. 이에 따라 접합부 내력 산정 시 강접합이 아닌 반강접에 해당하도록 보수적으로 계산해야 한다고 판단된다.

3.3 변형률 분석

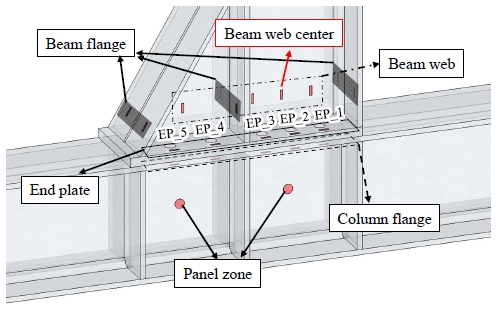
부재의 변형을 측정하고자 실험에 영향을 미치지 않도록 주의하여 부재의 도장면을 벗겨내고 강재에 직접 스트레인 게이지를 부착하였다. Fig. 11과 같이 각 실험체의 보 단부 웨브와 플랜지, 접합부의 단부판과 기둥 플랜지, 패널 존의 변형을 측정해 항복 여부를 확인하였다. 항복변형률(ε_y)은 Table 2의 SS275 항복강도를 참조하여 산정한 값이다.

Fig. 11.

Gauge attachment position

모든 실험체의 기둥 플랜지에서 우선적으로 항복하는 양상이 나타났으며, 잇따라 패널 존이 항복하였다. 반면 보나 헌치의 플랜지는 실험이 종료될 때까지 탄성영역에 존재한 것으로 나타났으며 단부판과 웨브는 일부 항복했다. 따라서 실험체의 강도를 결정함에 있어 기둥 플랜지와 패널 존의 강도가 우선적으로 관여한다고 판단된다.

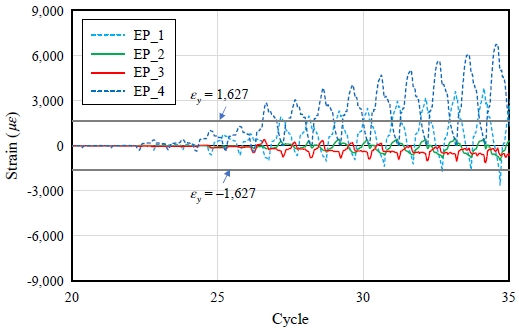
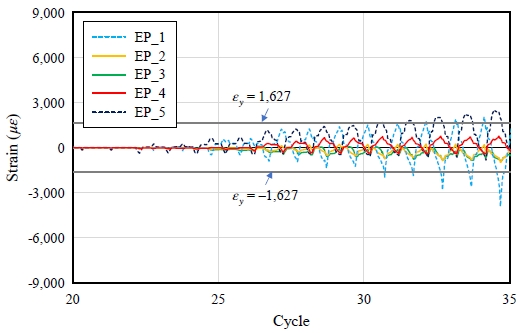
FN 실험체의 경우 엔드플레이트가 모두 항복하지 않은 것으로 확인되었다. 반면 FH2와 FH4의 경우 엔드플레이트가 비교적 두꺼워 모든 영역을 탄성영역으로 추측했지만, Fig. 12 및 Fig. 13과 같이 중심부를 제외한 접합부의 양 끝에 있는 게이지(EP_1, EP_4 또는 EP_5)가 항복한 것으로 나타났다. 이는 앞서 본 Fig. 7의 형상과 같이 가력 시 볼트 접합부의 바깥쪽 엔드플레이트가 들뜨며 기둥 플랜지와 함께 소성변형된 것으로 파악되었다. 이로써 실험체의 강역이 넓어진 것을 실험을 통해 알 수 있었다.

Fig. 12.

Measured strain value at each cycle (FH2)

Fig. 13.

Measured strain value at each cycle (FH4)

또한 모든 실험체의 보 웨브 중심에 동일하게 부착한 게이지의 변형을 나타낸 Fig. 14을 보면 실험 종료 시까지 탄성영역인 FN에 반해 FH2와 FH4는 0.06 rad에서 항복한 것을 알 수 있다. 이와 같은 게이지 값을 이용하여 각 실험체의 중립축을 추정해 보았을 때 Fig. 15과 같이 나타나며, FN이 H형강의 중심부에 존재하지만 FH2와 FH4는 H형강의 하단부에 위치한 것을 확인할 수 있다. 이로 인해 헌치 보강에 따라 실험체의 중립축이 변화하였으며 기존 보-기둥 접합부에 비해 응력전달 메커니즘 또한 바뀌었다고 판단된다.

Fig. 14.

Measured strain value at each cycle (beam web center)

Fig. 15.

Neutral axis calculate by gauge

3.4 에너지소산능력

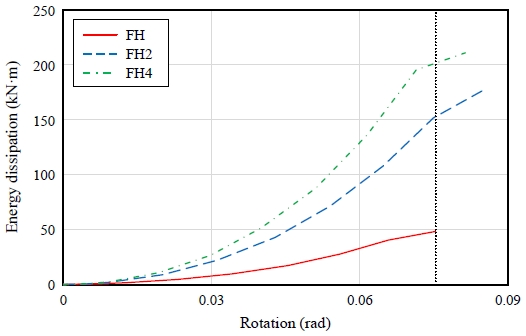
선행연구^[11]를 참고하여 에너지소산능력에 따른 각 실험체의 접합부 내력을 평가하고자 함수 식을 활용하여 Fig. 16과 같은 방법으로 하중-변위 곡선에서의 면적을 구하고 이를 Fig. 17과 같이 최대변위각에 대한 에너지소산량의 곡선으로 나타냈다. 그 결과 FN 실험체는 48.37 kN·m, FH2 실험체는 176.91 kN·m, FH4 실험체는 211.21 kN·m의 에너지를 소산하였다.

Fig. 16.

Calculation method of energy dissipation

Fig. 17.

Energy dissipation

동일한 조건에서 비교하기 위하여 FN 실험체의 최대 변위각 0.075 rad에서 각 실험체별로 에너지소산능력을 산정하면 FH2는 153.04 kN·m, FH4는 201.73 kN·m으로 산정된다. 따라서 FN에 비해 각각 3.16배, 4.17배 차이가 나므로 FH2에 비해 FH4가 약 32 % 더 효율적으로 에너지를 소산하는 것으로 보인다. 따라서 헌치의 유무에 따른 에너지소산능력 차이는 상당히 큰 것으로 보이며 헌치의 크기에 따라 달라지는 것으로 나타났다. 본 실험에서는 헌치의 크기가 가장 큰 FH4 실험체의 에너지소산능력이 가장 우수하다고 판단된다.