녹 면적율과 부식피트 형상비를 이용한 도장강재의 인장강도 추정법

2.1 인장실험시편 제작 및 인장실험 결과

강교량이 놓여진 부식환경, 적용된 도장계, 공용연수 등에 따라 강부재에 발생한 녹의 분포 및 밀도는 다양하다. ASTM D610^[6]에 따르면, 녹은 Fig. 1에 나타낸 것과 같이 점상(spot) 녹, 일반(general) 녹, 점(pinpoint) 녹과 이들의 조합(hybrid) 녹의 4가지로 분류할 수 있다. 녹 발생에 의한 단면감소는 점상 녹에 의해 가장 크게 발생할 것으로 추정되어, 인장시편 제작시의 녹 분포와 밀도에 적용하였다.

Fig. 1.

Visual samples of percentages of rusted surface areas (ASTM D 610)

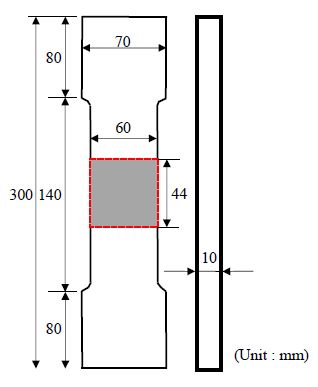
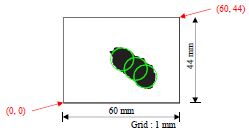
인장시편은 구조용 강재(KS SM 355A)로 KS B 0801-​7에 준하여 제작하였다(Fig. 2, Fig. 3 참조). 그리고 시편 중앙부의 가로 60 mm와 세로 40 mm의 편면에 기계 가공으로 부식 피트를 가공하여 부식손상(녹 발생)을 모사하였다.

Fig. 2.

Dimension of test specimen

Fig. 3.

Specimens with an aspect ratio of 1.0

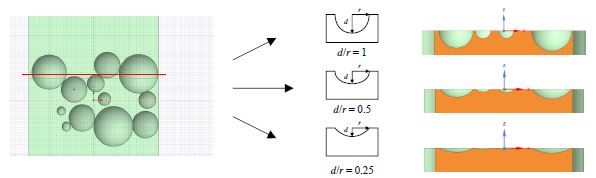
부식손상 모사의 편의를 위하여 ASTM D 610의 녹 면적율별 샘플을 시편 중앙부의 60 × 44 mm²에 중첩하여 여러 개의 원으로 이상화하였다. 녹 면적율은 ASTM D 610에 제시된 3 %, 10 %, 16 %, 33 %, 50 %로 하였으며 원의 좌표와 지름은 Table 1과 같다.

Table 1.

Coordinates and diameters of corrosion pits in the visual samples(Unit: mm)

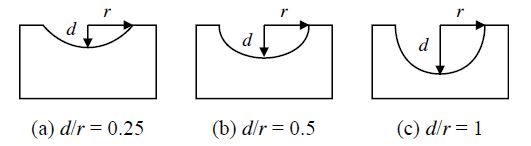
Nakai et al.^[7]은 선박에 발생한 부식피트를 측정하였으며, 그 결과 부식피트의 형상은 원뿔 모양과 유사하고, 반경과 깊이의 비는 0.2에서 0.5 사이에 분포함을 제시하였다. 이에 본 연구에서는 Fig. 4와 같이 부식피트 형상비는 부식피트의 깊이와 반경비(d/r)로 0.25, 0.5 및 1.0로 설정하였다.

Fig. 4.

Aspect ratio of depth to radius (d/r)

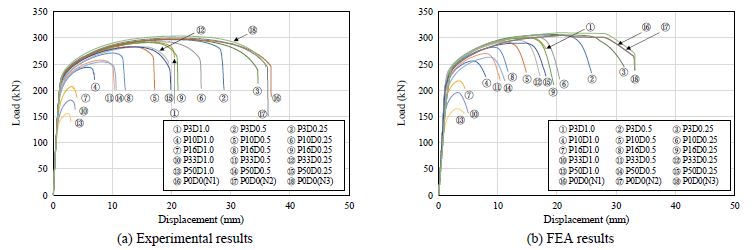
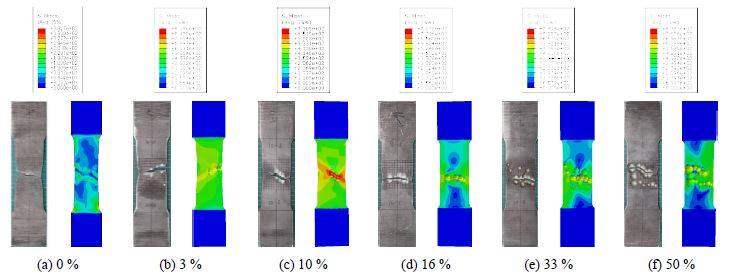
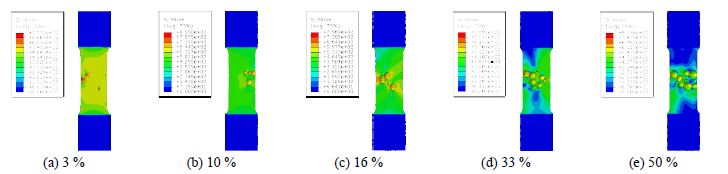
인장시편은 녹 면적율 3 %, 10 %, 16 %, 33 %, 50 %, 부식형상비 0.25, 0.5, 1.0의 각각 1개씩 15개를 제작하였다. 그리고 기준시편으로 무(無)부식(녹 면적율 0 %)을 모사한 시편 3개도 제작하였다. 단, 녹 면적율은 시편 중앙부 60 × 44 mm²에 대한 부식피트의 표면적 비율이다. 시편 18개의 인장실험 결과를 Fig. 5(a)에 하중-변위 곡선으로 나타냈으며, 파단형상을 Fig. 6에 나타냈다.

Fig. 5.

Load-displacement curves

Fig. 6.

Failure mode (left: experiment, right: FEA)

2.2 인장시편의 유한요소해석

2.2.1 유한요소해석 조건

인장시편의 유한요소해석에는 ABAQUS 유한요소 상용소프트웨어를 사용하였다. Fig. 7에 나타낸 것과 같이 해석모델의 기하학적 형상은 solid 요소(C3D10)를 이용하여 인장시편과 동일하게 인장시편 전체를 모델링하였다. 그리고 부식손상부 60 × 44 mm²의 요소 크기는 1 mm로 하고 그 이외 영역은 4 mm로 하였다.

Fig. 7.

ABAQUS mesh segmentation (P50D1.0)

유한요소해석에서는 von Mises 항복 기준과 등가소성변형경화규칙을 적용하여 재료의 비선형성을 고려하였다. 그리고 무부식 시편의 인장실험 결과에 근거하여 탄성계수와 푸아송비는 각각 205 GPa와 0.3으로 하였으며, 식 (1)과 식 (2)를 사용하여 진변형률과 진응력을 계산하여 적용하였다^[8]-[15]. 경계조건은 인장실험과 동일하게 양단 그립면에 대해 적용하였으며, 일단 축 변위를 제외하고 양단 고정으로 하였다.

$\[ {\sigma }_{true}={\sigma }_{eng}\left(1+{ϵ}_{eng}\right) \]$

(1)

$\[ {ϵ}_{true}=\ln \left(1+{ϵ}_{eng}\right) \]$

(2)

2.2.2 인장시편의 유한요소해석 결과

인장시편의 인장실험과 유한요소해석 결과를 Fig. 5, Fig. 6 및 Table 2에 나타냈다.

Table 2.

Comparison of error between experimental results and FEA results

Fig. 6에 나타낸 것과 같이 인장실험에 의한 파단형상은 녹 면적율과 부식형상비에 따라 다르지만, 폭방향으로 부식피트를 연결하는 형태로 나타났다. 그리고 유한요소해석에 의한 소성영역의 분포도와 유사하게 나타났다. 따라서 본 연구에서 수행한 유한요소해석에 의해 인장시편의 파단형상을 정도 높게 모사할 수 있음을 확인하였다.

녹 면적율과 부식형상비에 따른 인장시편별 항복하중과 극한하중을 Table 2에 나타냈다. 무부식 인장시편의 경우 인장실험에 대한 해석결과의 오차율은 2 %, 녹 면적율별 부식형상비 0.25와 0.5의 경우에는 모두 오차율이 5 % 이내로 잘 일치함을 알 수 있다.

한편 녹 면적율별 부식형상비 1.0의 경우에는 최대 약 7.52 %의 오차율이 발생하였다. 따라서, 녹 면적율 3 %, 10 %, 16 %, 33 %, 50 %와 부식형상비 0.25와 0.5인 경우에는 유한요소해석 오차율 5 % 이내로 항복강도와 극한강도를 추정할 수 있음을 확인하였고, 부식형상비 1.0의 경우에는 오차율 약 8 % 이내로 항복하중과 극한하중이 평가됨을 확인하였다.

3.1 부식 인장시편 생성

인장시편 18개를 대상으로 인장실험과 유한요소해석을 실시하였다. 녹 면적율 3 %, 10 %, 16 %, 33 %, 50 %와 부식형상비 0.25, 0.5, 1.0에 대해 각각 1개씩의 인장시편을 생성한 것으로 그 결과의 적용은 매우 제한적이라 할 수 있다. 그리고 녹 면적율이 동일한 경우에도 부식피트의 위치 및 분포에 따라 인장강도는 달라질 것이다^{[12],[14],[15]}. 또한 다양한 녹 면적율과 부식형상비에 대한 유한요소해석 모델시편을 생성하여 해석하는 것에는 많은 시간이 소요되므로, 본 연구에서는 상용 유한요소해석 소프트웨어를 사용하는 것과 동등한 정도를 가지는 간편식을 이용한 인장강도 추정법에 대해 검토한다.

본 절에서는 부식손상된 인장시편의 극한하중을 극한강도와 최소단면적의 곱으로 정도 높게 계산할 수 있는지에 대해 검토하고자 한다.

3.2 간이식을 이용한 극한하중 계산

먼저 인장실험에서 얻은 극한하중과 식 (3)으로 계산된 극한하중을 비교하였다. 인장강도(극한강도)는 무부식 시편의 인장실험으로 산출된 526 MPa이다. 최소단면적은 부식손상부 60 × 44 mm²을 축방향으로 1 mm 간격으로 절단하여 계산된 45개 단면적의 최솟값으로 녹 면적율과 부식형상비별 최소단면적을 도출하였다(Fig. 9 참조). 그리고 식 (3)으로 각 인장시편의 극한하중을 계산하였다.

Fig. 8.

Stochastic model analysis result

Fig. 9.

Determining the minimum cross-sectional area for different levels of corrosion depth

인장실험에 사용된 시편 개수가 각각 1개씩으로 매우 제한적이므로 녹 면적율 3 %, 16 %, 50 %와 부식형상비 0.25, 0.5, 1.0에 대해 각각 5개씩의 부식모델 시편을 추가 생성하였다.

부식모델 시편 45개에 대해 인장시편과 동일한 방법으로 유한요소해석을 실시하였다. 그리고 부식모델 시편의 극한하중을 식 (3)으로 계산하여 Fig. 10에 나타냈다.

Fig. 10.

Comparison of ultimate loads obtained from test, FEA and Eq. (3)

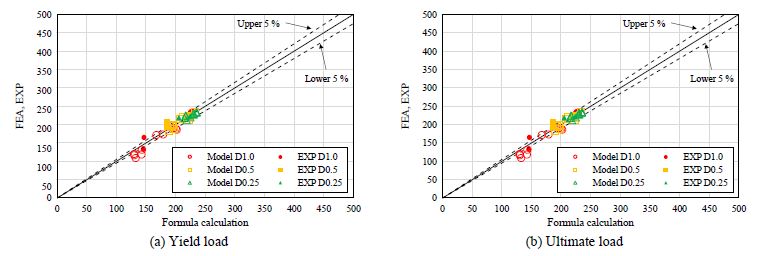
Fig. 10에 나타낸 것과 같이, 식 (3)으로 계산한 극한하중은 녹 면적율에 따른 부식형상비 0.25와 0.5의 경우에는 실험결과 또는 유한요소해석결과와 오차율 5 % 이내로 잘 일치한다. 한편, 부식형상비 1.0의 경우에는 해석결과와 비교하여 오차율이 10 %를 초과하는 경우도 있다. 이는 Fig. 8(e)에 나타낸 것과 같이 부식형상비가 1.0인 경우 파단면이 평평한 평면보다는 Z자 형태와 같이 입체적으로 발생하지만, 식 (3)에서 사용한 최소단면적은 축방향에 수직으로 절단된 최소단면적을 사용하므로 실제 파단형상이 고려되지 않았음에 기인하는 것으로 추정된다. 한편 Nakai et al.^[7]이 제시한 실제 강구조물에 발생하고 있는 부식형상비가 0.2 - 0.5임을 고려하면, 실제 강구조물의 극한하중은 5 % 이내로 추정할 수 있을 것이다. 단 본 연구에서는 극단적인 경우 또는 부식형상비에 따른 영향을 검토하기 위하여 부식형상비가 1.0인 경우에 대해서도 검토하였다. 따라서, 본 연구의 인장시편의 극한하중은 녹 면적율 50 % 이하 및 부식형상비 0.5 이하의 경우, 식 (3)을 이용하여 오차율 5 % 이내로 극한하중을 평가할 수 있음을 확인하였다.

3.3 부식시뮬레이션과 인장강도 평가

녹 면적율에 따른 도장강재의 인장강도 추정법을 검토하려면 다양한 부식피트의 분포(위치)에 대한 검토가 필수적이다. 본 연구에서는 녹 면적율 3 %, 10 %, 16 %, 33 %, 50 %에 대해 부식피트의 분포를 변화시켜 각각 500개씩의 부식모델시편을 생성하였다. 각각의 녹 면적율에 대해 Table 1과 동일한 지름과 개수를 사용하였으며, Python의 rand 함수를 통해 각 원(부식피트)의 중심점의 좌푯값에 대해 난수를 생성하고 이를 각 원의 중심점 좌표로 하였다. 단 각 원은 부식손상부 내에 위치하도록 하였다. 그리고 각각의 원은 서로 겹치지 않는 것으로 하여, 녹 면적율과 부식형상비 별 각각 500개씩의 부식손상 모델시편을 생성하였다(Fig. 11 참조).

Fig. 11.

Corrosion simulation and calculating minimum cross-sectional area

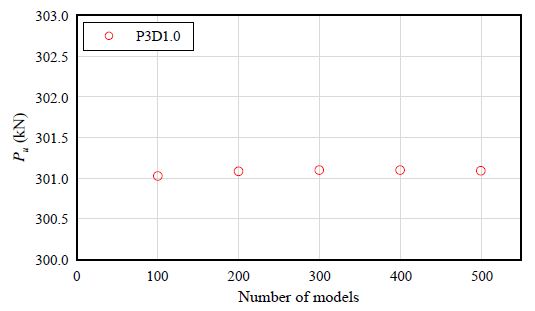
부식모델 시편은 최소단면적은 앞에서 설명한 것과 같이 부식손상부 44 × 60 mm²를 축 방향으로 1 mm씩 절단하고 단면적을 계산하여 45개 단면적 중 최솟값을 각 시편의 최소단면적으로 하였다. 부식모델 시편은 각각 500개씩 생성하였으며, 생성한 모델 개수의 적절성을 검토하기 위해 시편 수에 따른 극한하중의 변화를 녹 면적율 3 %와 형상비 1.0에 대해 산출하여 Fig. 12에 나타냈다. 부식모델 시편 수가 100개 이상이면 시편 수에 따른 극한하중의 변화는 거의 없음을 확인하였으며, 본 연구에서는 500개씩의 부식모델 시편을 이용하여 검토하였다.

Fig. 12.

Average ultimate load corresponding to different number

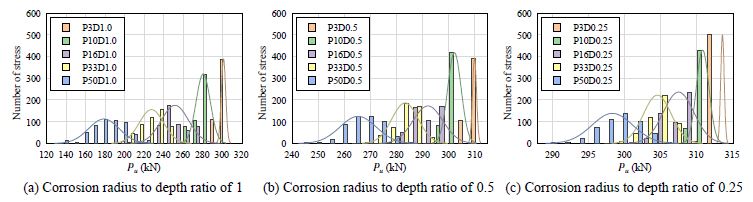
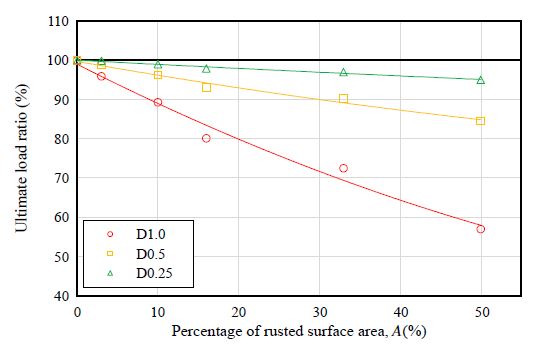
녹 면적율과 부식형상비별 부식모델 시편 500개의 극한하중을 식 (3)으로 계산하여 그 빈도 분포를 Fig. 13에 나타냈으며, 이들 데이터는 정규분포를 나타내고 있음을 알 수 있다. 또한 부식모델의 극한하중 평균값과 표준편차를 산출하여 Fig. 14에 나타냈다. Fig. 14에 나타낸 것과 같이 녹 면적율이 증가하면 인장시편의 극한하중은 선형적으로 감소함을 알 수 있다. 그리고 녹 면적율과 부식형상비가 0.25, 0.5, 1.0으로 증가함에 따라 표준편차도 증가하는 경향이 있음을 알 수 있다.

Fig. 13.

Distribution of ultimate loads

Fig. 14.

Ultimate load mean and mean deviation

4.1 인장강도 평가식 산출

부식모델 시편 500개씩을 이용하여 녹 면적율과 부식형상비에 따른 잔존 인장강도 추정법을 검토하였다. 즉, 녹 면적율과 부식형상비에 따른 500개의 극한하중의 평균값을 이용하여 잔존 인장강도 추정법을 검토하였다. 평균 극한하중비(P_r)는 인장실험으로 구한 무부식 시편의 평균 극한하중에 대한 식 (3)으로 계산한 부식모델 시편의 평균 극한하중의 비이다.

녹 면적율에 따른 극한하중비는 Fig. 15과 같으며, 부식형상비에 따른 평균 극한하중비는 Fig. 16과 같다. 그리고 각각의 데이터를 이용하여 선형, 지수, 로그 및 다항식 형태의 회귀곡선식을 적용하여 각각의 결정계수를 비교하였다. 그 결과 평균 극한하중비와 녹 면적율의 상관관계는 식 (4)의 회귀곡선식으로 나타낼 수 있으며, 평균 극한하중비와 부식형상비의 상관관계는 식 (5)로 정량화할 수 있음을 확인하였다. 회귀곡선식의 결정계수가 가장 큰 경우의 각 계수는 Tables 3-4와 같다.

Fig. 15.

Ultimate load ratio vs. percentage of rusted surface area

Fig. 16.

Ultimate load ratio vs. pitting corrosion aspect ratio

Table 3.

Constants of regression equation (Eq. (4)) of ultimate load ratio

Table 4.

Constants of regression equation (Eq. (5)) of ultimate load ratio

여기서, 극한하중비(P_r)는 부식 시편의 극한하중에 대한 무부식 시편의 극한하중의 백분율이고, R, α, β, A, γ, ϵ은 상수이다.

각 p–δ 곡선을 사용하여 P_r를 계산하고 Figs. 15-16에 녹 면적율(A)과 부식피트 형상비(R)에 대해 나타냈다.

식 (4), 식 (5) 및 Tables 3-4의 상수를 사용하여 녹 면적율과 부식형상비에 해당하는 극한하중 비율을 계산할 수 있다. 예를 들어, 녹 면적율이 25 %이고 부식형상비가 0.75인 인장강재의 극한하중비는 Fig. 17과 아래 절차로 계산할 수 있다.

Fig. 17.

Procedure to calculate ultimate load ratio for other cases

• (1) 25를 식 (4)의 A에 대입하고 부식형상비(R_i)가 0.25, 0.5, 1.0일 때의 극한하중비(P_r1, P_r2, P_r3)를 계산(Fig. 17(a) 참조).
• (2) 부식형상비와 극한하중비 (R_i, P_ri)의 (0.25, 98), (0.5, 91) 및 (1.0, 76)의 3점으로부터 구한 회귀곡선식을 통해 식 (4)와 식 (5)에서 상수(γ, ϵ) 결정.
• (3) (2)에서 얻은 상수(γ = –14.47, ϵ = –9.92)을 식 (4)에 대입하고 부식형상비 0.75를 식 (4)의 R에 대입하여 최종 극한하중비(P_r = 84.42)을 계산.

위 절차를 통해 본 연구의 검토대상인 녹 면적율 3 %, 6 %, 10 %, 16 %, 33 %, 50 %와 부식형상비 0.25, 0.5, 0.75, 1.0뿐만 아니라, 이외의 임의의 녹 면적율과 부식형상비에 대한 극한하중비도 계산할 수 있을 것이다.

4.2 녹 면적율에 따른 인장강도 평가

임의의 녹 면적율과 부식형상비에 대한 잔존 극한하중 계산방법을 제시하였다. 따라서 부식손상된 도장 강재의 표면 녹 면적율을 이용하여 도장 강재의 잔존 인장강도를 추정할 수 있을 것이다.

녹 면적율과 녹 등급에 따른 잔존 인장강도 추정법의 활용방법을 제시하기 위해 ASTM과 ISO의 녹 등급에 근거하여 잔존 인장강도를 평가하였다. Table 5에 나타낸 것과 같이, ASTM D610은 녹 면적율을 기준으로 녹 등급을 0~10등급으로 분류하고 있으며, ISO의 경우 Ri0 ~ Ri5등급으로 분류하고 있다. 그리고 ASTM과 ISO의 녹 등급에 대응하는 녹 면적율은 8등급(0 - 0.3, 0.3 - 1, 1 - 3, 3 - 10, 10 - 16, 16 - 33, 33 - 50, 50 - 100)으로 각 등급의 녹 면적율에 대한 인장강도 감소율을 계산하여, 그 결과 녹 면적율, ASTM과 ISO의 녹 등급에 따른 인장강재의 평균 극한하중 감소율을 Table 5에 나타냈다. 예를 들면, 녹 면적율 1 % - 3 %(ASTM 5등급, ISO Ri3등급)이고 부식형상비가 0.5인 경우 평균 극한하중 감소율은 1 % - 2 %이며, 잔존 극한하중은 98 % - 99 %로 인장강도 감소는 거의 발생하지 않음을 추정할 수 있다. 그리고 녹 면적율은 33 % - 50 %(ASTM 1등급, ISO Ri5등급)이고 부식형상비가 0.5인 경우 평균 극한하중 감소율은 9 % - 15 %이고 잔존 극한하중은 85 % - 91 %로 추정할 수 있다.

Table 5.

Reduction in tensile strength according to rusting grade and pitting corrosion aspect ratio

녹 면적율과 부식형상 별 각각 500개의 데이터로 계산한 평균 극한하중비와 표준편차(S)를 이용하여 이들 500개 데이터의 95 % 신뢰구간 하한치(평균 극한하중비 – 2S)을 계산하였다. 이 값을 이용하여 녹 면적율, ASTM과 ISO의 녹 등급과 부식형상비에 따른 극한하중 감소율을 계산하여 Table 6에 나타냈다. 예를 들면, 녹 면적율이 10 %(ASTM 4등급, ISO Ri4등급)이고 부식형상비가 0.5인 경우 극한하중 감소율의 하한값은 2 % - 5 %이고 잔존 극한하중은 95 % - 98 %로 추정할 수 있다.

Table 6.

Reduction in tensile strength according to corrosion grade and pitting aspect ratio (m – 2S)

이와 같이 Table 5와 Table 6를 이용하면, 녹 면적율 또는 ASTM 및 ISO 녹 등급에 따른 극한하중 감소율 또는 잔존 극한하중을 추정할 수 있을 것이다. 단, 여기서 부식형상비의 측정이 곤란한 경우에는 Nakai et al.^[7]의 결과에 근거하여 부식형상비를 0.5로 설정함으로써 극한하중을 안전측으로 평가할 수 있을 것이다.