이중 패널 벽체구조 무도류벽 원형 물탱크의 보강 및 구조 상세에 따른 거동특성 분석
Copyright © 2023 by Korean Society of Steel Construction
초록
이 연구는 이중 패널 벽체구조 원형 물탱크의 최적 설계를 위해 FEM 해석을 기반으로 보강 상세에 따른 거동 분석을 목표로 한다. 이중 패널 벽체구조 원형 물탱크의 내진설계를 위해 내진하중 산정 및 동수압의 분포를 정립하였으며, 이를 기반으로 실제 규모의 shell 요소 기반 유한요소해석모델을 구축하였다. 벽체 보강재인 X 브레이싱의 설치 상세에 따른 거동 분석을 기반으로 최적 설치 형태를 제시하였으며, L-앵글의 설치 간격에 따른 외벽 거동을 분석하였다. 또한, 이중 패널 벽체구조 원형 물탱크에서 정수압이 안팎으로 상쇄되는 내벽은 압축 방향 동수압에 의해 좌굴 위험에 노출됨에 따라, L-앵글을 사용한 내벽 좌굴 보강안을 제안하였다.
Abstract
The purpose of this study is to analyze behavior characteristics according to structural details based on FEM analysis for optimal design of a circular water tank with double panel wall. Design seismic load and distribution of hydrodynamic pressure from design codes are investigated in order to determine a proper application to the seismic design of the circular water tank. Based on the full-scale FEM analysis using shell elements, the influence of X-bracing and L-angle stiffener are investigated. From the numerical analysis, it is confirmed that using the X-bracing at the upper wall and the L-angle stiffener at the outer lower wall is more efficient to reinforce the tank. In addition, for the same capacity, the change in the behavior of the wall according to the spacing between interior and exterior walls is negligible. The inner wall, which hydrostatic pressure is balanced inside and outside, is exposed to buckling due to the hydrodynamic pressure in compression direction, and reinforcement details using the L-angle stiffener are proposed.
Keywords:
Double panel wall, Circular water tank, Seismic design, Hydrodynamic pressure, Finite element analysis키워드:
이중 패널 벽체구조, 원형 물탱크, 내진설계, 동수압, 유한요소해석1. 서 론
액체저장탱크는 지진에 의해 손상이 발생할 경우, 구조물 파손뿐만 아니라 내부 액체의 유출로 인한 인명 피해 등으로 이어지며 큰 사회경제적 손실이 발생할 수 있다. 현재 많은 물탱크는 위생성 및 내구성이 우수한 스테인리스 패널로 제작되는데, 스테인리스는 고강도로 경량화가 가능하나 두께의 감소로 인해 지진 시 발생하는 좌굴에 더욱 취약한 구조를 갖기 때문에 안전한 설계를 위해 강재 액체저장탱크의 내진설계 및 좌굴 거동에 대한 연구가 활발히 수행되고 있다[1]-[5].
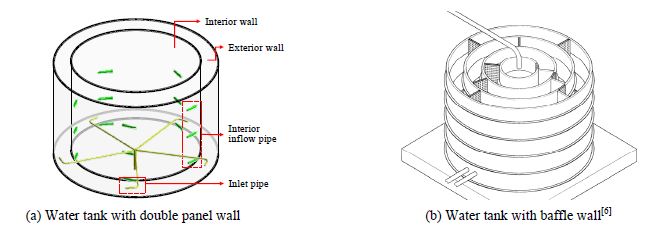
무도류벽 원형 물탱크는 기존 도류벽 원형 물탱크 대비 시공비 및 관리 비용 감소의 경제적 이점과 자체적 수류 형성으로 균일한 소독성능을 발휘하도록 고안되었으며 Fig. 1(a)와 같다. 기존 도류벽 원형 물탱크는 Fig. 1(b)와 같이 내부에 인위적 수류 형성을 위해 여러 개의 간벽이 설치되는데, 무도류벽 원형 물탱크는 이와 달리 각 벽체가 독립적인 이중 패널 벽체구조로 고안되었다. 따라서 자중 및 정수압, 지진 시 발생하는 동수압에 대한 구조적 안전성 확보가 요구되므로, 내벽 내부에 지붕을 지지하는 기둥이 설치되며, 횡방향 수압에 대한 보강재로 두 벽체를 연결하여 설치되는 X 브레이싱이 도입되었다. 내부 기둥과 달리, X 브레이싱의 경우 설치 높이에 따라 수조 내부의 유지 보수를 위한 이동성에 제약이 있을 수 있으므로, 설치 형태에 따른 보강 효과 분석을 통해 효율적인 설치안 결정이 필요하다. 나아가, 대용량화 및 내진에 대한 벽체의 추가 보강이 요구될 경우, 자재의 수급 및 시공성을 고려해 약 1 m 높이로 제작되는 단위 벽체 패널의 연결을 위한 L-앵글을 추가 설치함으로써 보강할 수 있다. 하지만, 벽체의 높이별 수압이 등분포로 작용하지 않으므로 설치 높이 및 간격에 따른 벽체 거동 분석이 선행되어야 하며, 얇은 패널 구조물로서 좌굴에 대한 검토도 필수적으로 요구된다.
국내 설계기준인 KS B 6283[7], 건축물내진설계기준(KDS 41 17 00)[8]에서는 지진 시 원형 물탱크에 작용하는 동수압 분포를 제시하지 않으며, 내진하중 산정 프로세스를 명확하게 제시하고 있지 않으므로, 이중 패널 벽체구조의 원형 물탱크에 대한 내진설계 프로세스 정립이 필요하다.
이 연구에서는 국내외 설계기준을 비교분석하여 원형 물탱크에 대한 내진설계 프로세스를 정립하였다. 이를 기반으로, 직경 40 m, 담수 높이 3.6 m의 5,000톤 규모 이중 패널 벽체구조 무도류벽 원형 물탱크를 대상으로 보강재 설치 상세에 따른 FEM 기반 변수해석을 수행하여 각 보강재의 보강 효과를 확인하였다. 나아가, 지진 시 정수압과 동수압의 조합으로 인해 발생할 수 있는 좌굴을 검토하여 좌굴 보강안을 제안하였으며, 내외벽 사이 간격에 따라 달라지는 동수압과 보강재의 보강 효과를 분석하여 무도류벽 물탱크의 효율적 보강방안을 제안하였다.
2. 원형 물탱크 내진설계 프로세스
2.1 원형 물탱크의 내진하중 산정 프로세스 정립
물탱크의 내진하중 산정법은 등가정적해석법과 동적해석법으로 구분되며, 동적해석법에는 응답스펙트럼해석법, 시간이력해석법 등이 있다. 국내 설계기준인 KS B 6283[7]에서는 등가정적해석법과 응답스펙트럼해석법에 따른 내진하중 산정법을 각각 제시하고 있다. 하지만, 전도모멘트에 대한 탱크 옆판(벽체)의 안정도 평가만을 포함함에 따라 벽체에 작용하는 동수압 분포를 제시하지 않는다. 동특성에 해당하는 충격 및 대류 성분의 유효중량(Wi, Wc)과 유효높이(hi, hc)는 등가정적해석법에 해당하는 식을 제시하고 있으며 식 (1) 및 식 (2)와 같다. 동특성 산정에 요구되는 등가질량비(m0/ml, m1/ml)와 등가작용높이비(h0/H, h1/H)는 설계변수인 직경(D)과 설계최고액면높이(H)의 비(D/H)에 따라 일대일 대응되는 값을 표로 제시하고 있다[7].
| (1a) |
| (1b) |
여기서, Wi: 저장액체의 충격 성분 유효중량(N),
Wc: 저장액체의 대류 성분 유효중량(N),
WL: 저장액체의 무게(N),
: 충격 등가질량비,
: 대류 등가질량비.
| (2a) |
| (2b) |
여기서, hi: 충격 성분 유효중량의 무게중심높이(m),
hc: 대류 성분 유효중량의 무게중심높이(m),
H: 탱크 내용액의 설계최고액면높이(m),
: 충격질량 등가작용높이비,
: 대류질량 등가작용높이비.
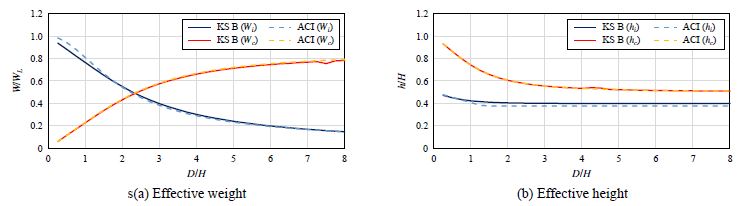
한편, 국외 설계기준인 ACI 350.3[9]에서는 응답스펙트럼해석법을 따르며, 벽체에 작용하는 동수압 분포를 포함한 내진하중 산정 프로세스를 상세히 제시하고 있다. 내진하중 산정 프로세스는 Fig. 2와 같으며, 탱크의 무게와 지진 시 유체 거동에 의한 동특성인 충격 성분과 대류 성분의 유효질량과 유효높이를 산정한 뒤, 지진 위험도, 지역 계수 등의 설계계수를 기반으로 산정한 설계 스펙트럼 가속도를 곱하여 내진하중을 산정한다. 이때, 충격 및 대류 성분의 유효중량과 유효높이 산정식은 식 (3)-(4)와 같으며, KS B 6283[7]에 제시된 식 (1)-(2)와 비교했을 때 Fig. 3와 같이 유사함을 확인하였다. 따라서, 벽체에 작용하는 동수압 분포를 제시하고 있는 ACI 350.3[9]의 동특성 산정식을 사용하되, 설계 스펙트럼 가속도 산정 시 요구되는 설계계수는 국내 설계기준을 따라 적용하였다.
| (3a) |
| (3b) |
| (4a) |
| (4b) |
설계 스펙트럼 가속도 산정을 위한 설계계수는 국내 설계기준인 KDS 41 17 00[8]에서 제시한 내진 특등급 기준의 지진위험도계수 2.0, 지역구역계수 0.11을 적용하였다. 또한, 충격 및 대류 성분에 의한 동수압은 실제 포물선 분포로 작용하나 ACI 350.3[9]에서 제시하는 등가 선형 분포를 따라 산정하였다. 최종적으로 산정된 동수압을 기준으로 건축구조기준 설계하중(KDS 41 10 15)[10]의 하중 조합에 따라 동수압에 계수 0.7을 적용하였다.
2.2 원형 물탱크의 동수압 분포 정립
원형 물탱크 벽체에 작용하는 동수압은 2.1절에서 정립한 프로세스에 따라 산정 가능하나, full-scale FEM 해석을 수행하기 위해서는 동수압의 원주 방향 분포가 요구된다. 하지만, 국내 설계기준에서는 이를 제시하지 않아 국외 설계기준인 ACI 350.3[9], IITK-GSDMA[11]를 참고하여 full-scale FEM 해석을 위한 동수압 분포를 정립하였다. Fig. 4(a) 및 Fig. 4(b)는 각각 ACI 350.3[9], IITK-GSDMA[11]에서 제시하는 동수압의 원주 방향 분포를 나타낸다. 두 설계기준은 충격 성분과 대류 성분에 의한 동수압의 합이 지진 작용 방향에 따라, 수조 중심부를 기준으로 1/2은 압축, 1/2은 인장 방향으로 작용함을 제시한다. 이때, ACI 350.3[9]에서 제시하는 분포는 벽체와 수조 중심축 사이 각이 커짐에 따라 동수압이 작아지고, 원주 방향으로 작용한다. 반면, IITK-GSDMA[11]의 경우 수조 전면에 걸쳐 지진과 동일한 한 축의 방향으로 최대 동수압이 작용하는 분포를 제시한다. 또한, IITK-GSDMA[11]에서는 Fig. 4(b)를 단순화하여 Fig. 4(c)와 같이 고려할 수 있음을 제시하고 있다.
이 연구에서는 full-Scale 모델의 FEM 해석을 통해 구조적 안전성 검토를 목표로 함에 따라, 지진의 방향성을 고려하며 보수적으로 최대 동수압을 사용한 Fig. 4(b)의 분포를 따라 하중을 재하하였다.
3. 무도류벽 원형 물탱크의 FEM 최적 설계
3.1 FEM 모델링
이 연구에서는 상용 구조해석프로그램인 ABAQUS를 사용하였으며, 무도류벽 물탱크는 모든 부재가 비교적 얇은 두께의 스테인리스로 제작되는 특성을 감안, 탄성계수 210,000 MPa, 단위중량 77.8 N/m3의 단일 재료를 적용하여 3D shell로 모델링하였다. 물탱크는 허용응력설계법에 따라 허용응력을 초과하는 응력이 발생하는 부재의 사용을 제한하여 설계하기 때문에 선형탄성해석을 수행하였으며, 각 부재의 두께가 형상 대비 얇으므로 기하 비선형 해석을 수행함으로써 좌굴에 대해 검토하였다.
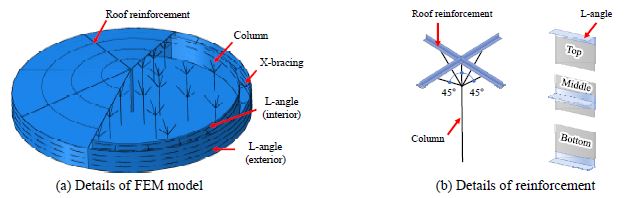
해석모델은 외벽 직경과 높이가 각각 40 m, 4 m인 약 5,000톤 규모 이중 패널 벽체구조 원형 물탱크로, 모델링 형상은 Fig. 5(a)와 같으며, 벽체, 지붕, 바닥 패널의 두께는 Table 1과 같다. 벽체 주요 보강재로 내벽과 외벽을 연결하는 X 브레이싱, 원주 방향으로 L-앵글이 설치되며, 내벽 내부에는 지붕을 4방향으로 지지하는 내부 기둥이 설치된다. 내부 기둥은 30 mm × 30 mm × 3 mm 규격의 사각관이며, 이외의 모든 보강재 규격은 30 mm × 30 mm × 3 mm L형 앵글로 동일하다. 지붕 보강재는 Fig. 5(a)와 같이 원주 방향으로 수조 중심에서 반경 5 m, 10 m, 15 m 위치에, 수평 방향으로는 8개가 설치된다. 보강재 설치 상세는 Fig. 5(b)와 같이, 내부 기둥은 두 방향의 지붕 보강재가 만나는 24개 지점에 설치되며, 벽체 보강 L-앵글은 최상단과 최하단만 1단으로 설치되고, 그 사이에서는 그림과 같이 2개가 겹쳐진 형태로 적용된다.
해석모델의 경계조건은 5,000톤 규모의 용수 무게를 고려하여 하부 패널의 모든 축 방향에 대한 회전과 변위를 제어하였으며, 모든 부재의 접촉조건은 용접 시공이 이루어짐에 따라 강결연결을 위해 Tie로 지정해주었다.
해석변수는 벽체 보강재인 X 브레이싱과 수조 외부 L-앵글의 설치안, 내외벽 간격으로 총 13개를 설정하였으며, 보강재의 설치 상세는 Figs. 6-7, 각 모델의 조건은 Table 2와 같다. 모든 모델의 정수압은 수조 높이의 90 %를 담수 높이로 가정하여 산정하였으며, Fig. 2의 내진하중 산정 프로세스에 따라 지진 시 조합 하중을 산정하였다. 내벽은 정수압이 안팎으로 상쇄되므로 평상시 정수압은 외벽에만 작용하며, 지진 시 조합 하중은 정수압과 0.7배 동수압이 합하여 산정되므로 외벽에 더 크게 작용한다.
3.2 유효 영향 부재 분석
무도류벽 물탱크는 여러 개의 간벽이 설치되는 기존 도류벽 물탱크와 달리 이중 패널 벽체구조로 고안되어 벽체에 작용하는 하중을 일부 분담하며, 벽체 하단에 집중되는 하중의 불균형을 분산시키기 위해 내외벽 상하단을 교차 지지하는 X 브레이싱을 벽체 보강재로 사용한다. X 브레이싱의 효율적 설치안을 제시하기 위해 Fig. 6와 같이 4개의 설치 형태로 해석을 수행하였다. 이는 벽체에 설치되는 높이에 따라 2 m 높이에서 외벽과 접하는 X1와 X2, 3 m 높이에서 외벽과 접하는 X3와 X4로 구분되며, X1, X3는 X 브레이싱이 2단으로 설치되고 X2, X4는 윗단만 1단으로 설치된다. 또한, 설치 개수에 따른 영향을 확인하기 위해 각 설치 형태가 21개, 42개 설치되는 경우로 해석을 수행하였다.
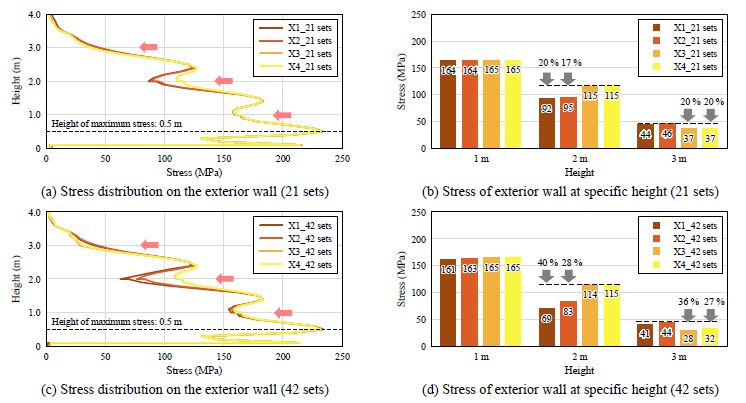
정수압이 안팎으로 상쇄되는 내벽은 외벽 대비 낮은 하중이 작용하므로, X 브레이싱의 보강 효과는 외벽 응력을 기준으로 확인하였다. 해석 결과, X 브레이싱 설치 형태에 따른 외벽 높이별 응력 분포는 Fig. 8(a), Fig. 8(c)와 같으며, 21개 및 42개 설치된 경우로 구분된다. 외벽 최대 응력은 모든 모델에서 약 0.5 m 높이로 동일하게 발생하였으며, 외벽 높이별 응력은 1 m 간격으로 감소하는 분포로 나타났다. 이는 Fig. 7(a)의 L1과 같이 1 m 간격으로 설치되는 수조 외부 L-앵글과 2 m 또는 3 m 높이에 설치되는 X 브레이싱이 외벽 응력을 분담하기 때문이다.
외벽 1 m, 2 m, 3 m 높이의 응력을 나타내는 Fig. 8(b), Fig. 8(d)에서 확인할 수 있듯, X 브레이싱이 설치되지 않은 1 m 높이의 외벽 응력은 161 MPa - 165 MPa로 모든 모델에서 유사하게 발생했다. 즉 X 브레이싱이 설치되지 않은 1 m 높이에서는 외벽에 설치되는 수조 외부 L-앵글의 영향이 지배적이다. 따라서 2 m 높이의 응력은 X3, X4의 경우 L-앵글의 응력 분담이 지배적이므로 유사한 응력이 발생했다. 반면 X 브레이싱이 설치된 X1, X2의 경우, X 브레이싱이 응력을 추가 분담함에 따라 X3, X4 대비 낮은 응력이 발생했다. 반대로 X3, X4의 설치 높이인 3 m에서는 X1, X2에 발생하는 응력은 유사하나, X3, X4에 발생하는 응력은 X1, X2 대비 낮은 것으로 확인된다.
즉, X1, X2의 경우 X 브레이싱이 설치되는 2 m 높이 외벽 응력을 최대 약 40 %, 28 % 감소시켰으며, X3, X4는 3 m 높이 외벽 응력을 최대 약 36 %, 27 % 감소시켰다. 또한, 이러한 응력 감소량은 Fig. 8(b)보다 X 브레이싱이 더 많이 설치된 Fig. 8(d)에서 X1은 약 20 %p, X2는 약 11 %p, X3는 약 16 %p, X4는 약 7 %p 크게 나타났다.
X 브레이싱의 설치 개수 및 형태에 따른 보강 효과는 확인되나, 외벽에 직접 설치되는 위치에서만 그 영향이 크기 때문에 외벽 최대 응력 발생 높이인 0.5 m에서는 그 영향이 미미하게 나타났다.
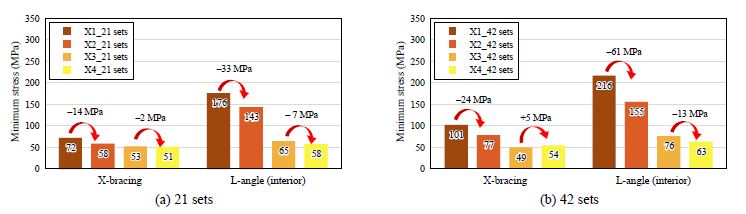
물탱크는 허용응력설계법이 적용되어 허용응력을 초과하는 부재의 사용을 제한하므로, X 브레이싱에 발생하는 최대 응력을 함께 확인하였다. Fig. 9은 X 브레이싱과 벽체 연결부에 설치되는 수조 내부 L-앵글에 발생하는 최대 응력을 나타내며, Fig. 9(a)와 Fig. 9(b)는 X 브레이싱이 21개, 42개 설치되는 경우로 구분된다.
X 브레이싱에 발생하는 최대 응력은 3 m 높이에 설치되는 X3, X4 대비 2 m 높이에 설치되는 X1, X2 형태에서 더 높게 발생했다. 이는 수조 하단으로 내려갈수록 수압이 증가함에 따라 X 브레이싱 설치 높이가 낮을수록 X 브레이싱이 분담하는 응력이 증가하기 때문이다. 이러한 경향은 X 브레이싱과 벽체 연결부에 설치되는 수조 내부 L-앵글에서도 동일하게 확인된다.
한편, X 브레이싱에 발생하는 최대 응력은 X 브레이싱이 21개 설치될 경우 X2 대비 X1에서 약 14 MPa 높게 발생했으나, X3, X4의 경우 2 MPa로 그 차이가 미소하였다. X 브레이싱이 42개 설치된 경우에도 X2 대비 X1에서 약 24 MPa 높게 나타났으며, X3, X4의 경우 5 MPa 차이로 나타났다. 즉, X 브레이싱이 수조 상단에 설치될 경우, 1단 대비 2단으로 설치했을 때 X 브레이싱에 발생하는 최대 응력의 변화는 거의 없는 것으로 나타났다.
X 브레이싱 설치 상세에 따른 해석 결과, X 브레이싱은 직접 설치되는 높이의 외벽 보강에 효과적으로, 외벽 최대 응력 감소를 위해선 약 0.5 m 높이에 설치되어야 한다. 하지만, 약 1 m 이하 높이에 X 브레이싱이 설치될 경우 내부 이동성의 제약으로 수조 유지 보수에 어려움이 있을 수 있으므로 이를 고려할 때 수조 상단 보강에 적합하다고 판단된다. 또한, X 브레이싱으로 수조 상단을 보강할 경우, 1단과 2단 설치 시 나타나는 각 부재의 최대 응력 변화가 미미하므로, 경제성을 고려하였을 때 1단으로 설치하는 것이 더욱 효율적이라고 판단된다.
3.2.1에서 X 브레이싱은 수조 내부 이동성의 제약으로 인해 외벽 하단 보강에는 한계가 있음을 확인하였다. 한편 Table 2의 작용 하중에서 알 수 있듯이, 지진 시에는 외벽 하단에 정수압과 동수압이 조합하여 39.56 kN/m2의 수압이 작용하나, 원주 방향으로 작용하는 정수압이 35.32 kN/m2로 지배적이다. 수조 외부 L-앵글은 X 브레이싱과 달리 수조 외부에 설치되어 설치 위치의 제약이 없으며, 원주 방향으로 물탱크를 둘러 설치됨에 따라 추가 설치를 통해 정수압의 영향이 지배적인 외벽 보강에 적용할 수 있다. 하지만 벽체 하부에 최대 수압이 작용하는 물탱크 특성상 경제성을 고려하여 외벽 두께는 높이별로 다르게 제작되고, Fig. 8(a)와 Fig. 8(c)에서 확인한 바와 같이 높이별 응력 분포가 상이하므로 L-앵글을 전 높이 등간격으로 설치하여 보강하는 것은 비효율적이다.
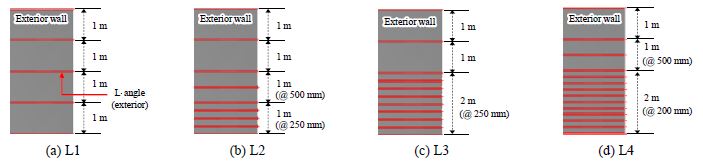
따라서 Fig. 7과 같이 수조 외부 L-앵글의 설치 간격을 하단부터 감소시키며 L1, L2, L3, L4의 4가지 설치안으로 해석을 수행하였다. L1의 경우 4 m 높이 외벽에 1 m 간격으로 앵글이 설치되며, L2, L3, L4는 L1을 기준으로 하단부터 앵글이 추가 설치된다. L2는 높이 0 m - 1 m, 1 m - 2 m에 각각 250 mm, 500 mm 간격, L3는 2 m 높이까지 250 mm 간격, L4는 0 m - 2 m, 2 m - 3 m 높이에 각각 200 mm, 500 mm 간격으로 앵글이 추가 설치된 경우이며, 모든 모델의 X 브레이싱은 X4의 형태로 21개 설치되었다.
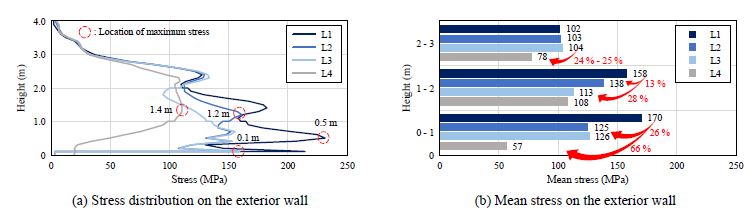
해석 결과, 수조 외부 L-앵글 설치 상세에 따른 외벽 높이별 응력 분포는 Fig. 10(a)와 같으며, Fig. 10(b)는 외벽 평균 응력을 0 m - 1 m, 1 m - 2 m, 2 m - 3 m 구간별로 나타낸다. 앵글이 1 m 간격으로 설치된 L1의 외벽 응력 분포는 얇은 패널에서 발생하는 멤브레인 거동에 의해 설치된 앵글 사이에서 응력이 크게 증가하는 분포를 보이며, 최대 응력은 약 0.5 m 높이에서 발생하였다.
Fig. 10에서 L2, L3의 경우 앵글 간격이 동일한 0 m - 1 m 구간에서 높이별 응력 분포가 유사하게 나타나는데, 0 m - 1 m 구간에 앵글이 250 mm 간격으로 3개 추가 설치될 때 L1 대비 평균 응력이 약 26 % 감소하는 것으로 나타났다. 반면, 1 m - 2 m 구간 평균 응력의 경우 L1 대비 L2에서 약 13 % 감소하였으며, L2보다 1 m - 2 m 높이에 2개의 앵글이 더 설치되는 L3에서는 약 28 % 감소하였다. 즉, 앵글이 동일하게 설치된 구간의 외벽 거동은 앵글 간격이 다르게 설치되는 주변 구간의 영향을 거의 받지 않고 동일한 수준의 거동을 보였다.
Fig. 10(a)에 나타난 바와 같이, 외벽의 최대 응력 발생 높이는 L2의 경우 약 1.2 m로 0 m - 1 m의 촘촘한 보강구간을 벗어나 나타났다. L3의 경우 마찬가지로 1 m - 2 m 구간까지 촘촘하게 보강됨에 따라 외벽의 최대 응력 발생지점이 보강구간의 위 또는 아래에 발생하는데, 이 경우 수두의 영향과 외벽의 휨거동 조합으로 외벽 최하단 앵글 보강재 사이, 약 0.1 m 높이에서 발생하였다.
한편 L3보다 0 m - 2 m 구간을 촘촘히 보강한 L4의 경우 그 구간에서 외벽 패널의 멤브레인 거동이 거의 나타나지 않아 0 m - 2 m 구간에서 급작스런 응력의 변동이 발생하지 않았다. 즉, 외벽의 두께가 증가한 것과 같은 거동을 보이며, 외벽의 최대 응력은 약 1.4 m에서 발생하였다. L4에서 0 m - 1 m 구간 평균 응력 또한 L1 대비 약 66 %, L2 및 L3 대비 약 40 % 감소함을 확인할 수 있다. 이러한 경향은 각 해석모델의 2 m - 3 m 구간에서도 확인되는데, 앵글이 추가 설치되지 않은 L1, L2, L3의 경우 102 MPa - 104 MPa의 유사한 평균 응력이 발생했으나, 해당 구간에 앵글이 하나 추가 설치된 L4에서 평균 응력이 약 24 % - 25 % 감소하는 것으로 나타났다.
L-앵글의 설치 상세에 따른 해석 결과, 외벽 두께 증가 없이 약 0.5 m 높이에서 발생하는 외벽의 최대 응력을 감소시키기 위하여 0 m - 1 m 구간에 앵글을 추가 설치하는 것은 효과적이나, 앵글이 추가 설치된 구간을 제외한 이외의 구간은 높이별 응력 분포가 동일 수준으로 유지되는 것으로 나타났다.
3.3 동수압에 의한 이중 패널 벽체구조의 거동 특성
이중 패널 벽체구조의 원형 물탱크에서 외벽에 작용하는 조합 하중은 정수압이 약 90 %를 차지하며 수조 중심에서 바깥으로 인장 방향의 정수압이 외벽 거동에 지배적 영향을 미친다. 반면, 내벽은 정수압이 안팎으로 상쇄됨에 따라 지진 시 동수압만 작용하기 때문에 외벽 대비 낮은 수압이 작용하지만, 동수압의 작용 방향으로 내벽 1/2면은 압축 방향의 수압이 작용하게 된다. 따라서, 이중 패널 벽체구조의 원형 물탱크는 내진설계 시 내벽과 외벽에 작용하는 조합 하중의 크기와 작용 방향에 큰 차이를 보임에 따라 동수압 작용 시 발생할 수 있는 벽체의 상세 거동 분석이 필요하다.
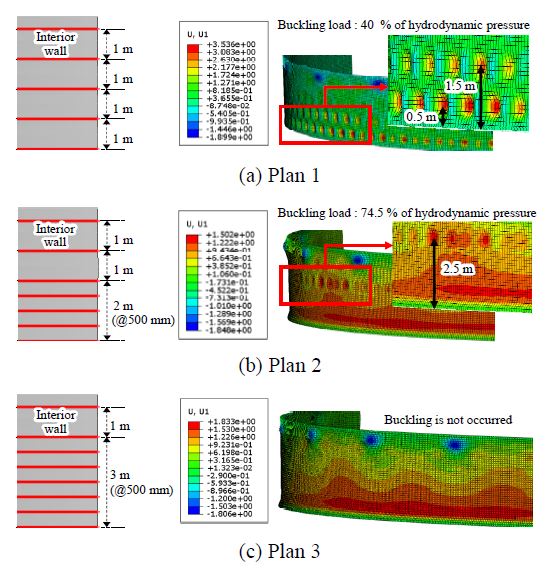
L-앵글을 내외벽에 1 m 간격으로 동일하게 설치하여 해석한 결과, 외벽에 정수압만 작용하는 평상시에는 좌굴이 발생하지 않았으나, Fig. 11(a)와 같이 동수압이 약 40 % 작용 시 동수압이 압축 방향으로 작용하는 내벽 1/2면에서 좌굴이 발생하였으며, 동수압 작용 방향의 변위가 내벽 하단 약 0.5 m, 1.5 m 높이에서 크게 발생함을 확인하였다. 즉, 벽체에 작용하는 수압의 크기보다는 작용 방향이 좌굴에 큰 영향을 미치며, 압축 방향의 수압이 작용하는 내벽이 좌굴에 취약한 것으로 나타났다.
지진 시 수조 상부에서 발생하는 대류거동 및 슬로싱 현상으로 인해 동수압은 담수 높이에서도 일부 작용하나, 수조 하단에서 최대 수압이 작용하는 분포는 정수압과 동일하다. 따라서 동수압에 의해 발생하는 내벽 좌굴을 보강하기 위해 L-앵글을 내벽 하단부터 500 mm 간격으로 추가 설치하였다. 내벽 2 m 높이까지 500 mm 간격으로 L-앵글을 추가 설치한 결과, Fig. 11(b)와 같이 동수압이 약 34.5 %p 더 작용했을 때 좌굴이 발생하며 좌굴 발생 시점이 늦어졌고, 동수압 작용 방향의 최대 변위 발생 높이도 약 2.5 m로 높아졌다. 최종적으로 Fig. 11(c)와 같이 내벽 3 m 높이까지 500 mm 간격으로 L-앵글을 설치했을 때 좌굴이 발생하지 않음을 확인하였다.
L-앵글은 단위 벽체 패널의 연결부, X 브레이싱과 벽체 연결부, 추가 구조 보강용으로 사용된다. 일반적으로 폭 1 m의 단위 벽체 패널을 사용하기 때문에 L-앵글은 기본 1 m 간격으로 설치된다. 하지만, 높이 4 m의 5,000톤 규모 이중 패널 벽체구조 원형 물탱크는 내진설계 시 압축 방향 동수압의 영향으로 내벽에 발생하는 좌굴을 보강하기 위해 내벽 3 m 높이까지 500 mm 간격의 L-앵글 설치가 필수적으로 요구됨을 확인하였다.
3.4 내외벽 간격에 따른 벽체 거동
이중 패널 벽체구조의 원형 물탱크는 내외벽 간격이 달라짐에 따라 각 벽체에 작용하는 동수압과 보강재의 보강 효과가 달라질 수 있다. 5,000톤의 동일 규격에서 내외벽 간격의 영향을 분석하기 위하여 외벽의 직경은 40 m로 유지하였다. 이와 더불어 내벽 직경을 36 m에서 각각 33 m, 30 m로 감소시킨 두 개의 해석모델을 추가하였으며, 대상 해석모델은 Table 2의 7번, 12번, 13번 모델과 같다. 각 모델의 보강 상세는 X 브레이싱의 경우 X4의 형태로 21개를 설치하였으며, 수조 외부 L-앵글은 1 m 간격의 L1 형태로 동일하나, Fig. 5(a)와 같이 경사 지붕으로 내벽 직경이 감소함에 따라 지붕과 접하는 내벽 높이는 달라진다.
해석 결과, 내외벽 간격에 따른 외벽과 내벽의 최대 응력은 Fig. 12와 같다. 외벽의 최대 응력은 Fig. 12(a)와 같이 내외벽 간격이 증가함에 따라 정수압이 작용하는 평상시와 조합 하중이 작용하는 지진 시 모두 그 영향이 매우 작은 것으로 나타났다. Table 2의 외벽에 작용하는 정수압과 조합 하중에서 알 수 있듯이, 정수압은 담수 높이로 산정되므로 모든 모델에서 동일하게 산정되나, 동수압은 내부 용수 무게에 의해 산정되기 때문에 외벽에 작용하는 조합 하중은 내외벽 간격이 증가함에 따라 증가한다. 하지만 이 물탱크의 설계에서는 Fig. 12(a)와 같이 그 수준이 매우 미미한 것으로 나타났다. 이는 앞서 언급한 바와 같이 조합하중에서 지진하중의 비중이 약 10 % 수준으로 비교적 작기 때문이다.
내벽은 평상시 정수압이 안팎으로 상쇄되지만 내외벽 상하단을 교차 지지하는 X 브레이싱으로 인해 외벽에만 작용하는 정수압을 일부 분담하며, 지붕 무게에 의해 내벽 상단부에서 최대 응력이 발생하는데, Fig. 12(b)와 같이 외벽에만 정수압이 작용하는 평상시 내벽의 최대 응력은 내외벽 간격이 증가함에 따라 감소하는 것으로 나타났다.
Fig. 13은 내외벽 간격에 따른 세 모델의 평상시 내벽에 발생하는 응력을 나타낸다. 내외벽 간격이 2 m로 가장 좁은 경우, 내벽 최대 응력은 Fig. 13(a)와 같이 X 브레이싱이 설치된 축의 최상단에서 발생했다. 하지만 내외벽 간격이 증가하면서 내벽 최대 응력은 Fig. 13(b), Fig. 13(c)와 같이 점차 감소하며, X 브레이싱 사이 최상단에서 발생하는 것으로 나타났다. 이는 내외벽 간격이 증가함에 따라 경사 지붕과 접하는 내벽 높이가 높아지기 때문에, 4 m 높이로 고정된 X 브레이싱 설치 높이와 지붕과 접하는 내벽 최상단의 거리가 멀어짐에 따라 두 하중을 더 넓은 면적이 분담하기 때문이다. 동수압이 추가로 작용하는 지진 시에는 내외벽 간격이 증가함에 따라 내벽 작용 동수압이 감소하므로, 지진 시에도 내벽의 최대 응력은 감소하는 것으로 나타났다.

Stress on interior wall by hydrostatic pressure according to spacing between interior and exterior wall
경사 지붕을 갖는 5,000톤 규모 이중 패널 벽체구조 원형 물탱크에서 내외벽 간격이 2 m, 3.5 m, 5 m로 증가할 때 벽체의 최대 응력 증감은 확인되나, 그 수준이 매우 작은 것으로 나타났다. 즉, 이중 패널 벽체구조 원형 물탱크에서 내외벽 간격은 벽체 거동에 매우 낮은 수준의 영향을 미치므로, 내외벽 간격은 두 벽체 사이에 설치되는 보강재의 시공성 등을 고려하여 결정하는 것이 합리적일 것으로 판단된다.
4. 결 론
이 논문에서는 국내외 설계기준을 비교 분석하여 원형 물탱크의 내진하중 산정 프로세스 및 동수압 분포를 정립하였다. 이를 기반으로 5,000톤 규모 이중 패널 벽체구조 무도류벽 원형 물탱크의 FEM 모델을 구축하였으며, X 브레이싱과 L-앵글의 설치 상세에 따른 보강 효과를 외벽 응력을 기준으로 분석하였다. 또한, 이중 패널 벽체구조에서 동수압의 영향으로 발생할 수 있는 좌굴에 대한 보강안을 제안하였으며, 나아가 내외벽 간격에 따른 벽체 거동을 분석하였다.
- (1) 이중 패널 벽체구조 물탱크의 내외벽을 교차로 지지하는 X 브레이싱의 설치 형태에 따른 보강 효과는 X 브레이싱이 21개 설치되었을 경우 X1과 X2는 2 m 높이의 외벽 응력을 약 20 %, 17 % 감소시켰으며, X3와 X4는 3 m 높이의 외벽 응력을 약 20 % 감소시켰고, X 브레이싱이 42개 설치된 경우엔 X1, X2, X3, X4의 보강 효과가 약 20 %p, 11 %p, 16 %p, 7 %p 더 크게 나타났지만, 이러한 보강 효과는 각 설치 형태가 외벽과 만나는 설치 높이의 외벽 응력 감소에 효과적인 것으로 나타났다. 따라서, X 브레이싱을 통해 외벽에 발생하는 최대 응력의 감소를 목표로 할 경우 1 m 높이 이하에 설치되어야 하나, 수조 내부의 보수보강을 위한 이동성이 고려되어야 하므로, X 브레이싱은 수조 상단 보강에 적합할 것으로 사료된다.
- (2) L-앵글은 설치 높이가 자유로워 수압이 크게 작용하는 외벽 하단부에 일부 구간에만 추가 설치함으로써 경제적 보강이 가능하며, 이때 보강 효과는 L-앵글이 추가 설치된 구간에서는 확인되지만, 이외의 구간은 동일 수준의 응력 분포를 유지하는 것으로 나타났다.
- (3) 이중 패널 벽체구조 원형 물탱크에서 내벽은 정수압이 안팎으로 상쇄됨에 따라 지진 시 지진의 방향성을 고려한 동수압만 작용하여, 정수압과 동수압이 조합하여 작용하는 외벽 대비 작은 수압이 작용하였다. 하지만 수조 중심에서 바깥으로 인장 방향의 정수압이 지배적인 외벽과 달리, 내벽 1/2면은 동수압이 압축 방향으로 작용하여 좌굴에 대한 보강이 필요한 것으로 나타났으며, L-앵글의 추가 설치를 통한 내벽 좌굴 보강안을 제안하였다.
- (4) 5,000톤 규모의 이중 패널 벽체구조 원형 물탱크에서 내외벽 간격은 2 m - 5 m까지 증가해도 벽체의 거동에 큰 영향을 미치지 않는 것으로 나타났으므로, 내외벽 간격은 벽체 간 보강재의 시공성 등을 고려하여 결정하는 것이 합리적일 것으로 사료된다.
- (5) 제시한 보강 및 구조 상세에 따른 이중 패널 벽체구조 원형 물탱크의 거동 분석은 설계기준에서 제시하는 동수압을 기준으로 내진에 대해 검토하였으나, 유체-구조의 상호작용을 추가적으로 고려함으로써 보다 정확한 거동 분석이 가능할 것으로 생각된다.
Acknowledgments
본 연구는 중소벤처기업부와 중소기업기술정보진흥원의 “지역특화산업육성+(R&D, S3090747)”사업과 ㈜포스코의 지원을 받아 수행된 연구결과임.
References
-
Bae, D., Park, J.H., and Oh, C.K. (2016) Comparison of Design Standards for Seismic Design of Steel Liquid Storage Tanks, Journal of Korean Society of Steel Construction, KSSC, Vol.28, No.3, pp.195-202 (in Korean).
[https://doi.org/10.7781/kjoss.2016.28.3.195]

-
Bae, D., Park, I.G., Park, J.H., and Oh, C.K. (2016) Comparison of Wind Load Provisions Based on the Wind Buckling Behaviors of Plant Tank, Journal of Korean Society of Steel Construction, KSSC, Vol.28, No.3, pp.203-211 (in Korean).
[https://doi.org/10.7781/kjoss.2016.28.3.203]

-
Moslemi, M., and Kianoush, M.R. (2012) Parametric Study on Dynamic Behavior of Cylindrical Ground-Supported Tanks, Engineering Structures, Elsevier, Vol.42, pp.214-230.
[https://doi.org/10.1016/j.engstruct.2012.04.026]

-
Bakalis, K., Fragiadakis, M., and Vamvatsikos, D. (2017) Surrogate Modeling for the Seismic Performance Assessment of Liquid Storage Tanks, Journal of Structural Engineering, American Society of Civil Engineers, Vol.143, No.4, 04016199.
[https://doi.org/10.1061/(ASCE)ST.1943-541X.0001667]

-
Heo, S.J., Yoh, K.Y., and Kim, J.K. (2022) Design of Large Capacity Water Tank with Stainless Corrugated Panel Wall, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.1, pp.55-66 (in Korean).
[https://doi.org/10.7781/kjoss.2022.34.1.055]

- Woo, Y.B. (2005) Republic of Korea Patent No. 1020050044781, Korea (in Korean).
- Korean Agency for Technology and Standards (2016) Design Requirements for Windpressure-Proof and Earthquake-Proof of Liquid Storage Tanks (KS B 6283: 2016), Korea (in Korean).
- Ministry of Land, Infrastructure and Transport (2019) Seismic Design Standard for Buildings (KDS 41 17 00: 2019), Korea (in Korean).
- American Concrete Institute (2006) Seismic Design of Liquid-Containing Concrete Structures and Commentary (ACI 350.3-06), USA.
- Ministry of Land, Infrastructure and Transport (2019) Building Structure Standards – Design Load (KDS 41 10 15: 2019), Korea (in Korean).
- National Information Center of Earthquake Engineering (2007) Guidelines for Seismic Design of Liquid Storage Tanks (IITK-GSDMA), India.