교통신호등주 지지부 피로응력집중도 해석

1. 서 론

교통신호등주의 지주(pole)와 기초판(base plate)은 용접을 통해 연결되며, 지주에 작용하는 휨모멘트에 의해 연결부에 인접한 지주에 면외휨이 발생하여 높은 응력집중이 발생할 수 있다^[1],[2]. 이러한 높은 응력집중으로 인해 용접부에 발생하는 응력 수준이 높아져 피로균열로 인한 파괴가 발생할 수 있으므로, 교통신호등주의 피로수명이 감소하고 차량 및 인명 사고가 발생할 수 있다^[3],[4].

교통신호등주에 휨모멘트를 발생시키는 주요한 요인은 바람이 신호등주를 통과하면서 발생하는 와류(vortex shedding)와 차량이 신호등주를 통과하면서 발생시키는 돌풍(wind gust)이다. 교통신호등주는 단면의 두께에 비해 길이가 매우 긴 세장한 형상을 나타내며 고유 감쇠비가 1 % 이하로 매우 낮아 진동이 시작되면 매우 긴 시간 동안 지속적으로 진동이 유지되는 특성이 있다^[5],[6]. 따라서 단기간에 많은 반복하중을 받을 수 있으므로 피로에 취약하다.

교통신호등주의 지주-기초판 용접 연결부에 대한 피로강도를 규명하기 위해 다수의 실험 및 수치해석 연구가 수행되었다. Koenigs et al.^[4]은 피로실험을 통해 기초판의 두께를 51 mm 이상 확보해야만 AASHTO^[7]에서 제시하는 피로범주 E’를 확보할 수 있다는 것을 밝혔다. 이후 피로실험을 통해 지주 및 기초판의 크기와 형상 및 기초판과 기초를 연결하는 볼트의 수에 따라 피로강도가 달라질 수 있음을 여러 연구자들^{[5],[6],[8]-[11]}이 실험적으로 확인했다. 지주-기초판 용접 연결부의 피로강도에 영향을 주는 인자가 다수 존재하기 때문에, 피로실험을 통해 각 인자의 영향을 규명하는 것은 많은 비용과 시간이 소요된다.

Ocel et al.^[9], Park^[10], Roy et al.^[11]은 상용 유한요소해석 프로그램을 이용하여 지주-기초판 용접 연결부에 발생하는 피로응력집중계수를 확보하고 비선형 회귀분석을 통해 각 인자들에 대한 피로응력집중계수를 추정할 수 있는 식을 제안하였다. 특히 Park^[10]과 Roy et al.^[11]은 피로실험으로 확보한 피로강도와 피로응력집중계수의 상관성을 분석하여 응력집중계수에 따른 피로강도를 제안하였고 AASHTO의 교통신호등주 설계기준^[12]에 반영되었다. 그러나 응력집중계수 추정식은 미국에서 사용하는 지주의 크기를 반영하여 지주의 지름이 203 mm 이상의 지주에 대해서 유효하다. 국내에 사용되는 교통신호등주의 지름은 최소 91 mm로 AASHTO의 교통신호등주 설계기준의 식을 적용할 수 없다^[13],[14].

이 연구에서는 AASHTO의 교통신호등주 설계기준^[12]에서 제시하고 있는 피로응력집중계수의 적용 범위를 확장하여 국내에서 사용하는 교통신호등주의 피로설계에도 적용하고자 한다. Park^[10]과 Roy et al.^[11]가 확보한 지주-기초판 용접 연결부의 피로응력집중계수와 국내에서 사용하는 지주-기초판 용접 연결부의 피로응력집중계수를 추가하고 비선형 회귀분석을 통한 피로응력집중계수를 도출하였다.

2. 해석방법 및 피로응력집중 영향인자

2.1 피로응력집중계수 해석 및 유한요소모델링 방법

각 지주-기초판 용접 연결부의 피로응력집중계수를 얻기 위해 상용 유한요소해석 프로그램 ABAQUS 2021^[15]을 사용하여 유한요소 상세해석을 진행하였다. 피로응력집중의 크기의 정확한 확인을 위해 글로벌 모델(global model) 및 서브 모델(submodel)을 생성하여 2단계 해석을 실시했다.

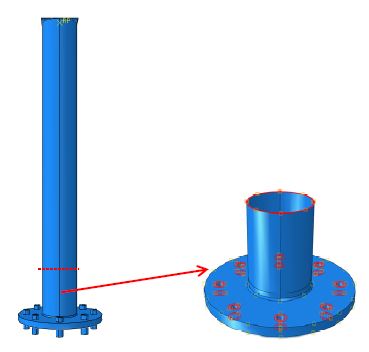
글로벌 모델(Fig. 1)은 지주의 길이를 지름의 8배가 되도록 했으며 기초판의 반대편의 지주면에 강체로 만든 하중재하판(loading plate)에 지주 길이의 직각 방향으로 집중하중을 재하하였다. 교통신호등주의 지지부를 정확히 모사하기 위해 체결력을 도입한 앵커볼트가 기초판을 지지하도록 하였으며 앵커볼트의 아랫면은 모든 방향으로 고정하였다. 앵커볼트와 기초판이 닿는 면은 모두 접촉(contact)하게 만들어 기초판과 앵커볼트의 상호작용을 모사할 수 있도록 했다. 하중의 크기는 지주-기초판 연결부의 지주 단면에 최대 10 MPa의 공칭인장응력이 발생하도록 하였다.

Fig. 1.

Part details

서브 모델(Fig. 2)은 기초판 위로부터 지주의 길이가 지름의 1.5배가 되도록 하였으며, 앵커볼트를 제거하고 Fig. 2에서 붉은색 면으로 표시된 면에 글로벌 모델에서 얻은 변위를 재하하였다. 격자의 크기는 지주의 두께 방향으로 2층으로 구성하고 격자의 최대 가로-세로 비율이 1:4를 넘지 않도록 하였으며 수렴성테스트를 통해 연결부에 발생하는 국부응력이 수렴하는 것을 확인하였다.

Fig. 2.

Global model and submodel

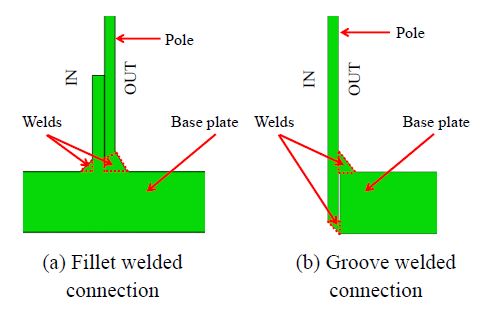
지주-기초판 용접 연결부는 지주를 기초판에 삽입하고 기초판 상하면에서 필릿용접을 하는 경우(Fig. 3(a))와 지주를 기초판 위에 올려놓고 지주 단부에 홈을 판 후 지주 안쪽에 백킹 링(backing ring)을 설치하여 용접을 하는 그루브용접(Fig. 3(b))의 두 경우를 고려했다. 그루브용접의 경우에는 기초판의 강성이 필릿용접의 경우보다 크기 때문에 지주 단면에 작용하는 휨응력으로 인한 기초판의 변형이 상대적으로 작아서 연결부의 응력이 낮은 장점이 있다^[1],[3].

Fig. 3.

Two types of pole-to-base plate welded connections

지주-기초판 용접 연결부의 피로응력집중계수는 연결부의 지주 표면에서 발생하는 최대주응력을 연결부 단면에서의 최대 공칭인장응력으로 나눈 값으로 정의하였다^{[8],[10],[11]}. 최대주응력은 용접 노치에서 발생하며 노치가 뾰족할 경우 이론적으로 무한대의 응력이 발생한다. 따라서 국부피로응력은 용접 노치에서 얻을 수 없으며 이 연구에서는 DNV-RP-C203^[16]에서 제안하는 용접 노치로부터 지주 길이방향으로 $$ 0.1\sqrt{\left(RT\right)}$$만큼 떨어진 위치에서의 최대주응력을 연결부의 피로응력으로 결정했다(Fig. 4). 여기서 R은 지주의 반지름, T는 지주의 두께를 의미한다.

Fig. 4.

Location of local fatigue stress

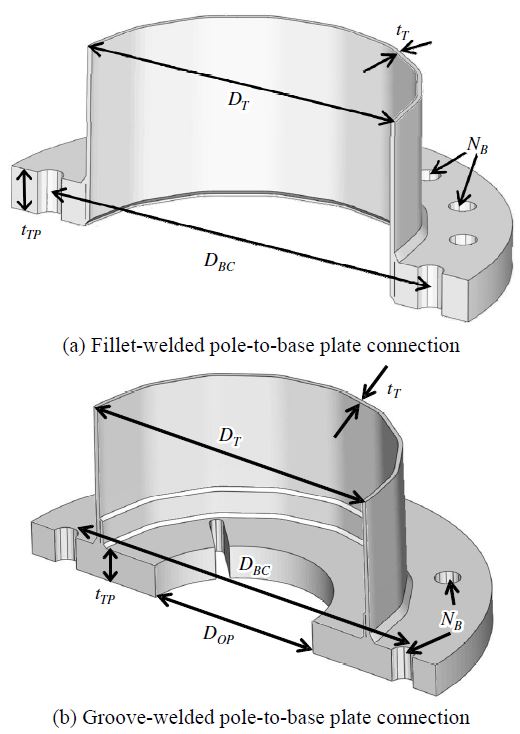
AASHTO의 교통신호등주 설계기준^[12]에 따르면 지주-기초판 연결부의 피로강도에 영향을 주는 영향인자들은 강관의 지름(D_T), 두께(t_T), 기초판의 두께(t_TP), 볼트 개수(N_B), 기초판 내부 구멍 지름(D_OP), 볼트 배열 지름(D_BC)이다. 기초판 내부 구멍 지름(D_OP)과 볼트 배열 지름(D_BC)은 각각 지주의 지름보다 작거나 클 수 없기 때문에 각각의 지름을 지주의 지름으로 나누어 지주 지름에 대한 비율로 정의했으며 이들을 기초판 내부 구멍 지름비(base plate opening ratio, C_OP)와 볼트 배열 지름비(bolt circle ratio, C_BC)로 정의하였다.

Fig. 5.

Identified geometric parameters[12]

기존 지주-기초판 용접 연결부에 대한 피로설계식을 국내 실정에 맞게 확장하기 위해 국내에서 사용하는 지주 및 기초판에 대한 인자들을 적용했다. 지주의 지름과 두께는 Fig. 6와 같이 기존 설계식에서 고려하지 않은 작은 크기의 지주 지름과 두께를 포함하였다. 기초판 또한 기존 식에서 고려하지 않은 25 mm, 30 mm, 32 mm의 얇은 두께의 기초판을 고려했다. 기초판 내부 구멍 지름비는 0.36, 0.63, 0.9를 적용했으며, 볼트 배열 지름비는 국내 교통신호등주 설계^[13],[14]에 따라 1.27부터 1.92까지 다양하게 적용했다.

Fig. 6.

Detailed analysis model according to diameter

3. 용접 형태에 따른 피로응력집중계수

3.1 기존 피로응력집중계수 식 분석

이 연구에서는 기존 지주-기초판 용접 연결부의 피로설계식의 유효범위가 우리나라에서 사용되는 교통신호등주에 적용될 수 없기 때문에 우리나라에서 교통신호등주 설계에 사용되는 영향인자들에 대한 유한요소해석을 수행하고 피로응력집중계수를 확보하였다.

먼저 기존 설계식과 이 연구에서 구한 피로응력집중계수를 비교하고 기존 식을 그대로 사용할 수 있는지 확인하였다. 유한요소해석을 통하여 얻은 피로응력집중계수는 SCF(stress concentration factor)로 표기하였고 기존 설계식으로 구한 피로응력집중계수는 GSCF(geometric stress concentration factor)로 표기하였다. 필릿용접 및 그루브용접에 대한 기존 설계식은 각각 식 (1), 식 (2)와 같으며 영향인자 값을 대입하면 피로응력집중계수를 구할 수 있도록 만들어져있다^[12]. Table 1은 식 (1)와 식 (2)의 영향인자들의 유효범위를 나타낸다.

$\[ \begin{array}{ll}GSCF=& 2.16+\left(1.17\times D_T^{1.15}-14.6\right)\\ & \times \left(0.924\times C_{BC}^{0.0474}\times N_B^{-0.0105}-0.908\right)\\ & \times \left(4.54+52.1\times t_T\right)\times t_{TP}^{-2.36}\end{array} \]$

(1)

$\[ \begin{array}{ll}GSCF=& 1.35+\left(C_{BC}^{0.00674}\times N_B^{-0.0029}-0.982\right)\\ & \times \left(\frac{1.0}{-0.764+C_{OP}^{-0.689}}\right)\\ & \times \left(0.446\times D_T^{1.12}-2.6\right)\\ & \times \left(1.0+17.3\times t_T\right)\times t_{TP}^{-1.95}\end{array} \]$

(2)

Table 1.

Effective ranges of the influence factors consider in AASHTO[12]

Fig. 7은 지주두께가 5.5 mm, 볼트 배열 지름비가 1.92, 기초판의 두께가 25 mm - 32 mm, 지주 지름이 170 mm - 360 mm인 필릿용접 지주-기초판 연결부에 대해 기존 설계식과 유한요소해석으로 구한 피로응력집중계수를 보여준다. 기초판의 두께와 지주의 지름이 AASHTO^[12]에서 제시하는 영향인자의 유효범위를 벗어난 경우이다. 전반적으로 지주 지름이 커짐에 따라 응력집중계수가 증가하는 경향을 모두 보여준다. 그러나 기존 설계식의 경우 유한요소해석결과보다 계수값의 크기가 작다. 이는 기존 설계식이 얇은 기초판에 대해 응력집중을 과소평가하고 있음을 나타낸다.

Fig. 7.

Influence of pole diameter on SCF and GSCF of fillet-welded pole-to-base plate connection for various base plate thickness

또한 기초판 두께가 25 mm인 경우 지주 지름이 줄어듦에 따라 응력집중계수가 1 이하로 줄어들고 더 두꺼운 기초판의 응력집중계수보다 낮은 값을 나타낸다. 지주-기초판 연결부는 휨모멘트를 받을 경우 연결부 인근에서 면외휨이 발생하므로 응력집중이 반드시 발생하며^[2] 기초판의 두께가 얇을수록 면외휨의 크기가 커지기 때문에 더 높은 응력이 발생한다^[3]-[6]. 이러한 현상을 유한요소해석결과는 정확히 반영하는데 반하여 기존 설계식은 그렇지 못하다.

기존 설계식을 분석해보면 필릿용접과 그루브용접 모두 식 (3) 및 식 (4)와 같이 지주의 지름이 커짐에 따라 응력집중계수가 커지는 경향을 나타내도록 되어있다. 그러나 지주의 지름이 필릿용접의 경우 약 227 mm 그리고 그루브용접의 경우 약 123 mm 이하인 경우에는 해당 항이 음수가 된다. 이러한 이유로 기존 식은 작은 지름의 지주에 대해서 정확하지 않은 피로응력집중계수값을 나타낼 수밖에 없다. 따라서 기존 설계식은 영향인자들의 유효범위를 벗어나는 경우 사용할 수 없음을 알 수 있다. 우리나라에서 주로 사용하는 얇은 기초판과 작은 지름의 지주에 대한 피로설계를 위해서는 기존 식에 대한 수정이 불가피하다.

$\[ {∆}_F=1.17\times D_T^{1.15}-14.6 \]$

(3)

$\[ {∆}_G=0.446\times D_T^{1.12}-2.6 \]$

(4)

3.2 피로응력집중 식의 수정

기존 설계식을 수정하기 위해 지주 지름에 해당하는 항에서 음의 값이 발생하지 않도록 상수항을 삭제하였다. 새로운 설계식을 만들기 위해 기존 설계식을 만들 때 사용한 데이터에 추가하여 국내에서 사용하는 지주 및 기초판의 제원에 대해 필릿용접의 경우 162개 그리고 그루브 용접의 경우 486개의 유한요소해석결과를 활용하여 비선형 회귀분석을 실시했다. 새로운 설계식 도출에 활용한 데이터의 개수는 필릿용접의 경우 852개, 그루브 용접의 경우 3,007개이다. 비선형 회귀분석은 상용 통계분석 프로그램인 SigmaPlot v10^[17]을 사용하였다. 비선형 회귀분석 결과 필릿용접과 그루브용접에 대한 피로응력집중계수는 각각 식 (5), 식 (6)과 같이 얻을 수 있었다.

$\[ \begin{array}{ll}GSCF=& 2.05+\left(0.355D_T^{1.89}\right)\times \left(0.907+0.197t_T\right)\\ & \times \left(0.417C_{BC}^{0.456}\times N_B^{-0.0644}-0.34\right)\times t_{TP}^{-2.21}\end{array} \]$

(5)

$\[ \begin{array}{ll}GSCF=& 1.3+\left(1.21C_{BC}^{0.0956}\times N_B^{-0.0062}-1.17\right)\\ & \times \left(\frac{2.1}{-0.967+C_{OP}^{-0.104}}\right)\times \left(0.021D_T^{1.45}\right)\\ & \times \left(0.821+0.416t_T\right)\times t_{TP}^{-1.79}\end{array} \]$

(6)

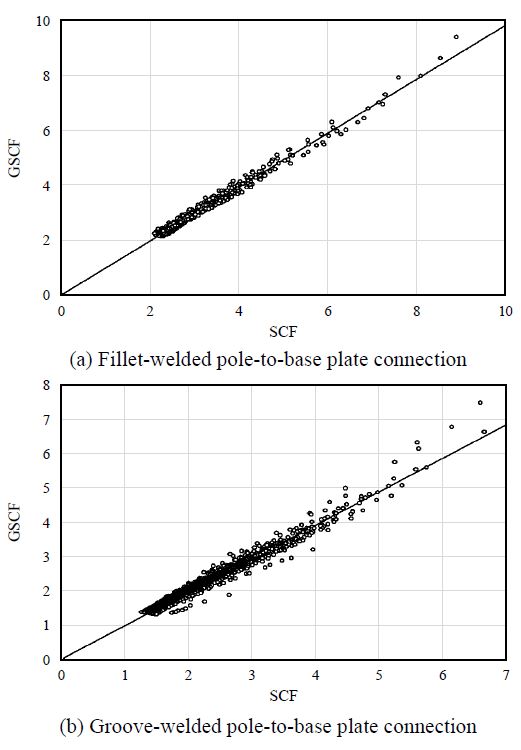
각 식의 정확도를 확인하기 위하여 유한요소해석과 식 (5), 식 (6)으로 구한 피로응력집중계수를 Fig. 8에 나타냈다. 필릿용접의 경우 추정의 표준오차는 약 4.3 %, 결정계수(R²)는 0.998이었고, 그루브용접의 경우 추정의 표준오차는 약 8.5 %, 결정계수(R²)는 0.978이었다.

Fig. 8.

Regression results of Eqs. (5)-(6)

식 (5)와 식 (6)을 적용할 수 있는 범위는 Table 2와 같으며 우리나라에서 적용하는 모든 교통신호등주 설계에 적용할 수 있도록 확장하였다.

Table 2.

Effective ranges of the influence factors from this study

4. 결 론

AASHTO의 교통신호등주 설계기준에서 제시하고 있는 지주-기초판 용접 연결부에 대한 피로설계식은 지주의 지름이 작아질수록 정확하지 않은 피로응력집중계수를 제시하는 것을 확인하였다. 우리나라의 경우 미국보다는 작은 지름을 가지는 지주를 사용하므로 AASHTO에서 제시하는 피로설계식을 사용하는 경우 정확하지 않은 피로설계를 할 가능성이 있다. 따라서 우리나라에서 사용하는 작은 지름의 지주를 가지는 지주-기초판 연결부에 대한 유한요소해석을 통해 연결부에 발생하는 피로응력집중계수를 확보하고 기존 설계식을 수정하여 작은 지름의 지주에도 적용 가능한 피로응력집중계수를 제안하였다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단(No.2020R1A4A4079299)과 2022년도 인하대학교의 지원을 받아 수행된 연구임.

References

• Hall III, J.H. (2004) The Effect of Baseplate Flexibility on the Fatigue Performance of Welded Socket Connections in Cantilevered Sign Structures, Master’s Thesis, Lehigh University, USA.
• Irvine, N.M. (1981) Review of Stress Analysis Techniques Used in UKOSRP, Proceedings of Conference on Fatigue in Offshore Structural Steels, Institute of Civil Engineers, UK, pp.47-57.
• Kaczinski, M.R., Dexter, R.J., and van Dien, J.P. (1998) Fatigue-Resistant Design of Cantilevered Signal, Sign and Light Supports, NCHRP Report 412, Transportation Research Board, USA.
• Koenigs, M.T., Botros, T.A., Freytag, D., and Frank, K.H. (2003) Fatigue Strength of Signal Mast Arm Connections, FHWA/TX-04/4178-2, Texas Department of Transportation, USA.
• Roy, S., Park, Y.C., Sause, R., and Fisher, J.W. (2012) Fatigue Performance of Stiffened Pole-to-Base Plate Socket Connections in High-Mast Structures, Journal of Structural Engineering, American Society of Civil Engineers, Vol.138, No.10, pp.1203-1213. [https://doi.org/10.1061/(ASCE)ST.1943-541X.0000554]
• Roy, S., Park, Y.-C., Sause, R., and Fisher, J.W. (2010) Fatigue Performance of Groove-Welded Tube-to-End Plate Connections in Highway Sign, Luminaire, and Traffic Signal Structures, Transportation Research Record, Sage, Vol.2152, No.1, pp.​63-70. [https://doi.org/10.3141/2152-08]
• American Association of State Highway and Transportation Officials (2001) Standard Specification for Structural Supports for Highway Signs, Luminaires, and Traffic Signals (4th Ed.), USA.
• Ocel, J.M., Dexter, R.J., and Hajjar, J.F. (2006) Fatigue-Resistant Design for Overhead Signs, Mast-Arm Signal Poles, and Lighting Structures, MN/RC-​2006-07, Minnesota Department of Transportation, USA.
• Stam, A.P., Richman, N., Pool, C., Rios, C., Anderson, T., and Frank, K. (2011) Fatigue Life of Steel Base Plate to Pole Connections for Traffic Structures, FHWA/TX-11/9-1526-1, Center for Transportation Research, University of Texas at Austin, USA.
• Park, Y.C. (2015) Developing Fatigue Tube-to-​Transverse Plate Welded Connections for Highway Sign, Signal, and Luminaire Support Structures, Ph.D. Dissertation, Lehigh University, USA.
• Roy, S., Park, Y.C., Sause, R., Fisher, J.W., and Kaufmann, E.J. (2011) Cost-Effective Connection Details for Highway Sign, Luminaire, and Traffic Signal Structures, NCHRP Web-Only Document 176, Transportation Research Board, USA.
• American Association of State Highway and Transportation Officials (2015) LRFD Specifications for Structural Supports for Highway Signs, Luminaires, and Traffic Signals (1st Ed.), USA.
• Korean National Police Agency (2017) Installation and Maintenance Manual for Traffic Signals, Korea (in Korean).
• Korea Road Traffic Facility Industry Cooperatives (2018) Integrated Traffic Light Poles (SPS-F RTSFA-​002-7268: 2018), Korea (in Korean).
• Dassault Systèmes Simulia Corp. (2021) Abaqus 2021 Abaqus/CAE User’s Guide, DSS, USA.
• Det Norske Veritas (2011) Fatigue Design of Offshore Steel Structures (DNV-RP-C203), Norway.
• Systat Software, Inc. (2006) SigmaPlot 10 – User’s Manual, USA.