휨 실험 모사를 위한 파형강판 볼트 이음부 모델링

1. 서 론

파형강판은 일정 크기의 구조용 강판재를 정해진 규격의 파형모양으로 성형하여 파형성형 전 평평한 강판의 강성을 증가시킨 건설 부재로서 일반 강판에 비해 단면계수가 10~30배 커 하중에 대한 내하력과 저항력이 우수하다^[1]-[4]. 이러한 파형강판 구조물은 구조 특성상 제작된 여러 개의 강판을 서로 이어 붙여 완성하는데, 주로 볼트를 이용하여 강판을 연결하므로 볼트 이음부 강도는 구조물에 중요한 설계변수가 된다^[5].

볼트 이음부 강도평가는 지금까지 실험을 통해 타당성을 검증하고 설계근거를 마련해왔지만^[6]-[9], 비용 및 시간 등이 많이 할애되는 단점이 존재한다. 이 연구에서는 휨 실험 대신 유한요소해석을 통해 경제적이면서도 효율적인 휨강도 평가를 수행하기 위해 볼트 이음부를 모델링하는 방법을 연구하였다.

유한요소해석 방법의 유효성 검증 및 볼트 이음부를 모사하는 모델링 방법을 찾기 위해 선행연구^[6],[9]에서 진행된 실험체를 바탕으로 유한요소해석모델을 모델링하였으며 구조물의 형상, 물성치, 경계조건 및 변위조건 모두 실험과 동일하게 진행하였다.

볼트 이음부의 모델링 과정을 진행할 때 강판 사이의 상호작용과 좌굴 형상 그리고 강도를 구현하는 것이 중요하다. 모델링 과정에서 실험과 똑같이 볼트 모양을 만들어 넣는 방법은 해석이 힘들고 제한적이지만, 유한요소해석 프로그램에서 제공하는 구속조건 옵션들을 사용하여 실제 볼트를 체결한 것과 같은 상황을 모사할 수만 있다면 유효한 해석결과 도출은 물론 수월한 모델링으로 인한 시간 절감도 가능하다.

유한요소해석 프로그램에서 제공하는 이음부의 구속조건 옵션들이 다양하기 때문에 실험과 유한요소해석 결괏값들을 비교하여 볼트를 구현할 수 있는 구속조건을 찾는 방법으로 진행하였으며, 휨 실험 특성상 강체에 좌굴이 발생하기 때문에 좌굴 형상 및 좌굴로 인해 생기는 강도감소 현상 또한 구현하는 방법을 찾는 연구를 진행하였다.

2. 유한요소 휨 구조해석

2.1 해석모델

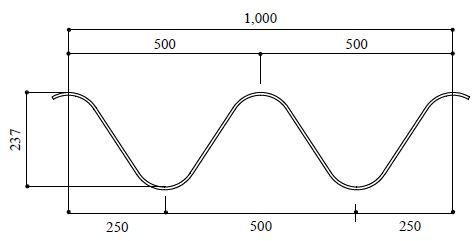
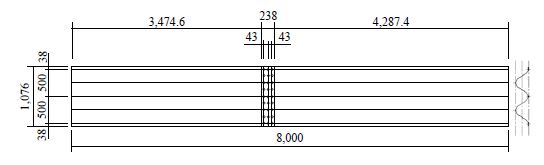
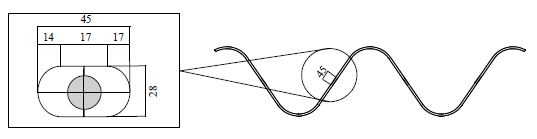
본 연구의 휨 해석을 진행할 모델은 두께 6.0 mm를 사용하여 Fig. 1과 같이 골 깊이 240 mm, 골 간격 500 mm인 슈퍼 대골형 파형강판(extra-deep corrugated steel plate, EXDEC)^[10]에서 적용 가능한 ASTM^[11] 설계기준에 따른 실험체 Fig. 2를 사용하였다.

Fig. 1.

Cross-section and dimensions of EXDEC (Unit: mm)

Fig. 2.

Specimen for the bolted connection (3 rows, with web bolt, Unit: mm)

2.2 휨 구조해석 모델링 방법

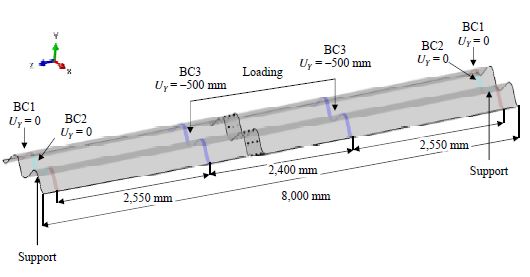
전 세계적으로 가장 널리 사용되는 상용 유한요소구조해석 프로그램인 ABAQUS 2021^[12]를 이용하여 Fig. 3와 같이 4점재하 휨 구조해석 제원 및 경계조건(BC)을 구현했으며 구조물의 형상, 물성치, 경계조건 및 하중조건 모두 실험과 동일하게 하였다. 강판의 탄성계수는 210 GPa를 적용하였으며 항복강도는 두께별로 인장시험을 통해 구한 값(Table 1)을 사용하였다. 재료 모델은 재료가 항복한 후에는 일정한 항복고원을 가지는 bi-linear 모델을 적용하였다. 요소는 선형형상함수를 가지는 6면체 모양의 3차원 요소를 사용했으며, 강판의 두께 방향으로 2개의 요소층을 가지도록 하였다. 요소의 형상비는 1:4를 넘지 않도록 하였으며 수렴성 테스트를 통해 과다한 변형이 발생하는 볼트 구멍 주변에서 응력값이 수렴하는 것을 확인했다. 각 BC마다 자세한 모델링 방법을 아래에 설명하였다.

Fig. 3.

Four-point loading test setup and dimensions (Unit: mm)

Table 1.

Measured yield strengths for each plate thickness

Fig. 4는 지지부(BC1, BC2)를 유한요소해석 프로그램으로 모사한 것이다. 강판하부 지지부 라인을 따라 BC1를 만든 후 높이 방향 변위를 고정시켜 지지부를 모사하였고, 파형모양의 지그장치로 인해 고정되는 BC2를 만들어 너비 방향 변위를 고정시켰다.

Fig. 4.

Support realized by finite analysis software

Fig. 5는 가력부(BC3)를 유한요소해석 프로그램으로 모사한 것이다. 강판상부 가력부 라인 중심에 reference point​(RP)를 만들고 RP를 기점으로 가력부 라인을 coupling시켜 가력부 라인 전체가 coupling된 RP를 따라 거동하도록 하였다. BC3는 RP에 높이 방향 변위 –500 mm를 재하시켜 가력부를 모사하였다.

Fig. 5.

Loading realized by finite analysis software

볼트 이음부는 휨 실험 진행 중 강판이 서로 접촉되기 때문에 강판의 마찰계수 0.4를 적용한 Contact 옵션을 사용하였다. Fig. 6와 같이 상부판 이음부 하부면과 하부판 이음부 상부면을 서로 contact하여 변형형상을 실험과 동일하게 나타내도록 하였다.

Fig. 6.

Bolted joint contact realized by finite analysis software

2.3 휨 구조해석 방법

휨 실험을 진행할 때 이음부 주변에서 좌굴이 발생한다. 유한요소해석 프로그램에서 정적해석을 진행할 수 있는 옵션은 General 해석, Riks 해석으로 진행할 수 있다.

General 해석은 모델에 존재하는 모든 비선형성의 영향을 포함할 수 있는 단계이다^[12]. 쉽게 말해 일반적인 구조해석을 진행할 때 General 옵션을 사용한다.

Riks 해석은 구조물의 불안정하고 기하학적 비선형 붕괴를 예측하는데 사용된다^[12]. Arc-length 기법이라고도 불리는 것으로, 하중을 자동으로 증감하면서 평형점을 찾아가는 기법이다. 따라서 하중값을 부여하여 구조물의 좌굴이 발생하거나 분기될 때 해석할 수 있는 방법이다. 이 해석방법은 좌굴 발생 시 구조물의 강성에 음의 값이 발생할 경우에도 해석이 가능하다는 장점이 있다. 그러나 구조모델이 복잡한 경우에 해석결과의 수렴성이 떨어지는 단점이 존재한다.

본 연구에서 진행하는 실험체는 하중재하가 아니라 변위재하이기 때문에 변위를 재하하는 위치에서의 반력을 구하여 General 해석으로도 좌굴이 발생한 구조물에서 음의 강성이 발생하는 하중-변위 그래프를 도출할 수 있었다. 이 방법을 증명하기 위해 두께 6.0 mm의 강체를 가지고 변위재하 방법으로 General 옵션과 Riks 옵션의 해석을 각각 진행하였다.

Fig. 7을 보면 하중-변위 그래프에서 General 해석방법과 Riks 해석방법이 동일한 극한강도를 구현하고 있으며 General 해석이 좌굴로 인해 생기는 하중감소 현상을 표현한다는 것이 확인되었다. 그러나 Riks 해석을 수행하는 경우 Contact 옵션이 추가된 모델에서는 수렴성에 문제가 있어 국부좌굴 발생 후 강성이 음의 값이 되는 것을 모사할 수 없다.

Fig. 7.

General and Riks load-displacement graph

3. 볼트 이음부 상세 모델링

3.1 개요

실험에 사용된 볼트 이음부의 볼트 구멍 크기는 M22, F13T의 고장력 볼트의 규격을 참고하여 ASTM^[11] 기준으로 Fig. 8과 같이 구현된다. 실험 파형강판의 볼트 구멍 모양은 타원형이지만 유한요소해석모델은 모델링의 편의성과 볼트 이음부 구속조건 설정에 있어 볼트 몸통부 크기만 고려하여 Fig. 9과 같이 지름 20 mm의 원형으로 하였다.

Fig. 8.

Slotted hole according to ASTM standard (D28×45)

Fig. 9.

Bolted joint realized by finite analysis software

유한요소해석 프로그램에서 제공하는 이음부의 구속조건 옵션들이 다양하기 때문에 실험과 유한요소해석 결괏값을 비교하여 볼트의 축력 및 체결력을 구현할 수 있는 구속조건을 찾는 방법으로 진행하였다. 두께 6.0 mm의 강판으로 타당성 검사를 실시하였고, 모델링한 강판에 구속 옵션들을 바꿔가며 실시하였다. 구속 옵션의 종류로는 이론상 볼트 연결과 적합하다고 생각한 Tie, Coupling, MPC_Beam, MPC_Pin, Connect_Axial을 서로 비교실험하였다.

3.2 해석방법

모델링한 파형강판에 볼트 이음부 구속 옵션을 바꿔서 진행하는 방법으로 진행하였으며, 해석결과를 하중-변위 그래프로 나타내어 실험 그래프와 비교 분석하였다. 여러 가지 구속조건 중 볼트의 성질을 모사할 수 있는 구속조건을 찾는 방법으로 진행하였다.

3.2.1 Tie constraints

Tie는 맞닿은 두 surface의 node들을 하나로 고정하는 역할을 한다. 볼트의 체결력을 구현하기 위해 이 방법을 시도하였고 Fig. 10은 유한요소해석 프로그램을 이용하여 맞닿은 두 edge의 node들을 하나로 고정시킨 tie constraint이다.

Fig. 10.

Tie constraint

3.2.2 Coupling

Coupling은 관성 모멘트 표현 식으로 하중 분포를 설명할 수 있는 모델에 하중을 분산하고 이러한 경우의 예로 볼트 및 용접 등을 표현할 수 있다^[12]. Fig. 11과 같이 볼트 중간 부분에 RP를 하나 만들어 RP를 기준으로 두 볼트 구멍의 가장자리를 연결하여 볼트 이음부를 모사하였다.

Fig. 11.

Coupling

3.2.3 MPC_Beam

MPC(multi-point constraints)는 모델의 서로 다른 자유도 사이에 구속조건을 부과할 수 있다. 유한요소해석 프로그램은 서로 다른 구속조건을 연결하는 여러 가지 옵션을 제공한다. 그중 하나인 MPC_Beam은 두 node 사이에 강체 빔을 제공하여 첫 번째 node의 변위 및 회전을 두 번째 node의 변위 및 회전으로 제한하고 두 node 사이에 강체 빔이 존재하는 것과 같은 형상을 표현한다^[12].

Fig. 12는 유한요소해석 프로그램으로 구현한 MPC_​Beam 이음으로, 그림과 같이 각 볼트 구멍 가장자리를 하나의 RP로 연결한 후 두 RP를 MPC_Beam으로 이은 것이며 이러한 특성이 볼트와 비슷하다고 생각하여 해석을 진행하였다.

Fig. 12.

MPC_Beam

3.2.4 MPC_Pin

MPC_Pin은 두 node 사이에 고정된 조인트를 제공하며 전체 변위를 동일하게 만들지만, 회전이 있는 경우 서로 독립적으로 유지한다^[12]. 파형강판 휨 실험 특성상 4점재하 방식이기 때문에 복부볼트에서 두 볼트 구멍 node에서 회전이 발생한다. 앞서 실험했던 Coupling과 MPC_​Beam은 두 node의 변위와 회전까지 제어했지만, MPC_​Pin은 각 회전 방향에 대한 거동을 독립적으로 유지하기 때문에 재하 과정에서의 기울기 차이를 줄일 수 있다고 생각하여 실험을 진행하였다. Fig. 13은 유한요소해석 프로그램으로 구현한 MPC_Pin 이음이며, MPC_Beam과 마찬가지로 각 볼트 구멍 가장자리를 하나의 RP로 연결한 후 두 RP를 MPC_Pin으로 이은 것이다.

Fig. 13.

MPC_Pin

3.2.5 Connector

지금까지 선행내용에서 진행되었던 볼트 이음부 모델링 실험은 볼트 가장자리의 두 node들을 고정만 시켰다. 하지만 Connector는 두 connection의 물성치 값을 입력할 수 있어 볼트변형에 의한 슬라이드를 구현할 수 있고, 두 connection의 조임축력까지 구현 가능하여 두 판을 겹침 이음했을 때 발생하는 골 부분의 간격감소까지 구현할 수 있다.

Connection의 구성요소는 변환 connection, 회전 connection, 특수회전 connection 세 가지 범주로 나뉜다. 첫 번째 변환 connection 구성요소는 두 node의 변환 자유도에 영향을 미치고 첫 번째 node 또는 두 node의 회전 자유도에 영향을 줄 수 있다. 두 번째 회전 connection 구성요소는 두 node의 회전 자유도에만 영향을 준다. 세 번째 특수회전 connection 구성요소는 node의 회전 자유도 및 기타 자유도에도 영향을 미친다^[12]. 이 세 가지 중 정의를 참고하여 볼트를 연결한 것과 같은 결과를 낼 수 있다고 판단된 변환 connection을 사용하였다.

변환 Connection에도 여러 가지 구성요소가 존재한다. 그중 Axial 요소는 node를 연결하는 선을 따라 작용하는 두 node 사이의 연결을 제공하므로 볼트의 역할을 대신할 수 있다고 판단하여 Axial 요소로 실험을 진행하였다. 두 node 연결은 Fig. 14과 같이 MPC와 동일하게 볼트 구멍 가장자리를 하나의 RP로 연결한 후 두 RP를 connector로 이은 것이며 connector의 elastic은 200 GPa, 연결된 두 부분의 조임 축력은 실험에 M22, F13T의 고장력 볼트를 사용하였기 때문에 도로교 표준시방서^[13]를 참고하여 290 kN으로 하였다.

Fig. 14.

Connector_Axial

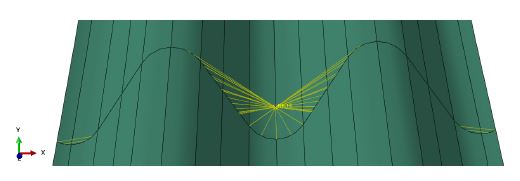
이전에 실험했던 구속옵션과는 다르게 Connector는 볼트의 물성치, 조임축력을 입력할 수 있기 때문에 두 단계로 나눠서 해석이 진행된다. 첫 번째 단계는 볼트의 물성치와 조임축력을 해석하여 서로 겹침이음되어 생기는 골 부분 간격에 대해 간격감소를 구현한 후 두 번째 단계에서 휨 재하 해석을 진행한다. 첫 번째 단계에서 구현한 이음부 골 부분 간격감소결과를 Fig. 15에 나타냈다.

Fig. 15.

Gap reduction due to tightening axial force

4. 휨 구조해석결과

4.1 구속조건 휨 해석결과

모든 구속조건의 해석을 완료하여 실험결과와 해석결과를 비교해 Fig. 16에 나타냈다. 모두 실험과 비슷한 극한하중은 도출하지만 재하과정에서 기울기 차이가 발생한다. 하지만 Connector는 실험과 비슷한 기울기를 도출하였고, 이음부 국부좌굴로 인한 음의 강성도 실험과 비슷하게 모사하고 있어 Connector가 볼트를 모사하는 옵션으로 적합하다고 판단하였다.

Fig. 16.

Thickness 6.0 mm test and analysis load-displacement graph

Connector로 진행된 실험은 좌굴 형상 또한 실험과 비슷하게 나타난다. Fig. 17은 실험과 유한요소해석의 하부판 볼트 이음부 좌굴 형상을 비교한 사진이고, Fig. 18은 실험과 유한요소해석 상부판 볼트 이음부 좌굴 형상을 비교한 사진이다. 두 모델의 해석결과를 시각적으로 비교해 봤을 때 볼트 이음부 쪽 좌굴 형상이 매우 유사하게 보인다.

Fig. 17.

Comparison of bottom plate buckling shape

Fig. 18.

Comparison of top plate buckling shape

4.2 휨 구조해석 분석

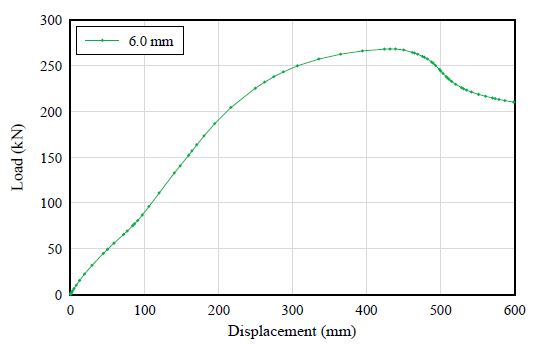
Fig. 19에는 유한요소해석 프로그램으로 해석한 두께 6.0 mm 강판 하중-변위 그래프를 나타냈다. 변위재하 시 그래프의 기울기가 부분적으로 증가하다 줄어드는 것을 볼 수 있다.

Fig. 19.

Thickness 6.0 mm finite analysis software load-displacement graph

실험과 유한요소해석의 강성도를 비교하여 Fig. 20에 나타냈다. 강성그래프의 전체적인 경향성을 살펴보면 변위가 증가할수록 전체적인 하향곡선을 그리다 지간 중앙부의 변위가 80 mm - 200 mm 사이에서 일시적으로 강성이 증가하는 현상이 나타난다.

Fig. 20.

Thickness 6.0 mm test and analysis stiffness-displacement graph

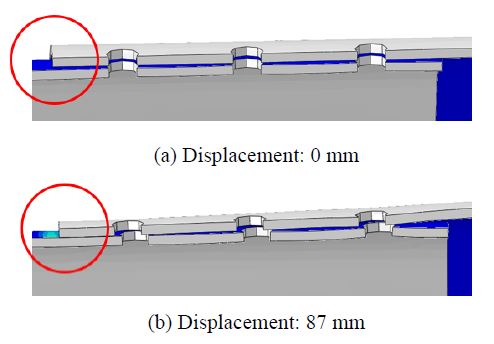
Fig. 21은 변위에 따른 하부판 볼트이음부 contact pressure 분포도이다. 똑같은 제원의 파형강판 두 판을 겹침 이음했을 때 골 부분에서 상부판과 하부판의 간격이 생기는데 이 상태로 4점재하 실험을 실시하면 지간 중앙부의 변위가 87 mm가 될 때 상부판 골이 하부판 골에 닿아 응력이 발생하는 것을 Fig. 21과 Fig. 22의 붉은 원을 통해 확인하였다. 이 때문에 지간 중앙부 변위의 저항이 생겨 강성이 일시적으로 증가하는 현상이 나타나는 것으로 보인다.

Fig. 21.

Distribution of contact pressure at the bolted joint of the bottom plate

Fig. 22.

Side contact pressure distribution of bolted joint

5. 결 론

파형강판 볼트 이음부의 휨강도 평가를 실험이 아닌 유한요소해석으로 구하기 위한 해석방법을 찾는 연구를 수행했다. 기존 볼트 이음부 휨 실험결과를 바탕으로 유한요소프로그램의 해석결과를 비교하는 방법으로 진행하였으며 결과를 종합하면 다음과 같다.

• (1) 휨 실험을 진행할 때 이음부 주변에서 발생하는 국부좌굴을 모사하기 위해서는 Riks 해석을 수행하는 것이 일반적이다. 그러나 Contact 옵션을 추가한 모델에서는 해석의 수렴성 문제가 발생해 좌굴 이후의 음의 강성을 모사할 수 없다. 그러나 변위를 재하하는 General 해석을 실시하는 경우 하중 재하부의 변위에 대한 반력값을 통해 하중-변위 관계를 확인할 수 있고 국부좌굴 발생 이후에 반력이 줄어드는 것을 모사할 수 있다.
• (2) 볼트 연결을 모사하기 위해 유한요소분석 프로그램에서 제공하는 구속 옵션 중 Tie, Coupling, MPC_​Beam, MPC_Pin, Connect_Axial을 실험하였는데 Connect_Axial 옵션이 볼트의 축력, 조임축력, 볼트의 물성치를 모두 모사할 수 있음을 확인하였고, 해석결과 또한 실험과 비슷한 결과를 도출할 수 있음을 확인하였다.
• (3) 실험체 변위재하 과정에서 이론상으로 좌굴이 생기기 전 하중-변위 그래프의 기울기가 선형으로 나타나야 하지만 실험은 비선형으로 나타난다. Tie, Coupling, MPC_Beam, MPC_Pin 옵션은 볼트의 축력, 조임축력, 볼트의 물성치를 모사할 수 없고 두 볼트 구멍 사이의 구속만 모사할 수 있기 때문에 하나의 강판을 재하한 것과 같은 그래프 형상을 나타냈다. 하지만 볼트의 축력, 조임 축력, 볼트의 물성치를 구현할 수 있는 Connect_Axial 옵션은 좌굴이 생기기 전 하중-변위 그래프가 비선형으로 나타났고 이 결과 역시 실험과 비슷하다. 이점으로 미루어 봤을 때 하중-변위 그래프에서 비선형 그래프가 생기는 이유는 볼트 이음부에서의 볼트 손상, 슬라이드가 원인으로 보인다.
• (4) 강성그래프의 전체적인 경향성을 살펴보면 변위가 증가할수록 전체적인 하향곡선을 그리다 지간　중앙부의 변위가 80 mm - 200 mm 사이에서 일시적으로 강성이 증가하는 현상이 나타난다. 같은 제원의 파형강판 두 판을 겹침이음했을 때 골 부분에서 상부판과 하부판의 간격이 생기는데 이 상태로 4점재하 실험을 실시하면 지간 중앙부의 변위가 80 mm - 200 mm 사이가 될 때 상부판 골 부분이 하부판 골 부분에 닿는 것을 확인하였다. 이 때문에 지간 중앙부 변위의 저항이 생겨 강성이 일시적으로 증가하는 현상이 나타나는 것으로 보인다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단(No.2020R1A4A4079299)과 2022년도 인하대학교의 지원을 받아 수행된 연구입니다. 실험결과를 제공해주신 청암이앤씨에도 감사드립니다.

References

• Kim, G.N. (2000) A Study on the Behavior and Force Analysis of Long-Span Corrugated Steel Plate Arch Structures, Master’s Thesis, Hanyang University, Korea (in Korean).
• Lee, P.G., Yoon, T.Y., Park, C.H., Lee, W.J., and Doh, S.K. (2002) Practical Study of Long Span Corrugated Plate Structures, Research Institute of Industrial Science and Technology, Korea (in Korean).
• Hwang, W.S., Kang, S.P., and Wi, Y.M. (2004) Strength and Stress Distribution Behavior for the Connections of Corrugated Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.16, No.3, pp.365-375 (in Korean).
• Choi, D.-H., Park, S.-I., and Yoon, H.-D. (2004) Evaluation of Present Design Method for Encased-​Concrete Corrugated Steel Plate Structures, Journal of the Korean Society of Civil Engineers A, KSCE, Vol.24, No.2A, pp.321-333 (in Korean).
• Park, Y.-S., Cui, G., and Park, Y.-C. (2018) Experimental Study on Compressive Seam Strength of Bolted Connections in Extra-Deep Corrugated Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.30, No.5, pp.309-316 (in Korean). [https://doi.org/10.7781/kjoss.2018.30.5.309]
• Cui, G. (2017) Experimental Study on the Compressive Seam Strength and Flexural Strength of Extra Deep Corrugated Steel Plate, Master’s Thesis, Myongji University, Korea (in Korean)
• Jang, J.M. (2014) A Study on Flexural Strength for Deep Corrugated Steel Plate of Reinforcement Type, Master’s Thesis, Myongji University, Korea (in Korean).
• Oh, H.S., Lee, J.W., and Jun, B.G. (2011) An Experimental Assessment on the Structural Behavior of Bolt Connected Deep Corrugated Steel Plate, Journal of the Korea Institute for Structural Maintenance Inspection, KSMI, Vol.15, No.3, pp.79-87 (in Korean). [https://doi.org/10.11112/jksmi.2011.15.3.079]
• Park, Y.-S., Cui, G., and Park, Y.-C. (2018) Experimental Study on Flexural Strength of Bolted Connection in Extra-Deep Corrugated Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.30, No.5, pp.317-323 (in Korean). [https://doi.org/10.7781/kjoss.2018.30.5.317]
• Hwang, S.M., Rhee, J.W., and Kim, M.K. (2017) Verification of Structural Performance of Extra Strength Corrugated Plate, Proceedings of 2017 KSCE Convention, Korean Society of Civil Engineers, pp.145-146 (in Korean).
• American Society for Testing and Materials (2018) Standard Specification for Corrugated Steel Structural Plate, Zinc-Coated, for Field-Bolted Pipe, Pipe-​Arches, and Arches (ASTM A761/A761M-18), USA.
• Dassault Systèmes Simulia Corp. (2021) Abaqus 2021, DSS, USA.
• Ministry of Land, Infrastructure and Transport (2016) Standard Specifications for Highway Bridges, Korea (in Korean).