십자형 수직 다이어프램이 적용된 콘크리트 각형강관(CFT) 기둥-H형보 접합부 개발 및 구조성능

1. 서 론

콘크리트충전강관(concrete filled tubular, CFT) 기둥은 강관 내부에 콘크리트를 충전한 구조로, 중력하중에 대해 콘크리트는 압축력을 부담하고 강재의 구속효과로 구조성능이 향상되며, 수평하중에 대해서는 강재의 휨거동에 의해 강도 및 연성능력이 증진된다. 충전된 콘크리트는 외부 강관의 의한 구속 효과로 더 많은 축하중을 분담하여 강재기둥에서 발생할 수 있는 국부적인 응력집중을 완화할 수 있는 동시에, 강관의 국부좌굴을 억제하여 부재의 연성능력 및 내력을 크게 향상시킨다. 따라서, CFT 기둥은 타 종류의 구조단면에 비해 작은 단면적을 갖고 동등한 구조성능 발휘가 가능하며, 강관이 콘크리트 타설시 거푸집 역할을 하여 공기단축 효과를 발생시켜 시공성 및 경제성을 크게 향상시킬 수 있다^[1].

이러한 이점들로 인하여 최근 고층화, 대형화가 요구되는 건축물에 CFT 기둥이 사용되는 빈도가 증가하고 있다^[2],[3]. 그러나, 폐단면 특성상, 고장력볼트를 사용하기 어려워 철골보-기둥 접합부 상세가 H형강 기둥에 비해 제한적이고 복잡한 접합형태를 지니고 있어 현장 적용에 어려움이 있다. 또한, 각 절주별로 제작된 부재의 이음 방식도 폐단면인 강관 내부에 뒷댐재를 설치한 후 맞댐 완전용입용접(complete joint penetration, CJP) 상세가 적용됨으로써 시공성이 저하되는 문제를 가지고 있다.

CFT 기둥의 강재보 접합부 방식은 일반적으로 관통다이어프램, 외다이어프램과 내다이어프램이 있다^[4]. 외다이어프램의 경우 콘크리트 충전성에 큰 문제를 초래하지 않지만, 관통다이어프램과 내다이어프램을 사용한 강재보-기둥 접합부의 경우, 상·하부플랜지와 같은 레벨에 보 플랜지 두께 이상의 판재를 수평으로 설치하는 방식이기 때문에, 접합부의 구성이 복잡하여 각형강관기둥 내부의 콘크리트 충전성이 저하되는 문제점을 가지고 있다^[5].

다이어프램 접합부 상세와 관련하여 기존 연구를 보면, Choi et al.^[6]은 시공성 및 응력흐름이 개선된 복합십자형 다이어프램 접합부를 제안하였고 연구결과로 CFT 기둥 내부에 유공판을 수직, 수평으로 설치하여 콘크리트 충전성을 개선하고, 기둥-보 접합부에서 강축에는 관통다이어프램, 약축에는 내다이어프램을 적용하여 응력집중 현상을 완화시켰다. Kim et al.^[7]은 보 플랜지 좌우에 T형 스티프너로 보강한 외다이어프램 접합부를 제안하고 실험과 유한요소해석을 통해 접합부의 파괴거동을 조사하였다. Wang and Lee^[5]는 원형 CFT 기둥-보 접합부에서 강재보의 상부플랜지에는 외다이어프램과 하부플랜지에는 관통다이어프램이 사용된 혼합다이어프램 접합형식을 제안하여 구조성능을 검증하였다.

기존에 제안된 이들 접합부 상세는 제작과정이 복잡하고, 각형강관기둥의 두께와 다이어프램 구간의 두께가 상이한 경우, 균일한 용접 품질을 확보하기 쉽지 않을 것으로 판단된다. CFT 적용 확대를 위해서는 이러한 제작과정과 시공과정에서 발생 가능한 문제점을 해결할 수 있는 접합상세가 필요하다.

따라서, 이 연구에서는 CFT 기둥-H형 강재보 접합부에 사용되는 수직 내다이어프램의 용접 작업성을 개선하기 위하여, 십자형 수직 내다이어프램을 사용한 보-기둥 접합부 상세를 제안하고, 실험 수행 전 해석적 연구를 통해 변수에 따른 기둥-보 접합부의 내진성능을 비교하고 제안된 접합부의 적용 가능성을 분석하고자 한다.

2. 접합부 상세 제안

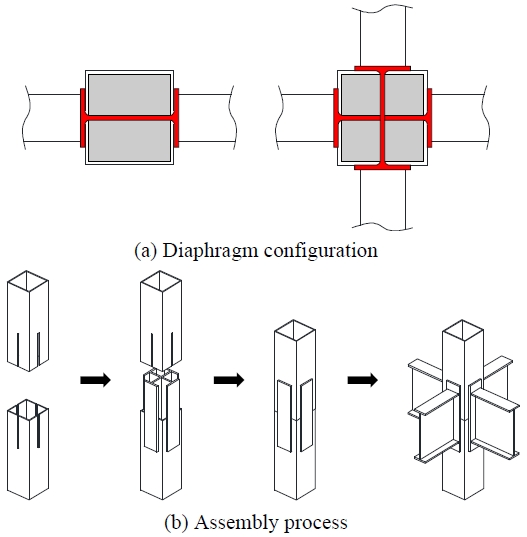
이 연구에서 제안하는 십자형 다이아프램을 갖는 기둥-보 접합상세는 Fig. 1과 같다. 폐단면 형태의 강관기둥과 기존의 수직 다이어프램 사이의 접합은 필릿용접이나 모서리 개선 후 부분용입용접 작업이 필요하여 제작 비용 증가와 용접작업에 필요한 공간 확보에 어려움이 있었다.

Fig. 1.

Proposed diaphragm

따라서, 시공성을 개선하기 위해 용접조립형 각형강관 기둥 단부에 슬릿을 설치하고 십자형 수직 다이어프램을 삽입하였다. 십자형 수직다이어프램의 플랜지와 CFT 기둥 사이는 필릿용접 상세가 적용된다. 다이어프램의 플랜지와 H형 강재보가 직접 연결되는 형식을 갖는 십자형 수직 다이어프램 형식의 접합부는 H형강 기둥에 강재보가 강축 방향으로 접하는 형식과 유사하게 하중 전달이 비교적 명확하며 다이어프램의 플랜지와 CFT 기둥 외부면에 용접접합이 가능하여 시공성을 크게 향상시킬 수 있다.

3. 유한요소해석

3.1 십자형 수직 다이어프램 해석모델링 및 주요 변수

십자형 수직 다이어프램 형상에 따른 용접 CFT 기둥-​H형 강재보 접합부의 반복이력 거동을 고찰하기 위해 정적 및 동적 해석에 널리 사용되고 있는 비선형 유한요소해석 프로그램인 ABAQUS/Standard^[8]를 사용하여 수치해석을 수행하였다.

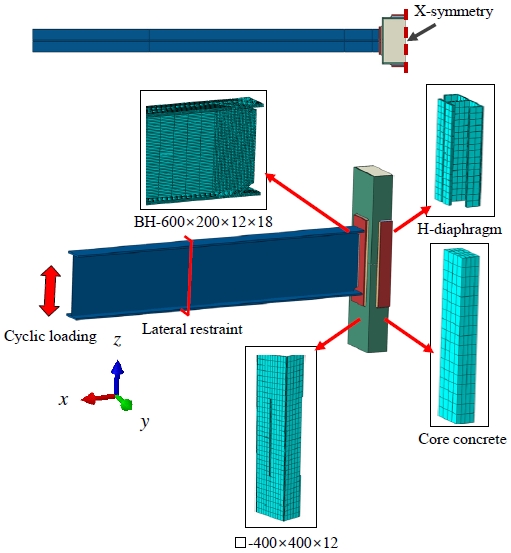
Table 1과 같이 다이어프램 플랜지 두께(T_d), 웨브 두께(T_vd), 콘크리트 충전여부를 주요 해석변수로 선정하여 총 6개의 실험체를 모델링하였다. 해석에 사용된 용접조립형 박스기둥(□-400×400×12), 용접조립 H형 강재보(BH-​600×200×12×18) 및 다이아프램 모두 동일한 건축구조용 압연강재인 SN355 강재를 적용하였고, 강관 내부에 충전된 콘크리트의 설계압축강도는 45 MPa로 설정하였다.

Table 1.

Details of FE modeling

Fig. 2에 유한요소해석모델과 사용된 경계 및 하중조건을 나타냈다. 각형강관기둥, 충전된 콘크리트, 다이어프램 등 주요 구성원들 모두 솔리드요소(C3D8R)를 적용하여 모델링하였다. 해석시간을 최소화하기 위하여 CFT 기둥 단면을 1/2 대칭단면으로 구성하였다.

Fig. 2.

Finite element model and mesh

콘크리트에 매립된 다이어프램의 거동을 고려하기 위해 ‘Embeded region’을 사용하였다. 접촉면의 경우, 강재와 용접부위는 ‘Tie’를 사용하여 일체 거동하는 것으로 가정하였고 용접 이외의 각 구성요소들의 접촉면의 수직방향은 ‘Normal behavior’의 ‘Hard contact’를, 수평방향은 Coulomb 마찰모델을 사용하여 Tangential 거동을 모사하였다. 선행연구결과^[9]를 바탕으로 강재-강재와 강재-콘크리트의 마찰계수는 각각 0.3, 0.6으로 설정되었다.

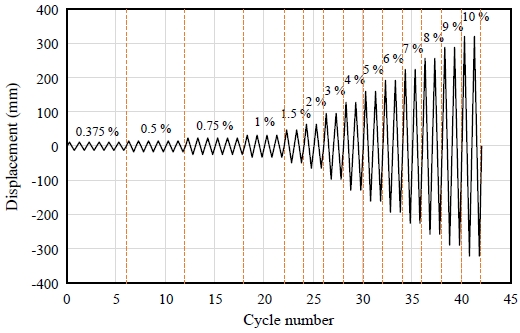
해석모델의 경계조건으로는 기둥의 양단을 핀(U_x = U_y = U_z = 0) 지지로 설정하고, 보의 횡좌굴을 방지하기 위하여 가력 중심에서 1,000 mm 떨어진 곳에 보 플랜지의 횡방향을 구속(U_y = 0)하였다. 가력방법은 KDS 41 31 00: 2019^[10]의 강구조 보-기둥 접합부 성능검증 시험방법에 따라서 기둥 중심에서 가력중심 길이 L = 3,200 mm를 기준으로 층간 변위각을 정의하여, 반복가력을 실시하였다(Fig. 3 참조).

Fig. 3.

Loading protocol

3.2 재료모델

3.2.1 콘크리트

반복하중 하에서 콘크리트의 압축연화, 소성팽창, 강성감소, 인장강화 등의 특성을 반영한 파괴거동을 분석하기 위하여 콘크리트 손상소성모델(concrete damaged plasticity model)을 적용하였다. 콘크리트 강성감소는 0과 1 사이의 스칼라값을 가진 손상계수를 사용하여 초기강성에 대한 할선비로 손상정도를 표현한다.

$\[ E-\left(1-d\right)E_0 \]$

(1)

여기서, E₀: 콘크리트 초기탄성계수, d: 손상계수.

다축 응력상태에 놓인 콘크리트 요소의 파괴 기준면은 편심율(m, eccentricity), 팽창각(β, dilation angle), 응력비(f = f_b0/f_c), 1축 압축강도에 대한 2축 압축강도의 비(k_c) 등의 변수들을 일축압축/인장(uniaxial tension and compression), 삼축응력 상태에서의 콘크리트 재료시험을 통하여 산정한다. 이 연구에서는 Jankowiak and Lodygowski^[11]에 의하여 적용성이 검증된 콘크리트 손상소성모델을 적용하여 45 MPa 압축강도를 갖는 콘크리트 거동을 모사하였다. 사용된 콘크리트 손상소성모델의 변수는 Table 2에 정리하였다.

Table 2.

CDP model[11]

3.2.2 강재

비선형 재료경화모델의 적용은 반복하중을 받는 강재부재의 탄소성 유한요소해석결과의 신뢰성에 크게 영향을 미친다. 이 연구에서는 일반적으로 많이 사용되는 Chaboche 모델^[12]에 기초하여 이동경화와 등방경화를 모두 고려한 복합경화모델을 적용하였다. 응력 공간에서 소성변형에 의한 항복면 중심의 이동을 모사하기 위하여 아래 식 (2)와 같이, 비선형 함수로 산정된 배응력(α, back stress)을 사용하여 정의한다.

$\[ \alpha =C\frac{1}{\gamma }\left(1-e^{-\gamma {\epsilon }^{pl}}\right) \]$

(2)

여기서, C: 이동경화 계수, γ: 소성변형률의 증가에 따른 이동 경화계수의 감소분, ε^pl: 소성변형률.

반복하중으로 인한 팽창된 항복면(σ_y)은 초기 항복면(σ_y0, initial size of yield surface)에 누적 소성변형률(ε^cpl, cumulative plastic strain)에 대한 비선형 함수를 고려하여 산정된 항복면 크기 변화량을 더하여 아래와 같이 표현한다.

$\[ {\sigma }_y={\sigma }_{y0}+Q_{\infty }\left(1-e^{-b{\epsilon }^{cpl}}\right) \]$

(3)

여기서, Q_∞: 등방경화로 인해 팽창된 항복면의 크기, b: Q_∞ 값으로 수렴할 때까지의 증가속도.

이 연구에서는 SN355 강재 시험결과^[13]를 토대로 복합경화모델 변수를 Table 3와 같이 정의하였다.

Table 3.

Parameters of the Chaboche model[12]

4. 기둥-보 접합부 해석결과

이 논문은 실대형 실험을 수행하기 전에 제안된 기둥-보 접합부의 구조적 거동을 조사하기 위하여 선행적으로 이루어진 해석적 연구이다. 비록 기존 선행연구를 통해 검증된 재료모델을 해석모델에 적용하였으나, 실제 H형 수직 다이어프램의 구조적 거동에 대한 신뢰성 평가는 제한적이다.

각 해석모델에 대한 모멘트-회전각 간의 관계 결과를 Table 4에 나타냈다. Fig. 4와 같이 실험체의 항복모멘트와 항복 시 회전각은 ‘general yield moment method’^[14]를 사용하여 산정하였다. 모멘트-회전각 포락곡선(envelope curve)에서 최대모멘트(M_max)의 수평선과 초기강성 구배를 갖는 직선의 교점을 항복모멘트(M_y)로 정의하였고 이에 대응되는 회전각을 항복회전각(θ_y)으로 정의하여 산정하였다. 실험체의 극한모멘트(M_u) 및 한계상태에서의 회전각(θ_u)은 최대모멘트 85 % 지점에서의 모멘트와 회전각이다.

Table 4.

FEA results of proposed cruciform diaphragm welded joints

Fig. 4.

General yield moment method diagram

4.1 접합부 이력거동 및 파괴양상

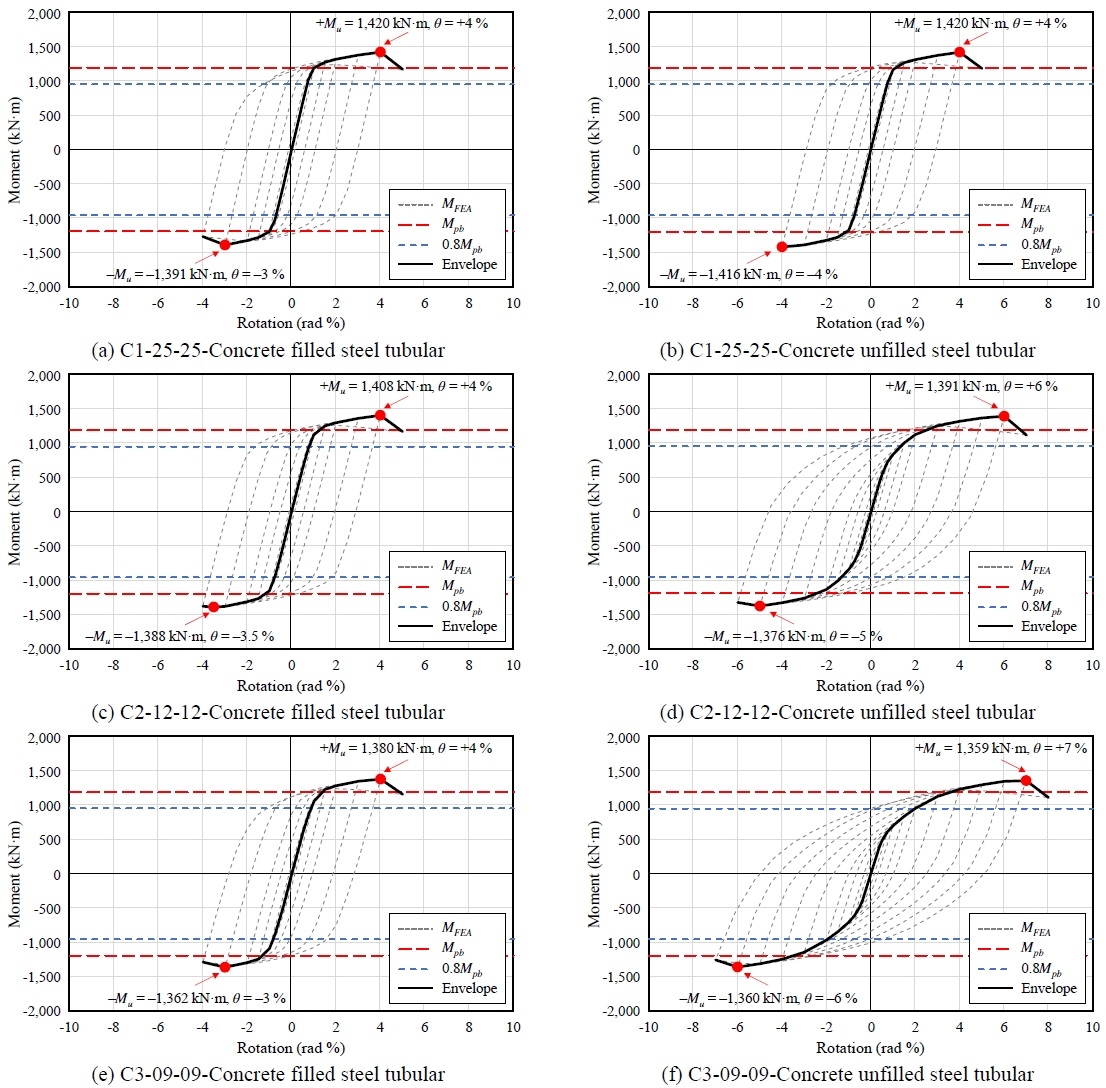
각 해석모델의 모멘트-회전각 이력곡선을 Fig. 5에 나타냈다. 접합부의 휨모멘트는 AISC 341-16^[15] 기준에 따라 기둥면에서 가력점까지의 거리를 기준으로 산정하였다. KDS 41 31 00: 2019^[10] 기준에서 규정하는 합성구조 중간모멘트 접합부의 최소 층간변위각 3 %이며, AISC 341-16^[15] 규정의 경우, 층간변위각 2 %에서 접합부의 최대내력은 강재보 전소성모멘트(M_pb)의 80 % 이상 확보되어야 한다.

Fig. 5.

Beam moment at the column face versus rotation angles

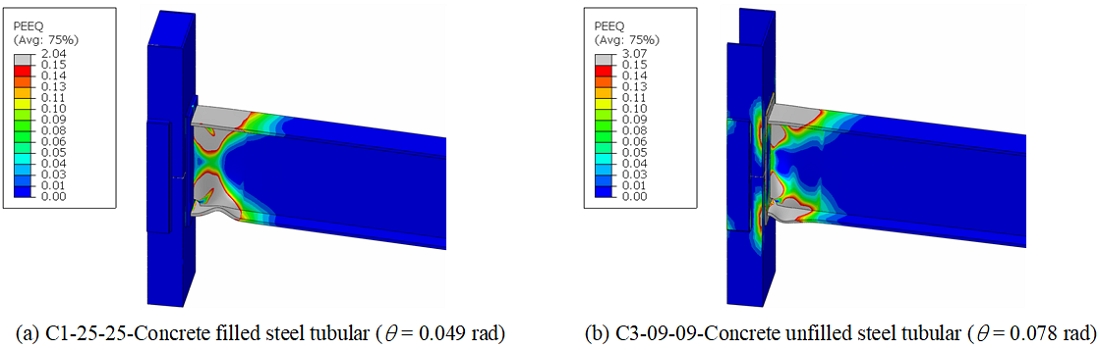
해석 결과, 모든 실험체의 정모멘트 구간에서 최대내력(M_max)은 회전각 4 % - 7 %에서 강재보의 전소성모멘트의 114 % - 119 % 값에 도달하여, AISC^[15]와 KDS^[10] 기준의 합성구조 중간모멘트골조 접합부 내진성능을 충족하는 것으로 나타났다. 주요 설계변수에 따른 접합부의 손상도를 평가하기 위하여 최대내력시점에서 등가소성변형률(equivalent plastic strain, PEEQ) 분포를 Fig. 6에 나타냈다.

Fig. 6.

PEEQ distributions at the ultimate limit state

등가소성변형률은 일반적으로 재료의 비탄성변형을 나타내는데 사용되는 스칼라 변수이다^[16],[17]. 강재 재료의 한계상태를 직관적으로 표현하기 위하여 인장시험결과에서 얻은 한계소성변형률(0.15) 값을 초과하는 부위는 회색으로 나타냈다.

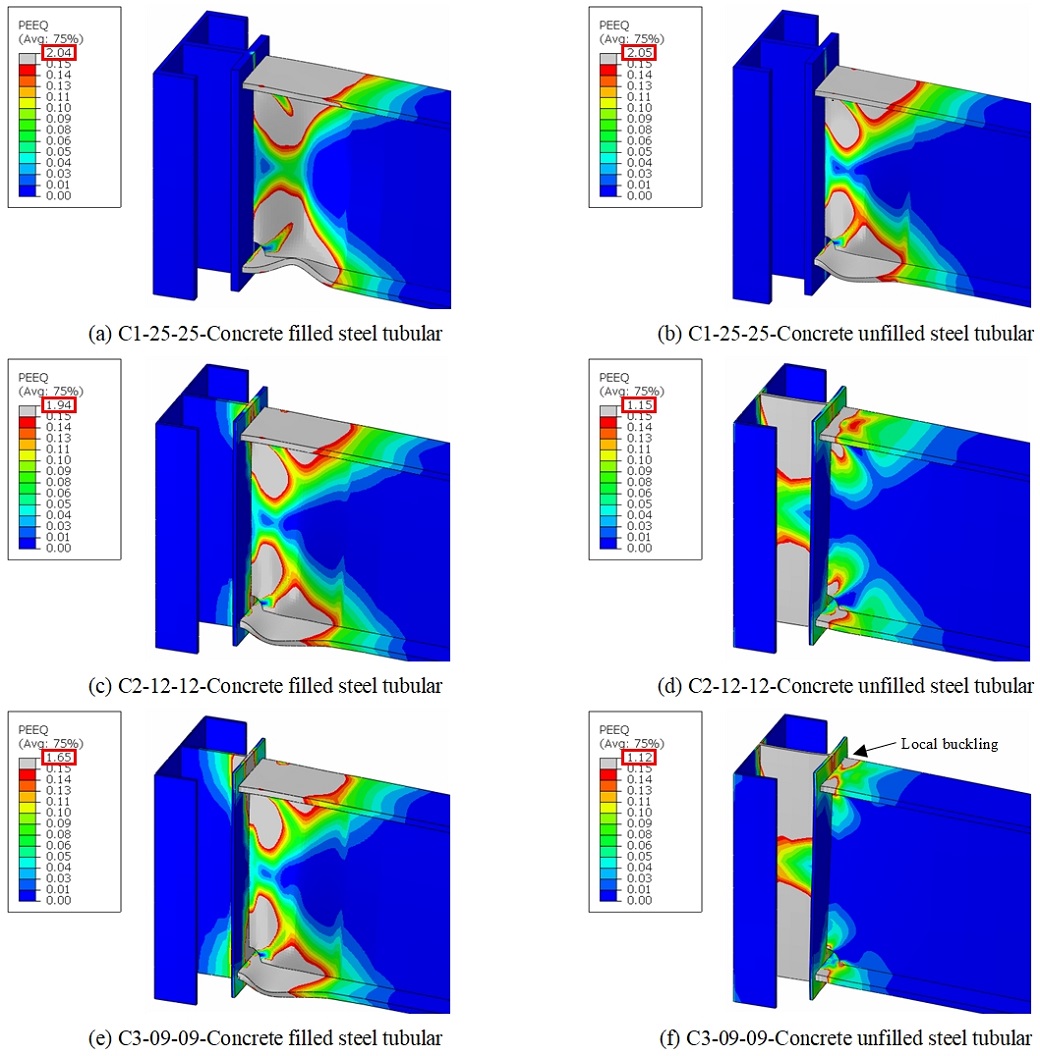
콘크리트가 충전된 모든 해석모델의 보 단부에서 소성힌지가 발생과 기둥의 패널 존에서 제한적인 항복변형을 보여주었다. 따라서, 기둥과 접합부보다는 보의 휨항복에 의한 비탄성변형을 가정하는 합성중간모멘트골조에 대한 현행기준의 이상적인 구조거동을 발휘하는 것으로 판단된다. 그러나, 콘크리트가 충전되지 않는 해석모델의 경우 기둥의 패널 존에서 일부 항복변형이 발생하였다. 콘크리트 구속효과와 다이어프램의 플랜지 및 웨브 두께 변화에 따른 다이어프램 내의 하중흐름을 파악하기 위하여 회전각 5 %에 해당하는 변위에서의 등가소성변형률 분포를 Fig. 7에 나타냈다.

Fig. 7.

PEEQ distributions at 5 % story drift angle

AISC 341-16^[15] 기준을 준용하여 다이어프램을 사용할 경우, 다이어프램의 두께는 보 플랜지의 두께 이상이어야 한다. 다이어프램의 플랜지와 웨브가 H형 강재보 플랜지 두께(t_f = 18 mm)보다 두꺼운 C1-25-25 해석모델은 콘크리트 구속이 구조거동에 미치는 영향이 다른 해석모델에 비해 상대적으로 작은 것으로 나타났다.

콘크리트의 충전한 경우와 충전하지 않은 경우, 모두 보에서 상당한 크기의 항복변형이 발생하였으며, 다이어프램의 변형은 극히 미미하였다. 또한, 소성변형률 분포도를 비교해보면 유사한 양상을 나타내는 것으로 확인되었다. 다이어프램의 웨브와 플랜지 두께가 낮아질수록 비탄성 변형은 보에서 다이어프램의 웨브로 전이되었으며, 손상도를 가리키는 최대 등가소성변형률 값은 작아졌다. 보 플랜지 두께의 1/2를 갖는 C3-09-09 해석모델은 강재보의 플랜지보다 다이어프램의 웨브가 먼저 항복하였으며, 국부좌굴이 플랜지에서 발생하는 것을 확인할 수 있었다.

4.3 연성 및 에너지소산능력

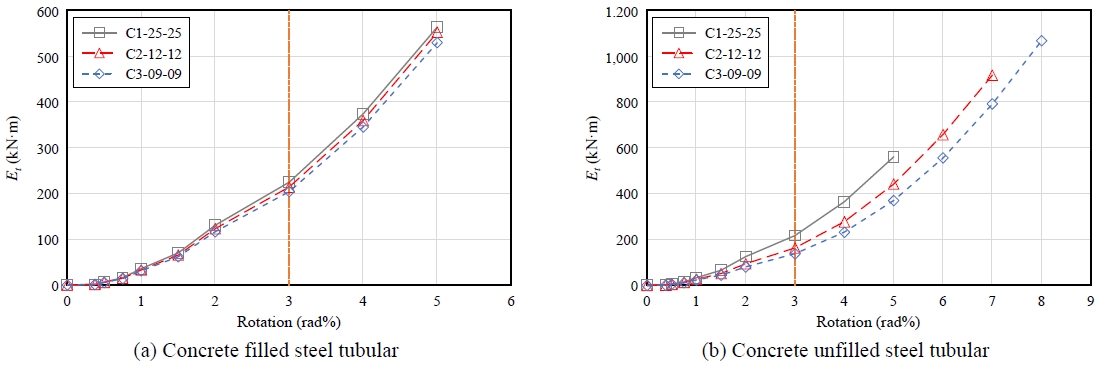
반복하중을 받는 강구조 보-기둥 접합부의 연성능력(μ)은 다음의 식으로 평가할 수 있으며^[19], 에너지소산능력(E_t)은 한계상태(최대내력의 85 %)까지 해석모델 내에 국부취성파괴가 발생하지 않는다는 가정하에 하중-변위 이력곡선으로부터 사이클별 면적을 누적시켜 산정하였다.

$\[ \mu =\frac{{\theta }_u}{{\theta }_y} \]$

(5)

각 해석모델의 연성 및 에너지소산능력을 Table 4에 정리하였다. 콘크리트가 충전된 해석모델의 경우, 다이어프램의 플랜지 및 웨브 두께 변화는 연성능력 및 소산능력에 큰 영향을 미치지 않는 것으로 나타났으나, 콘크리트가 충전되지 않을 때, 다이어프램의 두께가 작아질수록 에너지소산능력이 최대 91 %(C3-09-09의 E_t 1068.9/​C1-25-25의 E_t/561.0 = 1.91) 증가하여, 앞서 콘크리트 충전된 경우와 대비되는 양상을 보여주었다.

이러한 결과는 보 단부에서 소성힌지가 발생하기 전에 다이어프램이 비탄성 거동을 하여 접합부의 에너지소산에 기여한 것으로 판단된다. 비록 내부 콘크리트가 충전되지 않은 조건에서 두께가 낮은 해석모델이 한계상태까지 우수한 에너지소산능력을 발휘하는 것으로 확인되었으나, Fig. 7과 같이 목표변위 3 %에서는 AISC 341-16^[15] 내진규정에 준용하여 보 플랜지 이상의 두께를 갖는 C1-​25-25 해석모델이 높은 강성과 최대내력을 발휘하면서 가장 많은 소성변형으로 에너지소산능력을 발휘하는 것으로 나타났다.

Fig. 8.

Comparison of energy dissipation of joints

5. 결 론

이 연구에서는 콘크리트 충전 각형강관기둥과 H형강보의 접합부에 사용하는 수직 내 다이어프램의 시공성을 개선하기 위하여 십자형으로 제작한 H형 수직다이어프램과 슬릿이 설치된 각형강관기둥을 조립하여 구성한 접합방법을 제안하였으며, 실대형 실험을 수행하기 전에 제안된 콘크리트 충전 각형강관기둥-H형 강재보 접합부의 구조적 성능을 해석적 연구를 바탕으로 확인하였다.

• (1) 십자형으로 제작한 H형 수직다이어프램을 갖는 접합부 해석모델들은 층간변위각 2 %와 3 %에서 강재보의 전소성모멘트와 비교하였을 때 1.14배~​1.19배 높은 값을 확보하였고 KDS 2019와 AISC 341-16의 합성구조 중간모멘트골조에서 요구하는 내진성능을 만족하는 것으로 나타났다.
• (2) 콘크리트를 충전한 조건에서 모든 접합부의 소성힌지는 보 단부에서 발생하였으며, 9 mm - 25 mm 범위의 다이어프램 두께는 기둥-보 접합부의 최대내력과 연성도에 큰 영향을 미치지 않음을 확인하였다.
• (3) 콘크리트를 충전하지 않는 조건에서 다이어프램 두께가 보 플랜지 두께보다 작은 경우에는 소성힌지는 보 단부에서 다이어프램 웨브로 전이되었으며, 다이어프램의 소성변형으로 층간변위각이 상승되어 최대접합부의 전체 에너지소산능력은 최대 91 % 증가하였다.
• (4) 접합부의 강성, 강도 및 목표변위 3 %에서의 에너지소산능력을 종합적으로 고려할 때, AISC 341-​16 기준을 준용하여 보 플랜지 두께 이상을 갖는 다이어프램 사용이 합리적인 것으로 판단된다.

References

• Moon, A.H., Shin, J., Lim, C.G., and Lee, K. (2022) Finite Element Analysis Study of CJS Composite Structural System with CFT Columns and Composite Beams, Journal of the Earthquake Engineering Society of Korea, EESK, Vol.26, No.2, pp.71-82 (in Korean). [https://doi.org/10.5000/EESK.2022.26.2.071]
• Kim, S.-B., Kim, S.-S., Lee, W.-R., Kim, J.-Y., Lee, S.-B., Ryu, D.-S., and Kim, D.-H. (2012) Study on the Flexible Strength of U-Shape Hybrid Composite Beam, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.5, pp.521-534 (in Korean). [https://doi.org/10.7781/kjoss.2012.24.5.521]
• Architectural Institute of Korea (2004) Commentary for Concrete Filled Tube (CFT) Steel Structures, Kimoondang, Korea (in Korean).
• Morino, S., and Kawaguchi, J. (2005) Research on and Construction of the Concrete-Filled Steel Tube Column System in Japan, International Journal of Steel Structures, KSSC, Vol.5, No.4, pp.277-298.
• Wang, N., and Lee, M.J. (2015) Structural Characteristics of Beam-to-Column Connection of Circular CFT Columns by Using Mixed Diaphragms, Journal of Korean Society of Steel Construction, KSSC, Vol.​27, No.3, pp.299-310 (in Korean). [https://doi.org/10.7781/kjoss.2015.27.3.299]
• Choi, S.M., Jung, D.S., Kim, D.J., and Kim, J.H. (2005) A Study on the Equations for Load Carrying Capacities of Concrete Filled Tubular Square Column-to-Beam Connections with Combined Cross Diaphragm and Sleeves, Journal of Korean Society of Steel Construction, KSSC, Vol.17, No.4, pp.419-429 (in Korean).
• Kim, Y.-J., Shin, K.-J., and Kim, W.-J. (2008) Effect of Stiffener Details on Behavior of CFT Column-​to-Beam Connections, International Journal of Steel Structures, KCCS, Vol.8, No.2, pp.119-133.
• Dassault Systèmes Simulia Corp. (2018) Abaqus Analysis User’s Manual, DSS, USA.
• Rong, B., Zhang, Y., Sun, J., and Zhang, R. (2022) Experimental and Numerical Research on Hysteretic Behavior of CFST Frame with Diaphragm-Through Connections, Journal of Building Engineering, Elsevier, Vol.45, 103529. [https://doi.org/10.1016/j.jobe.2021.103529]
• Ministry of Land, Infrastructure and Transport (2019) Steel Structures Design Standard (KDS 41 31 00: 2019), Korea (in Korean).
• Jankowiak, T., and Łodygowski, T. (2005) Identification of Parameters of Concrete Damage Plasticity Constitutive Model, Foundations of Civil and Environmental Engineering, Publishing House of Poznan University of Technology, Vol.6, No.1, pp.53-69.
• Lemaître, J., and Chaboche, J.-L. (1994) Mechanics of Solid Materials, Cambridge University Press, UK.
• Kim, T.J., Park, J.W., Cho, J.H., and Kim, H.D. (2008) Seismic Performance Evaluation of Welded Beam-​Column Connections Fabricated with SHN Steel Sections, Journal of Korean Society of Steel Construction, KSSC, Vol.20, No.6, pp.829-838 (in Korean).
• Wang, J., Yang, J., and Cheng, L. (2019) Experimental Study of Seismic Behavior of High-Strength RC Columns Strengthened with CFRP Subjected to Cyclic Loading, Journal of Structural Engineering, American Society of Civil Engineers, Vol.145, No.2, 04018240. [https://doi.org/10.1061/(ASCE)ST.1943-541X.0002251]
• American Institute of Steel Construction (2016) Seismic Provisions for Structural Steel Buildings (ANSI/​AISC 341-16), USA.
• Liang, G., Lu, Z., Guo, H., Liu, Y., Yang, D., Li, S., and Pan, X. (2021) Experimental and Numerical Investigation on Seismic Performance of Extended Stiffened End-Plate Joints with Reduced Beam Section Using High Strength Steel, Thin-Walled Structures, Elsevier, Vol.169, 108434. [https://doi.org/10.1016/j.tws.2021.108434]
• Karami, B., Hashemi, B.H., Ramhormozian, S., and Zarabimanesh, Y. (2022) Numerical Study on Prequalification and Cyclic Performance of Column-Tree Connections, Structures, Elsevier, Vol.41, pp.331-348. [https://doi.org/10.1016/j.istruc.2022.04.089]
• American Institute of Steel Construction (2016) Specification for Structural Steel Buildings (ANSI/​AISC 360-16), USA.
• Chen, J., Chan, T.-M., Su, R.K.L., and Castro, J.M. (2019) Experimental Assessment of the Cyclic Behaviour of Concrete-Filled Steel Tubular Beam-​Columns with Octagonal Sections, Engineering Structures, Elsevier, Vol.180, pp.544-560. [https://doi.org/10.1016/j.engstruct.2018.10.078]