T-Stub의 형상변수에 따른 초기강성 예측모델 제안

1. 서 론

최근 국내에서는 T-stub 접합부를 완전강접합부(rigid connection)로 사용 가능 여부를 확인하는 연구, 전단탭이 없는 상·하부 T-stub 접합부에 대한 연구가 진행되고 있다. 반면에 T-stub 접합부의 반강접합(semi-rigid connection)에 대한 국내 설계지침이 명확하지 않아 T-stub을 사용하지 않고 있는 상황이며, T-stub 접합부 설계에 중요한 요소라고 판단되는 초기강성 예측모델에 대한 국내 기초자료가 미비한 실정이다^[1]-[6].

따라서, 본 연구에서는 T-stub 접합부의 초기강성 예측모델을 제안하기 위해 축 방향 인장력을 받는 T-stub 접합부 실험을 진행하였다. 이를 기반으로 유한요소해석을 진행하여 신뢰성을 검증하고 T-stub의 플랜지(flange) 두께와 고장력볼트 게이지 거리를 동시에 고려한 초기강성 예측모델을 제안한다.

T-stub 접합부의 파괴 양상은 일반적으로 고장력볼트의 인장 파단, 플랜지 필릿(fillet)부의 항복 후 고장력볼트의 인장 파단, 플랜지 필릿부와 고장력볼트부의 휨 황복으로 분류되며. 이는 Thornton^[9]과 Astaneh^[7]가 제안한 매개변수 α^′ 식 (1)로 T-stub 접합부의 파괴 양상을 예측할 수 있다. 또한 T-stub 접합부의 기하학적 형상 변수는 Fig. 1과 같다^[7]-[16].

Fig. 1.

Geometric shape of T-stub

α^′에 따른 T-stub 접합부의 파괴 양상은 Fig. 2와 같이 나타내고 있으며, Fig. 2(b), Fig. 2(c)와 같은 플랜지의 휨 항복이 되는 경우에는 T-stub 접합부는 지레작용에 의한 영향을 고려해야 하며 서로 다른 거동 양상을 보인다. 본 연구에서는 T-stub 플랜지의 충분한 소성이 발생하는 α^′ > 1인 경우의 T-stub 접합부에 대해서 연구를 진행한다.

Fig. 2.

Failure mode of T-stub

2. T-stub 접합부의 단순가력실험

2.1 T-stub 접합부의 축 방향 인장하중 실험모델 상세

실험에 사용된 강재의 기계적 성질은 KS B 0801 5호 인장시험편을 사용하여 인장시험을 진행하였으며, 해당 기계적 성질은 Table 1에 정리하였다. 또한 실험에 사용된 T-stub 접합부의 기하학적 형상 변수는 Table 2와 같이 정리하였다^[17],[18].

Table 1.

Material properties of T-stub

Table 2.

Shape parameter of T-stub connections

고장력볼트는 F10T-M20을 사용하였으며, 초기 도입 장력은 165 kN으로 하였다. Fig. 3와 같이 T-stub 접합부의 축 방향 인장하중실험은 T-stub 웨브에 연결된 2,000 kN 급 UTM을 통하여 실험을 진행하였으며 예상 최대 인장하중은 833 kN으로 진행하였다.

Fig. 3.

T-stub connection experimental test

2.2 유한요소해석을 통한 해석 및 실험 비교

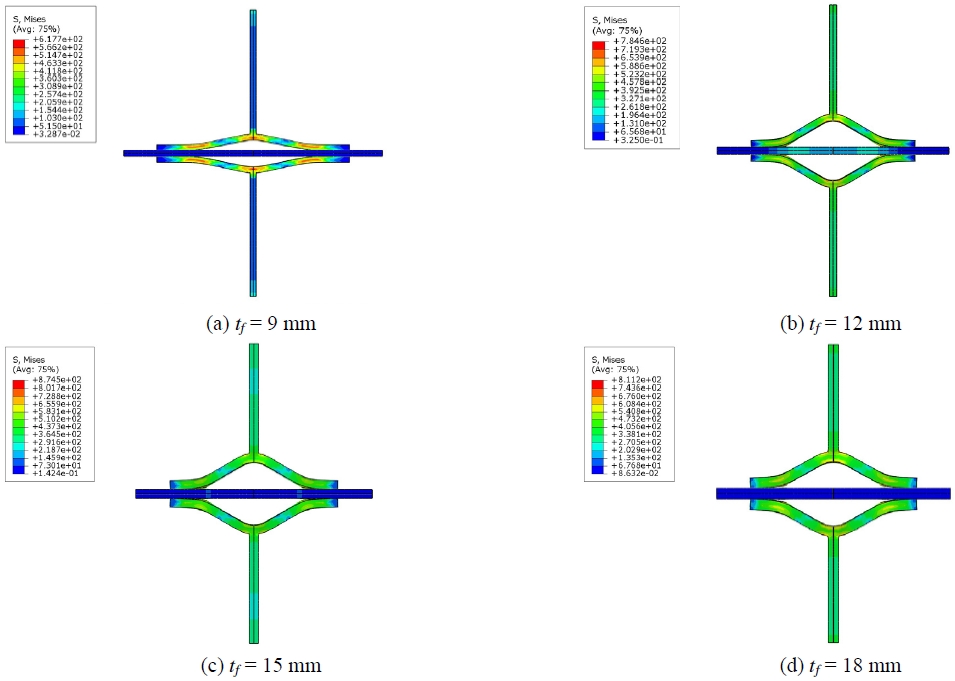
T-stub 접합부는 상용프로그램인 ABAQUS(ver. 2017)를 사용하여 유한요소해석을 진행하였다. 이때 적용한 옵션은 Table 3에 정리하였으며, Fig. 4는 FEA(finite element analysis) 모델의 최대 응력 분포상태를 나타내었다. Fig. 5는 각 실험체와 유한요소해석결과를 비교한 그래프이며 Table 4에 정리한 수치는 식 (7)과 같이 정의되는 Richard 해석모델을 적용하여 회귀분석을 수행하였다^[19]-[21].

Table 3.

Abaqus option

Fig. 4.

Stress distribution of the T-stub

Fig. 5.

Deformation–tensile load curves of the T-stub

Table 4.

Comparison data of the experimental and FEA

T-stub 접합부의 전이 구간 이전의 변위-인장력 관계 곡선의 기울기는 초기강성을 나타내며, 전이 구간 이후 곡선의 기울기는 소성강성을 나타낸다. T-stub 접합부의 초기강성은 플랜지 두께가 12 mm인 경우에는 최대 7.1 %의 오차를 나타내며, 플랜지 두께가 15 mm인 경우에는 최대 10.2 %의 오차를 나타낸다.

$\[ K\left(∆\right)=\frac{\left(K_e-K_p\right)\cdot ∆}{{\left(1+{\left|\frac{\left(K_e-K_p\right)\cdot ∆ }{y_0}\right|}^n\right)}^{1/n}}+K_p\cdot ∆ \]$

(7)

• 여기서, K: 강성(kN/mm),
• 　 　 　y₀: 참조강도(kN),
• 　 　 　K_e: 초기강성(kN/mm),
• 　 　 　K_p: 소성강성(kN/mm),
• 　 　 　∆: 변위(mm),
• 　 　 　n: 곡선형태변수.

3. T-stub 접합부의 유한요소해석

3.1 T-stub 접합부의 해석모델 상세

Table 4에 의하면 T-stub 접합부 실험과 유한요소해석의 초기강성은 최대 10 %의 오차가 나타난 것으로 확인된다. 축 방향 인장력을 받는 T-stub 접합부의 다양한 기하학적 형상을 변수로 유한요소해석을 진행하였다. 유한요소해석은 Table 3와 동일한 설정으로 진행하였으며, 유한요소해석의 사용한 기계적 성질은 Table 5, 기하학적 형상 변수는 Table 6에 정리하였다.

Table 5.

Material properties of T-stub used in FEA

Table 6.

Shape parameter of T-stub used in FEA

3.2 T-stub 접합부의 유한요소해석결과

Table 5의 기하학적 형상 변수를 기반으로 유한요소해석을 진행하여 다음과 같은 결과가 나타났다.

Fig. 6(a) - Fig. 6(d)는 플랜지 두께가 동일한 T-stub의 하중-변위 관계를 게이지 거리별로 분류하였으며, Table 7은 각각의 기하학적 형상 변수에 따른 T-stub 접합부의 초기강성과 소성강성을 식 (7)을 이용하여 나타낸 것이다. 또한 Fig. 7은 게이지 거리 210 mm를 기준으로 두께에 따른 각 모델의 최대 응력분포를 나타낸 것이다.

Fig. 6.

Load–displacement curve of T-stub used in FEA

Table 7.

Initial stiffness and plastic stiffness of T-stub used in FEA

Fig. 7.

Stress distribution of T-stub used in FEA

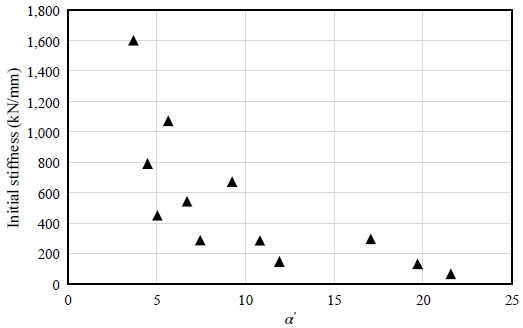
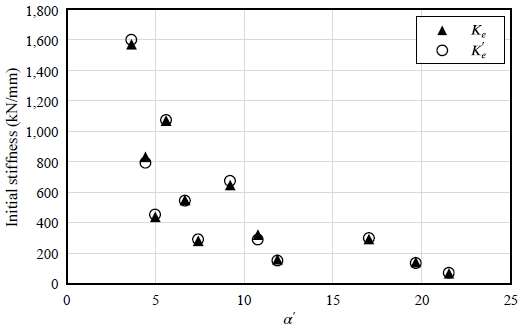
T-stub 접합부의 플랜지 두께 및 게이지 거리와 초기강성의 관계를 그래프로 나타내기 위해 식 (1)을 이용하여 플랜지 두께와 게이지 거리를 매개변수 α^′으로 나타내었다. T-stub 접합부의 초기강성과 α^′의 관계를 Fig. 8에 정리하였다.

Fig. 8.

α′–initial stiffness relationship

Fig. 8에서 보이는 것과 같이, T-stub 접합부의 매개변수 α^′과 초기강성은 반비례하는 형태를 나타낸다. 또한 Table 6 및 식 (1)에 의하면 매개변수 α^′과 T-stub 접합부의 플랜지 두께는 반비례하며, α^′과 게이지 거리는 비례한다. 이러한 관계성을 이용하여 T-stub 접합부의 초기강성에 따른 플랜지 두께 및 게이지 거리의 관계를 분석하였다.

4. T-stub 접합부의 초기강성 예측모델

4.1 플랜지 두께에 따른 초기강성 분석

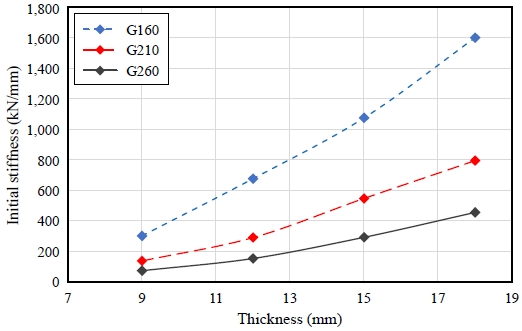
기하학적 형상 변수가 T-stub 접합부의 초기강성에 미치는 영향을 분석하기 위해 게이지 거리에 따라 플랜지 두께를 변수로 하여 정리하였다. T-stub 접합부의 초기강성-플랜지 두께의 관계는 Fig. 9에 정리하였으며, 초기강성은 두께에 따라 증가하는 형태를 보이지만 게이지 거리에도 영향을 받는 것을 보인다.

Fig. 9.

Initial stiffness–flange thickness relationship

플랜지 두께에 따른 초기강성은 Table 6에 정리하였듯이 게이지 거리의 영향을 고려하지 않으면 플랜지 두께가 9 mm에서 12 mm로 증가하는 경우에 초기강성은 평균 117 % 증가하며, 12 mm에서 15 mm로 증가하는 경우 초기강성은 평균 81.5 % 증가한다. 또한 플랜지 두께가 15 mm에서 18 mm로 증가하는 경우에는 평균 54 % 증가하는 경향으로 나타난다.

4.2 게이지 거리에 따른 초기강성 분석

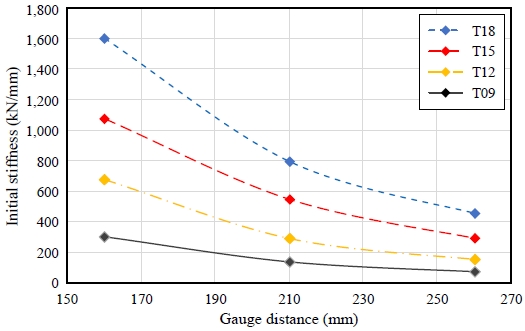
T-stub 접합부의 플랜지 두께에 따라 게이지 거리를 변수로 하여 T-stub 접합부의 초기강성에 미치는 영향을 Fig. 10에 정리하였다. Fig. 10에서 볼 수 있듯이 T-stub 접합부의 초기강성은 게이지 거리가 증가함에 따라 감소하는 형태를 보이며, 이는 플랜지 두께에 영향을 받는 것으로 보인다.

Fig. 10.

Initial stiffness–gauge distance relationship

Table 6에서 볼 수 있는 것처럼, 플랜지 두께와 관계없이 게이지 거리가 160 mm에서 210 mm로 증가함에 따라 T-stub 접합부의 초기강성은 평균 53 % 감소하였다. 한편 게이지 거리가 210 mm에서 260 mm로 증가할 경우 초기강성은 평균 46 % 감소하였다.

4.3 T-stub 접합부의 초기강성 예측모델 제안

Fig. 9과 Fig. 10 및 Table 6에 의하면 T-stub 접합부의 초기강성은 플랜지 두께에 비례하며, 게이지 거리에는 반비례한다. 이 관계를 Fig. 8과 비교하였을 때 플랜지 두께가 증가함에 따라 α^′은 감소하는 반면에 T-stub 접합부의 초기강성은 증가한다. 또한 게이지 거리가 증가할 때 α^′도 증가하지만, 초기강성은 감소하는 경향이 나타난다.

위의 내용을 정리하면 T-stub 접합부의 플랜지의 두께와 게이지 거리에 따른 축 방향 인장하중을 받는 초기강성은 식 (8)과 같이 나타난다.

$\[ K_e^{\text{'}}=1000\left(t_f-6\right)\cdot e^{-\left(0.0163-0.002t_f\right)\cdot g} \]$

(8)

Table 8은 식 (8)을 이용하여 제안한 T-stub 접합부의 초기강성과 FEA 모델에 식 (7)을 이용한 초기강성을 비교하였다. 이에 따르면 T-stub 접합부의 플랜지 두께와 게이지 거리를 동시에 고려한 초기강성은 최대 10.52 %, 최소 0.29 %의 오차가 나며 0.99의 R²값을 나타난다. 또한 Table 8의 초기강성과 제안된 초기강성의 관계를 매개변수 α^′을 이용하여 Fig. 11에 정리하였다.

Table 8.

Initial stiffness and plastic stiffness of T-stub used in FEA

Fig. 11.

Initial stiffness comparison

5. 결 론

이 연구는 T-stub의 기하학적 형상 변수가 T-stub 접합부의 초기강성에 미치는 영향을 파악하고, 이에 따른 T-​stub 접합부의 초기강성 예측모델을 제안하였다. 이 연구를 통하여 다음과 같은 결론을 얻었다.

• (1) 3차원 비선형 유한요소해석모델은 실험결과와 매우 유사한 회귀분석값을 제공하므로 이를 활용하여 다양한 변수를 적용하는 것은 적절하다고 판단한다.
• (2) T-stub 접합부의 초기강성은 플랜지 두께가 증가함에 따라 증가하는 것으로 보인다.
• (3) T-stub 접합부의 초기강성은 게이지 거리가 증가함에 따라 감소하는 것으로 보인다.
• (4) T-stub 접합부의 플랜지 두께와 게이지 거리를 동시에 고려한 초기강성 값은 3차원 비선형 유한요소해석모델의 회귀분석을 이용한 초기강성값과 매우 유사한 값을 제공하므로 이를 활용하여 T-stub 접합부의 국내 설계지침을 위한 기초자료로 적절하다고 판단한다.

Acknowledgments

이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단-기본 연구의 지원을 받아 수행된 연구임(No. 2016R1D1A1B03930555).

References

• Lee, M.J. (2006) Initial Stiffness Evaluation of T-​Stub Connection, Journal of Korean Society of Steel Construction, KSSC, Vol.18, No.6, pp.805-813 (in Korean).
• Yang, J.G., Lee, H.D., Kim, Y.B., and Pae, D.S. (2015) Proposal of Connection Details for a Double Split Tee Connection Without a Shear Tap, Journal of Korean Society of Steel Construction, KSSC, Vol.​27, No.5, pp.423-433 (in Korean). [https://doi.org/10.7781/kjoss.2015.27.5.423]
• Yang, J.G., and Kim, Y.B. (2016) Development of Connection Details for a Double Split Tee Connection Without a Shear Tab, Journal of Korean Society of Steel Construction, KSSC, Vol.28, No.1, pp.53-​64 (in Korean). [https://doi.org/10.7781/kjoss.2016.28.1.053]
• Yang, J.G., and Kim, Y.B. (2016) Design of a Steel Structural Building Using Double Split Tee Connections Without Shear Tabs, Journal of Korean Society of Steel Construction, KSSC, Vol.28, No.2, pp.85-96 (in Korean). [https://doi.org/10.7781/kjoss.2016.28.2.085]
• Yang, J.G., Hwang, K.S., and Lee, J.H. (2017) Comparison and Analysis of the Energy Dissipation Capacity of a Double Split Tee Connection Without a Shear Tab, Proceedings of the 28th Annual Conference of Korean Society of Steel Construction, KSSC, pp.77-78 (in Korean).
• Yang, J.G., and Lee, J.H. (2018) Behavioral Characteristics for the Energy Dissipation Capacity of a Double Split Tee Connection Without a Shear Tab, Proceedings of the 29th Annual Conference of Korean Society of Steel Construction, KSSC, pp.119-120 (in Korean).
• Astaneh, A. (1985) Procedure for a Design and Analysis of Hanger-Type Connections, Engineering Journal, American Institute of Steel Construction, Vol.22, No.2, pp.63-66.
• Kulak, G.L., Fisher, J.W., and Struik, J.H.A. (2001) Guide To Design Criteria for Bolted and Riveted Joints (2nd Ed.), American Institute of Steel Construction, USA.
• Thornton, W.A. (1985) Prying Action: A General Treatment, Engineering Journal, American Institute of Steel Construction, Vol.22, No.2, pp.67-75.
• Yang, J.-G., Park, J.-H., Choi, J.-H., and Kim, S.-M. (2011) Characteristic Behavior of a T-Stub Connection Under Shear, Including the Effects of Prying Action and Bolt Pretension, Proceedings of the 6th International Symposium on Steel Structures, KSSC, Korea, pp.1086-1092.
• Yang, J.-G., Park, J.-H., Kim, H.-G., and Back, M.-C. (2013) A Prying Action Force and Contact Force Estimation Model for a T-Stub Connection with High-Strength Bolts, Journal of Asian Architecture and Building Engineering, Taylor & Francis, Vol.12, No.2, pp.309-316. [https://doi.org/10.3130/jaabe.12.309]
• Faella, C., Piluso, V., and Rizzano, G. (2000) Structural Steel Semirigid Connections: Theory, Design, and Software, CRC Press, USA.
• Piluso, V., Faella, C., and Rizzano, G. (2001) Ultimate Behavior of Bolted T-Stubs. I: Theoretical Model, Journal of Structural Engineering, American Society of Civil Engineers, Vol.127, No.6, pp.686-693. [https://doi.org/10.1061/(ASCE)0733-9445(2001)127:6(686)]
• Piluso, V., Faella, C., and Rizzano, G. (2001) Ultimate Behavior of Bolted T-Stubs. II: Model Validation, Journal of Structural Engineering, American Society of Civil Engineers, Vol.127, No.6, pp.694-704. [https://doi.org/10.1061/(ASCE)0733-9445(2001)127:6(694)]
• Piluso, V., Rizzano, G., and Sabatino, R. (2009) Influence of Bolt Preloading and Flexural Effects on the Ultimate Behaviour of Bolted T-Stubs, Proceedings of ICASS 2009 (Sixth International Conference on Advances in Steel Structures), The Hong Kong Polytechnic University, Hong Kong.
• Yang, J.-G., Kim, Y., and Park, J.-H. (2012) Prediction Model for the Initial Rotational Stiffness of a Double Split T Connection, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.3, pp.279-​287 (in Korean). [https://doi.org/10.7781/kjoss.2012.24.3.279]
• Korean Agency for Technology and Standards (2007) Test Pieces for Tensile Test for Metallic Materials (KS B 0801: 2007), Korea (in Korean).
• Korean Agency for Technology and Standards (2003) Method of Tensile Test for Metallic Materials (KS B 0802: 2003), Korea (in Korean).
• Richard, R.M., and Abbott, B.J. (1975) Versatile Elastic-Plastic Stress-Strain Formula, Journal of Engineering Mechanics Division, American Society of Civil Engineers, Vol.101, No.4, pp.511-515. [https://doi.org/10.1061/JMCEA3.0002047]
• Richard, R.M., Hsia, W.-K., and Chmielowiec, M. (1988) Derived Moment Rotation Curves for Double Framing Angles, Computers and Structures, Elsevier, Vol.30, No.3, pp.485-94. [https://doi.org/10.1016/0045-7949(88)90281-7]
• Jaspart, J.-P., and Maquoi, R. (1991) Plastic Capacity of End-Plate and Flange Cleated Connections: Prediction and Design Rules, Connections in Steel Structures II (Proceedings of the 2nd International Workshop on Connections in Steel Structures), American Institute of Steel Construction, USA, pp.225-235.