조관 물성 변화를 고려한 원형 강관의 휨 성능 평가

1. 서 론

원형 강관은 구조물의 자중을 감소시키고 단면 축에 대해 재료가 균질하게 분포되는 약축이 없는 단면으로 풍하중, 지진하중에 대해 우수한 단면 형태를 가지며^[1] 휨, 축력, 비틀림에 대한 저항성이 높은 구조적 장점을 가져 다양한 구조물에 사용되고 있다^[2]-[4]. 원형 강관의 조관 방법 중 하나인 전기저항용접(electronic resistance welding, ERW) 방법은 coiling된 강판을 풀어 성형용 롤러를 통과시키며 원형으로 변형하고, 용접과 sizing 과정을 통해 강관을 완성하는데^[5], 이러한 조관 과정을 통해 강판은 D/t에 따라 높은 수준의 소성변형 이력을 겪으며, 가공경화 현상 및 바우싱거 효과에 의해 조관 전후 강관의 길이 방향 및 원주 방향으로 항복강도 등의 물성 및 항복면의 변화가 발생한다. Oh et al.^[6]은 직경 318.5 mm - 609.6 mm, 두께 7 mm - 15.3 mm인 철탑용 고장력강 강관에 대해 조관 전 coiling된 강판과 조관 후 강관에서 82개의 재료 시험편을 채취하여 인장시험을 수행하였고, 강관의 길이 방향 및 원주 방향 항복강도가 조관 전에 비해 증가하거나 감소함을 확인하였다. 조관 과정 중 발생하는 항복강도 등 주요 물성의 변화는 강관의 구조적 성능을 저하시킬 수 있으므로^[5], 조관 과정에 따른 주요 물성 변화의 추적은 강관의 성능 유지에 있어 매우 중요하며, 많은 연구자들에 의해 관련 연구가 활발히 수행되고 있다^[7]-[12].

특히, 강관의 휨 성능은 강관의 길이 방향으로 발현되는 인장 및 압축 성능에 영향을 받게 되는데, 조관 과정 중 발생하는 인장 및 압축 측의 비대칭성을 고려하지 않는다면 강관의 휨 거동을 정확히 평가하지 못할 수 있으므로, 비대칭성 재료 물성을 고려하는 해석 방법이 제시되어야 할 필요성이 있다.

국내 건축물 강구조 설계기준인 KDS 41 31 00^[13]은 원형 강관에 적용하는 강재로 KS D 3632^[14]를 따르도록 규정하고 있는데, KS D 3632^[14]에서는 강재의 항복비(yield ratio, YR)를 SNT275, SNT355는 85 % 이하, SNT460의 경우 90 % 이하로 규정하고 있으며, 국제 구조 설계기준인 Eurocode 3^[15]에서는 강재의 항복강도 대비 인장강도의 비율을 1.1 이상, 연신율을 15 % 이상, 항복 변형률 대비 최대 변형율의 비율을 15 이상으로 규정하여 강구조물이 충분한 연성과 내하력을 확보하도록 하고 있다. 강재의 항복비가 높을 경우, 구조물이 항복한 이후 소성 영역에 진입하여 최대강도까지 도달하는 데에 충분한 변형이 일어나지 않고, 추가적인 하중을 흡수하지 못하여 구조물의 안정성을 확보하지 못할 수 있는데^[16]-[19], 강관은 그 조관 과정에 따라 변화하는 항복강도에 의해 항복비가 변하게 되므로, 항복비의 변화가 강관의 휨 성능에 미치는 영향을 평가할 필요성이 있다.

이 연구에서는 조관 중 발생하는 원형 강관의 압축 및 인장 물성 변화 특성을 고려한 휨 성능 평가를 위하여 직경 406.4 mm, 두께 15.7 mm의 SNT355E ERW 강관에서 채취한 재료 시험편의 압축 및 인장 시험을 수행하였고, 강관의 4점 재하 휨 실험을 수행하였다. 유한요소해석을 통해 응력-변형률 곡선에 따른 강관의 거동특성 분석과 더불어 ERW 강관의 휨 거동을 보다 정확히 평가하기 위한 해석방법을 제시하였다. 나아가 조관에 따라 발생할 수 있는 항복강도 변화, 즉, 항복비의 변화와 강관 휨 성능에 있어 중요 인자 중 하나인 D/t를 변수로 매개변수해석을 실시하였다. 설계변수에 따른 강관의 휨 성능 분석을 위해 하중-변위 곡선과 더불어 연성거동 특성을 비교할 수 있는 지표인 변위연성비와 연성지수를 비교 분석함으로써 설계변수에 따른 성능변화를 정량화하고자 하였다.

2. 실험설계 및 수행

2.2 재료시험

조관 후 제거한 길이 600 mm의 강관으로부터 Fig. 1(a)와 같이 재료 시험편을 채취하여 편평화하였으며, 제원은 Fig. 1(b)와 같다. 재료시험을 통해 측정된 응력-변형률 곡선은 Fig. 2와 같고, 주요 물성은 Table 1과 같다. 인장시험은 KS B 0802^[20]에 따라 수행되었으며, 0.2 % offset 방법을 통해 산정된 인장항복응력(f_0.2,T)은 406 MPa, 최대응력은 567 MPa로 측정되었다. 항복비(YR)는 SNT355E의 상한값인 85 %보다 13 %p 작은 72 %로 나타났다. 한편, 압축항복응력(f_0.2,C)은 510 MPa로 인장항복응력보다 약 26 % 크게 나타났다. 압축시험은 항복 이후에 좌굴 영향을 크게 받기 때문에 Fig. 2와 같이 항복 이후 변형률이 2 %에 도달하였을 때 실험을 조기 종료하였다. 이후 유한요소해석 시 압축재료 물성은 실험값 이후에 대해 완전소성으로 가정하였다.

Fig. 1.

Material test specimen

Fig. 2.

Stress-strain curve

Table 1.

Material test result

2.3 휨 실험

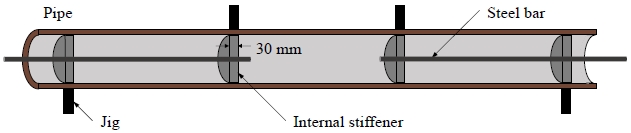
휨 실험은 POSCO 글로벌R&D센터 강구조실험동에서 10,000 kN UTM을 사용하여 수행하였으며, 실험 시 전단력에 의한 영향을 고려하지 않은 순수 휨 모멘트 저항성을 평가하기 위하여 Fig. 3와 같이 가력점 간 거리를 1,600 mm, 지점 간 거리를 4,800 mm로 4점 재하 휨 실험을 수행하였다. 실험 중 발생할 수 있는 가력부 및 지점부의 집중하중에 의한 국부적인 좌굴을 방지하기 위하여 강관 외부에 Fig. 4와 같이 지그를 용접하였으며, 강관 내부에도 Fig. 5와 같이 지그와 같은 위치에 30 mm의 두께를 갖는 보강재를 삽입하였다.

Fig. 3.

Schematic of 4-point-bending test (Unit: mm)

Fig. 4.

Steel pipe with welded jig and internal stiffener

Fig. 5.

Internal stiffener

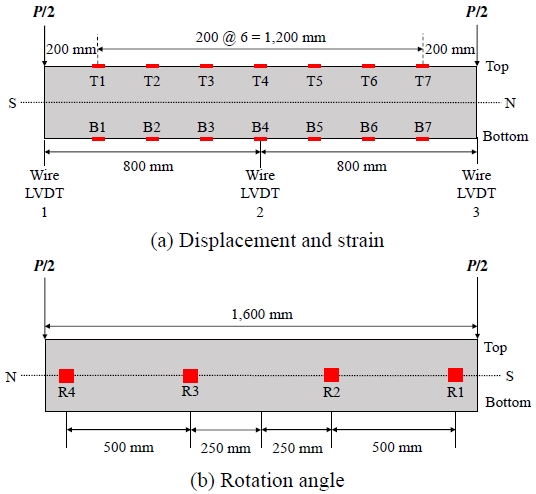
실험 중 하중 재하에 따른 변위 및 변형률 계측을 위해 Fig. 6와 같이 순수 모멘트 작용부 중 실험체 중앙 및 가력점 하부의 3개소에 줄변위계를 설치하였고, 상면 압축 연단의 7개소, 하면 인장 연단의 7개소에서 종방향 변형률을 계측하였다. 또한 실험체의 측면 4개소에 경사계를 부착하여 가력 중 기기 변위 20 mm마다 재하를 중지하고 육안으로 경사각을 확인하였다.

Fig. 6.

Measurement location of displacement, strain and rotation angle

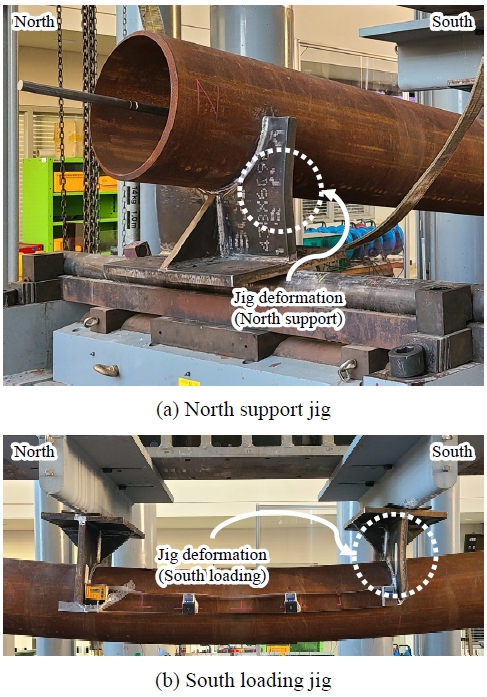
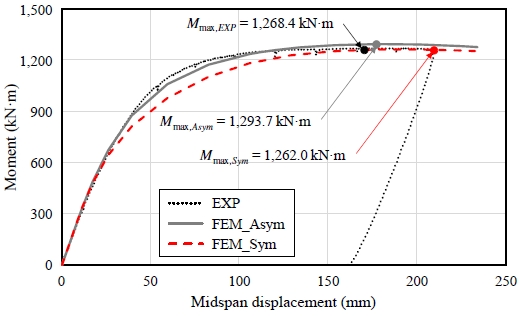
하중 재하는 변위 제어를 통하여 기기 변위 100 mm까지 0.03 mm/sec로, 기기 변위 100 mm 이후 0.05 mm/sec의 속도로 단조 가력하였다. 최대모멘트는 실험체 중앙 처짐 169.9 mm에서 1,268.4 kN·m로 나타났다. 실험체에 용접된 북측 지점부 지그와 남측 가력부 지그에 Fig. 7(a), Fig. 7(b)와 같이 소성변형이 발생하여 시험기 가력 변위 200 mm에서 가력을 중지하였다.

Fig. 7.

Deformation of jig in experiment

3. 유한요소해석을 통한 휨 거동 모사

3.1 유한요소해석 모델링

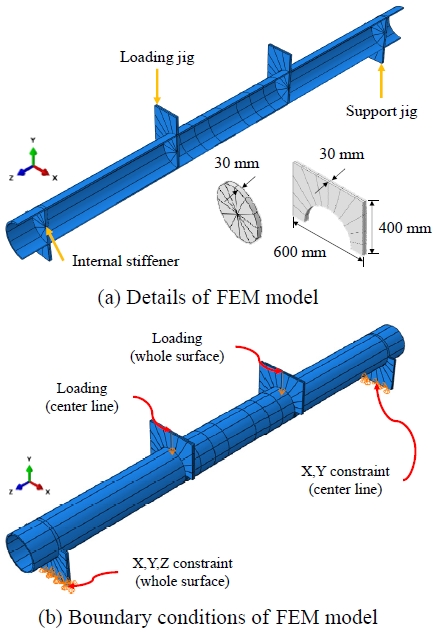
이 연구에서는 상용 구조해석프로그램인 ABAQUS(Ver. 2021)를 사용하여 실험 강관에 대해 응력-변형률 곡선에 따른 휨 거동 해석을 실시하였고, 항복비, D/t를 변수로 매개변수해석을 실시하였다. Fig. 8(a)와 같이 강관과 내부 보강재는 실험체와 동일한 제원으로 모델링하였다. 실험 중 지그에 발생한 소성변형에 대한 경계조건을 알맞게 부여하기 위해 각 부재는 3D Solid 요소로 모델링하였다. 3D Solid 요소의 기본 element type인 8절점 적분 저감 요소의 적분점 부족으로 인한 모래시계(hourglass) 현상으로 발생하는 수치해석 오류를 감소시키기 위해 완전 적분(full integration) 요소를 사용했으며, 완전 적분 요소에서 발생할 수 있는 shear locking 현상을 예방하기 위해 절점 사이 2차 보간을 통해 휨 변형을 정확히 구현할 수 있는^[21] 20절점 요소인 C3D20 요소를 사용했다. 요소의 크기는 해석의 효율성을 위해 모든 부재를 40 mm로 설정했다.

Fig. 8.

FEM model

실험 중 발생한 지그의 변형 형상을 도출하기 위하여 Fig. 8(b)와 같이 해석모델의 좌측 지점부는 하단 전면에 모든 축방향 변위를 제어하였고, 우측 지점부는 횡방향 중심선에 종방향을 제외한 모든 변위를 제어하였다. 또한 좌측 가력부는 횡방향 중심선에 하중을 재하하였으며, 우측 가력부는 상단 전면에 하중을 재하하였다. 하중 재하는 실험과 동일하게 변위 제어로 200 mm를 재하하였다. 기하 비선형이 고려되었으며, 강관의 재료 모델은 2.2절의 재료시험을 통해 산정된 Fig. 2와 같은 응력-변형률 곡선에서 인장 및 압축 물성을 모두 반영한 비대칭성 재료 모델과, 인장 측 물성만을 반영한 대칭성 재료 모델을 적용해 상호 비교하여 비대칭성 재료 물성의 반영 효과를 비교하였다. 이때 압축 측 응력-변형률 곡선은 시험값 이후 완전 소성으로 가정하였으며, 지그 및 내부 보강재는 항복강도 275 MPa의 완전 소성 재료를 적용하였다.

3.2 유한요소해석결과

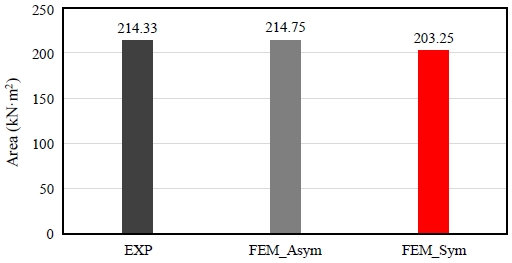
휨 실험과 유한요소해석으로 도출된 모멘트-변위 곡선은 Fig. 9과 같이 나타났다. 비대칭성 해석모델의 최대모멘트는 중앙 처짐 177.3 mm에서 1,293.7 kN·m로 실험 최대모멘트보다 약 2 % 높게 나타났으며, 대칭성 해석모델의 최대모멘트는 중앙 처짐 232.4 mm에서 1,262.0 kN·m로 실험 최대모멘트보다 약 0.5 % 낮게 나타났다. 하지만 Fig. 10에서 확인할 수 있는 바와 같이, 중앙 처짐 200 mm까지의 모멘트-변위 곡선 면적은 실험체가 214.33 kN·m²로 나타났으며, 비대칭성 해석모델이 214.75 kN·m²로 실험체와 약 0.2 %, 대칭성 해석모델이 203.25 kN·m²로 실험체와 약 5.2 % 차이가 발생했다. 따라서 비대칭성 해석모델이 실험체의 휨 거동을 보다 유사하게 구현하는 것으로 판단된다. 즉, 강관의 휨 거동을 정확히 예측하기 위해서는 강관의 길이 방향 압축 및 인장 응력-변형률 곡선을 모두 사용해 모델링하는 것이 적절할 것으로 판단된다.

Fig. 9.

Moment-displacement curves of experiment and FEM

Fig. 10.

Area of moment-displacement curves up to 200 mm

조관 중 발생하는 물성 변화는 강관의 D/t 및 항복강도에 따라 그 영향이 달라진다^[11]. 하지만 D/t 및 항복강도가 조관 과정 중 발생하는 강관의 길이 방향 압축 및 인장 응력-변형률 곡선의 비대칭성에 미치는 영향에 관한 연구는 미흡한 실정이기에, 이를 정량화할 수 있는 추가 연구가 필요할 것으로 사료되며, 이후 매개변수해석 시 인장 및 압축응력-변형률 곡선의 비대칭성은 고려하지 않았다.

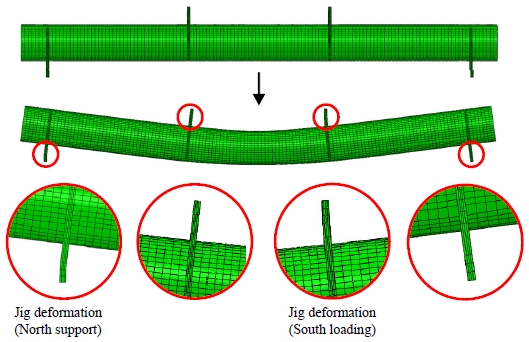
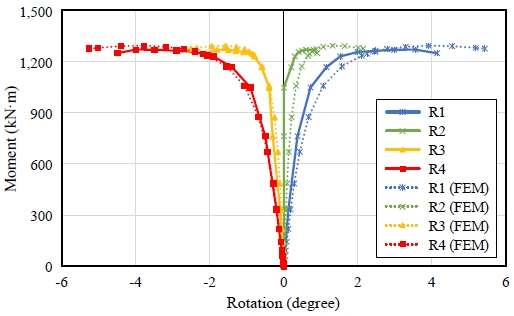
추가적으로, 비대칭성 해석모델의 변형 형상, 하중 단계별 변형률, 경사각을 통해 유한요소해석의 타당성을 검토하였다. Fig. 11은 해석모델의 변형 형상을 나타낸다. 상면 압축 연단에는 국부좌굴이 발생하지 않았으며, 지그의 변형 형상 역시 실험체의 변형 형상과 유사한 것을 확인할 수 있다. Fig. 12는 실험체 및 해석모델의 상면 및 하면 중앙에서의 모멘트-종방향 변형률 곡선을 나타내며, 모멘트 증가에 따른 상면 압축 연단 및 하면 인장 연단의 종방향 변형률은 실험과 유사하게 나타났다. Fig. 13은 실험체와 해석모델의 모멘트-경사각 곡선을 나타낸다. R3 경사계와 R4 경사계의 경우 실험과 유한요소해석에서 모두 유사한 결과를 보였다. 반면, 실험 중 R2 경사계의 계측 오류로 하중 재하 초반 지속적으로 0°의 경사각이 계측되었으며, R1 경사계의 경우 소성변형이 일어난 가력 지그와 근접한 위치에서 계측하여 가력 지그의 변형으로 인해 강관의 순수 휨 변형이 비교적 적게 발생하여, 대칭되는 위치의 R4 경사계보다 동일한 하중에서 비교적 낮은 경사각이 계측된 것으로 판단된다. 모멘트-변위 곡선과 변형 형상 및 하중 재하에 따른 변형률 및 경사각을 검토한 결과 모든 결과가 실험과 해석모델에서 유사함을 확인하였고, 추가 매개변수해석을 통해 강관의 휨 성능을 평가하였다.

Fig. 11.

Deformed shape of FEM model

Fig. 12.

Moment-longitudinal strain curves

Fig. 13.

Moment-rotation curves

4. 매개변수해석

4.1 매개변수 설정

이 연구에서는 강관의 휨 성능을 평가하기 위하여 조관 과정에 따라 변화할 수 있는 항복비와 휨 성능의 주요 인자 중 하나인 D/t를 매개변수로 설정하였다. 매개변수 해석모델은 휨 실험 및 3장의 모델과 동일한 직경 406.4 mm, 내부 보강재 및 지그가 병합된 강관이며, 지그의 변형이 발생하지 않도록 지점 및 가력부의 횡방향 중심선에 경계조건을 부여하고 하중을 재하하였다.

강재의 항복비는 KS D 3632^[14]에 명시된 SNT 강재의 항복비 한곗값을 참고하여 75 %, 80 %, 85 %, 90 %의 네 가지로 설정하였다. KS D 3632^[14]는 SNT275, SNT355 강재의 항복비를 85 % 이하로 규정하고 있는데, 해당 기준 이상의 항복비가 강관의 휨 성능에 주는 영향을 비교하기 위해 90 %의 항복비 역시 매개변수에 포함시켰다. 또한 KS D 3632^[14]가 규정하는 모든 강재에 대해 재료 인장시험을 수행하지 않았으므로, 매개변수해석에서는 공칭 탄성계수인 210,000 MPa, 인장강도는 KS D 3632^[14]가 규정하는 인장강도 범위의 평균값을 적용하여 SNT275는 480 MPa, SNT355는 565 MPa, SNT460은 655 MPa로 설정했고, 항복비에 따라 항복강도를 변화시키며 매개변수해석을 수행하였다. 항복비에 따른 항복강도는 336 MPa - 432 MPa(SNT275), 395.5 MPa - 508.5 MPa(SNT355), 458.5 MPa - 589.5 MPa(SNT460)이다.

직경 406.4 mm의 강관을 기준으로 항복비 매개변수를 통해 산정된 항복강도에 따른 폭-두께비의 한곗값은 Table 2와 같다. 항복강도에 따라 조밀 단면의 폭-두께비 한곗값은 24.94 - 43.75의 범위에서 산정되었으며, 비조밀 단면의 폭-두께비 한곗값은 110.43 - 193.75의 범위로 산정되었다. 각 항복강도에 대해 조밀 단면과 비조밀 단면의 거동을 모두 고려하기 위하여 20, 35, 50, 65, 80의 D/t를 매개변수로 설정하였으며, D/t에 따른 강관의 두께는 D/t = 20일 때 20.32 mm, 35일 때 11.61 mm, 50일 때 8.13 mm, 65일 때 6.25 mm, 80일 때 5.08 mm이다.

Table 2.

Limit of D/t ratio in KDS 41 31 00

비조밀 단면에 해당하는 강관의 경우 조관 과정 중 발생하는 초기 결함(initial imperfection)의 크기에 따라 국부좌굴 강도가 영향을 받게 되는데, 초기 결함을 매개변수로 함께 고려할 경우 방대한 양의 해석이 요구된다. 따라서 이 연구에서는 강관의 초기 결함을 고려하지 않고 D/t 및 항복비의 변화가 휨 성능에 미치는 영향만을 평가하였다.

4.2 휨 성능 평가

이 연구에서는 D/t와 항복비의 변화에 따른 강관의 휨 성능을 하중-변위 곡선과 더불어, 연성 거동 평가가 가능한 지표인 변위연성비 및 연성지수로 정량화하여 평가하였다.

4.2.1 하중-변위 곡선

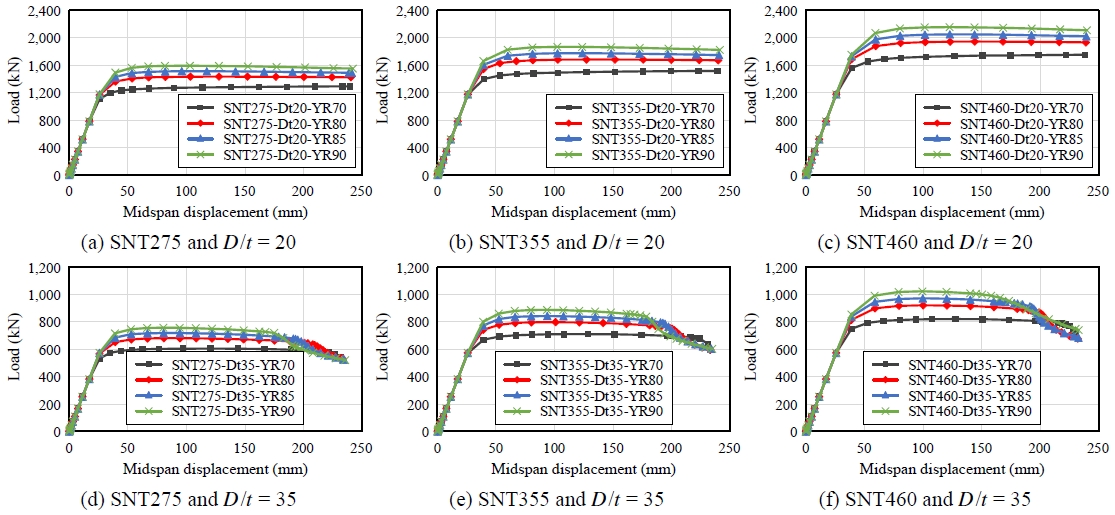
Fig. 14은 D/t = 20, 35인 강관의 하중-변위 곡선을 나타낸다. D/t = 20인 경우 강도에 관계 없이 조밀단면에 해당하며, 항복 이후 항복비에 따라 하중-변위 곡선의 기울기에 있어 약간은 차이가 발생하나 그 수준은 미미한 것으로 나타났다. 한편 D/t = 35인 경우, SNT275는 모든 경우 조밀, SNT355는 YR이 70을 초과하는 경우 비조밀, SNT460은 YR이 70 이상인 경우 모두 비조밀로 구분되고, 해석 결과 대변형에서 국부좌굴에 의해 급격한 강도 저하가 발생하는 것으로 평가되었다. 이러한 특성은 조밀단면 기준값에서 멀어질수록 더 크게 나타난 것으로 평가된다. 그러나 이러한 특성은 대변형 발생에 따른 것으로 이 D/t 범주에서는 항복비에 의한 국부좌굴에 대한 영향과 국부좌굴에 의한 최대강도에 대한 영향은 미미한 것으로 판단된다. 한편, D/t가 상대적으로 높아 세장판 단면에 가까운 비조밀 단면이거나 세장판 단면의 경우 항복강도 영향이 작기 때문에, 이 경우에서 또한 항복비에 의한 최대강도 영향은 미미할 것이다. 따라서 항복비와 D/t에 따른 강관의 휨 성능은 강도 이외에 연성 특성을 중심으로 추가적인 고려가 요구된다.

Fig. 14.

Load-displacement curves

4.2.2 변위연성비(displacement ductility ratio)

변위연성비(μ_∆, displacement ductility ratio)는 강관의 하중-변위 곡선에서 항복 이후 최대하중에 이르기까지 강관의 변형특성을 평가하기 위한 지표이며, Fig. 15에서 나타낸 바와 같이 다음의 식으로 산정된다^[22].

$\[ {\mu }_{∆}={∆}_{P_{\mathrm{m}\mathrm{a}\mathrm{x}}}/{∆}_y \]$

(1)

• 여기서, μ_∆: 변위연성비(displacement ductility ratio),
• 　 　 　∆_Pmax: 최대 하중 시 변위,
• 　 　 　∆_y: 항복 시 변위.

Fig. 15.

Definition of displacement ductility ratio[22] and ductility factor[23]

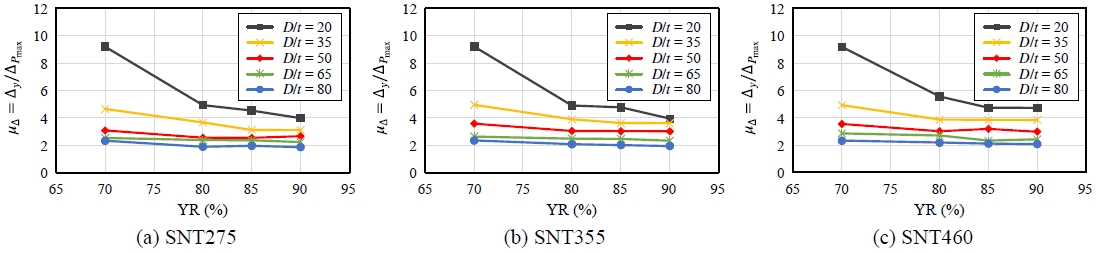
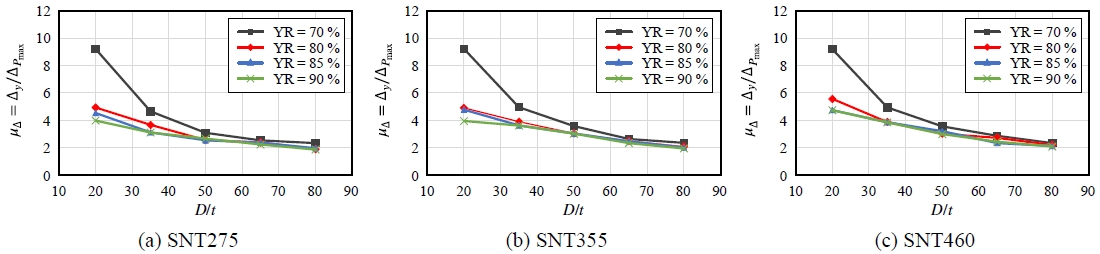
Fig. 16과 Fig. 17은 변위연성비를 각각 항복비와 D/t의 변화에 따라 나타냈다. D/t = 20인 강관은 항복비가 70 %에서 80 %로 증가함에 따라 SNT275의 경우 약 46.4 %, SNT355의 경우 약 46.8 %, SNT460의 경우 약 39.5 % 감소하며 평균적으로 변위연성비가 44.2 % 감소하는 것으로 나타났다. 항복비가 80 %에서 85 %로 증가하는 경우 SNT275, SNT355, SNT460은 각각 8.1 %, 2.7 %, 14.7 % 감소하였으며, 85 %에서 90 %로 증가하는 경우 SNT275, SNT355, SNT460은 각각 12.2 %, 17.6 %, 0.2 % 감소하는 것으로 나타났다. D/t = 35인 강관은 항복비가 70 %에서 80 %로 증가하며 SNT275의 경우 약 21.3 %, SNT355의 경우 약 21.4 %, SNT460의 경우 약 21.6 % 감소하여 평균 약 21.4 % 감소하였으며, 항복비가 80 %에서 85 %로 증가함에 따라 각각 14.8 %, 7.0 %, 0.3 % 감소하였다. 한편, 항복비가 85 %에서 90 %로 증가할 경우 SNT275, SNT355, SNT460 모두 0.3 % 내외로 감소하여 유사한 변위연성비를 나타냈다. D/t = 50, 65, 80인 강관은 항복비에 따라 변위연성비에 약간의 차이는 발생하나 그 수준이 미미하였다. 즉, 설계기준상 내진강재 기준인 항복비 85 %를 기준으로 볼 때, D/t = 20인 경우 SNT460은 항복비 85 % - 90 % 사이에서 항복비의 변위연성비에 대한 영향은 무시할 만한 수준으로 작았다. 한편, SNT275, SNT355이고 D/t = 20인 경우, 항복비 85 % - 90 % 사이에서 항복비의 영향은 약 15 % 내외로 존재하나, D/t = 35 이상에서는 항복비 85 % - 90 % 사이에서 항복비의 영향이 매우 미미한 것으로 나타났다. 따라서 SNT460의 경우 항복비 85 % - 90 % 사이에서 항복비의 변위연성비에 대한 영향은 별도로 고려하지 않아도 될 것으로 판단된다.

Fig. 16.

Displacement ductility ratios with respect to yield ratio

Fig. 17.

Displacement ductility ratios with respect to D/t ratio

D/t와 항복비별 단면 분류에 따라 조밀단면에 해당하는 강관은 항복비 증가로 인해 항복 이후 빠르게 최대강도에 도달하여 변위연성비가 감소하지만, Fig. 14의 하중-변위 곡선에서 확인할 수 있듯 최대강도 이후에도 대변형까지 충분한 내하력을 확보하는 것으로 판단되므로 에너지 흡수능력을 나타내는 연성지수까지 고려한 비교를 통해 보다 정확한 성능비교가 이뤄져야 할 것이다. 한편, 비조밀단면으로 분류되는 강관의 경우 휨 거동이 국부좌굴에 의해 지배되며 항복비의 증가가 변위연성비에 주는 영향이 상대적으로 작거나 미미한 것으로 평가되었다.

4.2.3 연성지수(ductility factor)

연성지수(ductility factor, DF)는 Fig. 15에 나타낸 바와 같이 하중-변위 곡선에서 최대하중 이후 최대하중의 80 %에 도달했을 때까지의 면적을 항복 하중까지의 면적으로 나눈 값으로, 극한 상태까지 구조물이 받을 수 있는 에너지를 나타내는 지표로 간주될 수 있다^[23].

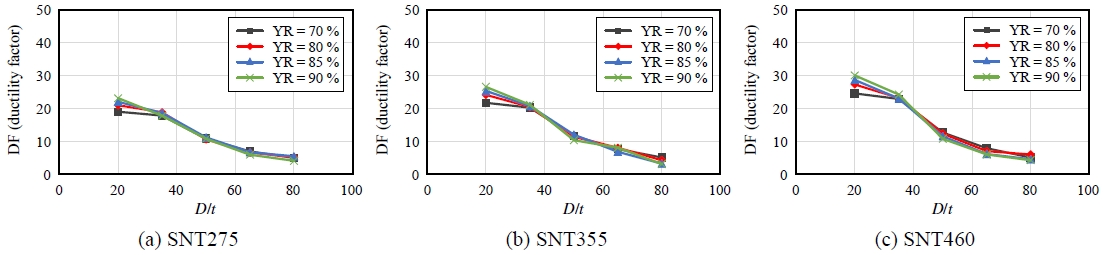
Figs. 18-19에 항복비와 D/t의 변화에 따른 연성지수를 나타냈다. D/t = 20인 강관은 항복비가 70 %에서 80 %까지 증가함에 따라 연성지수는 SNT275의 경우 약 10.4 %, SNT355의 경우 약 11.3 %, SNT460의 경우 약 11.1 % 증가하며 평균 약 10.9 % 증가하였다. 항복비가 80 %에서 85 %로 증가하는 경우 SNT275, SNT355, SNT460은 각각 5.1 %, 5.1 %, 5.0 % 증가하였으며, 85 %에서 90 %로 증가하는 경우 5.0 %, 4.9 %, 4.7 % 증가하였다. 이러한 특성은 최대 강도 이후 대변형까지 강도 저하가 크지 않아 항복비에 따른 연성지수 또는 에너지 흡수능력 감소 또한 크지 않았던 것으로 판단된다. 한편, D/t = 35 이상인 강관은 항복비의 증가에도 연성지수가 유사하게 나타났다.

Fig. 18.

Ductility factors with respect to yield ratio

Fig. 19.

Ductility factors with respect to D/t ratios

즉, 설계기준상 내진강재 기준인 항복비 85 %를 기준으로 볼 때, D/t = 20인 경우 SNT275, SNT355, SNT460은 모두 항복비 85 % - 90 % 사이에서 항복비의 영향은 5 % 이내로 비교적 작고, D/t = 35 이상인 경우엔 매우 미미한 수준으로 항복비 85 % - 90 % 사이에서 항복비에 따른 연성지수에 대한 영향은 별도로 고려하지 않아도 될 것으로 판단된다. 연성지수는 변위연성비와 달리 대변형 시 강관의 국부좌굴 이후 강도 저하까지 고려하게 되는데, 35 이상의 D/t 범주에서는 항복비가 국부좌굴에 미치는 영향이 상대적으로 작아 항복비의 증가가 강관의 연성지수에 주는 영향이 상대적으로 미미한 것으로 평가되었다.

5. 결 론

이 연구에서는 조관 중 발생하는 원형 강관의 물성 변화 특성을 고려한 강관의 휨 해석 방법 제안 및 휨 성능 평가를 위하여 직경 406.4 mm, 두께 15.7 mm의 SNT355E ERW 강관에서 채취한 재료 시험편의 압축 및 인장 시험을 수행하였고, 강관의 4점 재하 휨 실험과 유한요소해석을 수행하였다. 또한 항복비와 D/t를 변수로 매개변수해석을 실시하였고, 설계변수에 따른 강관의 휨 성능을 하중-변위 곡선과 더불어 변위연성비와 연성지수를 통해 정량적으로 분석함으로써 다음과 같은 결론을 도출하였다.

• (1) 인장 및 압축 물성을 모두 반영하는 비대칭성 해석모델과, 인장 물성만을 반영하는 대칭성 해석모델의 최대하중은 실험체와 각각 2 %, 0.5 %의 차이를 보였으나, 중앙 처짐 200 mm까지의 모멘트-변위 곡선의 면적을 비교한 결과 각각 0.2 %, 5.2 % 차이로 비대칭성 해석모델이 실험체와 더욱 유사한 휨 거동을 나타냈다. 이와 더불어 전체적인 모멘트-변위 변형특성 또한 유사하게 나타났다. 따라서 강관의 휨 거동을 보다 정확히 예측하기 위해서는 강관의 길이 방향 압축 및 인장 응력-변형률 곡선을 모두 사용한 모델링이 적절할 것으로 판단된다.
• (2) D/t와 항복비에 따른 강관의 휨 성능을 하중-변위 곡선을 통해 분석한 결과, 조밀단면의 경우 항복비 변화에 따른 최대강도 영향이 비교적 큰 반면, D/t가 조밀단면 기준값과 멀어질수록 국부좌굴에 의해 강도감소가 더욱 급격하게 나타났다. 그러나 이 D/t 범주에서 항복비에 의한 국부좌굴에 대한 영향과 국부좌굴에 의한 최대강도에 대한 영향은 미미한 것으로 판단된다.
• (3) 설계기준상 내진강재 기준인 항복비 85 %를 기준으로 볼 때, D/t = 20 이상인 경우 SNT460은 항복비 85 % - 90 % 사이에서 항복비의 변위연성비에 대한 영향은 무시할만한 수준으로 작아 설계 시 이에 대한 별도 고려는 하지 않아도 될 것으로 판단된다. 한편, SNT275, SNT355는 D/t = 20인 경우, 항복비 85 % - 90 % 사이에서 항복비의 영향은 약 15 % 내외로 존재하나, D/t = 35 이상에서는 항복비 85 % - 90 % 사이에서 항복비의 영향이 매우 미미한 것으로 나타났다.
• (4) 에너지 흡수능력을 나타내는 연성지수는 D/t = 20인 경우, SNT275, SNT355, SNT460은 모두 항복비 85 % - 90 % 사이에서 항복비의 영향은 5 % 이내로 비교적 작고, D/t = 35 이상인 경우에는 매우 미미한 수준으로 항복비 85 % - 90 % 사이에서 항복비에 따른 연성지수에 대한 영향은 별도로 고려하지 않아도 될 것으로 판단된다.
• (5) 강관의 휨 성능은 항복비보다는 D/t에 더욱 지배적인 영향을 받는 것으로 판단되며, 현행 설계기준에서 명시하는 항복비 제한에 대해 추가적인 다양한 연구를 통해 보다 세밀한 구분이 필요할 것으로 사료된다.

Acknowledgments

본 연구는 ㈜포스코와 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 21CTAP-C163558-​01).

References

• Lee, S.J., Kim, J.W., Kim, S.S., Lee, M.J., and Yang, J.G. (2011) In-Plane Bending Moment Capacity of T-Joints in the Circular Hollow Section of New High Strength Steel Subjected to Cyclic Loadings, Journal of Korean Society of Steel Construction, KSSC, Vol.​23, No.2, pp.169-177 (in Korean).
• Khalaf, M.S., Ibrahim, A.M., Najm, H.M., Hassan, A., Sabri, M.S.S., Alamir, M.A., and Alarifi, I.M. (2022) Evaluation and Prediction of the Bending Behavior of Circular Hollow Steel Tube Sections Using Finite Element Analysis, Materials, MDPI, Vol.15, No.11, 3919. [https://doi.org/10.3390/ma15113919]
• Kim, J.H., Lee, C.H., Han, K.H., and Kim, S.H. (2019) Experimental Study of High-Strength Steel RHS X-Joints Under Axial Compression, Journal of Korean Society of Steel Construction, KSSC, Vol.31, No.2, pp.75-84 (in Korean). [https://doi.org/10.7781/kjoss.2019.31.2.075]
• Suk, C.H., Lee, C.H., and Kim, S.H. (2022) Analytical Modeling and Strength Prediction of CHS XX-​Joints Subjected to Brace Axial Compression, Journal of Korean Society of Steel Construction, KSSC, Vol.34, No.3, pp.129-140 (in Korean). [https://doi.org/10.7781/kjoss.2022.34.3.129]
• Kyriakides, S., and Corona, E. (2007) Mechanics of Offshore Pipelines, Volume 1: Buckling and Collapse (1st Ed.), Elsevier, Netherlands. [https://doi.org/10.1016/B978-008046732-0/50001-5]
• Oh, J.Y., Lee, S.J., Jung, J., Park, D.G., and Yang, I.S. (2019) Structural Performance Analysis of Steel Plates with Deformation of Circular Steel Tube, Journal of the Korean Society of Advanced Composite Structures, KOSACS, Vol.10, No.6, pp.78-83 (in Korean). [https://doi.org/10.11004/kosacs.2019.10.6.078]
• Zou, T., Li, D., Wu, G., and Peng, Y. (2016) Yield Strength Development from High Strength Steel Plate to UOE Pipe, Materials and Design, Elsevier, Vol.89, pp.1107-1122. [https://doi.org/10.1016/j.matdes.2015.10.095]
• Lee, J., Kim, D., Quagliato, L., Kang, S., and Kim, N. (2017) Change of the Yield Stress in Roll Formed ERW Pipes Considering the Bauschinger Effect, Journal of Materials Processing Technology, Elsevier, Vol.244, pp.304-313. [https://doi.org/10.1016/j.jmatprotec.2017.01.022]
• Yi, J., Kang, S.-C., Park, W., and Choo, J.F. (2019) Yield Strength Tracking of UOE Pipe Considering Various Thickness-to-Diameter Ratios, Marine Structures, Elsevier, Vol.68, 102616. [https://doi.org/10.1016/j.marstruc.2019.04.004]
• Han, S.-W., Park, Y.C., Kim, H.-K., and Kang, S.-C. (2020) Effect of Strain Hardening on Increase in Collapse Pressure During the Manufacture of ERW Pipe, Applied Science, MDPI, Vol.10, No.14, 5005. [https://doi.org/10.3390/app10145005]
• Kim, J., Kang, S.-C., Kim, J.-K., and Song, J. (2021) Yield Strength Estimation of X65 and X70 Steel Pipe with Relatively Low t/D Ratio, Steel and Composite Structures, Techno-Press, Vol.38, No.2, pp.151-164.
• Choi, H., Choi, S., Kang, S.-C., Kim, C., and Lee, M.-G. (2021) Prediction of Anisotropic Strengths of Steel Plate After Prior Bending-Reverse Bending Deformation: Application of Distortional Hardening Model, International Journal of Mechanical Sciences, Elsevier, Vol.204, 106512. [https://doi.org/10.1016/j.ijmecsci.2021.106512]
• Ministry of Land, Infrastructure and Transport (2019) Steel Structures Design Standard (KDS 41 31 00: 2019), Korea (in Korean).
• Korean Agency for Technology and Standards (2019) Carbon Steel Tubes for Building Structure (KS D 3632: 2019), Korea (in Korean).
• European Committee for Standardization (2003) Eurocode 3: Design of Steel Structures, Part 1-1: General Rules and Rules for Buildings (Final Draft, prEN 1993-1-1: 2003(E)), Belgium
• Kim, Y.M., Kim, S.K., Lim, Y.J., and Kim, N.J. (2002) Effect of Microstructure on the Yield Ratio and Low Temperature Toughness of Linepipe Steels, ISIJ International, The Iron and Steel Institute of Japan, Vol.42, No.12, pp.1571-1577. [https://doi.org/10.2355/isijinternational.42.1571]
• Oh, S.H., Kim, J.W., and Moon, T.S. (2005) An Experimental Study of Flexible-Stiff Mixed System of High Yield Ratio-High Strength Steel for the Practical Use, Journal of Korean Society of Steel Construction, KSSC, Vol.17, No.4, pp.395-405 (in Korean).
• Tong, M.W., Venkatsurya, P.K.C., Zhou, W.H., Misra, R.D.K., Guo, B., Zhang, K.G., and Fan, W. (2014) Structure-Mechanical Property Relationship in a High Strength Microalloyed Steel with Low Yield Ratio: The Effect of Tempering Temperature, Material Science and Engineering: A, Elsevier, Vol.609, pp.​209-216. [https://doi.org/10.1016/j.msea.2014.05.004]
• Han, S.H., Lee, C.H., and Kim, S.H. (2020) P-M Interactive Strength of Steel Plate-to-CHS X-Joints Including 600 MPa Tensile Strength Steel, Journal of Korean Society of Steel Construction, KSSC, Vol.32, No.6, pp.385-396 (in Korean). [https://doi.org/10.7781/kjoss.2020.32.6.385]
• Korean Agency for Technology and Standards (2018) Method of Tensile Test for Metallic Materials (KS B 0802: 2018), Korea (in Korean).
• Dassault Systems Simulia Corp. (2021) Abaqus Analysis User’s Manual, Ver. 2021, DSS, USA
• Mun, J.-H., and Yang, G.-H. (2014) Design Approach for Boundary Element of Flexure-Governed RC Slender Shear Walls Based on Displacement Ductility Ratio, Journal of the Korea Concrete Institute, KCI, Vol.26, No.6, pp.687-694 (in Korean). [https://doi.org/10.4334/JKCI.2014.26.6.687]
• Tafsirojjaman, T., Fawzia, S., and Thambiratnam, D. (2020) Investigation on the Behavior of CFRP Strengthened CHS Members Under Monotonic Loading Through Finite Element Modelling, Structures, Elsevier, Vol.28, pp.297-308. [https://doi.org/10.1016/j.istruc.2020.08.059]