수평 긴장력이 도입된 강선을 이용한 교량 처짐 측정기법에 관한 기초적 연구
Copyright © 2022 by Korean Society of Steel Construction
초록
기존의 처짐 측정 방법은 해상교량, 과선교 등에 적용이 어려워 직접 처짐을 측정하지 못하는 문제점이 있다. 본 연구는 직접 처짐을 측정하기 어려운 구간에 적용할 수 있는 변위측정법 개발을 목적으로 하며, 측정방법은 수평으로 설치된 강선에 수직으로 스프링과 변위계를 설치하여 변위를 측정하는 방법이다. 실험은 단기계측과 장기계측으로 나누어 연구를 수행하였고, 단기계측은 경간장 및 강선 긴장력 차이에 의한 변위 보정을 목적으로 수행하였으며, 장기계측은 대기온도 및 풍속변화 차이에 의한 변위 보정을 목적으로 수행하였다. 실험결과로부터 경간장 및 강선 긴장력, 온도변화에 따른 보정계수 계산식을 제안하였다.
Abstract
The existing deflection measurement method has a problem in that it is difficult to directly measure the deflection because it is difficult to apply to offshore bridges and overbridges. The purpose of this study is to develop a displacement measurement method that can be applied to a section where it is difficult to measure deflection directly. The experiment was conducted by dividing the experiment into short-term measurement and long-term measurement. Short-term measurement was performed for the purpose of correcting displacement due to the difference in span and steel wire tension, and long-term measurement was performed for the purpose of correcting displacement due to difference in atmospheric temperature and wind speed. From the experimental results, it was proposed to calculate the correction factor according to the span length, the tension force of the steel wire, and the temperature change.
Keywords:
Steel wire, Tension force, Air temperature, Bridge, Deflection키워드:
강선, 긴장력, 대기온도, 교량, 처짐1. 서 론
교량 구조물의 구조 안전성 평가에 있어서 실시간으로 전체적인 구조거동을 관리하기 위해 교량의 처짐 측정은 매우 중요한 평가지표로 활용되고 있다. 교량 처짐 측정은 변위측정 자기센서(linear variable differential transformer, LVDT; 이하 변위계)를 이용한 방법이 높은 정밀도로 폭넓게 활용되고 있으나, 기존 처짐측정 방법은 해상교량, 과선교와 같이 수심이 깊은 교량 등에서 적용이 어려워 직접 처짐을 측정하지 못하는 문제점이 있다[1],[2].
직접 처짐 측정이 어려운 교량에서 처짐 데이터를 확보하는 것은 교량의 유지관리 측면에서 매우 중요한 요소이다. 따라서 직접 처짐을 측정하기 어려운 구간에 적용할 수 있는 교량 하부 비접촉 변위측정법의 개발은 교량 구조물의 안전성 및 사용성 평가에 매우 중요하며, 최근 처짐 측정에 대한 다양한 연구개발이 이루어지고 있다.
처짐 측정에 대한 대표적인 연구동향으로는 처짐형상을 간접적으로 추정하기 위해 광섬유 브래그 격자 센서(fiber bragg-grating strain sensor, FBG)를 이용하여 변형률 측정을 통해 처짐형상을 추정하는 방법[3],[4], 기하학적인 구조물의 형상변화를 추정하기 위해 하중재하에 대한 경사변형과 처짐량을 측정, USN 기반의 무선 경사 센서 모듈을 이용하여 처짐을 추정하는 방법[5], 차량 주행에 따른 가속도 계측자료를 이용하여 교량의 고유진동수를 진동모드별로 파악하고 모드중첩법에 의한 비감쇠 강제진동 이론의 처짐 계산식으로 처짐을 예측하는 방법 등 간접적으로 처짐을 추정하는 방법들이 대표적이다[6].
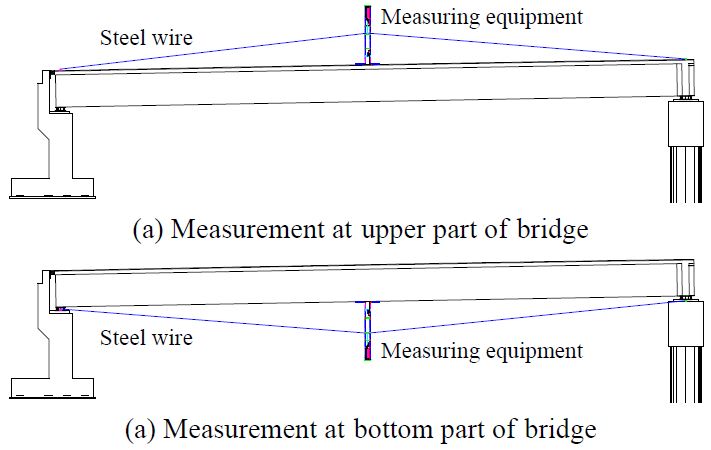
본 연구는 직접 처짐을 측정하기 어려운 구간에 적용할 수 있는 교량 하부 비접촉 변위측정법 개발을 위한 것으로 간접적인 처짐 추정방법이 아닌 직접 처짐 측정법으로 보다 정확한 교량 구조물의 내하력 및 안전성 평가를 실시하는데 목적이 있다. 비접촉 변위측정이란 Fig. 1과 같이 교량의 상부 또는 하부에서 교량의 교대 또는 교각에 수평으로 설치된 강선 중앙부에 수직으로 강선을 설치한 후, 강선 상부에 스프링과 변위계를 설치하여 거더가 하중에 의해 변형될 때 스프링의 변위를 변위계에 의해 측정하는 방법이다. 이때 스프링에 발생하는 변위와 실제 변위 간에 오차가 발생하며 이에 대한 보정계수가 필요하게 된다.
2. 측정시스템 개요
2.1 측정시스템 구성 및 원리
교량 하부 비접촉 변위측정 원리는 Fig. 2와 같이 교량의 교대 또는 교각에 수평으로 설치된 강선 중앙부에 수직으로 강선을 설치한 후, 강선 상부에 스프링과 변위계 A를 설치하여 거더가 하중에 의해 변형될 때 스프링의 변위를 변위계 A에 의해 측정하는 방식이다.
교량 하부 비접촉 변위측정을 위한 측정시스템은 수평 강선, 수평장력 윈치, 수평 로드셀, 하중 측정 인디케이터, 고정프레임, 처짐 측정 인디케이터(변위·온도·풍속 측정), 고탄성 스프링, 변위계 A, 변위계 B, 변위계 거치용 반력철판 및 수직강선 등으로 구성된다.
측정장치 설치는 다음과 같이 이루어진다. 교대 및 교각으로부터 수평으로 설치된 강선에 일정 장력을 도입하기 위해 한쪽에는 장력을 주기 위한 윈치를 설치하고, 다른 한쪽에는 하중을 측정하기 위한 로드셀과 인디케이터를 설치하여 초기장력을 도입한다. 수평강선 중앙부에 고정프레임과 처짐 측정 인디케이터(변위·온도·풍속 측정), 고탄성 스프링, 변위계 A, 변위계 거치용 반력철판 및 수직강선 등을 설치하고, 고정프레임 하부에 상하로 높이 조절이 가능한 장치를 설치한 후, 높이 조절에 따른 변위를 측정하기 위해 하부에 변위계 B를 설치한다.
측정원리는 다음과 같다. Fig. 2와 같이 교량의 상부구조물에서 처짐이 발생할 경우, 교량의 상부구조물에 설치된 고정프레임도 함께 하강하게 된다. 이때 교대와 교각을 잇는 수평강선과 연결된 수직강선은 상대적으로 상승하게 되고, 반력철판을 통해 수직강선과 연결된 고탄성 스프링이 압축력을 받아 짧아진다. 여기서 반력철판도 고탄성 스프링에 의해 상승하게 되고, 반력철판의 거치판과 맞붙은 변위계 A의 인출핀도 상승하면서 변위계 A와 연결된 인디케이터에서 변위를 계측하게 된다.
이때 스프링에 발생하는 변위와 실제 변위 간에 오차가 발생하며 이에 대한 보정계수가 필요하게 된다. 이를 위해 실제 측정 전에 데이터 보정측정을 실시하여 보정계수를 파악한다. 높이 조절장치를 상하로 움직이면서 변위계 A와 변위계 B의 변위를 동시에 측정하여 변위계 B에서 측정되는 실제 변위값과 변위계 A에서 측정되는 변위값의 차이를 보정하여 보정계수를 구하고, 변위계 A에 보정계수를 입력한 후, 실제 측정을 실시한다.
실제 측정에서는 교량에 차량하중을 재하하여 처짐이 발생하면 고탄성 스프링이 압축력을 받아 짧아지게 되고, 보정계수가 적용된 변위계 A에 변위가 발생하여 처짐을 측정하게 된다. 보정계수의 경우 현장요건에 따라 보정 측정과 실제 측정에서 측정 경간장, 강선 긴장력, 대기온도 및 풍속의 변화 등에 영향을 받아 다양하게 분포하며, 사전에 보정계수 특성을 명확히 파악함으로써 현장 측정에 있어서 측정데이터 정밀도의 품질을 확보해야 한다.
본 연구에서는 실험을 통해 경간장, 강선 긴장력 및 대기온도 변화에 따른 비접촉 변위 보정계수의 특성을 파악하고자 단기계측과 장기계측으로 나누어 연구를 수행하였다. 단기계측은 측정 경간장과 수평강선 장력 차이로 발생되는 오차에 대한 검증과 보정을 위한 목적으로 수행하였으며, 장기계측은 대기온도 및 풍속변화에 의해 발생하는 오차에 대한 검증과 보정을 위한 목적으로 수행하였다.
3. 실험방법
3.1 단기계측실험
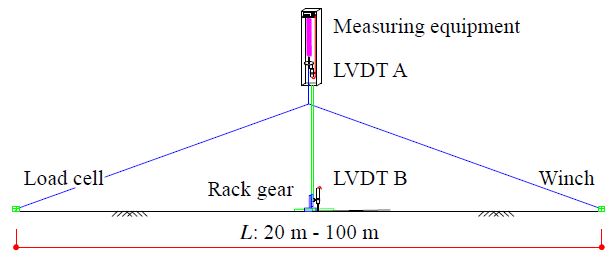
단기계측실험은 강선 긴장력과 경간장을 변수로 하였다. 실험을 위해 지면에 수평으로 설치된 강선에 윈치로 일정 축력을 도입시킨 후, 바닥면에 고정되어 랙 기어에 의해 상하로 이동되는 실험체 고정장치에 스프링과 변위계 A를 설치하였다. 실험계측은 강선 중앙부에서 실험체 고정장치에 설치된 스프링으로 수직으로 긴장력을 가한 후, 랙 기어를 상하로 움직이면서 스프링에서 발생하는 비접촉 상대처짐을 변위계 A에서 측정하고, 지면과 랙 기어 사이에서 발생하는 직접처짐을 변위계 B에서 측정하는 방식으로 수행하였다. 단기계측 실험체 세팅도를 Fig. 3에, 대표적인 세팅현황을 Fig. 4에 나타냈다. 계측에 사용된 강선은 직경 2.38 mm, 인장하중 4.63 kN이며, 스프링은 외경 16 mm, 직경 2.0 mm의 인장스프링을 사용하였다. 수평강선의 긴장력 차이와 경간장 차이에 따른 영향을 파악하기 위하여 수평강선 긴장력 4종류(600 N, 800 N, 1,000 N, 1,200 N)에 대해 각각 경간장 7종류(20 m, 30 m, 50 m, 60 m, 70 m, 80 m, 100 m)를 적용하여 총 28개 실험변수에 대해 실험을 실시하였다. 수직강선 긴장력은 수직 스프링을 사용하여 모든 실험변수에 동일하게 200 N의 수직 긴장력을 도입시킨 상태에서 실험을 실시하였다.
3.2 장기계측실험
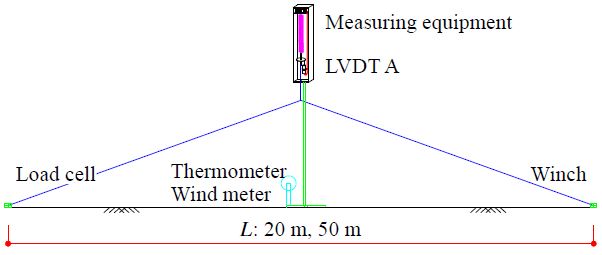
장기계측실험은 온도변화 및 풍속의 영향을 분석하기 위하여 실시하였으며, 1,000 N의 수평 긴장력이 도입된 경간장 20 m 및 50 m의 실험체에 200 N의 수직 긴장력을 수직 스프링으로 도입시킨 상태에서 약 1개월에 걸쳐 대기온도, 풍속변화에 따른 변위계 A의 처짐량 변화를 1분당 1회 측정하여 분석하였다. 장기계측 실험체 세팅도를 Fig. 5에 나타냈고, 세팅현황을 Fig. 6에 나타냈다.
4. 결과분석 및 고찰
4.1 강선 긴장력 및 경간장 차이에 따른 검토
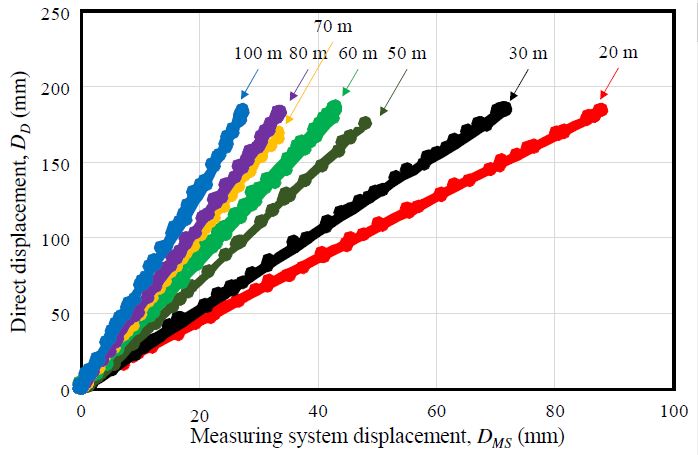
강선 긴장력 및 경간장을 변수로 하여 실시한 단기계측 실험을 실시, 분석한 결과 측정시스템을 이용하여 측정된 변위계 A의 처침(DMS)과 직접 변위에 해당하는 변위계 B의 처짐(DD) 사이에는 선형의 비례관계가 성립하는 것을 확인하였다. 실험결과로 구한 총 28개의 실험변수에 대한 실험계측결과를 1차식으로 선형 회귀분석하였다. 강선 긴장력과 경간장 차이에 따른 회귀분석을 통해 얻어진 보정계수(DD/DMS)를 정리하여 Table 1에 나타냈고, 대표적으로 강선 긴장력 1.000 N에서의 경간장별 처짐 측정 비교 곡선을 Fig. 7에 나타냈다. Fig. 7에서 수평축은 본 연구에서 교량 중앙부의 직접 처짐 측정을 위해 개발된 측정시스템을 이용하여 측정된 변위계 A의 처짐(DMS)이며, 수직축은 직접 변위에 해당하는 변위계 B의 처짐(DD)을 나타낸다. Fig. 7에서 변위계 A의 처짐(DMS)과 변위계 B의 처짐(DD) 사이에는 선형의 비례관계가 성립하는 것을 알 수 있다.
실험결과를 집계한 Table 1의 각 기울기값을 토대로 강선 긴장력별로 경간장 변화에 따른 보정계수(DD/DMS)의 영향을 파악하기 위하여 경간장-보정계수(DD/DMS) 곡선을 Fig. 8에 나타냈다. Fig. 8에서 경간장과 보정계수(DD/DMS)는 선형 비례관계에 있는 것을 알 수 있다.
Fig. 8으로부터 각각의 긴장력별로 이를 다시 1차식으로 선형 회귀분석하고, 경간장 L을 변수로 보정계수 k1을 계산하는 1차 추정식으로 변환, Table 2에 나타냈다. Table 2에서 α는 이후 분석을 위해 각각의 보정계수 추정식 k1의 (기울기×104), β는 (y절편×104)로 표현하였다.
Table 2의 α 및 β값과 강선 긴장력의 관계를 Fig. 9에 나타냈다. Fig. 9에서 α 및 β값과 강선 긴장력도 선형 비례관계에 있음을 알 수 있으며, 이를 다시 선형 회귀분석한 결과는 α = –0.00003165 × C + 0.08851, β = 0.00025295 × C + 0.66827로 표현할 수 있으며, 경간장 L과 강선 긴장력 C를 변수로 보정계수 k1을 계산하는 추정식은 식 (1)과 같다.
| (1) |
여기서, k1: 경간장 및 강선 긴장력에 따른 보정계수,
- L: 경간장(m, 20 ≤ L ≤ 100),
- C: 강선 긴장력(N, 600 ≤ C ≤ 1200).
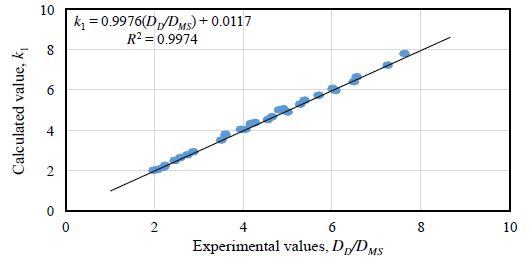
식 (1)을 이용하여 계산된 보정계수 계산값을 Table 3에 나타냈으며, Table 1의 실험결과를 집계한 보정계수(DD/DMS)와 Table 3 상의 보정계수 계산값 k1 간의 상관관계를 Fig. 10에 나타냈다. Fig. 10에서 계산결과와 실험결과가 높은 정밀도로 거의 일치하는 것을 알 수 있으며, 식 (1)은 경간장 및 강선 긴장력의 변화에 따른 현장측정에서 변위측정 보정계수 유효성을 판단하는 기초자료로 활용할 수 있을 것으로 판단된다.
4.2 온도변화 및 풍속변화에 따른 검토
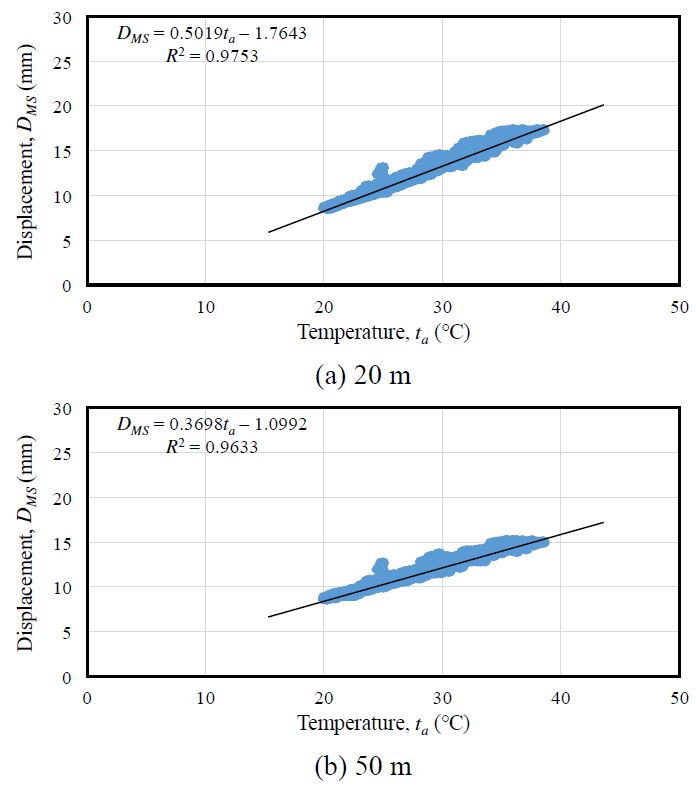
장기계측결과로부터 얻어진 대기온도 변화에 따른 처짐변화 측정결과 중에 대표적으로 경과일수 30~32일 시점의 대기온도(ta)-장기처짐(DMS) 곡선을 Fig. 11에 나타냈다. 선형 회귀분석하여 얻어진 1차식과 상관계수(R2)를 Fig. 11에 같이 표기하였으며, 경과일수에 따른 온도변화-장기처짐 곡선의 선형 회귀분석으로 구한 1차식의 기울기를 집계하여 Table 4에 나타냈다. 데이터 집계는 풍속을 영향을 배제하기 위하여 풍속 0.1 m/s 이하에서의 데이터만을 사용하였다. Fig. 11에서 대기온도와 장기처짐 사이에는 선형의 비례관계가 성립하는 것을 알 수 있으며, Table 4에서 경과일수가 누적되어도 경간장별로 온도변화 기울기값이 거의 동일한 양상을 나타내는 것을 알 수 있다. 이로부터 측정데이터 간의 온도변화에 의한 오차를 보정계수를 통하여 측정결과에 반영할 수 있을 것으로 판단된다.
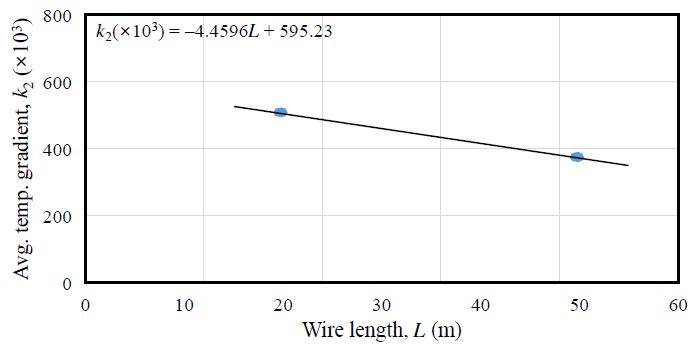
측정데이터 간 온도변화를 보정계수를 통하여 측정결과에 반영하기 위해 Table 4의 결과로부터 경간장별 온도변화 기울기 평균값을 Fig. 12에 나타내고, 1차식으로 선형 회귀분석하였다. Fig. 12에 나타난 경간장과 온도변화 기울기 평균값의 상관관계로부터 측정데이터 간 온도변화에 따른 기울기 보정값 k2를 산정하면 식 (2)와 같다.
| (2) |
여기서, k2: 온도변화에 따른 보정계수,
- L: 와이어 길이(m),
- T: 데이터 측정 전후 온도변화
- (℃, 예: 25 ℃ → 22 ℃일 때 T = –3).
풍속에 따른 영향을 검토하기 위해 각각의 경간장별로 장기계측결과로부터 얻어진 처짐값 중에서 동일한 온도조건에 풍속차이에 따른 처짐값을 집계함으로써 대기온도의 영향을 배제하였다. 풍속-장기처짐 측정결과를 경간장별로 집계하고, 1차식의 선형 회귀분석으로 분석하였으며, 대표적인 풍속(vw)-장기처짐(DMS) 추세선을 Fig. 13에 나타냈다. Fig. 13을 통해 풍속에 따른 장기처짐 측정값이 거의 일정한 양상을 나타내는 것을 알 수 있으며, 직경 2.38 mm 강선에 순간적으로 작용하는 풍속의 변화는 처짐에 미치는 영향이 미소하여 풍속에 대한 검토는 본 연구에서 배제하기로 하였다.
4.3 보정계수 계산식
교량 중앙부 직접 처짐 측정이 가능한 계측시스템을 개발하기 위하여 강선 긴장력 및 경간장을 변수로 한 실험계측결과와 대기온도 및 풍속의 영향을 고려한 장기계측결과로부터 식 (1)과 식 (2)를 종합하여 강선 긴장력, 경간장 및 대기온도 변화에 따른 보정계수는 식 (3)과 같다.
| (3) |
여기서, k1: 경간장 및 강선 긴장력에 따른 보정계수,
- k2: 온도변화에 따른 보정계수,
- C: 강선 긴장력(N),
- L: 경간장(m),
- T: 데이터 측정 전후 온도변화
- (℃, 예: 25 ℃ → 22 ℃일 때 T = –3).
식 (3)은 강선 긴장력, 경간장 및 대기온도 변화에 따른 보정계수 산정식으로, 현장측정에서 변위측정 보정계수 유효성을 판단하는 기초자료로 활용할 수 있을 것으로 판단된다.
다만 현시점에서 본 연구결과로 얻어진 보정계수를 현장에 바로 적용하기에는 무리가 있다. 본 연구에 사용된 강선은 재료적 특성 차이를 배제하기 위해 직경 2.38 mm 1종류만을 사용하였다. 강선은 직경 차이 및 동일한 직경이라도 형상에 따라 강도 및 강성이 다양하게 분포하지만, 식 (3)에는 강선 직경 및 형상에 따른 초기강성, 항복강도, 인장강도 등의 재료적 특성이 반영되지 않았기 때문에 이에 따른 추가적인 오차가 발생할 것으로 판단된다.
재료적 특성이 반영된 보정계수 산정식은 향후 연구과제로 남아 있으며, 강선의 직경 및 형상 차이에 따른 재료실험을 통해 초기강성, 항복강도, 인장강도를 명확히 하고, 이러한 재료성질과 강선에 도입되는 긴장력과 경간장 차이에 따른 상관관계를 실험을 통해서 검증하여야만 한다. 또한 강선의 긴장 전후로 경과시간에 따라 발생하는 초기 릴랙세이션 등에 의한 긴장력 차이, 경간장 100 m 이상에서의 거동 특성 등에 대해서도 추가적인 연구가 필요한 상태이다.
5. 결 론
본 연구는 직접 처짐을 측정하기 어려운 구간에 적용할 수 있는 교량 하부 비접촉 변위측정법 개발의 일환으로 실험을 통한 경간장, 강선 긴장력, 대기온도 변화, 풍속 변화에 따른 변위 특성을 파악하는 것을 목적으로 연구를 수행하였으며, 다음과 같은 결론을 얻었다.
- (1) 실험계측에서 초기 강선에 도입하는 긴장력의 차이에 따라 발생하는 오차 등에 대한 검증과 보정을 위해 실험을 실시하였으며, 실험결과로부터 강선 긴장력과 경간장 차이에 따른 보정계수 계산식을 제안하였다.
- (2) 장기계측에서 대기온도 변화 및 풍속의 영향을 분석하기 위한 실험을 실시하였으며, 실험결과로부터 경간장에 따른 온도변화 기울기 보정계수 계산식을 제안하였다.
본 기술개발에서는 직경 2.38 mm의 강선으로 최대 경간장 100 m까지 실험을 실시하여 분석하였으나, 비접촉 변위측정법의 보다 높은 신뢰성 확보를 위해서는 향후 추가적인 연구가 필요할 것으로 판단된다.
Acknowledgments
이 논문은 ㈜홍익기술단의 연구비 지원으로 수행되었으며, 이에 감사드립니다.
References
- Korea Authority of Land & Infrastructure Safety (2008) Manual for Utilization and Management of Diagnostic Equipment, Korea (in Korean).
- Ministry of Land, Infrastructure and Transport, and Korea Authority of Land & Infrastructure Safety (2019) Detailed Guidelines for Safety Management and Maintenance of Facilities: Safety Inspection and Diagnosis, Chapter 1: Bridge, Korea (in Korean).
- Cho, N.-S., and Kim, N.-S. (2008) Prediction of the Static Deflection Profiles on Suspension Bridge by Using FBG Strain Sensors, Journal of the Korean Society of Civil Engineers, KSCE, Vol.28, No.5A, pp.699-707 (in Korean).
- Kim, N.-S., and Cho, N.-S. (2002) Estimation of Bridge Deflection Using Fiber Optic Bragg-Grating Sensors, Journal of the Korean Society of Civil Engineers, KSCE, Vol.22, No.6A, pp.1357-1366 (in Korean).
-
Jo, B.W., Yoon, K.W., Kim, Y.J., and Lee, D.Y. (2011) A Study on the Ubiquitous Wireless Tilt Sensors’s Application for Measuring Vertical Deflection of Bridge, Journal of the Korea Institute for Structural Maintenance and Inspection, KSMI, Vol.15, No.3, pp.116-124 (in Korean).
[https://doi.org/10.11112/jksmi.2011.15.3.116]

-
Yun, Y.K., and Ryu, H.J. (2011) Calculation of Deflection Using the Acceleration Data for Concrete Bridges, Journal of the Korea Institute for Structural Maintenance and Inspection, KSMI, Vol.15, No.5, pp.92-100 (in Korean).
[https://doi.org/10.11112/jksmi.2011.15.5.092]