[ Article ]

Journal of Korean Society of Steel Construction - Vol. 34, No. 5, pp.289-300

ISSN: 1226-363X (Print) 2287-4054 (Online)

Print publication date 27 Oct 2022

Received 14 Sep 2022 Revised 04 Oct 2022 Accepted 04 Oct 2022

DOI: https://doi.org/10.7781/kjoss.2022.34.5.289

비대칭 합성거더의 단면성능 향상을 위한 도심축 구성에 관한 정식화

정순록¹ ; 박상현² ; 이승용³^{, *}

1박사과정, 한국교통대학교, 토목공학과
2대표이사, 티에이치디㈜
3교수, 한국교통대학교, 건설환경융합공학과

Formulation of Neutral Axis for the Improvement of Sectional Properties of Asymmetric Composite Girders

Jung, Soon Log¹ ; Park, Sang Hyun² ; Lee, Seung Yong³^{, *}

1Graduate Student (Ph.D Course), Dept. of Civil Engineering, Korea National University of Transportation, Chungju, 27469, Korea
2CEO, THD Co., Ltd., Uiwang, 16006, Korea
3Professor, Dept. of Civil and Environmental Convergence Engineering, Korea National University of Transportation, Chungju, 27469, Korea

Correspondence to: ^* Tel. +82-43-841-5189 Fax. +82-43-841-5180 E-mail. sylee@ut.ac.kr

초록

이 논문은 시공 단계에 따라 합성 전과 후로 구분되는 강재 거더의 역학적 성질을 증가시킬 목적으로 수행되었다. 주부재의 상단에 소형의 추가부재를 부착함에 있어 합성된 거더의 형상이 비대칭인 점으로 인해서 오히려 단면계수가 감소되는 부분을 개선하고자 하였다. 소형부재의 설치로 인한 비대칭 합성거더와 주부재인 경우의 단면계수, 단면2차모멘트 차이 값이 (+)의 값을 가져야 한다는 명제를 통해 역학적 성질을 유도하였으며, 이로부터 비대칭 합성거더의 도심축 구성위치 및 이를 만족시킬 수 있는 추가부재의 사용단면적에 관한 정식화 연구결과를 도출하였다.

Abstract

This study was conducted with the purpose of increasing the mechanical properties of steel girder, which are divided into before and after composite according to the construction stage. When attaching a small additional member to the upper end of the main member, it was intended to improve the part where the section modulus was decreased due to the asymmetric shape of the composite girder. The mechanical properties were derived through the proposition that the difference between the section modulus and the moment of inertia in the case of the asymmetric composite girder and the main member due to the installation of small members should have a positive value. From this, the results of a formal study on the position of the central axis of the asymmetric composite girder and the cross-sectional area of additional members that can satisfy it were derived.

Keywords:

Asymmetric composite girder, Inertia moment, Sectional modulus, Neutral axis

키워드:

비대칭 합성거더, 단면휨강성, 단면계수, 도심축

1. 서 론

본 연구는 강재를 이용하는 국내 교량 산업을 활성화하고 경제적인 구조물 공사를 할 수 있는 근간을 다지기 위한 것으로, 강재를 이용한 대표적인 교량 형식은 경간장 규모별로 50 m - 90 m는 강박스거더, 30 m - 50 m 내외는 플레이트 거더, 90 m 이상은 트러스, 아치교, 사장교 및 현수교 등으로 구성되고 있다. 국내·외 콘크리트를 주재료로 사용한 특수교량 분야도 사용되고 있지만, 경간장이 장경간화할수록 고정하중의 부담이 있어 실상, 특수교량의 거더인 보강형 거더는 다수의 경우 강재를 사용하는 것이 보편적인 현상이다.

한편 최근 국내·외에서는 H형강을 이용하여 교량 혹은 건축구조물로서 활용하려고 하는 연구 및 상용화가 활발하게 진행 중이다^[1]-[3]. 그러나 이러한 참고문헌 상의 연구내용은 H형강보의 상부플랜지에 이종의 재료를 혼합한 연구내용^[4], 즉 기본부재인 강재거더 자체의 역학적 성질을 개선한 것은 아닌 연구 또는 콘크리트를 타설하는 것에 관한 연구 등이다. 이와는 달리 기본부재인 강재거더의 역학적 성질을 향상시키려는 연구^[5]-[8] 등이 있다. 그러나 선행연구결과는 모두 단면2차모멘트 또는 단면계수를 향상시킴에 있어 그 효과의 범위가 형강 혹은 소정의 폭을 가진 H형강 수준으로 제한적이었다.

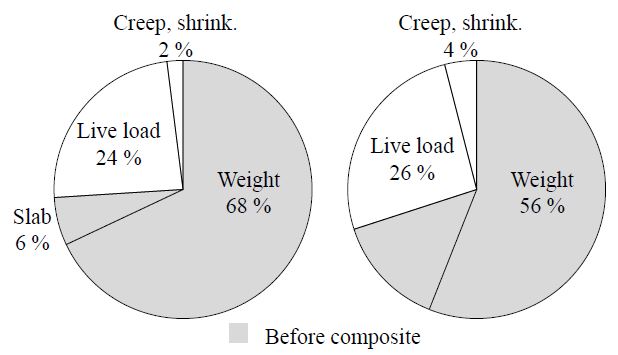
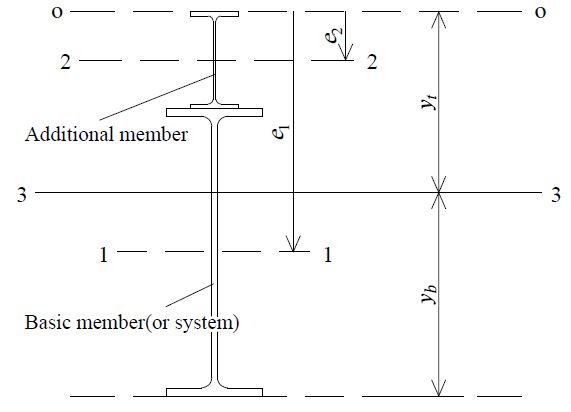
이에 본 논문에서는 기본부재의 역학적 성질 향상에 대한 범용성을 추구하기 위해 그 근간에 관한 연구를 진행하였다. 기본부재의 역학적 성질 향상을 위해 본 연구에서 먼저 주목한 것은 Fig. 1 및 Fig. 2와 같이 강박스거더 및 플레이트거더교에서 기본부재인 강재거더가 설계하중 종류별로 받는 응력 분포에 따른 비중이다.

Fig. 1.

Stress distribution of steel box girder

Fig. 2.

Stress distribution of steel plate girder

Figs. 1-2의 응력 분포도는 국토해양부에서 편찬한 ‘도로설계편람 제5편 교량편: 강박스거더 및 플레이트 거더교 기술내용’을 참조하였다^[9]. 여기서 기본부재인 강재거더는 합성 전 구조계에서 65 % - 76 %(색상 표시 부분)의 응력을 이미 받고 있다. 이러한 응력분포는 지간장 70 m 미만인 조건에서는 보편적으로 나타나는 현상으로, 본 연구에서 주목할 점은 합성 전 구조계에서 기본부재인 강재거더에 이미 전체 설계응력 크기의 70 % 정도를 지지해야 한다는 점이다.

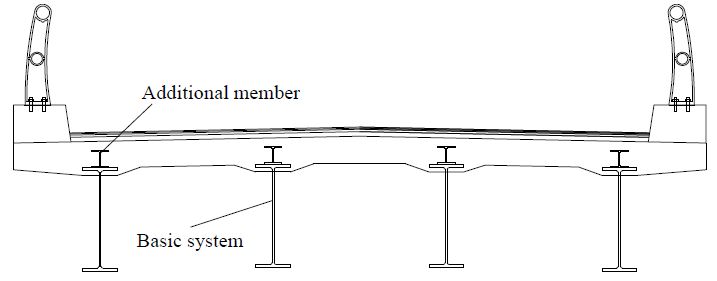
따라서 강재거더 형식에 대한 역학적 성질의 향상은 바닥판 콘크리트가 합성되거나 데크가 설치되어 작용하는 구조계가 아닌 합성 전에 작용하는 구조계의 성질을 개량해야 한다. 이에 본 논문에서는 합성 전 구조계의 성질을 개량할 수 있도록 연구를 진행했다. 다음의 Fig. 3 및 Fig. 4 는 기본부재인 강재거더의 역학적 성질을 개량할 목적으로 시공된 거더 횡단면도이다^[5]-[8].

Fig. 3.

Section view of plate girder with I (or H)

Fig. 4.

Section view of steel box girder with T-shape

통상적인 물리적 현상으로는 Figs. 3-4와 같이 기본부재(혹은 시스템)가 I 형상이든 혹은 □ 형상이든 그것에 소형부재가 추가로 단면적이 증가하고, 합성거더의 형고가 증설하게 되면 단면2차모멘트가 증가함으로써 그로 인한 처짐 감소와 더불어 합성된 거더 상·하연에 발생하는 응력이 감소하여야 하는 것이 보편적인 결과이다. 그러나 다음의 Table 1-3에 나타난 결과를 보면 반드시 그러한 결과가 보장되지는 않음을 알 수 있다. 먼저 기본시스템이 H형상인 플레이트 거더인 경우에 대해서 살펴보면 다음과 같다.

Table 1.

Check conditions of plate girder with H-shape

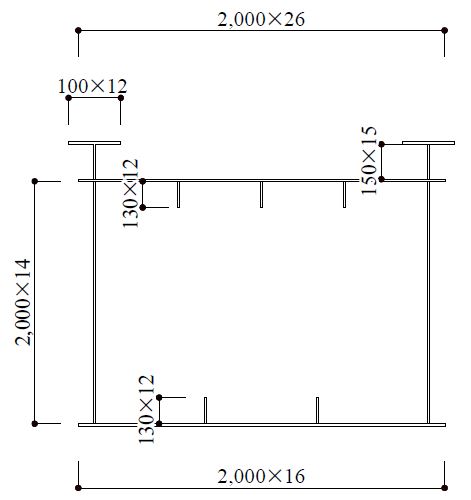
Table 2에 나타난 결과를 보면 기본시스템으로 H형강 700×300을 사용하고 소형형강 H-200×100을 추가 설치한 경우, 전술한 바와 같이 합성거더로서의 사용 단면적과 전체 거더 높이 증가로 인해 단면2차모멘트는 당초와 비교해 125 % 증가하였으나, 합성거더의 응력 크기를 나타내는 척도인 단면계수는 상연 13 % 감소, 하연 10.2 % 증가를 나타냈다. 기본시스템 형상이 구형인 박스거더에 대해서도 Fig. 5와 같은 규격일 때 비교 검토를 실시하였다.

Table 2.

Results of comparison of asymmetric plate girder

Fig. 5.

Check conditions of box girder with T-shape (Unit: mm)

Table 3에 나타난 결과를 보면 단면2차모멘트는 당초와 비교해 6 % 증가하였으나, 합성거더의 응력 크기를 나타내는 척도인 단면계수는 상연 17 % 감소와 하연 2 % 증가를 나타냈다.

Table 3.

Results of comparison of asymmetric box girder

상기 결과에서 보듯 비대칭 합성거더인 경우의 구조물의 응력상태는 하연의 경우 안정적인 감소를 나타내지만 상연의 경우 응력검토 위치의 거리 증가가 단면2차모멘트 증가효과보다 커서 매우 불리한 구조를 나타내고 있다. 이에 본 연구에서는 비대칭 합성거더 상연의 응력이 지배인자라고 판단하였다. 특히 허용응력설계법, 한계상태설계법, 하중저항계수설계법 등 강구조물에 대한 설계기준과 관계 없이 세장한 규격으로 사용되는 특성으로 인해 압축응력을 받는 위치에서 응력이나 소성모멘트 저항강도 등이 재질 본래의 성능에 비해서 약화된다. 따라서 기본시스템에 추가부재를 설치하는 경우의 지배요소를 합성거더의 상연응력 제어 및 향상으로 하였다. 또한 Table 1 - Table 3에서 발생한 현상을 개선할 뿐 아니라 범용성 있는 비대칭 합성거더의 성능을 개선하기 위해 본 연구를 진행하였다.

2. 비대칭 합성거더의 단면특성치 감소 원인

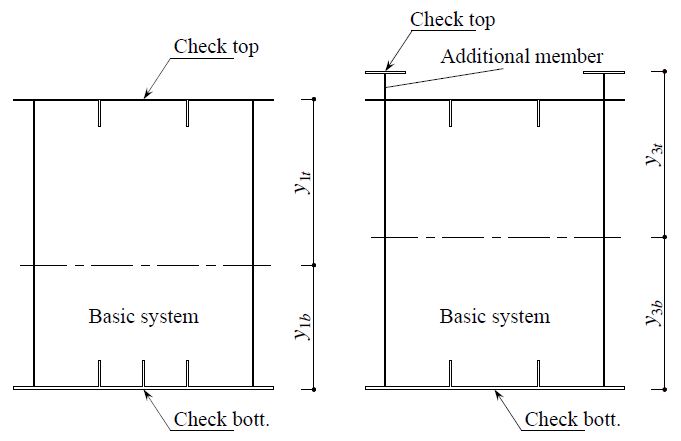
전술한 바와 같이 추가부재의 사용으로 강재량 및 형고 증설로 인해 거더 상단에 발생하는 휨응력이 오히려 증가하는 물리적 이유를 Figs. 6-7에 나타내어 설명하면 다음과 같다. Figs. 6-7에서 나타난 바와 같이 기본시스템과 비대칭 합성거더의 차이점을 보면, 추가부재로 인한 형고증설로 인해 플레이트 거더 및 박스 거더 모두(기본시스템 형상에 구애받지 않음을 의미) 단면2차모멘트가 증가함은 불변이나 그로 인해서 수반되는 현상이 도심축 위치의 상향 이동 및 거더 상연의 응력검토 위치가 기본시스템과 비교해 비대칭 합성거더인 경우의 단면2차모멘트 크기가 증가한 양보다 상대적으로 검토위치의 상향 이동거리가 더 커서 발생하는 기하학적 물리적 현상으로 보면 y_1t < y_3t 비율이 더 큰 값으로 발생한 현상이다.

Fig. 6.

Neutral axis of the asymmetric plate girder

Fig. 7.

Neutral axis of the asymmetric box girder

Fig. 8과 같이 추가부재의 사용이 기본시스템과 서로 동일한 규격인 경우의 결과를 보면 Table 4와 같다.

Fig. 8.

Representation of the symmetric composite girder

Table 4.

Results of comparison of symmetric plate girder

Table 4의 결과를 보면, 추가부재가 기본시스템과 동일한 규격인 경우 단면2차모멘트 및 단면계수가 매우 큰 폭으로 증가함을 알 수 있다. 이러한 현상은 Fig. 7 및 Fig. 8에 나타낸 바와 같이 기하학적인 특성으로 나타나는 현상이다. 현실적으로 건축, 토목, 플랜트와 같은 건설환경 등의 공학적 조건이 무한으로 구조물의 형고, 사용량을 증설할 수 있는 것이 아니므로 경제성을 고려한 구조물 건설이 중요하다. 그러기 위해서는 기본시스템에 소량의 부재 사용량으로도 충분한 내구성을 발휘할 수 있도록 해야 한다. 따라서 본 연구의 목적은 이러한 조건 즉, 기본시스템 Ⅰ에 소량의 추가부재 IⅠ와의 합성으로도 성능이 향상된 비대칭 합성거더 III을 완성하는 것이다.

3. 비대칭 합성거더의 단면특성치 산정

통상적으로 합성거더의 임의 축에 관한 단면2차모멘트는 이 축과 평행한 도심축에 대한 관성모멘트와 평행축의 정리에 의해 구해진다.

Fig. 9과 같은 면적을 생각하고 i-i 축의 원점을 C에 잡고, 여기서 Z-Z 축은 i-i 축에 평행하고 떨어진 거리는 d라고 하면 Z-Z 축에서의 관성모멘트 즉, 단면2차모멘트는 다음과 같이 구해진다.

Fig. 9.

Derivation of parallel-axis theorems

I Z = ∫ y + d 2 d A = ∫ y 2 d A + 2 d ∫ y d A + d 2 ∫ d A

(1)

식 (1)의 우변 첫 적분항은 x축에 관한 관성모멘트 I_x이며, 둘째 적분항은 x축이 도심을 지나므로 0이 되고 셋째 적분항은 그림의 면적이다. 따라서 앞의 식은 다음과 같으며, 식 (2)는 관성모멘트에 대한 평행축 정리^[10]이다.

I Z - Z = I i - i + A ⋅ d 2

(2)

4. 비대칭 합성거더 도심축 구성에 관한 정식화

4.1 단면2차모멘트 차이에 대한 정의

앞서 2장에서 살펴본 바와 같이 합성거더로 인한 형고 증설 효과가 온전히 발생하지 못하는 원인은 시스템 간 합성으로 인한 단면2차모멘트 증가율보다도 상대적으로 비대칭 합성거더의 휨응력 검토 위치가 기본시스템에 비해서 큰 값으로 증가했기 때문이다. 이것을 해소하려면 합성거더의 도심축과 휨응력 검토 상단인 상연까지의 편심거리가 조화를 이루어야 한다. 이러한 조화를 이루려면 단면계수 증가를 발휘할 수 있도록 합성거더 내에서의 도심축 위치가 결정적 인자가 된다. 그러나 도심축 위치라는 변수는 단면2차모멘트, 단면적, 단면계수 등에 미치는 영향이 상호 복합적이며, 그 관계가 범용성이 있으려면 일정한 패턴의 함수로 유도되어야 할 것이다.

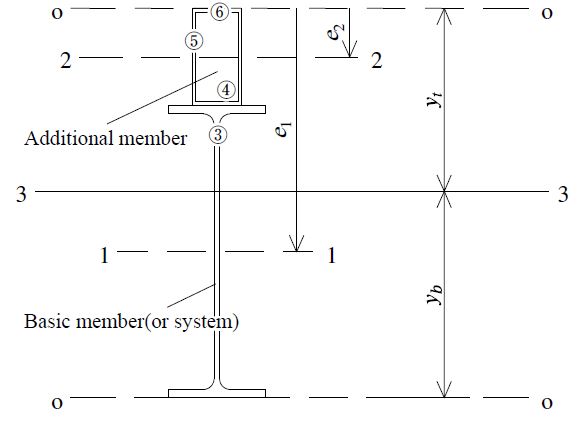
기호 정리(Notation) 및 평행축 정리 식 (1)을 참고하여 Figs. 10-12와 같은 비대칭 합성거더의 단면2차모멘트를 정의하면 식 (3)과 같다.

Fig. 10.

Asymmetric composite girder with H & H

Fig. 11.

Asymmetric composite girder with H & □

Fig. 12.

Asymmetric composite girder with □ & T

I 3 = ∑ I i + ∑ A i ⋅ e i 2 - ∑ A i ⋅ y t 2

(3)

또한 기본부재의 단면2차모멘트와 합성거더간 단면2차모멘트 차이에 대해서 정의하면 다음과 같다.

∆ I = I 3 - I 1 = ∑ I i + ∑ A i ⋅ e i 2 - ∑ A i ⋅ y t 2 - I 1

(4)

E q . 4 = I 1 + I 2 + ∑ A i ⋅ e i 2 - ∑ A i ⋅ y t 2 - I 1

(5)

E q . (5) = I 2 + ∑ A i ⋅ e i 2 - ∑ A i ⋅ y t 2

(6)

식 (6)을 y_t에 관해 이항하면 단면2차모멘트의 차이를 합성거더의 도심축 위치의 함수로 다음과 같이 정의할 수 있다.

y t 2 = I 2 + ∑ A i ⋅ e i 2 ∑ A i

(7)

4.2 단면계수의 차이

4.2.1 ΔZ > 0

기호 정리를 참고하여 기본시스템 및 합성거더에서 발생하는 휨응력을 표현하면 식 (8)과 같다.

f i = M 3 ⋅ y t o r b I i

(8)

식 (8)은 단면계수 도입으로 식 (9)와 같이 표현할 수 있다.

f i = M 3 Z 3 t o r f i = M 3 Z 3 b

(9)

여기서,

Z = y t I i o r Z = y b I i

(10)

이때 추가부재를 사용한 가치가 발생하려면 기본부재와 합성거더 간 단면계수 차이인 식 (11)은 0보다 커야 한다.

∆ Z = Z 3 - Z 1 ≻ 0

(11)

비대칭 합성거더로 형성될 때 단면특성치가 감소하는 경우는 합성거더 III의 상연이며, 이것이 지배인자이기에 본 연구의 이론 정식화 과정은 합성거더 III 상연의 단면계수 차이 값을 가지고 연구를 진행했다.

Z_3t는 식 (3)을 합성거더의 상면부터 중립축까지의 거리 y_t로 나눈 값이므로 식 (12)와 같다.

Z 3 t = ∑ I i + ∑ A i ⋅ e i 2 - ∑ A i ⋅ y t 2 y t

(12)

이에 반해 기본부재의 거더 상단의 단면계수인 Z_1t는 식 (13)과 같다.

Z 1 t = I 1 y 1 t

(13)

식 (11)의 ∆Z를 합성거더 상단에 대한 것으로 표현하여 식 (12)와 식 (13)을 대입해서 정리하면 다음과 같다.

Z 3 t = ∑ I i + ∑ A i ⋅ e i 2 - ∑ A i ⋅ y t 2 y t - Z 1 t ≻ 0

(14)

식 (14)의 양변에 y_t를 곱해서 정리하면 식 (15)와 같으며, 식 (15)는 y_t를 구하는 2차 방정식이다.

- ∑ A i ⋅ y t 2 - Z 1 t ⋅ y t + ∑ I i + ∑ A i ⋅ e i 2 ≻ 0

(15)

여기서 $D = - ∑ A i, E = - Z 1 t, F = ∑ I i + ∑ A i ⋅ e i 2$ 라고 하면, 식 (15)의 해는 다음과 같다.

y t = - E ± D 2 - 4 ⋅ D ⋅ F 2 ⋅ D

(16)

한편 식 (14)의 $y t 2$ 에 식 (7)을 대입하여 정리하면 다음과 같다.

∑ I i - I 2 y t - Z 1 t ≻ 0

(17)

I 1 + I 2 - I 2 y t - Z 1 t ≻ 0

(18)

식 (17)을 y_t에 대해 이항해서 정리하면 식 (19)와 같이 y_t의 범위를 구하게 된다.

y 1 t = I 1 Z 1 t ≻ y t

(19)

4.2.2 y_t의 미분

식 (15)는 비대칭 합성거더의 도심축 위치를 독립변수로, 두 시스템 간 단면계수 차이 값을 종속변수로 하는 2차 방정식이므로 미분에 의해서 ∆Z가 극대화될 수 있는 조건을 구할 수 있다.

d Δ Z 3 t d y t = 2 ⋅ D y 3 t + E ≻ 0

(20)

∆Z가 극대값을 가지는 y_t 조건은 다음과 같다.

y t ≻ - E 2 ⋅ D

(21)

4.3 추가부재의 필요 단면적 정의

비대칭 합성거더의 도심축인 y_t는 합성도형의 중립축이 단면의 도심을 통해야 하는 성질과 합성단면의 임의 축에 대한 단면1차모멘트가 합력의 모멘트와 분력의 모멘트의 합과 같아야 하는 성질에 의해서 다음과 같다.

y t = ∑ A i ⋅ e i ∑ A i

(22)

식 (22)를 다시 추가부재의 사용 단면적 A₂에 관해 정리하면, 추가부재 II에서 필요한 단면적 조건을 식 (23)과 같이 구할 수 있다.

A 2 = A 1 ⋅ y t - e 1 e 2 - y t

(23)

4.4 정식화 결과

본 연구에서는 비대칭 합성거더 III의 도심축 위치인 y_t의 조건과 그것을 만족시킬 수 있는 추가부재 II의 필요단면적 A₂에 대해 식 (16), 식 (19), 식 (21), 식 (23)을 통해서 결정하는 방법을 유도해냈다. 식 (19)의 경우 비대칭 합성거더의 도심축 위치가 합성거더 상단인 추가부재 상면을 원점으로 했을 때 기본시스템 Ⅰ의 위치인 y_1t보다 작아야 한다는 것은 합성거더 상단의 도심축 위치가 합성 전에 비해서 상향에 위치함을 물리적으로 의미한다. 식 (16)은 비대칭 합성거더와 기본시스템 Ⅰ 간 단면계수 차이가 양질의 결과를 얻으려면 비대칭 합성거더의 도심축 위치 y_t의 조건 음의 근과 양의 근 사이에 있어야 함을 나타낸다.

식 (23)은 기본시스템 Ⅰ의 형상에 관계 없이 식 (16)을 만족시키기 위한 제반 조건으로 추가부재 II의 단면적에 대한 필요조건이다.

5. 유도된 정식화 검증

본 연구에서 유도한 정식화 결과가 모든 구조물 사용조건에 대해서 만족하는지 여부를 알아보기 위해서, 국내·외에서 생산되는 일반적인 H형강 및 □각관 등의 압연형강 등을 대상으로 각각의 모든 제품 등이 기본시스템 I 및 추가부재 II 등에 사용되는 조합에 관한 매개변수 연구를 통해서 그 조합인 비대칭 합성거더 III가 발휘하는 단면특성치를 분석해서 증가 여부를 검토하였다. 이때 앞서 식 (16) - 식 (23) 등으로 구해지는 비대칭 합성거더 III의 도심축 위치(y_t)와 추가부재 II의 단면적 A₂ 등의 성립 여부를 검토하였고, 또한 압연형강이 아닌 임의의 규격으로 플레이트를 가지고 제작하는 강박스 거더에 대해서도 상기 유도된 식이 성립하는지를 검토하는 순서로 본 연구의 정식화 이론의 범용성을 검증하였다.

5.1 압연형강(H형강 및 □각관) 제원표

국내·외에서 공용하고 있는 H형강 및 □각관 제원 규격을 다음 Table 5와 같이 정리하여 상호 간 모든 조건에 대한 단면 특성치 변화를 분석하였다. 상매개변수 연구결과를 정리한다(일람표에서 ①~㉙: H형강, ㉚~㉟: □각관).

Table 5.

Size and sectional properties about H & □

5.2 정식화 검토결과

5.2.1 압연형강을 사용한 비대칭 합성거더 검증결과

Table 5에 나타난 압연형강 중 ⑮~㉙까지를 기본시스템 I으로 하고, 그 상면에 ①~⑭, ㉛~㉟를 추가부재 II로 조합해서 합성한 비대칭 합성거더 III에 대한 단면특성치 산출결과 등을 Table 6-16에 요약 기술하였다. Table 6-17에서 I₁, I₁₃ 및 ∆I의 단위는 ×10⁴ mm⁴, Z_1t, Z_3t 및 ∆Z_3t의 단위는 ×10³ mm³, 식 (16) 및 Used y_3t의 단위는 mm, Used A₂ 및 식 (23)의 단위는 ×10² mm²이다.

Table 6.

Basic system Ⅰ – ⑮ & additional system II

Table 7.

Basic system Ⅰ – ⑯ & additional system II

Table 8.

Basic system Ⅰ – ⑰ & additional system II

Table 9.

Basic system Ⅰ – ⑱ & additional system II

Table 10.

Basic system Ⅰ – ⑲ & additional system II

Table 11.

Basic system Ⅰ – ㉒ & additional system II

Table 12.

Basic system Ⅰ – ㉔ & additional system II

Table 13.

Basic system Ⅰ – ㉕ & additional system II

Table 14.

Basic system Ⅰ – ㉖ & additional system II

Table 15.

Basic system Ⅰ – ㉗ & additional system II

Table 16.

Basic system Ⅰ – ㉘ & additional system II

5.2.2 제작 구조물의 정식화 검증결과

5.2.1에서는 압연형강인 35가지의 부재를 대상으로 상호 교차조합 검토에 의해 식 (16)과 식 (23)에 대한 검증을 실시하였다. 식 (16)과 식 (23) 등이 범용성에 대한 검토를 위해서 Fig. 13과 같이 임의 치수로 제작인 부재 조건에 대해서 단면특성치 증감 여부를 검토하였다.

Fig. 13.

Check condition of the built-up member (Unit: mm)

Fig. 13에서 추가부재를 사용한 경우는 2가지를 서로 다르게 적용한 경우를 표현하였다. 그에 따른 검토결과는 Table 17에 나타냈다.

Table 17.

Built-up member ① & ②

5.3 정식화 검증결과 고찰

본 연구에서 기본부재에 추가부재를 합성한 비대칭 합성거더에 대해서 단면특성치가 증가할 수 있는 조건을 정식화에 대한 검증을 전술한 바와 같이 국내·외 통용되는 모든 기성 형강 조합과 강박스 거더와 제작부재 등을 상대로 실시하였으며(Table 6-17), 의미하는 개요를 Figs. 14-15을 대상으로 설명한다. 먼저 Figs. 14-15은 기본시스템 I로 H-588×300(일람기호 ㉕)를 대상으로 한 것이며, Fig. 14은 추가부재로 H-200×100×5.5×8, Fig. 15은 □-200×100×9×9 부재를 사용한 것이다.

Fig. 14.

Verification result of Eq. (16), Eq. (21), and Eq. (23) in case of ㉕ + additional member ⑥

Fig. 15.

Verification result of Eq. (16), Eq. (21), and Eq. (23) in case of ㉕ + additional member ㉜

Fig. 14의 그래프는 실제 적용한 중립축 위치가 이보다 큰 445 mm로 정식화에서 제시하는 조건인 비대칭 합성거더의 중립축 위치 436 mm(식 (16)의 해)를 만족시키지 못하기에 비대칭 합성거더의 단면계수가 12.3 % 감소했음을 나타내고 있다. 이에 반해 Fig. 15은 동일한 기본시스템 I에서 추가부재 II만을 변경 설치한 결과, 식 (16)과 식 (23)에서 제시하는 조건을 만족시키기에 기본시스템 I보다 비대칭 합성거더 III의 단면2차모멘트는 53.1 %, 단면계수는 8.6 % 증가된 결과를 나타내고 있다.

6. 결 론

압연형강, 공장 및 현장 제작부재 등을 대상으로 지간 40 m 미만에 주로 사용하는 간편한 소교량, 소형 구조물 외에 강재를 사용한 보편적인 사용 지간 60 m - 200 m 등에 적용하는 강박스 거더 및 사장교 주형으로 사용되는 보강거더의 역학적 성질을 향상시키기 위한 연구를 수행하였다. 그 결과, 대칭으로 동일한 부재를 직렬회로와 같이 합성하는 경우 단면2차모멘트의 증가와 함께 단면계수도 비례해서 증가하는 양상을 보이나, 추가부재의 규격이 기본시스템에 비해 매우 작은 크기로 사용해야 하는 조건이라면 합성거더의 역학적 성질이 오히려 기본시스템보다 작은 값으로 퇴보하게 됨을 분석하였고, 그러한 원인은 합성거더의 중립축에 관한 비대칭 형상에 기인한 것이었다.

또한 비대칭 합성거더에 대해 단면계수가 단면2차모멘트와 함께 증가할 수 있는 물리적 메커니즘을 정식화하였다. 압연형강 및 제작 부재 등에 대해서 모든 검증을 실시한 결과, 정식화에서 제시하는 합성거더의 도심축 범위와 도심축 범위를 가능케 하는 추가부재의 단면적 사용량 조건을 적용한다면 소형 구조물부터 대형 구조물까지 토목 및 건축 등의 구조물 전 분야에 걸쳐서 역학적 성질이 향상된 거더를 제공할 수 있을 것으로 판단된다.

기 호(Notation)


I₁ :	기본시스템 I의 단면2차모멘트(mm⁴)
I₂ :	추가부재 II의 단면2차모멘트(mm⁴)
I₃ :	합성거더 III의 단면2차모멘트(mm⁴)
∆I :	합성거더와 기본부재간 단면2차모멘트 차이(mm⁴)
A_i :	개별 부재의 단면적(mm²)
A₁ :	기본시스템 I의 단면적(mm²)
A₂ :	추가부재 II의 단면적(mm²)
h₁ :	기본시스템 I의 형고(mm)
h₂ :	추가부재 II의 형고(mm)
H :	합성거더 III의 형고(mm)
I_i :	개별 부재의 단면2차모멘트(mm⁴)
e_i :	기준점으로부터 각 부재 중심까지의 거리(mm)
y_1t :	기본시스템 I의 중립축으로부터 상연까지의 거리(mm)
y_1b :	기본시스템 I의 중립축으로부터 하연까지의 거리(mm)
y_2t :	추가부재 II의 중립축으로부터 상연까지의 거리(mm)
y_2b :	추가부재 II의 중립축으로부터 하연까지의 거리(mm)
y_3t :	합성거더 III의 중립축으로부터 상연까지의 거리(mm)
y_3b :	합성거더 III의 중립축으로부터 하연까지의 거리(mm)
y_t :	이론해에서 구한 합성거더 III의 중립축으로부터 상연까지의 거리(mm)
y_b :	이론해에서 구한 합성거더 III의 중립축으로부터 하연까지의 거리(mm)
f_i :	구조물에 발생하는 휨모멘트에 의한 휨응력(MPa)
M₃ :	합성거더 III의 구조물에 발생하는 휨모멘트(kN·m)
Z :	단면계수(mm³)
Z₁, Z₃ :	기본시스템 Ⅰ과 합성거더 III의 단면계수(mm³)
Z_1t, Z_1b :	기본시스템 I의 상·하연 단면계수(mm³)
Z_3t, Z_3b :	합성거더 III의 상·하연 단면계수(mm³)
∆Z :	합성거더 III와 기본시스템 I 사이의 단면계수 증감(mm³)
∆Z_3t :	합성거더 III와 기본시스템 I 사이의 상연 단면계수 증감(mm³)
∆Z_3b :	합성거더 III와 기본시스템 I 사이의 하연 단면계수 증감(mm³)
Used A₂ :	추가부재 II의 단면적(mm²)
Req. A₂ :	이론해에서 구한 효과적인 합성거더 III에 필요한 추가부재 II의 단면적(mm²)

References

Research Institute of Industrial Science & Technology (2005) Republic of Korea Patent No.10-0486448, Korea (in Korean).
3D Engineering Co., Ltd. (2021) Republic of Korea Patent No.10-2296057, Korea (in Korean).
University Industry Foundation of Yonsei University (2022) Republic of Korea Patent No.10-2412385, Korea (in Korean).
Kyung, Y.S., Ahn, B.K., Bang, J.H., and Kim, M.Y. (2005) Development of a Prestressed Plate Girder Forming Hybrid Sections of Hot-Rolled H Beam and High-Strength Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.17, No.5, pp.637-648 (in Korean).
Steel Korea Co., Ltd. (2007) Republic of Korea Patent No.10-0758994, Korea (in Korean).
With-Hyeon Co., Ltd. (2012) Republic of Korea Patent No.10-1122958, Korea (in Korean).
THD Co., Ltd. (2019) Republic of Korea Patent No.10-2061515, Korea (in Korean).
Lee, S.Y., Park, Y.H., and Park, S.H. (2013) Estimation of Structural Behavior of the Long Span Temporary Bridge Superstructure Stiffened by Composite Double H-Beam, Journal of the Korean Society of Civil Engineers, KCSE, Vol.33, No.1, pp.1-11 (in Korean). [https://doi.org/10.12652/Ksce.2013.33.1.001]
Ministry of Land, Transport and Maritime Affairs (2008) Handbook for Road Design, Vol. 5: Bridge, pp.506-57-506-148 (in Korean).
Gere, J.M., and Timoshenko, S.P. (1991) Mechanics of Materials (3rd Ed.), Champman and Hall, USA, pp.250-261, pp.740-741. [https://doi.org/10.1007/978-1-4899-3124-5_5]

Item	Size (mm)	Area (×10² mm²)	Inertia moment (×10⁴ mm⁴)
Additional member	H-200×100	27.2	1,840
Basic system	H-700×300	235.5	201,000

Item	Height (mm)	Section modulus (×10³ mm⁴)		Inertia moment (×10⁴ mm⁴)
Item	Height (mm)	Top	Bottom	Inertia moment (×10⁴ mm⁴)
Basic member	700	5,743	5,743	201,000
Composite system	900	4,997	6,332	251,369
Comparison (%)	-	–13.0	+10.2	+25.0

Item	Section modulus (×10³ mm⁴)		Inertia moment (×10⁴ mm⁴)
Item	Top	Bottom	Inertia moment (×10⁴ mm⁴)
Basic member	124,222	93,578	10,898,593
Composite system	115,851	95,452	11,534,261
Comparison (%)	–17.0	+2.0	+6.0

Item	Height (mm)	Section modulus (×10³ mm⁴)		Inertia moment (×10⁴ mm⁴)
Item	Height (mm)	Top	Bottom	Inertia moment (×10⁴ mm⁴)
Basic member	700	5,743	5,743	201,000
Composite system	1,400	13,985		978,975
Comparison (%)	-	+244		+487

No.	H (mm)	B (mm)	t₁ (mm)	t₂ (mm)	A (×10² mm²)	I_i (×10⁴ mm⁴)	Z_i (×10³ mm⁴)
①	100	100	6	8	21.90	383	76.5
②	125	125	6.5	9	30.31	847	136
③	150	75	5	7	17.85	666	88.8
④	148	100	6	9	26.84	1,020	138
⑤	150	150	7	10	40.14	1,640	219
⑥	200	100	5.5	8	27.16	1,840	184
⑦	194	150	6	9	39.01	2,690	277
⑧	200	200	8	12	63.53	4,720	472
⑨	250	125	6	9	37.66	4,050	324
⑩	244	175	7	11	56.24	6,120	502
⑪	250	250	9	14	92.18	10,800	867
⑫	300	150	6.5	9	46.78	7,210	481
⑬	298	201	9	14	83.36	13,300	893
⑭	350	175	7	11	63.14	13,600	775
⑮	300	300	10	15	119.8	20,400	1,360
⑯	340	250	9	14	101.5	21,700	1,280
⑰	350	350	12	19	173.9	40,300	2,300
⑱	400	200	8	13	84.12	23,700	1,190
⑲	390	300	10	16	136	38,700	1,980
⑳	450	200	9	14	96.76	33,500	1,490
㉑	440	300	11	18	157.4	56,100	2,550
㉒	500	200	10	16	114.2	47,800	1,910
㉓	488	300	11	18	163.5	71,000	2,910
㉔	600	200	11	17	134.4	77,600	2,590
㉕	588	300	12	20	192.5	118,000	4,020
㉖	700	300	13	24	235.5	201,000	5,760
㉗	800	300	14	26	267.4	292,000	7,290
㉘	900	300	16	28	305.8	404,000	8,990
㉙	918	303	19	37	387.4	535,000	11,700
㉚	200	100	4.5	4.5	25.67	1,330	133
㉛	200	100	6	6	33.63	1,710	171
㉜	200	100	9	9	48.67	2,350	235
㉝	200	150	4.5	4.5	30.17	1,760	176
㉞	200	150	6	6	39.63	2,270	227
㉟	200	150	9	9	57.67	3,170	317

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	20,400	28,931	8,531	41.8	1,360	1,068	–291.7	–21.5	26.2	27.1	58.2	17.9	24.6	N.G
⑥		36,078	15,678	76.9		1,188	–172.4	–12.7	29.9	30.4	59.7	27.2	31.0	N.G
⑧		51,067	30,667	150.3		1,939	579.0	42.6	27.7	26.3	55.4	63.5	49.5	O.K
㉛		38,522	18,122	88.8		1,305	–55.1	–4.0	29.4	29.5	58.7	33.6	34.9	N.G
㉟		47,901	27,501	134.8		1,782	422.3	31.1	27.9	26.9	55.8	57.7	47.5	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	21,700	31,478	9,778	45.1	1,277	1,111	–165.6	–13.0	27.7	28.3	56.6	17.9	21.3	N.G
⑥		39,160	17,460	80.5		1,251	–25.4	–2.0	31.2	31.3	57.8	27.2	27.7	N.G
⑫		61,700	40,000	184.3		1,672	395.4	31.0	38.1	36.9	59.5	46.8	39.2	O.K
㉛		41,825	20,125	92.7		1,381	10⁴.8	8.2	30.6	30.3	56.7	33.6	31.4	O.K
㉟		51,679	29,979	138.2		1,899	622.3	48.7	28.9	27.2	53.5	57.7	43.7	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
⑥	40,300	59,905	19,605	48.6	2,303	1,773	–529.7	–23.0	32.6	33.8	59.3	27.2	37.3	N.G
⑧		80,209	39,909	99.0		2,661	358.2	15.6	30.8	30.1	56.0	63.5	56.2	O.K
⑫		86,447	46,147	114.5		2,129	–174.2	–7.6	40.3	40.6	61.9	46.8	49.8	N.G
㉛		63,321	23,021	57.1		1,916	–386.6	–16.8	32.2	33.0	58.6	33.6	41.2	N.G
㉟		76,222	35,922	89.1		2,487	183.9	8.0	31.0	30.7	56.3	57.7	53.9	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	23,700	35,502	11,802	49.8	1,190	1,176	–8.9	–0.8	30.1	30.2	54.8	17.9	18.0	N.G
⑥		44,018	20,318	85.7		1,347	162.0	13.7	33.3	32.7	55.5	27.2	24.2	O.K
⑫		67,736	44,036	185.8		1,807	621.7	52.5	39.6	37.5	56.5	46.8	35.8	O.K
㉛		47,033	23,333	98.4		1,496	311.9	26.3	32.6	31.4	54.3	33.6	27.8	O.K
㉟		57,663	33,963	143.3		1,185	889.3	75.0	30.4	27.8	50.7	57.7	39.5	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	38,700	50,869	12,169	31.4	1,985	1,622	–363.0	–18.3	30.4	31.4	56.3	17.9	24.5	N.G
⑥		60,241	21,542	55.7		1,742	–243.0	–12.2	34.0	34.6	57.5	27.2	31.5	N.G
⑫		87,339	48,639	125.7		2,148	163.0	8.2	41.1	40.7	59.5	46.8	44.0	O.K
㉚		58,822	20,122	52.0		1,690	–295.0	–14.9	34.0	34.8	57.7	25.7	30.9	N.G
㉜		72,242	33,542	86.7		2,277	293.0	14.7	32.4	31.7	54.9	48.7	43.1	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	47,800	64,771	16,971	35.5	1,910	1,819	–92.9	–4.9	35.3	35.6	54.3	17.9	19.2	N.G
⑥		76,519	28,719	60.1		1,999	87.2	4.6	38.5	38.3	55.1	27.2	25.9	O.K
⑪		130,329	82,530	172.7		2,008	392.0	105.0	37.3	33.3	49.7	92.2	58.5	O.K
㉛		81,335	33,535	70.2		2,196	284.0	14.9	37.8	37.0	54.1	33.6	29.3	O.K
㉜		91,954	44,154	92.4		2,662	750.2	39.2	36.5	34.5	52.1	48.7	36.8	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	77,600	100,425	22,825	29.4	2,590	2,473	–113.4	–4.4	40.3	40.6	53.7	17.9	19.3	N.G
⑥		115,591	37,991	49.0		2,671	84.4	3.3	43.5	43.3	54.4	27.2	26.1	O.K
⑪		187,163	109,563	141.2		4,963	2,376.0	91.9	37.7	42.0	49.5	92.2	58.9	O.K
㉜		137,119	59,519	76.7		3,483	896.5	34.7	41.4	39.4	51.7	48.7	36.8	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	118,000	140,908	22,908	19.4	4,014	3,414	–599.2	–14.9	40.1	41.3	54.3	17.9	25.4	N.G
⑥		156,789	38,789	32.9		3,523	–492.5	–12.3	43.6	44.5	55.3	27.1	33.3	N.G
⑫		199,401	81,401	69.0		3,931	–82.2	–2.0	50.6	50.7	57.0	46.8	47.8	N.G
㉜		180,656	62,656	53.1		4,359	344.9	8.6	42.0	41.4	53.4	48.7	44.2	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
③	201,000	231,636	30,636	15.2	5,743	4,927.8	–815.0	–14.2	45.7	47.0	53.8	17.9	26.5	N.G
⑥		252,152	51,152	25.4		5,008	–734.6	–12.8	49.2	50.3	54.7	27.2	34.8	N.G
⑧		307,036	106,037	52.8		6,757	1,014.2	17.7	46.8	45.4	52.0	63.5	52.3	O.K
㉜		285,027	84,027	41.8		6,027	284.0	4.9	47.7	47.3	53.0	48.7	45.6	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
⑥	292,000	355,479	63,479	21.7	7,300	6,418	–882.2	–12.1	54.2	55.4	54.2	27.2	35.4	N.G
⑧		425,055	133,055	45.6		8,433	1,133.0	15.5	51.8	50.4	51.8	63.5	52.5	O.K
㉛		368,392	76,392	26.2		6,770	–530.0	–7.3	53.7	54.4	53.7	33.6	38.6	N.G
㉜		397,289	105,289	36.1		7,596	296.2	4.1	52.7	52.3	52.7	48.7	45.8	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
⑥	404,000	481,297	77,297	19.1	8,978	7,954	–1,024.2	–11.4	59.2	60.5	53.9	27.2	35.7	N.G
⑧		567,841	163,841	40.6		10,224	1,246.0	13.9	56.9	55.5	51.7	63.5	52.7	O.K
㉛		497,361	93,362	23.1		8,352	–626.0	–7.0	58.8	59.6	53.4	33.6	38.9	N.G
㉜		533,362	129,362	32.0		9,284	306.4	3.4	57.8	57.4	52.5	48.7	46.1	O.K

No.	I₁	I₃	∆I	∆I (%)	Z_1t	Z_3t	∆Z_3t	∆Z_3t (%)	Eq. (16)	Used y₃t	y_t/H (%)	Used A₂	Eq. (23)	Effect
①	18,649,099	19,441,324	792,225	10⁴.2	206.023	188,041	–17,982	–8.7	100.6	103.4	45.2	78	148.7	N.G
②	18,649,099	20,872,887	2,223,788	111.9	206.023	215,161	9,138	4.4	98.3	97.0	44.1	234.0	221.8	O.K