저항복강 및 축소 심재를 갖는 좌굴방지가새의 설계변수에 대한 해석적 연구

1. 서 론

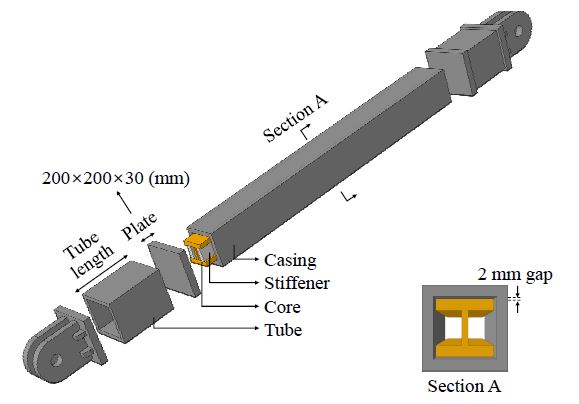
좌굴방지가새는 골조의 강성에 기여하는 가새 및 비탄성 변형을 통해 에너지 소산이 가능한 댐퍼의 두 가지 기능을 수행할 수 있어 널리 사용되는 제진 시스템이다^[1]. 좌굴방지가새는 충전재 사용 여부에 따라 충전형과 비충전형 좌굴방지가새로 구분이 가능한데, 충전형 좌굴방지가새는 하중에 의한 변형을 부담하는 심재(core), 심재의 좌굴을 구속하는 보강재(casing), 심재 변형시 마찰에 의해 보강재에 하중이 전달되는 것을 방지하는 비부착물질(debonding material), 보강재와 함께 심재 좌굴 구속에 기여하는 모르타르 등의 충전재(infilling material)로 구성된다^[2]. 충전재 사용 시 흔히 사용되는 모르타르의 양생 기간 및 자중에 의한 시공성의 저하로 인하여 비충전형 좌굴방지가새가 선호되는 추세^[3],[4]이다. 본 논문에서도 비충전형 좌굴방지가새를 제안하고자 한다.

Fig. 1.

Example of buckling restrained braces with H-section core

또한 본 논문에서는 충전재를 사용하지 않으며 심재 양단에 튜브를 설치하여 심재의 길이를 줄이고, 항복 변위가 작아짐에 따라 에너지 소산이 이른 시점에서 발생하는 튜브형 좌굴방지가새(Tube-BRB)를 제안하고, 설계변수에 따른 거동을 분석하였다. 앞서 언급한 바와 같이 심재 양단에 탄성 영역에서 거동하는 튜브를 설치함으로써 항복 변위가 작아짐에 따라 골조 내에 적용 시 보와 기둥에 비해 이른 시점에 항복하여 골조 내 소성 힌지가 좌굴방지가새에서 발생하도록 유도할 수 있고, 초기 불완전성이 줄어들며 좌굴 하중의 증가로 축력을 받는 동안 안정적인 거동을 기대할 수 있다(Fig. 2 참조).

Fig. 2.

Concepts of Tube-BRB

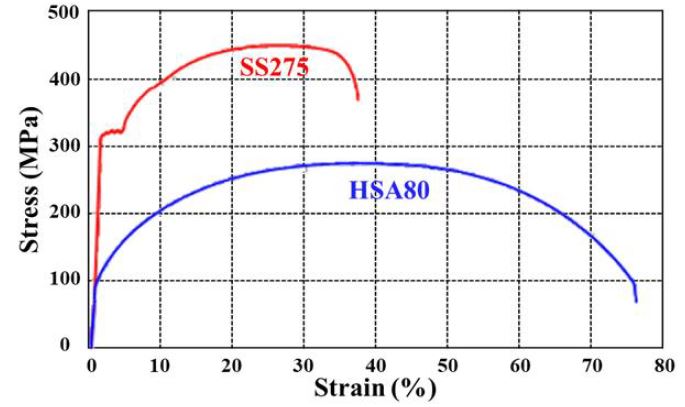
또한 심재의 변위 부담 길이가 줄어듦에 따라 높은 연성 및 우수한 에너지 소산 능력을 갖는 것으로 알려져 있는 저항복강인 HSA80^[5]을 심재로 사용함으로써 항복 하중이 줄어들고 에너지 소산이 증가하여, 축소 심재를 적용하여 발생하는 이점인 좌굴방지가새 내 소성 힌지 유도, 초기 불완전성 저감, 좌굴하중 증가 등의 효과를 극대화할 수 있을 것으로 판단하였다(Fig. 3 참조).

Fig. 3.

Stress-strain curve of normal and low yield point steel[6]

그 외 기본적인 설계 내용은 다음과 같다. 플레이트형 심재에 비해 단면2차모멘트 확보가 용이하며 제작이 간편한 H형강 심재를 계획하였다. 초기 불완전성의 영향을 줄이고 설계변수의 영향에 집중하기 위해 전체 길이 2,000 mm의 축소실험을 계획하였으며 심재 변형의 골조에 전달되는 것을 막기 위하여 부재 양단을 핀(pin) 접합으로 설정하였다. 심재는 저항복강 HSA80으로, 보강재 및 그 외 모든 부재는 일반 강재 SS275를 사용하고 폴리에틸렌을 비부착물질로 사용하여 인장 및 압축 하중 모두에서 대칭적으로 거동할 수 있게 하였다.

2. 유한요소해석

2.1 유한요소해석 개요

설계변수에 따른 거동 분석을 위하여 상용 유한요소해석 프로그램인 ABAQUS 2020^[7]을 사용하여 해석을 진행하였다. 실험 셋업을 고려하여 좌굴방지가새 부분골조실험의 물리적인 형상을 구현하였고, 용접에 의한 열변형 등을 고려하여 L/500의 초기 불완전성을 반영하였다. 기하, 재료 비선형이 예상되는 심재, 스티프너 부분은 상세한 거동 분석을 위하여 mesh를 Quadratic Element로 설정하였고 그 외의 부분은 Linear Element로 설정하였다.

강재 재료 특성은 소성 영역에서의 거동을 묘사하기에 적합한 Chaboche Model^[8]을 사용하여 구현하였다. SS275 및 HSA80의 Chaboche factor는 선행연구결과^[9],[10]를 참조하여 Table 1과 같이 적용하였다.

Table 1.

Chaboche model of SS275 and HSA80

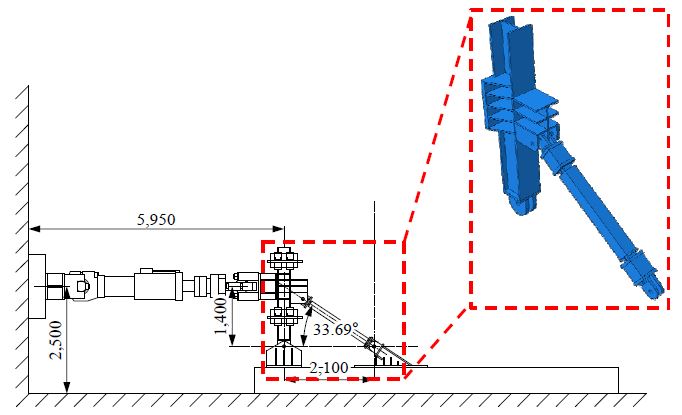
강구조설계기준(KDS 41 31 00)^[11]에 명시된 좌굴방지가새의 성능 인증기준 중 부분 골조 시험을 계획함에 따라 지간 2,100 mm 및 높이 1,400 mm의 1:1.5 비율 프레임을 설정하고 기준에 따라 가력 변위를 설정하였다. 준정적(quasi-static) 조건에서 실험이 진행됨을 고려하여 Static, General 조건으로 각 스텝을 설정하였다.

Fig. 4.

Experiment set-up and FEM Model

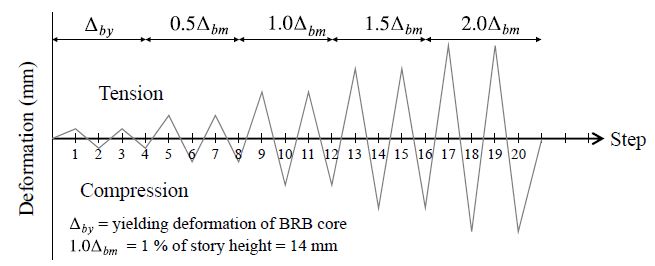
강구조설계기준에서 가력 프로토콜은 심재의 항복 변위(∆_by) 및 골조의 설계 층간 변위(∆_bm)에 따라 정의된다. 설계 층간 변위 설정의 경우 골조의 탄성해석을 통해 얻은 값과 층고의 1 % 중 큰 값을 사용하게 되어 있는데, 골조의 탄성해석 수행에 제한이 있으므로 일반적으로 층고의 1 %를 설계 층간 변위로 간주하여 가력을 진행한다^[12].

전체 가력 프로토콜은 Fig. 5와 같이 ∆_by로 2회 반복 가력 후 0.5∆_bm에서부터 2.0∆_bm까지 0.5∆_bm씩 증가하도록 2회 반복 가력하여 진행된다.

Fig. 5.

Loading protocol of BRB Test

2.2 유한요소해석 검증

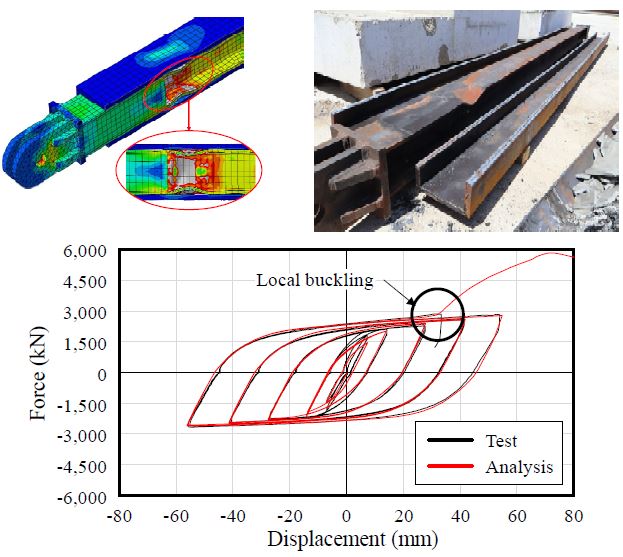
유한요소해석모델의 신뢰성 검증을 위하여 유사한 형태를 갖는 좌굴방지가새의 부분골조실험을 수행한 선행연구의 실험조건을 모델링한 해석결과^[9]를 Fig. 6와 같이 비교하였다. 해석 결과 국부좌굴 발생 이전까지의 하중 이력 곡선과 국부좌굴 발생 시점 및 위치 등이 실험결과와 일치하는 것을 확인하였다.

Fig. 6.

Comparing experiment and FEM result

2.3 변수 설정 과정

H형강 심재를 갖는 좌굴방지가새의 주요한 파괴 모드는 심재의 국부좌굴 및 무보강 구간에서의 파괴^[13]로 알려져 있다. 심재에서의 국부좌굴 발생은 심재의 판폭두께비에 가장 큰 영향을 받는 것으로 알려져 있음^[14]에 따라 제작 가능한 저항복강의 두께를 고려하여 변수를 설정하였다. 축소실험으로 진행할 것을 고려하여 심재 단면의 높이와 폭은 표준 형강 중 최소 단면과 같도록 100 mm로 설정한 채 판폭두께비가 변수가 되도록 설정하였다. 웨브의 두께는 생산 가능한 저항복강의 최소 두께인 12 mm로 고정하고 플랜지의 두께를 10 mm에서 24 mm까지 2 mm씩 증가하도록 변수를 구성하여 판폭두께비와 국부좌굴 발생 간의 영향을 분석하였다.

이후 Tube-BRB에 대하여 tube 길이 및 스티프너 길이에 따른 거동을 분석하였다. 같은 튜브 길이를 갖더라도 판폭두께비가 달라질 때 하중 변화에 의한 거동의 차이가 예상되어 플랜지 두께가 12 mm, 16 mm, 20 mm, 24 mm인 모델에 대해 100 mm, 200 mm, 300 mm, 400 mm, 500 mm의 튜브 길이를 갖는 8개의 모델에 대해 해석을 진행하였다. 튜브의 폭은 실제 실험체 제작 시 용접 등 제작성을 고려하여 플레이트보다 10 mm씩 짧은 180 mm로 설정하였으며 튜브를 사용하지 않고 판폭두께비를 변수로 진행된 해석의 하중 이력 곡선 상의 최대 하중에서도 단면이 항복하지 않도록 두께를 17 mm로 설정하였다.

마지막으로 튜브 사용에 따라 좌굴방지가새 전체 길이 중 변위를 부담하는 길이가 줄어들고, 이에 따라 피로에 의한 파괴에 취약할 것으로 예상하여 변위 부담 길이의 영향을 분석하고자 하였다. 심재의 길이 중 스티프너가 존재하는 부분은 강성의 차이로 인하여 실질적으로 변형을 부담하지 못하므로 스티프너의 길이를 변수로 설정하였다. 핀 접합의 영향으로 스티프너의 길이가 짧아질수록 압축 하중에 의한 소성 힌지의 발생 가능성이 증가하고^[15] 길어질수록 변위 부담 길이가 짧아짐에 따라 인장 하중에 의한 파괴 가능성이 증가할 것으로 예측되었다. 튜브 길이에 따른 스티프너 길이의 상한값과 하한값을 분석하기 위해 해석을 진행하였다. 전체 해석모델 및 각 모델의 제원은 Table 2와 같다.

Table 2.

Total FEM models and variables

Table 3.

FEM result by width-thickness ratio(Unit: mm)

3. 유한요소해석결과

3.1 Tube-BRB 해석결과

3.1.1 판폭두께비에 따른 결과

해석 결과 플랜지 두께가 18 mm 이하, 판폭두께비가 1.89 이상인 모든 모델에서 2.0∆_bm의 두 번째 압축 하중에 의한 심재 국부좌굴 및 그에 따른 내력 저하가 발생했다. 좌굴방지가새 인증에 관한 기준 중 ‘실험체의 하중-변위 이력 곡선은 강성이 증가하는 안정적이며 반복적인 거동을 보여주어야 한다’는 내용에 근거하여 내력 저하 발생 시 기준을 만족하지 못하는 것으로 간주하였으며 플랜지 두께가 20 mm 이상이며 판폭두께비가 1.7 이하인 모델에서 내력 저하 현상 없이 기준을 만족하는 것을 확인하였다.

Fig. 7.

FEM model for width-thickness ratio

3.1.2 무보강구간 및 튜브 길이에 따른 결과

판폭두께비에 이어 튜브의 길이에 따른 거동을 분석하고자 해석을 진행하였다. 또한 해석과정에서 무보강구간이 좌굴방지가새의 거동에 중요한 영향을 미치는 요인으로 판단되었다. 무보강구간이 양단에 존재할 경우 플랜지 두께가 24 mm인 모델은 튜브의 길이가 100 mm일 때부터, 플랜지 두께가 20 mm인 모델은 튜브의 길이가 200 mm일 때부터 심재에 소성 힌지가 발생하며 파괴되는 양상을 보였다.

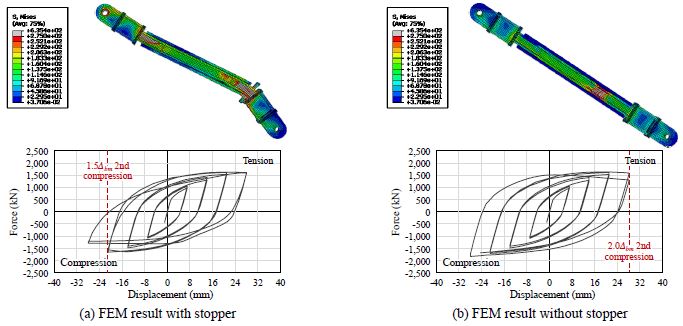
따라서 각각의 모델에 대해 스토퍼(stopper)를 사용하여 (Fig. 8 참조) 보강재가 심재의 중앙에 위치하며 무보강구간이 양단에 존재하는 모델과 스토퍼 없이 무보강구간이 한 단에 존재하는 모델 두 가지에 대해 해석을 진행하였으며 해석결과는 Table 4와 같다.

Fig. 8.

Stopper and unconstrained section

Table 4.

FEM result by tube length and unconstrained section

스토퍼의 유무와 관련 없이 튜브 길이 100 mm인 모델 중 플랜지 두께가 12 mm인 모델은 국부좌굴에 의해 파괴가 발생하였고 16 mm, 20 mm인 모델은 인장 파단에 의한 내력 저하 현상이 발생하였다. 그 외 플랜지 두께가 24 mm인 모델 및 튜브 길이가 200 mm 이상인 모델은 심재 단부에 소성 힌지가 발생하는 파괴 양상을 보였는데, 스토퍼를 사용하지 않을 경우 Fig. 9과 같이 해당 현상이 효과적으로 제어되며 내력 저하 발생 시점이 미뤄지는 것을 확인할 수 있다. 달리 말하자면, 국부좌굴 및 인장 파단과 달리 심재에 소성 힌지가 발생하여 파괴되는 양상은 무보강구간의 영향을 크게 받는 것으로 판단된다. 따라서 3.1.3절부터의 Tube-BRB 해석모델은 스토퍼를 상용하지 않고 무보강구간이 한 단에만 존재하도록 설정하여 진행하였다.

Fig. 9.

Different FEM result by unconstrained section

핀 접합으로 설계하여 압축 하중에 의해 심재에 좌굴 모드가 발현되었을 때 튜브는 변형되지 않고 회전하며 좌굴 모드 발현 이후 심재 단부에 모멘트가 발생할 때 튜브의 길이와 튜브, 심재 사이의 플레이트의 두께를 합친 길이가 모멘트의 팔길이와 같이 작용하여 튜브의 길이가 길어질수록 불리하게 작용하는 것으로 분석하였다. 또한 같은 길이의 튜브에 대해 플랜지 두께에 따라 파괴 양상에 차이가 발생하는 것을 확인하였다. 이에 대한 자세한 분석을 위하여 3.1.1절에서 국부좌굴이 발생하지 않은 3개의 모델에 대해 튜브 길이를 변수로 진행하여 판폭두께비에 따른 튜브 길이의 영향을 Table 5와 같이 분석하였다.

Table 5.

FEM result by tube length

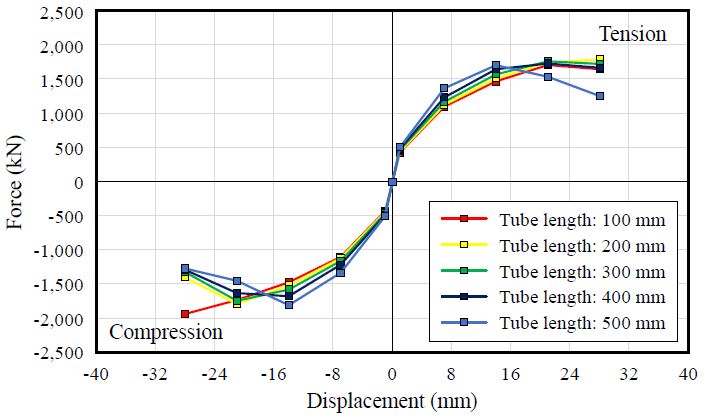
Table 5와 같이 플랜지 두께가 24 mm인 경우 심재에 소성 힌지가 발생함에 따른 파괴 양상이 발견되었다. Fig. 10을 통해 튜브 길이가 길어질수록 압축 영역에서 내력 저하 발생 시점이 빨라지는 것을 확인할 수 있으며, 강구조설계기준에서 좌굴방지가새의 부분 골조실험 시 변위를 만족하도록 가력을 진행하게 하여 플랜지 두께가 증가함에 따라 단면적이 증가하고, 이에 따라 하중이 같이 증가하여 위와 같이 불리하게 작용하는 것으로 분석된다. 따라서 Tube-BRB 설계 시 단면적 및 판폭두께비의 산정이 중요한 변수가 될 것으로 판단된다. 플랜지 두께가 20 mm인 모델과 22 mm인 모델은 튜브 길이에 따른 파괴 양상 및 발생 시점이 동일하게 나타난 것을 확인할 수 있다.

Fig. 10.

Skeleton curve of FEM models (24 mm flange thickness)

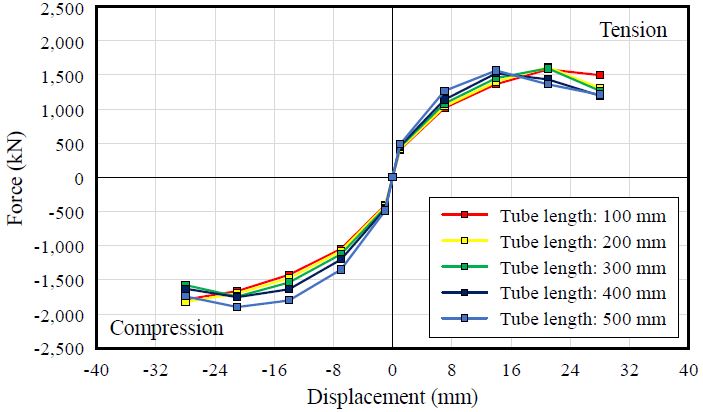
Fig. 11을 통해 튜브 길이가 증가함에 따라 인장 영역에서의 내력 저하 현상 발생 시점이 빨라지고, 내력 저하의 정도도 커지는 것을 알 수 있다. 튜브 길이가 길어질수록 변위 부담 길이가 줄어들어 이러한 양상을 보이는 것으로 생각할 수 있다. 인장에서의 내력 저하 현상이 나타났다는 것은 한계 상태에 진입한 단면이 발생하였음을 의미하며 이어지는 압축 하중 재하 시 해당 부분이 힌지와 같이 거동하여 불안정한 거동을 보이게 될 것을 예측할 수 있고, 이는 Fig. 11을 통해 확인된다. 따라서 변위 부담 길이의 확보를 통해 인장에서의 내력 저하 현상이 발생하지 않도록 하는 것이 저항복강 심재를 사용한 Tube-BRB 설계 시 중요한 고려사항이 될 것으로 분석할 수 있다.

Fig. 11.

Skeleton curve of FEM models (20 mm flange thickness)

Fig. 12와 같이 심재 중 스티프너가 존재하는 부분과 심재 양단의 튜브는 강성의 차이로 인하여 변형이 거의 발생하지 않음에 따라 실질적으로 하중에 의한 변형을 부담하는 구간의 길이는 두 부분을 제외한 만큼으로 간주된다. 튜브를 사용하는 것이 목적이므로 스티프너의 길이를 줄임으로써 변위 부담 길이를 확보할 수 있으나 특정 값 이하로 줄어들게 되면 무보강구간에서의 파괴가 발생할 것을 예상할 수 있다. 따라서 인장 파단이 발생하지 않는 변위 부담 길이와 압축 하중에 의한 소성 힌지 발생 등 파괴 양상 없이 거동할 수 있게 하는 스티프너 길이를 규명하고자 이를 변수로 해석을 진행하였다.

Fig. 12.

Stiffener length and yielding length

3.1.3 스티프너 길이에 따른 결과

스티프너 길이를 변수로 진행된 해석결과는 Table 6와 같다. 튜브를 사용하지 않은, 튜브의 길이가 0 mm인 모델에 대해 먼저 해석을 진행하여 변위 부담 길이가 1,100 mm 이상일 때 인장 파단이 발생하지 않는 것을 확인하였다. 또한 스티프너의 길이가 전체 좌굴방지가새 길이의 5 %에 해당하는 100 mm만 존재하여도 소성 힌지 발생에 의한 파괴를 방지할 수 있을 정도의 압축 내력을 확보할 수 있음을 확인하였다. 이에 이어 100 mm의 튜브를 설정하였을 때의 거동 변화를 분석하였다.

Table 6.

FEM result by stiffener length

튜브 길이가 100 mm일 때도 1,100 mm의 변위 부담 길이를 만족할 때 인장 파단이 발생하지 않고 안정적으로 거동하는 것이 확인되었다. 그러나 튜브를 사용하지 않은 경우 스티프너의 길이가 100 mm로 설정되어도 충분한 압축 내력을 보이며 안정적인 거동을 보인 것과 달리 스티프너 길이가 150 mm 미만이고 심재의 7.5 %보다 짧은 경우 소성 힌지 발생에 의한 파괴가 발생함을 확인하였다. 이러한 결과에 비추어 볼 때 튜브 길이가 길어질수록 압축 내력 확보를 위한 스티프너의 길이도 함께 증가하여야 안정적인 거동을 기대할 수 있을 것으로 판단된다.

이러한 경향성을 통해 튜브 길이가 200 mm일 경우 스티프너의 길이가 심재의 7.5 %에 해당하는 150 mm보다 길 때 압축 내력이 확보되어 안정적인 거동을 보일 수 있을 것으로 예측할 수 있다. 그러나 스티프너 길이가 150 mm일 때 변위 부담 길이는 900 mm가 되어 압축 내력을 확보하지 못한 채 인장 파단이 발생하지 않는 변위 부담 길이 또한 확보하지 못하게 된다. 따라서 소성 힌지 발생 및 인장 파단 모두 예측이 가능하고, 해석 결과 소성 힌지 발생에 의한 내력 저하가 먼저 발견되었다. 150 mm보다 길어질 경우 소성 힌지 발생은 제어할 수 있었으나 인장 파단이 발생하여 예상했던 결과와 일치하는 거동을 보이는 것을 확인하였다.

결과적으로 100 mm의 튜브 길이 및 150 mm의 스티프너 길이를 갖는 Tube-BRB에 대해 앞서 언급되었던 국부좌굴, 인장 파단, 소성 힌지 발생 등의 파괴 모드가 발견되지 않고 인증기준을 만족하는 것을 확인하였다. 해당 모델을 프로토타입으로 실험을 진행하여 유한요소해석결과와 비교하는 과정을 거쳐 해석의 미비점을 보완하고, 더욱 상세한 거동을 분석할 수 있을 것으로 생각된다.

4. 결 론

본 논문에선 저항복강 심재를 사용한 새로운 형태의 비충전형 좌굴방지가새로서 심재의 양단에 튜브를 사용하여 변위 부담 길이를 줄이고 좌굴에 대한 안정성을 증가시킨 Tube-BRB를 제안하였으며 실제 실험을 통한 성능 입증에 앞서 유한요소해석을 통해 인증기준 만족을 위한 설계변수를 분석하였다. 설계변수에 따른 거동을 분석한 내용 및 본 논문의 결론은 다음과 같다.

• (1) 본 연구를 수행하면서 Tube-BRB의 파괴 모드로서 심재의 국부좌굴과 인장 파단, 소성 힌지 발생 등을 발견할 수 있었다. 심재 국부좌굴 및 인장 파단은 각각 심재의 판폭두께비 및 변위 부담 길이에 가장 큰 영향을 받는 것으로 분석되었다. 소성 힌지에 의한 파괴는 심재 변형에 따른 골조의 파괴를 방지하기 위해 양단을 핀 접합으로 설계함에 따라 발생하는 파괴 모드인 것으로 생각되며 스티프너 길이 및 무보강구간에 영향을 받는 것으로 분석되었다. 특히 무보강구간이 좌굴방지가새의 전체적인 거동에 큰 영향을 주는 것으로 분석되어 가력 변위를 고려한 최소한의 길이로 설정하는 것이 성능 확보에 유리할 것으로 판단된다.
• (2) 강구조설계기준에서 정의한 좌굴방지가새의 성능 인증 조건에 따라 골조의 높이에 기반한 설계 층간 변위를 기준으로 가력하여 낮은 항복 강도를 갖는 저항복강을 심재로 사용할 경우 일반 강재에 비해 더 이른 하중에서 항복이 발생하며 더 많은 누적 소성 변형을 부담해야 한다. 이에 따라 인장 하중에 의한 좌굴방지가새의 내력 저하 현상이 발견된 모델이 있는 것으로 분석할 수 있다.
• (3) 심재 양단에 튜브를 적용한 Tube-BRB의 경우 튜브가 길어질수록 모멘트의 팔길이가 증가하는 효과에 의하여 압축 내력 확보를 위한 스티프너 길이가 함께 증가해야 함에 따라 변위 부담 길이의 확보에 불리하게 작용하는 것으로 분석되었다.
• (4) 상기 언급된 좌굴방지가새의 파괴 모드에 대해 각각을 지배하는 설계변수를 분석하였고, 인증기준을 만족하는 Tube-BRB의 프로토타입을 도출하였다. 위의 (2)항에서 언급한 바와 같이 저항복강을 사용함으로써 부담해야 하는 누적 소성 변형의 크기에서 불리함이 있으나 높은 연성으로 인하여 기준을 만족하는 프로토타입을 도출할 수 있었던 것으로 사료된다.
• (5) 실제 실험을 수행하여 유한요소해석의 결과와 비교하여 해석의 신뢰성을 입증하고, 더욱 자세한 설계변수 분석이 가능할 것으로 생각된다. Tube-BRB의 설계를 위한 튜브 설계 상세 또한 실험 및 이론적인 연구를 통하여 제안할 수 있을 것으로 생각되며 추후 골조에의 적용을 통해 Tube-BRB 적용 시의 거동을 분석할 수 있을 것이다.

Acknowledgments

이 논문은 2022년도 정부(과학기술정보통신부)의 재원으로 한국연구재단(NRF-2020R1A2C3005687, NRF-2021R1A2C1095145)에 의해 수행되었습니다.

References

• Zhou, Y., Shao, H., Cao, Y., and Lui, E.M. (2021) Application of Buckling-Restrained Braces to Earthquake-Resistant Design of Buildings: A Review, Engineering Structures, Elsevier, Vol.246, 112991. [https://doi.org/10.1016/j.engstruct.2021.112991]
• Xie, Q. (2005) State of the Art of Buckling-Restrained Braces in Asia, Journal of Constructional Steel Research, Elsevier, Vol.61, No.6, pp.727-748. [https://doi.org/10.1016/j.jcsr.2004.11.005]
• Huang, F., Duan, H., Cheng, B., and Teng, N. (2021) Hysteretic Performance of All-Steel Assembled Double-Cores Buckling-Restrained Braces Using Q195 Low-Yield Core, Journal of Constructional Steel Research, Elsevier, Vol.187, 106925. [https://doi.org/10.1016/j.jcsr.2021.106925]
• Gao, J., Xi, J., Ding, J., Xu, Y., Zhu, J., and Chang, Y. (2022) Analytical and Experimental Studies on All-Steel Buckling Restrained Brace with Double Steel Tubes, International Journal of Steel Structures, KSSC, Vol.22, No.1, pp.280-293. [https://doi.org/10.1007/s13296-021-00573-z]
• Kim, G., Ryu, H., and Kim, D. (2021) A Study on the Hysteretic Characteristics of Hybrid Steel Damper System Using the High Ductile Low-Yield-Point Steel, Journal of Korean Society of Steel Construction, KSSC, Vol.33, No.4, pp.203-214 (in Korean). [https://doi.org/10.7781/kjoss.2021.33.4.203]
• Ryu, H.-S., Choi, K.-Y., Kim, Y.-J., Kim, H.-J., and Oh, S.-H. (2021) The Characteristics and Application Technology of Low Yield Point Steel HSA80, Magazine of the Korean Society of Steel Construction, KSSC, Vol.33, No.1, pp.8-14 (in Korean).
• Dassault Systèmes Simulia Corp. (2020) Abaqus/CAE, Version 2020, Software for Technical Computation, DSS, USA.
• Chaboche, J.L. (1986) Time-Independent Constitutive Theories for Cyclic Plasticity, International Journal of Plasticity, Elsevier, Vol.2, No.2, pp.149-188. [https://doi.org/10.1016/0749-6419(86)90010-0]
• Alemayehu, R.W., Kim, Y., Bae, J., and Ju, Y.K. (2020) Cyclic Load Test and Finite Element Analysis of NOVEL Buckling-Restrained Brace, Materials, MDPI, Vol.13, No.22, 5103. [https://doi.org/10.3390/ma13225103]
• Kim, S.H., and Lee, C.H. (2021) Material Parametrization of LYP Steel HSA80 for Use in Concentrically Braced Frame, Proceedings of the 32th Annual Conference, KSSC, pp.71-72 (in Korean).
• Ministry of Land, Infrastructure and Transport (2019) Steel Structures Design Standard for Building Structure (KDS 41 31 00: 2019), Korea (in Korean).
• Bashiri, M., and Toufigh, V. (2020) Numerical and Experimental Investigation on a BRB Confined with Partially Carbon Fiber Reinforced Polymer (CFRP), Engineering Structures, Elsevier, Vol.223, 111150. [https://doi.org/10.1016/j.engstruct.2020.111150]
• Mansouri, A., and Moosavi, G. (2021) Analytical Study of the Seismic Performance of All-Steel Buckling-Restrained Braces with H-Shaped Cores, Canadian Journal of Civil Engineering, Canadian Science Publishing, Vol.48, No.5, pp.494-511. [https://doi.org/10.1139/cjce-2019-0642]
• Lee, I.G., Alemayehu, R.W., and Ju, Y.K. (2021) Structural Behavior of Buckling-Restrained Braces​(BRB) with Low-Yielding Steel Under Cyclic Loading, Proceedings of the 32th Annual Conference, KSSC, pp.15-16.
• Zhao, J., Wu, B., and Ou, J. (2012) Flexural Demand on Pin-Connected Buckling-Restrained Braces and Design Recommendations, Journal of Structural Engineering, American Society of Civil Engineers, Vol.138, No.11, pp.1398-1415. [https://doi.org/10.1061/(ASCE)ST.1943-541X.0000549]