초탄성 니티놀 형상기억합금의 준정적 거동에 대한 수치해석적 재현
Copyright ⓒ 2015 by Korean Society of Steel Construction
초록
초탄성 형상기억합금은 상온에서 소성 범위를 초월하여 상당량의 변위를 가하더라도 하중을 제거 후에 별도의 열처리를 가하지 않더라도 원상태로 복원이 가능한 특수한 금속이다. 자동치유가 가능한 형상기억합금의 특유한 재료적인 성질로 인하여 구조물에서 변위가 집중되는 부분에 기존에 주로 사용되는 강재를 대체하여 이러한 특수 합금 재료가 널리 활용되기 시작하였다. 하지만 형상기억합금을 활용한 구조물의 기본적인 설계와 성능 검증을 하기 위해 고등적인 구조해석에 필요한 재료적인 모델의 개발과 연구의 노력이 부족하기 때문에 본 재료를 현장에서 적용하기에는 여전히 많은 제약을 받고 있다. 따라서 본 연구에서는 초탄성 형상기억합금의 거동을 수치해석적인 방법으로 재현이 가능한 구성적인 재료 모델의 소개와 프로그램 코딩에 대하여 다루고자 한다. 또한 본 연구에서 제시된 재료 모델의 타당성을 입증하기 위하여 수치해석적으로 재현된 물리적인 거동을 실험에서 얻어진 데이터에 비교 및 보정 작업도 수행하였다. 아울러 이러한 재료 모델로 구현된 초탄성 형상기억합금의 물리적인 물성치를 구조 해석에 적용하고 정확성을 검증하여 현장 적용의 타당성을 입증하였다.
Abstract
Superelastic shape memory alloys (SMAs) are metallic materials that can automatically recover to their original condition without heat treatment only after the removal of the applied load. These smart materials have been wildly applied instead of steel materials to the place where large deformation is likely to concentrate. In spite of many advantages, superelastic SMA materials have been limited to use in the construction filed because there is lack of effort and research involved with the development of the material model, which is required to reproduce the behavior of superelastic SMA materials. Therefore, constitutive material models as well as algorithm codes are mainly treated in this study for the purpose of simulating their hysteretic behavior through numerical analyses. The simulated curves are compared and calibrated to the experimental test results with an aim to verify the adequacy of material modeling. Furthermore, structural analyses incorporating the material property of the superelastic SMAs are conducted on simple and cantilever beam models. It can be shown that constitutive material models presented herein are adequate to reliably predict the behavior of superelastic SMA materials under cyclic loadings.
키워드:
형상기억합금, 초탄성 거동, 복원 효과, 구성적인 재료 모델, 수치해석Keywords:
Shape memory alloy (SMA), Superelastic behavior, Constitutive material model, Numerical analysis1. 서 론
초탄성(Superelastic) 형상기억합금은(Shape Memory Alloy, 이하 SMA) 상온에서 소성 범위를 초과하여 상당량의 변위를 본 합금 소재에 가하더라도 하중 제거 후에 원형으로 스스로 복원이 가능한 금속 재료이다[1],[2]. 이러한 스마트한 첨단 금속 소재를 구조물 내에서 변형이 집중되는 부위에 기존에 주로 사용된 강재를 대신하여 사용한다면 복원력에 의한 자동 치유(Self-healing) 효과를 기대할 수 있다. 게다가 초탄성 형상기억합금은 에너지 소산에 의한 부가적인 충격 흡수와 뛰어난 내부식성(Corrosion Resistance) 및 피로(Fatigue) 파괴에 대한 우수한 저항력을 가지고 있어 최근에 건설 현장에서의 소재의 활용이 점진적으로 증가하고 있는 추세이다[3],[4],[5],[6]. 이러한 첨단 소재의 활용 요구가 증대됨에도 불구하고 설계와 성능 검증에 필수적인 수치해석에 대한 재료 모델의 개발이 여전히 부족한 실정이다. 일부분의 연구자에 의해 완성된 사용자 정의에 의한 재료 모델에 의하여 초탄성적인 효과를 극히 일부분 제한적으로 재현하고 있는 상황이다. 따라서 본 연구에서는 온도와 응력에 의존하는 형상기억합금의 상변위를(Phase Transformation) 고려하여 초탄성 효과를 수치해석적으로(Numerical Analysis) 구현하는 재료 모델을 제시하고 이를 프로그램 코딩화하여 구조해석을 수행하고 해석의 정확성을 입증하는 대 주안점을 두고자 한다.
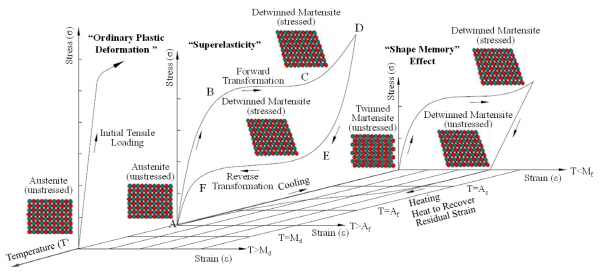
Fig. 1은 일반적인 니켈-티타늄의 합금 소재인 니티놀(Nitinol) 형상기억합금의 응력-변형률-온도와의 관계를 보여주고 있다[2]. 니티놀은 니켈과(Nickel) 티타늄이(Titanium) 동일한 분포로 혼합하여 제작하며 형상기억합금 소재 중에서 비교적 현장에서 널리 사용되고 있다. 니티놀 형상기억합금은 온도와 응력에 따라서 비교적 약한 마르텐자이트와(Martensite) 상대적으로 강한 오스테나이트(Austenite) 결정 상태를 가지고 있다. 그림에서 보는 바와 같이 마르텐자이트 상변위 이하에서의 온도에서는(T<Mf) 비교적 낮은 응력 고원과(Stress Plateau) 하중 제거 후에 단지 탄성적인 복원이 발생할 뿐 실제로 상당량의 잔류변위가 발생한다. 여기에 별도의 열처리를(Heating) 가할 경우 마르텐자이트에서 오스테나이트 상변위가 발생하여 원형으로 복원이 되는 형상기억 효과를(Shape Memory Effect, 이하 SME) 보여주고 있다[2]. 반면에 오스테나이트 상변위(Phase Transformation) 온도를 초과할 경우(T>Af) 상당량의 소성 변형을 재료에 가하더라도 별도의 열처리를 가하지 않더라도 원형으로 복원이 되는 초탄성(Superelasticity) 거동을 보여주고 있다. 초탄성 형상기억합금은 변형률 1% 이내에서 발생하는 탄성거동 구간(AB구간 참고), 응력 고원에서 오스테나이트에서 마르텐자이트로 변형하는 순방향 상변위 구간(BC구간, Forward Transformation), 재탄성 거동에 의한 응력경화 구간(CD구간), 하중 제하시(Unloading) 탄성변형 회복구간(DE구간), 응력 회복이 발생하여 오스테나이트 상태로 돌아가는 역방향 상변위 구간(EF구간), 잔류 변형이 없는 탄성회복 구간(FA) 등 총 6개 구간으로 구성된 깃발 모양의 이력 거동을(Flage-shaped Hysteresis Behavior) 보여준다[7]. 오스테나이트 상태의 형상기억합금은 최대 8% 이내로 변형률을 재하(Loading) 할 경우에 별도의 열처리를 가하지 않더라도 단지 응력 제거만으로도 잔류 변형이 거의 없고 원형으로 자동 복원되는 성질을 가지고 있다. 마지막으로 상변위 온도가 Md 이상으로 올라갈 경우에는 강도가 오스테나이트 상태의 응력의 슬립에 의해 발생되는 고원구간 이상으로 증가하며 하중 제하시 일반적인 소성 변형이(Ordinary Plastic Deformation) 발생한다[2],[7],[8].
본 연구에서는 일정한 온도 내에서 재료적으로 우수한 초탄성 형상기억합금의 상변위 상태를 고려하여 깃발 모양의 이력 곡선을 재현할 수 있는 1차원적인 구성방정식 모델을 제시하고 상용 프로그램에서 사용자 정의의 재료(User-defined Material, 이하 UMAT) 모델을 개발하고 자 한다. 형상기억합금 내에서 마르텐자이트의 함유 비율에(Fraction) 따라서 순방향 혹은 역방향 상변위 과정을 나타내고자 한다. Aurichio에 의하여 개발된 강성(Stiffness) 모델을 기반으로 한[9] 준정적 시간-이산(Quasi-static Time Discrete) 방정식을 사용하여 마르텐자이트의 함유 비율을 점진적으로 조절한다. 따라서 본 연구 논문에서는 수치해석에 직접 적용할 수 있는 알고리듬을(Algorithm) 포함하여 시간-이산 구성 방정식(Constitutive Equation) 모델에 대하여 집중적으로 논의하고 자 한다. 아울러 UMAT 모델을 사용하여 수치해석적으로 재현된 초탄성 형상기억합금의 준정적 거동을 재료 실험에 의하여 얻어진 데이터와 비교한다. 마지막으로 본 재료 모델을 활용하여 구조 해석을 실시하고 응력측정 및 이론식 비교를 통하여 본 연구에서 제시된 재료 모델의 정확성을 입증하고 자 한다.
2. 재료모델
이번 장에서는 일축하중 상태하에서 초탄성 형상기억합금의 응력-변형율에 의한 준정적 거동에 대하여 논의하고 자 한다. Fig. 2에서 보이는 바와 같이 오스테나이트 상태의 니티놀 형상기억합금은 초기 탄성계수(E), 마르텐자이트 상변위의 시작과 완성이 되는 응력(σsSAand σfSA), 오스테나이트 상변위의 시작과 완성이 되는 응력과(σsASand σfAS) 응력고원 내에서 변형률 슬립(εL) 등의 총 6개의 파라미터로(Parameter) 형상화 된 깃발 모양의 이력을 일련의 직선들로 이상화하여 거동을 재현할 수 있다[9]. 일정한 간격으로 이산되어 나누어진 시간 간격이 증가함에 따라서 마르텐자이트의 비율을 점진적으로 변화 시키는 방식을 재료의 구성 방정식에 도입하여 모델 내에서 상변위 과정을 반영하였다. 구체적인 이론 설명과 수식은 다음 장에서 논의한다.
2.1 초탄성 형상기억합금의 상변위
앞에서 언급한 대로 순방향 및 역방향의 상변위 과정을 형상기억합금 내에서 0에서부터 1까지의 범위를 가지는 마르텐자이트 비율을(
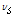 ) 내부 변수로 가정하여 수식화 할 수 있다. 여기서 오스테나이트에서 마르텐자이트 결정으로 전환되는 과정을 순방향 상변위라고 정의하며(A → S) 반대의 과정을 역방향 상변위라고 정의한다(S → A). 2개의 상변위 과정은 응력에 대하여 시간에 따른 선형적인 운동 법칙이(Kinetic Rule) 존재한다고 가정한다. 재료 모델에 대한 구성 방정식에서 순방향 상변위 과정은 응력에 대하여 다음과 같이 정의한다.
) 내부 변수로 가정하여 수식화 할 수 있다. 여기서 오스테나이트에서 마르텐자이트 결정으로 전환되는 과정을 순방향 상변위라고 정의하며(A → S) 반대의 과정을 역방향 상변위라고 정의한다(S → A). 2개의 상변위 과정은 응력에 대하여 시간에 따른 선형적인 운동 법칙이(Kinetic Rule) 존재한다고 가정한다. 재료 모델에 대한 구성 방정식에서 순방향 상변위 과정은 응력에 대하여 다음과 같이 정의한다.
 (1)
(1)
여기서
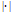 는 응력의 절대값을 의미하며 점 모양의 위 첨자는 응력을 시간에 대하여 미분한 속도의 개념을 나타낸다. 시간의 흐름에 따른 마르텐자이트의 비율 변화를 나타내는 방정식은 다음과 같이 표현한다.
는 응력의 절대값을 의미하며 점 모양의 위 첨자는 응력을 시간에 대하여 미분한 속도의 개념을 나타낸다. 시간의 흐름에 따른 마르텐자이트의 비율 변화를 나타내는 방정식은 다음과 같이 표현한다.
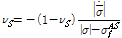 (2)
(2)
반면에 역방향 상변위와 이에 상응하는 마르텐자이트의 비율 변화에 대한 방정식은 다음과 같이 나타낸다.
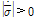 (3)
(3)
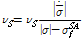 (4)
(4)
2.2 시간-이산 모델에서의 응력-변형률 관계
탄성 변형률과(
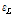 ) 포함하는 총 변형률은 싸인 함수를(sgn(・)) 사용하여 다음과 같이 정의할 수 있다.
) 포함하는 총 변형률은 싸인 함수를(sgn(・)) 사용하여 다음과 같이 정의할 수 있다.
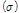 (5)
(5)
여기서 싸인 함수는 응력의 흐름을 고려하고 마르텐자이트 비율에 선형적으로 비례하는 소성 변형률을 결정하기 위하여 사용된다. 탄성 범위에서의 응력은 훅의 법칙을(Hook’s Law) 고려하여 다음과 같이 표현한다.
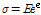 (6)
(6)
여기서 E는 형상기억합금의 탄성계수를 의미한다. 이산적인 시간 간격 내에서 소성 변형률에 의하여 제어를 받는 마르텐자이트의 비율을 수치해석적인 적분을 수행하기 위하여 시간-이산 모델을 도입한다. 마르텐자이트 비율에서 이산적인 시간 구간 내에서의 증분은(Increment) 다음과 같은 수식으로 나타낼 수 있다.
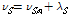 (7)
(7)
여기서
 은 이산적인 시간구간 내에서 마르텐자이트 비율의 증분을 의미하여 아래의 적분 수식으로 나타낼 수 있다.
은 이산적인 시간구간 내에서 마르텐자이트 비율의 증분을 의미하여 아래의 적분 수식으로 나타낼 수 있다.
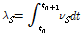 (8)
(8)
시간적인 흐름 순서를 정의하기 위하여 시간의 아래 첨자에
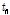 의 이산적인 구간 내에서 다음 시간의 흐름을 의미한다.
의 이산적인 구간 내에서 다음 시간의 흐름을 의미한다.
식 (6)에서의 응력-변형률 간에 선형적인 관계는 아래의 수식으로 재정리 할 수 있다.
 (9)
(9)
위의 수식을 시간에 대한 미분을 수행하여 응력의 증분을 나타낸다면 아래의 수식으로 정리할 수 있다.
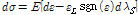 (10)
(10)
재료에 항복이 발생한 이후에 마르텐자이트 비율의 증분은(
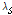 ) 소성 변형률이 발생한 양에 비례하므로 시간 미분에 따라서 아래와 같이 정의할 수 있다.
) 소성 변형률이 발생한 양에 비례하므로 시간 미분에 따라서 아래와 같이 정의할 수 있다.
 (11)
(11)
여기서
 는 항복 이후에 응력-변형률 선도에 대한 접선탄성 계수의 스칼라 양을 의미하며 식 (9)을 아래의 수식으로 변환할 수 있다.
는 항복 이후에 응력-변형률 선도에 대한 접선탄성 계수의 스칼라 양을 의미하며 식 (9)을 아래의 수식으로 변환할 수 있다.
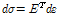 (12)
(12)
접선 탄성계수는 다음과 같이 정의할 수 있다.
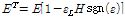 (13)
(13)
스칼라 양인
 는 초탄성 형상기억합금에 소성변위가 발생한 이후에 등온에서의 1차원적인 시간-이력 모델에서 응력-변형률 선도의 선형적인 상관관계를 적용하여 상변위 과정을 반영한다면 다음과 같은 관계식으로 나타낼 수 있다.
는 초탄성 형상기억합금에 소성변위가 발생한 이후에 등온에서의 1차원적인 시간-이력 모델에서 응력-변형률 선도의 선형적인 상관관계를 적용하여 상변위 과정을 반영한다면 다음과 같은 관계식으로 나타낼 수 있다.
 (14)
(14)
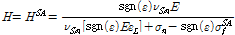 (15)
(15)
위의 수식을 변환하여 상변위 과정 동안에 마르텐자이트의 비율의 변화는 선형적인 상관 관계를 적용하여 다음과 같이 정의한다.
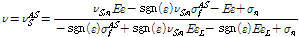
(16)
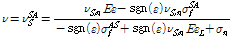 (17)
(17)
수식에 대한 타당성을 검증하기 위하여 각각의 상변위 과정에서의 응력의 변화가 없다고 가정을 하여(
 Case) 위의 수식을 적용한다면 완벽한 탄성-소성(Perfectly Elasto-plastic) 응력-변형률 선도를 가진 평형사변형 형태의 깃발모양의 이력 곡선으로 초탄성 형상기억합금의 거동을 재현할 수 있다. 마지막으로 순방향 혹은 역방향 상변위 내에서 변형률의 경계 값은 마르텐자이트 비율을 기준하여 직선으로 보간하여 나타낸다. 마지막으로 각각의 상변위 한계에서의 변형률은 아래의 식으로 정의할 수 있다.
Case) 위의 수식을 적용한다면 완벽한 탄성-소성(Perfectly Elasto-plastic) 응력-변형률 선도를 가진 평형사변형 형태의 깃발모양의 이력 곡선으로 초탄성 형상기억합금의 거동을 재현할 수 있다. 마지막으로 순방향 혹은 역방향 상변위 내에서 변형률의 경계 값은 마르텐자이트 비율을 기준하여 직선으로 보간하여 나타낸다. 마지막으로 각각의 상변위 한계에서의 변형률은 아래의 식으로 정의할 수 있다.
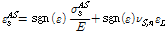 (18)
(18)
 (19)
(19)
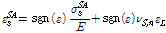 (20)
(20)
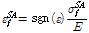 (21)
(21)
3. 프로그램 코딩
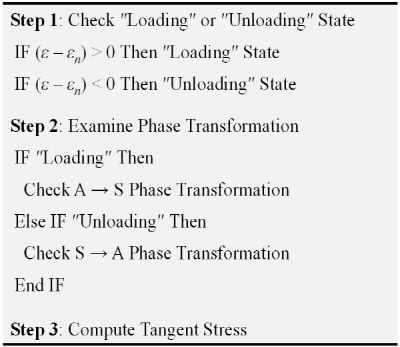
이번 장에서는 시간-이력 방정식 모델을 사용자 정의의 코드로 실행하는 프로그래밍 과정과 방법에 대하여 살펴본다. 준정적인 하중 상태에서 초탄성 형상기억합금의 거동을 재현하기 위하여 OpenSEES라는 상용 프로그램을 사용하여[10] C++ 프로그램 언어를 사용하여 사용자 정의 코드를 제작하고 상용 프로그램 내에서 소스 코드에(Source Code) 장착하여 재료 모델을 생성한다. Table 1은 하중과 상변위 과정에서의 변형률을 변수로 한 논리 제어를 보여주고 있으며 Table 2에서는 전반적인 사용자 정의 재료 모델의 논리의 흐름과 핵심 알고리듬을 보여주고 있다. 하중의 재하시 시간당 변형률의 증가와(
 ) 역방향 상변위가(S → A) 발생한다. 각 과정에서 일어나는 응력과 변형률의 변화를 Table 2에서 단계별도 요약 정리하였다. 상변위의 시작과 완성이 되는 시점의 변형률을 기준으로 논리 제어의 한계치를 설정하여 제어된 구간 내에서의 응력, 접선 탄성계수 및 마르텐자이트 비율 등을 산정한다.
) 역방향 상변위가(S → A) 발생한다. 각 과정에서 일어나는 응력과 변형률의 변화를 Table 2에서 단계별도 요약 정리하였다. 상변위의 시작과 완성이 되는 시점의 변형률을 기준으로 논리 제어의 한계치를 설정하여 제어된 구간 내에서의 응력, 접선 탄성계수 및 마르텐자이트 비율 등을 산정한다.
4. 재료 모델의 평가
형상기억합금 중에서 비교적 널리 사용되고 있는 니티놀 재료의 초탄성적인 거동을 재현하기 위하여 해석 프로그램에서 사용자 정의의 재료 모델을 제작하고 이를 사용하여 수치해석적으로 재현된 거동을 실험 데이터와 비교하여 정확성을 검증하고 자 한다. 본 연구에서는 미국 조지아 공과 대학에서(Georgia Institute of Technology) 수행된 구조 실험 중에서 25mm 직경을 가진 형상기억합금 봉에 반복적인 사이클 하중을 재하하여 얻어진 실험 데이터를 사용하여[2] 해석에 의하여 얻어진 결과를 분석 비교하였다. 구조 실험에서 얻어진 응력-변형률 선도의 결과 데이터를 기반으로 재료 모델 내에서 시간-이력 방정식을 표현하는 주요 파라미터들의 입력 값은 다음과 같이 산정할 수 있다.
 7%
7%
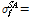 520MPa
520MPa
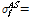 240MPa
240MPa
Fig. 2에서 보는 바와 같이 초탄성 형상기억합금은 인장과 압축에서 동일하고 대칭적인 거동을 한다고 가정한다.
재료 실험에 의하여 얻어진 결과 그래프와 OpenSEES 프로그램 내에서 제작한 사용자 정의 재료 모델을 사용하여 수치해석적으로 재현된 그래프를 Fig. 3에서 비교하였다. 전반적으로 Fig. 3(a)와 (b)에서 제시된 실험 및 해석에 의하여 얻어진 초탄성 형상기억합금의 응력-변형률 거동이 비교적 잘 일치함을 알 수 있다. 해석에 의하여 재현된 그래프의 경우에는 재료의 상변위의 거동에 따라 일련의 직선으로 이상화 하여 원형으로 완벽하게 복원되어 잔류 변형이 없는 깃발 모양의 이력 곡선으로 재현하였다. 다만 하중을 제거한 이력 곡선에서 수치해석적 재현이 실험결과 곡선과 비교하여 다소 비대한 경향이 있다. 항복 이전에 초기의 탄성 기울기가 하중 제거 후에 역방향 상변위가 시작되는 지점까지의 기울기를 동일하게 간주하여 모델링 하였기 때문에 이러한 경향을 보여주고 있다.
5. 활용 및 해석검증
이번 장에서는 프로그램 내에서 설치된 사용자 정의 재료 모델을 실제 구조 해석에 활용하고 모델링의 타당성을 검증하고 자 한다. 이를 위해서 초탄성 형상기억합금으로 제작된 양단 힌지의(Hinge) 단순보와(Simple Beam) 한쪽이 고정된 캔틸레버보에(Cantilever Beam) 각각 중앙과 자유단 끝단에 준정적인 반복 하중을 가하여 특이점에서의 하중-변위와 응력-변형률의 변화를 측정 하였다. 이러한 구조 해석도 상용 프로그램인 OpenSEES를 사용하여 수행하였다.
5.1 모델링 방법
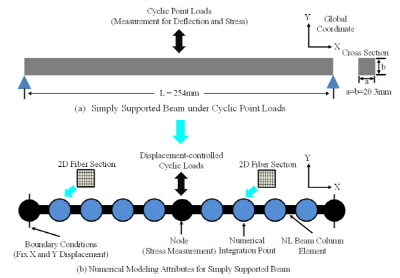
Fig. 4와 5에서는 양단이 힌지로 구속된 단순보와 한쪽 단이 고정된 캔틸레버보의 모델링을 보여주고 있다. 4장에서 언급된 초탄성 형상기억합금의 물성치를 각각의 수치해석 모델에 입력하였으며 비선형적인 재료 모델을 포함하고 있다. 각각의 수치해석 모델은 대변형을 고려한 비선형 보-기둥 요소를(Nonlinear Beam-column Element) 사용하여 모형화 하였고 그 단면은 각 변의 길이가 20.3mm인 정사각형이며 이를 해석 모델에서 2차원적인 단면 파이버로(Fiber) 모형화 하였다. 이러한 단면 파이버는 비선형적인 재료 모델을 포함하고 있으며 요소들 내에서 수치적분 지점들에(Numerical Integration Point) 배열하고 또한 해석을 수행하는 동안에 응력-변형률의 수치를 직접적으로 측정 가능하다. 단순보 중앙에 위치한 절점에(Node) 변위로 제어된 반복 하중을 직접적으로 재하하고 동일한 절점에서 응력과 변형률을 측정한다. 캔틸레버보의 경우에는 자유단 끝단에서 반복 하중을 재하하며 수치적분 포인트를 포함하는 고정단 절점에서 응력과 변형률을 측정한다. 단순보와 캔틸레버보의 길이를 각각 254mm와 127mm로 설계하였다. 마지막으로 해석 모델들의 지점들은 경계 조건들을 사용하여 모형화 하였다.
5.2 해석 및 결과분석
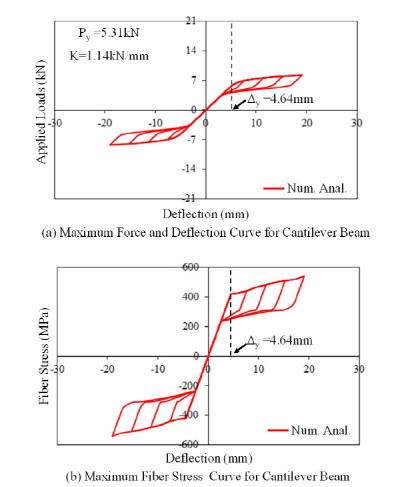
해석 모델에서 준정적인 반복 하중을 절점에 가하여 하중과 변위를 측정하고 또한 최대의 응력이 발생하는 지점에서 응력을 측정하였다. Fig. 5와 6은 단순보와 캔틸레버보 모델에서 수행한 해석 결과를 보여주고 있다. 각각의 모델에 상당량의 변위 하중을 가하더라도 탄성뿐만 아니라 소성범위에서도 우수한 복원 효과를 보여주고 있으며 역방향 상변위 과정을 거치면서 잔류 변형이 거의 발생하지 않고 원형으로 복원됨을 그래프에서 확인할 수 있다. 일정 변위에서 최대의 응력이 발생하는 지점에서 측정한 응력과 하중을 재하하는 지점에서 측정한 변위와 조합한 그래프에서는(Fig. 6(b), 7(b) 참고) 초탄성 형상기억합금 재료의 본연의 이력 곡선과 동일한 깃발 모양의 이력 곡선을 보여주고 있으며 각각의 상변위 경계에서의 응력 파라미터들과 동일한 결과 값들이 측정되었다.
순방향 상변위가 발생되는 시점에서 재료의 항복이 발생한다고 간주할 수 있으며 항복이 발생하는 시점에서의 항복 변위를(
 ) 해석을 통하여 측정된 결과 값과 비교 검증하였다. 단순보에서 보의 중앙과 캔틸레버보에서 보 끝단에서의 하중과 처짐에 대한 초기의 강성은(Stiffness) 다음과 같다.
) 해석을 통하여 측정된 결과 값과 비교 검증하였다. 단순보에서 보의 중앙과 캔틸레버보에서 보 끝단에서의 하중과 처짐에 대한 초기의 강성은(Stiffness) 다음과 같다.
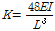 (22)
(22)
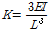 (23)
(23)
여기서
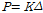 ) 항복 상태에서의 하중을 계산할 수 있다. 위에서 제시한 이론식에 의하여 계산된 단순보와 캔틸레버보의 초기 강성은 각각 2.29kN/mm와 1.14kN/mm이며 하중과 처짐의 상관 관계를 이용한다면 항복 하중은 11.8kN과 5.31kN으로 예측할 수 있다. Fig. 6(a)와 7(a)에서 보이는 바와 같이 이론식에 의해서 계산된 항복 하중은 항복 변위에서 도식화하여 얻은 항복 하중과 거의 동일하다고 판단할 수 있다. 따라서 해석에 대한 결과의 관측을 종합해볼 때 사용자 정의의 재료 모델이 초탄성 형상기억합금의 거동을 정확하게 재현하며 구조 해석에 적용함에 있어서 적절하다고 결론 내릴 수 있다.
) 항복 상태에서의 하중을 계산할 수 있다. 위에서 제시한 이론식에 의하여 계산된 단순보와 캔틸레버보의 초기 강성은 각각 2.29kN/mm와 1.14kN/mm이며 하중과 처짐의 상관 관계를 이용한다면 항복 하중은 11.8kN과 5.31kN으로 예측할 수 있다. Fig. 6(a)와 7(a)에서 보이는 바와 같이 이론식에 의해서 계산된 항복 하중은 항복 변위에서 도식화하여 얻은 항복 하중과 거의 동일하다고 판단할 수 있다. 따라서 해석에 대한 결과의 관측을 종합해볼 때 사용자 정의의 재료 모델이 초탄성 형상기억합금의 거동을 정확하게 재현하며 구조 해석에 적용함에 있어서 적절하다고 결론 내릴 수 있다.
6. 결 론
본 연구에서는 초탄성 형상기억합금의 이력 거동을 정확하게 재현하는 시간-이산 구성 방정식과 이를 프로그램 내에서 활용 가능하게 하는 사용자 정의의 재료 모델에 대하여 논의하였다. 상변위 과정에 따른 마르텐자이트의 비율을 변수로 하여 구성 방정식에서 응력과 변형률의 관계를 정의하였다. 재료 실험에 의하여 얻어진 결과값을 바탕으로 입력 파라미터를 설정하고 해석에 의하여 초탄성 형상기억합금의 거동을 정확하게 재현하였다. 사용자 정의의 재료 모델이 프로그램 내에서 적절하게 구현됨을 검증하기 위해서 초탄성 형상기억합금 재질의 단순보와 캔틸레버보의 수치해석 모델을 제작하고 반복적인 사이클의 변위 하중을 가하여 구조 해석을 수행하였다. 모델의 요소들 내에서 최대 응력이 발생하는 지점에 수치적분 지점을 설치하고 응력과 변형률의 변화를 관찰한 결과 재료의 원래 물성치와 동일한 거동의 이력 곡선을 측정하였으며 항복 응력이 발생하는 시점에서 전체 하중-변위 곡선에서 동시에 소성 변형이 발생하였다. 마지막으로 이론식으로 계산된 항복 강도는 구조 해석에 의해 측정된 항복 강도와 거의 동일한 수치를 보여주고 있다. 따라서 본 연구에서 제시한 구성 방정식과 이를 활용한 재료 모델이 구조 해석에 적절하게 활용할 수 있다고 판단된다.
Acknowledgments
본 연구는 국토교통부 국토교통기술촉진연구사업의 연구비 지원에(14CTAP-C078944-01)의해 수행되었습니다. 연구 지원에 대하여 깊은 감사를 드립니다.
References
-
Song, G., Ma, N., and Li, H.-N. (2006) Applications of Shape Memory Alloys in Civil Structures, Engineering Structures, Elsevier, Vol.28, No.9, pp.1266-1274.
[https://doi.org/10.1016/j.engstruct.2005.12.010]

-
DesRoches, R., McCormick, J., and Delemont, M. (2004) Cyclic Properties of Superelastic Shape Memory Alloy Wires and Bars, Engineering Structures, American Society of Civil Engineers, Vol.130, No.1, pp.38-46.
[https://doi.org/10.1061/(ASCE)0733-9445(2004)130:1(38)]

-
Hu, J.W. (2014) Seismic Analysis and Evaluation of Several Recentering Braced Frame Structures, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Sage, Vol.228, No.5, pp.781-798.
[https://doi.org/10.1177/0954406213490600]

-
Hu, J.W. (2015) Response of Seismically Isolated Steel Frame Buildings with Sustainable Lead-Rubber Bearing (LRB) Isolator Devices Subjected to Near-Fault (NF) Ground Motions, Sustainability, MDPI AG, Vol.7, No.1, pp.111-137.
[https://doi.org/10.3390/su7010111]

-
Hu, J.-W., and Choi, E. (2014) Seismic Design, Nonlinear Analysis, and Performance Evaluation of Recentering Buckling-Restrained Braced Frames (BRBFs), International Journal of Steel Structures, KSSC, Vol.14, No.4, pp.683-695.
[https://doi.org/10.1007/s13296-014-1201-3]

-
Hu, J.W., and Leon, R.T. (2011) Analysis and Evaluations for Composite-Moment Frames with SMA PR-CFT Connections, Nonlinear Dynamics, Springer, Vol.65, No.4, pp.433-455.
[https://doi.org/10.1007/s11071-010-9903-3]

-
Hu, J.W., Choi, E., and Leon, R.T. (2011) Design, Analysis, and Application of Innovative Composite PR Connections Between Steel Beams and CFT Columns, Smart Materials and Structures, IOP Publishing, Vol.20, No.2, 025019.
[https://doi.org/10.1088/0964-1726/20/2/025019]

-
Duerig, T.W., Melton, K.N., Stökel, D., and Wayman, C.M. (1990) Engineering Aspects of Shape Memory Alloys, Butterworth-Heinemann, UK.
[https://doi.org/10.1016/B978-0-7506-1009-4.50015-9]

-
Auricchio, F., and Sacco, E. (1997) A One-Dimensional Model for Superelastic Shape-Memory Alloys with Different Properties Between Martensite and Austenite, International Journal of Non-Linear Mechanics, Elsevier, Vol.32, No.6, pp.1101-1114.
[https://doi.org/10.1016/S0020-7462(96)00130-8]

- Mazzoni, S., McKenna, F., Scott, M.H., and Fenves, G.L. (2006) OpenSEES Command Language Manual, Ver. 1.7.3., University of California, Berkeley, USA.