볼트 전단파단이 지배하는 지압형식 볼트접합부의 힘-변형 관계

1. 서 론

강구조물은 철근콘크리트 구조에 비하여 구조재료적 특성과 조립구조법이라는 점에서 많은 장점을 가지고 있다. 이러한 조립구조법을 가능케 하는 강구조물의 접합과 이음의 대표적인 두 가지 방법으로 용접접합과 볼트접합이 있다. 이 중 볼트접합은 볼트를 조이는 것만으로 접합이 가능하기 때문에 시공 시 특별한 기술을 요구하지 않는다. 따라서 품질을 확보하는데 있어 작업 숙련도와 작업환경에 큰 영향을 받지 않을 뿐만 아니라 건설공기절감에도 유리하여 강구조 현장에서 선호되고 있는 방식이다. 이러한 볼트접합은 현대 건축물에서 일상적으로 대량 소비되는 부분이고, 구조적인 측면에서 볼 때 볼트의 전단파단과 모재의 전단파단 또는 인장파단만 잘 제어되면 지압메커니즘에 의해 강도 상승이 수반되면서 소성변형하는 연성거동을 보인다(Fig. 1). 이러한 접합부의 거동 특성을 잘 활용하여 해석과 설계를 합리화할 수 있다면 매우 큰 구조비용의 절감이 가능하다.

가령, 국내외 실무에서 양단을 전단탭으로 기둥에 접합된 보는 통상 단순보로 가정하여 설계하지만, 실제로는 단부의 지압거동에 의해 반강접 접합부가 되어 일정 부분의 부모멘트를 분담하므로 이를 고려하면 훨씬 경제적이고 합리적인 설계가 가능하다. 그러나 볼트접합부의 지압거동이 설계에 제대로 반영되지 못하고 있는 것은 신뢰성이 있고 간편한 해석적 모델링 방안이 아직 없기 때문이다. 또한 국내의 경우 이와 관련된 연구는 더욱 희소하다. Lee and Kim(2005)^[1]은 보-웨브를 볼트접합하고 플랜지는 용접한 철골모멘트접합부의 취성파단에 보-웨브 볼트접합부의 슬립이 미치는 영향을 실험적/해석적으로 연구하였고, Shin et al.(2011)^[2]은 웨브-볼트, 플랜지-용접 상세를 갖는 보-기둥 접합부에 대한 유한요소해석을 통해 슬립-지압거동이 플랜지의 취성파단지수(rupture index)에 미치는 연구를 수행하였다. Yang(2012)^[3]은 과대공을 갖는 볼트접합부의 강도평가를 위해 표준공과 과대공을 갖는 볼트접합부의 실험을 실시하였으며 설계기준과 비교･평가하였다. 페라이트계 스테인리스강(STS430) 박판 볼트접합부에 대해 김태수와 Kim and Kim(2013)^[4]은 볼트배열에 따른 이면전단 강도평가 및 파괴모드를 고찰하였으며, Kim et al.(2013)^[5]은 일면전단에 대한 강도평가 및 유한요소해석을 수행하였다.

본 연구에서는 기존의 단일 볼트로 구성된 지압 접합부의 힘-변형 관계식을 고찰하고 한계점을 규명한 후, 다양한 변수를 갖춘 실험결과를 통해 범용 가능한 힘-변형 관계식을 제안하여 합리적인 편심하중을 받는 군볼트 접합부의 설계 방안을 제안하고자 한다.

2. 순간중심회전법 고찰

본 장에서는 편심하중을 받는 볼트접합부의 극한강도해석법으로서 Crawford and Kulak(1971)^[6]가 선행연구로 제안한 순간중심회전법을 고찰한다.

2.1 순간중심회전법(ICRM)

Crawford와 Kulak(1971)은 볼트접합부의 연성능력에 주목하여 편심하중을 받는 군볼트 설계에 볼트간의 힘의 재분배를 활용하는 순간중심회전법(ICRM, Instantaneous Center of Rotation Method)이란 선구적 방안을 제시하였다. 먼저 순간회전중심(Instantaneous Center)을 가정하고 그 위치에서 각 볼트의 지압력을 산정한다(Fig. 2). 그리고 가정한 순간회전중심에서 힘의 평형조건 만족여부를 시행착오적으로 확인하여(식 (1)) 정확한 순간회전중심의 위치를 결정하고 각 볼트부에 작용하는 지압력, 하중방향 및 접합부 변형량을 산정한다(식 (2)).

 (1.a)

       (1.b)

            (1.c)

                       (2)

여기서,    :볼트 중심으로부터 순간회전중심까지의 거리

       :순간회전중심에서 가장 멀리 떨어진 볼트의 중심으로부터 순간회전중심까지의 거리

       :볼트접합부의 변형

      :볼트접합부의 최대변형량(0.34in, 8.75mm)

가장 멀리 떨어진 볼트부에서 최대하중을 받게 되므로 이 부분에서 최대변형량에 도달함을 가정하여 볼트간 작용하고 있는 힘을 재분배시킨다. 따라서 순간중심회전법을 적용하기 위해서는 전제조건으로 단일볼트 접합부의 힘-변형 관계가 규정되어야 한다.

2.2 선행연구의 문제점 및 한계

Crawford와 Kulak은 미국 소재 A325 단일볼트(직경 3/4in, 19.05mm), A36 단일강재만을 이용한 실험으로 단일볼트의 힘-변형 관계식을 제안하였다(식 (3)).

 (3)

여기서,   : 볼트의 최대전단강도(74kips)

          : 자연 대수(base of natural logarithms)

          : 회귀계수 10

          : 회귀계수 0.55

         : 볼트의 변형(in.)

Crawford와 Kulak은 실험결과를 통해 단일볼트의 최대변형량을 0.34in(8.75mm)로 규정하였다. 이것은 매우 제한된 조건에서 이루어진 실험을 토대로 한 것이므로, 볼트접합부 조건이 국내 실정에 맞게 변경 될 경우에는 Crawford와 Kulak이 제안한 힘-변형 관계식 및 최대변형량 제한의 적합성 여부가 불분명하다. 또한 압축실험결과만을 통해 힘-변형 관계식을 제안하여 편심하중을 받는 볼트군의 경계조건에 따른 실제 변형거동을 잘 모사하지 못한다. 실제로 최근 UCSD (Univ. of Calif., San Diego)의 Uang 그룹(Sato and Uang, 2010^[7], Uang et al., 2010^[8], Hong and Uang 2004^[9])은 내진설계에 박판 강재 볼트접합부의 지압을 통한 에너지소산 메커니즘을 활용하는 방안을 연구하였는데 제한된 실험조건으로 도출된 Crawford와 Kulak의 힘-변형 관계식을 일반화하여 적용할 수 없음을 분명히 보여주었다.

따라서 본 연구에서는 볼트접합부의 경계조건을 반영한 단일볼트 압축･인장실험을 통하여 국내에 적용할 수 있는 단일볼트의 힘-변형 관계를 도출하고자 한다.

3. 단일볼트 접합부 압축실험

3.1 압축실험 개요

Crawford와 Kulak의 실험이 단일강재 및 두께, 단일볼트 직경에 국한된 것과는 달리 강종, 모재의 두께, 볼트 직경을 변수로 압축실험을 수행하였다. 실험은 만능재료시험기(Universal Testing Machine, 이하 UTM)를 사용하여 가력 하였으며, 하중과 변위는 UTM에서 측정된 값을 사용하였다. Fig. 4와 Table 1은 각각 실험체 셋업과 제원을 나타낸 것으로 모재의 좌굴이 발생치 않고 볼트의 전단파단이 선행하도록 설계하였으며, 볼트 나사산이 전단면에 포함되지 않도록 하였다. 실험 지그는 두께 30mm의 인장강도 800MPa급 강재로 제작하였으며, 실험 후에도 탄성 상태로 유지하여 가력 시 계측에 미치는 영향을 최소화하였다.

3.2 압축실험 결과 및 분석

대부분의 변형은 실험체의 볼트 구멍부 지압변형 및 볼트 전단변형으로 나타났으며(Fig. 5(a)~(c)) 실험체 변형에 비하여 지그의 일그러짐이나 변형은 확인할 수 없었다(Fig. 5(d)).

Table 2는 압축실험 결과를 표로 정리한 것이다. 실험체 플레이트 구멍부의 과도한 변형에 의해 지그가 UTM head에 접촉하여 가력이 중지된 네 가지의 경우(C400-15-22 등)를 제외하고는 모든 종국파괴모드는 예상대로 볼트 전단파단으로 나타났으며, 각 최대 강도는 F10T 볼트(D20, D22, D24)의 전단강도를 나타내었다(Fig. 6). 강재의 두께가 두꺼울수록 강재의 강도가 높을수록 초기 강성이 크게 나타났으며 최대강도에서의 변형값이 작게 나타났다. 이는 최대강도에서의 변형 값은 강재 및 볼트의 강도, 강재 두께 및 연단거리 등 접합부의 기하학적 형상에 의존한다는 것을 의미한다. 또한 실험 결과에서 보여주는 최대강도에서의 변형값은 Crawford와 Kulak이 제안한 최대변형값인 0.34in.(8.75mm)를 하회하는 경우도 있음을 보여주고 있으므로(Table 2) Crawford와 Kulak의 최대변형값 0.34in.(8.75mm)을 일률적으로 사용하는 것은 타당하지 못하다.

3.3 단일볼트 접합부 힘-변형관계

압축력을 받는 단일볼트 접합부의 일반화된 힘-변형 관계식을 제안하기 위해 모재의 공칭인장강도를 통하여 정규화를 실시하였다. 지압강도로 정규화된 그래프에서 보수적으로 힘-변형 관계식을 도출하기 위해 실험결과의 하한치를 선택하여(Fig. 7) 식 (4)와 같이 제안하였다.

 (4.a)

 (4.b)

여기서,  : 무차원화 된 볼트의 지압강도

         :모재의 공칭인장강도(MPa)

          :볼트의 직경(mm)

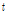          :모재의 두께(mm)

          :자연 대수(base of natural logarithms)

          :회귀계수 0.1

          :회귀계수 0.55

3.4 최대변형값 제한

Crawford와 Kulak은 볼트접합부의 최대변형값을 0.34in로 규정하였으나 제한된 조건에서 실험한 결과를 토대로 도출된 결과이므로 볼트의 직경 또는 모재의 강종이 바뀔 경우에도 적용될 수 있는지는 판단하기 어렵다. Table 2 및 Fig. 6을 보면 같은 강종과 두께의 실험체에서는 볼트의 직경이 커질수록 변형능력이 상승하고 같은 볼트 직경일 경우에는 강재 두께가 두꺼워짐에 따라 변형능력이 감소하는 경향을 보인다. 이를 토대로 실험결과를 볼트의 전단강도와 지압강도의 비로 정규화를 실시하였다(식 (5.a)).

단일볼트의 최대변형값이 지압강도와 볼트의 전단강도비에 반비례하는 경향이 나타나므로 하한값을 선택하여 식 (5.b)를 제안하였다. 단 최대변형값의 상한은 20mm로 제한을 두어 과도한 변형을 방지하였다.

                      (5.a)

       (5.b)

4. 단일볼트 접합부 인장실험

4.1 인장실험 개요

단일볼트 압축실험체의 예상되는 파괴모드는 볼트의 전단파단 및 볼트 구멍 주위의 과도한 변형인 반면 단일볼트 인장실험체의 경우는 모재의 두께 및 플레이트의 직경에 따라 볼트의 전단파단 및 연단부의 찢어짐 파괴로 실험이 종료될 것으로 예측된다. 이렇든 볼트 접합부의 경계조건에 따라 단일볼트 실험체의 힘-변형관계는 상이하게 다른 결과를 보일 것으로 예측된다. 따라서 본 장에서는 단일볼트 압축실험체와는 다른 세팅으로 실험을 수행하였다.

압축실험과 마찬가지로 인장실험 역시 모재 강종, 두께 및 F10T 볼트 직경을 설계변수로 하였다(Table 3). 모재의 총단면 항복과 순단면 파단 및 블록 전단파괴를 제어하여 지압파괴가 선행하도록 설계하였다. 실험지그는 800MPa급 고강도 강재(30t)를 용접하여 제작하였으며, 탄성 상태로 유지하여 실험체의 변위 계측에 미치는 영향을 최소화하였다.

4.2 인장실험 결과 및 분석

SM490 및 SS400 인장 실험체의 종국파괴모드는 실험체의 연단부파단 또는 볼트 전단파단으로 나타났으며 (Fig. 10(a)~(c)) 인장강도 800MPa급 고강도강 지그에서는 변형이 거의 발생하지 않았다(Fig.10(d)). Table 4는 실험의 결과를 요약한 것으로 각 실험체의 최대변형과 최대하중을 살펴보면 파괴양상이 전단파단의 경우 연단부 파괴에 비하여 변형 능력이 떨어짐을 알 수 있다.

Fig. 11은 인장실험에서 파괴모드가 볼트의 전단파단인 실험체들의 결과를 표시한 것이다. 종국파단 모드가 볼트의 전단파단인 경우 압축실험결과와 비교하였을 때 인장실험의 최대하중은 볼트의 전단강도를 하회하는 것으로 나타났다. 이는 압축실험과는 달리 인장실험 지그와 실험체에 이격거리가 존재하였기 때문에 볼트에 전단변형 뿐만 아니라 휨변형 또한 수반되었으며, 800강 지그에 작용한 지레반력(prying action)이 볼트에 인장력을 추가적으로 유발함^[10]에 따라 강도가 저감된 것으로 사료된다.

4.3 단일볼트 접합부 힘-변형관계

압축실험과 마찬가지로 무차원 정규화를 통해 인장력을 받는 볼트접합부의 일반화된 힘-변형 관계를 도출하였다(식 (6.a)). 지압강도로 정규화한 그래프를 살펴보면(Fig. 13) 대부분의 실험체들이 유사한 거동을 보이며, 볼트가 전단파단된 실험체의 힘-변형관계의 경우 연단부파단된 실험체의 힘-변형관계와 유사한 거동을 보인 후 볼트파단이 일어남을 알 수 있다. 연단파단으로 실험종료된 실험체의 경우 최대강도의 값이 로 규정하는 것과 잘 부합하는 결과이다.

인장을 받을 시 지압강도-변형식은 볼트의 전단파단으로 실험이 종료된 실험체들을 바탕으로 하여 보수적으로 Fig. 13과 같이 실험결과의 하한치를 통해 제안하였다(식 (6.b)).

 (6.a)

 (6.b)

여기서,  : 무차원화 된 볼트의 지압강도

         : 모재의 공칭인장강도(MPa)

         : 연단거리(mm)

          : 모재의 두께(mm)

          : 자연 대수(base of natural logarithms)

          : 회귀계수 0.1

          : 회귀계수 0.55

4.4 최대변형값 제한

인장실험의 결과를 지압강도( )와 단일볼트의 전단강도 비로 정규화하였을 시 연단부파단인 경우와 볼트의 전단파단인 경우로 군이 나뉘는 경향을 보인다(Fig. 14). 압축실험과 마찬가지로 볼트 전단파단된 실험체들의 결과를 이용하여 최대변형 산정식(식 (7))을 마련하였으며 과도한 변형을 방지하기 위해 상한값을 20mm로 제한하였다. 볼트접합부에서 볼트 구멍 주위에 20mm이상의 변위가 발생한다는 것은 실험에서 사용한 볼트의 최소 직경 이상의 변형을 갖는 것을 의미하며 이는 더 이상 지압 메커니즘에 의한 힘-변형 거동을 보이지 못한다고 볼 수 있다.

 (7.a)

 (7.b)

압축실험의 힘-변형 관계식(식 (4))과 최대변형 산정식(식 (5)), 그리고 인장실험결과를 통한 식 (6)과 식 (7)을 이용한다면 합리적인 순간중심회전법에 의한 군볼트 접합부 설계가 가능할 것이다.

5. 제안한 힘-변형 관계식의 활용

본 연구에서 제안한 힘-변형 관계식의 ICRM으로의 적용절차는 다음과 같다.

(1)순간회전중심(I.C.)의 위치를 가정한다. 이때 볼트의 배치가 x축 및 y축 대칭이어도 순간회전 중심의 위치는 x축 방향뿐만 아니라 y축 방향으로도 바뀔 수 있음에 유의한다. 이는 Crawford와 Kulak은 압축실험만을 통해 하나의 경계조건만을 고려한 것과 달리 본 연구에서는 인장실험을 통하여 압축실험과는 다른 경계조건도 고려했기 때문이다.

(2)가정된 순간회전중심으로부터 각 볼트까지의 거리( )를 산정한다.

(3)최대변형 산정식을 이용하여 각 볼트의 변형량을 산정한다. 이때 각 볼트의 변형량은 순간중심에서 각 볼트중심까지의 거리의 비를 사용하여 구한다(식 (2)). Fig. 15에서 상단의 사각형 내의 볼트군은 압축실험보다는 인장실험의 경계조건과 흡사하다고 볼 수 있으므로 인장실험의 결과를 토대로 제안된 식 (7)을 사용하고 하단의 사각형 내의 볼트군은 압축실험의 결과로부터 제안된 식 (5)를 이용한다. 이후부터는 상단의 볼트군과 같은 경우를 열린경계, 나머지 볼트군과 같은 경우를 닫힌경계로 칭한다.

(4)제안된 힘-변형 관계를 이용하여 각 볼트에 걸리는 힘을 산정한다. 열린경계의 볼트군은 인장실험의 결과인 식 (6)을 이용하고 닫힌경계의 볼트군은 압축실험의 결과인 식 (4)를 이용한다.

(5)평형조건 및 적합조건에 맞지 않을 경우 단계 (1)부터 재수행한다.

기존의 순간중심회전법과는 다르게 y축 방향으로도 순간회전중심이 바뀔 수 있기 때문에 반복작업이 조금 더 복잡해지지만 합리적인 설계가 가능하다.

6. 예제를 통한 힘-변형 제안식의 확인

편심하중을 받는 브래킷 설계 예제를 통하여 연구결과의 활용방안을 예시하여 이해를 돕고, 본 연구 결과의 타당성을 보이고자 한다. 예제는 Fig. 16과 같은 조건을 갖는 편심하중을 받는 볼트접합부에서 최대하중 P를 산정하는 문제이며 강재는 두께 15mm의 SS400, 볼트는 M20(F10T)이다. 기둥 플랜지의 경우 충분한 내력을 받을 수 있는 것으로 가정하여 브래킷 설계문제로만 국한하기로 한다.

6.1 탄성해석법에 의한 풀이

기존의 탄성해석법은 모재를 강체로, 볼트를 탄성체로 이상화하고, 두 부재 사이에 마찰이 없는 것으로 가정하여 해석한다. 회전중심이 군볼트의 도심에 위치한다고 가정한 후 편심하중을 집중하중과 우력 모멘트의 조합으로 보고 각각의 외력벡터의 합으로 볼트접합부의 강도를 산정하는 방법이다(Fig. 17).

 (8)

 (9)

탄성해석법으로 Fig. 16의 예제를 풀면 접합부가 받을 수 있는 최대하중 (2, 8번 볼트가 설계전단강도에 도달할 때의 하중)는 243.21kN이 된다.

6.2 Crawford와 Kulak의 순간중심회전법에 의한 풀이

순간중심회전법을 이용하여 예제를 풀기 위해서는 2.1절에서 설명했던 것처럼 순간회전중심을 가정해야 한다. 그 후 반복해법을 통하여 순간회전중심의 위치를 찾는다. 순간회전중심의 위치를 7번 볼트로부터 x축 반대 방향으로 3mm 떨어져 있다고 가정을 했을 경우(r_o=40.75mm)에 각 볼트에 걸리는 지압력을 Table 5에 나타냈다. 최외각 볼트(2번, 8번 볼트)의 최대변위는 0.34in.(8.75mm)로 제한되었다.

x축 힘의 평형조건은 여덟 개의 볼트가 x축 및 y축을 기준으로 대칭을 이루어 자동으로 만족시킨다. y축 힘 및 모멘트 평형조건을 만족하는지 확인하기 위해 식 (1.b) 및 식 (1.c)를 수직분력 P_y 및 하중 P에 대해 정리하면 식 (10)과 같다.

 (10.a)

 (10.b)

가 42.117mm일 때가 된다(Fig. 18).

앞선 과정과 마찬가지로 식 (1.c)를 이용하면

 (11)

식 (10.a)와 비교하면 순간회전중심의 위치 가 42.117mm일 때 힘의 평형을 만족시키는 것으로 나타난다. 1019.76kN의 하중은 접합부의 파단하중으로 최단부 볼트부(2번, 8번)가 극한하중상태에 이르렀을 때에 기초한 것이다. 따라서 선행연구의 제안식을 따른다면 볼트의 전단강도(식 (8))와 A325볼트의 최대전단강도인 74kips(식 (12))를 기준으로 강도저감을 실시해야 한다.

 (12)

강도저감을 실시하면 접합부가 지지할 수 있는 최대하중은 식 (13)과 같다.

 (13)

6.3 제안식을 적용한 순간중심회전법에 의한 풀이

본 연구에서는 볼트접합부의 최대변형값을 지압강도와 전단강도의 비로 규정하였다. 이를 통해 경계조건에 따라 서로 다른 최대변형값 산정식과 힘-변형 관계식을 적용한다.

예제에서 1~6번 볼트는 닫힌경계로 보고 압축실험에서 나온 식을 사용하고, 7번과 8번 볼트는 열린경계로 판단하여 인장실험을 통해 도출된 식을 사용한다.

압축실험의 결과(식 (5))를 활용하면 닫힌경계의 최대변형( )은 9.51mm의 값이 구해진다. 이 최대변형값을 이용하여 6.2절과 마찬가지로 순간회전중심의 위치를 가정하고 반복해법을 수행한 결과를 Table 6에 정리하였다.

식 (1.c)를 이용하여 P를 구하면 식 (14)와 같다.

 (14)

이를 다시 식 (1.b)에 대입하면 가 42.168mm일 때 y축 힘의 평형조건을 만족시키는 순간회전중심의 위치임을 알 수 있다. x축 힘의 평형조건 또한 만족시키기 위해서는 순간회전중심이 y축 방향으로 4.285mm 내려간 위치에 존재해야한다(Fig. 19).

앞서 Crawford와 Kulak의 방법과 마찬가지로 볼트 설계전단강도로 강도저감을 한다(식 (15)).

 (15)

본 연구에서 제안한 방법으로 예제를 풀 경우 브래킷 접합부가 지지할 수 있는 최대하중은 266.42kN이다. 이 값은 탄성해석법의 결과(243.21kN)보다 약 9%의 강도증진 효과를 보이나 Crawford와 Kulak의 방법에 의한 결과(291.86kN)보다는 낮은 수치이다. 힘-변형 거동양상은 볼트직경, 모재의 강종, 두께 및 경계조건에 따라서 변한다. 이러한 변수가 고려되지 않고 압축실험만을 통해 제안된 Crawford와 Kulak의 힘-변형관계식은 A36강재, A325 단일볼트(직경 3/4in., 19.05mm)로 이루어진 닫힌경계의 군볼트에만 유효하며, 열린경계부에 적용 시에는 그 강도를 과대평가하는 문제가 발생한다.

볼트의 지압강도와 전단강도의 비를 이용하여 최대변형을 제한하였고 접합부의 경계조건 및 여러 가지 변수에 따른 힘-변형관계를 반영하였기 때문에 본 연구의 제안식은 국내소재 접합부에 적용가능하다.

7. 결 론

본 연구에서는 지압형식 볼트접합부의 거동 및 힘-변형 관계에 대하여 실험적, 해석적으로 고찰하였다. 범용가능한 단일볼트 접합부의 힘-변형 관계식을 제안하고 기존 선행연구의 한계점을 보완한 설계방안을 제시하였다. 연구결과를 요약하면 다음과 같다.

(1)현행의 볼트접합부의 탄성설계법은 보수적이므로 접합부가 지닌 연성능력을 활용하여 구조비용의 경제성을 제고할 필요가 있다. 편심하중을 받는 군볼트 접합부의 설계에 있어서 Crawford와 Kulak(1971)이 제안한 방법은 탄성해석법에 비하여 훨씬 합리적이고 경제적이지만 A325 단일볼트(직경 3/4in, 19.05mm), A36강재로 이루어진 접합부에만 유효한 것으로 국내의 다양한 강종에 적용했을 때 타당성 여부가 불분명하다.

(2)본 연구에서는 군볼트 접합부의 두 가지 경계조건을 고려하기 위해 단일볼트 접합부의 압축 및 인장실험을 모재의 강종 및 두께, 볼트직경을 변수로 수행하였다. 종국모드가 볼트 전단파단인 실험체의 최대강도는 볼트의 직경에 관련 있음을 보였으며 볼트 접합부의 변형능력은 모재의 강종과 두께, 볼트의 직경 및 연단거리 등에 의존함을 보여주었다.

(3)닫힌경계에서는 단일볼트의 압축실험의 결과를 로 정규화한 힘-변형 관계식을 활용하는 방안을 제시하였다.

(4)선행연구에서는 볼트접합부의 최대 변형능력을 0.34in (8.75mm)로 제한하여 볼트 접합부의 변형능력을 과소 또는 과대평가하는 한계점을 보였다. 본 연구에서는 각각의 경계조건에 따라서 전단강도와 지압강도의 비를 이용한 최대변형값 산정식을 제안하였다.

(5)하나의 브래킷 설계예제를 세 가지 방법(탄성해석법, 순간중심회전법, 본 연구에서 제안한 방법을 적용한 순간중심회전법)으로 풀어봄으로써 선행연구에서 제안한 방법이 국내 소재에 적용될 수 없는 이유와 상기 제시한방법의 타당성을 검증하였다.

(6)그러나 실험조건이 2면 전단으로만 이루어진 점과 두께가 15mm 이하인 박판의 경우에 대한 검증이 이루어지지 않은 한계를 지닌다. 또한 데이터 수가 부족하고 닫힌 경계와 열린 경계에 대한 정확한 구분이 미흡한 상황으로 신뢰성 확보를 위해 다양한 변수에 대한 추가적인 실험 및 수치해석 연구가 필요하다. 또한 순간회전중심을 간단명료하게 찾는 방법에 대한 추후 연구가 필요하다.

Acknowledgments

본 연구는 교육과학기술부가 주관하고 한국연구재단이 시행하는 기초연구사업(No.0415-20120036)의 지원으로 이루어진 것으로 이에 감사드립니다.

References

• 이철호, 김재훈(2005) 웨브를 볼트로 접합한 보 플랜지 절취형(RBS) 철골모멘트접합부의 내진설계 및 성능평가, 한국강구조학회논문집, 한국강구조학회, 제17권, 제6호, pp.​689-697.
  Lee, C.H., and Kim, J.H. (2005) Seismic Design and Testing of Reduced Beam Section Steel Moment Connections with Bolted Web Attachment, Journal of Korean Society of Steel Construction, KSSC, Vol.17, No.6, pp.689-697 (in Korean).
• 신경재, 임보혁, 이수헌, 최성모(2011) 웨브를 볼트로 접합한 보-기둥 접합부의 유한요소해석, 한국강구조학회논문집, 한국강구조학회, 제23권, 제3호, pp.305-316.
  Shin, K.J., Lim, B.H., Lee, S.H., and Choi, S.M. (2011) FEA of Beam-Column Connection with Bolted Web, Journal of Korean Society of Steel Construction, KSSC, Vol.23, No.3, pp.305-316 (in Korean).
• 양승현(2012) 표준공과 과대공을 갖는 고장력볼트 접합부의 강도변화, 한국강구조학회논문집, 한국강구조학회, 제24권, 제5호, pp.605-612.
  Yang, S.H. (2012) Change of Strength of High-Strength Bolted Connection Depending of Standard and Over Bolt Hole, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.5, pp.605-612 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.5.605 ]
• 김태수, 김민성(2012) 페라이트계 스테인리스강(STS430) 이면전단 볼트접합부의 구조거동에 관한 실험적 연구, 한국강구조학회논문집, 한국강구조학회, 제25권, 제5호, pp.​463-474.
  Kim, T.S., and Kim, M.S. (2012) An Experimental Study on Structural Behaviors of Double Shear Bolted Connections Fabricated with Ferritic Stainless Steel (STS430), Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.5, pp.463-474 (in Korean). [ https://doi.org/10.7781/kjoss.2013.25.5.463 ]
• 김지훈, 김태수, 강현식(2013) 페라이트계 스테인리스강 2행 2열 일면전단 볼트접합부의 최대내력평가, 한국강구조학논문집, 한국강구조학회, 제25권, 제6호, pp.659-669.
  Kim, J.H., Kim, T.S., and Kang, H.S. (2013) Ultimate Strength Estimation of Ferritic Stainless Steel Single Shear Bolted Connections Fastened with Four Bolts, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.6, pp.659-669 (in Korean). [ https://doi.org/10.7781/kjoss.2013.25.6.659 ]
• Crawford, S.F., and Kulak, G.L. (1971) Eccentrically Loaded Bolted Connections, Journal of the Structural Division, American Society of Civil Engineers, Vol.97, No.3, pp.765-783.
• Sato, A., and Uang, C.-M. (2010) Seismic Performance Factors for Cold-Formed Steel Special Bolted Moment Frames, Journal of Structural Engineering, American Society of Civil Engineers, Vol.136, No.8, pp.961-967. [https://doi.org/10.1061/(ASCE)ST.1943-541X.0000191]
• Uang, C.-M., Sato, A., Hong, J.-K., and Wood, K. (2010) Cyclic Testing and Modeling of Cold-Formed Steel Special Bolted Moment Frame Connections, Journal of Structural Engineering, American Society of Civil Engineers, Vol.136, No.8, pp.953-960. [https://doi.org/10.1061/(ASCE)ST.1943-541X.0000190]
• Hong, J.-K., and Uang, C.-M. (2004) Cyclic Testing of a Type of Cold-Formed Steel Moment Connections for Pre-​Fabricated Mezzanines, Report No. TR-04/03, University of California, San Diego, USA.
• Wallaert, J.J., and Fisher, J.W. (1964) Shear Strength of High-Strength Bolts, Report No. 288.20, Fritz Engineering Laboratory (Lehigh University), USA.
• American Institute of Steel Construction (2010) Specification for Structural Steel Buildings (ANSI/AISC 360-​10), USA.
• 한국강구조학회(2009) 강구조기준에 따른 고력볼트 접합시공지침, 한국강구조학회.KSSC (2009) Fabrication Guide for Structural Joints Using High-Strength Bolts, KSSC, Korea (in Korean).