
HSB800 및 HSB600 강재를 적용한 하이브리드거더의 휨강도 평가
Copyright ⓒ 2014 by Korean Society of Steel Construction
초록
HSB800과 HSB600 강재를 플랜지와 웨브에 적용하고 균일휨모멘트를 받는 하이브리드거더의 휨강도 평가를 위한 연구를 수행하였다. 비조밀 및 조밀플랜지와 세장, 비조밀 및 조밀 웨브를 갖는 이축 및 일축대칭 단면들을 대상으로 하였으며, 3차원 쉘요소 모델에 초기처짐과 잔류응력의 영향을 고려하여 ‘단면 휨강도’ 및 ‘횡비틀림좌굴 강도’를 비선형해석으로부터 평가하였다. 수치해석 결과는 AASHTO LRFD 및 Eurocode 3 기준과 비교하였으며, 비조밀 및 조밀 웨브를 갖는 단면에 대해서는 AASHTO LRFD 부록 A6 기준의 적용성을 분석하였다.
Abstract
In this paper, flexural resistance of hybrid girder under uniform bending moment was evaluated, which is composed of HSB800 and HSB600 steel for the flange and web, respectively. Doubly-symmetric and monosymmetric sections with noncompact or compact flange and slender, noncompact or compact web were considered. Nonlinear analyses with 3-dim. shell element model were performed to determine the ‘flexural resistance of section’ and the ‘lateral torsional buckling strength’ by taking initial imperfection and residual stress into account. The numerical results were compared with the AASHTO LRFD and Eurocode 3 specifications and also the applicability of AASHTO LRFD appendix A6 was examined for the sections with noncompact and compact web.
키워드:
HBS800 및 HSB600 강재, 하이브리드거더, 휨강도, 이축 및 일축대칭단면, AASHTO LRFD, Eurocode 3Keywords:
HSB800 and HSB600 steel, Hybrid girder, Flexural resistance, Doubly- and monosymmetric section, AASHTO LRFD, Eurocode 31. 서 론
I-단면 플레이트거더에서 웨브가 단면2차모멘트에 기여하는 정도는 일반적으로 20% 내외 수준이다. 고강도강을 적용한 거더에서 플랜지에 비해 웨브에는 항복강도가 낮은 강재를 적용하는 하이브리드거더는 균질단면(homogeneous section)에 비해 휨강도의 저하 대비 경제성의 향상 정도가 더 커서 경제적인 휨부재로 인정되고 있다[1].
I-단면 플레이트거더의 휨강도는 압축플랜지의 좌굴(Flange Local Buckling, 이하 FLB) 강도와 횡비틀림좌굴(Lateral-Torsional Buckling, 이하 LTB) 강도로부터 결정되며, 이들 강도는 웨브의 세장비와도 관계가 있다. 하이브리드거더의 역학적인 장점으로는 웨브에 상대적으로 저강도 강재를 사용하면 웨브의 한계세장비가 커지므로 웨브의 좌굴강도 측면에서 유리하다[2]. 또한, 횡비틀림좌굴강도는 주로 단면의 기하학적 특성과 관계되므로 동일한 두께를 갖는 웨브에 상대적으로 저강도 강재를 사용하여도 균질단면에 비해 LTB 강도의 저하는 매우 적다[3].
하이브리드거더에 대한 기준으로 먼저, Eurocode 3[4]에서는 웨브의 항복강도가 플랜지 항복강도의 0.5배까지 작은 강재를 허용하고 있으며, 판(웨브 및 플랜지)의 세장비에 따라 class 1~4로 구분하고 세장비가 낮은 class 1 및 2 단면의 휨강도는 소성모멘트(
 )로 제한하는 탄성설계법을 적용하고 있다. 이러한 문제점을 보완하기 위해 항복강도가 485MPa를 초과하지 않는 경우 비조밀 및 조밀웨브 단면에 대해서는 웨브소성화계수(web plastification factor)를 적용함으로써 단면의 조밀도에 따라 휨강도를 최대 소성모멘트까지 허용하는 부록 A6 규정을 별도로 제시하고 있다. 하지만 항복강도가 이보다 큰 고강도 강재를 적용하는 경우, 최대 휨강도는 여전히 항복모멘트로 제한되므로 고강도 강재를 적용한 플레이트거더의 경제적 설계에 걸림돌이 되고 있다.
)로 제한하는 탄성설계법을 적용하고 있다. 이러한 문제점을 보완하기 위해 항복강도가 485MPa를 초과하지 않는 경우 비조밀 및 조밀웨브 단면에 대해서는 웨브소성화계수(web plastification factor)를 적용함으로써 단면의 조밀도에 따라 휨강도를 최대 소성모멘트까지 허용하는 부록 A6 규정을 별도로 제시하고 있다. 하지만 항복강도가 이보다 큰 고강도 강재를 적용하는 경우, 최대 휨강도는 여전히 항복모멘트로 제한되므로 고강도 강재를 적용한 플레이트거더의 경제적 설계에 걸림돌이 되고 있다.
최근 국내에서도 HSB800(항복강도 690MPa)과 HSB600 (항복강도 450MPa) 고강도 강재가 생산되어 교량구조물에 적용되기 시작하였다. 고강도 강재를 적용한 플레이트거더의 휨강도 평가에 대한 연구로서 Cho and Shin[6]은 세장웨브(slender web)를 갖는 이축대칭 HSB800 및 HSB600의 균질단면 거더와 HSB800(플랜지)-SM570TMC (웨브)의 하이브리드거더의 LTB 강도를 해석적으로 평가하고 해석치가 Eurocode 3 및 AASHTO LRFD 본문 기준의 휨강도를 만족함을 제시하였다. 한편, Park et al.[7],[8]은 이축 및 일축대칭 HSB800 균질단면 거더의 비탄성 LTB 강도 평가 연구를 수행하였으며, 압축플랜지 단면이 인장플랜지 단면에 비해 작은 경우를 제외하고는 비조밀 및 조밀웨브를 갖는 단면에 대해 AASHTO LRFD 부록 A6 규정을 적용할 수 있다고 제안한 바 있다.
본 연구에서는 HSB800과 HSB600 강재를 플랜지와 웨브에 적용한 하이브리드거더의 비지지길이에 따른 휨강도를 해석적으로 평가하였다. 두 강재의 항복강도 비는 0.65로서 전술한 Eurocode 3의 하이브리드거더 강재 조건은 만족하지만, AASHTO LRFD 조건에는 위배된다. 균일 휨모멘트를 받는 이축대칭 및 일축대칭단면을 고려하였으며, 비조밀 및 조밀 플랜지와 세장, 비조밀 및 조밀 웨브로 구성된 단면들을 고려하였다. 일축대칭 단면은 플랜지의 폭 및 두께 차이에 의해 압축플랜지 단면이 인장플랜지에 비해 작은 경우와 큰 경우를 각각 고려하였다. 해석 결과를 Eurocode 3 및 AASHTO LRFD 기준과 비교하였으며, 특히 비조밀 및 조밀웨브를 갖는 경우 HSB800-HSB600 하이브리드거더의 경제적 설계를 위해 AASHTO LRFD 부록 A6의 적용 가능성을 평가하였다.
2. 설계기준 현황
비지지길이(
 )가 짧아 LTB가 발생하지 않을 때의 휨강도를 ‘단면 휨강도’로 지칭하기로 하고 비지지길이가 큰 경우에는 LTB가 휨강도를 지배하므로 이 때의 강도를 ‘횡비틀림좌굴(LTB) 강도’로 구분하여 본 논문에서는 지칭하기로 한다.
)가 짧아 LTB가 발생하지 않을 때의 휨강도를 ‘단면 휨강도’로 지칭하기로 하고 비지지길이가 큰 경우에는 LTB가 휨강도를 지배하므로 이 때의 강도를 ‘횡비틀림좌굴(LTB) 강도’로 구분하여 본 논문에서는 지칭하기로 한다.
2.1 Eurocode 3 기준
2.1.1 단면 휨강도
EN 1993-1-1[4]에서는 플랜지와 웨브의 세장비에 따라 단면을 class 1~4로 구분하며, 이 때 class 1 및 2 단면의 휨강도는 소성모멘트(
 )로 고려하고 있으며, 웨브가 class 3이고 플랜지가 class 1 또는 2일 때는 effective class 2 단면으로 고려한다. 하이브리드거더의 ‘단면 휨강도’ 개념을 Fig. 1에 제시하였다.
)로 고려하고 있으며, 웨브가 class 3이고 플랜지가 class 1 또는 2일 때는 effective class 2 단면으로 고려한다. 하이브리드거더의 ‘단면 휨강도’ 개념을 Fig. 1에 제시하였다.
2.1.2 횡비틀림좌굴 강도
EN 1993-1-1[4]에서 균일 휨모멘트를 받는 플레이트거더의 LTB 강도(
 )는 다음과 같다.
)는 다음과 같다.
 (1)
(1)
여기서
 는 다음과 같다.
는 다음과 같다.
 (2)
(2)
여기서,
 은 탄성 LTB 강도[9]로서 다음과 같다.
은 탄성 LTB 강도[9]로서 다음과 같다.
 (3)
(3)
여기서,
 :일축대칭단면에 관한 변수이며[10] 이축대칭단면에서는 0이다.
:일축대칭단면에 관한 변수이며[10] 이축대칭단면에서는 0이다.
2.2 AASHTO LRFD 기준
압축플랜지와 인장플랜지의 항복에 대한 모멘트 중 작은 값을 ‘단면 휨강도’로 고려하며, 압축플랜지에 대한 휨강도는 FLB와 LTB 강도 중 작은 값으로 고려한다.
2.2.1 본문 6.10.8 기준
1) 단면 휨강도
응력으로 제시된 압축플랜지의 FLB 강도는 다음과 같다.
・
 (4a)
(4a)
・그 밖의 경우 :
 (4b)
(4b)
한편, 인장플랜지의 휨강도는 다음과 같다.
 (5)
(5)
여기서,
 .
.
2) 횡비틀림좌굴 강도
압축플랜지의 LTB 강도는 다음과 같다.
・
 (6a)
(6a)
・
 인 경우 :
인 경우 :
 (6b)
(6b)
여기서,
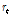 : 압축플랜지와 압축웨브 높이의 1/3단면의 연직축에 대한 단면회전반경.
: 압축플랜지와 압축웨브 높이의 1/3단면의 연직축에 대한 단면회전반경.
2.2.2 부록 A6 기준
다음 조건들을 만족하는 조밀 또는 비조밀 웨브를 갖는 단면은 부록 A6 규정을 적용할 수 있다.
 (7a)
(7a)
 (7b)
(7b)
 (7c)
(7c)
여기서,
 : 인장플랜지의 연직축에 대한 단면2차모멘트.
: 인장플랜지의 연직축에 대한 단면2차모멘트.
1) 단면 휨강도
모멘트로 제시된 압축플랜지의 FLB 강도는 다음과 같다.
・
 (8a)
(8a)
・그 밖의 경우 :
 (8b)
(8b)
한편, 인장플랜지의 휨강도는 다음과 같다.
 (9)
(9)
여기서,
 : 플랜지좌굴계수이다.
: 플랜지좌굴계수이다.
비조밀웨브의 한계세장비(
 )는 식 (7b)와 같고, 조밀웨브의 한계세장비는 다음과 같다.
)는 식 (7b)와 같고, 조밀웨브의 한계세장비는 다음과 같다.
 (10)
(10)
비조밀 및 조밀 웨브 단면의 압축 및 인장플랜지의 웨브소성화계수는 AASHTO LRFD 부록 A6에 제시되어 있다.
2) 횡비틀림좌굴 강도
비지지길이에 따른 LTB 강도는 다음과 같다.
・
 (11a)
(11a)
・
 인 경우 :
인 경우 :
 (11b)
(11b)
여기서,
 : 본문규정과 동일,
: 본문규정과 동일,
 (12)
(12)
여기서
 : 플랜지 중심간 거리이다.
: 플랜지 중심간 거리이다.
2.3 Eurocode 3와 AASHTO LRFD의 LTB 강도 기준 차이
Eurocode 3에서 LTB 강도를 결정하는 식 (3)은 단일패널에 대한 탄성 횡비틀림좌굴강도이다. 반면에, AASHTO LRFD의 LTB 강도는 본 연구에서 적용한 모델과 같이(뒤의 Fig. 2 참조) 중앙패널 구간 양측에 사이드패널을 갖는 보에 대해 4점재하 실험으로부터 결정된 것이다. 이 때, 사이드패널은 중앙패널 구간 압축플랜지의 횡방향 회전을 구속하는 효과가 있어 단일패널에 비해 큰 LTB 강도를 보이게 된다. 따라서, Eurocode 3는 AASHTO 기준에 비해 LTB 강도를 작게 평가하며, 이는 단일패널과 연속패널에 대한 휨강도 평가 연구로부터 입증된 바 있다[7],[8].
3. 해석 모델 및 해석 방법
3.1 해석 모델
I-단면 교량 거더는 일정 간격으로 수직브레이싱이나 가로보로 횡지지되므로 본 연구에서는 Fig.2와 같이
 간격으로 수직보강재를 편측에 부착하였다. 모델들의 지지조건은 Table 1과 같고 Dx, Dy, Dz는 각각 x,y,z축 이동변위이다.
간격으로 수직보강재를 편측에 부착하였다. 모델들의 지지조건은 Table 1과 같고 Dx, Dy, Dz는 각각 x,y,z축 이동변위이다.
3.2 초기처짐 및 잔류응력
초기처짐은 Yura[10]가 제시한 초기처짐 형상을 적용하였으며, Fig. 3에 보인 바와 같이 중앙패널부의 중앙점을 기준으로 웨브의 상단에서
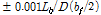 의 연직방향 처짐을 고려하였다.
의 연직방향 처짐을 고려하였다.
한편, 용접 제작에 따른 잔류응력의 분포는 Fig. 4(a)와 같이 고려하였다. HSB800 강재를 적용한 플랜지의 인장 및 압축잔류응력 크기는 Kang et al.[11]의 연구로부터 각각
 와
와
 로 고려하였으며, 폭 c2와 c3는 인장-압축 평형조건으로부터 결정된다. HSB600 강재를 적용한 웨브의 인장잔류응력 크기는
로 고려하였으며, 폭 c2와 c3는 인장-압축 평형조건으로부터 결정된다. HSB600 강재를 적용한 웨브의 인장잔류응력 크기는
 으로 고려하였고 압축잔류응력은 White et al.[12]이 웨브의 폭-두께비(D/tw)에 따라 제시한 값을 토대로 Fig. 4(b)의 크기로 고려하였으며, 폭 c4와 cfw는 인장-압축 평형조건으로부터 결정된다.
으로 고려하였고 압축잔류응력은 White et al.[12]이 웨브의 폭-두께비(D/tw)에 따라 제시한 값을 토대로 Fig. 4(b)의 크기로 고려하였으며, 폭 c4와 cfw는 인장-압축 평형조건으로부터 결정된다.
3.3 재료모델 및 비선형해석
HSB800 및 HSB600 강재의 재료모델은 Fig. 5에 보인 바와 같이 multi-linear 모델로 고려하였으며, 상세한 응력-변형률 관계는 Table 2에 제시하였다. 강재의 탄성계수는
 을, 항복기준은 Von Mises 기준을 적용하였으며 변형률 경화 구간에서는 isotropic strain hardening 모델을 사용하였다.
을, 항복기준은 Von Mises 기준을 적용하였으며 변형률 경화 구간에서는 isotropic strain hardening 모델을 사용하였다.
비선형해석은 ABAQUS/Standard[13]를 사용하였으며, 모든 부재는 S4R 쉘요소를 사용하여 모델링하였다. 본 연구에서 고려한 거더의 상세 제원은 4.1절에서 제시하겠지만 웨브 순높이는 2.000mm, 플랜지 폭은 400~600mm로 고려하였다. Fig. 4의 잔류응력분포를 적절히 고려하기 위해 플랜지는 폭에 따라 10~16열의 요소로 분할하였으며, 웨브는 51열의 요소로 분할하였다. Fig. 6는 구축된 유한요소모델에 의한 해석 예이다.
3.4 적용 모델의 검증해석
본해석에 앞서 본 연구에서 설정한 모델링 방법의 타당성을 검증하기 위해 기존 실험 연구 예에 대하여 해석을 수행하였다. 대상 거더는 Ito et al.[14]등의 실험 중 1개의 거더를 대상으로 하였으며 재료모델은 Coupon Test 결과를 그대로 적용하였다. 거더 제원은 플랜지 폭 121mm, 두께 11.2mm, 복부판 높이 377mm, 두께 6.2mm이며 플랜지에는 SM570Q 강재를, 웨브에는 SM400 강재를 적용하였다. 비지지길이는 950mm, 전체 거더의 길이는 3,800mm이며, Fig. 3의 초기처짐을 고려하고 Fig. 4의 잔류응력을 고려하여 해석한 결과를 Fig. 7에 제시하였다. 본 연구의 모델링 방법에 의한 해석결과는 실험결과에 비해 약 4% 작게 평가되었으며, 본 연구의 모델링 기법을 적용하는데 무리는 없을 것으로 판단된다.
4. 휨강도 평가 해석
4.1 해석 대상 거더 제원
이축 및 일축대칭 단면들에 대해 고려하였으며 일축대칭 단면은 압축플랜지 단면적이 인장플랜지 단면적에 비해 작은 경우(이하
 인 경우로 제한하였다. 모든 단면에서 웨브의 순높이는 2,000 mm로 하였으며, 이축대칭 단면과 일축대칭단면의 플랜지 두께를 변화시킨 경우는 상․하 플랜지 폭을 500mm로, 일축대칭 단면은 플랜지 폭을 변화시킨 경우 각각 400mm와 600mm로 고려하였다. 해석 대상 거더의 단면 제원은 Table 3과 같고 AASHTO LRFD 기준과 Eurocode 3에 따른 단면 특성치를 제시하였다.
인 경우로 제한하였다. 모든 단면에서 웨브의 순높이는 2,000 mm로 하였으며, 이축대칭 단면과 일축대칭단면의 플랜지 두께를 변화시킨 경우는 상․하 플랜지 폭을 500mm로, 일축대칭 단면은 플랜지 폭을 변화시킨 경우 각각 400mm와 600mm로 고려하였다. 해석 대상 거더의 단면 제원은 Table 3과 같고 AASHTO LRFD 기준과 Eurocode 3에 따른 단면 특성치를 제시하였다.
각 단면 경우에서 플랜지의 세장비는 비조밀 및 조밀 플랜지를, 웨브는 세장, 비조밀 및 조밀 웨브의 조합을 고려하였다. 참고로 HSB800 강재 적용 플랜지의 조밀 및 비조밀플랜지 한계세장비는 각각
 이고, 조밀 한계세장비는 식(10)으로부터 결정되며 단면에 따라 한계값이 변한다.
이고, 조밀 한계세장비는 식(10)으로부터 결정되며 단면에 따라 한계값이 변한다.
한편, 비지지길이는 ‘단면 휨강도’ 평가를 위해
 의 총 6개 경우를 고려하였다.
의 총 6개 경우를 고려하였다.
4.2 이축대칭단면 해석 결과
이축대칭단면 HSB800-HSB600 하이브리드거더의 비지지길이에 따른 LTB 강도는 Fig. 8에 제시하였으며, ‘단면 휨강도’가 지배적인 경우 각 기준의 단면 휨강도를 고려한 것이다.
Fig. 8(a)의 세장웨브를 갖는 NFSW 단면은 AASHTO LRFD 본문 기준의 휨강도를 만족하는 것으로 평가되었다. Fig. 8(b)와 (c)의 비조밀웨브를 갖는 NFNW 및 CFNW 단면은 모두 AASHTO LRFD의 부록 A6에 준하는 휨강도가 얻어졌다.
한편, Fig. 8(d)로부터 조밀웨브를 갖는 CFCW 단면 역시 AASHTO LRFD 부록 A6의 휨강도가 얻어졌다.
따라서, 플랜지 항복강도가 485MPa를 초과하고,
 인 이축대칭단면 하이브리드거더는 AASHTO LRFD 본문 기준을 만족하며, 비조밀 및 조밀웨브를 갖는 단면은 부록 A6의 적용이 가능한 것으로 평가되었다.
인 이축대칭단면 하이브리드거더는 AASHTO LRFD 본문 기준을 만족하며, 비조밀 및 조밀웨브를 갖는 단면은 부록 A6의 적용이 가능한 것으로 평가되었다.
한편, Fig. 8로부터 Eurocode 3 기준은 비지지길이가 짧은 경우 고강도강을 적용한 하이브리드거더의 ‘단면 휨강도’를 적절히 평가하는 것으로 나타났다. 하지만, LTB 강도는 비지지길이가 증가할수록 상당히 안전측으로 평가하는 것으로 나타났으며, 그 이유는 2.3절에서 기술한 바와 같다.
4.3 일축대칭단면 해석 결과-플랜지 폭 변화 경우
4.3.1 압축플랜지 폭이 작은 경우
 )인 경우 비지지길이에 따른 LTB 강도의 비교는 Fig. 9에 제시하였으며, 역시 ‘단면 휨강도’가 지배적인 경우 이를 고려한 것이다.
)인 경우 비지지길이에 따른 LTB 강도의 비교는 Fig. 9에 제시하였으며, 역시 ‘단면 휨강도’가 지배적인 경우 이를 고려한 것이다.
먼저, Fig. 9(a)로부터 세장웨브를 갖는 NFSW 단면은 AASHTO LRFD 본문 기준의 ‘단면 휨강도’는 대체로 만족하지만 비지지길이
 구간에서 LTB 강도가 기준에 미소하게 미치지 못하였다. Fig. 9(c)로부터 CFNW 단면은 본문 기준 강도는 만족하나 부록 A6 강도를 만족하는 것으로 판정하기에는 곤란하다. 마지막으로 Fig. 9(d)의 CFCW 단면은 부록 A6 규정의 휨강도에 도달하였는데 단, 이 단면은 매우 조밀한 압축플랜지를 갖는 단면이다.
구간에서 LTB 강도가 기준에 미소하게 미치지 못하였다. Fig. 9(c)로부터 CFNW 단면은 본문 기준 강도는 만족하나 부록 A6 강도를 만족하는 것으로 판정하기에는 곤란하다. 마지막으로 Fig. 9(d)의 CFCW 단면은 부록 A6 규정의 휨강도에 도달하였는데 단, 이 단면은 매우 조밀한 압축플랜지를 갖는 단면이다.
따라서,
 인 단면에서 이러한 경향은 HSB800 균질단면 플레이트거더에서도 유사한 결과를 보였다[8]. 따라서 본 조건의 단면에 대해서는 실험 등을 통한 보완 연구가 필요할 것으로 판단된다.
인 단면에서 이러한 경향은 HSB800 균질단면 플레이트거더에서도 유사한 결과를 보였다[8]. 따라서 본 조건의 단면에 대해서는 실험 등을 통한 보완 연구가 필요할 것으로 판단된다.
한편, Fig. 9로부터 Eurocode 3 기준은 본 경우에도 ‘단면 휨강도’를 비교적 적절히 평가하는 것으로 나타났다. 하지만, 비지지길이가 증가할수록 LTB 강도는 역시 상당히 안전측으로 평가하는 것으로 나타났다.
4.3.2 압축플랜지 폭이 큰 경우
 )인 경우 비지지길이에 따른 LTB 강도의 비교는 Fig. 10에 제시하였으며, ‘단면 휨강도’가 지배적인 경우 이를 고려한 것이다.
)인 경우 비지지길이에 따른 LTB 강도의 비교는 Fig. 10에 제시하였으며, ‘단면 휨강도’가 지배적인 경우 이를 고려한 것이다.
먼저, Fig. 10(a)로부터 세장웨브를 갖는 NFSW 단면은 AASHTO LRFD 본문 기준의 강도를 만족하였으며, 비지지길이가
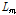 이하 구간에서는 AASHTO LRFD A6 규정을 적용하더라도 휨강도를 상당히 안전측으로 평가하였다. Fig. 10(c)의 CFNW 단면도 부록 A6 강도를 충분히 만족하며, 역시 비지지길이가 짧은 경우 휨강도를 안전측으로 평가하였다. 마지막으로 Fig. 10(d)의 CFCW 단면 역시 부록 A6 규정의 휨강도를 충분히 만족하였다.
이하 구간에서는 AASHTO LRFD A6 규정을 적용하더라도 휨강도를 상당히 안전측으로 평가하였다. Fig. 10(c)의 CFNW 단면도 부록 A6 강도를 충분히 만족하며, 역시 비지지길이가 짧은 경우 휨강도를 안전측으로 평가하였다. 마지막으로 Fig. 10(d)의 CFCW 단면 역시 부록 A6 규정의 휨강도를 충분히 만족하였다.
따라서,
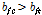 이며 비조밀 및 조밀 웨브를 갖는 일축대칭 하이브리드거더는 부록 A6의 적용하여도 충분히 여유가 있는 것으로 나타났다.
이며 비조밀 및 조밀 웨브를 갖는 일축대칭 하이브리드거더는 부록 A6의 적용하여도 충분히 여유가 있는 것으로 나타났다.
한편, Fig. 10로부터 Eurocode 3 기준은 본 경우 역시 비지지길이가 짧은 경우 ‘단면 휨강도’를 적절히 평가하였으며, 비지지길이가 증가할수록 LTB 강도를 상당히 안전측으로 평가하는 것으로 나타났다.
4.4 일축대칭단면 해석 결과-플랜지 두께 변화 경우
4.4.1 압축플랜지 두께가 얇은 경우
일축대칭단면의 경우 플랜지 두께 차이에 따른 휨강도와 플랜지 폭의 차이에 따른 휨강도의 양상이 다를 수 있어 본 절에서는 플랜지 두께가 다른 일축대칭단면의 휨강도를 평가하였다.
 )인 경우 비지지길이에 따른 휨강도 결과는 Fig. 11에 제시하였으며, 역시 ‘단면 휨강도’가 지배적인 경우 이를 고려한 것이다.
)인 경우 비지지길이에 따른 휨강도 결과는 Fig. 11에 제시하였으며, 역시 ‘단면 휨강도’가 지배적인 경우 이를 고려한 것이다.
먼저, Fig. 11(a)로부터 세장웨브를 갖는 NFSW 단면은 AASHTO LRFD 본문 기준의 ‘단면 휨강도’와 ‘LTB 강도’를 대체로 만족하였다. Fig. 11(b)의 NFNW 단면에서는 AASHTO LRFD의 본문 기준의 휨강도를 만족하며, 부록 A6 기준강도도 대체로 만족하였다. Fig. 11(c)로부터 CFNW 단면 역시 부록 A6 강도를 대체로 만족하였다. 마지막으로 Fig. 11(d)의 CFCW 단면 역시 부록 A6의 휨강도를 만족하였다.
따라서, 플랜지 두께 차이에 따른
 단면에서는 플랜지 폭을 변화시킨 경우와 달리 세장웨브 단면은 본문 기준의 강도가, 비조밀 및 조밀웨브 단면은 부록 A6의 휨강도가 대체로 얻어졌다.
단면에서는 플랜지 폭을 변화시킨 경우와 달리 세장웨브 단면은 본문 기준의 강도가, 비조밀 및 조밀웨브 단면은 부록 A6의 휨강도가 대체로 얻어졌다.
한편, Fig. 11로부터 Eurocode 3 기준은 본 경우에도 역시 비지지길이가 짧은 경우 ‘단면 휨강도’를 적절히 평가하였으며, 비지지길이가 증가할수록 LTB 강도는 안전측으로 평가하였다.
4.4.2 압축플랜지 두께가 두꺼운 경우
 이하 구간에서는 휨강도를 비교적 안전측으로 평가하였다. 한편, Fig. 12(b)의 NFNW 단면은 부록 A6 기준을 대체로 만족하였다. Fig. 12(c)의 CFNW 단면도 부록 A6 강도를 적절히 만족하며, 마지막으로 Fig. 12(d)의 CFCW 단면 역시 부록 A6 규정의 휨강도를 적절히 만족하였다.
이하 구간에서는 휨강도를 비교적 안전측으로 평가하였다. 한편, Fig. 12(b)의 NFNW 단면은 부록 A6 기준을 대체로 만족하였다. Fig. 12(c)의 CFNW 단면도 부록 A6 강도를 적절히 만족하며, 마지막으로 Fig. 12(d)의 CFCW 단면 역시 부록 A6 규정의 휨강도를 적절히 만족하였다.
따라서,
 인 경우는 기준강도를 상회하는 정도가 거의 없거나 크게 줄어 들었다.
인 경우는 기준강도를 상회하는 정도가 거의 없거나 크게 줄어 들었다.
한편, Fig. 12로부터 Eurocode 3 기준은
 인 경우 역시 비지지길이가 짧은 경우 ‘단면 휨강도’를 적절히 평가하였으며, 비지지길이가 증가할수록 LTB 강도는 안전측으로 평가하였다.
인 경우 역시 비지지길이가 짧은 경우 ‘단면 휨강도’를 적절히 평가하였으며, 비지지길이가 증가할수록 LTB 강도는 안전측으로 평가하였다.
5. 휨강도 분석
단면 종류별 해석 결과를 종합하여 AASHTO LRFD 본문기준과 부록 A6 기준을 적용한 값을 Fig. 13과 Fig. 14에 각각 나타내었다. 또한, 앞 장에서 이축대칭 단면과 일축대칭 단면 중
 )의 최소값을 나타내었다.
)의 최소값을 나타내었다.
먼저 Fig. 13으로부터 이축대칭 단면은 모두 기준강도를 적절히 만족하였으나
 인 경우는 플랜지 폭을 변화시킨 경우는 비교적 여유가 많고, 두께를 변화시킨 경우는 대체로 기준강도에 부합하는 수준의 휨강도를 보였다.
인 경우는 플랜지 폭을 변화시킨 경우는 비교적 여유가 많고, 두께를 변화시킨 경우는 대체로 기준강도에 부합하는 수준의 휨강도를 보였다.
한편, 비조밀 및 조밀웨브를 갖는 단면에 대해서는 Fig. 14에 제시한 바와 같이 부록 A6 기준과 해석결과를 비교했을 때 이축대칭 단면의 경우 전체적으로 기준에 비교적 잘 부합하였다.
 인 경우는 모두 부록 A6 기준강도를 만족하였다.
인 경우는 모두 부록 A6 기준강도를 만족하였다.
6. 결 론
본 연구에서는 HSB800과 HSB600 고강도 강재를 각각 플랜지와 웨브에 적용한 하이브리드거더의 휨강도 평가를 위한 해석 연구를 수행하였으며, 주요 결론은 다음과 같다.
(1)HSB600과 HSB800 강재의 항복강도 비는 0.65로서 AASHTO LRFD 기준에서 웨브 강재의 항복강도가 플랜지 항복강도의 0.7 이상이어야 하는 규정을 만족하지 않지만, 이축대칭단면의 ‘단면 휨강도’ 및 ‘LTB 강도’는 모두 본문 6.10.8의 기준 강도를 만족하였으며, 비조밀 및 조밀웨브를 갖는 단면은 부록 A6의 강도를 만족하였다.
(2)
 인 일축대칭단면은 ‘단면 휨강도’는 만족하였으나, ‘LTB 강도’는 기준강도에 최대 7% 정도 못미치는 경우가 있었다. 이러한 결과는 HSB800 강재를 적용한 균질단면 거더에서도 동일한 결과를 보인 것으로 보아 웨브와 플랜지의 항복강도 비보다는 단면 특성으로 인한 것으로 판단된다.
인 일축대칭단면은 ‘단면 휨강도’는 만족하였으나, ‘LTB 강도’는 기준강도에 최대 7% 정도 못미치는 경우가 있었다. 이러한 결과는 HSB800 강재를 적용한 균질단면 거더에서도 동일한 결과를 보인 것으로 보아 웨브와 플랜지의 항복강도 비보다는 단면 특성으로 인한 것으로 판단된다.
(3)
 인 단면은 설계기준강도 대비 비교적 큰 여유를 보였다.
인 단면은 설계기준강도 대비 비교적 큰 여유를 보였다.
(4)이상으로부터
 인 단면에 대해서는 실험 등을 통한 보완 연구가 필요하다.
인 단면에 대해서는 실험 등을 통한 보완 연구가 필요하다.
(5)Eurocode 3는 이축 및 모든 일축대칭단면에서 ‘단면 휨강도’를 적절히 평가하는 것으로 나타났다. 하지만, ‘LTB 강도’는 인접패널에 의한 플랜지 회전 구속효과가 없는 단일패널의 횡비틀림좌굴강도로 고려하기 때문에 연속패널 개념을 적용한 AASHTO LRFD 기준에 비해 상당히 안전측으로 평가되었다.
Acknowledgments
본 연구는 국토해양부가 출연하고 한국건설교통기술평가원에서 위탁 시행한 R&D정책인프라사업(과제번호11 기술표준화01-01)의 지원에 의해 수행되었습니다.
References
-
Veljkovic, M., and Johansson, B. (2004) Design of Hybrid Steel Girders, Journal of Constructional Steel Research, Elsevier, Vol.60, pp.535-547.
[https://doi.org/10.1016/S0143-974X(03)00128-7]

-
김재구(2010) 고성능강재 적용 플레이트거더의 극한 휨, 전단저항력, 박사학위논문, 고려대학교.
Kim, J.G. (2011) Ultimate Flexural and Shear Strength of High Strength Steel Plate Girders, Ph.D. Dissertation, Korea University, Korea (in Korean). - Nethercot, D.A. (1976) Buckling of Welded Hybrid Steel I-Beams, Journal of the Structural Division, American Society of Civil Engineers, Vol.102, No.3, pp.461-474.
- European Committee for Standardization (2005) Eurocode 3: Design of Steel Structures, Part 1.1: General Rules and Rules for Buildings (EN 1993-1-1: 2005), Belgium.
- American Association of State Highway and Transportation Officials (2012) AASHTO LRFD Bridge Design Specifications (6th Ed.), USA.
-
조영은, 신동구(2011) HSB 강거더의 비탄성 횡비틂좌굴에 의한 휨강도-세장 복부판 단면, 한국강구조학회논문집, 한국강구조학회, 제24권, 제2호, pp.217-231.
Cho, E.Y., and Shin, D.K. (2011) Flexural Strength of HSB Steel Girders Due to Inelastic Lateral-Torsional Buckling - Sections with Slender Web, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.2, pp.217-231 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.2.217 ]
-
박용명, 이건준, 최병호, 황민오(2013) 이축대칭단면 HSB800 강재 플레이트거더의 비탄성 횡비틂좌굴강도의 해석적 평가, 한국강구조학회논문집, 한국강구조학회, 제25권, 제2호, pp.141-151.
Park, Y.M., Lee, K.J., Choi, B.H., and Hwang, M.O. (2013) Numerical Analysis of Inelastic Lateral Torsional Buckling Strength of HSB800 Steel Plate Girder with Doubly Symmetric Section, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.2, pp.141-151. [ https://doi.org/10.7781/kjoss.2013.25.2.141 ]
-
박용명, 이건준, 최병호, 황민오(2013) 일축대칭단면 HSB800 강재 플레이트거더의 비탄성 횡비틂좌굴강도의 해석적 평가, 한국강구조학회논문집, 한국강구조학회, 제25권, 제2호, pp.153-164.
Park, Y.M., Lee, K.J., Choi, B.H., and Hwang, M.O. (2013) Numerical Analysis of Inelastic Lateral Torsional Buckling Strength of HSB800 Steel Plate Girder with Monosymmetric Section, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.2, pp.153-164 (in Korean). [ https://doi.org/10.7781/kjoss.2013.25.2.153 ]
- Anderson, J.M., and Trahair, N.S. (1972) Stability of Monosymmetric Beams and Cantilevers, Journal of the Structural Division, American Society of Civil Engineers, Vol.98, No.1, pp.269-286.
- Yura, J.A. (2001) Fundamentals of Beam Bracing, Engineering Journal, Vol.38, No.1, pp.11-26.
- Kang, S.-C., Kim, K.-S., and Lee, J.-K. (2011) Experimental Investigation of Residual Stresses in HSB800 Structures by the Sectioning Method, Engineering Journal, International Association for Bridge and Structural Engineering/International Association of Student Surgical Societies, UK, p.552
- White, D.W., Zureick, A.H., Phoawanich, N., and Jung, S.-K. (2001) Development of Unified Equations for Design of Curved and Straight Steel Bridge I-Girders, Final Report Prepared for AISI Transportation and Infrastructure Committee, Professional Service Industries, Inc. and Federal Highway Administration, Georgia Institute of Technology, USA.
- Dassault Systèmes Simulia Corp. (2004) Abaqus Analysis User’s Manual, Ver. 6.5, DSS, USA.
-
Ito, M., Nozaka, K., Shirosaki, T., and Yamasaki, K. (2005) Experimental Study on Moment-Plastic Rotation Capacity of Hybrid Beams, Journal of Bridge Engineering, American Society of Civil Engineers, Vol.10, No.4, pp.490-496.
[https://doi.org/10.1061/(ASCE)1084-0702(2005)10:4(490)]










 )
) )
) )
)



 2)
2)

 )
)

 )
)
 )
)
 )
)
 )
)
 )
)
 )
)
 )
) )
)
 )
)
 )
)
 )
)
 )
) )
)
 )
)
 )
)
 )
)
 )
) )
)
 )
)
 )
)
 )
)
 )
) )
)
 )
)
 )
)
 )
)
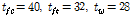 )
) )
)

 )
)




