일련의 주행 차량에 의한 현수교의 충격계수 평가
Copyright ⓒ 2014 by Korean Society of Steel Construction
초록
본 연구에서는 중앙경간 404m 및 1545m의 현수교에 일련의 차량이 차로하중 형태로 주행하는 상태에 대해 차량-교량 상호작용해석을 수행하고 주케이블, 행어 및 보강거더의 충격계수를 평가하였다. 활하중 모델은 도로교한계상태설계기준을 참고하였으며, KL-510 트럭은 6-자유도 모델로, 차로하중은 일련의 1축 차량이 연행해서 주행하는 것으로 모사하였다. 주탑부에서 보강거더의 연결 및 지지 형식에 따른 충격계수의 차이를 평가하기 위해 중앙경간 404m 교량에 대해서는 hinge-type과 floating-type 거더 형식을 고려하였다. 해석에서 고려한 매개변수는 활하중 형식-트럭 단독 주행시와 트럭과 차로하중의 주행, 차량의 편심 주행, 노면조도 그리고 주행속도를 고려하였다. 노면조도는 ISO 8608 규정에 근거하여 랜덤 생성하였으며 차량-교량 상호작용해석 시 노면조도는 트럭하중에만 적용하였다. 한편, 케이블교량의 충격계수 평가를 위해 일반적으로 사용되는 영향선 기법에 의해 충격계수를 산출하고 차량-교량 상호작용해석에 의한 결과와 비교하였다.
Abstract
In this paper, vehicle-bridge interaction analysis under a series of moving vehicles to simulate a lane load was performed to estimate impact factor of the main cable, hanger and girder for the selected suspension bridges with 404m and 1545m main span. Korea Bridge Design Code(Limit State Design) was selected for the live model in which KL-510 truck was modeled 6-d.o.f. vehicle and a lane load was simulated by a series of single-axle vehicles. For the 404m main span bridge, hinge-type and floating-type girders at the tower were considered to examine the impact factor according to the connection and supporting type of the girders. The parameters considered herein are the types of live load-a truck only and a truck plus lane load, eccentricity of moving vehicles, road surface roughness and vehicle speed. The road surface roughness was randomly generated based on ISO 8608 and it was applied to the truck only. The impact factors were also evaluated by using the influence line method that is commonly used in cable-supported bridges and compared with those from vehicle-bridge interaction analysis.
키워드:
현수교, 충격계수, 일련 이동차량, 차량-교량 상호작용 해석, 노면조도, 영향선 기법Keywords:
Suspension bridge, Impact factor, Series of moving vehicles, Vehicle-bridge interaction analysis, Road surface roughness, Influence line method1. 서 론
현수교는 케이블의 유연한 거동 특성으로 인하여 기타 형식의 교량에 비해 활하중에 의한 처짐이 크게 발생하고 진동이 발생하기 쉬운 교량 형식이다. 참고문헌[1]에 따르면 도로교용 현수교에서 주케이블과 주탑은 고정하중에 의한 응력이 지배적이고 최대응력을 유발하는 활하중의 재하길이가 길기 때문에 충격의 영향이 작고, 또한 보강거더는 일반 거더교에 비해 장주기이므로 활하중에 의한 충격은 일반적으로 고려하지 않는다고 기술하고 있다. 이와 같은 맥락으로 도로교설계기준[2]에서는 주케이블과 보강거더에 대해서는 충격계수를 고려하지 않고, 행어에 대해서는 가로보를 지간으로 하여 일반 거더교의 충격계수 산정식으로 평가하는 것으로 규정하고 있으며, 케이블강교량 설계지침[3]에서는 행어에 대해서도 충격효과를 무시하여도 된다고 제시하고 있다.
차량하중에 의한 현수교의 동적 거동을 연구한 국내외 사례를 살펴보면 대부분 트럭하중만이 주행하는 경우를 고려하였다. 먼저, Karoumi[4]는 중앙경간 1624m의 타정식 현수교를 대상으로 2대의 1축 트럭이 연행하는 조건에 대해 차량-교량 상호작용 해석을 수행하고 교량의 충격계수를 평가하였다. 교량의 감쇠비, 노면조도, 차량 속도 등의 매개변수를 고려하여 동적 해석을 수행한 결과, 케이블교량의 충격계수는 노면이 규칙적으로 유지 관리되는 조건에서도 30%를 넘어설 수 있다고 제시하였다. Hayashikawa and Watanabe[5]는 중앙경간 315m, 770m 및 1100m의 현수교 모델을 대상으로 이동하는 하나의 집중하중을 고려하여 교량의 충격계수를 평가한 결과, 충격계수는 이동하중의 속도가 증가할수록 커지며, 특히 지간이 긴 교량에 비해 짧은 교량의 충격계수가 크다고 제시하였다.
한편, 국내에서는 Chang et al.[6]이 중앙경간 300m의 자정식 현수교를 대상으로 차량-교량 상호작용해석을 수행하고 주케이블과 행어 및 보강거더의 충격계수를 평가하였는데, 해석시 고려한 차량하중은 6-d.o.f.를 갖는 트랙터-트레일러 형식의 트럭 1대이며, 매개변수로는 차량속도와 차량중량을 고려하였고 노면조도는 실제 노면의 스펙트럼으로부터 생성된 노면형상을 고려하였다. 그 결과, 현수교의 충격계수는 주행 차량의 속도 변수에 따라 크게 증폭될 수 있으며, 특히 행어 부재에서 그 영향이 두드러진다는 결론을 도출하였다. Suh and Kim[7]은 중앙경간 404m의 타정식 현수교와 중앙경간 300m의 자정식 현수교를 대상으로 주케이블의 정착 형식이 충격계수에 미치는 영향을 평가하였다. 동적 해석시 6-d.o.f.를 갖는 트럭 1대를 고려하였으며, 매개변수로는 노면조도, 차량속도 및 차량중량을 고려하였다. 그 결과, 교량의 정착 형식에 상관없이 노면조도가 나빠질수록 충격계수는 증가하였다고 제시하였다.
이와 같이 대부분의 기존 연구에서는 주로 1대 또는 2대의 차량하중만을 고려하여 현수교의 충격계수를 평가하였는데, 장대 현수교에서 최대 응력을 유발하는 활하중 조건은 주로 차로하중이므로 이를 감안한 현수교의 충격계수 평가가 필요하다. 이에 본 연구에서는 중앙경간 404m 및 1545m의 타정식 현수교를 대상으로 일련의 차량이 주행하는 차로하중 형태에 대해 차량-교량 상호작용 해석을 수행하고 주케이블과 행어 및 보강거더의 충격계수를 평가하였다.
이를 위해 본 연구에서는 도로교한계상태설계기준[8]의 활하중 모델을 고려하였다. 본 기준에서는 1) KL-510 트럭하중(100%), 2) KL-510 트럭하중의 75%와 차로하중을 동시에 재하하는 두가지 재하 조건을 규정하고 있으며, 충격계수는 차로하중에 대해서는 적용하지 않고 트럭하중에만 적용하도록 규정하고 있다. 본 연구에서는 차량-교량 상호작용해석을 위해 KL-510 트럭은 6-d.o.f. 차량 모델로 고려하였으며, 차로하중은 일련의 1축 차량이 연행해서 주행하는 것으로 모사하였다.
한편, 주탑부에서 보강거더의 연결 및 지지 형식에 따른 충격계수의 비교를 위해 중앙경간 404m 교량에서는 hinge-type과 floating-type 거더를 각각 고려하였다. 매개변수해석에서 주행 편심이 충격계수에 미치는 영향을 평가하였으며, 노면조도와 차량 속도를 고려하였다. 노면조도는 ISO 8608 기준[9]에 따라 랜덤 생성하였으며, 한계상태설계기준에 따라 노면조도는 트럭하중에만 적용하였다. 한편, 실무에서 케이블교량의 충격계수 산정에 사용되고 있는 영향선 기법으로 충격계수를 산정하고 차량-교량 상호작용해석에 의한 결과와 비교하였다.
2. 차량-교량 상호작용해석 방법
2.1 노면조도
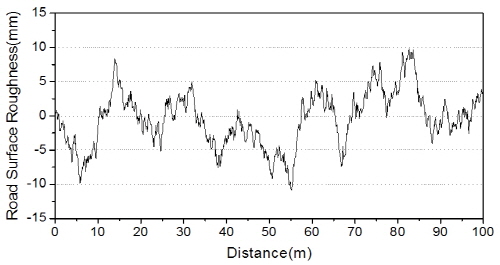
차량 주행 시 노면조도는 교량의 동적 거동을 증폭시키는 주요 인자로서[4],[10], 평균값이 영인 정상확률과정으로 가정한 파워스펙트럼밀도 함수로 구현하는 방법이 일반적으로 사용되고 있다[11]. 본 연구에서는 Table 1에 제시된 ISO 8608[9]의 등급에 따라 노면조도를 랜덤 생성하였으며, Fig. 1에 노면조도 class B의 예를 제시하였다.
2.2 차량모델
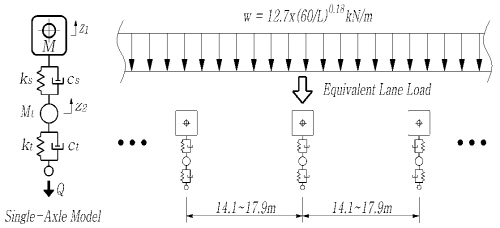
본 연구에서는 한계상태설계기준[8]의 활하중 모델을 고려하였는데, 트럭하중 단독 주행의 경우는 Fig. 2(a)에 제시된 KL-510 1대를, 트럭하중과 차로하중의 조합에 대해서는 KL-510의 75% 하중과 Fig. 2(b)에 보인 바와 같이 1축 차량이 일정한 간격으로 주행하는 등가차로하중(
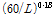 kN/m)의 조합으로 고려하였다. 참고로 차로하중을 일련의 1축 차량으로 모사하는 방법은 참고문헌[12]에서 제시된 기법으로 본 연구에서도 이와 같이 고려하였다.
kN/m)의 조합으로 고려하였다. 참고로 차로하중을 일련의 1축 차량으로 모사하는 방법은 참고문헌[12]에서 제시된 기법으로 본 연구에서도 이와 같이 고려하였다.
KL-510 트럭모델의 상세한 물성치는 참고문헌[13]과 같고, 차체(car body)의 운동은 연직운동(bouncing)과 전후방향 회전운동(pitching)을 고려하고, 차축(axle)은 연직운동만을 하는 것으로 고려하여 6-d.o.f. 차량모델로 구성하였다. 한편, 등가차로하중의 모사를 위한 1축 트럭하중의 물성치도 참고문헌[13]에 제시되어 있다. 참고로 이들 차량의 물성치는 참고문헌[14],[15]의 분석으로부터 1차모드 고유진동수가 2.2Hz 수준이 되도록 현가장치를 결정하였다.
2.3 교량모델
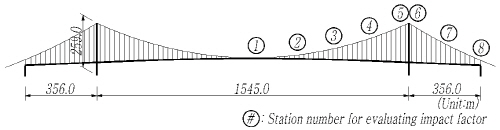
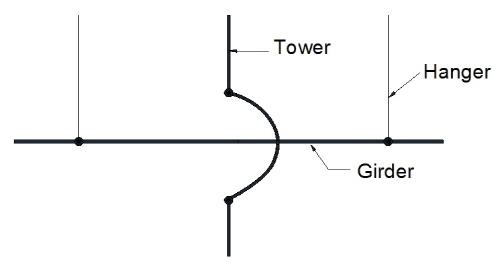
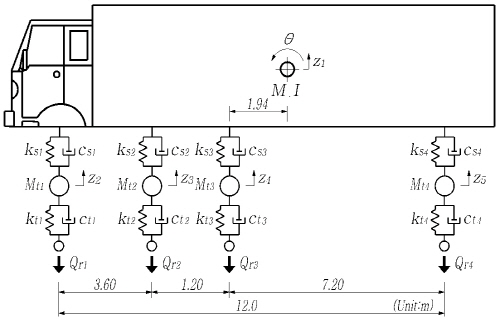
본 연구에서 고려한 해석 대상 교량은 중앙경간 404m 및 1545m의 강박스형 보강거더를 가지는 타정식 현수교이다. 보강거더가 주탑부에서 연결 및 지지되는 형식에 따라 교량의 충격계수에 미치는 영향을 비교하기 위하여 중앙경간 404m의 현수교는 hinge-type과 floating-type을 각각 고려하였으며, 중앙경간 1545m의 현수교는 floating-type 만을 고려하였다. Fig. 3에 교량의 개략적 제원과 구성 부재별 충격계수의 평가위치를 나타내었고, Fig. 4에 hinge-type 및 floating-type 거더의 개념도를 나타내었으며, Table 2에 각 교량별 구성 부재의 주요 물성치를 제시하였다.
차량-교량 상호작용 해석을 위하여 각 교량은 3차원 모델로 고려하였다. 주케이블과 행어는 각각 탄성현수선요소 및 등가트러스요소를 사용하였으며, 초기평형상태해석으로부터 주케이블과 행어의 초기장력값을 산출하여 해석시 기하강성으로 변환하였다. 또한, 보강거더와 주탑은 보요소, 교량 받침은 링크요소, 보강거더와 행어의 연결은 fish-bone 모델로 고려하였다.
한편, 교량의 감쇠행렬은 식 (1)의 Rayleigh damping[16]을 사용하였다.
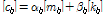 (1)
(1)
여기서,
 는 질량 및 강성비례 Rayleigh 감쇠계수로서 다음과 같다.
는 질량 및 강성비례 Rayleigh 감쇠계수로서 다음과 같다.
 (2)
(2)
 (3)
(3)
여기서,
 는 1차 및 2차모드의 댐핑비로서 본 연구에서는 현수교의 댐핑비에 대한 식 (4)[4]로부터 결정하였다.
는 1차 및 2차모드의 댐핑비로서 본 연구에서는 현수교의 댐핑비에 대한 식 (4)[4]로부터 결정하였다.
 (4)
(4)
한편, 본 연구에서 고려한 교량의 연직방향 1차 및 2차 모드의 고유주기를 Table 3에 나타내었으며, 중앙경간 1545m 교량의 연직방향 모드형상 예를 Fig. 5에 제시하였다.
2.4 차량-교량 상호작용 해석 방법
차량-교량 상호작용 해석을 위해 본 연구에서는 교량과 차량의 운동방정식을 별개로 구성하는 방법을 적용하였으며, 교량의 운동방정식은 다음과 같다.
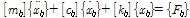 (5)
(5)
여기서,
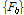 는 차량 바퀴의 동적 접촉력에 의한 동적하중벡터이다.
는 차량 바퀴의 동적 접촉력에 의한 동적하중벡터이다.
한편, 차량의 운동방정식은 Lagrange 운동방정식으로부터 식 (6)의 차량 운동방정식을 유도하였다.
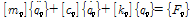 (6)
(6)
여기서,
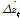 는 시간증분 동안의 노면조도와 교량의 동적거동에 의한 변위 및 속도벡터이다.
는 시간증분 동안의 노면조도와 교량의 동적거동에 의한 변위 및 속도벡터이다.
차량과 교량의 운동방정식 해는 Newmark
 -method[16]를 적용하였으며, 각 시간증분 단계에서 타이어와 노면의 변위적합조건을 만족할 때까지 반복해석하는 방법을 적용하였다. 자세한 차량-교량 상호작용해석 알고리듬은 Yang 등[17]과 같다.
-method[16]를 적용하였으며, 각 시간증분 단계에서 타이어와 노면의 변위적합조건을 만족할 때까지 반복해석하는 방법을 적용하였다. 자세한 차량-교량 상호작용해석 알고리듬은 Yang 등[17]과 같다.
3. 충격계수의 정의 및 평가 방법
3.1 차량-교량 상호작용해석에 의한 충격계수
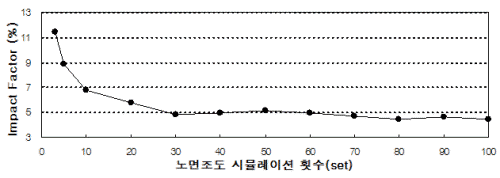
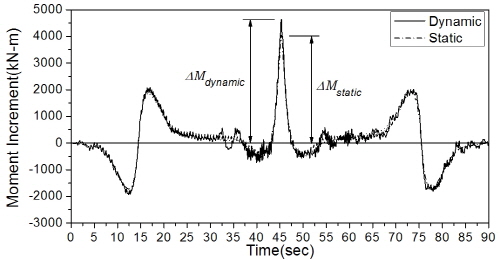
Fig. 6(a)에 보인 예와 같이 차량-교량 상호작용 해석으로부터 케이블 장력의 변동치(
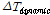 )에 대한 시간이력곡선이 얻어지며, 주케이블 및 행어의 충격계수는 정적 대비 동적 해석시의 최대 장력 증가치를 기준으로 다음 식과 같이 정의하였다.
)에 대한 시간이력곡선이 얻어지며, 주케이블 및 행어의 충격계수는 정적 대비 동적 해석시의 최대 장력 증가치를 기준으로 다음 식과 같이 정의하였다.
 (7)
(7)
여기서,
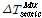 는 정적 재하시 케이블 또는 행어 장력의 최대 증분이다.
는 정적 재하시 케이블 또는 행어 장력의 최대 증분이다.
한편, Fig. 6(b)는 보강거더의 모멘트 변동치에 대한 시간이력곡선의 일례를 나타낸 것이며, 거더의 충격계수는 정적 대비 동적 해석시의 정모멘트 또는 부모멘트 변동치의 최대값을 기준으로 다음 식과 같이 정의하였다.
 (8)
(8)
여기서,
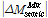 는 각각 동적 및 정적 활하중에 의한 거더 정모멘트 또는 부모멘트 변동치의 최대값이다.
는 각각 동적 및 정적 활하중에 의한 거더 정모멘트 또는 부모멘트 변동치의 최대값이다.
3.2 영향선을 이용한 충격계수 산정법
케이블교량의 합리적인 충격계수 평가는 차량-교량 상호작용해석에 의하여야 하나, 상용 툴의 부재로 인해 현재 설계 실무에서는 영향선을 이용하여 충격계수를 평가하고 있다. 본 기법으로 주케이블과 행어, 보강거더의 충격계수를 산출하는 일례로, 중앙경간 중앙부에서의 주케이블과 행어의 충격계수 산출시 Fig. 7(a) 및 (b)에 보인 바와 같이 그 지점의 주케이블 및 행어의 장력에 대한 영향선을 작성하고 각 부재에 최대 인장 증분이 발생하는 활하중 재하길이(
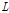 )를 산정하여 식 (9)에 대입하여 보강거더의 충격계수를 산출하는 방식이다.
)를 산정하여 식 (9)에 대입하여 보강거더의 충격계수를 산출하는 방식이다.
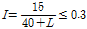 (9)
(9)
여기서,
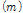 이다.
이다.
4. 매개변수 해석
본 연구에서는 hinge-type과 floating-type 거더를 갖는 현수교에 대해 차량-교량 상호작용 해석에서 활하중 형식, 주행차선의 편심, 노면조도, 그리고 차량속도의 매개변수를 고려하였다. 노면조도는 ISO 8608에 따라 노면조도 class A, B, C에 대해 각각 5 set를 랜덤 생성하였으며, 이후 제시한 모든 결과는 각 노면조도에 대한 해석 결과의 평균값이다.
한편, 트럭 및 차로하중의 조합하중은 Fig. 8에 보인 바와 같이 트럭하중이 교량을 주행하는 동안에는 차로하중이 교량의 전 구간에 걸쳐 재하되어 주행하는 조건으로 고려하였으며, 차로하중에는 노면조도를 고려하지 않았다.
4.1 활하중 형식의 영향
전술한 바와 같이 도로교한계상태설계기준[8]에서는 교량의 활하중을 KL-510 트럭 한 대 또는 KL-510 트럭의 75%와 차로하중의 조합에 의한 영향 중 큰 값을 사용하도록 제시하고 있다. 현수교와 같은 장대교량에서는 후자의 경우가 최대응력을 유발하지만, 활하중 형식이 교량의 충격계수에 미치는 영향을 평가하기 위해 KL-510 1대 주행, KL-510 2대 연행, 그리고 KL-510 트럭의 75%와 차로하중이 동시에 주행하는 3가지 경우에 대한 해석을 수행하였다. 해석 시 고려한 노면조도는 class B 조건이며, 차량은 80km/h의 속도로 거더 중심축을 따라 주행하는 것으로 하였다. KL-510 2대 연행 시 차량 간격은 참고문헌[18]에 제시된 공진차두간격(
 : 주행속도)으로 고려하였다. 즉, 차량간격은 Table 3에 제시한 각 교량의 1차 고유주기에 차량속도 22.22m/sec를 곱한 거리로 고려하였으며, 이로부터 중앙경간 404m 교량은 각각 89m(hinge-type)와 92m (floating-type), 1545m 교량은 193m이 된다.
: 주행속도)으로 고려하였다. 즉, 차량간격은 Table 3에 제시한 각 교량의 1차 고유주기에 차량속도 22.22m/sec를 곱한 거리로 고려하였으며, 이로부터 중앙경간 404m 교량은 각각 89m(hinge-type)와 92m (floating-type), 1545m 교량은 193m이 된다.
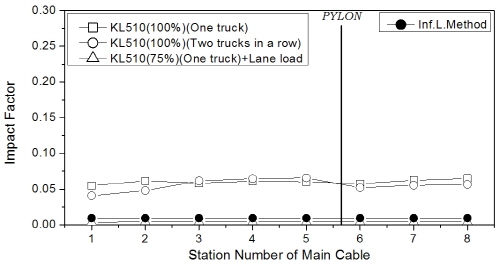
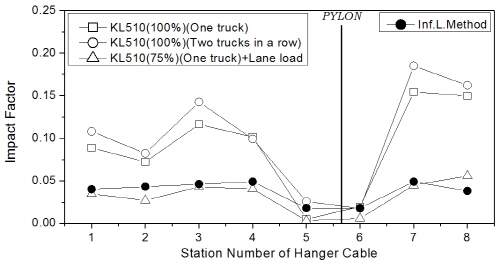
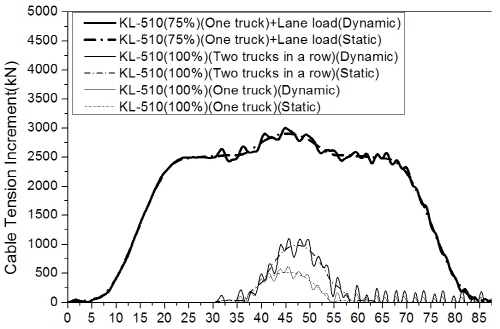
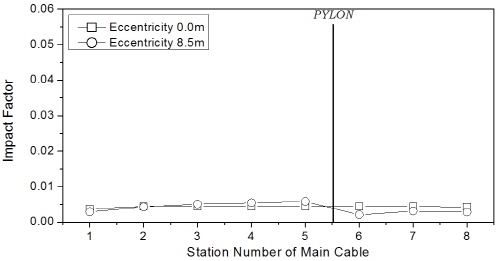
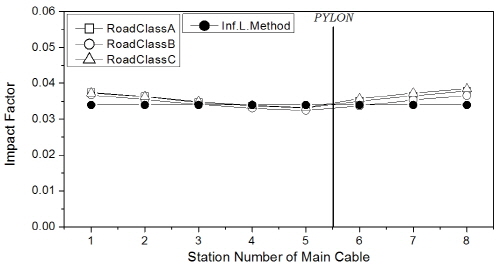
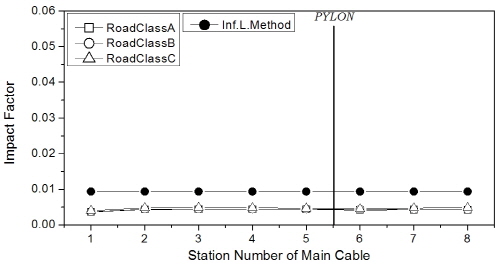
먼저, 주케이블의 충격계수 결과를 Fig. 9에 나타내었는데, 트럭과 차로하중의 조합하중이 주행하는 경우에 비해 트럭 1대 또는 2대 연행 경우의 충격계수가 훨씬 크게 평가되었으며, 특히 조합하중에 의한 결과는 영향선 기법 결과와 유사하였다. 이 때 주케이블의 충격계수는 지간 404m에서 보강거더의 지지 방식(hinge 또는 floating type)에 관계없이 4% 이내였고, 1545m의 장대지간에서는 충격계수를 거의 무시할 수 있는 수준이었다.
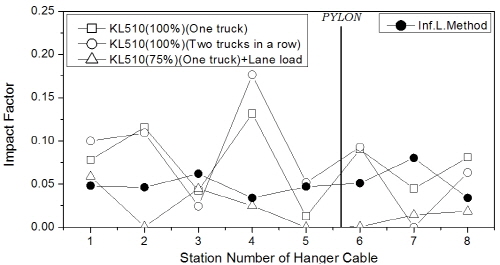
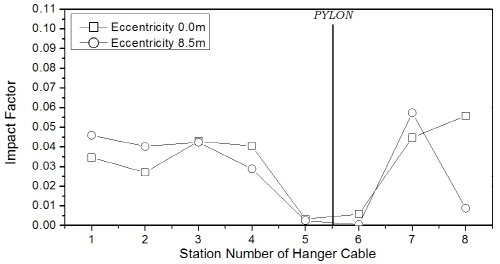
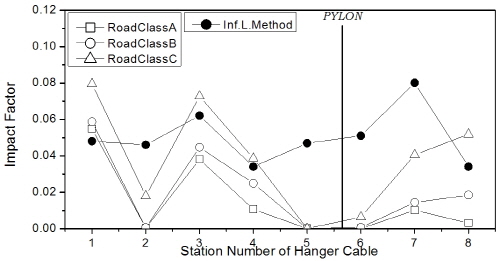
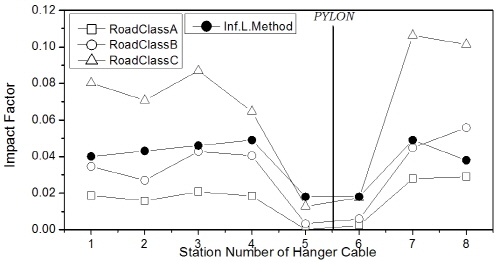
행어의 충격계수는 Fig. 10에 제시하였는데, 대부분의 평가 위치에서 역시 차로하중이 고려된 조합하중에 비해 트럭 1대 또는 2대 연행 경우에 충격계수가 크게 산출되었으며, 특히 조합하중에 의한 결과는 영향선 기법 결과에 비해 대체적으로 조금 작게 평가되었다. 한편, hinge-type에 비해 floating-type에서 주탑 부근 행어의 충격계수는 훨씬 작게 도출되었다. 차로하중이 포함된 경우에 대해 Fig 10(b)와 (c)로부터 행어의 최대 충격계수는 지간장에 따른 차이는 크지 않았으나, 교폭이 상대적으로 넓은 1545m 교량에서 조금 작은 값을 보였다.
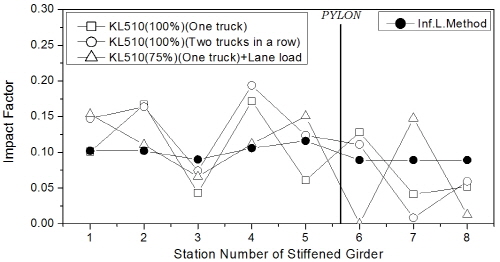
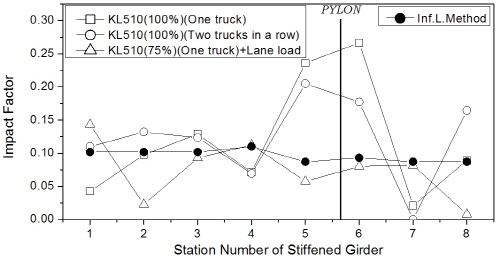
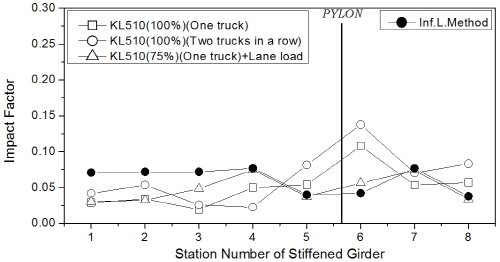
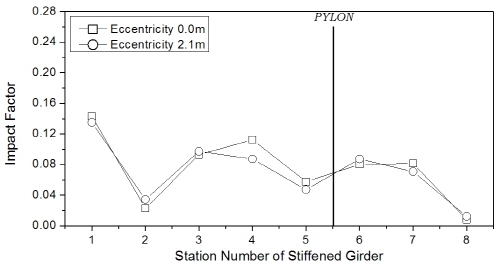
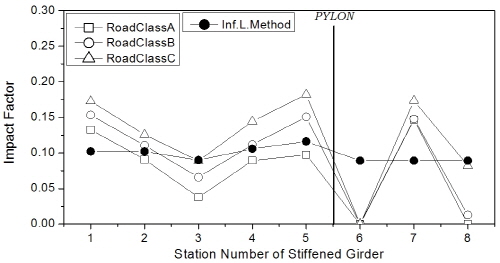
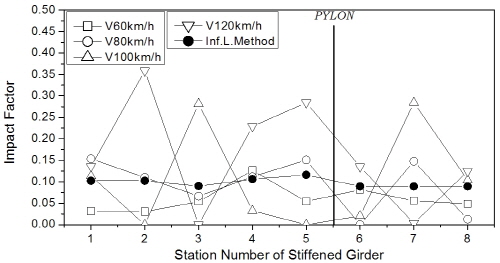
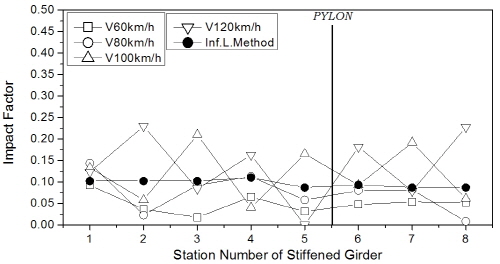
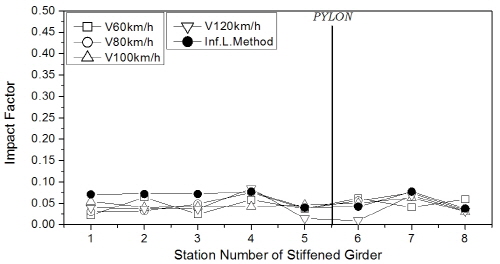
한편, 보강거더의 충격계수는 Fig. 11에 나타내었는데, 주케이블 및 행어와는 달리 거더에서는 차량하중 조합 방식에 따라 일정한 추이는 보이지 않았다. 하지만 충격계수의 최대값은 트럭 1대 또는 2대 연행 경우에 발생하였으며, 404m (floating-type) 교량의 주탑 부근에서 25% 수준의 큰 값을 보였다. 차로하중이 포함된 경우에 대해 분석하면 Fig 11(b)와 (c)로부터 보강거더의 충격계수는 주케이블과 마찬가지로 지간이 장대화됨에 따라 감소하는 경향을 보였다.
기존 연구[4],[6],[7]와 마찬가지로 트럭 1대 또는 2대가 주행하는 경우 충격계수는 대체로 큰 값을 보였다. 하지만, Fig. 12에 예시한 바와 바와 같이 교량 부재에 최대 응력을 발생시키는 경우는 트럭과 차로하중의 조합하중에 의한 것이므로 실제 적용에서는 이러한 점을 고려하여야 할 것으로 판단된다. 따라서, 이후 매개변수해석에서는 KL-510(75%)과 차로하중의 조합에 대해서만 고려하기로 한다.
4.2 편심 차량하중의 영향
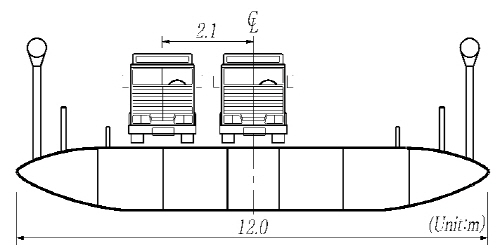
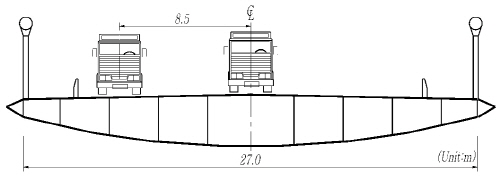
보강거더에 비틀림을 발생시키는 주행 차량의 편심이 교량의 충격계수에 미치는 영향을 평가하였다. 트럭 및 차로하중의 편심 위치를 Fig. 13에 나타내었는데, 편심이 없는 경우는 차량이 보강거더 단면의 중심으로 주행하는 경우이다. 매개변수해석시 고려한 노면조도는 class B 조건이며, 차량 속도는 80km/h의 속도를 고려하였다.
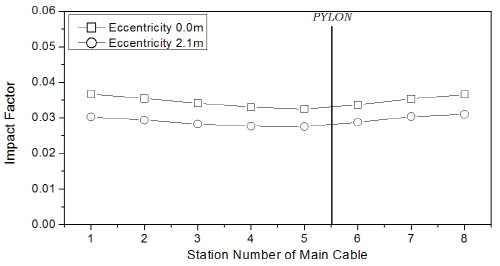
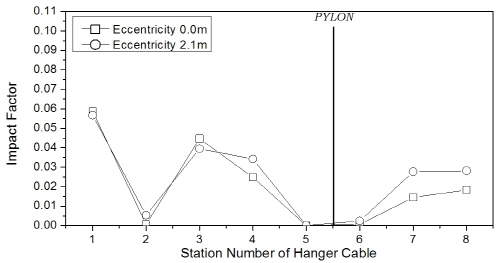
먼저, 편재하측 주케이블의 충격계수 결과를 Fig. 14에 나타내었는데, 중앙경간 404m 교량의 경우 hinge-type과 floating-type 모두 편심이 없는 경우에 충격계수가 크게 평가되었으나, 충격계수의 차이는 1% 이내로 미소하였으며, 중앙경간 1545m 교량의 경우도 편심에 의한 영향은 미소하였다.
행어의 충격계수는 Fig. 15에 제시하였는데, 충격계수의 평가위치에 따라 일관적 추세는 보이지 않았으며, 중앙경간 1545m 교량의 측경간 단부 행어를 제외하면 대부분 위치에서 충격계수는 2% 이내의 차이를 보였다. 한편, 보강거더의 충격계수는 Fig. 16에 나타내었는데, 역시 대부분의 평가 위치에서 2% 이내의 차이를 보였다.
앞서 살펴본 바와 같이 주행 차량의 편심이 충격계수에 미치는 영향은 미소하였는데, 이는 비틀림 강성이 강한 박스형 거더의 영향인 것으로 판단되며, 이후 매개변수해석에서는 주행 차량의 편심에 의한 영향은 배제하고 보강거더 단면의 중심축을 따라 주행하는 조건만을 고려하였다.
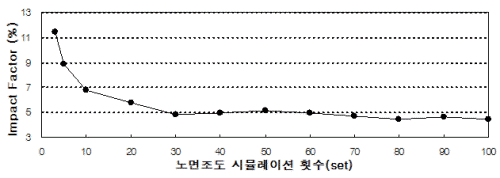
4.3 노면조도의 영향
노면조도는 교량의 충격계수에 큰 영향을 미치는 주요 인자 중 하나인데, 장대교량의 경우 노면관리가 양호한 것으로 가정하여 노면조도는 class A, B, C 조건만을 고려하였으며, 트럭 및 차로하중의 주행속도는 80km/h의 속도를 고려하였다.
먼저, 주케이블의 충격계수를 Fig. 17에 제시하였는데, 주케이블의 충격계수는 노면조도에 의한 영향이 매우 미소한 것으로 나타났다. 한편, 중앙경간 404m 교량의 경우 영향선 기법 결과와 상당히 일치하였으며, 중앙경간 1545m 교량의 경우는 영향선 기법 결과보다 조금 작게 평가되었다.
행어의 충격계수는 Fig. 18에 나타내었는데, 주케이블과는 달리 노면조도가 class C로 나빠질수록 증가하였으며, 노면조도 class A, B의 조건에서는 대부분의 평가위치에서 영향선 기법 결과보다 작게 평가되었다.
한편, 보강거더의 충격계수는 Fig. 19에 제시하였는데, 역시 노면조도가 나빠질수록 충격계수는 증가하였다. 그리고 floating-type 교량의 충격계수는 노면조도 class A, B의 조건에서 영향선 기법 결과보다 대부분 위치에서 작게 평가되었으나, hinge-type에서는 다수 위치에서 상회하는 결과를 보였다.
4.4 차량 속도의 영향
차량의 주행속도 또한 교량의 충격계수에 큰 영향을 미치는 주요 인자이다. 본 연구에서 고려한 차량들의 속도는 60, 80, 100, 120km/h이며, 노면조도는 class B 조건을 고려하였다.
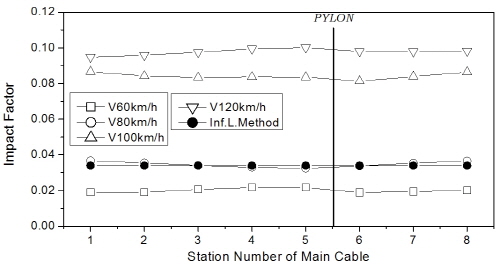
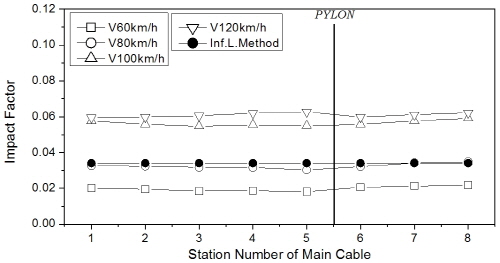
먼저, 주케이블의 충격계수를 Fig. 20에 나타내었는데, 차량 속도가 증가함에 따라 충격계수는 증가하였으며, 특히 중앙경간 404m hinge-type 교량의 충격계수는 floating-type에 비해 차량 속도 100km/h 이상의 속도에서 큰 폭으로 증가하였다. 반면, 중앙경간 1545m floating-type 교량은 차량 속도의 영향이 상대적으로 미소하였다. 한편, 영향선 기법 결과는 차량 속도 80km/h의 결과와 거의 일치하는 것으로 나타났다.
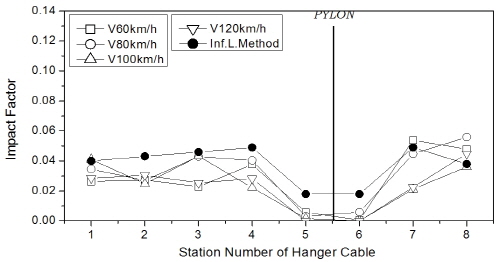
행어의 충격계수는 Fig. 21에 제시하였는데, 충격계수는 차량 속도에 따라 일정한 추이는 보이지 않았으나 대체로 100km/h 이상의 경우가 80km/h 이하의 경우에 비해 큰 값을 보였다. 특히 중앙경간 404m hinge-type 교량의 충격계수는 floating-type에 비해 속도별 변동폭이 컸으며, 중앙경간 1545m 교량은 중앙경간 404m 교량에 비해 속도별 변동폭이 훨씬 작은 결과를 보였다. 또한, 차량 속도 80km/h 이하의 경우에는 거더 연결 형식 및 지간장에 상관없이 대부분의 평가 위치에서 영향선에 의한 결과보다 작게 평가되었다.
한편, 보강거더의 충격계수는 Fig. 22에 나타내었는데, 행어와 마찬가지로 차량 속도에 따라 일정한 추이는 보이지 않았으나 대체로 100km/h 이상의 경우가 80km/h 이하의 경우보다 큰 값을 보였다. 또한 행어의 경우와 유사하게 중앙경간 404m hinge-type 교량의 충격계수는 404m floating- type에 비해 속도별 변동폭이 컸으며, 중앙경간 1545m 교량은 중앙경간 404m 교량에 비해 속도별 변동폭이 훨씬 적었다. 또한, 교량의 지간에 상관없이 floating-type 교량은 차량 속도 80km/h 이하의 경우 대부분의 평가 위치에서 영향선 기법 결과보다 작게 평가 되었다.
5. 결 론
본 연구에서는 중앙경간 404m 및 1545m의 현수교에 대해 차량-교량 상호작용해석을 수행하고 구성 부재의 충격계수를 평가하였으며, 설계지배 활하중은 차로하중을 일련의 1축 차량 하중으로 고려하되 도로교한계상태설계기준[8]의 활하중 모델을 고려하였다. 본 연구에서 도출된 주요 결론은 다음과 같다.
(1)트럭과 차로하중의 조합하중이 주행하는 경우에 비해 트럭 1대 또는 2대 연행 시 주케이블 및 행어의 충격계수는 훨씬 크게 평가되었다. 하지만 장대교량에서 최대응력을 유발하는 경우는 차로하중이 포함되는 경우이므로 장대 현수교의 충격계수는 차로하중이 포함된 조건에 대해 평가하는 것이 합리적이라고 판단된다.
(2)주행 차량의 편심이 교량의 충격계수에 미치는 영향은 교량 대부분의 평가 위치에서 2% 이내로 미소하였다.
(3)노면조도가 나빠짐에 따라 행어 및 보강거더의 충격계수는 크게 증가하였으나 주케이블에서는 그 영향이 미소하였다.
(4)차량의 속도가 증가함에 따라 주케이블의 충격계수는 증가하였는데, 특히 지간이 짧은 교량에서 그 영향이 큰 것으로 나타났다. 한편, 행어와 보강거더의 충격계수는 차량 속도 변수에 대해 일정한 추이는 보이지 않았으나, 대체로 속도가 빠를수록 충격계수는 증가하였다. 또한, floating-type 교량에 비해 hinge-type 교량에서, 그리고 지간장이 짧은 교량에서 속도별 충격계수의 변동폭이 큰 것으로 나타났다.
(5)Floating-type 교량에 대해 노면조도 class B, 차량속도 80km/h 이하의 조건에서 교량의 지간에 따라 주케이블의 충격계수는 3%∼0.5%, 행어의 충격계수는 6%∼4%, 보강거더의 충격계수는 10%∼5% 수준이었다. 한편, 케이블교량의 충격계수 평가를 위해 흔히 사용되는 영향선 기법으로 평가한 충격계수는 상기 값을 대부분 포괄하였으며, 따라서 영향선 기법은 floating-type 현수교에 대해서는 상기 조건(노면조도 class B, 차량속도 80km/h)의 범위에서 적용 가능할 것으로 평가되었다.
본 연구에서는 도로교한계상태설계기준에서 제시된 이상화한 활하중 모델을 고려하였으나, 향후 과제로서 실제 차량의 특성(중량, 고유주기 등)과 주행 차량의 대수 및 차량 주행간격을 매개변수로 한 추가 연구가 필요할 것으로 판단된다.
Acknowledgments
이 논문은 2012년도 정부(교육과학기술부)의 재원으로 한국연구재단의 이공분야기초연구사업 일반연구자지원사업 기본연구(과제번호: 2012R1A1A2003942, 과제명: 케이블지지 도로교 및 철도교의 충격계수 평가 연구)의 지원으로 수행되었으며, 이에 감사드립니다.
References
-
이승우(2003) 현수교의 계획과 해석, 도서출판 한기술.
Lee, S.W. (2003) Planning and Analysis of Suspension Bridge, Hangisul, Korea (in Korean). -
국토해양부(2010) 도로교설계기준.
Ministry of Land, Transport and Maritime Affairs (2010) Highway Bridge Design Standard, Korea (in Korean). -
대한토목학회(2005) 케이블 강교량 설계 지침 작성 연구, 대한토목학회.
Korean Society of Civil Engineers (2005) Research on Making Guidelines for Steel Cable-Supported Bridges, KSCE, Korea (in Korean). - Karoumi, R. (1999) Response of Cable-Stayed and Suspension Bridges to Moving Vehicles-Analysis Methods and Practical Modeling Techniques, Ph.D. Dissertation, Royal Institute of Technology, Sweden.
- Hayashikawa, T., and Watanabe, N. (1982) Dynamic Behavior of Suspension Bridges Under Moving Loads, Memoirs of the Faculty of Engineering, Hokkaido University, Hokkaido University, Vol.16, No.1, pp.1-12.
-
장승필, 김호경, 서정인(1995) 불규칙한 노면조도위를 주행하는 차량에 의한 자정식 현수교의 진동특성, 한국강구조학회논문집, 한국강구조학회, 제7권, 제1호, pp.117-123.
Chang, S.P., Kim, H.K., and Suh, J.I. (1995) Self-Anchored Suspension Bridge Vibration Due to a Vehicle Load Running on Irregular Road Surface, Journal of Korean Society of Steel Construction, KSSC, Vol.7, No.1, pp.117-123 (in Korean). -
서정인, 김호경(2000) 현수교의 정착 형식에 따른 이동하중에 의한 동적 응답의 비교, 한국강구조학회논문집, 한국강구조학회, 제12권, 제1호, pp.103-110.
Suh, J.I., and Kim, H.K. (2000) Comparison of Dynamic Response According to Anchorage Type of Suspension Bridges, Journal of Korean Society of Steel Construction, KSSC, Vol.12, No.1, pp.103-110 (in Korean). -
국토해양부(2012) 도로교설계기준(한계상태설계법).
Ministry of Land, Transport and Maritime Affairs (2012) Highway Bridge Design Standard (Limit State Design), Korea (in Korean). - International Organization for Standardization (1995) Mechanical Vibration – Road Surface Profiles – Reporting of Measured Data (ISO 8608: 1995), Switzerland.
-
Wang, T.-L., and Huang, D. (1992) Cable-Stayed Bridge Vibration Due to Road Surface Roughness, Journal of Structural Engineering, American Society of Civil Engineers, Vol.118, No.5, pp.1354-1374.
[https://doi.org/10.1061/(ASCE)0733-9445(1992)118:5(1354)]

-
Dodds, C.J., and Robson, J.D. (1973) The Description of Road Surface Roughness, Journal of Sound and Vibration, Elsevier, Vol.38, No.2, pp.175-183.
[https://doi.org/10.1016/S0022-460X(73)80373-6]

-
小松定夫, 川谷充郎(1978) 斜張橋の自動車走行による動的応答と衝撃係数に関する研究, 土木学会論文報告集, 土木学会, 第275券, pp.13-28.
Komatsu, S., and Kawatani, M. (1978) Study on Dynamic Response and Impact of Cable-Stayed Girder Bridges Under Moving Vehicles, Proceedings of Japanese Society of Civil Engineers, JSCE, Vol.275, pp.13-28 (in Japanese). [ https://doi.org/10.2208/jscej1969.1978.275_13 ]
-
박재봉, 박용명, 김동현, 이종한(2013) 신뢰도 기반 활하중모델에 의한 강합성 사장교의 충격계수 평가, 한국강구조학회논문집, 한국강구조학회, 제25권, 제4호, pp.335-346.
Park, J.B., Park, Y.M., Kim, D.H., and Lee, J.H. (2013) Evaluation of Impact Factor in Composite Cable-Stayed Bridges Under Reliability-Based Live Load Model, Journal of Korean Society of Steel Construction, KSSC, Vol.25, No.4, pp.335-346 (in Korean). [ https://doi.org/10.7781/kjoss.2013.25.4.335 ]
-
Calçada, R., Cunha, A., and Delgado, R. (2005) Analysis of Traffic-Induced Vibrations in a Cable-Stayed Bridge, Part II: Numerical Modeling and Stochastic Simulation, Journal of Bridge Engineering, American Society of Civil Engineers, Vol.10, No.4, pp.386-397.
[https://doi.org/10.1061/(ASCE)1084-0702(2005)10:4(386)]

-
彦坂熙, 吉村虎蔵, 内谷保(1979) 連行自動車荷重による単純桁橋の非定常ランダム応答と衝撃係数, 土木学会論文報告集, 土木学会, 第290券, pp.31-41.
Hikosaka, H., Yoshimura, T., and Uchitani, T. (1979) Non-Stationary Random Response and Impact Coefficient of Simple Girder Highway Bridge Under a Series of Moving Vehicle Loads, Proceedings of Japanese Society of Civil Engineers, JSCE, Vol.290, pp.31-41 (in Japanese). [ https://doi.org/10.2208/jscej1969.1979.290_31 ]
- Chopra, A.K. (1995) Dynamics of Structures: Theory and Applications to Earthquake Engineering (2nd Ed.), Prentice Hall, USA.
-
Yang, F., and Fonder, G.A. (1996) An Iterative Solution Method for Dynamic Response of Bridge-Vehicles Systems, Earthquake Engineering and Structural Dynamics, John Wiley & Sons, Vol.25, No.2, pp.195-215.
[https://doi.org/10.1002/(SICI)1096-9845(199602)25:2<195::AID-EQE547>3.0.CO;2-R]

-
深田宰史, 梶川康男, 角本周(1998) 2径間連続PC斜張橋の車両走行時の振動特性と動的増幅率, 土木学会論文集, 土木学会, 第605/I-45号, pp.37-47.
Fukuda, S., Kajikawa, Y., and Tsunomoto, M. (1998) Vibration Characteristics and Dynamic Increment Factor of 2 Span Continuous Cable-Stayed Bridge Under Moving Vehicles, Doboku Gakkai Ronbunshu, Vol.605/I-45, pp.37-47 (in Japanese). [ https://doi.org/10.2208/jscej.1998.605_37 ]


 (m2)
(m2)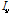 (m4)
(m4) (m4)
(m4) are moment of inertia of steel girder with respect to the horizontal and vertical axis, respectively.
are moment of inertia of steel girder with respect to the horizontal and vertical axis, respectively. are moment of inertia of pylon with respect to the longitudinal and transverse axis, respectively.
are moment of inertia of pylon with respect to the longitudinal and transverse axis, respectively.