BWIM시스템의 현장 적용성 및 영향인자에 관한 연구
Copyright ⓒ 2014 by Korean Society of Steel Construction
초록
BWIM에서 중량 추정결과에 영향을 미치는 것으로는 변형률 응답파형과 관계가 있는 차량 주행특성, 교량특성 및 계측조건을 고려할 수 있다. 이 연구에서는 이들 영향인자가 BWIM에 의한 차량 정보추정에 미치는 정도를 평가하고자 이론적인 연구 및 현장실측을 실시하였다. 이러한 평가를 통하여 BWIM에 의한 차량정보추정에서의 정밀도 향상을 위한 방안을 제시하고자 한다. 연구결과, 교량의 거더형식, 경간의 연속유무에 따른 차량정보추정의 차이는 거의 없는 것으로 나타났다. 그러나 교량의 평면형상 때문에 사교가 직교보다 높은 오차율을 나타내었다. 또한 차량의 주행속도는 2축과 3축사이의 간격이 짧은 축간거리의 산정에는 큰 영향을 미치지만, 총중량 추정에는 영향이 거의 없는 것으로 나타났다.
Abstract
It has been considered that factors affecting accuracy of the estimated weight of moving vehicle by BWIM system are vehicle and bridge characteristics, and measurement conditions which is related to the strain curve. In this study, theoretical review and field test were performed to evaluate effect of these factors in BWIM system. From these evaluations, we proposed a way to improve accuracy of the estimated vehicle information in BWIM system. As the results, it was known that girder type and continuity of spans in bridge are not governing factor, but its plane shape gives large influence on accuracy of the estimated vehicle information. In addition, running speed of vehicle has also large effect on the estimated accuracy of axle distance if the distance between second and third axles is short. However, weight sum of the two axles can be estimated reasonably by assuming them as one axle.
키워드:
BWIM, 변형률 측정, 차량정보, 차량중량, 강교량Keywords:
BWIM (Bridge Weigh-in-Motion), Strain measurement, Vehicle information, Vehicle weight, Steel bridge1. 서 론
도로를 통행하는 차량의 중량을 판별하는 방법은 크게 WIM방식과 BWIM(Bridge Weigh-In-Motion, 이하 BWIM)방식으로 나눌 수 있다. WIM방식은 비교적 정밀한 중량계측이 가능하지만 유지관리비용이 높은 것이 단점으로 지적되고 있다. BWIM방식은 초기설치비용 및 유지관리비용이 적다는 장점이 있으나, 중량추정 판정에 미치는 영향인자가 많아 정확도가 아직 WIM방식에 비해 떨어지는 단점이 있다.
BWIM시스템에 적용되는 기본개념은 1970년대 말 Moses (1979)[1]에 의해 처음 제안되었다. Peters(1986)[2]는 BWIM시스템을 암거에 적용한 바 있으며, Znidaric and Moses(1991)[3] 및 Dempsey et al.(1995)[4] 등은 BWIM시스템에 대한 연구를 통해 지간이 긴 교량에서는 중량추정의 정확성이 저하되는 등의 문제로 인하여 개선이 필요하다고 보고하였다. 유럽에서는 Jacob(2002)[5]의 WAVE(Weigh-in-motion of Axles and Vehicle for Europe) PROJECT와 COST323 Action[6]을 통하여 BWIM의 의한 중량 추정의 정확성이 많이 향상되었다(McNulty and O’Brien(2003))[7]. Znidaric et al.(2002[8], 2008[9])의 연구에서는 강교량 뿐만 아니라 콘크리트교량, 합성교량에까지 BWIM기술을 적용시켰으며, DAF(Dynamic Amplification Factor)을 적용하여 BWIM의 기능을 향상시켰다.
일본에서는 Kobayashi(2003)[10]는 실시간으로 측정한 변형률 응답 특성을 이용하여 차량의 중량특성을 분석하고, 교량의 피로평가에 활용하였다. 또한 Ojio(2006)[11] 등은 BWIM개발과 관련된 일련의 연구에서 중량추정을 위한 다양한 알고리즘을 제시하고 이에 대한 타당성을 검증하였다.
국내에서도 인공신경망 이론을 적용한 Park(2008)[12]의 연구와 밀도추정함수와 평균보정계수를 적용하여 알고리즘을 개발한 Han and Shin(2011)[13]의 연구 등이 수행된 바 있으며, Jung(2012)[14], Hwang et al.(2013)[16]의 연구에서는 동적해석 전용프로그램(DAP-1)을 사용하여 차량형식(축수), 주행위치, 온도 및 노이즈 등이 차량 중량 추정의 정확도에 미치는 영향에 대해 이론적인 연구를 수행하였다.
이들 선행연구는 모두 BWIM에 의한 중량추정의 실용성은 입증하였으나, 차량의 중량추정의 정확성을 향상시키기 위한 다양한 매개변수적 연구는 그다지 수행되어 있지 않다.
BWIM에서 중량추정에 영향을 미치는 것으로는 변형률 응답과 관계가 있는 차량 주행특성, 교량특성 및 계측조건을 고려할 수 있다. Lee et al.(2012)[15]의 연구에서는 주행차량에 따른 교량의 국부거동 특성을 분석하였으며, 차량 주행특성과 관련하여 Hwang et al.(2013)[16]의 연구에서 검토한 영향인자 이외의 것으로 주행속도, 주행패턴(연행/병행) 등이 있다. 교량특성으로는 거더형식, 경계조건(단순교/연속교), 평면형상(직교/사교), 지간길이, 하중분배 능력 등을 영향인자로서 고려할 수 있다. 또한 계측조건에서는 거더 및 수직보강재에서의 계측위치, 데이터 Sampling Rate 등이 영향인자라고 생각된다.
일반적으로 BWIM기법은 직교의 단순지지 강교량에서 그 적용성이 우수한 것으로 알려져 있다. 그리고 중량추정을 위한 데이터 측정은 대부분 거더를 대상으로 하고 있어서 총중량은 비교적 정확하게 추정되지만 축중량에 대한 정확성은 다소 저하되는 경향을 나타내고 있다.
Kim et al.(2010)[17]의 연구에서는 축중량의 추정오차를 감소시키기 위해 차륜하중에 대해 민감하게 응답하는 강바닥판을 대상으로 BWIM기법을 적용하여 전체중량 및 축중량 추정에 대한 정확성을 향상시켰다.
이 연구에서는 Hwang et al.(2013)[16]의 연구에 기초하여 앞에서 기술한 인자 중 교량의 평면형상, 주행속도, 주행패턴, 계측위치 및 데이터 Sampling rate가 BWIM에 의한 차량정보 추정에 미치는 영향을 평가하고자 이론적인 연구 및 현장실측을 실시하였다. 이러한 평가를 통하여 BWIM에 의한 차량정보 추정시 정밀도를 향상시키는 방안을 제시하고자 한다.
2. BWIM System
2.1 BWIM의 개요
BWIM은 기지의 중량을 갖는 차량을 통과시켜 단위하중에 의한 교량부재의 응답을 구한 후, Calibration을 실시하여 임의 통과차량의 중량, 속도 및 차종 등을 추정하는 방법이다.
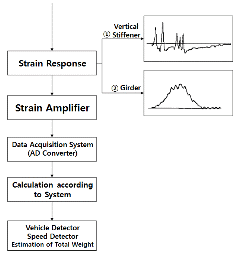
Fig. 1에 기본적인 BWIM시스템의 흐름을 나타내었다. 차량주행에 의한 거더 및 수직보강재의 응답이력곡선을 도출하고, 거더의 응답이력곡선을 이용하여 기지차량에 대한 기준영향선을 작성한 후 이를 사용하여 미지차량의 중량을 추정한다. 또한 수직보강재의 응답이력곡선을 이용하여 차량의 주행차로, 속도 및 축간거리를 검지하고, 차량을 판별한다.
2.2 차량의 속도, 축간거리 및 중량 추정방법
이 연구의 주행차량 속도, 축간거리 및 중량 추정방법은 Moses[1]이론에 기초한 선행연구(Jung, 2012[14], Hwang et al., 2013[16])와 동일하다. 이것을 사용하여 이 연구에서 대상으로 하는 영향인자가 BWIM에 의한 중량추정에 미치는 영향을 분석하였다.
2.3 주행패턴에 따른 응답이력곡선의 도출
일반도로의 교량에서 차량의 교통흐름은 차량이 단독으로 주행하는 경우보다는 2대 이상의 차량이 연행 또는 병행하는 것이 일반적인 차량 주행패턴이다. 그러므로 BWIM에서 연행 또는 병행 등의 주행패턴이 차량의 중량추정에 미치는 영향을 정확하게 평가하기 위해서는 각 주행차량에 대한 응답이력곡선을 정확하게 도출하고 이를 평가하는 것이 중요하다.
차량이 교량 위의 임의의 점을 통과 할 때 차량의 영향선
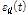 은 식 (2)와 같이 계산된다.
은 식 (2)와 같이 계산된다.
 (1)
(1)
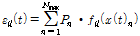 (2)
(2)
여기서,
 : 시간
: 시간
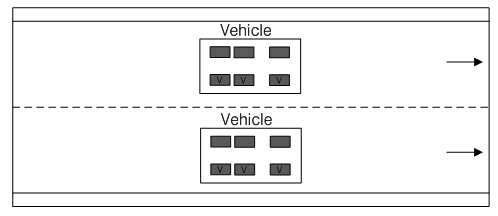
중량을 알고 있는 기지의 차량이 2차로를 주행하는 경우, 주행차량에 의한 변형률은
 은 Fig. 2(c)와 같이 2대의 차량에 의한 변형률이 중첩되어 나타나므로 다음과 같이 중첩된 변형률을 각각의 차량에 의한 변형률로 분리하는 과정이 필요하다.
은 Fig. 2(c)와 같이 2대의 차량에 의한 변형률이 중첩되어 나타나므로 다음과 같이 중첩된 변형률을 각각의 차량에 의한 변형률로 분리하는 과정이 필요하다.
(1)1차로를 단독 주행할 때 측정지점
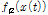 ]를 각각 도출한다.
]를 각각 도출한다.
(2)기준영향선 ①과 ②의 비율을 구한다.
(3)(2)에서 구한 비율을 병행에 의해 발생하는 변형률
 에 각각 곱하면 각 차량에 의한 영향을 분리할 수 있다(Fig. 2(c)).
에 각각 곱하면 각 차량에 의한 영향을 분리할 수 있다(Fig. 2(c)).
연행의 경우에는 2차로를 단독 주행할 때의 기준영향선
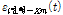 에 곱해주면 각각의 변형률응답곡선을 추출할 수 있다.
에 곱해주면 각각의 변형률응답곡선을 추출할 수 있다.
2.4 BWIM에 의한 중량추정에서의 영향인자 및 오차분류
BWIM에 의한 중량추정 결과에 영향을 미치는 인자가운데 이 연구에서 고려한 영향인자를 Table 1에 나타내었다. 이들 인자는 주로 교량의 변형률 응답이력곡선의 파형에 영향을 미치는 것들이다.
Table 2에 WIM에 의한 차량중량 추정시의 발생오차에 대한 유럽의 COST 323에서의 등급분류[18] 및 각 등급에 대한 허용오차의 범위를 나타내었다. 여기서, Class A는 법적인 목적으로 사용가능한 수준으로 가장 오차가 낮은 수준이며, 아래 등급인 B+, B, C, D 등급은 각각의 목적에 맞추어 등급을 분류한 것이다.
3. BWIM 현장실험
3.1 현장실험의 개요
이 연구에서 고려한 인자가 BWIM시스템의 중량추정 결과에 미치는 영향을 평가하기 위해 상부구조형식이 다른 2개의 교량을 선정하여 현장실험을 실시하였다.
현장실험으로부터 변형률 데이터를 얻기 위해 전기저항식 변형률 센서를 거더 및 수직보강재에 부착하고, 부착된 센서를 브릿지 박스를 통해 동적계측기기(EDX-100A)에 연결하였다. 또한 주행차량의 실제 속도를 파악하기 위해 신뢰성이 인증된 스피드건(Bushnell Speed Gun 101911)을 사용하였다.
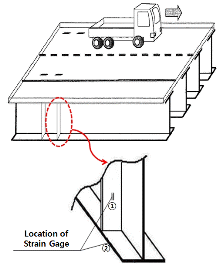
3.1.1 대상교량 I
대상교량 I은 PSC Box Girder와 Steel Box Girder가 혼재된 과선교량이며, 본 연구에서 대상으로 하는 Steel Box 교량은 3 Cell의 2경간 연속교량이다. Table 3 및 Fig. 3에 각각 대상교량 I의 현황 및 측정위치를 나타내었다.
BWIM에 의해 주행차량의 속도 및 축간거리를 추정하기 위하여 Fig. 3(b)에 나타낸 것과 같이 대상교량 I의 P7에서 P8 방향으로 0.45m(A-A단면) 및 2.45m(B-B단면) 이격된 박스거더 내부의 수직보강재를 대상으로 상부플랜지 하면에서 20mm 이격된 위치에 변형률 센서를 수직방향으로 부착하였다. 측정대상 수직보강재 간격은 2m이다.
그리고 주행차량의 중량을 추정하기 위하여 최대모멘트 발생위치인 3L/8(C-C단면) 및 경간 중앙 위치인 L/2(D-D단면)의 거더 하부플랜지에 변형률 센서를 교축방향으로 부착하였다. 변형률 데이터의 Sampling Rate는 모두 200Hz로 하였다.
대상교량 I의 현장실험에 사용된 주행차량은 토사를 적재한 3축의 덤프트럭 A 및 B이며, 차량주행은 실제 주행차로를 고려하여 P9에서 P7 방향으로 실시하였다. 주행차량의 제원 및 중량을 Table 4, 그리고 주행방법을 Table 5에 나타내었다.
3.1.2 대상교량 II
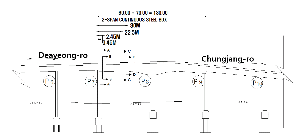
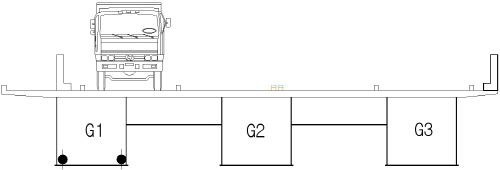
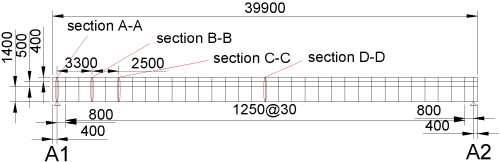
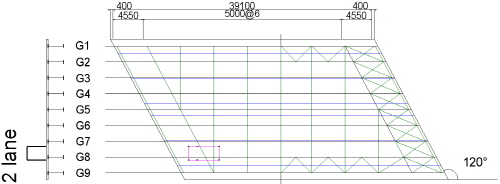
플레이트 거더교 형식의 대상교량 II는 일반국도 39호선에 위치한 교장 40m의 단경간 플레이트거더교이며, 120°의 사각을 갖는 사교이다. Table 6 및 Fig. 4에 각각 대상교량 Ⅱ의 현황 및 측정위치를 나타내었다.
BWIM에 의해 주행차량의 속도 및 축간거리를 추정하기 위하여 Fig. 4(c)에 나타낸 것과 같이 대상교량 Ⅱ의 지점 A1에서 A2 방향으로 3.30m(B-B단면) 및 5.80m(C-C단면) 이격된 수직보강재를 대상으로 상부플랜지 하면에서 200mm 이격된 위치에 변형률 센서를 수직방향으로 부착하였다. 측정대상 수직보강재 간격은 2.5m이다.
그리고 주행차량의 중량을 추정하기 위하여 최대모멘트 발생위치인 L/2(D-D단면)의 거더 하부플랜지에 변형률 센서를 교축방향으로 부착하였다. 변형률 데이터의 Sampling Rate는 모두 100Hz로 하였다.
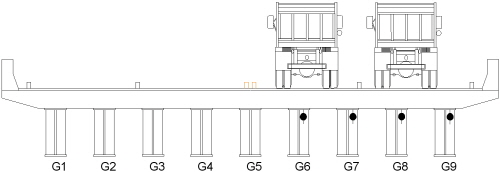
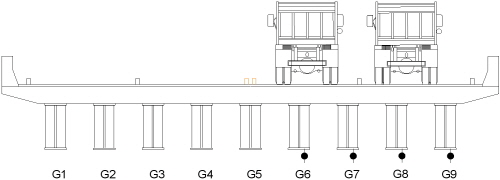
대상교량 II의 현장실험에서도 3축의 덤프트럭 2대를 사용하였으며, 한 대는 만차(트럭 C), 다른 한 대는 공차(트럭 D)이다. 차량의 제원 및 중량을 Table 7에, 그리고 주행방법을 Table 8에 나타내었다. 대상교량 II의 현장실험에서는 실제 교통흐름의 다양성 및 변동성을 반영하기 위하여 다양한 주행방법에 의한 현장실험을 실시하였다. 차로내의 주행차량 위치는 모두 각 차로의 중앙이며, 주행방향은 A1에서 A2 방향이다.
4. 현장실험 결과 및 분석
4.1 대상교량 I
4.1.1 주행차량의 속도 및 축간거리 추정
수직보강재에서 얻어진 변형률 응답이력곡선을 이용하여 주행차량의 속도 및 축간거리를 계산하였다.
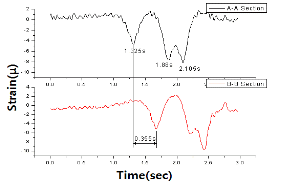
수직보강재에서 얻어진 변형률 응답이력곡선의 일례 및 주행차량의 속도와 축간거리의 추정 결과를 각각 Fig. 5 및 Table 9에 나타내었다. Table 9에 나타낸 바와 같이 수직보강재의 변형률을 이용하면 실제의 속도 및 1축과 2축 사이의 축간거리는 비교적 정확하게 추정할 수 있지만, 2축과 3축 사이의 축간거리 추정 오차는 속도가 증가할수록 커진다는 것을 알 수 있다. 그 이유는 2축과 3축 사이의 거리가 짧아 속도가 증가할수록 계측된 변형률에 각 축의 영향이 뚜렷이 나타나지 않고 인접 축의 축중의 영향이 중첩되어 나타나기 때문으로 판단된다.
4.1.2 주행차량의 중량 추정
주행차량의 속도가 중량 추정결과에 미치는 영향을 파악하기 위하여 주행차량 B가 사용된 Load Case 1을 기준으로 하여 속도와 중량이 다른 주행차량 A를 사용한 Load Case 2, 4에 대해 중량을 추정하고, 그 결과를 Table 10에 나타내었다.
두 경우 모두 Table 2에 나타낸 유럽에서 사용되는 오차분류등급의 A를 만족하며, 동일 차량 형식의 경우에는 주행차량의 속도 및 중량의 차이, 계측위치의 차이가 차량의 중량추정에 영향을 거의 미치지 않음을 알 수 있다. 향후 연구에서는 다양한 차량 종류 및 차량별 중량 특성에 대한 연구가 필요할 것으로 판단된다.
4.2 대상교량 II
4.2.1 주행차량의 속도 및 축간거리 추정
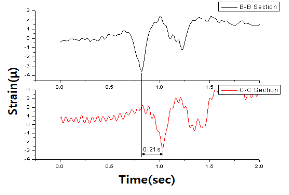
대상교량 II의 수직보강재에서 얻어진 응답이력곡선의 일례 및 주행차량의 속도와 축간거리의 추정 결과를 각각 Fig. 6 및 Table 11에 나타내었다. Table 11에 의하면 속도에 대한 추정 오차는 10% 내외이나, 축간거리 추정 오차는 최대 33% 정도로 나타나고 있다.
4.2.2 주행차량의 중량 추정
대상교량 II에서는 Fig. 4에 나타낸 거더 8번(G8)의 변형률 응답이력곡선을 이용하여 주행차량의 중량을 추정하고, 그 결과를 분석하였다.
Table 12에 대상교량 II에 대한 속도 및 중량 차이에 따른 중량추정의 결과를 나타내었다. 대상교량 I에 비하여 대상교량 II에서는 속도 및 중량의 차이에 따른 축중량 및 전체중량의 추정오차가 크게 발생하였는데, 이는 사교인 대상교량 II의 구조적인 특성에 기인하는 것으로 판단된다. 즉, Fig. 4에 나타낸 것과 같이 차량의 주행속도 및 중량의 차이에 관계없이 사교의 구조적 특성에 의하여 거더 상호간 주행차량의 축중 분포 및 하중전달이 간섭되기 때문으로 판단된다. 이러한 결과는 기존 외국의 연구인 Tamakoshi et al.(2004)[19]에서 지적한 것과 같이 사교인 교량에는 BWIM시스템 적용에 어려움이 있다는 보고와도 일치하고 있다.
4.3 BWIM시스템에 영향을 미치는 인자
4.3.1 교량특성(평면형상)
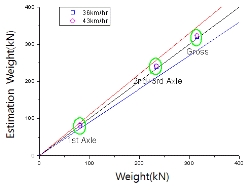
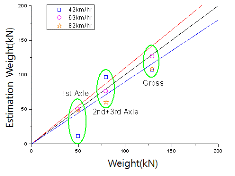
이 연구에서는 교량 평면형상(직교, 사교)이 주행차량의 중량 추정결과에 미치는 영향을 조사하였으며, 직교 및 사교에 대한 중량 추정결과를 Fig. 7에 나타내었다.
Fig. 7에 나타낸 것과 같이 직교의 경우에는 Table 2의 오차분류등급 A를 만족하는 매우 양호한 중량 추정결과는 나타내지만 사교의 경우에는 중량 추정오차가 다소 커지는 것을 알 수 있다. 이러한 원인은 사각으로 인한 하중 횡분배의 차이라고 사료된다. 이로부터 향후 BWIM시스템 적용은 직교를 대상으로 하는 것이 바람직하며, 사교를 선정해야만 하는 부득이한 경우에는 충분한 이론적 검토 후에 하중전달이 명확한 위치를 선정하는 것이 중요하다고 판단된다.
4.3.2 차량 주행특성
(1) 주행속도에 따른 영향
대상교량 I 및 대상교량 II의 경우, Table 9 및 Table 11에 나타낸 것과 같이 차량의 주행속도가 빨라져도 차량의 축간거리 산정에는 유의한 차이가 없었으나, 축간거리가 짧은 2축-3축의 축간거리 산정에는 오차가 증가하는 것으로 나타났다. 또한 각 축중에 대한 추정오차도 속도가 증가하면 약간 증가하는 경향을 나타내었으나, Table 10에 나타낸 것과 같이 2축과 3축을 하나의 축으로 하여 중량을 산정하면 축중량 및 전체중량의 산정결과에 주행속도는 거의 영향을 미치지 않는 것으로 나타났다.
(2) 주행패턴에 따른 영향
차량의 주행패턴이 중량 추정결과에 미치는 영향을 분석하기 위하여 대상교량 II에서 실시한 Load Case 5의 변형률 응답이력곡선을 사용하여 검토하였다.
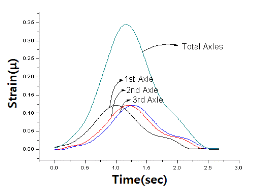
Fig. 8(a)에 대상교량 II의 Load Case 5에 대한 변형률 응답이력곡선 및 주행차량 C, D가 각각 단독 주행할 때 얻어진 응답이력곡선을 나타내었다. Fig. 8(b) 및 (c)에는 주행차량 C 및 D가 각각 1차로 및 2차로를 단독 주행하는 경우에 얻어진 각 차축 및 전체차축에 대한 기준영향선을 나타내었다.
대상교량 II에서의 Load Case 5~7에 대한 차량주행패턴으로부터 얻어진 응답이력곡선에 대하여 2장에서 기술한 차량주행패턴에 따른 응답이력곡선을 분리하고 각 주행차량의 중량을 추정하였다. Table 13에 주행차량 D에 대한 중량 추정결과를 나타내었다(Before의 항목으로 표시). Table 13에 나타낸 것과 같이 총중량 추정오차는 ±10% 내외로서 Table 2에 나타낸 유럽에서의 오차등급분류 B를 만족한다. 그러나 추정된 축중의 정확도는 대상교량 I에 비하여 떨어지는 것을 알 수 있다. 이것은 앞에서 기술한 것과 같이 교량의 평면형상 등에 의한 영향으로 판단된다.
축중에 대한 추정 정확도를 향상시키기 위하여 수직보강재의 응답을 사용하였다. Fig. 5 및 6에 나타낸 것과 같이 수직보강재의 응답은 하중이 부재의 바로 위를 통과할 때만 발생하므로 차량의 주행패턴과는 관계없이 통과차량의 차축에만 반응한다. 특히 지점부에 위치한 수직보강재는 교량의 진동특성 등의 영향이 적으므로 지점부인 A-A단면에 설치한 수직보강재의 응답을 분석하여 축중 분배율을 검토하고, 이를 활용하여 주행차량의 중량을 재차 추정하였다.
축중 분배율의 평가결과, 3가지 Load Case에서의 1축의 분배율은 30%~31%, 2축+3축의 분배율은 68%~69%로 나타났다. 이것에 기초하여 추정된 축중을 Table 13(After의 항목)에 나타내었다. 이 방법은 앞에서 사용된 기본방법에 비하여 추정 축중의 정확도를 향상시킬 수 있는 것으로 나타났다. 그러나 사교 등의 영향으로 추정 오차를 감소시키기에는 한계가 있는 것으로 판단된다. 향후 사교에서의 추정오차의 정밀도 향상을 위해서는 추가적인 연구가 필요할 것으로 판단된다.
4.3.3 계측조건
(1) Sampling Rate에 따른 영향
Sampling Rate가 속도 추정결과에 미치는 영향을 조사하기 위하여 동적해석 전용프로그램(DAP-1)[20],[21],[22],[23], [24],[25],[26]을 사용하여 시간이력해석을 수행하였다. 해석에서는 차량속도를 60km/h로 일정하게 하고 해석시간간격을 변화시켜가면서 그 영향을 평가하였다.
Table 14에 Sampling Rate에 따른 오차율을 나타내었다. Sampling Rate가 100Hz 이상에서는 추정오차가 2% 미만으로 매우 양호한 결과를 나타내는 반면에 50Hz에서는 속도 추정 오차가 4% 이상으로 커지는 것으로 나타났다.
한편 현장측정에서는 Sampling Rate를 100Hz 및 200Hz로 실시하여 이 연구의 중량추정에서는 Sampling Rate의 영향은 없는 것으로 판단된다.
(2) 측정위치에 대한 영향
연속교인 대상교량 I에 대하여 첫 번째 경간의 최대응답 발생위치인 3L/8 및 스팬 중앙인 L/2의 위치에서 변형률 응답이력곡선을 측정하고, 측정위치에 따른 중량추정의 정밀도를 검토하였다.
Table 10에 나타낸 것과 같이 거더에 대한 응답측정 위치에 따른 중량추정결과는 큰 차이가 없으므로, 최대응답이 발생하는 곳의 변형률 값을 사용하여 중량을 추정하는 것이 추정오차를 감소시킬 수 있을 것으로 판단된다.
Jung(2012)[14], Hwang et al.(2013)[16]의 연구에서도 경간의 L/2 및 L4에 대해 검토한 결과 유사한 경향이 나타나는 것으로 보고되었다.
한편, 교량의 거더형식은 상이하나 대상교량 I 및 대상교량 II의 수직보강재를 대상으로 상부플랜지 하면에서 각각 20mm 및 200mm 이격된 위치에 변형률 센서를 부착하여 차량정보 추정 결과의 차이를 조사하였다. 그 결과, 수직보강재에서의 센서 부착위치 차이로 인한 추정결과의 차이는 없는 것을 알 수 있었다
5. 결 론
이 연구에서는 BWIM알고리즘을 현장계측결과에 적용하고 차량주행 특성, 교량특성 및 계측조건의 영향인자가 BWIM에 의한 중량 추정결과에 미치는 정도를 비교 분석하여 다음과 같은 결론을 도출하였다.
(1)차량정보 추정시 교량특성의 영향인자에서 오차에 가장 큰 영향을 주는 것은 교량의 평면형상이다. 이는 평면형상의 차이로 인한 하중 횡분배 차이 때문이다. 향후 차량정보 추정을 위한 대상교량 선정시 직교를 선정하는 것이 바람직할 것으로 판단된다.
(2)수직보강재 변형률을 이용할 경우, 실제의 속도 및 1축과 2축 사이의 축간거리는 비교적 정확하게 추정할 수 있지만, 2축과 3축 사이의 축간거리는 양축의 간격이 좁아 각 축의 영향이 뚜렷이 나타나지 않고 추정오차도 속도가 증가할수록 커진다. 그러나 2축과 3축을 하나의 축으로하여 중량을 추정하면 만족할만한 중량추정결과를 얻을 수 있다.
(3)차량의 주행패턴에 따른 영향은 주행차로에 대한 영향선의 비를 이용하면 각 차량의 응답이력곡선을 추출할 수 있다. 축중량은 수직보강재의 응답을 이용하여 계산된 축중 분배율을 이용하면 정확도를 향상시킬 수 있을 것으로 판단된다.
(4)거더의 응답 측정위치 및 수직보강재의 센서 부착위치 차이는 차량정보 추정결과에 영향을 미치지 않는다.
(5)차량정보 추정을 위한 현장계측시 Sampling Rate는 100Hz 이상으로 하는 것이 바람직하다.
Acknowledgments
이 연구는 교육과학기술부와 한국연구재단의 지역혁신인력양성사업으로 수행된 연구결과입니다.
References
- Moses, F. (1979) Weigh-in-Motion System Using Instrumented Bridges, Transportation Engineering Journal of ASCE, American Society of Civil Engineers, Vol.105, No.3, pp.233-249.
- Peters, R.J. (1986) CULWAY – An Unmanned and Undetectable Highway Speed Vehicle Weighing System, Proceedings of the 13th ARRB Conference, Australian Road Research Board, Australia, pp.70-83.
- Žnidarič, A., and Moses, F. (1995) Bridge Weigh-in-Motion Testing of Vehicle Gross Weights in Slovenia, Proceedings of the 1st European Conference on Weigh-in-Motion of Road Vehicles, Swiss Federal Institute of Technology, Switzerland, pp.55-62.
- Dempsey, A.T., O’Brien, E.J., and O’Connor, J.M. (1995) A Bridge Weigh-in-Motion System for the Determination of Gross Vehicle Weights, Proceedings of the 1st European Conference on Weigh-in-Motion of Road Vehicles, Swiss Federal Institute of Technology, Switzerland, pp.239-249.
- Jacob, B. (Ed.) (2002) Weigh-in-Motion of Axles and Vehicles for Europe (WAVE), General Report, Laboratoire Central des Ponts et Chaussees, France, p.103.
- Jacob, B., O’Brien, E.J., and Jehaes, S. (Eds.) (2002) Weigh-in-Motion of Road Vehicle: Final Report of the COST 323 Action, Laboratoire Central des Ponts et Chaussees, France, p.538.
-
McNulty, P., O’Brien, E.J. (2003) Testing of Bridge Weigh-in-Motion System in Sub-Arctic Climate, Journal of Testing and Evaluation, American Society for Testing and Materials, Vol.31, No.6, pp.497-506.
[https://doi.org/10.1520/JTE12377J]

- Žnidarič, A., Lavrič, I., and Kalin, J. (2002) The Next Generation of Bridge Weigh-In-Motion System, Proceedings of the 3rd International Conference on Weigh-in-Motion (ICWIM3), Center for Transportation Research and Education (Iowa State University), USA, pp.219-229.
-
Žnidarič, A., Lavrič, I., and Kalin, J. (2008) Measurements of Bridge Dynamics with a Bridge Weigh-in-Motion System, Proceedings of the 5th International Conference on Weigh-in-Motion (ICWIM5), Laboratoire Central des Ponts et Chaussées, France, pp.485-498.
[https://doi.org/10.1002/9781118623305.ch39]

- Kobayashi, Y. (2003) Development of an Automatic Continuous Real-time Remote Monitoring System for Bridge Maintenance, Ph.D. Dissertation, Tokyo Institute of Technology, Japan, pp.28-32.
-
小塩達也(2006) 新しいBridge Weigh-in-Motionの開発と道路構造物の維持管理支援に関する研究, 博士学位論文, 名古屋大学大学院, 日本.
Ojio, T. (2006) Development of new Bridge Weigh-in-Motion Methods and its Applications to Maintenance of Highway Structures, Ph.D Dissertation, Nagoya University, Japan (in Japanese). -
박민석(2008) 인공신경망을 이용한 교량의 주행중 차량하중분석시스템 개발, 박사학위논문, 한양대학교.
Park, M.-S. (2008) Development of Bridge Weigh-in-Motion Systems without Axle Detector Using Artificial Neural Network, Ph.D. Dissertation, Hanyang University, Korea, pp.120-130 (in Korean). [ https://doi.org/10.1201/9781439828434.ch432 ]
-
한아름샘, 신수봉(2011) 밀도추정함수와 평균보정계수를 이용한 BWIM 알고리즘의 현장실험 적용, 구조물진단학회지, 한국구조물진단유지관리공학회, 제15권, 제2호, pp.70-78.
Han, A.R.S., and Shin, S. (2011) Application for a BWIM Algorithm Using Density Estimation Function and Average Modification Factor in the Field Test, Journal of the Korea Institute for Structural Maintenance Inspection, KSMI, Vol.15, No.2, pp.70-78 (in Korean). [ https://doi.org/10.11112/jksmi.2011.15.2.070 ]
-
정민선(2012) 교량의 이론적 응답에 기초한 BWIM 활용방안에 관한 연구, 석사학위논문, 한국해양대학교.
Jung, M.-S. (2012) A Study on the Utilization of BWIM Using Theoretical Response of Bridge, Master’s Thesis, Korea Maritime & Ocean University, Korea (in Korean). -
이성진, 경갑수, 박진은, 이희현(2012) 주행차량에 따른 개단면 강바닥판 교량의 국부거동 특성, 한국강구조학회논문집, 한국강구조학회, 제24권, 제1호, pp.101-108.
Lee, S.J., Kyung, K.S., Park, J.E., and Lee, H.H. (2012) Characteristic of Local Behavior in Orthotropic Steel Deck Bridge with Open Ribs according to Running Vehicle, Journal of Korean Society of Steel Construction, Vol.24, No.1, pp.101-108 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.1.101 ]
-
황효상, 경갑수, 이희현, 전준창(2013) BWIM방법을 이용한 차량 정보 추정시 정밀도 향상 방안에 관한 연구, 한국안전학회지, 한국안전학회, 제28권, 제1호, pp.63-73.
Hwang, H.-S., Kyung, K.-S., Lee, H.-H., and Jeon, J.-C. (2012) A Study on Accuracy Improvement for Estimation of Vehicle Information Using BWIM Methodology, Journal of the Korea Society of Safety, KOSOS, Vol.28, No1, pp.63-73 (in Korean). [ https://doi.org/10.14346/JKOSOS.2013.28.1.063 ]
-
김병화, 박민석, 여금수, 김수진(2010) 교량바닥판의 동적 변형률응답을 이용한 민감도 기반 BWIM 시스템, 한국소음진동공학회지, 한국소음진동공학회, 제20권, 제7호, pp.620-628.
Kim, B.H., Park, M.S., Yeo, K.S., and Kim, S.J. (2010) Sensitivity-Based BWIM System Using Dynamic Strain Responses of Bridge Deck Plate, Transactions of the Korean Society for Noise and Vibration Engineering, KSNVE, Vol.20, No.7, pp.620-628 (in Korean). [ https://doi.org/10.5050/KSNVE.2010.20.7.620 ]
- COST 323 Management Committee (1997) European Specification on Weigh-in-Motion of Road Vehicles, Draft 2.2, EUCO-COST/323/6/97, Laboratoire Central des Ponts et Chaussées, France.
-
玉越隆史, 中洲啓太, 石尾真理, 中谷昌一(2004) 道路橋の交通特性評価手法に関する研究: 橋梁部材を用いた車両重量計測システム, 国土技術政策総合研究所資料 第188号, 国土交通省国土技術政策総合研究所, 日本.
Tamakoshi, T., Nakasu, K., Ishio, M., and Nakatani, S. (2004) Study on Evaluation Method of the Traffic Characteristics on Highway Bridges: Bridge Weigh-in-Motion System, Technical Note of NILIM No.188, National Institute for Land and Infrastructure Management, Japan (in Japanese). - Lee, H.H. (1985) Impact Factor of Moving Load Due to Surface Roughness of Girder Bridge of Variable Span, Master’s Thesis, Asian Institute of Technology, Thailand, pp.12-16.
-
이희현(1990) 도로형교의 동적 거동에 관한 연구, 박사학위논문, 한양대학교, pp.624-635.
Lee, H.H. (1990) A Study on Dynamic Behavior of Highway Girder Bridges, Ph.D. Dissertation, Hanyang University, Korea, pp.624-635 (in Korean). -
Lee, H.-H., Jeon, J.-C., and Kyung, K.-S. (2012) Determination of a Reasonable Impact Factor for Fatigue Investigation of Simple Steel Plate Girder Railway Bridges, Engineering Structures, Elsevier, Vol.36, pp.316-324.
[https://doi.org/10.1016/j.engstruct.2011.12.021]

-
Chang, D., and Lee, H. (1994) Impact Factor for Simple-Span Highway Girder Bridges, Journal of Structural Engineering, American Society of Civil Engineers, Vol.120, No.3, pp.704-715.
[https://doi.org/10.1061/(ASCE)0733-9445(1994)120:3(704)]

-
李熙賢(2007) 桁形式鋼道路橋の疲労寿命評価法と疲労設計用衝撃係数の検討, 博士学位論文, 法政大学, 日本, pp.1-6.
Lee, H.H. (2007) Investigation of Fatigue Life Evaluation Method and Impact Factor for Fatigue Design of Steel Highway Girder Bridges, Ph.D. Dissertation, Hosei University, Japan, pp.1-6 (in Japanese). -
전준창, 경갑수, 강신화, 이희현(2011) 플레이트 거더교 수직보강재 응답의 BWIM 시스템 적용성 연구, 대한토목학회 2011년 학술발표대회 논문집, 대한토목학회, pp.82-85.
[https://doi.org/10.1111/j.1600-0390.2011.00406.x]