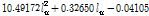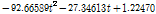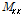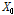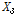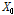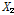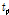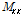폐단면 리브 보강판의 국부 거동 특성

1. 서 론

보강판은 콘크리트 바닥판 대신 사용하면 자중을 줄일 수 있다는 장점이 있어 교량, 주차 시설 등 건설 분야에서 많이 사용되고 있으며, 바닥판으로 사용하는 보강판의 경우 보강재가 촘촘히 배치되어 기하학적 직교이방성 거동을 나타내게 된다^[1],[2].

이러한 성질을 이용하여 강바닥판을 간편하게 직교이방성 판으로 해석하는 경우 강판에서 발생하는 국부 거동을 고려할 수 없다는 등의 문제점을 갖게 되며, 이러한 강바닥판의 직교이방성 해석에 대한 여러 문제점을 해결하기 위하여 연구가 활발히 진행되어 왔으나, 대부분 개단면 리브를 갖는 보강판에 국한되어 연구가 진행되어 왔다^[3],[4].

또한 큰 비틀림 강성으로 효율적인 구조를 갖게 된다는 장점으로 실 교량의 강바닥판에 사다리꼴 형태의 폐단면 리브가 많이 사용되고 있음에도 불구하고, 폐단면 리브를 갖는 보강판의 경우 그 거동 분석이 어려워 강바닥판 연결부 상세에 대한 국부 거동, 피로 거동 등 주로 실험적 연구가 진행되어 왔다^[5],[6].

본 연구에서는 사다리꼴 리브를 갖는 여러 보강판의 국부 처짐과 국부 모멘트에 대한 분석을 통하여 국부 거동 특성을 파악하고, 이를 정형화하여 사용자가 쉽게 폐단면 리브 보강판의 국부 거동을 예측할 수 있는 방법을 제공함으로써 폐단면 리브 보강판을 직교이방성 판으로 해석하는 경우에도 국부 거동을 고려할 수 있도록 하고자 한다.

2. 해석 예제

2.1 예제 제원

폐단면 리브를 갖는 보강판의 치수를 Fig. 1과 같이 정의하고, 실 교량에 적용된 사례를 나타내면 Table 1과 같다.

본 연구에서는 Table 1의 실 교량 사다리꼴 리브 제원을 고려하여 리브 안쪽 각도 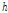는 200~300mm를 고려하였으며, 해석 예제의 각 제원을 정리하여 나타내면 Table 2와 같다.

2.2 하중 Case

하중은 양변 단순지지된 폭 6m, 길이 3m의 폐단면 리브 보강판에 총 100kN을 작용시켰으며, Fig. 2(a)와 같이 보강판 중앙에 위치한 강판 위 10cm×10cm의 정사각형에 하중 가 리브 위에 작용하는 경우 전체 거동(G)만 발생한다고 가정하여 그 차이를 국부 거동(L)으로 정의하였다^[7].

리브 배치에 따라 폐단면 리브가 보강판 중앙에 위치하는 경우를 모델 A로, 중앙에 리브 사이 강판이 위치하게 되는 경우를 모델 B로 정의하고, 하중 가 작용하는 경우에 대하여 강종 SM 490인 모든 부재를 12.5mm×12.5mm 크기의 4절점 판 요소로 모델링 한 뒤, 범용해석 프로그램인 MIDAS로 해석한 결과를 나타내면 Fig. 3 및 4와 같다.

본 연구에서는 Fig. 3 및 4에 나타낸 Model A와 B의 결과를 같은 기준으로 분석하기 위하여, 강판과 리브 복부가 이루는 각도를 로 표현된다.

3. 국부 거동 특성 분석

기존 연구^[7]에 따르면 하중이 작용하는 패널의 폭이 폐단면 리브 보강판의 국부 거동에 미치는 영향이 가장 크므로, 본 연구에서는 Model A와 Model B를 같은 기준으로 분석하기 위하여, 하중이 작용하는 패널의 폭을 라 정의한 뒤 폐단면 리브 보강판의 국부 거동을 분석하고자 한다.

3.1 개별 함수

제원에 따른 여러 가지 보강판의 국부 거동을 분석하기 위하여, Table 2에 나타낸 폐단면 리브 보강판의 제원 중 하중이 작용하는 패널의 폭 는 250mm를 기준 제원으로 설정하고, 식 (1)～(5)에 나타낸 것과 같이 각각의 제원별로 다른 제원은 동일한 상태에서 해당 제원이 변화된 보강판의 결과를 기준 제원을 갖는 보강판의 결과로 나눈 비율을 구한 뒤, 그 비율들을 이용하여 폐단면 리브 보강판에서 발생하는 국부 거동 특성을 분석하고자 한다.

재하패널폭 (1)

판두께 (2)

리브두께 (3)

리브높이 (4)

재하옆패널폭 (5)

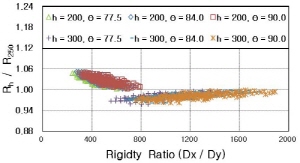
Table 2에 나타낸 총 1,296 가지 보강판에 대한 국부 처짐 해석 결과를 식 (1)～(5)에 정의한 바와 같이 다른 모든 제원은 동일한 경우에 각 제원별로 기준 제원을 갖는 보강판 대비 해당 제원이 변화한 보강판의 국부 거동 비율로 나타내면, Model A의 경우 Fig. 5, Model B의 경우 Fig. 6과 같다. 이때, 보강판의 양방향 휨강성 비( Rigidity Ratio: RR)는 식 (6)과 같이 정의하였다.

 (6)

Fig. 5와 6의 국부 처짐 비율을 살펴보면, Model A와 B 모두 재하 패널 폭( )와는 달리 강성비에 따른 차이는 거의 없음을 알 수 있다.

또한 Model A와 Model B 모두 재하 패널 폭( )의 비율은 강성비에 따라 약간의 분포 양상을 나타내나 그 차이가 크지 않음을 알 수 있으며, 그 비율 값과 양상 면에서 Model A와 B가 유사함을 알 수 있다.

각 제원별 국부 거동 비율을 나타낸 Fig. 5와 6에서 각 제원 크기별 비율의 중앙값을 구하여 Model A와 B에 대하여 각각의 리브 각도별로 나타내면 Fig. 7 및 Fig. 8과 같다.

Fig. 7 및 8을 살펴보면, 각 제원별 국부 거동 비율은 각 제원 변화에 따라 일정한 양상을 나타내고, Model A와 Model B 모두 각도에 따른 차이는 매우 작으며, Model A와 Model B 사이의 차이도 크지 않음을 알 수 있다.

이러한 양상은 국부 모멘트 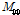에서도 유사하게 나타났으며, 이러한 점을 이용하여 각각의 국부 거동에 대하여 리브 각도별 기준 보강판의 값과 제원별 비율 함수를 나타내면, Model A의 경우 Table 3, Model B의 경우 Table 4와 같다.

Table 3 및 4에 나타낸 기준 보강판의 국부 처짐 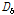를 이용하면, 임의 

제원 보강판의 국부 처짐( )은 식 (7)과 같이 기준값에 제원 변화에 따른 비율 함수를 곱하여 산정할 수 있다.

 (7)

국부 모멘트 는 식 (8) 및 (9)와 같이 구할 수 있다.

 (8)

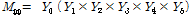 (9)

3.2  통합 함수

각 제원별 비율 함수는 Fig. 7 및 8에서 보듯이 강판과 리브 복부판이 이루는 각도( )의 함수로 표현하여 나타내면 Table 5와 같다. 이때, Model A의 90°와 Model B의 90° 는 두 값의 평균값을 대표 값으로 하였다.

앞서 Table 3과 4에 나타낸 개별 함수와 Table 5에 나타낸 각도 및 Model 통합 함수를 식 (7), (8), (9)에 대입하여 계산한 값을 실제 해석한 결과와 비교하여 각 각도별 오차율 범위로 표현하여 나타내면 Table 6과 같다.

Table 6에서 먼저 국부 처짐과 국부 모멘트의 오차율을 비교해보면, 국부 모멘트에 비하여 국부 처짐의 오차율 범위가 크다는 것을 알 수 있으며, 국부 모멘트의 경우 모두 ±1% 미만의 오차율 범위를 나타내어 상당한 정확도를 가짐을 알 수 있다.

국부 처짐의 오차율을 자세히 살펴보면, 각각의 Model별로 리브와 강판사이의 각도 에 따라 나타내었던 개별 함수를 사용한 경우 오차율 범위가 –2.31~+2.31%를 나타내었으며, 각도 및 Model 통합 함수를 사용한 경우 –4.06~+4. 07%를 나타내어 통합에 따라 약간의 오차율 증가가 발생하나, 그 크기가 크지 않음을 알 수 있다.

또한, 국부 모멘트 는 개별 함수를 사용하는 경우 오차율 범위가 –0.49~+0.49%를, 각도 및 Model 통합 함수를 사용한 경우 –0.57~+0.57%를 나타내어 통합에 따른 오차율 증가가 크지 않으며 실제 값과의 오차율이 모두 ±1% 미만으로 상당한 정확도를 나타냄을 알 수 있다.

국부 모멘트 와 마찬가지로 모든 경우에 오차율이 모두 ±1% 미만으로 상당한 정확도를 나타냄을 알 수 있다.

이상의 결과로부터, 각도( 는 ±1% 정도의 오차율 범위에서 국부 거동 결과를 얻을 수 있음을 알 수 있다.

3.3 임의 제원에 대한 적용성

본 연구에서 제안한 함수의 적용성을 살펴보기 위하여, Table 2에 나타낸 제원 이외의 다른 제원을 갖는 총 13가지 임의 제원 보강판을 선택하였으며, 그 중 Case 1～6은 예제 제원에서 하나의 제원만 임의 제원을 갖는 경우를, Case 7～13은 예제 제원에서 여러 제원이 동시에 변화된 경우를 고려하였으며, Table 7에 연구에서 사용한 기본 보강판과 임의 제원 보강판에 대한 제원 및 그 결과를 비교하여 나타내었다.

Table 7의 해석 결과 중 먼저 Case 1～6에 나타낸 하나의 제원만 변한 경우를 살펴보면, 리브 두께( )에 비하여 62.5% 만큼 큰 변화를 주었기 때문에 나타난 현상으로 판단되며, 그럼에도 불구하고 모든 국부 거동이 ±1% 이내의 오차율을 나타내어 상당한 정확도를 가짐을 알 수 있다.

또한 여러 개의 제원이 변하는 경우 중 Case 10과 11의 경우 기본 보강판에 비하여 국부 처짐에서 약간의 오차율 증가가 발생함을 알 수 있으나, 본 연구 해석 예제의 오차율 범위가 –4.06~+4.07% 임을 고려할 때, 임의 제원 보강판의  오차율은 타당한 범위의 값임을 알 수 있다.

이상의 결과로부터, 본 연구에서 제안한 통합 함수는 임의 제원을 갖는 보강판에도 잘 적용됨을 확인할 수 있었다. 

4. 재하 크기가 다른 경우에 대한 적용

본 연구에서 사용한 재하 크기와 다른 경우에 제안한 통합 비율 함수가 적용 가능한지 살펴보기 위하여, 먼저, 각 제원 변화에 따른 민감도 분석을 실시하고, 이를 이용하여 각각의 재하 크기에 맞는 보정 함수를 제안하고자 한다.

4.1 민감도 분석

민감도 분석을 위해 사용한 제원은 Table 8과 같으며, 리브 폭 방향 재하 크기를 라 하였을 때, 각각 10, 20, 30cm 씩 총 9가지 경우를 고려하였으며, 각 재하 크기별 기준값은 Table 9와 같다.

Table 9에 나타낸 각 재하 크기별 기준값과 Table 5의 통합 비율 함수를 적용하여 국부 거동을 계산한 뒤, 실제 해석 결과와 비교하여 오차율로 나타내면 Table 10과 같다.

Table 10에서 기본 재하 크기 10×10의 오차율과 비교하여 살펴보면, 리브 상부폭 )의 경우 재하 크기가 커짐에 따라 오차율이 2% 내외까지 증가하나 그 크기가 크지 않으며, 다른 제원들의 오차율 증가는 매우 작음을 알 수 있다.

따라서 재하 크기 10×10을 기준으로 제안한 통합 비율 함수 중 리브 상부폭 에 따라 보정할 필요가 있음을 알 수 있다.

4.2 재하 크기에 따른 통합 함수의 보정

Table 2에 나타낸 해석 예제 중 다른 제원은 동일하고, 각도( 로 표현됨을 알 수 있었다.

 (10)

 (11)

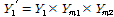 (12)

Table 11에 나타낸 재하 크기 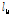)의 보정 함수를 적용한 뒤 그 결과를 적용하기 전과 비교하여 나타내면 Table 12와 같다.

Table 12 중 국부 처짐을 살펴보면, 최대 30%를 나타내던 오차율이 보정 함수 적용 후 약 6% 정도로 줄어들었음을 알 수 있으며, 국부 모멘트 도 최대 27%이던 오차율이 보정 함수 적용 후 약 4% 이내로 줄어들어 보정 함수의 효과를 확인할 수 있었다,

이상의 결과로부터 재하 크기가 다른 경우에도 Table 11에 나타낸 재하 패널 폭( 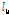)의 보정 함수와 Table 5에 나타낸 제원별 통합 함수 및 Table 9의 기준값을 사용하면 간편하게 타당한 결과를 얻을 수 있음을 알 수 있다.

5. 결 론

본 연구에서는 사다리꼴 폐단면 리브를 갖는 보강판에 대하여 제원 변화에 따른 국부 거동 양상을 파악하고, 재하크기 변화까지 고려한 보정 방법을 정형화하여 함수로 제안하였으며, 그 결과를 정리하여 나타내면 다음과 같다.

(1)폐단면 리브 보강판의 국부 처짐과 국부 모멘트는 하중재하 패널 폭, 판 두께, 리브 두께, 리브 높이, 옆 패널 폭 변화에 따라 일정한 비율을 나타내며, 기준 제원을 갖는 보강판의 국부 거동은 강판과 리브가 이루는 각도의 함수로 표현됨을 알 수 있었다.

(2)임의 제원을 갖는 폐단면 리브 보강판의 국부 거동은 기준 제원 보강판의 결과에 하중 재하 패널 폭, 판 두께, 리브 두께, 리브 높이, 옆 패널 폭에 대한 통합 비율 함수를 곱하여 간편하게 산정할 수 있었다.

(3)해석 예제에서 고려하지 않은 제원을 갖는 보강판에 통합 비율 함수를 적용한 결과 오차율 증가가 크지 않아 본 연구의 적용성을 확인할 수 있었으며, 재하 크기가 다른 경우에 적용한 결과 하중 재하 패널 폭의 비율 함수에 대한 보정이 필요함을 알 수 있었다.

(4)통합 비율 함수 중 재하 패널 폭의 비율 함수에 재하 크기에 따른 보정 함수를 곱한 결과 오차율이 국부 처짐은 6%, 국부 모멘트는 4% 정도로 크게 개선되어 재하 크기에 대한 보정 함수의 적용성을 확인 할 수 있었다.

따라서, 본 연구에서 제안한 기준값 및 통합 비율 함수와 보정 함수를 사용하면, 간편하게 임의 제원의 폐단면 리브를 갖는 보강판의 국부 처짐과 국부 모멘트를 산정할 수 있을 것으로 사료된다.

References

• Hambly, E.C. (1991) Bridge Deck Behaviour (2nd Ed.), E & FN SPON, UK.
• Troitsky, M.S. (1992) Orthotropic Bridges: Theory and Design, The James F. Lincoln Arc Welding Foundation, USA.
• 정충열(2008) 직교이방성 판요소를 이용한 개단면 리브 보강판의 정적 해석, 석사학위논문, 세명대학교.
  Jeong, C.Y. (2008) The Static Analysis of Plates Stiffened with Open Ribs Using the Orthotropic Plate Element, Master’s Thesis, Semyung University, Korea (in Korean).
• 주석범(2012) 보강판 제원에 따른 개단면 리브 보강판의 국부 처짐과 국부 모멘트의 정형화, 한국강구조학회논문집, 한국강구조학회, 제24권, 제6호, pp.659-670.
  Chu, S.B. (2012) Formulating the Local Displacement and Local Moments of a Plate Stiffened with Open Ribs According to the Dimensions of Stiffened Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.​6, pp.659-670 (in Korean). [ https://doi.org/10.7781/kjoss.2012.24.6.659 ]
• 오순택(2006) 강바닥판교의 설계 및 시공성 향상방안: 강바닥판교 3차원 실물 모형체의 피로강도, 한국강구조학회논문집, 한국강구조학회, 제18권, 제1호, pp.23-32.
  Oh, S.T. (2006) Improvement of the Design and Construction Technique of Orthotropic Steel Deck Bridges: Fatigue Strength of Three Dimensional Full-Scaled Model, Journal of Korean Society of Steel Construction, KSSC, Vol.18, No.1, pp.23-32 (in Korean).
• 선창원, 박경진, 경갑수, 김교훈(2008) 세로리브 내부 보강상세에 따른 강바닥판 연결부의 피로거동 특성에 관한 해석적 연구, 한국강구조학회논문집, 한국강구조학회, 제20권, 제1호, pp.105-119.
  Sun, C.W., Park, K.J., Kyung, K.S., and Kim, K.H. (2008) Analytical Study on the Characteristic of Fatigue Behavior in Connection Parts of Orthotropic Steel Decks with Retrofitted Structural Details in Longitudinal Rib, Journal of Korean Society of Steel Construction, KSSC, Vol.​20, No.1, pp.105-119 (in Korean).
• 주석범, 이중재, 윤안영(2011) 재하위치에 따른 폐단면 리브 보강판의 국부거동, 한국강구조학회 2011년 학술발표대회 논문집, 한국강구조학회, pp.231-232.
  Chu, S.B., Lee, J.J., and Yun, A.Y. (2011) The Local Behavior of Plates Stiffened with Closed Ribs According to the Loading Position, Proceedings of Annual Conference of Korean Society of Steel Construction, KSSC, pp.​231-232 (in Korean).