
내진 강판전단벽시스템의 변형모드에 따른 스트립앵글 변화
ⓒ KSSC 2013
초록
횡하중을 받는 고층건물에서의 인장역이 형성될 때 강판전단벽의 앵글 변화한다. 본 연구에서는 강판전단벽을 갖는 3층, 9층, 14층 및 20층의 4개 구조물에 대한 유한요소해석 연구를 하였다. 유한요소해석 결과와 각 모델들의 이론식으로 계산된 결과를 비교하여 전단변형 모드와 휨변형 모드로 분류하였다. 전단변형 모드의 모델에서는 주응력 벡터가 일정한 경사각을 이루며 인장역을 발생시킨 반면 휨변형 모델에서는 인장역의 변화는 기존의 이론식과 차이를 보였다.
Abstract
This study investigated the tension-field action induced strip angle changes and deformed mode shapes of SPSW for high-rise structures subjected to lateral forces. Based on the numerical analysis 3, 9, 14 and 20 story structures, shear and flexural modes were identified by comparing the numerical analysis results to the predicted strength by theory. Shear deformation mode exhibited a constant angle in tension-field; whereas, flexural mode of the numerical results, differed from the tension-field action theory.
키워드:
박강판전단벽, 인장역, 스트립앵글, 주응력벡터, 변형모드Keywords:
steel plate shear wall(SPSW), tension-field, strip angle, principal stress vector, deformation mode1. 서 론
1.1 연구배경
최근 건축물의 고층화 및 대형화 추세에 따라 연직하중 외에 지진이나 바람과 같은 횡하중에 저항하도록 설계하여야 하며, 사용성에 있어서 횡변위와 층간변위의 조절 또한 필수적인 요소가 된다. 일반적인 중층 이상의 건물에서 수평력과 횡변위를 제어하기 위한 횡력저항 시스템으로 가새골조시스템이 주로 사용되고 있으나 최근 미국 및 캐나다를 중심으로 강도와 강성이 크고 연성이 우수한 얇은 강판을 사용한 횡력저항시스템에 관한 연구가 활발하게 진행되고 있다[1],[2],[3]. 강판전단벽시스템(Steel Plate Shear Wall Systems, SPSW)은 풍하중과 지진하중과 같은 횡력에 효과적이며, 얇은 강판을 사용함으로써 자중감소 및 지진하중을 저감시킬 수 있는 내진저항성능이 뛰어난 시스템으로 알려져 있다[4],[5],[6],[7]. 하지만, 국내에서는 강구조의 내진설계 기준에 이 시스템이 포함되어 있으나 관련 연구 수준이 초기단계에 머물러 있으며, 강판전단벽 구조시스템을 보다 쉽게 적용할 수 있는 방법을 제시하지 못하고 있는 실정이다[4],[8].
1.2 이론적 배경
강판전단벽시스템은 내부패널의 형태에 따라 보강 강판전단벽과 무보강 강판전단벽으로 구분된다. 보강 강판전단벽은 강판을 스티프너로 보강하여 강판이 항복하기 전에 전단좌굴 현상을 방지하는 시스템인 반면, 무보강 강판전단벽은 강판의 전단좌굴 이후에 인장역작용(Tension Field Action)이 일어날 수 있도록 설계하여 외력에 의한 층전단력을 저항할 수 있도록 하는 시스템이다. 따라서 무보강 강판전단벽은 구조물의 파괴 시 강판의 대체만으로 보수보강이 이루어질 뿐만 아니라 얇은 강판의 인장역작용에 의해 큰 연성 능력을 확보할 수 있다. 무보강 강판전단벽은 Thorburn 등(1983)[1]에 의해 강판전단벽을 인장역작용에 따른 연속적인 트러스 부재로 대체하는 스트립모델로 대체할 수 있다고 제안하였다. 스트립모델은 Fig. 1과 같이 전단패널을 연속된 스트립으로 모델링하고 스트립은 단지 인장력만 받으며 패널 내에서 일정한 경사각을 갖는 모델이다. AISC Seismic Provision[9]에서는 스트립모델로 설계할 경우 인장역의 경사각과 스트립의 단면적을 고려하도록 구성되어 있다.
무보강 강판전단벽을 이용하려는 연구는 1980년대 이래로 Driver 등(1997)[10] 및 Berman and Bruneau(2003)[11]에 의해 많은 실험 및 해석연구가 진행되어 왔다. 기존의 연구는 저층 건물에서의 전단지배형 강판전단벽 구조물에 관한 연구가 대부분이었으며, 휨강성에 영향을 받는 고층건물에서는 정확한 강도 예측이 어렵다는 것을 Seilie and Hooper (2005)[12]가 제안한 바 있다. 강판전단벽에서 전도모멘트에 저항하기 위한 변수 폭을 경계면의 기둥을 사용하기 때문에 벽체의 휨이 전단을 지배할 때 전도모멘트에 의해 기둥에 더 큰 축력과 휨모멘트가 작용하게 된다. Fig. 2에서 보는 바와 같이 일반적으로 높이/경간 비가 작은 저층 구조물은 강판패널이 항복할 때 경계골조는 탄성범위에 있도록 설계되므로 최하층 기둥 단부에서 소성힌지를 형성하게 되는 이상적인 메커니즘을 갖는다. 그러나 고층구조물의 경우 작용하는 횡력에 따라 기둥에서 추가적인 전도 휨모멘트와 축력의 분배로 인하여 기둥 내부에서 소성힌지가 발생할 가능성이 높다[12].
이와 같이 휨강성이 전단력을 지배하는 고층구조물에서 횡력이 작용할 때 메카니즘의 변화는 Fig. 3과 같이 강판의 스트립앵글을 변화시킬 수 있을 것으로 판단된다[13].
1.3 연구 목적 및 내용
전도모멘트라 불리는 휨모멘트는 건물의 상부에서 하부로 갈수록 증가하며 벽체내부의 수직경계면 단부에서 인장력과 압축력을 발생시킨다. 높이와 수평길이의 비가 1이하인 짧고 강성이 큰 전단벽은 지진하중 작용 시 전단에 의해 지배된다. 반면 높이와 수평길이의 비가 2이상인 길고 유연한 전단벽은 Fig. 4와 같이 휨에 의해 지배된다. 하지만 기존의 연구에서는 휨에 영향을 받는 고층구조물의 강판전단벽시스템에 관한 연구는 거의 찾아볼 수 없다. 따라서 본 연구에서는 범용구조해석 프로그램인 ANSYS 14.5를 사용하여 강판전단벽시스템 고층구조물의 초기변형을 고려하여 비선형 해석에 적용할 수 있는 최적의 모델을 선정하고, 중․고층구조물의 강판전단벽 좌굴모드에 관한 연구와 높이 변화에 따른 스트립앵글의 변화에 관한 연구를 통하여 강판전단벽 설계 시 고려해야 할 기초 자료를 제시하고자 한다.
2. 유한요소해석 모델의 유효성 검증
2.1 검증모델의 개요
본 연구를 진행하기 전, Driver 등(1997)[10]에 의하여 수행되었던 4층의 강판전단벽 실물대 실험 및 해석결과를 비교․검토하여 본 연구에 사용될 모델의 적합성을 검증하고자 한다. 실험체의 형상은 실험체 하부에서 최상층 기둥까지의 높이 7.4m, 경간폭은 3.4m이고, 상부 3개 층의 층간 높이는 1.83m, 1층의 높이는 1.93m이고 기둥의 중심간 거리는 3.05m로서 Fig. 5와 같이 구조물의 1/2 축척으로 제작되었다. 모든 보와 기둥 단면은 캐나다 강구조 규준[14]의 class1 조밀단면을 사용하였다. 가력방법은 각 층의 보에 액츄에이터를 설치하여 횡방향 반복가력을 수행하였으며, P-Δ효과에 의한 전단벽의 거동을 고려하기 위해 기둥 상부에서 수직하중을 가하였다.
2.2 요소 설정
유효성 검증 해석을 위하여 기둥과 보는 beam요소를 사용하였고 강판전단벽은 shell 요소를 사용하여 모델링 하였다 (Fig. 6). 기둥과 보는 ANSYS 프로그램의 ‘BEAM 189’요소를 사용하여 축인장, 휨, 단면의 비틀림을 고려하였다. 이 요소는 각각의 절점에서 6개 또는 7개의 자유도를 갖고 면외변형을 고려할 수 있는 요소이다. 강판전단벽에 사용되는 얇은 강판을 해석하기 위해 ‘Shell 181’요소를 사용하였다. 이 요소는 x, y, z축의 변형과 회전에 대한 6개의 자유도를 가진 4절점 요소 이므로, 강판의 면외변형 거동을 설명할 수 있다.
2.3 재료 물성
모든 재료모델은 탄소성 변형도경화 효과를 고려하기 위하여 접선계수(
 )를 이용한 BKIN(Bilinear Kinematic Hard-ening)방법으로 모델링 하였고, Driver 등에 의해 수행된 인장시험결과를 바탕으로 응력-변형도 곡선을 생성하였다. 해석에 사용한 재료물성은 Table 1과 같다.
)를 이용한 BKIN(Bilinear Kinematic Hard-ening)방법으로 모델링 하였고, Driver 등에 의해 수행된 인장시험결과를 바탕으로 응력-변형도 곡선을 생성하였다. 해석에 사용한 재료물성은 Table 1과 같다.
2.4 모델 형상 및 요소 분할
모든 기둥과 보는 선 요소로 모델링 하였으며, 기둥요소는 강판요소와 직접 접합하기 위하여 기둥 단면의 중심축을 강판의 가장자리로 이동시켜 편심축 상에 놓이도록 하였다. 보 요소는 강판요소와의 접합을 위하여 보 단면을 중심으로 하여 상하로 수직의 Outrigger를 사용하여 강판요소에 직접 접합하였다. 또한 Fig. 7에서 보는 바와 같이 P-Δ효과를 고려하기 위하여 상부 기둥 끝에서 기둥 중심까지 내민보를 설치하였고, 요소의 분할은 1층의 강판요소를 6x9, 2층과 3층은 5x9, 최상층 강판요소는 4x9으로 분할하였다. 기둥요소는 강판요소와의 노드를 공유하기 위해 각각의 강판요소가 분할된 개수만큼 분할하였고, 보 요소는 Outrigger요소와의 연결을 위하여 18개의 요소로 분할하였다.
2.5 하중 및 경계조건
최하층 기둥과 강판의 밑면은 모든 자유도에 대하여 완전히 구속시켰다. 그 외의 다른 노드들은 모든 방향에서의 변위 및 회전에 자유로우며, P-Δ효과를 고려하기 위하여 Fig. 8(a)와 같이 최상층 내민보에 720kN의 수직하중을 적용하였다. 또한, 실제 구조물과 유사한 초기상태를 모델링하기 위하여 면내 방향으로 구조물에 크게 영향을 미치지 않도록 1kN의 단위하중을 적용하여 정적해석을 수행한 후, 전단벽에 대한 고유치 좌굴해석을 수행하였고, 이로 부터의 최하층 강판 면외변형은 초기결함(Initial Imperfection)을 고려한 초기변형으로 적용하였다. 소성해석을 위한 하중은 2층 바닥 보의 한 절점에서 80mm까지 변위제어를 통해 이루어졌다.
2.6 해석결과
유효성 검증을 위한 유한요소해석 결과는 Driver 등에 의해 수행된 실험결과에 비하여 Fig. 9와 같이 다소 낮은 초기강성을 보임을 알 수 있었다. 이는 경계골조의 실제 응력-변형률 특성과 낮은 응력단계에서 강판전단벽의 특성이 잘 고려되지 않았기 때문으로 사료된다. 또 다른 이유는, Driver 등의 실험은 기둥-보 모멘트접합을 사용한 반면, 본 해석에 사용된 모델은 강판의 가장자리에 발생하는 응력 집중현상을 막기 위하여 핀 접합으로 모델링하였기 때문이다.
하지만 연구에 사용된 본 모델은 Table 2에서 보는 바와 같이 실제 항복강도 및 극한강도에서 2.1%와 3.9%의 오차를 나타냄으로써 상당히 유사한 거동을 보임을 알 수 있었다.
해석을 통하여 강판전단벽의 재료물성은 전체 강도에 영향을 미치므로 정확하게 모델에 반영되어야함을 알 수 있었다. 비록 강판의 초기결함을 고려한 모델을 적용하였음에도 불구하고, 강판전단벽 구조물의 전반적인 강도에는 크게 영향을 미치지 못하였다. 따라서 유효성 검증 해석결과를 종합하여 볼 때, 본 해석모델이 강판전단벽을 적용한 고층구조물의 거동 예측을 위한 해석모델로 적합한 것으로 판단된다.
3. 변수 해석 연구
현재의 내진규정은 강판전단벽의 형상비(폭:높이)를 0.8∼2.5로 제한하고 있다. 기존 Rezai[15]가 수행한 연구에서와 같이 약한 경계골조와 형상비가 0.8 이하인 단순화된 스트립 모델을 사용하여 해석을 수행한 결과 정확한 스트립앵글을 예측하지 못하였다. 이는 휨지배형 고층구조물은 기둥에서 전도모멘트에 의하여 발생하는 큰 축력과 휨력에 의해 전단벽의 강성을 감소시키기 때문에 전단지배모드에서 강판 변형을 갖는 스트립 모델과는 다소 차이가 있고, 강판전단벽을 설치한 고층구조물은 저층의 큰 형상비를 갖는 강판전단벽 구조물에 비하여 경계골조의 큰 휨 성능이 요구된다. 이에 따라 강판이 부담하는 전단력 또한 커질 수 있기 때문에 강판전단벽 구조물의 항복 시 발생하는 강판의 인장역 변화에 대한 고찰이 필요하다. 이러한 고층구조물에서의 횡력에 의한 소성 메카니즘을 살펴보기 위해 높이 변화를 변수로 하는 모델을 선정하여 구조물 거동 및 강판의 변형에 관한 변수 해석연구를 수행하고자 한다. 강판의 면외변형에 대한 불완전한 모델을 적용하기 위하여 1차 정적해석(Static Analysis), 2차 고유치 좌굴해석(Eigen-value Buckling Analysis), 3차 소성해석 순으로 변수해석 연구를 진행하였다.
3.1 재료 모델
유효성 검증에 사용된 유한요소모델을 기초로, 전도모멘트의 영향을 살펴보기 위하여 층 높이 3.96m, 경간 4.57m의 3층, 9층, 14층, 및 20층의 구조물을 대상으로 유한요소해석을 수행하였다. 강판의 두께는 층전단력에 저항하기 위하여 AISC Provision에 규정된 요구성능을 만족하도록 설계하였고, 기둥과 보는 한계상태설계법에 근거하여 설계하였다. 변수해석에 사용된 강판의 재료모델은 SS400 강재의 물성치인 항복응력 235MPa, 탄성계수 205,000MPa, 2%의 변형도 경화효과를 나타내도록 접선계수를 사용 부재의 비선형성을 고려한 등방성 재료모델을 이용하였다(Fig. 10(a)). 경계골조는 항복응력 325MPa, 탄성계수 205,000MPa, 2%의 변형도 경화효과를 갖는 SM490 강재를 사용하여 강판과 동일하게 등방성 재료모델을 선정하였다(Fig. 10(b)).
3.2 모델개요 및 경계조건 입력
강판의 요소분할은 해석시간과 정확성을 고려하여 8x9으로 분할하였다. 경계골조는 강판의 구속을 위하여 강판의 분할된 요소 수만큼 같은 크기로 나누었다. 경계조건은 유효성 검증 해석모델과 같은 방법으로 강판의 면외변형을 고려하기 위하여 횡방향으로 1kN의 단위 하중을 적용한 후 고유치좌굴해석으로 부터의 1차 좌굴모드를 본 해석 모델에 초기결함으로 고려하였다.
소성해석의 진행을 위하여 최하층 강판의 밑면과 기둥단부를 모든 방향에 대하여 완전 구속시켰다. 하중은 P-Δ효과를 고려하기 위하여 720kN의 중력하중을 양쪽 Rigid Outrigger 요소 각각의 단부 노드에 수직방향으로 입력하였으며, 최상층 보 상부 플랜지 끝 부분의 노드를 구속하여 변위제어를 통하여 Fig. 11과 같은 경계조건을 갖는 강판전단벽의 이력거동을 살펴보았다.
3.3 해석 결과
3.3.1 고유치 좌굴해석결과
고유치 좌굴해석은 3차 모드까지의 좌굴형상을 입력 조건으로 사용하기 위하여 수행하였다. Fig. 12에서와 같이 모든 구조물에서의 초기 변형은 횡하중에 의한 전단력과 휨모멘트에 의하여 강판에서 인장역을 형성하며 면외변형이 발생하였다. 하지만 저층 구조물에서는 구조물의 상부에 횡력이 작용할 경우 경계골조가 갖는 큰 강성에 의해 최상층의 강판이 전단력에 저항하며 초기 면외 변형을 유발하였으나, 구조물의 높이가 높아질수록 경계골조가 휨모멘트에 의해 변형이 발생하면서 강판의 초기변형이 발생되는 지점이 내려감을 확인하였다.
3.3.2 응력분포 및 변형
모든 모델은 Fig. 12와 같이 최상층 강판에서 대각방향으로 인장역을 형성하며 가장 먼저 소성변형이 진행되었다. 그러나 3층 구조물에서는 보의 단부에서 적절한 소성힌지를 발생시키며 강판의 소성변형으로 인해 모든 층으로 하중의 분배가 잘 이루어졌다. 그러나 9층 이상의 구조물에서는 캔틸레버 거동을 보이며 상부 강판의 큰 전단강성으로 인해 저층부 기둥에서 소성힌지가 발생하였다. 이로 인하여 고층 강판전단벽시스템에서는 횡력에 의한 하중의 분배가 저층부 경계골조의 휨강성에 의해 지지되며 강판의 큰 전단강성을 제대로 발휘하지 못하고 상부의 강판에만 소성변형이 발생함을 확인하였다. 또한, 층고가 높아질수록 경계골조의 휨변형으로 인하여 상부에 작용하는 전단력이 커져서 소성화가 진행되는 강판의 수가 점차 증가함을 알 수 있었다.
Fig. 13에 각 모델별 층간변위를 나타내었다. 3층 강판전단벽 모델의 경우 단면형상이 변화되는 1층과 2층 경계면에서 층간변위율이 다소 낮게 형성되며 일정한 값을 유지하고 있다. 그러나 9층 이상의 구조물에서는 특정 층을 기점으로 급격한 층간변위가 일어나고 있다. 이는 부재 단면이 달라지는 경계층에서 기둥에 휨 변형이 발생하여 이후 급격한 층간변위에 의한 것으로 사료된다. 따라서 전단벽의 영향으로 층강성의 변화가 층간변위 변화에 크게 영향을 미침을 알 수 있었다.
3.3.3 밑면전단력의 비교․검토를 통한 변형모드 예측
강판전단벽의 강도는 전단강도(
 ) 중 작은 값으로 결정된다. 전단강도는 모든 강판이 인장역을 형성하면서 항복에 도달하고, 기둥의 양 끝단 및 보의 양단에서 소성힌지를 형성하면서 연성거동 시의 강판벽 강도이고, 휨강도는 시스템의 캔틸레버 거동에 의한 강도를 나타내며 주로 인장과 압축의 항복강도에 영향을 받는다.
) 중 작은 값으로 결정된다. 전단강도는 모든 강판이 인장역을 형성하면서 항복에 도달하고, 기둥의 양 끝단 및 보의 양단에서 소성힌지를 형성하면서 연성거동 시의 강판벽 강도이고, 휨강도는 시스템의 캔틸레버 거동에 의한 강도를 나타내며 주로 인장과 압축의 항복강도에 영향을 받는다.
1) 강판전단벽의 전단변형 강도
강판 전단벽의 전단강도는 Fig. 14와 같이 경계골조의 전단강도와 강판의 전단강도의 합으로 구할 수 있다[9].
강판의 좌굴응력은 식 (1)에 의해 구할 수 있다[16]. 식 (2)는 플레이트거더 강판의 좌굴계수(
 )로서 강판의 사면이 모두 단순지지 되었다는 가정 하에 유도된 식이다. 강판전단벽의 경우 강판이 플레이트가 아닌 보와 기둥의 경계골조에 접하기 때문에 외부 경계조건은 사면이 단순지지가 아닌 고정에 가깝다. 따라서 식 (3)에 의해 강판의 좌굴계수를 구하여야 한다.
)로서 강판의 사면이 모두 단순지지 되었다는 가정 하에 유도된 식이다. 강판전단벽의 경우 강판이 플레이트가 아닌 보와 기둥의 경계골조에 접하기 때문에 외부 경계조건은 사면이 단순지지가 아닌 고정에 가깝다. 따라서 식 (3)에 의해 강판의 좌굴계수를 구하여야 한다.
여기서, 강판의 후좌굴상태에서 인장역은 보와 일정한 각도를 이루며 전단면에 균일하게 발생하고, 기둥은 인장역방향으로 변형이 발생하지 않는다고 가정한다.
Fig. 15와 같이 강판이 항복할 때 인장역의 응력
 는 식 (4)~(6)으로 표현할 수 있다.
는 식 (4)~(6)으로 표현할 수 있다.
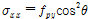 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
식 (4)∼(6)를 Von Mises 항복기준 식인 식 (7)에 대입하면 강판이 항복할 때 인장역의 응력은 강판의 인장응력과 같은 값을 갖게 된다. 따라서 강판의 전단강도(
 )는 식 (8)과 같이 구할 수 있으며, 이는 Berman과 Bruneau (2003)[11]가 제안한 식과 일치한다.
)는 식 (8)과 같이 구할 수 있으며, 이는 Berman과 Bruneau (2003)[11]가 제안한 식과 일치한다.
 (8)
(8)
골조의 전단강도를 계산하기 위하여 Fig. 16과 같이 골조의 기둥-보 접합부가 강접되었다고 가정하면, 각 부재 단부의 소성힌지에 의해 휨모멘트가 발생하므로 전단강도(
 )는 식 (9)에 의해 계산할 수 있다.
)는 식 (9)에 의해 계산할 수 있다.
 (9)
(9)
강판전단벽의 전단강도(
 )의 합으로 구할 수 있으며, 전체 강판전단벽시스템의 전단강도는 식 (10)과 같이 구할 수 있다.
)의 합으로 구할 수 있으며, 전체 강판전단벽시스템의 전단강도는 식 (10)과 같이 구할 수 있다.
2) 강판전단벽의 휨변형 강도
강판전단벽의 휨강도(
 )으로 정의하였다.
)으로 정의하였다.
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
3) 해석결과 비교
각 모델별 강판전단벽 구조물의 밑면전단력-변위 곡선을 Fig. 18에 나타내었다. 유한요소해석에서는 재료 모델의 특성을 탄소성 재료모델로 가정함에 따라 극한강도 이후에 발생되는 하중의 감소를 표현 할 수 없어서 최대 변위점은 하중이 최대하중의 80% 이하로 감소되는 점으로 정의하였다. Table 3에 각 모델별 항복강도와 극한하중의 해석값 및 이론값을 비교하였다.
Table 3에서 식 (10)과 식 (14)를 통한 이론값과의 강도 비교를 통하여 변형모드를 예측할 수 있었다. 예측강도는 전단강도(
 )가 증가할수록 연성이 증가하는 것을 예측할 수 있었다.
)가 증가할수록 연성이 증가하는 것을 예측할 수 있었다.
3.3.4 주응력분포를 통한 스트립앵글의 비교
Fig. 19는 최대하중 하에서 각 모델별 강판벽 Shell 요소의 주응력벡터를 보여주고 있다. 주응력의 방향은 강판벽의 인장역 경사각과 동일하며, 거동형태에 따라 강판에 발생되는 인장역의 변화를 도식화 하였다.
순수한 전단에 의해 강판이 저항할 경우 일정한 경사각을 이루며 주응력 분포를 형성하지만, 휨력을 동시에 받게 될 경우 곡선의 형태를 나타내며 인장역을 변화 시킨다.
Table 4는 각 모델별 스트립앵글과 AISC Seismic Provision 2005 기준식인 식 (15)에 의해 계산된 값이다. 전단에 의해 지배되는 3층 강판전단벽 구조물의 경우 해석값이 기준식에 매우 근사한 값을 보이고 있다. 그러나 전반적으로 휨에 지배되는 14층과 20층 강판전단벽 구조물의 경우 최하층 강판에서 기준값과 큰 차이를 보이고 있다. 이는 변형형상에서도 확인된 것처럼 고층 구조물의 경우 전도모멘트에 의한 추가적인 축력과 전단력이 최하층 기둥에 소성힌지를 발생시켜 휨거동이 발생되었기 때문으로 사료된다.
 (15)
(15)
기둥과 인장스트립의 각도,
 는 기둥과 보의 단면2차모멘트 이다.
는 기둥과 보의 단면2차모멘트 이다.
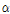 는
는
4. 결 론
본 연구는 강판의 면외변형을 고려한 강판전단벽 유한요소해석을 수행하여 기존의 Driver 등에 의해 수행된 실험연구와의 비교를 통해 모델의 적합성을 검증하고, 이 모델을 사용하여 구조물의 층고를 변수로 한 강판전단벽시스템의 변형모드별 스트립앵글의 변화에 관한 유한요소해석 변수연구를 통하여 다음과 같은 결론을 도출하였다.
(1)고유치 좌굴해석 결과 모든 해석모델들이 1차 모드에서 강판의 면외방향으로 좌굴하는 양상을 보였으며, 층고가 높아짐에 따라 하부의 강판에서 좌굴양상이 관찰되었다.
(2)비선형 유한요소해석을 통한 층고 변화에 따른 강판전단벽의 응력 및 변형양상은 우선 모든 해석모델의 최상층 강판에서 소성변형이 발생되었고, 9층 이상의 강판전단벽 구조물은 캔틸레버 거동을 보이며 상부 강판이 좌굴하는 양상을 보였다. 이로 인하여 고층의 강판전단벽 구조물에서는 횡력이 저층부의 경계골조가 지닌 휨강성에 의해 지지되며 강판이 지닌 큰 전단강성을 제대로 발휘하지 못하고 상부의 강판에서만 소성변형을 일으키는 양상을 나타내었다.
(3)3층 강판전단벽 모델의 층간변위를 확인한 결과, 단면형상이 변화되는 지점인 1층과 2층의 경계면에서 층간 변위가 다소 낮게 형성되며 일정한 값을 유지한 반면, 9층 이상의 구조물에서는 특정 층을 기점으로 급격한 층간변위가 발생하였다. 변형형상과 층간변위의 비교․검토 결과, 부재 단면이 변화하는 경계층에서 기둥의 휨변형이 발생하였으며, 이후 급격한 층간 변위를 나타내고 있음을 확인 할 수 있었다.
(4)AISC Seismic Provision 기준식에 따라 산출된 예측강도와 해석결과의 비교를 통하여 각 모델별 변형모드를 예측한 결과, 휨과 전단의 조합에 의해 저항하는 9층 강판전단벽 모델을 기준으로 전단지배모드와 휨지배모드로 분류할 수 있고 휨강도-전단강도의 비(
 )가 증가할수록 연성도가 증가함을 예측할 수 있었다.
)가 증가할수록 연성도가 증가함을 예측할 수 있었다.
(5)주응력 벡터를 확인함으로써 변형모드별 스트립앵글의 변화를 확인한 결과, 전단지배형 모델에서는 일정한 경사각을 이루며 인장역을 발생시켰으나, 휨지배형 모델에서는 기둥의 소성힌지 발생에 따라 휨 변형을 발생시키고 이에 따른 인장역의 변화는 기존의 이론식과 큰 차이를 보였다.
(6)현재 외국의 설계규정에는 전단지배형 강판전단벽의 스트립앵글 제안식에 관한 규정 밖에 존재하지 않아서 휨지배 강판전단벽 구조물은 스트립앵글의 변화를 유발한다는 결과를 근거로, 추후 해석 및 실험적 연구를 바탕으로 휨에 영향을 받는 스트립앵글에 관한 새로운 제안식이 필요할 것으로 사료된다.
Acknowledgments
이 논문은 2012년도 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2012 R1A1A4A01004350).
References
- Thorburn, L.J., Kulak, G.L., and Montgomery, C.J. (1983) Analysis of Steel Plate Shear Walls, Structural Engineering Report No. 107, Dept. of Civil Engineering, Univ. Alberta, Edmonton, Alberta, Canada.
- Timler, P.A. and Kulak, G.L. (1983) Experimental Study of Steel Plate Shear Walls, Structural Engineering Report No. 114, Dept. of Civil Engineering, Univ. Alberta, Edmonton, Alberta, Canada.
- Tromposch, E.W. and Kulak, G.L. (1987) Cyclic and Static Behavior of Thin Panel Steel Plate Shear Walls, Structural Engineering Report No. 145, Dept. of Civil Engineering, Univ. Alberta, Edmonton, Alberta, Canada.
- 위지은, 이명호, 오상훈, 허충, 오영석, 윤명호, 문태섭(2000) 전단 항복형 강판 내진벽의 거동, 대한건축학회추계학술발표대회 논문집, 대한건축학회, 제20권, 제2호, pp.377-380.Wi, J.E., Lee, M.H., Oh, S.H., Huh, C., Oh, Y.S., Yoon, M.H., and Moon, T.S. (2000) Behavior of Shear Yielding Steel Plate Seismic Wall, Proceedings of Fall Conference of Architectural Institute of Korea, AIK, Vol. 20, No, 2, pp.377-380 (in Korean).
- 이명호, 오상훈, 윤명호, 문태섭(2006) 스트립모델을 이용한 강판 전단패널의 해석, 대한건축학회지, 대한건축학회, 제22권, 제3호, pp.79-86.Lee, M.H., Oh, S.H., Yoon, M.H., and Moon, T.S. (2006) Analysis of Steel-Plate Shear Panels using Strip Model, Review of Architecture and Building Science, AIK, Vol. 22, No. 3, pp.79-86 (in Korean).
- 강헌성, 이명호, 김재건, 윤명호, 문태섭(2003) 스트립 모델에 의한 강판 전단벽의 해석, 한국강구조학회 2003년도 학술발표대회 논문집, 한국강구조학회, pp.372-379.Kang, H.S., Lee, M.H., Kim, J.K., Yoon, M.H., and Moon, T.S. (2003) Analysis of Steel Plate Shear Walls Based on Strip Model, Proceedings of Annual Conference Korean Society of Steel Construction, KSSC, pp.372-379 (in Korean).
- 황성래, 곽재혁, 김원기, 박홍근, 전상우(2003) 강판전단벽 골조의 해석과 분석, 한국강구조학회 2003년도 학술발표대회 논문집, 한국강구조학회, pp.428-434.Hwang, S.R., Kwak, J.H., Kim, W.K., Park, H.G., and Jeon, S.W. (2003) Structural Analysis and Evaluation of a Steel Plate Shear Wall Building, Proceedings of Annual Conference Korean Society of Steel Construction, KSSC, pp.428-434 (in Korean).
- 대한건축학회(2010) KBC 2009에 따른 강구조내진설계메뉴얼, 한국건축구조기술사회, 구미서관KSEA (2010) Seismic Design Manual of Steel Buildings per KBC2009, The Korean Structural Engineers Association, Goomibooks (in Korean).
- AISC (2005), AISC Seismic Provision 2005 for Structural Steel Buildings, American Institute of Steel Construction, USA.
- Driver, R.G., Kulak, G.L., Kennedy, D.J., and Elwi, A.E. (1997) Seismic Behavior of Steel Plate Shear Walls, Structural Engineering Report No. 215, Dept. of Civil Engineering, Univ. Alberta, Edmonton, Alberta, Canada.
-
Berman, J. and Bruneau, M. (2003) Plastic Analysis and Design of Steel Plate Shear Walls, Journal of Structural Engineering, ASCE, Vol. 129, No. 11, pp.1148-1456.
[https://doi.org/10.1061/(ASCE)0733-9445(2003)129:11(1448)]

- Seilie, I.F. and Hooper, J.D. (2005) Steel Plate Shear Wall: Practical Design and Construction, Modern Steel Construction, AISC, Vol. 45, No. 4, pp.37-45.
- 박홍근, 최인락, 전상우, 김원기(2006) 전단지배 강판벽의 연성능력, 한국강구조학회논문집, 한국강구조학회, 제18권, 제4호, pp.457-468.Park, H.G., Choi, I.R., Jeon, S.W., and Kim, W.K. (2006) Ductility Capacity of Shear-Dominated Steel Plate Walls, Journal of Korean Society of Steel Construction, KSSC, Vol. 18, No. 4, pp.457-468 (in Korean).
- CSA (2001), Limit State of Design of Steel Structure, Canadian Standards Association, Canada.
- Rezai, M. (1999) Seismic Behavior of Steel Plate Shear Walls by Shake Table Testing, Ph.D. Dissertation, University of British Columbia, Vancouver, Canada.
- Basler, K. (1963) Strength of Plate Girders under Combined Bending and Shear, Journal of Structural Division, ASCE, Vol. 87, No. 2, pp.181-197.


































 ) of frame
) of frame


 )
)






